Open-Circuit Fault-Tolerant Control of a Six-Phase Asymmetric Permanent Magnet Synchronous Motor Drive System
Abstract
:1. Introduction
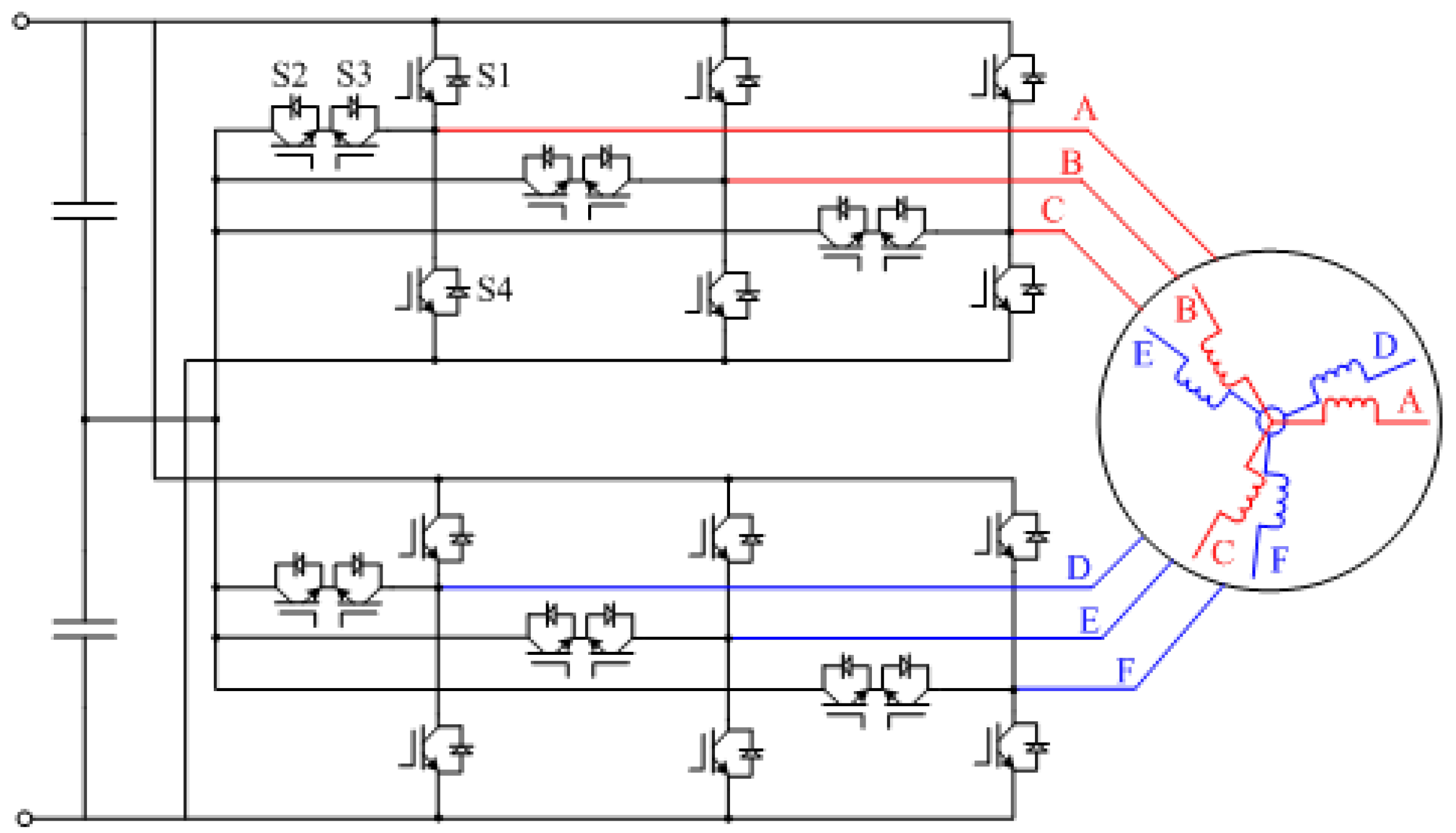
2. Six-Phase PMSM Drive System Configuration and Model
3. The SVM-DTC Control Method
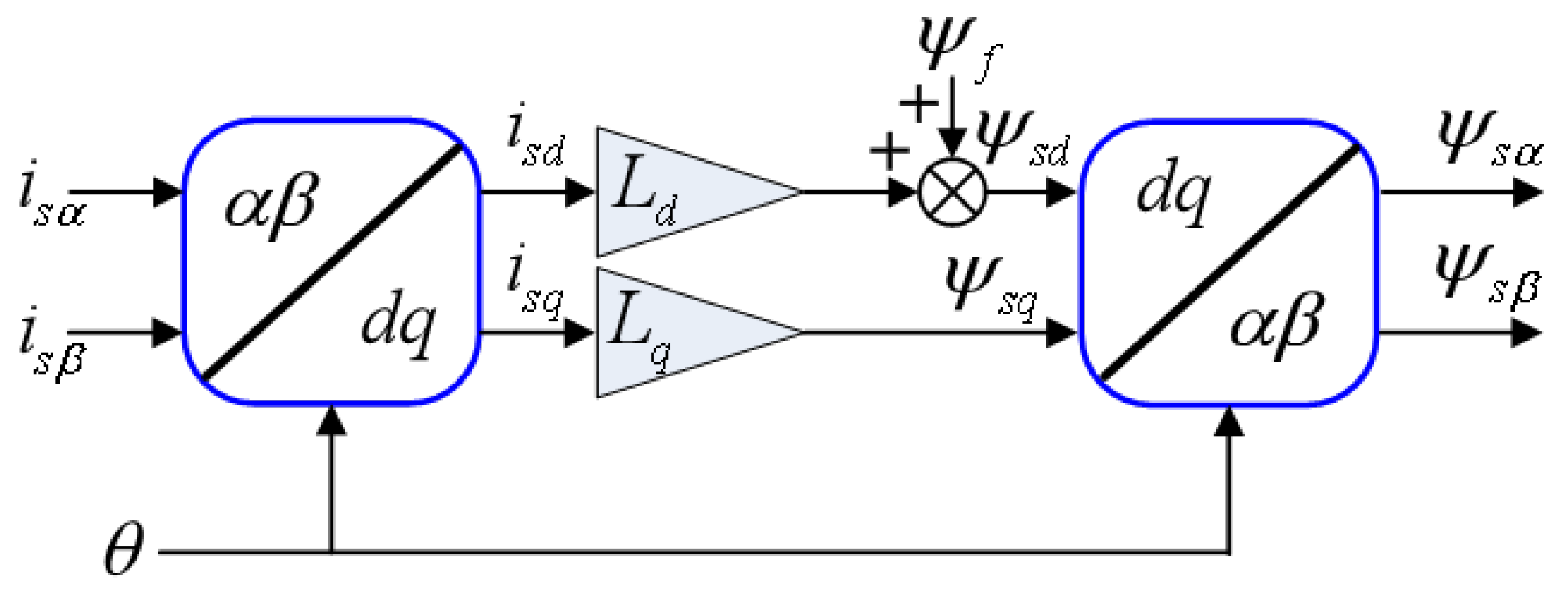
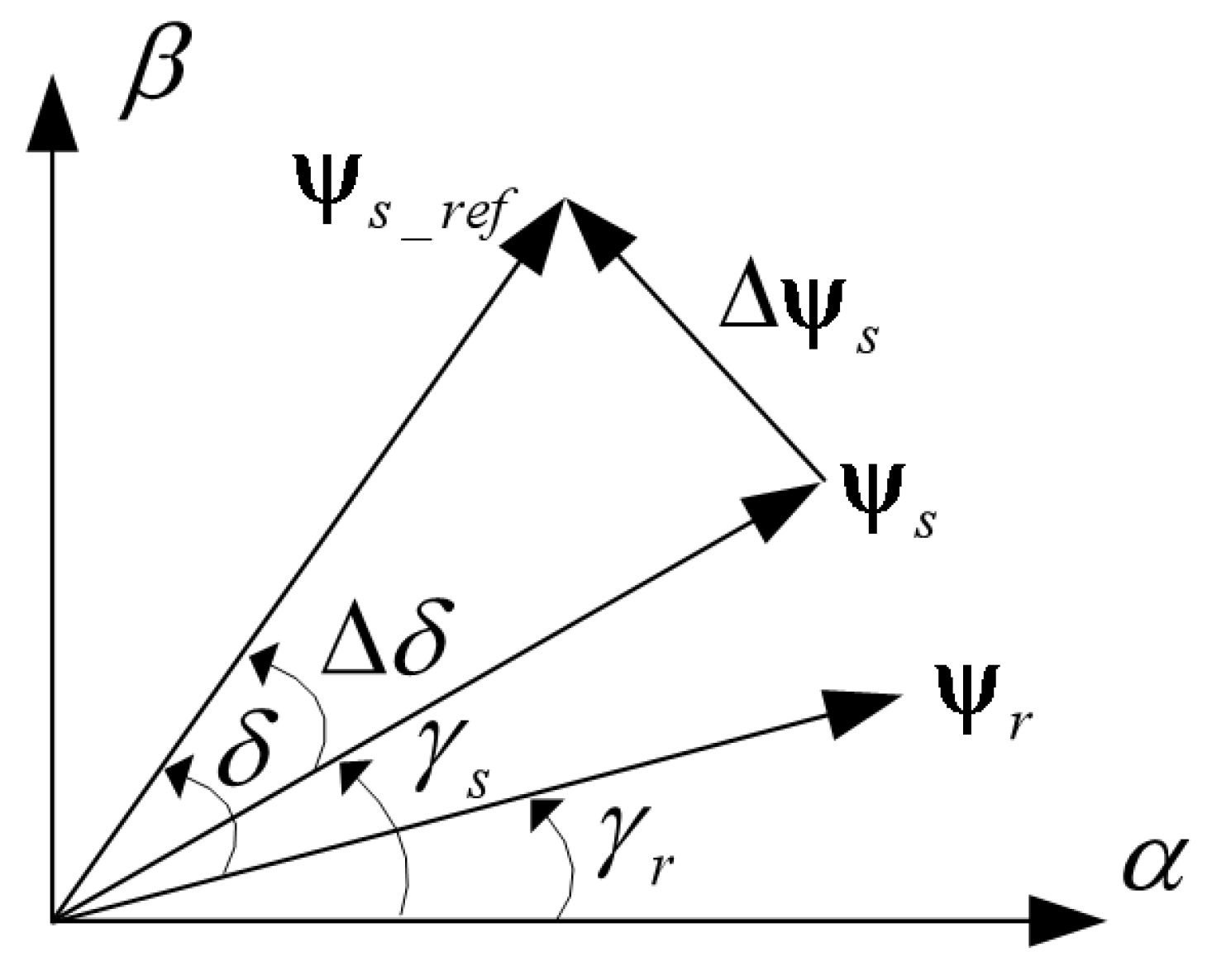
3.1. Torque and Magnetic Chain Estimation
3.2. Voltage Vector Prediction
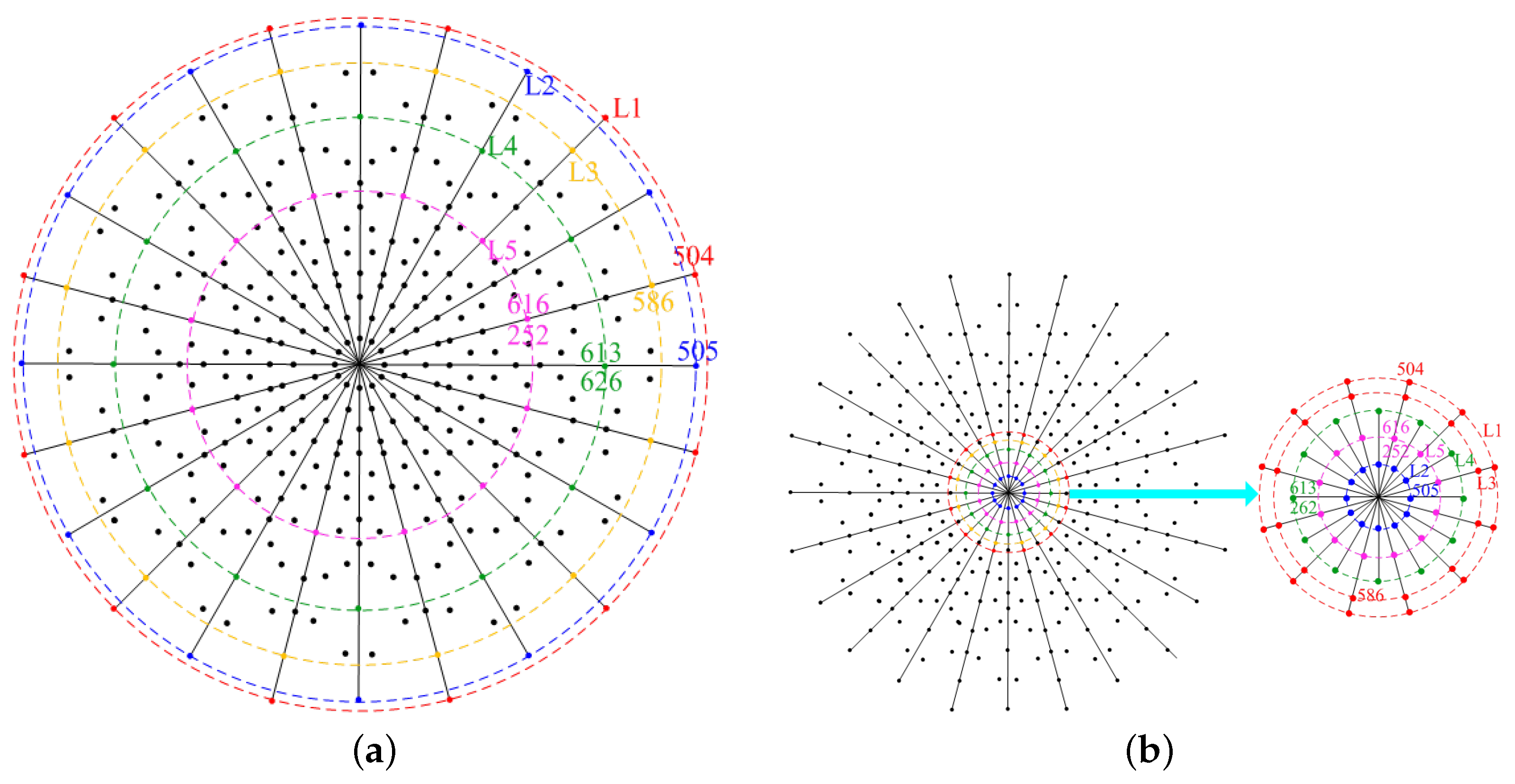
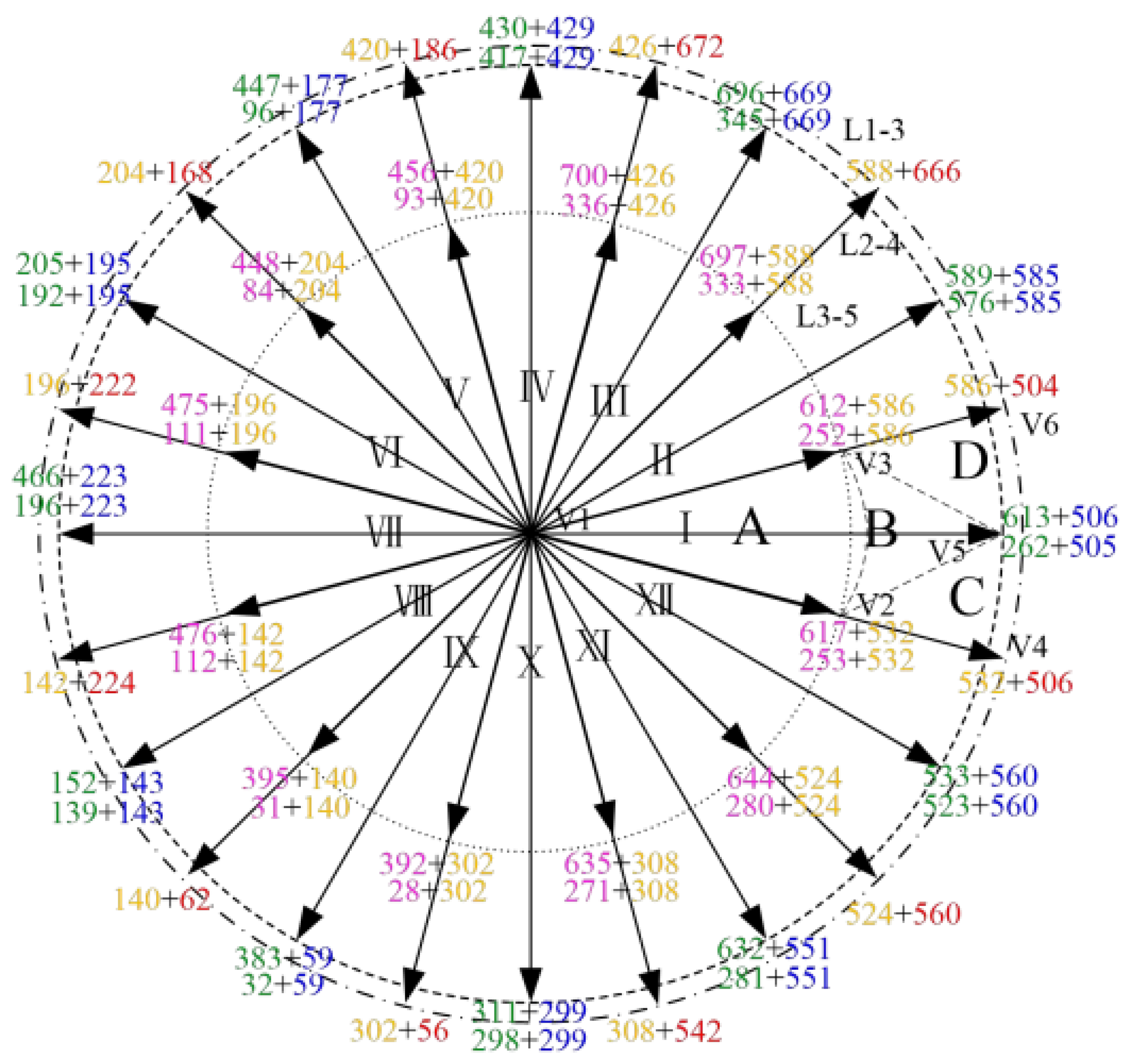
3.3. Simplified SVM
3.4. Current Harmonic Suppression
3.5. Neutral Voltage Balance Control Strategy
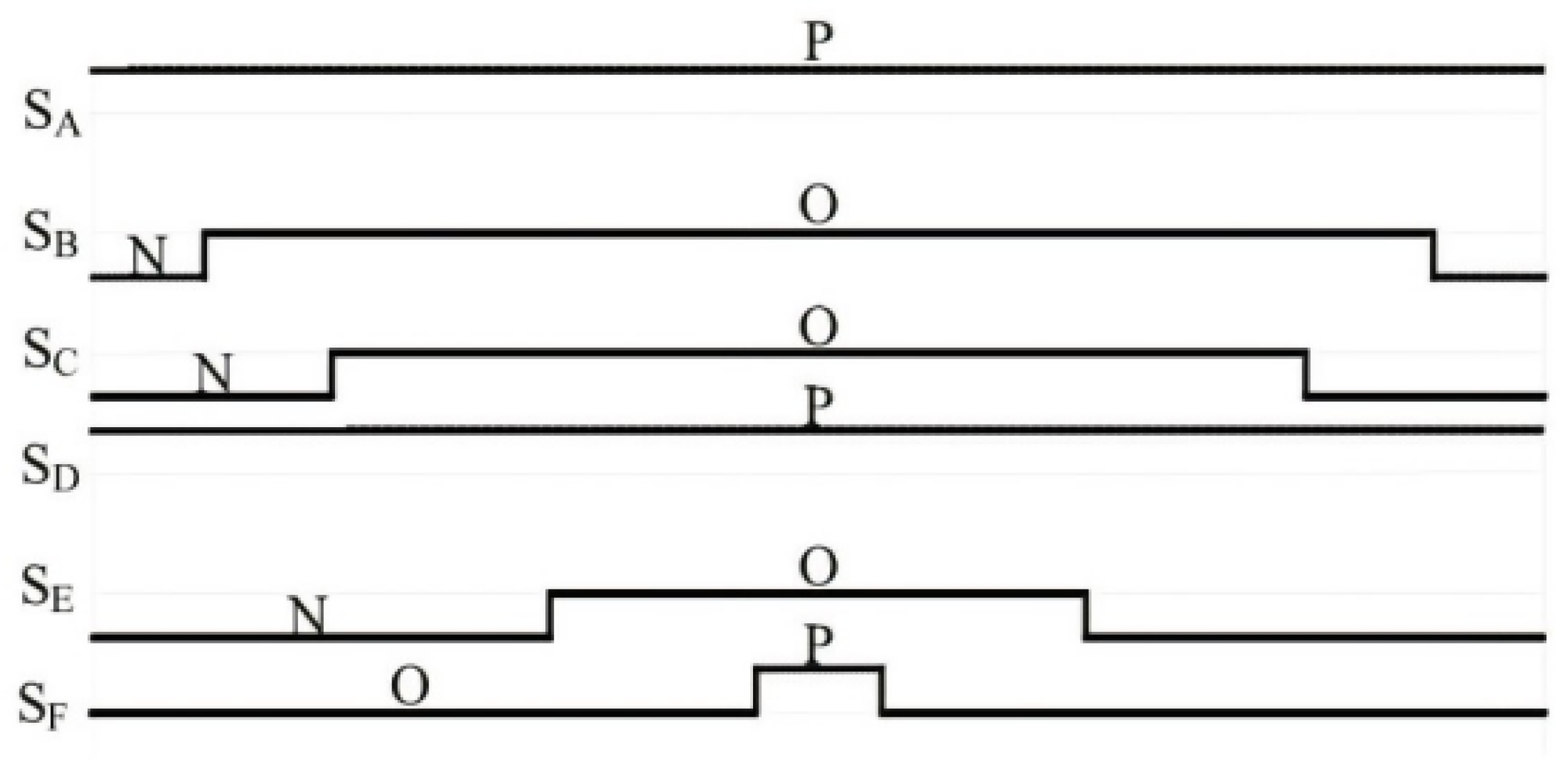
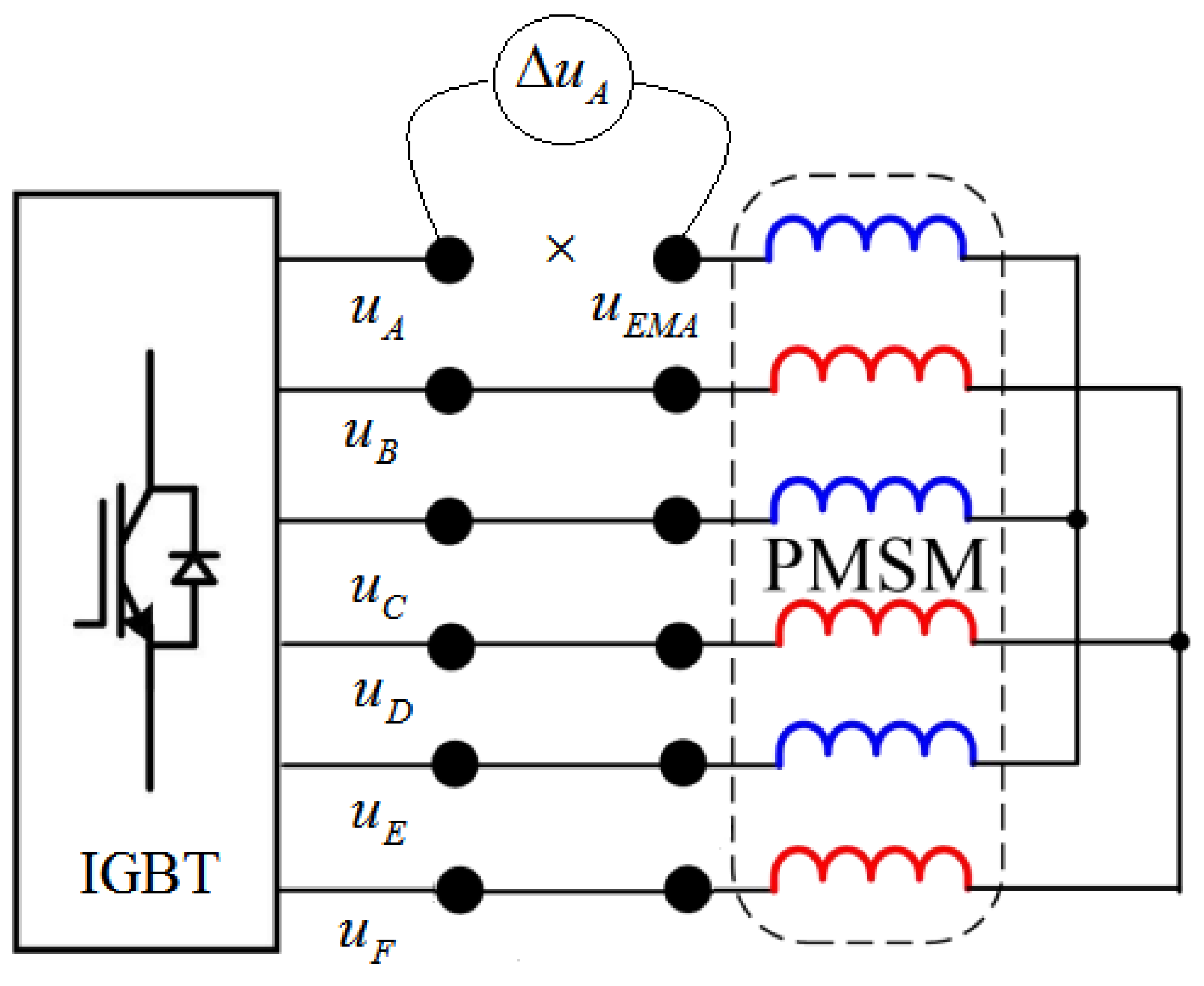
4. Open Circuit Fault Tolerance Strategy
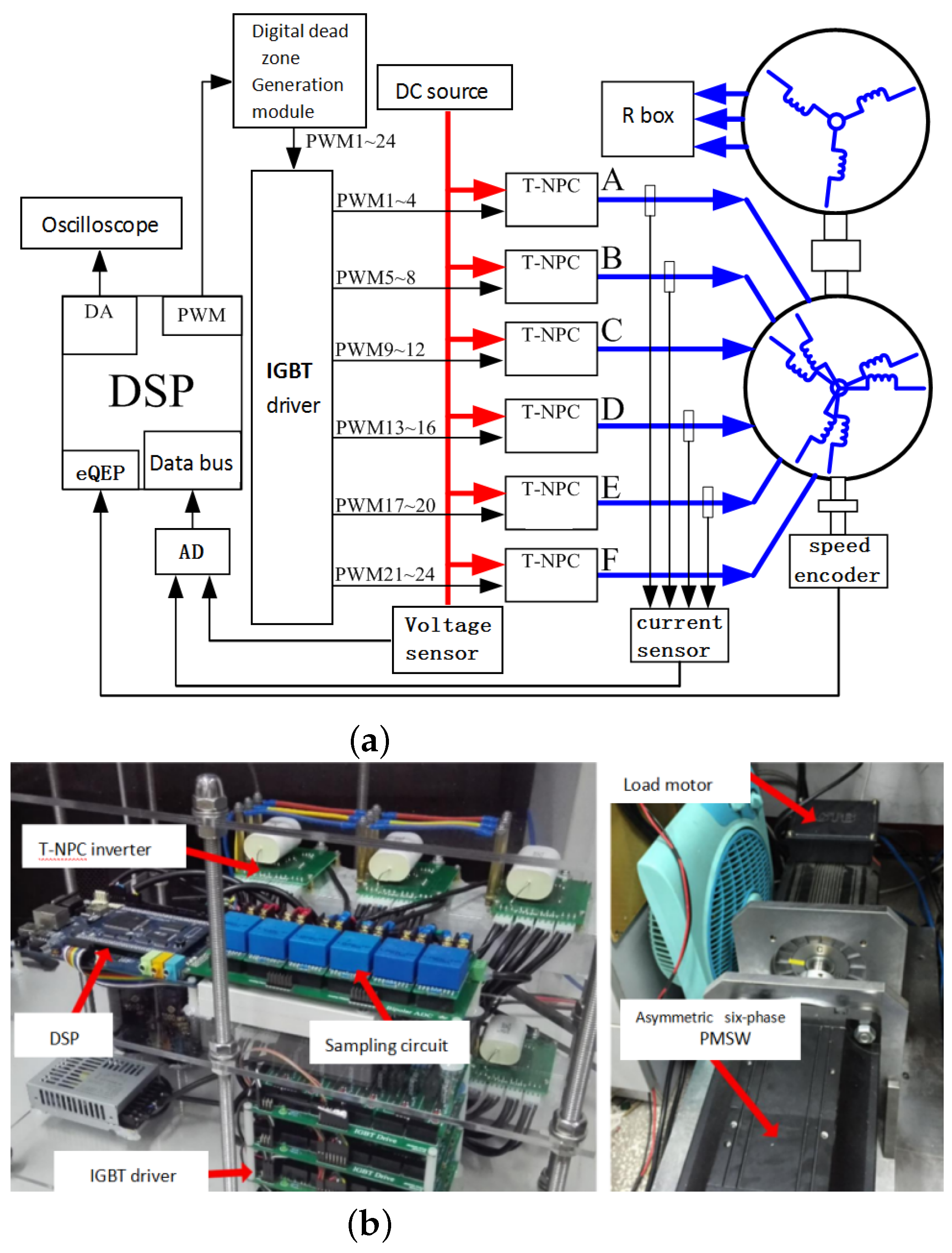
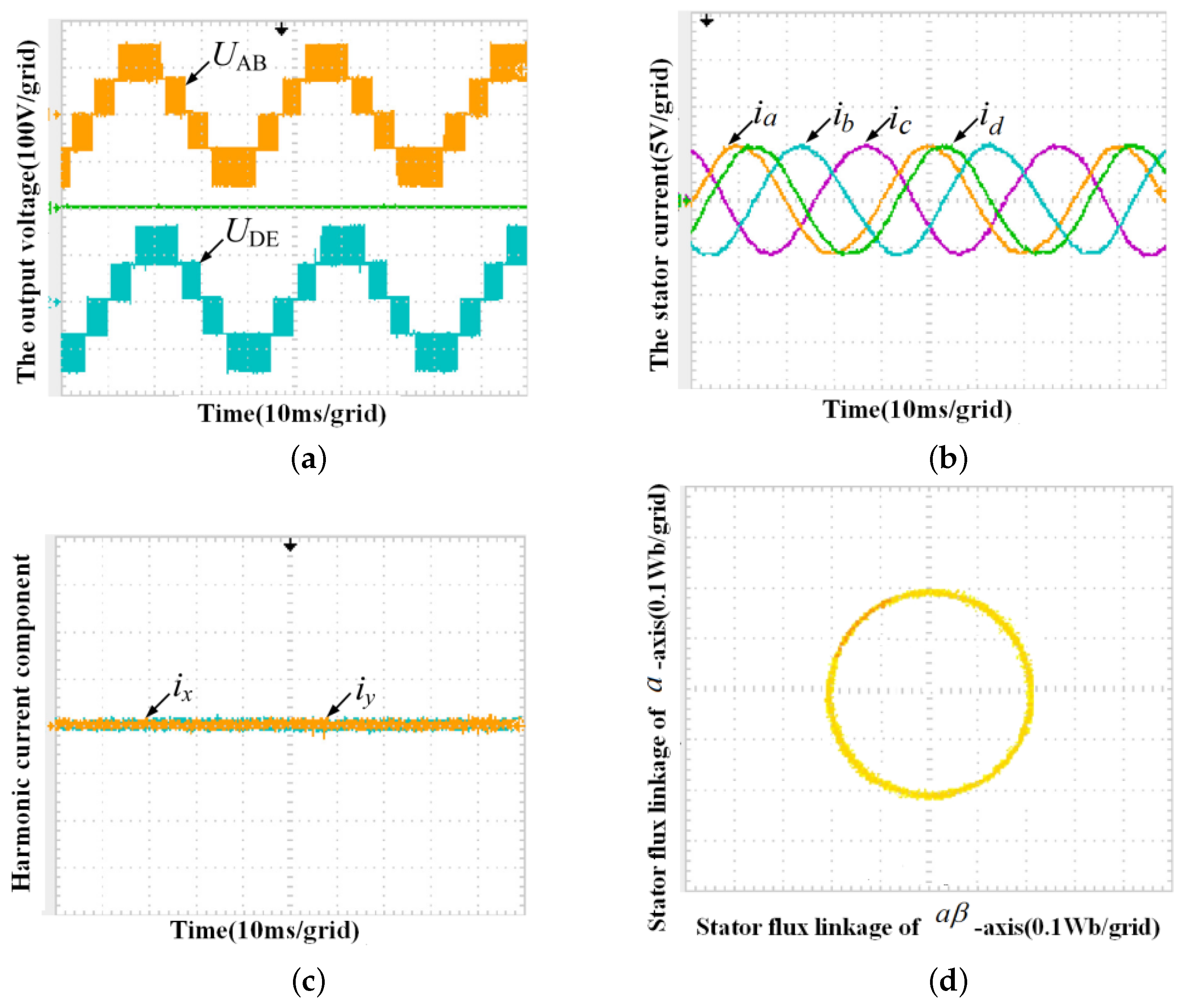
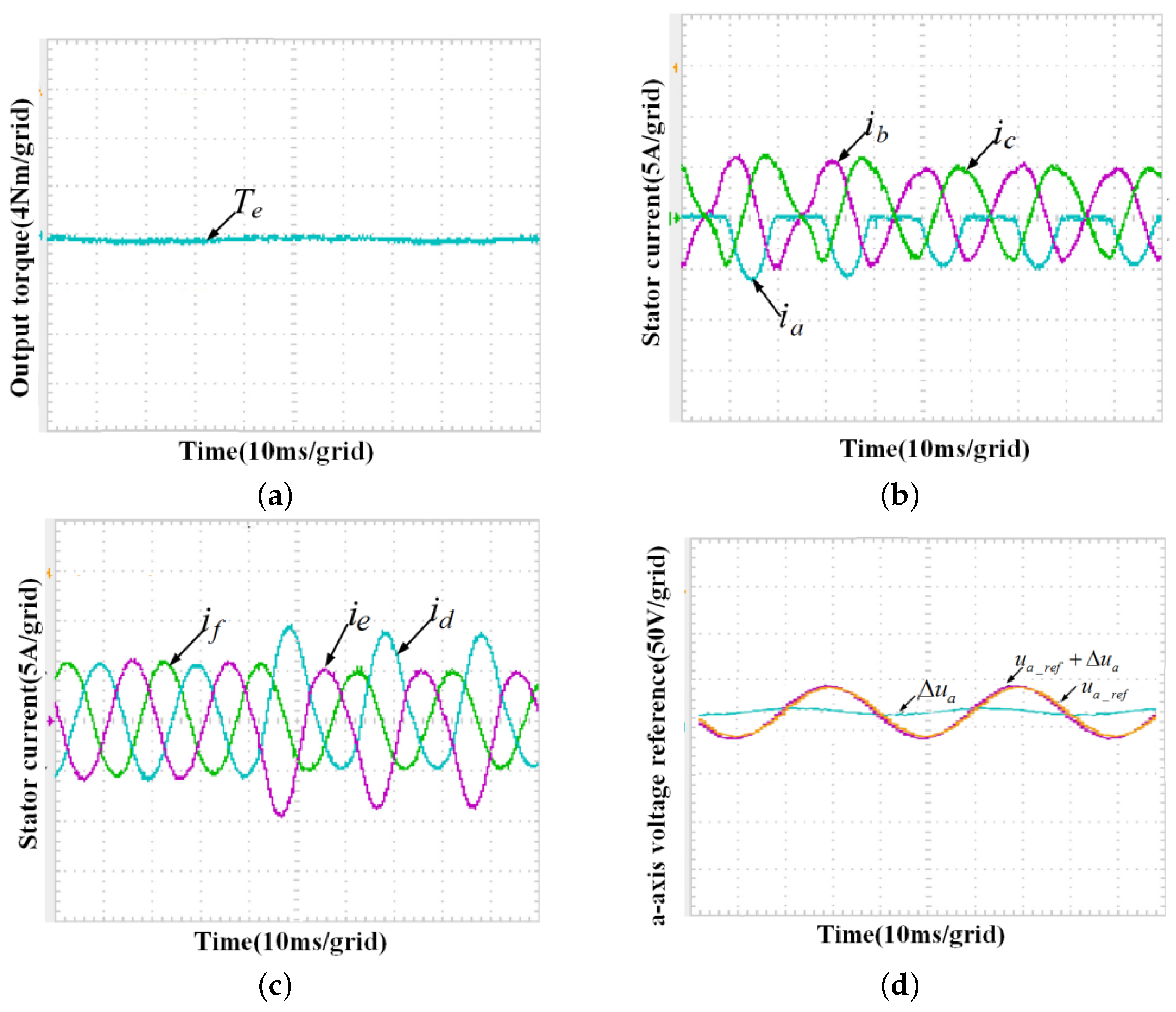
5. Test Verification
6. Conclusions and Further Research Directions
6.1. Conclusions
6.2. Further Research Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, P.; Lei, Y.; Wu, F. Analysis and Design of A Six-phase Fault-tolerant PM Machine Used for EVs. Electr. Mach. Control 2013, 17, 29–36. [Google Scholar]
- Zhang, Z.; Wu, Y.; Su, H.; Sun, Q. Research on Open-circuit Fault Tolerant Control of Six-phase Permanent Magnet Synchronous Machine Based on Fifth Harmonic Current Injection. CES Trans. Electr. Mach. Syst. 2022, 6, 306–314. [Google Scholar] [CrossRef]
- Guo, X.; Yin, C.; Shang, R.; Bian, Y.; Guo, B. Modeling and Optimized Harmonic Current Control for Six-Phase Permanent Magnet Synchronous Motor with Two Y-Connected Windings Displaced by 30° in Different Winding Types. Trans. China Electrotech. Soc. 2016, 31, 56–63. [Google Scholar]
- Zhang, X.; Wang, F.; Ji, W. SVPWM for T-NPC Inverter Control Based on Virtual Flux Vector. Power Electron. 2016, 50, 12–13. [Google Scholar]
- Yao, X.; Wu, X.; Du, Y. The Zero-Current-Transition Soft-Switching Technique for T-Type Neutral-Point-Clamped Inverter. Trans. China Electrotech. Soc. 2016, 31, 179–188. [Google Scholar] [CrossRef]
- Zheng, W.; Bing, Z.; Wang, Y.; Yue, Z.; Ming, C. Analysis and control of active neutral-point-clamping three-level inverters under fault tolerant operation modes. In Proceedings of the International Conference on Electrical Machines & Systems, Pattaya, Thailand, 25–28 October 2015. [Google Scholar]
- Lv, K.; Dong, X.; Zhu, C. Research on Fault-Tolerant Operation Strategy of Permanent Magnet Synchronous Motor with Common DC Bus Open Winding Phase-Breaking Fault. Energies 2022, 15, 2927. [Google Scholar] [CrossRef]
- Le, D.D.; Hong, S.; Lee, D.C. Fault detection and tolerant control for flying-capacitor modular multilevel converters feeding induction motor drives. J. Power Electron. 2022, 22, 947–958. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z. A Hybrid Direct Torque Control Scheme for DualThree-phase PMSM Drives with Improved Operation Performance. IEEE Trans. Power Electron. 2018, 34, 1622–1634. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Zhu, J. Enhanced Model Predictive Torque Controlof Fault-Tolerant Five-Phase Permanent Magnet SynchronousMotor With Harmonic Restraint and Voltage Preselection. IEEE Trans. Ind. Electron. 2019, 67, 6259–6269. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, C.; Wang, Y.; Han, S. Research on Fault-Tolerant Field-Oriented Control of a Five-Phase Permanent Magnet Motor Based on Disturbance Adaption. Energies 2022, 15, 3436. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z.; He, J.; Zhao, W. Diagnosis and Tolerance of Common Electrical Faults in T-Type Three-Level Inverters Fed Dual Three-Phase PMSM Drives. IEEE Trans. Power Electron. 2020, 35, 1753–1769. [Google Scholar] [CrossRef]
- Bao, J.; Gong, R.; Li, Q. Research on the Fault Recovery Strategy Based on Direct Torque Control for Fault Tolerant Permanent Magnet Motor. Small Spec. Electr. Mach. 2016, 44, 92–96. [Google Scholar]
- Kang, M.; Kong, W.-b.; Huang, J. Fault-tolerant Control of Five-phase Induction Motor for Electric Vehicles. Electr. Mach. Control. 2014, 18, 1–6. [Google Scholar]
- Bodo, N.; Jones, M.; Levi, E. A space vector PWM with common-mode voltage elimination for open-end winding five-phase drives with a single DC supply. IEEE Trans. Ind. Electron. 2014, 61, 2197–2207. [Google Scholar] [CrossRef] [Green Version]
- Jin, M.J.; Qiu, J.Q.; Shi, C.W.; Lin, R.G. A Novel Stator Flux Estimayor for Direct Torque Controlled Magnet Synchronous Motor Drives. Proc. CSEE 2005, 25, 139–143. [Google Scholar]
- Luo, Y.; Liu, C. Model Predictive Control for a Six-Phase PMSM Motor With a Reduced Dimension Cost Function. IEEE Trans. Ind. Electron. 2019, 67, 969–979. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W.; Liu, G.; Cheng, R.; Xie, Y. Remedial Field-Oriented Control of Five-Phase Fault-Tolerant Permanent-Magnet Motor by Using Reduced-Order Transformation Matrices. IEEE Trans. Ind. Electron. 2017, 64, 169–178. [Google Scholar] [CrossRef]
- Payami, S.; Behera, R.C.; Iqbal, A. DTC of three-level NPC inverter fed five-phase induction motor drive with novel neutral point voltage balancing scheme. IEEE Trans. Power Electron. 2018, 33, 1487–1500. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Chen, J.; Hu, Y. Decoupled Vector Space Decomposition Based Space Vector Modulation for Dual Three-Phase Three-Level Motor Drives. IEEE Trans. Power Electron. 2018, 33, 10683–10697. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Pre- and Post-Fault Tolerant Operation of a Six-Phase PMSM Motor Using FCS-MPC Without Controller Reconfiguration. IEEE Trans. Veh. Technol. 2018, 68, 254–263. [Google Scholar] [CrossRef]
- Engku Ariff, E.A.R.B.; Dordevic, O.; Jones, M. Space vector PWM algorithm for a three-level asymmetrical six-phase motor drive. IET Electr. Power Appl. 2019, 13, 1773–1782. [Google Scholar] [CrossRef]
- Hu, M.; Hua, W.; Huang, W.; Meng, J. Digital Current Control of an Asymmetrical Dual Three-Phase Flux-Switching Permanent Magnet Machine. IEEE Trans. Ind. Electron. 2020, 67, 4281–4291. [Google Scholar] [CrossRef]
- Hua, W.; Chen, F.; Huang, W.; Zhang, G.; Wang, W.; Xia, W. Multi-Vector-based Model Predictive Control with Geometric Solution of a Five-Phase Flux-Switching Permanent Magnet Motor. IEEE Trans. Ind. Electron. 2019, 67, 10035–10045. [Google Scholar] [CrossRef]
- Xue, C.; Song, W.; Wu, X.; Feng, X. A constant switching frequency finite-control-set predictive current control scheme of a five-phase inverter with duty-ratio optimization. IEEE Trans. Power Electron. 2018, 33, 3583–3594. [Google Scholar] [CrossRef]



| - | |||||
| x-y |
| - | |||
| x-y | 0 | 0 | 0 |
| Parameter | Numerical | Parameter | Numerical |
|---|---|---|---|
| Rated system power | 1.5 kW | DC voltage | 160 V |
| Motor phase current | 4.25 A | Permanent magnet flux linkage | 0.2 Wb |
| D axis inductance | 6.21 mH | A logarithmic | 3 |
| Q axis inductance | 6.21 mH | The rated load | 10 Nm |
| Stator resistance | 0.21 | Rated speed | 1000 r/min |
| A direct current capacity | 1000 F | Sampling frequency | 5 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhang, Q. Open-Circuit Fault-Tolerant Control of a Six-Phase Asymmetric Permanent Magnet Synchronous Motor Drive System. Electronics 2023, 12, 1131. https://doi.org/10.3390/electronics12051131
Liu L, Zhang Q. Open-Circuit Fault-Tolerant Control of a Six-Phase Asymmetric Permanent Magnet Synchronous Motor Drive System. Electronics. 2023; 12(5):1131. https://doi.org/10.3390/electronics12051131
Chicago/Turabian StyleLiu, Linyin, and Qinghui Zhang. 2023. "Open-Circuit Fault-Tolerant Control of a Six-Phase Asymmetric Permanent Magnet Synchronous Motor Drive System" Electronics 12, no. 5: 1131. https://doi.org/10.3390/electronics12051131
APA StyleLiu, L., & Zhang, Q. (2023). Open-Circuit Fault-Tolerant Control of a Six-Phase Asymmetric Permanent Magnet Synchronous Motor Drive System. Electronics, 12(5), 1131. https://doi.org/10.3390/electronics12051131






