Transmission Performance of Halbach Array Cylindrical Permanent Magnet Governor
Abstract
1. Introduction
2. Materials and Methods
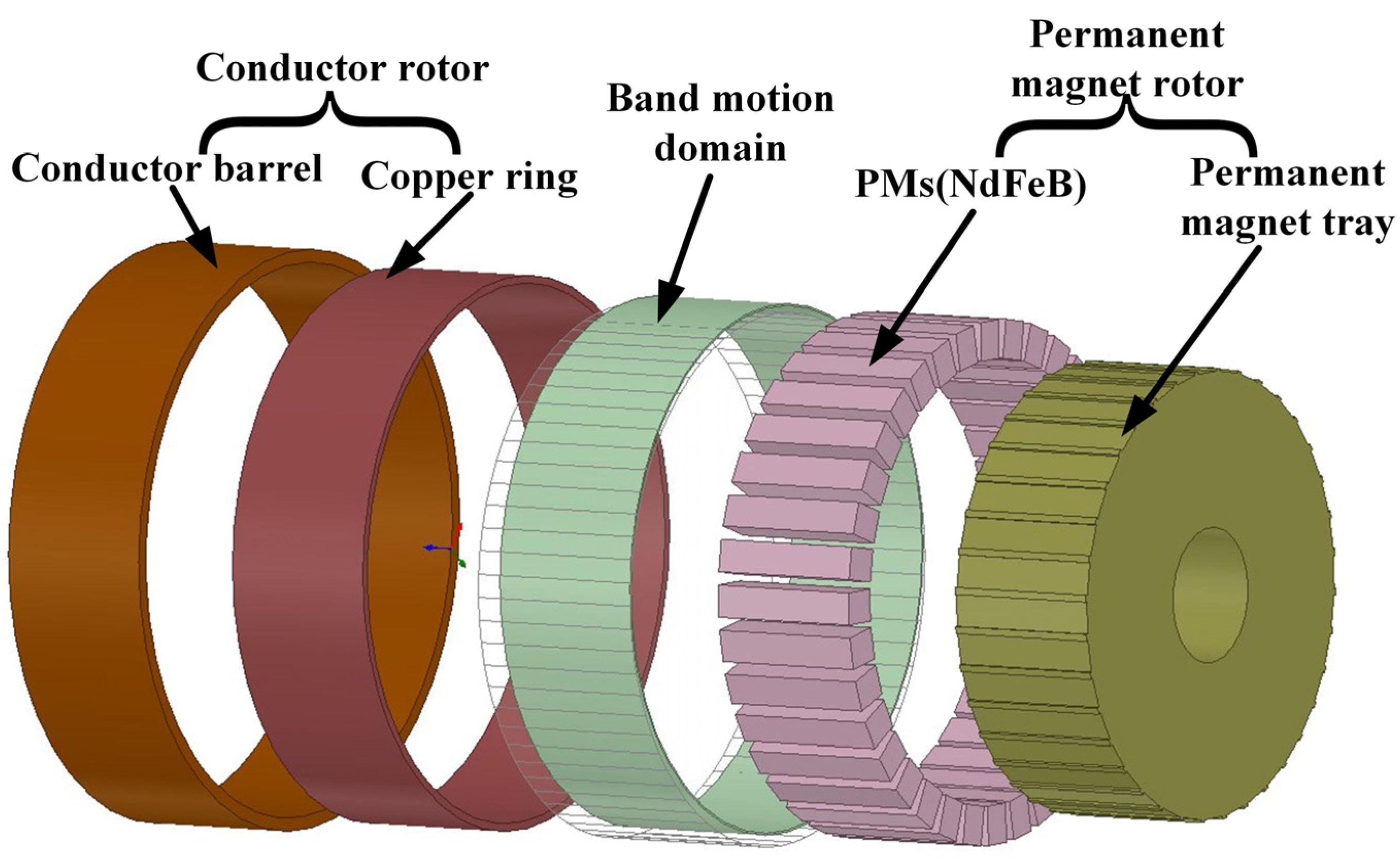
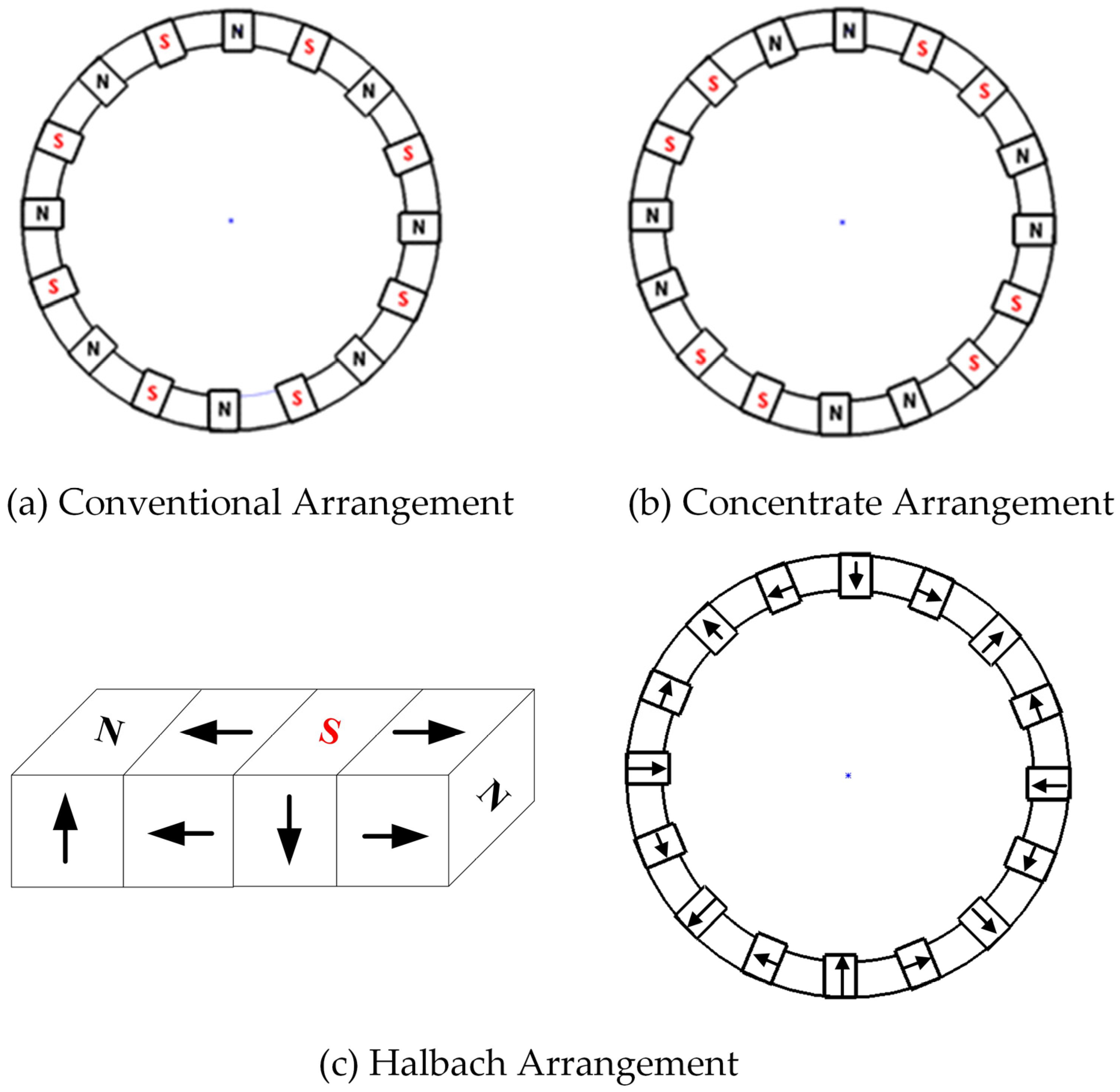
2.1. Cylindrical Permanent Magnet Governor with Halbach Magnet Array
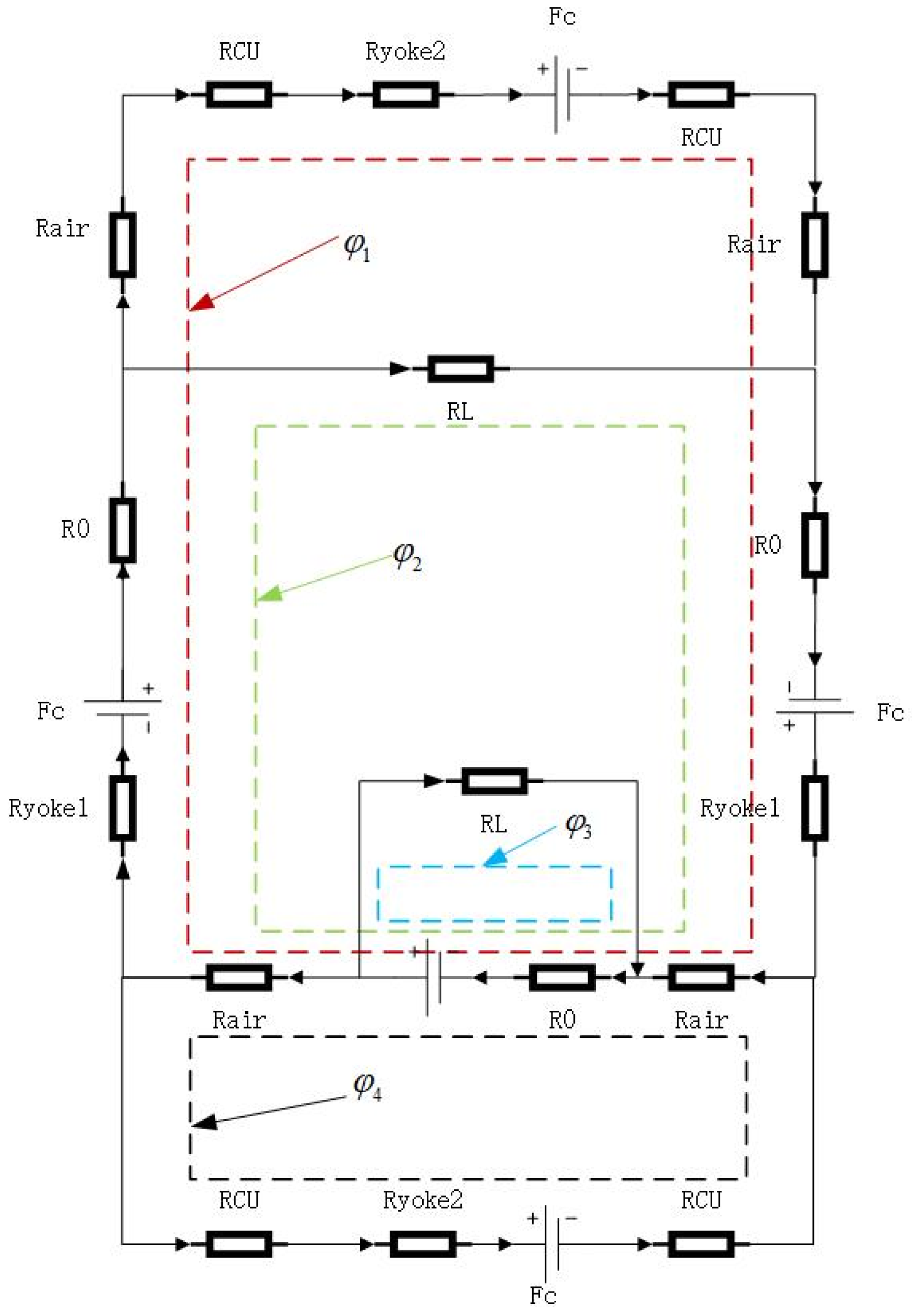
2.2. Equivalent Magnetic Circuit of Halbach Permanent Magnet Cell and Simulation Model
Simulation Model
3. Analysis of Results
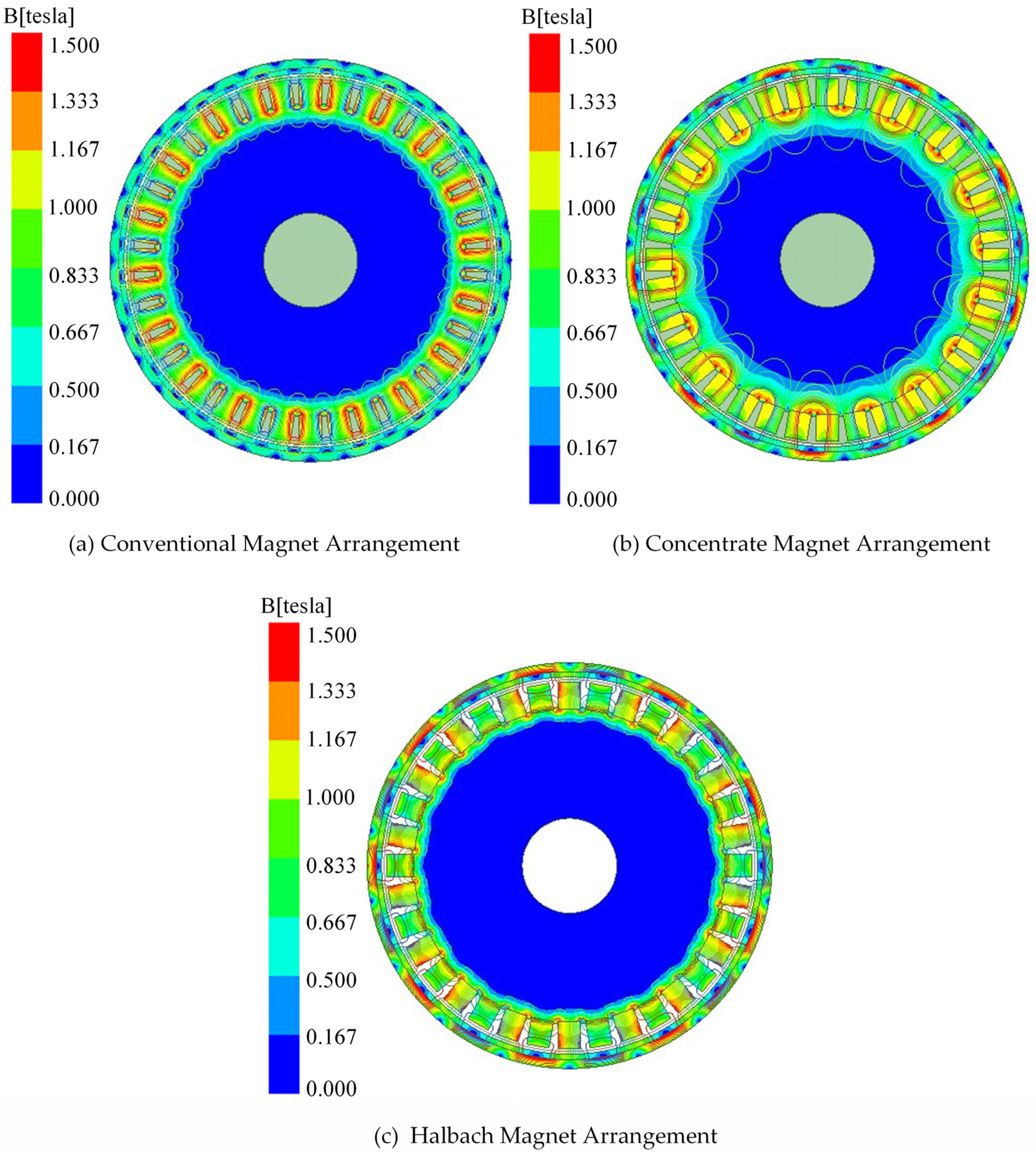
3.1. Magnetic Field Distribution
3.2. Eddy Current Density Distribution in the Copper Rings
3.3. Ohmic Loss in the Copper Ring
3.4. Output Torque of CPMG
3.5. Influence of Copper Ring Thickness on Transmission Performance
4. Experimental Analysis
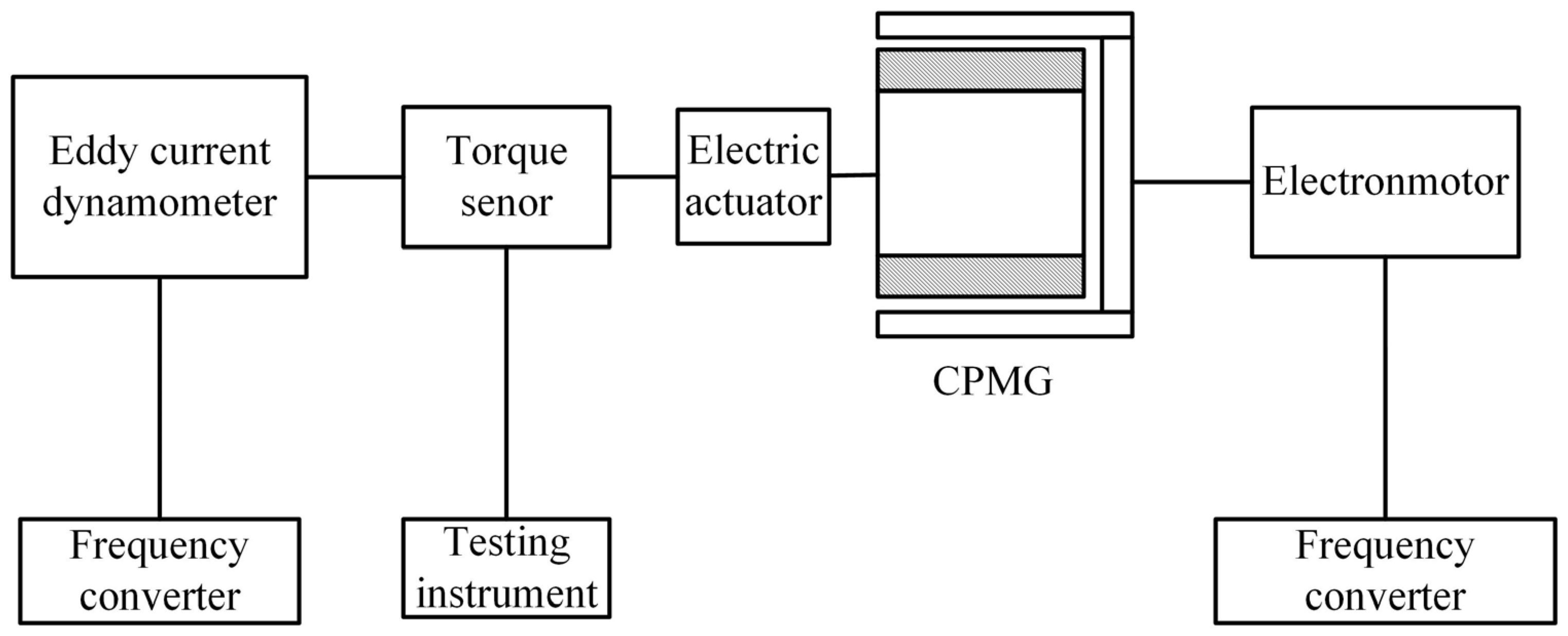
4.1. Setup of Experimental Platform
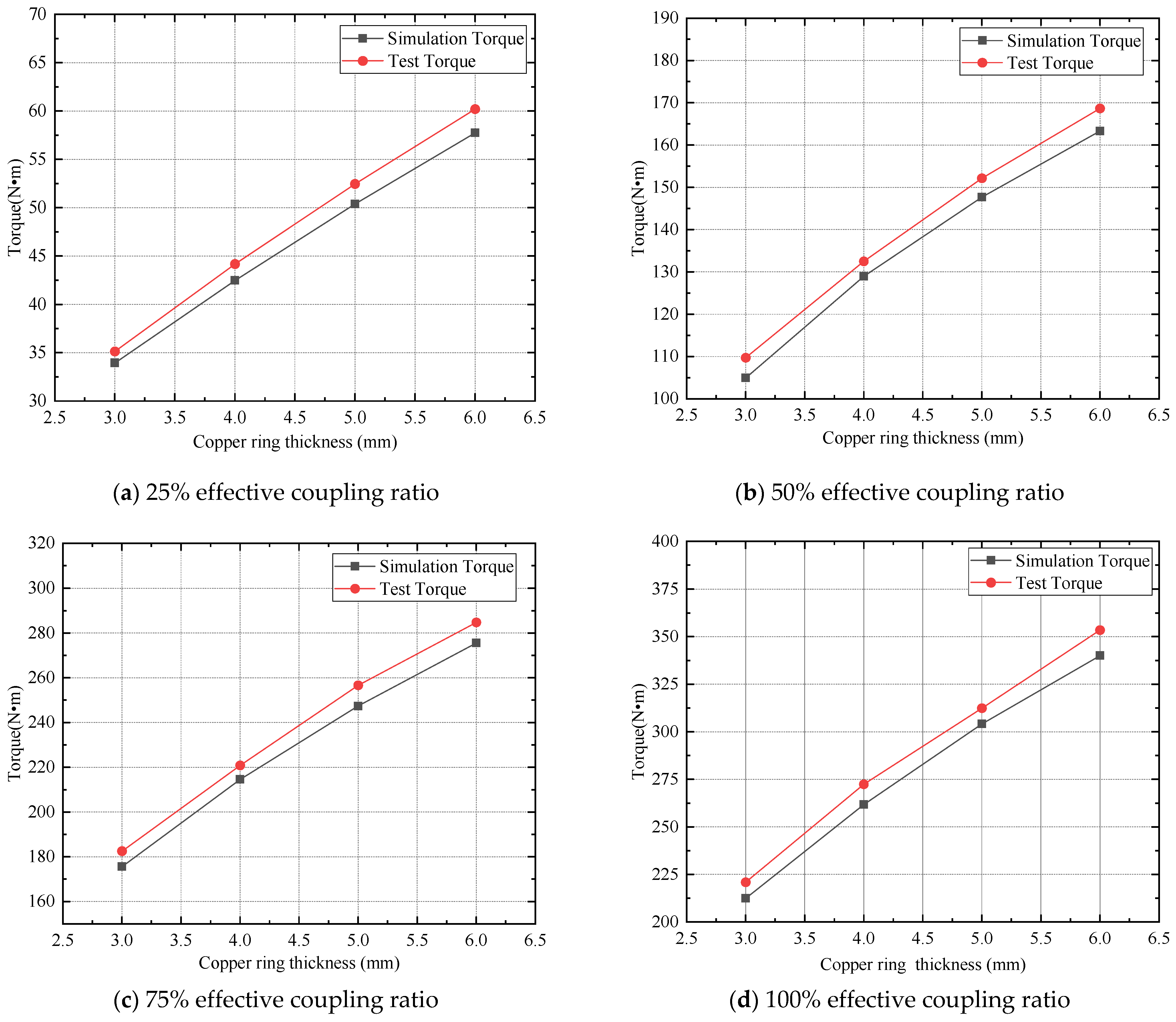
4.2. Output Torque Test
5. Conclusions
- The air gap flux density under the Halbach arrangement is 13% and 6.2% higher than the other two arrangements, respectively. The average output torque of the Halbach arrangement is increased by 15.89% and 10.31%, which is compared with the conventional arrangement and concentrate arrangement.
- When the effective coupling ratio and the thickness of the copper ring are constant, the output torque increases first and then drops with the slip rate increasing, which reaches the maximum torque of around 0.2. The results were consistent with the results of the simulation, and the error was kept within the range of 5%. The output torque of the Halbach array is higher than the magnets’ arrangement in Ref [1]. The peak torque of the Halbach array is 12.21% higher when compared to the magnets’ arrangement in Ref. [1].
- When the slip rate is constant, the output torque increases with the increase in the effective coupling ratio (between conductor and magnet), and the thickness of the copper ring increases.
Author Contributions
Funding
Conflicts of Interest
Sample Availability
Abbreviations
| DPMG | disk permanent magnet governor; |
| CPMG | cylindrical permanent magnet governor; |
| MEC | magnetic equivalent circuit; |
| MCT | marine current turbine; |
| PM | permanent magnet; |
| PMR | permanent magnet rotor; |
| KCL | Kirchhoff current law. |
References
- Cheng, X.; Liu, W.; Zhang, Y.; Liu, S.; Luo, W. A Concise Transmitted Torque Calculation Method for Pre-design of Axial Permanent Magnetic Coupler. IEEE Trans. Energy Convers. 2020, 35, 938–947. [Google Scholar]
- Seo, S.W.; Kim, Y.H.; Lee, J.H.; Choi, J.Y. Analytical torque calculation and experimental verification of synchronous permanent magnet couplings with Halbach arrays. AIP Adv. 2020, 8, 056609. [Google Scholar] [CrossRef]
- Wang, L.; Jia, Z.Y.; Zhang, L. Investigation on the accurate calculation of the temperature field of permanent magnet governor and the optimization method of heat conduction. Case Stud. Therm. Eng. 2019, 13, 100360. [Google Scholar] [CrossRef]
- Guo, B.; Li, D.; Shi, J.; Gao, Z. A Performance Prediction Model for Permanent Magnet Eddy-Current Couplings Based on the Air-Gap Magnetic Field Distribution. IEEE Trans. Magn. 2022, 58, 1–9. [Google Scholar] [CrossRef]
- Dolisy, B.; Mezani, S.; Lubin, T.; Levrque, J. A new analytical torque formula for axial field permanent magnets coupling. IEEE Trans. Energy Convers. 2015, 30, 892–899. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Wang, L. An Improved Analytical Model of Permanent Magnet Eddy Current Magnetic Coupler Based on Electromagnetic-Thermal Coupling. IEEE Access 2020, 8, 95235–95250. [Google Scholar] [CrossRef]
- Shi, J.; Suo, S.; Meng, G. The theoretical calculation model of torque transmission in permanent-magnet couplers. AIP Adv. 2021, 11, 025303. [Google Scholar] [CrossRef]
- Orlova, S.; Konuhova, M.; Kamolins, E.; Otankis, R. Design of magnetic couplings for bioreactors: Analytical treatment and optimization. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018. [Google Scholar]
- Sun, K.; Shi, J.; Cui, W.; Meng, G. Theoretical Computational Model for Cylindrical Permanent Magnet Coupling. Electronics 2021, 10, 2026. [Google Scholar] [CrossRef]
- Deshan, K.; Dazhi, W.; Wenhui, L.; Sihan, W.; Zhong, H. Analysis of a novel flux adjustable axial flux permanent magnet eddy current coupler. IET Electr. Power Appl. 2023, 17, 181–194. [Google Scholar] [CrossRef]
- Park, J.; Paul, S.; Chang, J.; Hwang, T.; Yoon, J. Design and comparative survey of high torque coaxial permanent magnet coupling for tidal current generator. Electr. Power Energy Syst. 2020, 120, 105966. [Google Scholar] [CrossRef]
- Taqavi, O.; Taghavi, N. Development of a Mixed Solution of Maxwell’s Equations and Magnetic Equivalent Circuit for Double-Sided Axial-Flux Permanent Magnet Machines. IEEE Trans. Magn. 2021, 57, 1–11. [Google Scholar] [CrossRef]
- Yang, C.; Peng, Z.; Tai, J.; Zhu, L.; Telezing, B.J.K. Torque characteristics analysis of slotted-type eddy-current couplings using a new magnetic equivalent circuit model. IEEE Trans. Magn. 2020, 56, 1–8. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. Experiment and analytical analyses of axial magnetic coupling under steady-state and transient operations. IEEE Trans. Ind. Electron. 2014, 61, 4356–4365. [Google Scholar] [CrossRef]
- Kim, I.C.; Wata, J.; Tongphong, W.; Yoon, J.S.; Lee, Y.H. Magnetic Coupling for a 10 kW Tidal Current Turbine: Design and Small Scale Experiments. Energies 2020, 13, 5725. [Google Scholar] [CrossRef]
- Lukočius, R.; Vilkauskas, A.; Marčiulionis, P.; Grigaliūnas, V.; Nakutis, Ž.; Deltuva, R. An Analysis of Axial Magnetic Coupling Force and Torque Dependencies on Its Structure Parameters Using a 3D FEM. Appl. Sci. 2022, 12, 6546. [Google Scholar] [CrossRef]
- Tian, M.; Zhao, W.; Wang, X.; Wang, D.; Yang, Y.; Diao, J.; Ma, X. Analysis on a Novel Flux Adjustable Permanent Magnet Coupler With a Double-Layer Permanent Magnet Rotor. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Lu, X.; He, X.; Jin, P.; Huang, Q.; Yang, Y.; Diao, J.; Ma, X. General 3D Analytical Method for Eddy-Current Coupling with Halbach Magnet Arrays Based on Magnetic Scalar Potential and H-Functions. IEEE Trans Magn. 2021, 14, 8458. [Google Scholar] [CrossRef]
- Lee, H.J.; Joung, H.K.; Kim, C.H. Optimal Design of the Halbach Array of the Halbach Array of Magnetic Coupling. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems(ICEMS), Shanghai, China, 29 November–2 December 2022; pp. 1–5. [Google Scholar]
- Li, Y.; Hu, Y.; Guo, Y.; Song, B.; Mao, Z. Analytical Modeling and Design of Novel Conical Halbach Permanent Magnet Couplings for Underwater Propulsion. J. Mar. Sci. Eng. 2021, 9, 290. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, L.; Qu, B.; Wang, D. Evaluation and analysis of novel flux-adjustable permanent magnet eddy current couplings with multiple rotors. IET Electr. Power Appl. 2021, 15, 754–768. [Google Scholar] [CrossRef]
- McGilton, B.; Crozier, R.; McDonald, A.; Mueller, M. Review of magnetic gear technologies and their applicants in marine energy. IET Reneaable Power Gener. 2018, 12, 174–181. [Google Scholar] [CrossRef]
- Mateev, V.; Marinova, I. Loss estimation of magnetic gears. Electr. Eng. 2020, 102, 387–399. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, S. Design and optimization of a new magnetic-geared pole-changing hybrid excitation machine. IEEE Trans. Ind. Electron. 2017, 12, 9943–9952. [Google Scholar] [CrossRef]
- Huang, J.; Fu, W.; Niu, S.; Zhao, X. Comparative Analysis of Different Permanent Magnet Arrangements in a Novel Flux Modulated Electric Machine. IEEE Access 2021, 1, 14437–14445. [Google Scholar] [CrossRef]
- Yang, K.; Zhao, F.; Wang, Y. Analysis of Double Layer Permanent Magnet Flux Reversal Machines with Different Permanent Magnet Arrangements in Stator. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Li, B.; Yang, B.; Xiang, F.; Guo, J. Optimal Design of a New Rotating Magnetic Beacon Structure Based on Halbach Array. Appl. Sci. 2022, 12, 10506. [Google Scholar] [CrossRef]




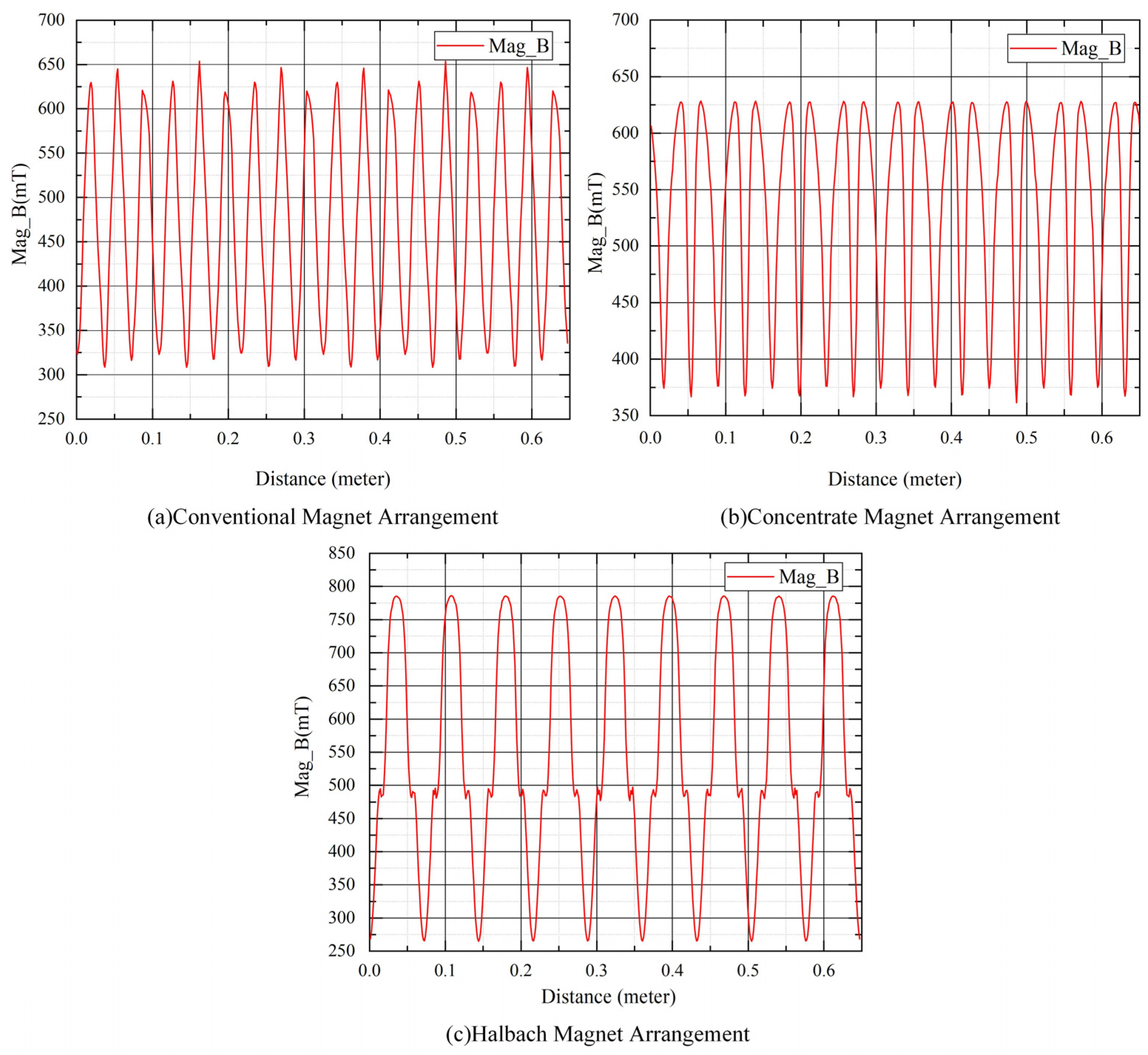
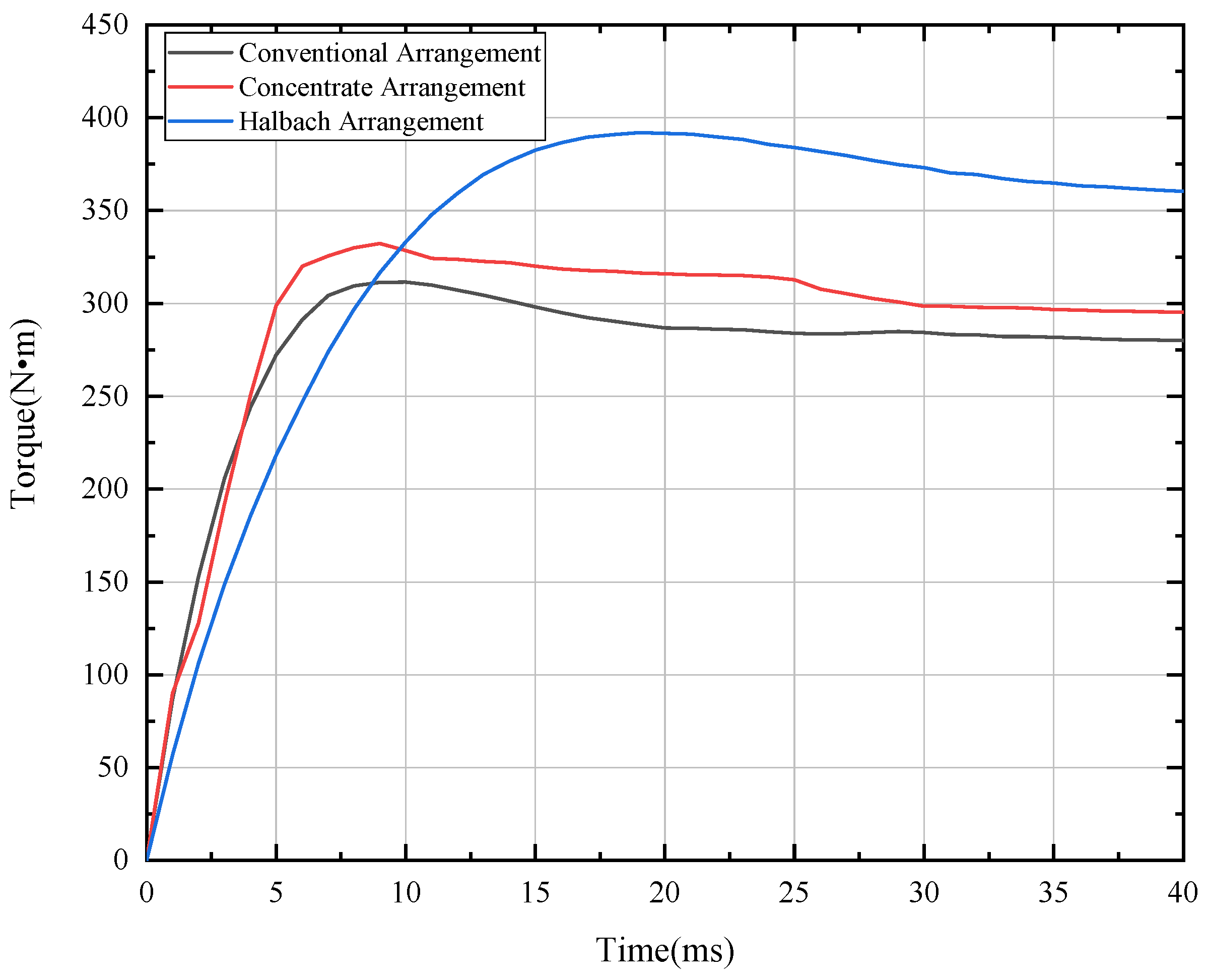
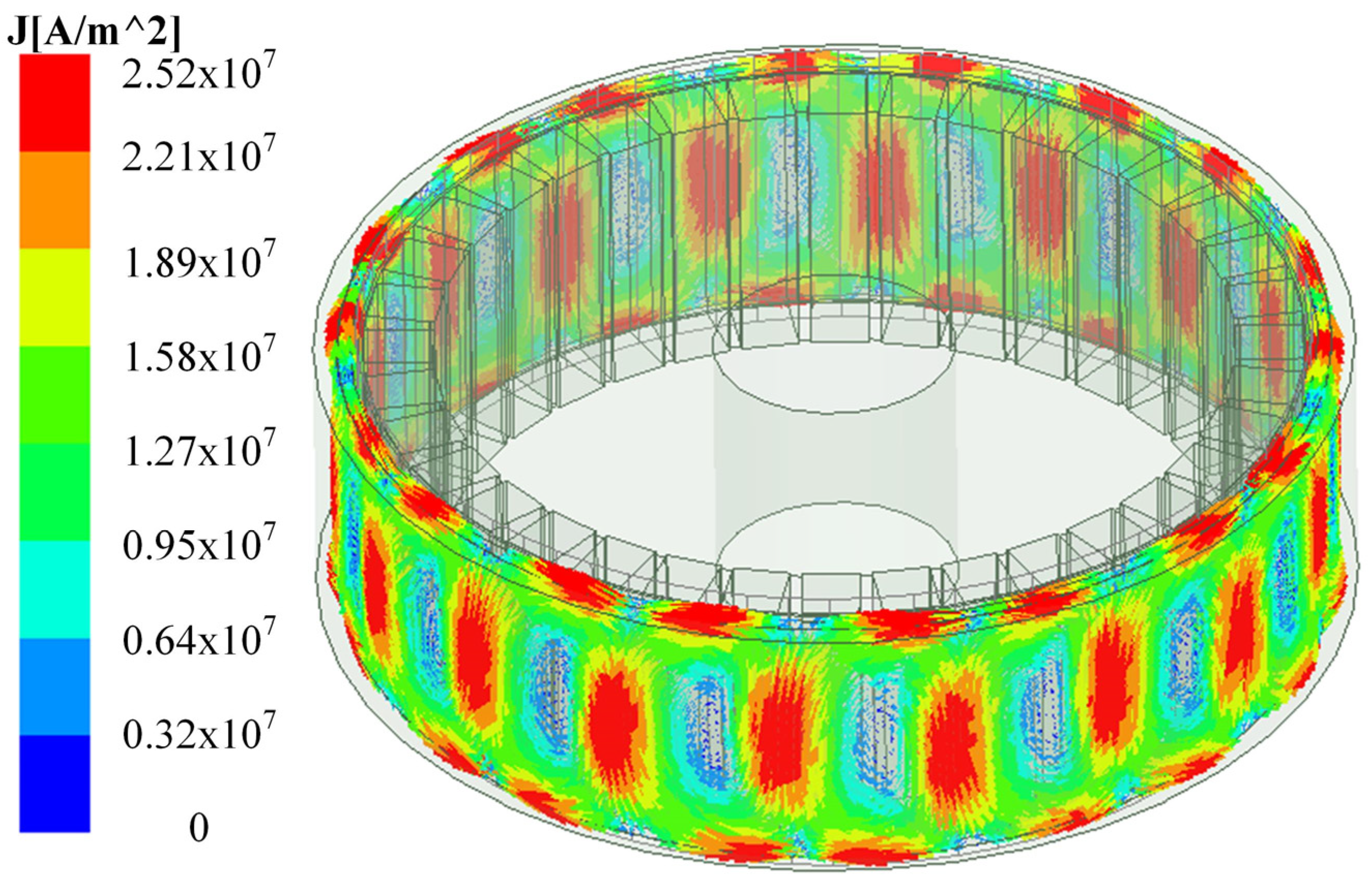


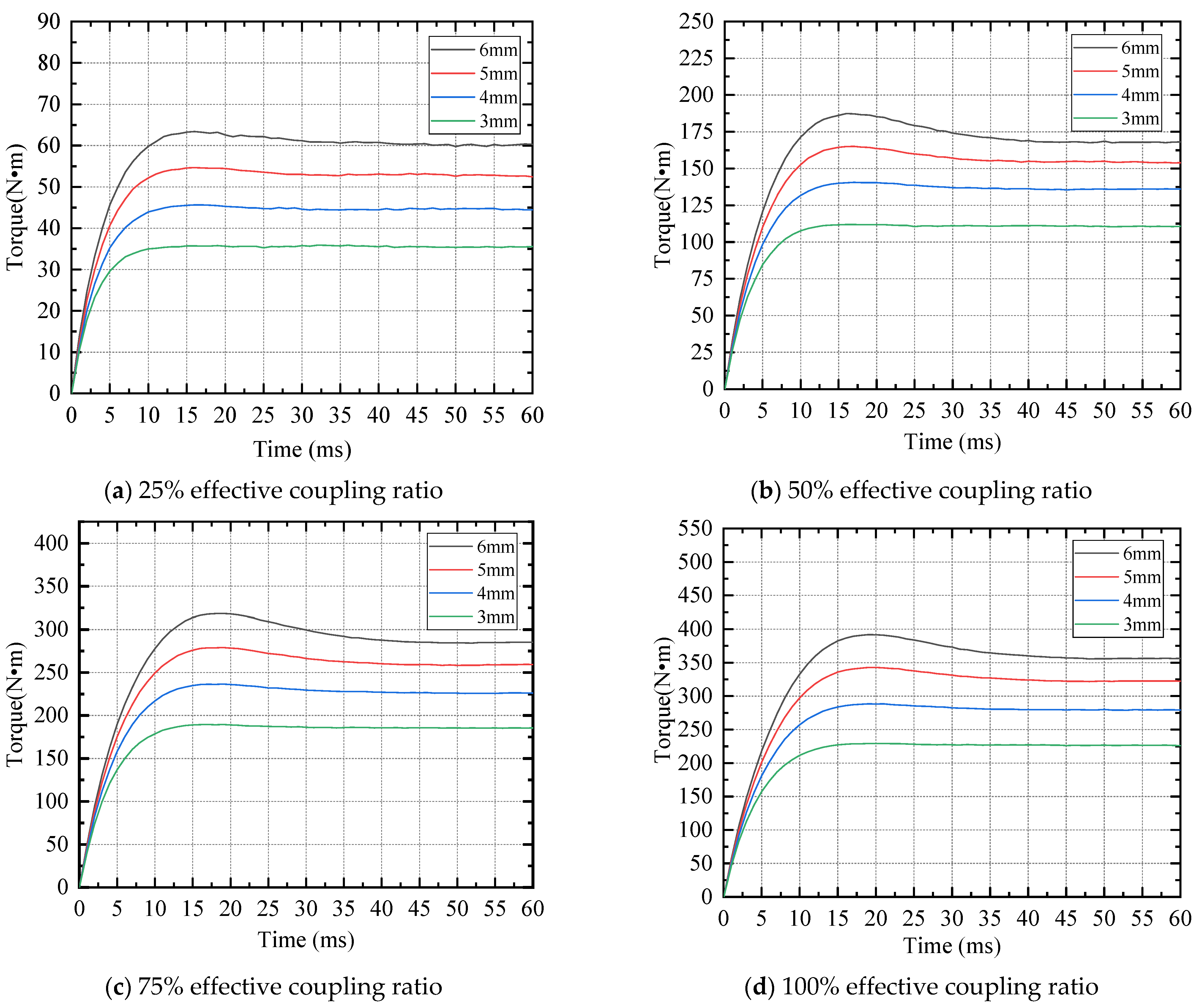


| Type of Permanent Magnet Arrangement | Conventional Arrangement | Concentrate Arrangement | Halbach Arrangement |
|---|---|---|---|
| peak magnetic induction line (Wb/m) | 0.012 | 0.013 | 0.015 |
| average magnetic flux density (mT) | 497.98 | 511.30 | 545.15 |
| Peak magnetic flux density (mT) | 653.59 | 610.65 | 785.88 |
| Average output torque (N·m) | 269.40 | 287.26 | 320.30 |
| Slip Rate | 25% | 50% | 75% | 100% |
|---|---|---|---|---|
| 0.05 | 30.10 | 89.83 | 149.51 | 179.49 |
| 0.1 | 53.75 | 153.95 | 258.58 | 320.30 |
| 0.15 | 67.42 | 179.15 | 307.52 | 384.38 |
| 0.16 | 67.84 | 184.23 | 314.96 | 388.46 |
| 0.17 | 68.12 | 185.04 | 315.95 | 390.26 |
| 0.18 | 69.48 | 185.20 | 316.01 | 390.28 |
| 0.19 | 70.12 | 184.74 | 313.28 | 388.82 |
| 0.2 | 72.64 | 180.70 | 307.63 | 386.12 |
| 0.25 | 73.13 | 172.62 | 289.09 | 364.51 |
| 0.3 | 71.31 | 162.94 | 267.45 | 340.86 |
| 0.35 | 68.54 | 152.96 | 250.59 | 317.23 |
| 0.4 | 65.08 | 141.98 | 230.19 | 291.81 |
| Copper Ring Thickness (mm) | Effective Coupling Ratio (%) | |||
|---|---|---|---|---|
| 25 | 50 | 75 | 100 | |
| 6 | 57.75 | 163.33 | 275.57 | 340.05 |
| 5 | 50.40 | 147.72 | 247.39 | 304.18 |
| 4 | 42.49 | 128.97 | 214.60 | 261.73 |
| 3 | 33.95 | 104.95 | 175.63 | 212.46 |
| Slip Rate | ||||||
|---|---|---|---|---|---|---|
| 0.05 | 174.89 | 138.75 | 179.49 | 183.62 | 2.63% | 4.99% |
| 0.1 | 328.62 | 281.41 | 320.30 | 334.82 | 2.53% | 1.89% |
| 0.15 | 391.25 | 325.48 | 384.38 | 402.77 | 1.75% | 2.94% |
| 0.2 | 396.73 | 348.25 | 386.12 | 404.42 | 2.67% | 1.94% |
| 0.25 | 370.43 | 331.38 | 364.51 | 375 | 1.74% | 1.23% |
| 0.3 | 347.52 | 298.82 | 340.86 | 353.13 | 1.92% | 1.61% |
| 0.35 | 323.56 | 274.89 | 317.23 | 329.35 | 1.96% | 1.79% |
| 0.4 | 303.21 | 259.63 | 291.81 | 310.23 | 3.75% | 2.31% |
| Effective Coupling Ratio (%) | Error (%) | |||
|---|---|---|---|---|
| 25 | 3 | 33.95 | 35.14 | 3.86 |
| 4 | 42.49 | 44.18 | 3.82 | |
| 5 | 50.40 | 52.47 | 3.94 | |
| 6 | 57.75 | 60.21 | 4.08 | |
| 50 | 3 | 104.95 | 109.72 | 4.34 |
| 4 | 128.97 | 132.51 | 2.67 | |
| 5 | 147.72 | 152.18 | 2.93 | |
| 6 | 163.33 | 168.69 | 3.18 | |
| 75 | 3 | 175.63 | 182.56 | 3.79 |
| 4 | 214.60 | 220.87 | 2.84 | |
| 5 | 247.39 | 256.64 | 3.6 | |
| 6 | 275.57 | 284.73 | 3.21 | |
| 100 | 3 | 212.46 | 220.94 | 3.84 |
| 4 | 261.73 | 272.42 | 3.93 | |
| 5 | 304.18 | 312.46 | 2.65 | |
| 6 | 340.05 | 353.48 | 3.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Wang, H.; Li, H.; Yang, C.; Gui, J. Transmission Performance of Halbach Array Cylindrical Permanent Magnet Governor. Electronics 2023, 12, 1161. https://doi.org/10.3390/electronics12051161
Zhu Y, Wang H, Li H, Yang C, Gui J. Transmission Performance of Halbach Array Cylindrical Permanent Magnet Governor. Electronics. 2023; 12(5):1161. https://doi.org/10.3390/electronics12051161
Chicago/Turabian StyleZhu, Yonglong, Hai Wang, Henian Li, Chunlai Yang, and Jingsong Gui. 2023. "Transmission Performance of Halbach Array Cylindrical Permanent Magnet Governor" Electronics 12, no. 5: 1161. https://doi.org/10.3390/electronics12051161
APA StyleZhu, Y., Wang, H., Li, H., Yang, C., & Gui, J. (2023). Transmission Performance of Halbach Array Cylindrical Permanent Magnet Governor. Electronics, 12(5), 1161. https://doi.org/10.3390/electronics12051161






