Unmanned-Aircraft-System-Assisted Early Wildfire Detection with Air Quality Sensors †
Abstract
1. Introduction
1.1. Background
1.2. Related Works
1.3. Main Contributions
- We built an energy-efficient patrol UAS for early-stage forest fire detection. The UAS platform is equipped with PM, CO, and a radio transceiver, enabling data exchange with the BSs.
- We formulated and solved an optimization problem that minimizes the overall UAS energy consumption while accounting for the detection threshold, achievable data rate quality, transmit power budget cap, and the communication link associations between the UAV and BSs.
- We developed a powerful algorithm to maximize the area covered by forest patrols while enhancing the effectiveness of UAS patrols for accurate fire detection and data exchange.
- We propose a software protocol to manage the resource allocation between the UAS and the selected BS.
- To avoid an infeasible solution of the transmitted power, we introduced a data rate loss factor to prevent the case of insufficient transmitted power in satisfying the data rate QoS.
1.4. Outline
2. System and Channel Model
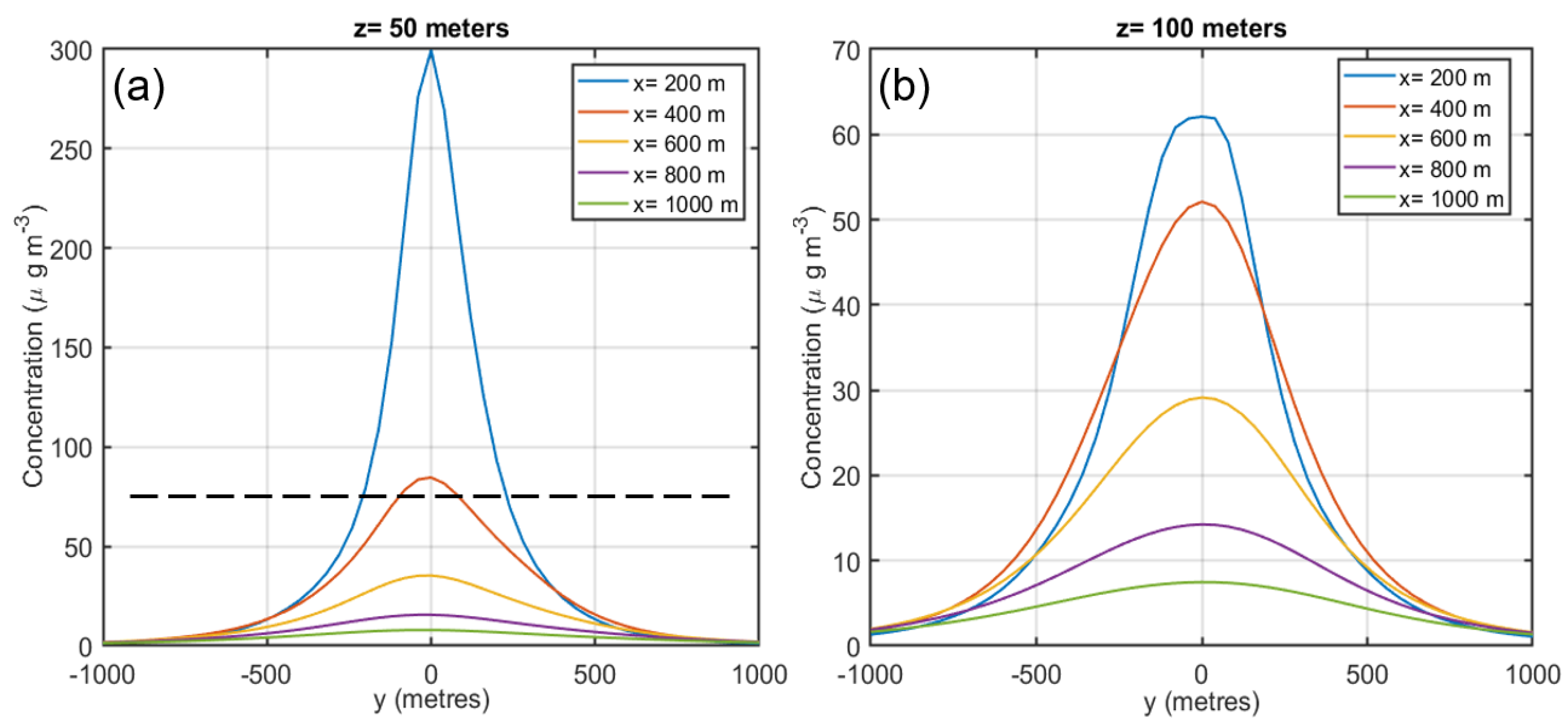
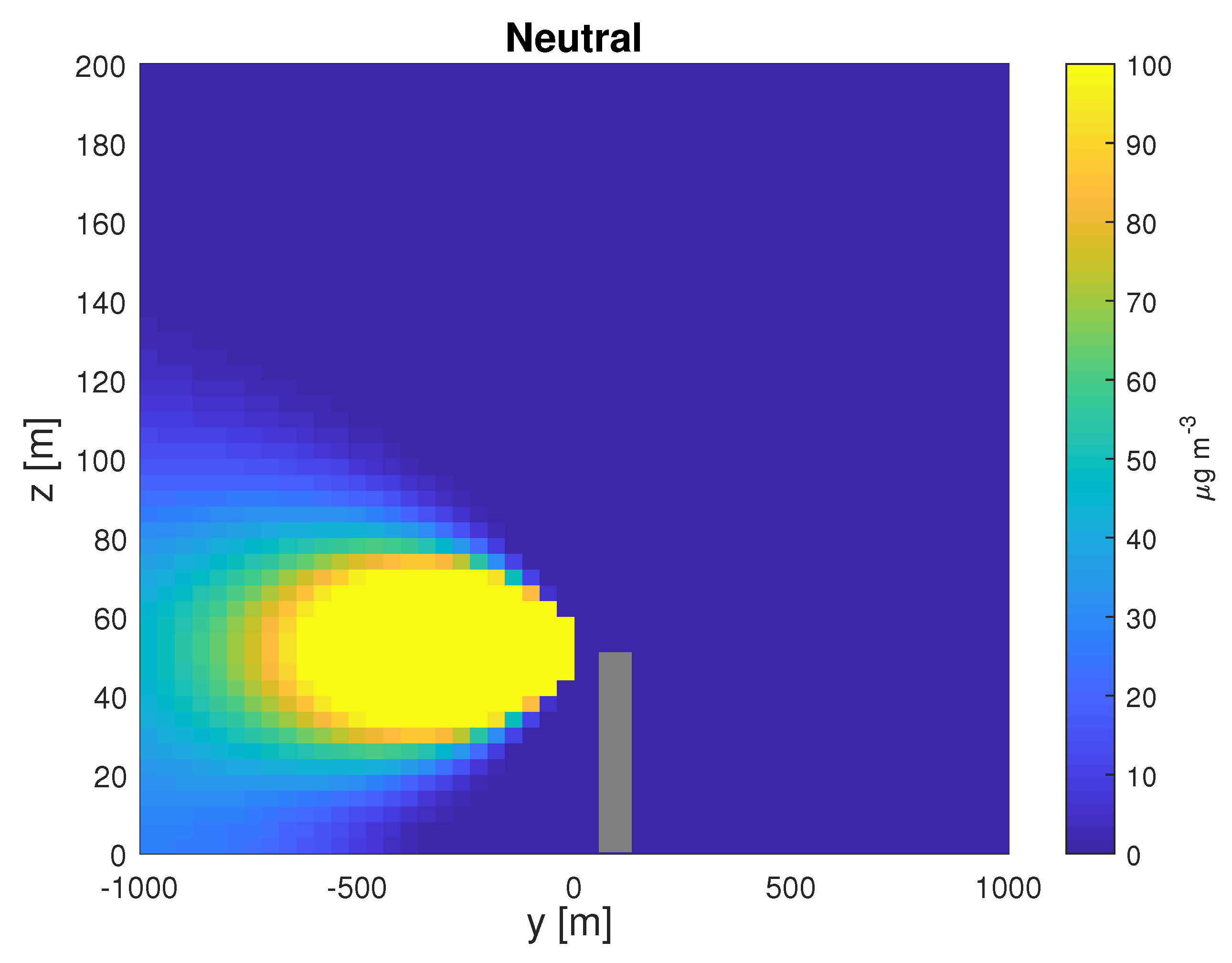
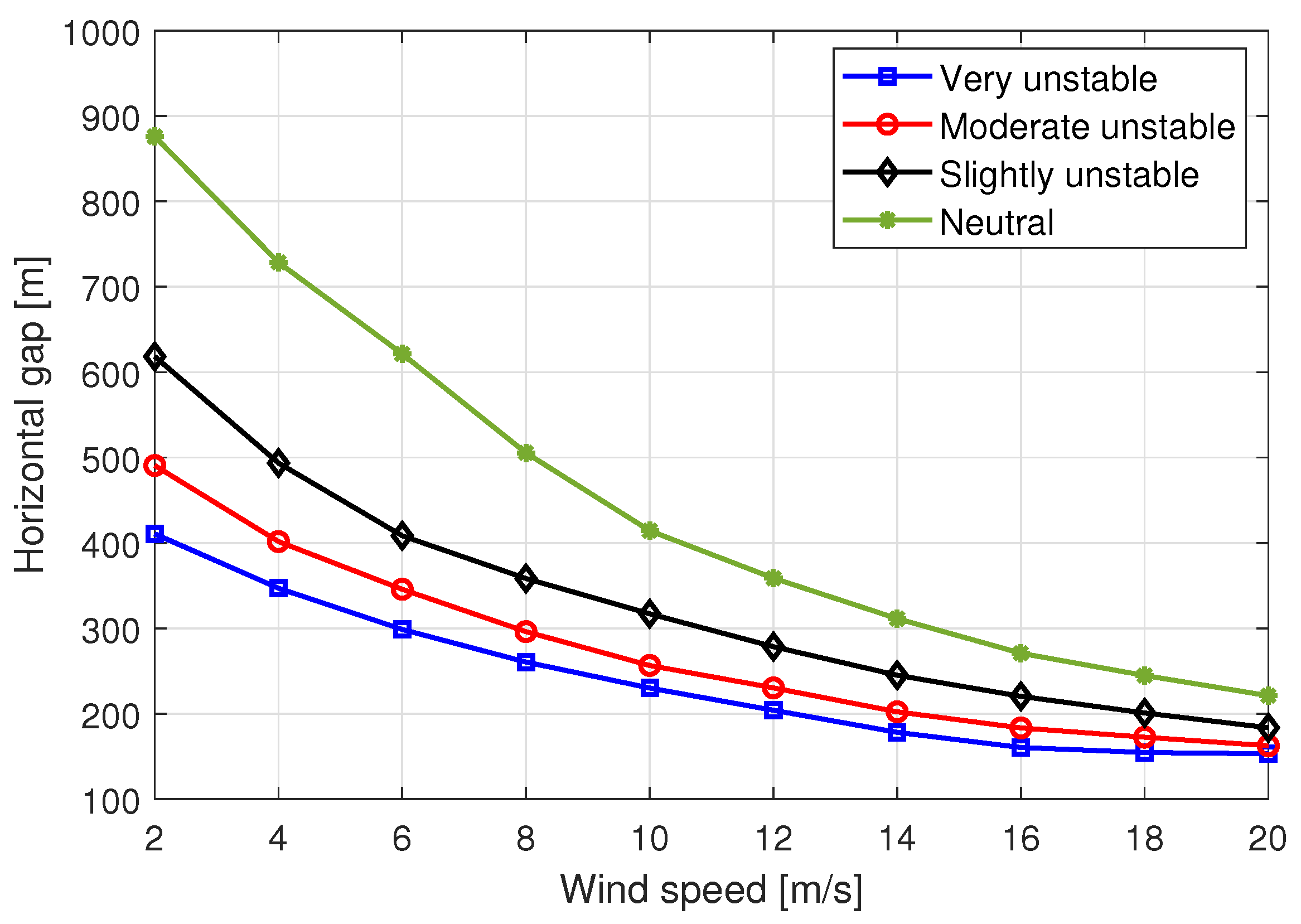
2.1. Pollutant Dispersion Model
2.2. UAS Communications Channel Model
2.3. Data Transmission
2.4. UAS Energy Model
3. Problem Formulation
3.1. General Optimization Problem
3.2. Trajectory Optimization
3.3. Data Transmission Optimization Problem
4. UAS Patrolling Solution
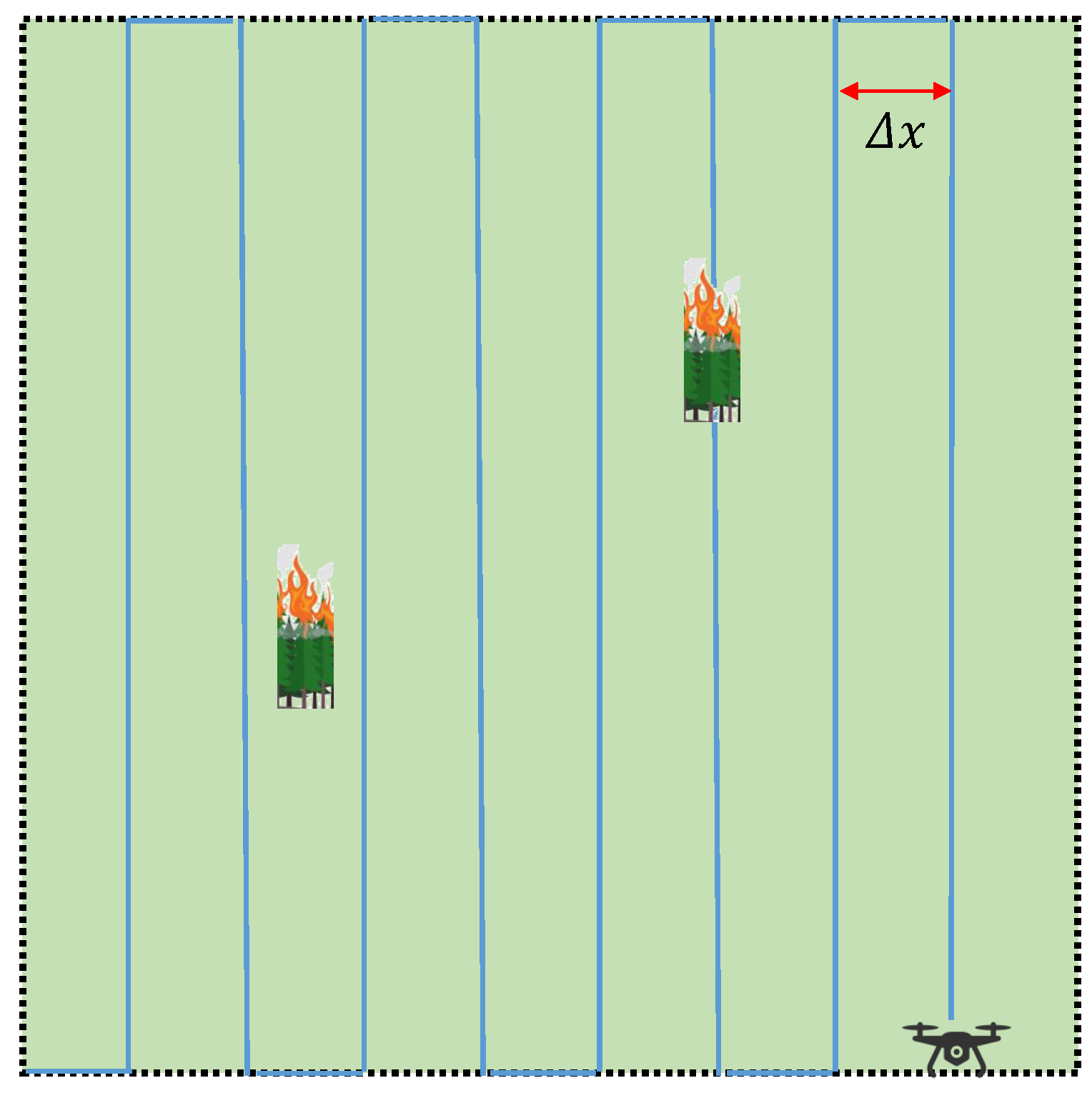
4.1. UAS Patrolling Algorithm
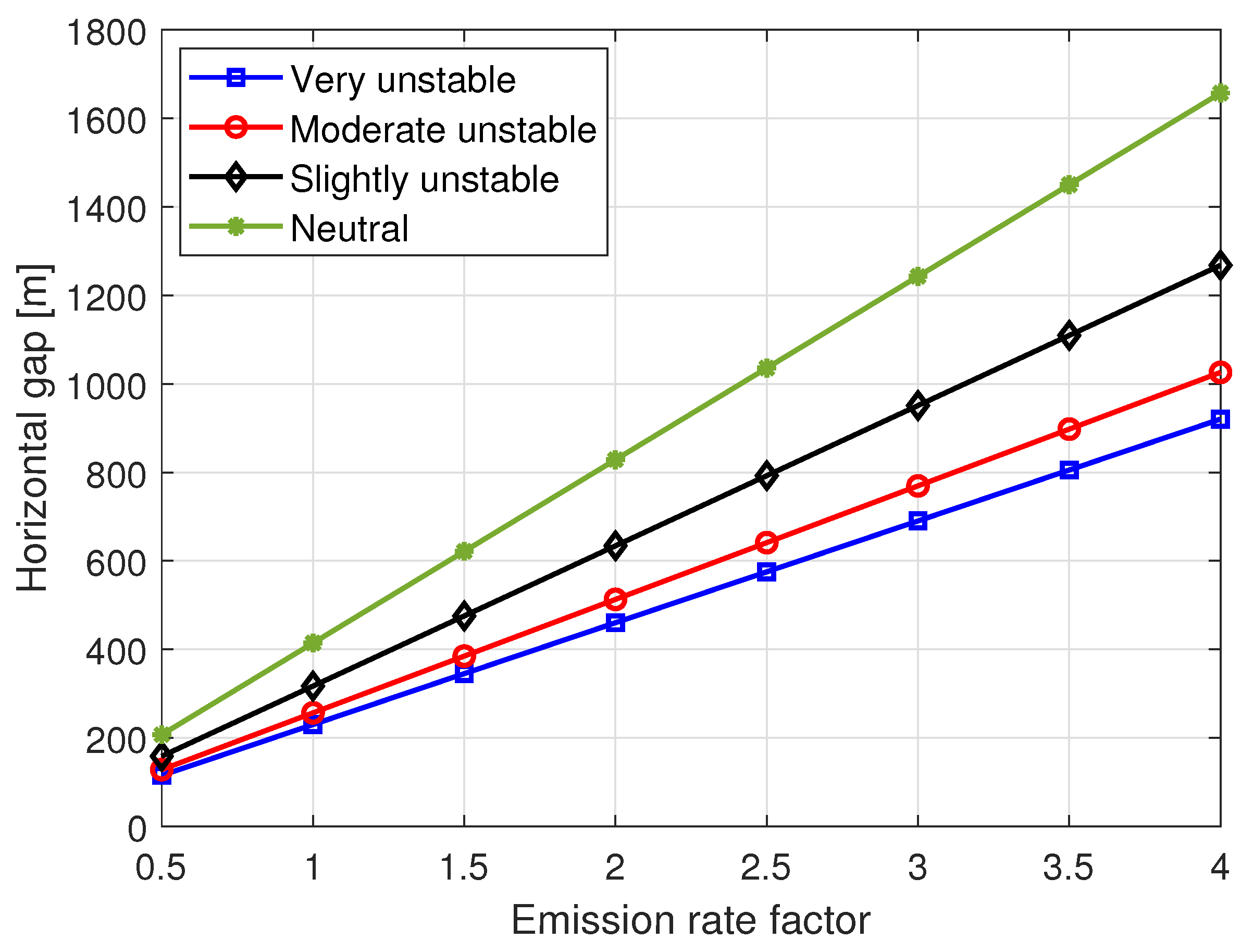
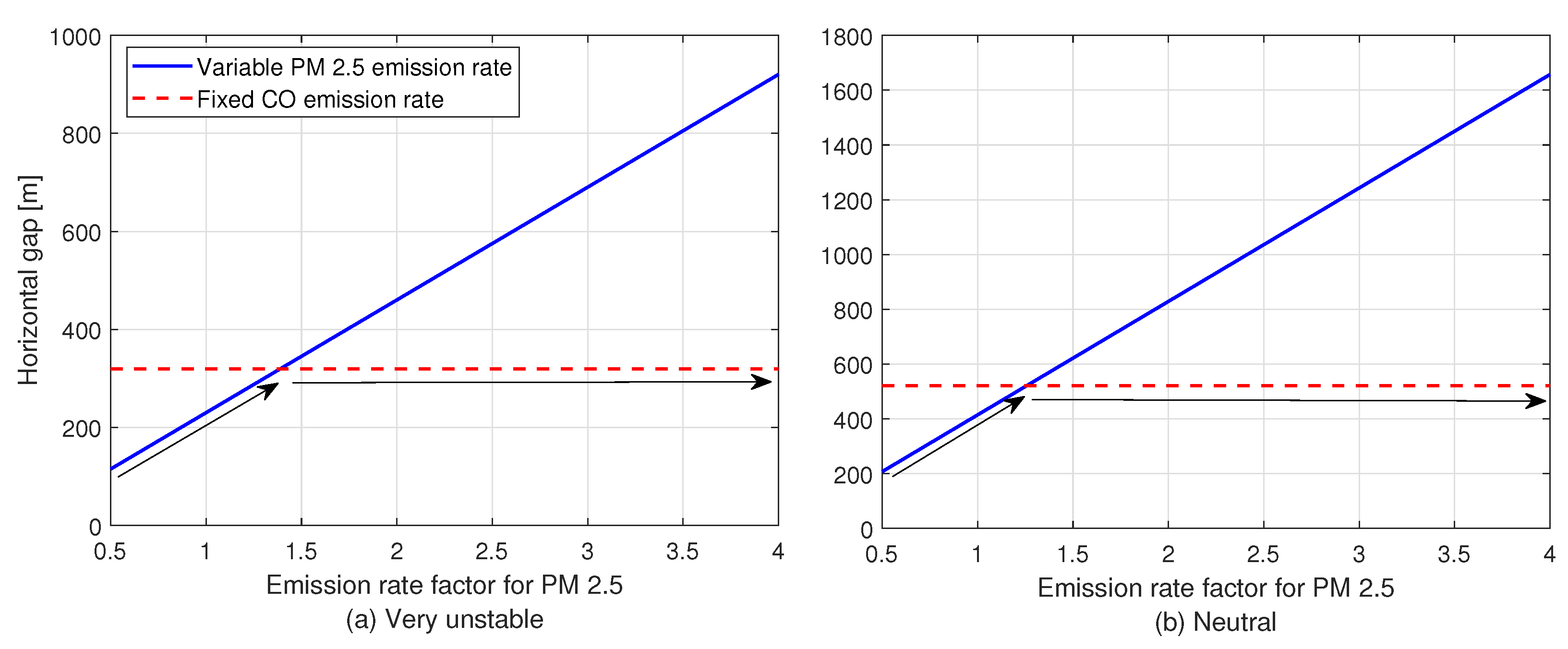
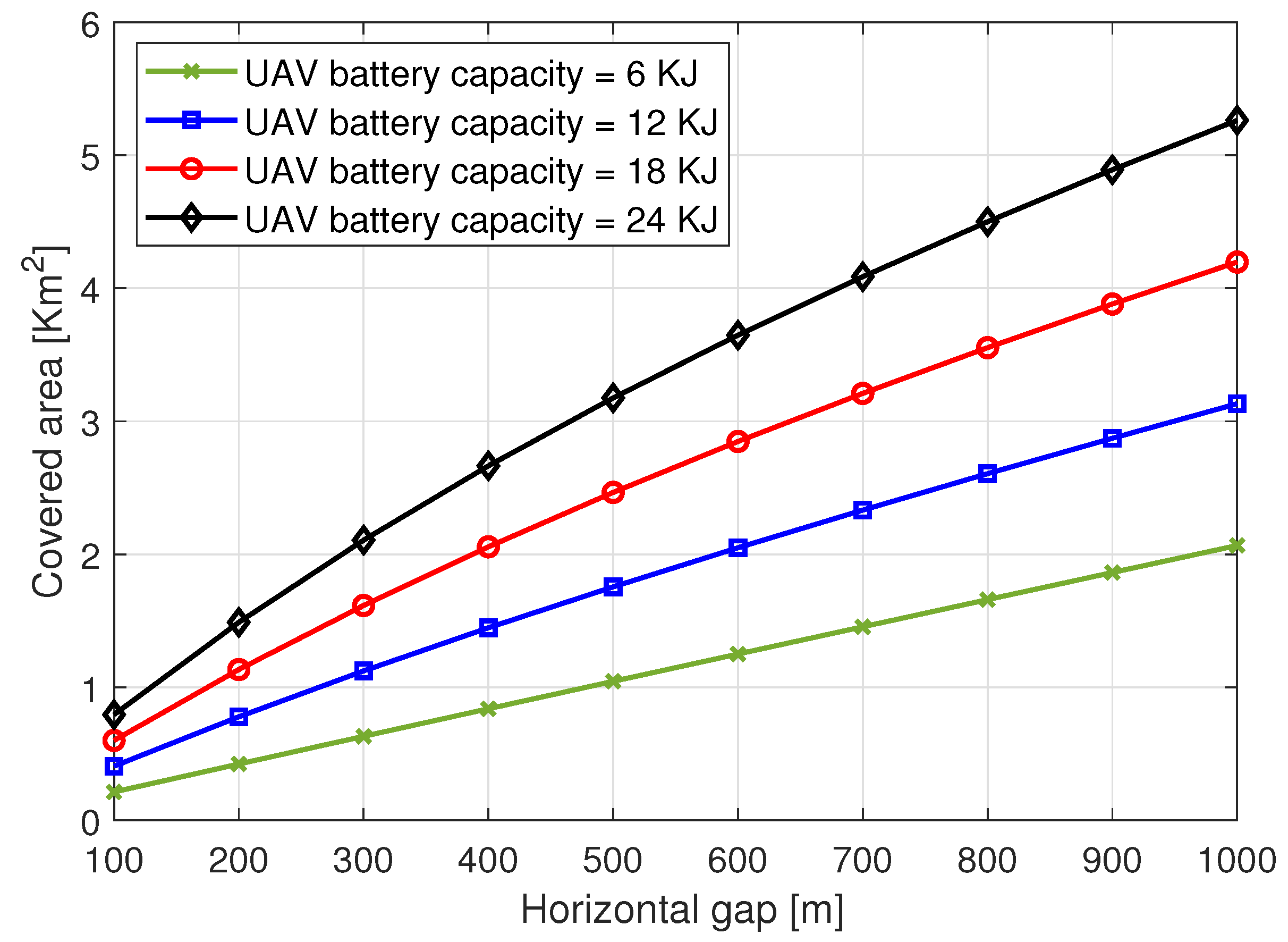
4.2. Patrolling Simulation Results
5. Data Communication Solution
5.1. UAS–BS Protocol
5.2. Establishment of the UAS–BS Link
5.3. Maintenance of the UAS–BS Link
5.4. Termination of the UAS–BS Link
5.5. Communication Optimization Solution
5.6. Data Transmission Optimization Solution
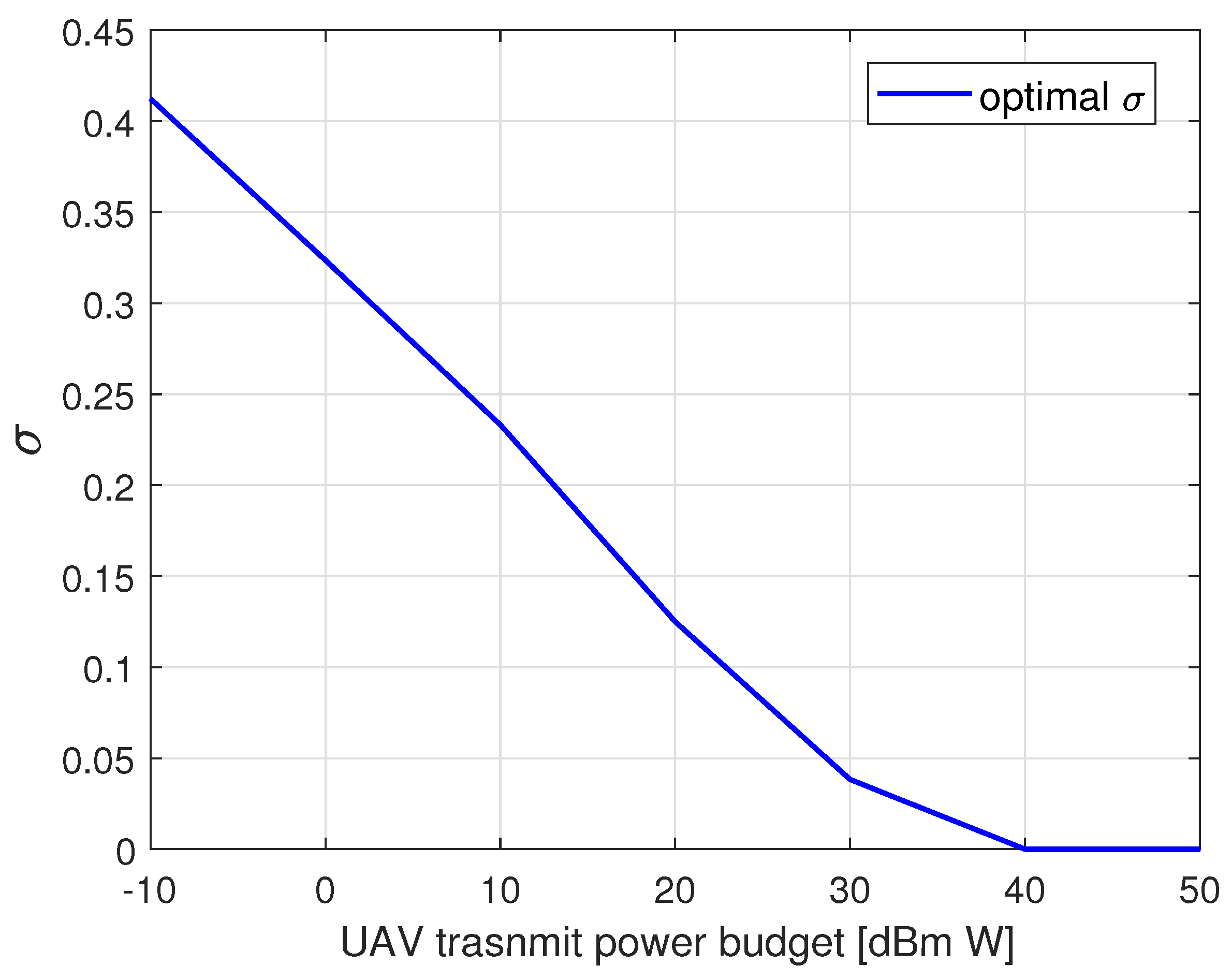
5.7. Communications Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kolaric, D.; Skala, K.; Dubravic, A. Integrated System For Forest Fire Early Detection and Management. Period. Biol. 2008, 110, 205–211. [Google Scholar]
- US Today. Two Dead Near Los Angeles as Saddleridge Fire Forces 100,000 People to Evacuate. Available online: https://www.usatoday.com/story/news/nation/2019/10/11/california-saddleridge-fire-spreading-evacuations-power-outages/3941274002/ (accessed on 27 February 2023).
- Center for Climate and Energy Solutions. Record Wildfires Push 2018 Disaster Costs to $91 Billion. 2019. Available online: https://www.c2es.org/2019/02/record-wildfires-push-2018-disaster-costs-to-91-billion/ (accessed on 27 February 2023).
- Rego, F.; Catry, F. Modeling the effects of distance on the probability of fire detection from look outs. Int. J. Wildland Fire 2006, 15, 197–202. [Google Scholar] [CrossRef]
- Matthews, S.; Sullivan, A.; Gould, J. Field evaluation of two image-based wildland fire detection systems. Fire Saf. J. 2012, 47, 54–61. [Google Scholar] [CrossRef]
- Murray, A. Optimising the spatial location of urban fire stations. Fire Saf. J. 2013, 62, 64–71. [Google Scholar] [CrossRef]
- Bao, S.; Xiao, N.; Lai, Z.; Zhang, H.; Kim, C. Optimizing watchtower locations for forest fire monitoring using location models. Fire Saf. J. 2015, 71, 100–109. [Google Scholar] [CrossRef]
- NASA. Techniques for Wildfire Detection and Monitoring. Available online: https://appliedsciences.nasa.gov/join-mission/training/english/arset-techniques-wildfire-detection-and-monitoring (accessed on 27 February 2023).
- Environment and Natural Resources. Detecting Wildfire. Available online: https://www.enr.gov.nt.ca/en/services/wildfire-operations/detecting-wildfire (accessed on 27 February 2023).
- Gao, Z.; Zhang, L.; Li, X.; Liao, M.; Qiu, J. Detection and analysis of urban land use changes through multi-temporal impervious. J. Remote Sens. 2010, 14, 593–606. [Google Scholar]
- Pardo, J.; Aguilar, W.; Toulkeridis, T. Wireless communication system for the transmission of thermal images from a UAV. In Proceedings of the 2017 CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Pucon, Chile, 18–20 October 2017; pp. 1–5. [Google Scholar]
- ALERTWildfire. ALERTWildfire Project. Available online: https://www.alertwildfire.org/ (accessed on 27 February 2023).
- Salavati, G.; Saniei, E.; Ghaderpour, E.; Hassan, Q.K. Wildfire Risk Forecasting Using Weights of Evidence and Statistical Index Models. Sustainability 2022, 14, 3881. [Google Scholar] [CrossRef]
- Malik, A.; Rao, M.R.; Puppala, N.; Koouri, P.; Thota, V.A.K.; Liu, Q.; Chiao, S.; Gao, J. Data-Driven Wildfire Risk Prediction in Northern California. Atmosphere 2021, 12, 109. [Google Scholar] [CrossRef]
- Onsterwisch, Z.; Maunteland, A.; Nisbett, N.; Dibbya, D.; Alsharoa, A. Particulate Matter Detection in Mines Using 3D Light Detection and Ranging Technology. In Proceedings of the 2023 IEEE Wireless Communications and Networking (WCNC), Glasgow, Scotland, UK, 26–29 March 2023; pp. 1–6. [Google Scholar]
- Zhang, L.; Wang, B.; Peng, W.; Li, C.; Lu, Z.; Guo, Y. A Method for Forest Fire Detection Using UAV. Adv. Sci. Technol. Lett. 2015, 81, 69–74. [Google Scholar]
- Alsharoa, A.; Yuksel, M. UAV-Direct: Facilitating D2D Communications for Dynamic and Infrastructure-less Networking. In Proceedings of the 4th ACM Workshop on Micro Aerial Vehicle Networks, Systems, and Applications, Mobile Systems, Applications, and Services (MobiSys), Munich, Germany, 10–15 June 2018; pp. 57–62. [Google Scholar]
- Selim, M.Y.; Alsharoa, A.; Kamal, A.E. Short-Term and Long-Term Cell Outage Compensation Using UAVs in 5G Networks. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Alsharoa, A.; Ghazzai, H.; Yuksel, M.; Kadri, A.; Kamal, A.E. Trajectory Optimization for Multiple UAVs Acting as Wireless Relays. In Proceedings of the 2018 IEEE International Conference on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Nait-Abdesselam, F.; Alsharoa, A.; Selim, M.Y.; Qiao, D.; Kamal, A.E. Towards enabling unmanned aerial vehicles as a service for heterogeneous applications. J. Commun. Netw. 2021, 23, 212–221. [Google Scholar] [CrossRef]
- Osterwisch, Z.; Rinchi, O.; Alsharoa, A.; Ghazzai, H.; Massoud, Y. Multiple UAV-LiDAR Placement Optimization Under Road Priority and Resolution Requirements. In Proceedings of the 2023 IEEE International Conference on Communications (ICC), Rome, Italy, 28 May–1 June 2023; pp. 1–6. [Google Scholar]
- Yuan, C.; Liu, Z.; Zhang, Y. Aerial Images-Based Forest Fire Detection for Firefighting Using Optical Remote Sensing Techniques and Unmanned Aerial Vehicles. J. Intell. Robot. Syst. 2017, 88, 635–654. [Google Scholar] [CrossRef]
- Allison, R.S.; Johnston, J.M.; Craig, G.; Jennings, S. Airborne Optical and Thermal Remote Sensing for Wildfire Detection and Monitoring. Sensors 2016, 16, 1310. [Google Scholar] [CrossRef] [PubMed]
- Kinaneva, D.; Hristov, G.V.; Raychev, J.; Zahariev, P. Early Forest Fire Detection Using Drones and Artificial Intelligence. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019; pp. 1060–1065. [Google Scholar]
- Yuan, C.; Liu, Z.; Zhang, Y. Fire detection using infrared images for UAV-based forest fire surveillance. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 567–572. [Google Scholar]
- Rjoub, D.; Alsharoa, A.; Masadeh, A. Early Wildfire Detection using UAVs Integrated with Air Quality and LiDAR Sensors. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–5. [Google Scholar]
- Gottuk, D.T.; Peatross, M.J.; Roby, R.J.; Beyler, C.L. Advanced fire detection using multi-signature alarm algorithms. Fire Saf. J. 2002, 37, 381–394. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, H.; Arnott, W.P.; Meyer, M.E.; Taylor, S.; Firouzkouhi, H.; Moosmüller, H.; Chow, J.C.; Watson, J.G. Evaluation of gas and particle sensors for detecting spacecraft-relevant fire emissions. Fire Saf. J. 2020, 113, 102977. [Google Scholar] [CrossRef]
- Gutmacher, D.; Hoefer, U.; Wöllenstein, J. Gas sensor technologies for fire detection. Sens. Actuators B Chem. 2012, 175, 40–45. [Google Scholar] [CrossRef]
- Mehadi, A.; Moosmüller, H.; Campbell, D.; Ham, W.; Schweizer, D.; Tarnay, L.; Hunter, J. Laboratory and field evaluation of real-time and near real-time PM2.5 smoke monitors. J. Air Waste Manag. Assoc. 2019, 70, 158–179. [Google Scholar] [CrossRef] [PubMed]
- Illingworth, S.; Allen, G.; Percival, C.; Hollingsworth, P.; Gallagher, M.; Ricketts, H.; Hayes, H.; Ładosz, P.; Crawley, D.; Roberts, G. Measurement of boundary layer ozone concentrations on-board a Skywalker unmanned aerial vehicle. Atmos. Sci. Lett. 2014, 15, 252–258. [Google Scholar] [CrossRef]
- Rhode, S. Drone Search-and-Rescue Study Reveals Potential, Limits; Aircraft Owners and Pilots Association: Frederick, MD, USA, 2018. [Google Scholar]
- Reisen, F.; Meyer, C.; Weston, C.; Volkova, L. Ground-Based Field Measurements of PM2.5 Emission Factors From Flaming and Smoldering Combustion in Eucalypt Forests. J. Geophys. Res. Atmos. 2018, 123, 8301–8314. [Google Scholar]
- David, C.C.; Alley, F.C. Air Pollution Control: A Design Approach; Waveland Press Inc.: Long Grove, IL, USA, 2010. [Google Scholar]
- Al-Hourani, A.; Kandeepan, S.; Jamalipour, A. Modeling air-to-ground path loss for low altitude platforms in urban environments. In Proceedings of the 2014 IEEE Global Communications Conference (GLOBECOM), Austin, TX, USA, 8–12 December 2014; pp. 2898–2904. [Google Scholar]
- Hourani, A.; Sithamparanathan, K.; Lardner, S. Optimal LAP altitude for maximum coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Holis, J.; Pechac, P. Elevation dependent shadowing model for mobile communications via high altitude platforms in built-up areas. IEEE Trans. Antennas Propag. 2008, 56, 1078–1084. [Google Scholar] [CrossRef]
- Cotton, S.L. Human Body Shadowing in Cellular Device-to-Device Communications: Channel Modeling Using the Shadowed κ − μ Fading Model. IEEE J. Sel. Areas Commun. 2015, 33, 111–119. [Google Scholar] [CrossRef]
- Obayashi, S.; Zander, J. A body-shadowing model for indoor radio communication environments. IEEE Trans. Antennas Propag. 1998, 46, 920–927. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Y.; Meng, F. Modeling and simulation of pathloss and fading for air-ground link of HAPs within a network simulator. In Proceedings of the 2013 IEEE International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), Beijing, China, 10–12 October 2013. [Google Scholar]
- Zeng, Y.; Zhang, R. Energy-Efficient UAV Communication With Trajectory Optimization. IEEE Trans. Wirel. Commun. 2017, 16, 3747–3760. [Google Scholar] [CrossRef]
- Hulens, D.; Verbeke, J.; Goedemé, T. Choosing the best embedded processing platform for on-board UAV image processing. In Proceedings of the 10th International Joint Conference on Computer Vision, Imaging and Computer Graphics, Berlin, Germany, 11–14 March 2015; Springer: Cham, Switzerland, 2015; pp. 455–472. [Google Scholar]
- Liu, X.; Yu, X.; Zhang, Z. PM2.5 concentration differences between various forest types and its correlation with forest structure. Atmosphere 2015, 6, 1801–1815. [Google Scholar] [CrossRef]
- Charland, A.; Clements, C. Kinematic structure of a wildland fire plume observed by Doppler LiDAR. IEEE/ACM Trans. Netw. 2013, 118, 3200–3212. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Beasley, D.; Bull, D.R.; Martin, R.R. An Overview of Genetic Algorithms: Part 2, Research Topics. Univ. Comput. 1993, 15, 170–181. [Google Scholar]
- Wotton, B.; Gould, J.; McCaw, L.; Cheney, P.; Taylor, S. Flame temperature and residence time of fires in dry eucalypt forest. Int. J. Wildland 2012, 22, 270–281. [Google Scholar] [CrossRef]
- Alsharoa, A.; Ghazzai, H.; Kadri, A.; Kamal, A.E. Spatial and Temporal Management of Cellular HetNets with Multiple Solar Powered Drones. IEEE Trans. Mob. Comput. 2020, 19, 954–968. [Google Scholar] [CrossRef]
- Boyd, S.; Mutapcic, A. Stochastic Subgradient Methods; Notes for EE364; Stanford University: Stanford, CA, USA, 2006. [Google Scholar]






| Method | Concerns |
|---|---|
| Watchtowers [4,5,6] | Expensive labor. |
| Workplace safety concerns. | |
| Prone to late detection of fires. | |
| Satellite Remote Sensing [7,8,9,10] | Insufficient spatial resolution. |
| The region being considered must be clear of clouds. | |
| Thermal Imaging [11,12,23,24] | Insufficient resolution. |
| There is some weather interference. | |
| Thick canopies may prevent the heat signal from the fire. | |
| AQSs [28,30] | A vast number of sensors must be deployed in order to cover a broad region. |
| Forests or dangerous places make deployment more difficult. | |
| AQSs + UAS (proposed solution) | Limited capacity of the UAS battery. |
| A base station is required for tracking and communication. |
| Constant | Value | Constant | Value | Constant | Value |
|---|---|---|---|---|---|
| V (m/s) | 5 | (m) | 15 | (m/s) | |
| (m) | (K) | (K) | |||
| (mb) | 1000 | (W) | (kg) | 1 | |
| (kg/m) | 4 |
| km | km | |||||||
|---|---|---|---|---|---|---|---|---|
| Stability | a | b | c | d | f | c | d | f |
| 1—Very unstable | 213 | 0.894 | 440.8 | 1.941 | 9.27 | 459.7 | 2.094 | −9.6 |
| 2—Moderate unstable | 156 | 0.894 | 106.6 | 1.149 | 3.3 | 108.2 | 1.098 | 2.0 |
| 3—Slightly unstable | 104 | 0.894 | 61.0 | 0.911 | 0 | 61.0 | 0.911 | 0 |
| 4—Neutral | 68 | 0.894 | 33.2 | 0.725 | −1.7 | 44.5 | 0.516 | −13.0 |
| W | W | |||||
|---|---|---|---|---|---|---|
| Data Type | (Mbits/s) | (W) | (Mbits/s) | (W) | ||
| 1 | 0.125 | 0.87 | 0.016 | 0.038 | 0.96 | 0.29 |
| 2 | 0.125 | 4.38 | 0.019 | 0.038 | 4.80 | 0.31 |
| 3 | 0.125 | 8.75 | 0.065 | 0.038 | 9.62 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rjoub, D.; Alsharoa, A.; Masadeh, A. Unmanned-Aircraft-System-Assisted Early Wildfire Detection with Air Quality Sensors. Electronics 2023, 12, 1239. https://doi.org/10.3390/electronics12051239
Rjoub D, Alsharoa A, Masadeh A. Unmanned-Aircraft-System-Assisted Early Wildfire Detection with Air Quality Sensors. Electronics. 2023; 12(5):1239. https://doi.org/10.3390/electronics12051239
Chicago/Turabian StyleRjoub, Doaa, Ahmad Alsharoa, and Ala’eddin Masadeh. 2023. "Unmanned-Aircraft-System-Assisted Early Wildfire Detection with Air Quality Sensors" Electronics 12, no. 5: 1239. https://doi.org/10.3390/electronics12051239
APA StyleRjoub, D., Alsharoa, A., & Masadeh, A. (2023). Unmanned-Aircraft-System-Assisted Early Wildfire Detection with Air Quality Sensors. Electronics, 12(5), 1239. https://doi.org/10.3390/electronics12051239









