Downlink Spectral Efficiency of Massive MIMO Systems with Mutual Coupling
Abstract
:1. Introduction
- As for the mutual coupling effect modeling, in contrast to the S-parameter-based method in [14] and the simulation plus impedance matrix-based in [23], which are highly reliant on the specific antenna array design and modeling, the impedance matrix-based method chosen in this paper can be utilized to perform the theoretical performance analysis of massive MIMO systems. In that case, closed-form expressions of SINRs can be driven. In addition, the MC effect modeling method in this paper is more realistic and flexible than the statistical distribution-based method in [24], which cannot evaluate the mutual coupling effect on system performance as a function of different antenna array configuration parameters, such as the number of antenna elements and inter-element spacing.
- In contrast to [14,16,23], the closed-form SINR expressions and corresponding lower bound of channel capacity is obtained based on the impedance matrix-based mutual coupling effect modeling. Especially, we give the closed-form SINR expression for maximal ratio transmission (MRT) combining based on the MMSE estimator.
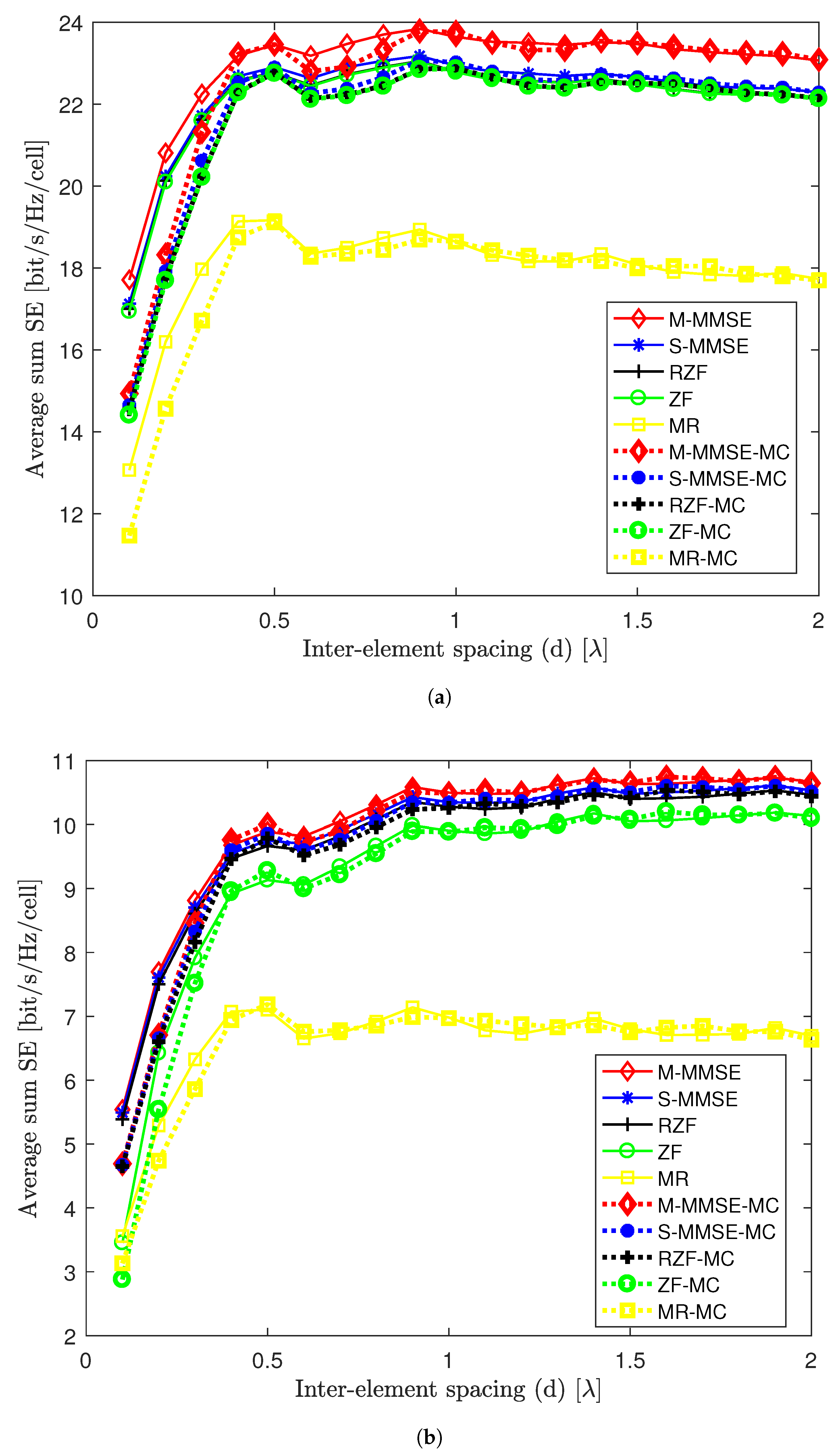
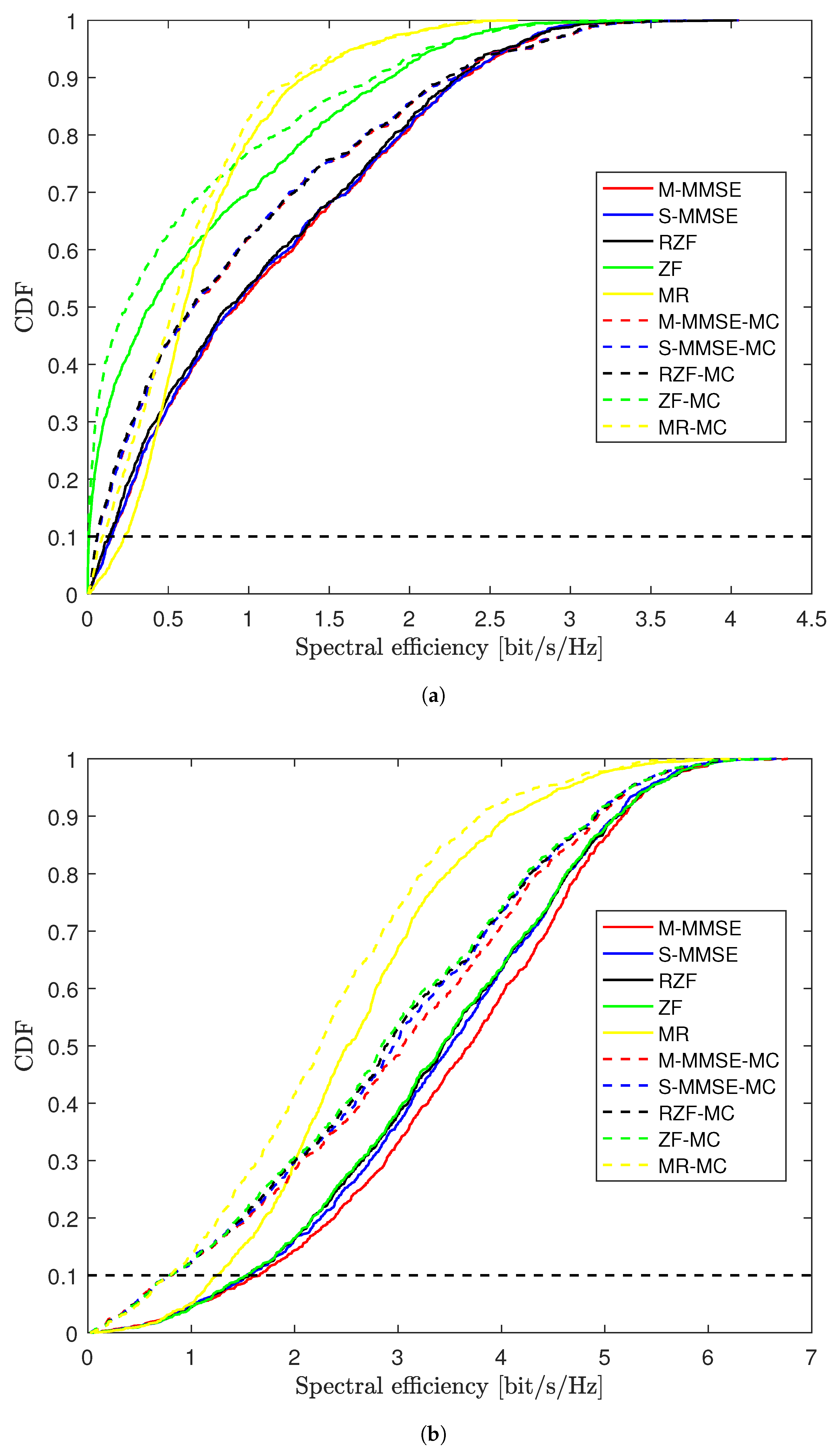
- In contrast to other previous works, a simulation performance comparison between MRT, zero-forcing (ZF), regularize ZF (RZF), single-cell minimum mean-squared error (S-MMSE), and multicell minimum mean-squared error (M-MMSE) precoding schemes are also carried out. The simulation results in this paper show the relative sensitivity of these precoders to the mutual coupling effect, which draws important technical insight and meaningful guidelines for the massive MIMO system design in practical scenarios.
2. System Model
2.1. Channel Model with Transmit Correlation
2.2. Mutual Coupling Model
2.2.1. Theoretical Approximation Based Mutual Coupling Matrix
2.2.2. S-Parameter-Based Mutual Coupling Matrix
2.3. Spatial Correlation with Mutual Coupling Effect
3. Channel Estimation
4. Downlink Spectral Efficiency and Transmit Precoding
5. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Björnson, E.; Matthaiou, M.; Ng, D.W.K.; Yang, H.; Love, D.J. Prospective multiple antenna technologies for beyond 5G. IEEE J. Sel. Areas Commun. 2020, 38, 1637–1660. [Google Scholar] [CrossRef]
- Shao, Z.; Yan, W.; Yuan, X. Markovian Cascaded Channel Estimation for RIS Aided Massive MIMO Using 1-Bit ADCs and Oversampling. ZTE Commun. 2022, 20, 48–56. [Google Scholar]
- Zhang, J.; Dai, L.; Li, X.; Liu, Y.; Hanzo, L. On low-resolution ADCs in practical 5G millimeter-wave massive MIMO systems. IEEE Commun. Mag. 2018, 56, 205–211. [Google Scholar] [CrossRef] [Green Version]
- Manteuffel, D.; Lin, F.H.; Li, T.; Peitzmeier, N.; Chen, Z.N. Characteristic Mode-Inspired Advanced Multiple Antennas: Intuitive insight into element-, interelement-, and array levels of compact large arrays and metantennas. IEEE Antennas Propag. Mag. 2022, 64, 49–57. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, S.; Li, Q. A review of mutual coupling in MIMO systems. IEEE Access 2018, 6, 24706–24719. [Google Scholar] [CrossRef]
- Chang, M.; Han, J.; Ma, X.; Xue, H.; WU, X.; Li, L.; Cui, T. Programmable Metasurface for Simultaneously Wireless Information and Power Transfer System. ZTE Commun. 2022, 20, 48–62. [Google Scholar]
- Hassan, S.u.; Mir, T.; Alamri, S.; Khan, N.A.; Mir, U. Machine Learning-Inspired Hybrid Precoding for HAP Massive MIMO Systems with Limited RF Chains. Electronics 2023, 12, 893. [Google Scholar] [CrossRef]
- Kassam, J.; Castanheira, D.; Silva, A.; Dinis, R.; Gameiro, A. A Review on Cell-Free Massive MIMO Systems. Electronics 2023, 12, 1001. [Google Scholar] [CrossRef]
- Clerckx, B.; Craeye, C.; Vanhoenacker-Janvier, D.; Oestges, C. Impact of Antenna Coupling on 2 × 2 MIMO Communications. IEEE Trans. Veh. Technol. 2007, 56, 1009–1018. [Google Scholar] [CrossRef]
- Masouros, C.; Sellathurai, M.; Ratnarajah, T. Large-Scale MIMO Transmitters in Fixed Physical Spaces: The Effect of Transmit Correlation and Mutual Coupling. IEEE Trans. Commun. 2013, 61, 2794–2804. [Google Scholar] [CrossRef]
- Neil, C.T.; Garcia-Rodriguez, A.; Smith, P.J.; Dmochowski, P.A.; Masouros, C.; Shafi, M. On the Performance of Spatially Correlated Large Antenna Arrays for Millimeter-Wave Frequencies. IEEE Trans. Antennas Propag. 2018, 66, 132–148. [Google Scholar] [CrossRef]
- Biswas, S.; Masouros, C.; Ratnarajah, T. Performance Analysis of Large Multiuser MIMO Systems With Space-Constrained 2-D Antenna Arrays. IEEE Trans. Wirel. Commun. 2016, 15, 3492–3505. [Google Scholar] [CrossRef] [Green Version]
- Gustafsson, M.; Aulin, J.; Högberg, M.; Alm, M.; Sihlbom, B. Impact of mutual coupling on capacity in large MIMO antenna arrays. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014; pp. 2723–2727. [Google Scholar] [CrossRef]
- Pfeiffer, C.; Dagefu, F.; Tomasic, B.; Twigg, J.N.; Wu, B.I. Virtual Impedance Method for Mutual Coupling Compensation. IEEE Trans. Antennas Propag. 2021, 69, 4569–4579. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, Y. Deep Learning-Based Mutual Coupling Modeling and Baseband Decoupling Algorithm for MIMO Systems. IEEE Commun. Lett. 2020, 24, 1986–1990. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Björnson, E.; Ai, B. Local partial zero-forcing combining for cell-free massive MIMO systems. IEEE Trans. Commun. 2021, 69, 8459–8473. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, R.; Chen, H.; Qin, Y.; Jin, M. Real-Valued DOA Estimation Utilizing Enhanced Covariance Matrix With Unknown Mutual Coupling. IEEE Commun. Lett. 2022, 26, 912–916. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, X.; Pedersen, G.F. Mutual Coupling Suppression With Decoupling Ground for Massive MIMO Antenna Arrays. IEEE Trans. Veh. Technol. 2019, 68, 7273–7282. [Google Scholar] [CrossRef]
- Chen, K.H.; Kiang, J.F. Effect of mutual coupling on the channel capacity of MIMO systems. IEEE Trans. Veh. Technol. 2015, 65, 398–403. [Google Scholar] [CrossRef]
- Wei, H.; Wang, D.; Zhu, H.; Wang, J.; Sun, S.; You, X. Mutual Coupling Calibration for Multiuser Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2016, 15, 606–619. [Google Scholar] [CrossRef]
- Ge, X.; Zi, R.; Wang, H.; Zhang, J.; Jo, M. Multi-User Massive MIMO Communication Systems Based on Irregular Antenna Arrays. IEEE Trans. Wirel. Commun. 2016, 15, 5287–5301. [Google Scholar] [CrossRef] [Green Version]
- Amani, N.; Wymeersch, H.; Johannsen, U.; Smolders, A.B.; Ivashina, M.V.; Maaskant, R. Multi-Panel Sparse Base Station Design With Physical Antenna Effects in Massive MU-MIMO. IEEE Trans. Veh. Technol. 2020, 69, 6500–6510. [Google Scholar] [CrossRef] [Green Version]
- Raeesi, O.; Gokceoglu, A.; Zou, Y.; Björnson, E.; Valkama, M. Performance Analysis of Multi-User Massive MIMO Downlink Under Channel Non-Reciprocity and Imperfect CSI. IEEE Trans. Commun. 2018, 66, 2456–2471. [Google Scholar] [CrossRef] [Green Version]
- Bjornson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO Networks Spectral, Energy, and Hardware Efficiency. In Foundations and Trends® in Signal Processing; Weizmann Institute: Rehovot, Israel, 2017; Volume 11, pp. 154–655. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2016. [Google Scholar]
- Ngo, H.Q.; Larsson, E.G. No Downlink Pilots Are Needed in TDD Massive MIMO. IEEE Trans. Wirel. Commun. 2017, 16, 2921–2935. [Google Scholar] [CrossRef] [Green Version]
- Hoydis, J.; ten Brink, S.; Debbah, M. Massive MIMO in the UL/DL of Cellular Networks: How Many Antennas Do We Need? IEEE J. Sel. Areas Commun. 2013, 31, 160–171. [Google Scholar] [CrossRef] [Green Version]
- Jose, J.; Ashikhmin, A.; Marzetta, T.L.; Vishwanath, S. Pilot Contamination and Precoding in Multi-Cell TDD Systems. IEEE Trans. Wirel. Commun. 2011, 10, 2640–2651. [Google Scholar] [CrossRef] [Green Version]




| MC Effect Ref. | MC Effect Modeling Method | Precoding Schemes | Closed-Form Expressions | Multi-User | Multi-Cell |
|---|---|---|---|---|---|
| [12] | Impedance matrix-based | HBF | Covered | Single user | Single cell |
| [13] | Impedance matrix-based | ZF and MRT | Covered | Multi-user | Single cell |
| [14] | S-parameter-based | Not covered | Not covered | Single user | Single cell |
| [23] | Simulation plus impedance matrix-based | ZF | Not covered | Multi-user | Single cell |
| [24] | Statistical distribution-based | ZF and MRT | Covered | Multi-user | Single cell |
| [16] | Deep learning-based | HBF | Not covered | Single user | Single cell |
| Our work | Impedance matrix-based | MRT, ZF, RZF, S-MMSE, M-MMSE | Covered | Multi-user | Multi-cell |
| Symbols | Parameters | Values |
|---|---|---|
| Carrier frequency | 2 GHz | |
| B | System Bandwidth | 200 MHz |
| ASD | angular standard deviation | 10 |
| M | the number of cells | 4 |
| K | the number of UEs | 5 |
| Transmit power per UE | 20 dBm | |
| Background noise density | −174 dBm/Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ai, B.; Zhang, J. Downlink Spectral Efficiency of Massive MIMO Systems with Mutual Coupling. Electronics 2023, 12, 1364. https://doi.org/10.3390/electronics12061364
Liu Y, Ai B, Zhang J. Downlink Spectral Efficiency of Massive MIMO Systems with Mutual Coupling. Electronics. 2023; 12(6):1364. https://doi.org/10.3390/electronics12061364
Chicago/Turabian StyleLiu, Yiru, Bo Ai, and Jiayi Zhang. 2023. "Downlink Spectral Efficiency of Massive MIMO Systems with Mutual Coupling" Electronics 12, no. 6: 1364. https://doi.org/10.3390/electronics12061364
APA StyleLiu, Y., Ai, B., & Zhang, J. (2023). Downlink Spectral Efficiency of Massive MIMO Systems with Mutual Coupling. Electronics, 12(6), 1364. https://doi.org/10.3390/electronics12061364







