URNet: An UNet-Based Model with Residual Mechanism for Monocular Depth Estimation
Abstract
:1. Introduction
- Supervised monocular depth estimation: The ultimate objective of supervised learning is to determine the relationship between the RGB (red–green–blue) image and depth map from the public RGB-D (red–green–blue depth) datasets, such as the KITTI dataset [9] and the NYU V2 dataset [10]. Several researchers have focused on and achieved great success with this technique. Eigen et al. [11] proposed the architectures of coarse-to-fine network and applied the concept of scale-invariant error to measure depth relations to significantly improve depth prediction performance. Fu et al. [12] proposed the spacing-increasing discretization (SID) method to save time and cost. Particualrly, the elimination of the sub-sampling layers and the incorporation of the dilated convolution enable SID to reduce cost and training time and improve accuracy. Teed et al. [13] proposed a DeepV2D model, which estimates monocular degrees on video by combining two classical geometric algorithms in an end-to-end architecture. Hence, DeepV2D needs additional information to produce its depth map.
- Self-supervised monocular depth estimation: Since the depth label is not required for the training procedure, data preparation and reprocessing can be reduced or eliminated. Thus it can save considerable time and energy in the training procedure. In the field of monocular depth estimation, self-supervised learning has gained popularity and made significant advancements. Godard et al. [14] proposed a flexible architecture, which can address the issue of dynamic object of self-supervised learning. They conceptualized, crafted, and enhanced the automatic mask loss and reprojection loss. Next, to improve the accuracy of depth prediction at the boundaries, Wong et al. [15] implemented the concept of residual-based adaptive weight and bilateral cyclic consistency constraint. Ling et al. [16] developed a model of deep learning for completion of monocular depth, which is incorporated with the attention block. To enhance the capabilities of the network, they also designed the notion of multi-warp loss for monocular depth estimation.
- We propose URNet, a novel model for monocular depth estimation based on the traditional UNet model and residual blocks. More specifically, we use the attention and ASPP (atrous spatial pyramid pooling) blocks to improve the prediction performance.
- We evaluate the performance of our URNet via the KITTI dataset and compare it with several existing researches.
2. Related Work
3. Our URNet
- Modifying the UNet-based nodes with the residual blocks.
- Adding connections between the encoder and decoder.
- Adding the attention blocks to the decoder.
- Utilizing the ASPP block to replace transfer blocks.
- Attention blocks: Natural language processing is the main area where the attention mechanism has been utilized [45,46,47]. Recently, it has also been used in depth estimation tasks, such as pixel-wise prediction [48,49,50]. The attention blocks are responsible for focusing and extracting additional features. Therefore, the implementation of attention blocks facilitates the enhancement of performance of our model. Because of the effectiveness of the attention blocks, in both the topics of natural language processing and computer vision, we decided to include the design of attention blocks in the decoder part of our architecture. This helps us to zero in on the most crucial aspects of the feature maps. More specifically, our attention blocks are composed of three smaller blocks, shown in Figure 3a. The first block receives the input from the encoder, and the second block receives the input from the decoder. Then, the outputs of the above two blocks will be concatenated as the input for the third block. Finally, the result will be the multiplication of the outputs of the third block and the second block.
- Atrous spatial pyramid pooling (ASPP): Chen et al. [51] came up with the idea of ASPP. Because of its benefits, ASPP has been used more in the topics of segmentation and depth prediction in the past few years [33,42,52]. The authors in [33] suggested a novel algorithm, called DenseASPP, for densely connected atrous spatial pyramid pooling. The blocks accept scales of various sizes, including larger and smaller sizes. In our model, the ASPP is used to extract multiple rates of network endpoint and transfer node characteristics. More specifically, our ASPP block is composed of three smaller blocks. Each block is comprised of the convolution, ReLU activation, and Batch normalization (Figure 3b), where the dilation parameters in the convolution layers of three blocks are set to 1, 2, and 3, respectively. Finally, the outputs of three blocks are concatenated and then subjected to the convolution.
4. Experiments and Results
4.1. Dataset
4.2. Detailed Settings
- Epochs: 50.
- Batch size: 4.
- Optimizer: AdamW [54].
- Values of power and momentum: 0.90 and 0.999.
- Values of weight decay: 0.0005 (encode) and 0 (decode).
- Values of learning rate: (initially) and (finally).
4.3. Evaluation Metrics
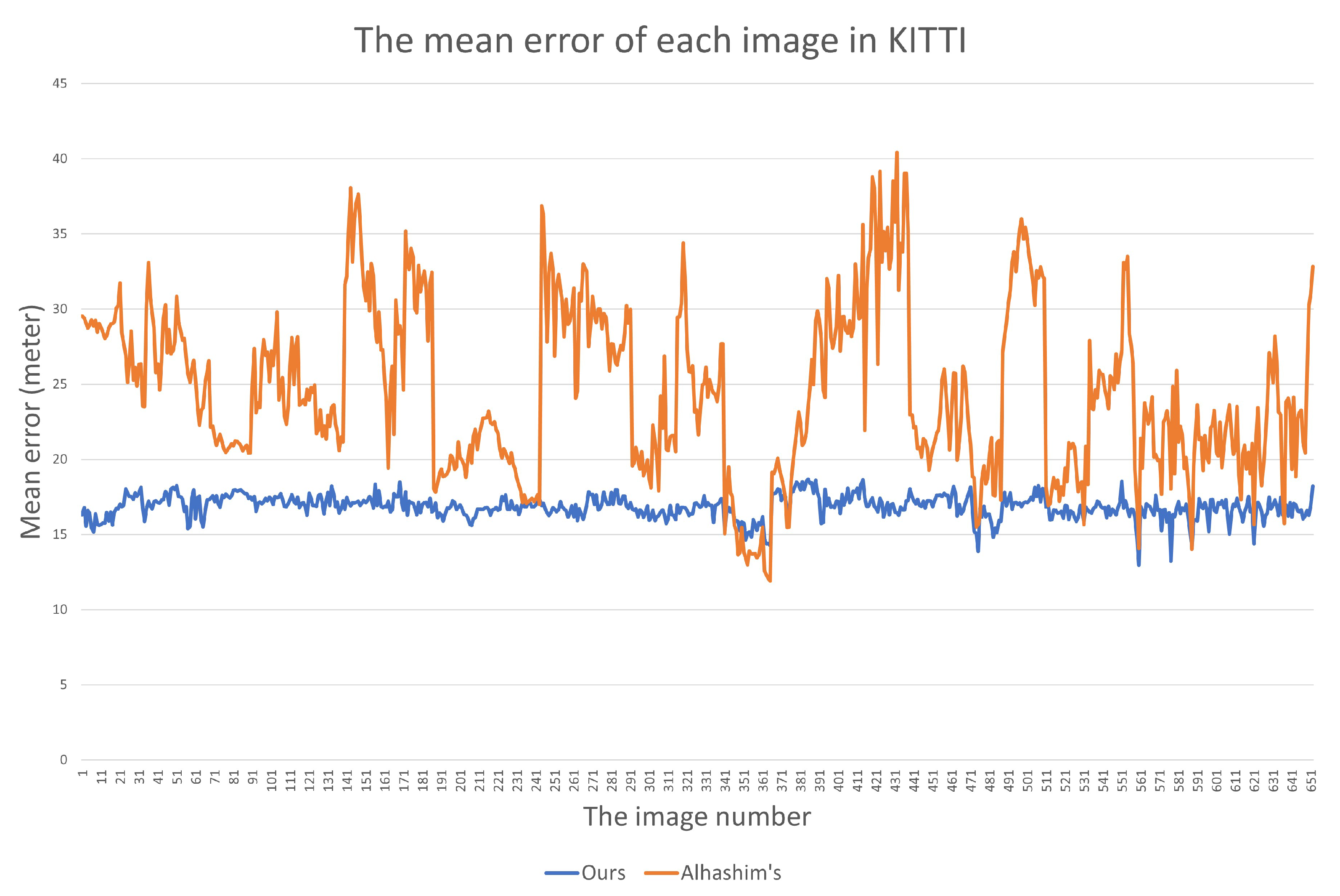
4.4. Depth Estimation Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bertels, M.; Jutzi, B.; Ulrich, M. Automatic Real-Time Pose Estimation of Machinery from Images. Sensors 2022, 22, 2627. [Google Scholar] [CrossRef] [PubMed]
- Avinash, A.; Abdelaal, A.E.; Salcudean, S.E. Evaluation of increasing camera baseline on depth perception in surgical robotics. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5509–5515. [Google Scholar]
- Chuah, W.; Tennakoon, R.; Hoseinnezhad, R.; Bab-Hadiashar, A. Deep learning-based incorporation of planar constraints for robust stereo depth estimation in autonomous vehicle applications. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6654–6665. [Google Scholar] [CrossRef]
- Scharstein, D.; Pal, C. Learning conditional random fields for stereo. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Xu, D.; Wang, W.; Tang, H.; Liu, H.; Sebe, N.; Ricci, E. Structured attention guided convolutional neural fields for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3917–3925. [Google Scholar]
- Kuznietsov, Y.; Stuckler, J.; Leibe, B. Semi-supervised deep learning for monocular depth map prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6647–6655. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Brostow, G. Unsupervised monocular depth estimation with left-right consistency. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6602–6611. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the European Conference on Computer Vision, Berlin, Germany, 7–13 October 2012; pp. 746–760. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth Map Prediction from a Single Image using a Multi-Scale Deep Network. Adv. Neural Inf. Process. Syst. 2014, 3, 2366–2374. [Google Scholar]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep ordinal regression network for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2002–2011. [Google Scholar]
- Teed, Z.; Deng, J. Deepv2d: Video to depth with differentiable structure from motion. arXiv 2018, arXiv:1812.04605. [Google Scholar]
- Godard, C.; Aodha, O.M.; Firman, M.; Brostow, G. Digging into self-supervised monocular depth estimation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 Octtober–2 November 2019; Volume 2019, pp. 3827–3837. [Google Scholar] [CrossRef] [Green Version]
- Wong, A.; Soatto, S. Bilateral cyclic constraint and adaptive regularization for unsupervised monocular depth prediction. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 5637–5646. [Google Scholar] [CrossRef] [Green Version]
- Ling, C.; Zhang, X.; Chen, H. Unsupervised Monocular Depth Estimation Using Attention and Multi-Warp Reconstruction. IEEE Trans. Multimed. 2022, 24, 2938–2949. [Google Scholar] [CrossRef]
- Tran, S.T.; Cheng, C.H.; Nguyen, T.T.; Le, M.H.; Liu, D.G. TMD-Unet: Triple-Unet with multi-scale input features and dense skip connection for medical image segmentation. Healthcare 2021, 9, 54. [Google Scholar] [CrossRef]
- Tran, S.T.; Cheng, C.H.; Liu, D.G. A multiple layer U-Net, U n-Net, for liver and liver tumor segmentation in CT. IEEE Access 2020, 9, 3752–3764. [Google Scholar] [CrossRef]
- Tran, S.T.; Nguyen, T.T.; Le, M.H.; Cheng, C.H.; Liu, D.G. TDC-Unet: Triple Unet with Dilated Convolution for Medical Image Segmentation. Int. J. Pharma Med. Biol. Sci. 2022, 11, 1–7. [Google Scholar] [CrossRef]
- Isensee, F.; Petersen, J.; Klein, A.; Zimmerer, D.; Jaeger, P.F.; Kohl, S.; Wasserthal, J.; Koehler, G.; Norajitra, T.; Wirkert, S.; et al. nnu-net: Self-adapting framework for u-net-based medical image segmentation. arXiv Preprint 2018, arXiv:1809.10486. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. arXiv Preprint 2021, arXiv:2105.05537. [Google Scholar]
- Yang, Y.; Wang, Y.; Zhu, C.; Zhu, M.; Sun, H.; Yan, T. Mixed-Scale Unet Based on Dense Atrous Pyramid for Monocular Depth Estimation. IEEE Access 2021, 9, 114070–114084. [Google Scholar] [CrossRef]
- Choudhary, R.; Sharma, M.; Anil, R. 2T-UNET: A Two-Tower UNet with Depth Clues for Robust Stereo Depth Estimation. arXiv Preprint 2022, arXiv:2210.15374. [Google Scholar]
- Zhao, T.; Pan, S.; He, X. ResUnet++ for Sparse Samples-based Depth Prediction. In Proceedings of the 2021 IEEE 15th International Conference on Electronic Measurement & Instruments (ICEMI), Harbin, China, 9–11 August 2021; pp. 242–246. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper depth prediction with fully convolutional residual networks. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 239–248. [Google Scholar]
- Torralba, A.; Oliva, A. Depth estimation from image structure. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1226–1238. [Google Scholar] [CrossRef] [Green Version]
- Saxena, A.; Sun, M.; Ng, A.Y. Make3d: Learning 3d scene structure from a single still image. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 824–840. [Google Scholar] [CrossRef] [Green Version]
- Karsch, K.; Liu, C.; Kang, S.B. Depth extraction from video using non-parametric sampling. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 775–788. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar] [CrossRef] [Green Version]
- Watson, J.; Firman, M.; Brostow, G.J.; Turmukhambetov, D. Self-Supervised Monocular Depth Hints. arXiv Preprint 2019, arXiv:arXiv.1909.09051. [Google Scholar]
- Tosi, F.; Aleotti, F.; Poggi, M.; Mattoccia, S. Learning Monocular Depth Estimation Infusing Traditional Stereo Knowledge. arXiv 2019, arXiv:1904.04144. [Google Scholar]
- Yang, M.; Yu, K.; Zhang, C.; Li, Z.; Yang, K. Denseaspp for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3684–3692. [Google Scholar]
- Ye, X.; Fan, X.; Zhang, M.; Xu, R.; Zhong, W. Unsupervised Monocular Depth Estimation via Recursive Stereo Distillation. IEEE Trans. Image Process. 2021, 30, 4492–4504. [Google Scholar] [CrossRef]
- Liu, J.; Li, Q.; Cao, R.; Tang, W.; Qiu, G. MiniNet: An extremely lightweight convolutional neural network for real-time unsupervised monocular depth estimation. Isprs J. Photogramm. Remote. Sens. 2020, 166, 255–267. [Google Scholar] [CrossRef]
- Fang, Z.; Chen, X.; Chen, Y.; Gool, L.V. Towards good practice for cnn-based monocular depth estimation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 1091–1100. [Google Scholar]
- Ye, X.; Chen, S.; Xu, R. DPNet: Detail-preserving network for high quality monocular depth estimation. Pattern Recognit. 2021, 109, 107578. [Google Scholar] [CrossRef]
- Alhashim, I.; Wonka, P. High quality monocular depth estimation via transfer learning. arXiv 2018, arXiv:1812.11941. [Google Scholar]
- Gan, Y.; Xu, X.; Sun, W.; Lin, L. Monocular Depth Estimation with Affinity, Vertical Pooling, and Label Enhancement; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Xu, H.; Li, F. Multilevel Pyramid Network for Monocular Depth Estimation Based on Feature Refinement and Adaptive Fusion. Electronics 2022, 11, 2615. [Google Scholar] [CrossRef]
- Pei, M. MSFNet:Multi-scale features network for monocular depth estimation. arXiv 2021, arXiv:2107.06445. [Google Scholar]
- Lee, J.H.; Han, M.K.; Ko, D.W.; Suh, H. From Big to Small: Multi-Scale Local Planar Guidance for Monocular Depth Estimation. arXiv 2019, arXiv:1907.10326. [Google Scholar]
- Chen, P.Y.; Liu, A.H.; Liu, Y.C.; Wang, Y.C.F. Towards scene understanding: Unsupervised monocular depth estimation with semantic-aware representation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2619–2627. [Google Scholar] [CrossRef]
- Zhu, S.; Brazil, G.; Liu, X. The edge of depth: Explicit constraints between segmentation and depth. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13116–13125. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Hu, D. An introductory survey on attention mechanisms in NLP problems. In Proceedings of the SAI Intelligent Systems Conference, London, UK, 5–6 September 2019; pp. 432–448. [Google Scholar]
- Lei, S.; Yi, W.; Ying, C.; Ruibin, W. Review of attention mechanism in natural language processing. Data Anal. Knowl. Discov. 2020, 4, 1–14. [Google Scholar]
- Liu, P.; Zhang, Z.; Meng, Z.; Gao, N. Monocular depth estimation with joint attention feature distillation and wavelet-based loss function. Sensors 2021, 21, 54. [Google Scholar] [CrossRef]
- Chen, S.; Fan, X.; Pu, Z.; Ouyang, J.; Zou, B. Single image depth estimation based on sculpture strategy. Knowl.-Based Syst. 2022, 250, 109067. [Google Scholar] [CrossRef]
- Makarov, I.; Bakhanova, M.; Nikolenko, S.; Gerasimova, O. Self-supervised recurrent depth estimation with attention mechanisms. Peerj Comput. Sci. 2022, 8, e865. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [Green Version]
- Song, M.; Lim, S.; Kim, W. Monocular depth estimation using laplacian pyramid-based depth residuals. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4381–4393. [Google Scholar] [CrossRef]
- Imambi, S.; Prakash, K.B.; Kanagachidambaresan, G.R. Pytorch. In Programming with TensorFlow: Solution for Edge Computing Applications; Springer: Cham, Switzerland, 2021; pp. 87–104. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]





| Node | Encoder | Decoder |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| Tr |
| Methods | Type | RMSE | MRE | RMLSE | |||
|---|---|---|---|---|---|---|---|
| Godard et al. [14] | Stereo | 4.863 | 0.115 | 0.193 | 0.877 | 0.959 | 0.981 |
| Watson et al. [31] | Stereo | 4.695 | 0.106 | 0.193 | 0.875 | 0.958 | 0.980 |
| Wong et al. [15] | Stereo | 4.172 | 0.126 | 0.217 | 0.840 | 0.941 | 0.973 |
| Tosi et al. [32] | Stereo | 4.714 | 0.111 | 0.199 | 0.864 | 0.954 | 0.979 |
| Ling et al. [16] | Stereo | 5.206 | 0.121 | 0.214 | 0.843 | 0.944 | 0.975 |
| Ye et al. [37] | Stereo | 4.810 | 0.105 | 0.196 | 0.861 | 0.947 | 0.978 |
| Eigen et al. [30] | Depth | 7.156 | 0.190 | 0.246 | 0.692 | 0.899 | 0.967 |
| Liu et al. [35] | Depth | 4.977 | 0.127 | NR | 0.838 | 0.948 | 0.980 |
| Fang et al. [36] | Depth | 4.075 | 0.098 | 0.174 | 0.889 | 0.963 | 0.985 |
| Ye et al. [34] | Depth | 4.978 | 0.112 | 0.210 | 0.842 | 0.947 | 0.973 |
| Pei et al. [41] | Depth | 4.054 | 0.098 | NR | 0.893 | 0.968 | 0.987 |
| Alhashim et al. [38] | Depth | 4.170 | 0.093 | NR | 0.886 | 0.963 | 0.986 |
| Chen et al. [49] | Depth | 3.597 | 0.0955 | 0.159 | 0.893 | 0.970 | 0.989 |
| Gan et al. [39] | Depth | 3.933 | 0.098 | 0.173 | 0.890 | 0.964 | 0.985 |
| Xu et al. [40] | Depth | 3.842 | 0.092 | 0.185 | 0.895 | 0.974 | 0.990 |
| Our results (URNet) | Depth | 3.249 | 0.088 | 0.131 | 0.912 | 0.981 | 0.995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duong, H.-T.; Chen, H.-M.; Chang, C.-C. URNet: An UNet-Based Model with Residual Mechanism for Monocular Depth Estimation. Electronics 2023, 12, 1450. https://doi.org/10.3390/electronics12061450
Duong H-T, Chen H-M, Chang C-C. URNet: An UNet-Based Model with Residual Mechanism for Monocular Depth Estimation. Electronics. 2023; 12(6):1450. https://doi.org/10.3390/electronics12061450
Chicago/Turabian StyleDuong, Hoang-Thanh, Hsi-Min Chen, and Che-Cheng Chang. 2023. "URNet: An UNet-Based Model with Residual Mechanism for Monocular Depth Estimation" Electronics 12, no. 6: 1450. https://doi.org/10.3390/electronics12061450
APA StyleDuong, H.-T., Chen, H.-M., & Chang, C.-C. (2023). URNet: An UNet-Based Model with Residual Mechanism for Monocular Depth Estimation. Electronics, 12(6), 1450. https://doi.org/10.3390/electronics12061450








