Parameter Identification of Li-ion Batteries: A Comparative Study
Abstract
:1. Introduction
- Proposing seven dynamic generic battery models for lithium-ion batteries;
- Analyzing each model’s equation to see how each term affects the final fitted curve.
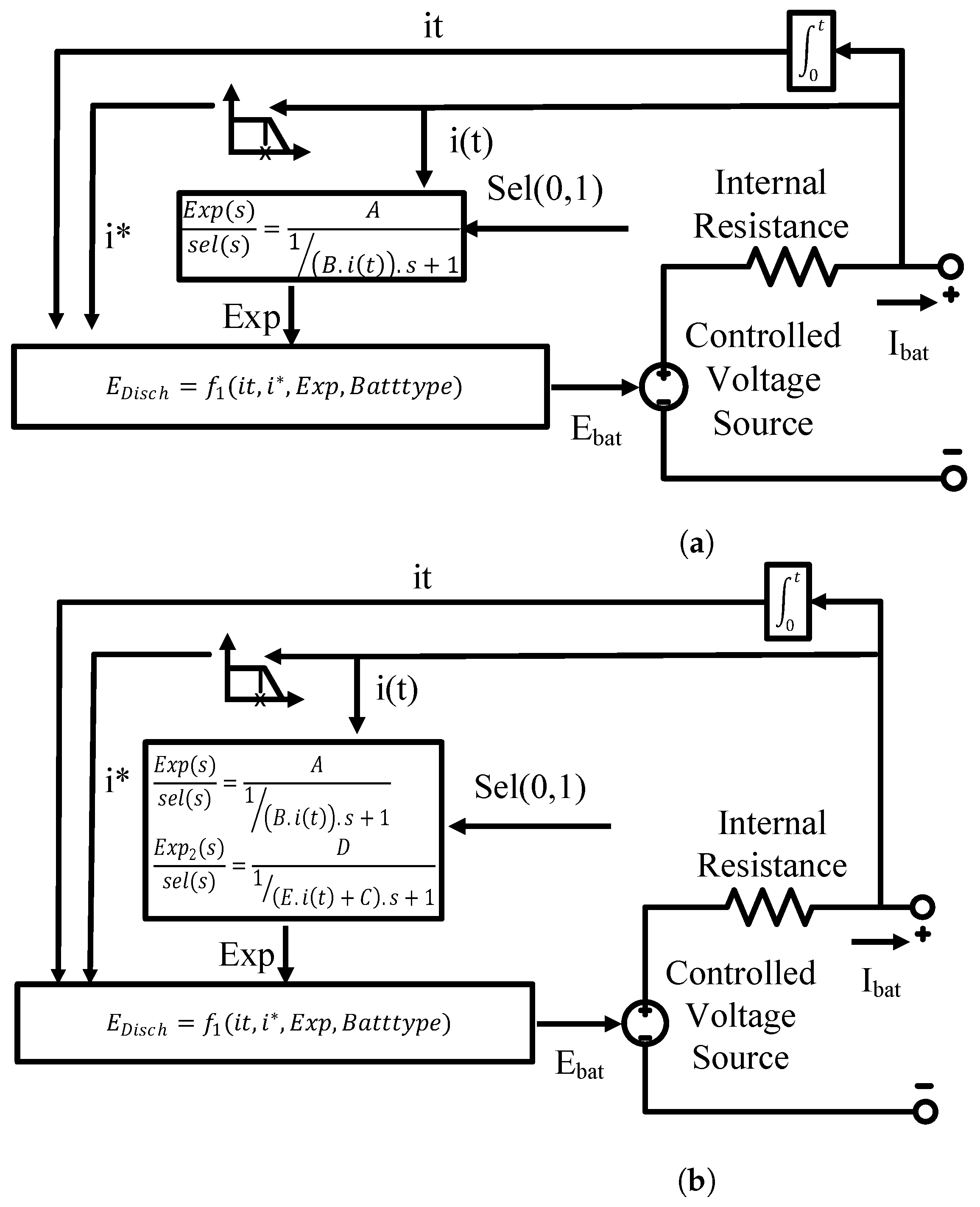
2. Generic Battery Model
2.1. Standard Generic Battery Model
2.2. Proposed Generic Battery Models
- Model 1 is the reference model, where it has 5 parameters only, which are , k, a, b, and q;
- Model 2 has the same equation as the reference model, except it has the k constant as two independent constants since they represent the polarization constant in V/Ah and the polarization resistance in , as witnessed in [15];
- Model 3 has as an additional term to the previous equation to consider the battery resistance;
- Model 4 has , and . It takes into account the aging effect on battery capacity and resistance;
- Model 5 adds term to the previous equation. It tries to find the polarization constant and resistance effects with the current battery capacity.
- Model 6 replaces the exponential term—in the previous equation—with a positive one;
- Model 7 adds the constant c to the positive exponential term;
- Model 8 has negative and positive exponential terms with the constant c.
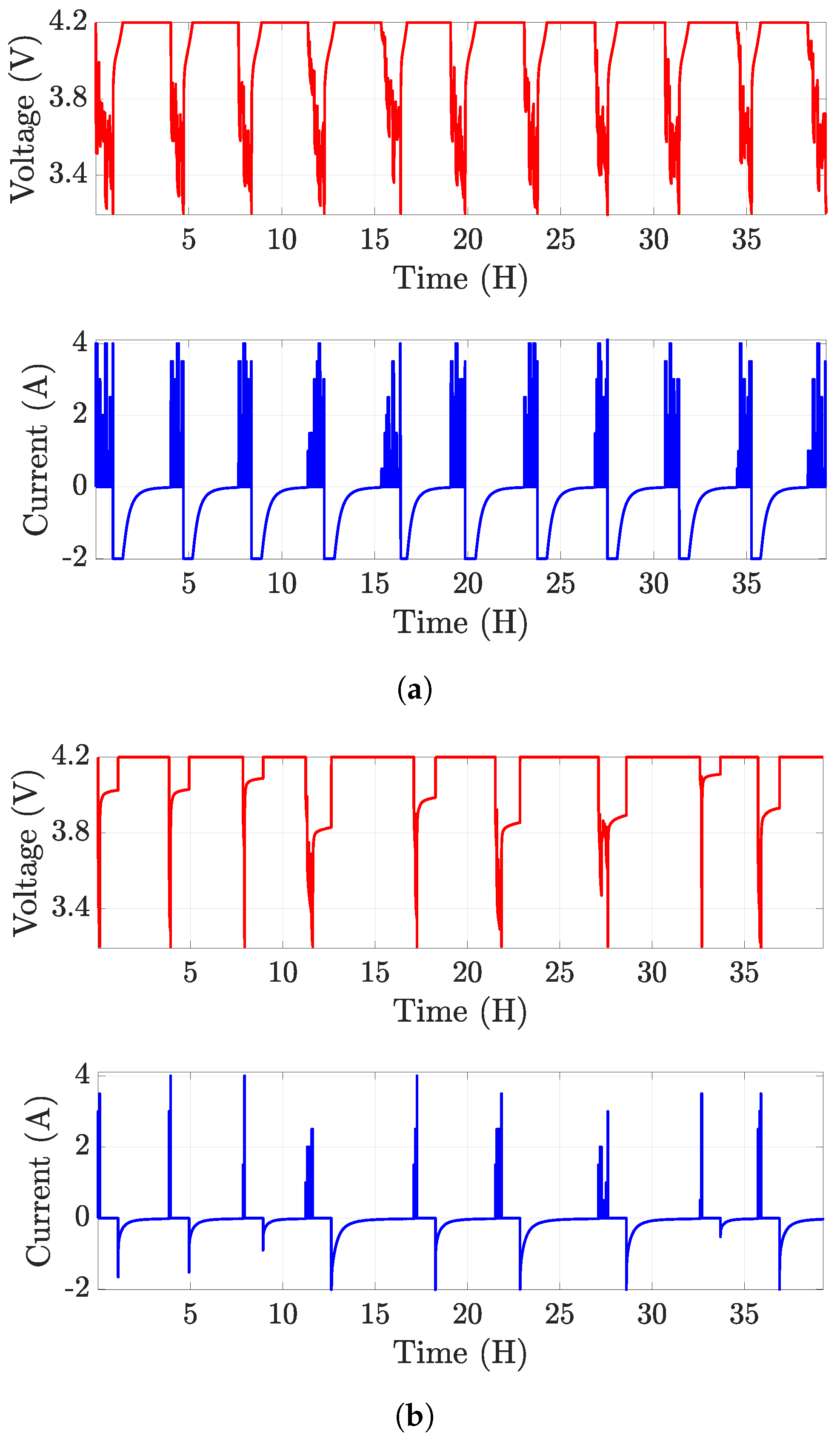
2.3. NASA Room Temperature Random Walk Discharging Datasets
2.4. Marine Predator Algorithm
2.5. Problem Formulation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thakur, A.K.; Prabakaran, R.; Elkadeem, M.; Sharshir, S.W.; Arıcı, M.; Wang, C.; Zhao, W.; Hwang, J.Y.; Saidur, R. A state of art review and future viewpoint on advance cooling techniques for Lithium–ion battery system of electric vehicles. J. Energy Storage 2020, 32, 101771. [Google Scholar] [CrossRef]
- Armand, M.; Tarascon, J. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar]
- Liu, Z.; He, H.; Xie, J.; Wang, K.; Huang, W. Self-discharge prediction method for lithium-ion batteries based on improved support vector machine. J. Energy Storage 2022, 55, 105571. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, B.; Li, Q.; Cartmell, S.; Ferrara, S.; Deng, Z.D.; Xiao, J. Lithium and lithium ion batteries for applications in microelectronic devices: A review. J. Power Sources 2015, 286, 330–345. [Google Scholar] [CrossRef] [Green Version]
- Allagui, A.; Freeborn, T.J.; Elwakil, A.S.; Fouda, M.E.; Maundy, B.J.; Radwan, A.G.; Said, Z.; Abdelkareem, M.A. Review of fractional-order electrical characterization of supercapacitors. J. Power Sources 2018, 400, 457–467. [Google Scholar] [CrossRef]
- AbdelAty, A.; Fouda, M.E.; Elbarawy, M.T.; Radwan, A. Optimal charging and discharging of supercapacitors. J. Electrochem. Soc. 2020, 167, 110521. [Google Scholar] [CrossRef]
- AbdelAty, A.; Fouda, M.; Elbarawy, M.; Attia, H.; Radwan, A. Parameter Identification of Flexible Supercapacitors with Fractional Cuckoo Search. In Proceedings of the IEEE 2020 32nd International Conference on Microelectronics (ICM), Aqaba, Jordan, 14–17 December 2020; pp. 1–4. [Google Scholar]
- Fouda, M.E.; Elwakil, A.S.; Allagui, A.; Rezk, H.; Nassef, A.M. Communication—Convolution-Based Estimation of Supercapacitor Parameters under Periodic Voltage Excitations. J. Electrochem. Soc. 2019, 166, A2267. [Google Scholar] [CrossRef]
- Fouda, M.; Elwakil, A.; Radwan, A.; Allagui, A. Power and energy analysis of fractional-order electrical energy storage devices. Energy 2016, 111, 785–792. [Google Scholar] [CrossRef]
- Jiang, Y.; Xia, B.; Zhao, X.; Nguyen, T.; Mi, C.; de Callafon, R.A. Data-based fractional differential models for non-linear dynamic modeling of a lithium-ion battery. Energy 2017, 135, 171–181. [Google Scholar] [CrossRef]
- Waag, W.; Käbitz, S.; Sauer, D.U. Application-specific parameterization of reduced order equivalent circuit battery models for improved accuracy at dynamic load. Measurement 2013, 46, 4085–4093. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.A. Experimental validation of a battery dynamic model for EV applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, T.; Ukyo, Y.; Novák, P. Memory effect in a lithium-ion battery. Nat. Mater. 2013, 12, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Romanenko, K.; Jerschow, A. Observation of memory effects associated with degradation of rechargeable lithium-ion cells using ultrafast surface-scan magnetic resonance imaging. J. Mater. Chem. A 2021, 9, 21078–21084. [Google Scholar] [CrossRef]
- Prieto, R.; Oliver, J.; Reglero, I.; Cobos, J. Generic battery model based on a parametric implementation. In Proceedings of the IEEE 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 603–607. [Google Scholar]
- Hannan, M.; Azidin, F.; Mohamed, A. Hybrid electric vehicles and their challenges: A review. Renew. Sustain. Energy Rev. 2014, 29, 135–150. [Google Scholar] [CrossRef]
- Song, D.; Sun, C.; Wang, Q.; Jang, D. A generic battery model and its parameter identification. Energy Power Eng. 2018, 10, 10. [Google Scholar] [CrossRef] [Green Version]
- Tremblay, O.; Dessaint, L.A.; Dekkiche, A.I. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar] [CrossRef]
- Scipioni, R.; Jørgensen, P.S.; Graves, C.; Hjelm, J.; Jensen, S.H. A physically-based equivalent circuit model for the impedance of a LiFePO4/graphite 26650 cylindrical cell. J. Electrochem. Soc. 2017, 164, A2017. [Google Scholar] [CrossRef] [Green Version]
- De Lima, A.B.; Salles, M.B.; Cardoso, J.R. State-of-charge estimation of a li-ion battery using deep forward neural networks. arXiv 2020, arXiv:2009.09543. [Google Scholar]
- Bhattacharjee, A.; Verma, A.; Mishra, S.; Saha, T.K. Estimating state of charge for xEV batteries using 1D convolutional neural networks and transfer learning. IEEE Trans. Veh. Technol. 2021, 70, 3123–3135. [Google Scholar] [CrossRef]
- Kollmeyer, P. Panasonic 18650pf li-ion battery data. Mendeley Data 2018, 1. [Google Scholar]
- Kollmeyer, P.; Vidal, C.; Naguib, M.; Skells, M. Lg 18650HG2 li-ion battery data and example deep neural network xEV SOC estimator script. Mendeley Data 2020, 3, 2020. [Google Scholar]
- Ely, J.J.; Koppen, S.V.; Nguyen, T.X.; Dudley, K.L.; Szatkowski, G.N.; Quach, C.C.; Vazquez, S.L.; Mielnik, J.J.; Hogge, E.F.; Hill, B.L.; et al. Radiated Emissions From a Remote-Controlled Airplane-Measured in a Reverberation Chamber; Technical report; 2011. Available online: https://ntrs.nasa.gov/api/citations/20110011513/downloads/20110011513.pdf (accessed on 1 March 2023).
- Hogge, E.F.; Bole, B.M.; Vazquez, S.L.; Celaya, J.R.; Strom, T.H.; Hill, B.L.; Smalling, K.M.; Quach, C.C. Verification of a remaining flying time prediction system for small electric aircraft. In Proceedings of the Annual Conference of the PHM Society, Coronado, CA, USA, 18–24 October 2015; Volume 7. [Google Scholar]
- Bole, B.; Kulkarni, C.; Daigle, M. Randomized battery usage data set. NASA AMES Progn. Data Repos. 2014, 70. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Yousri, D.; Babu, T.S.; Beshr, E.; Eteiba, M.B.; Allam, D. A Robust Strategy Based on Marine Predators Algorithm for Large Scale Photovoltaic Array Reconfiguration to Mitigate the Partial Shading Effect on the Performance of PV System. IEEE Access 2020, 8, 112407–112426. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A critical review of thermal issues in lithium-ion batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Bibin, C.; Vijayaram, M.; Suriya, V.; Ganesh, R.S.; Soundarraj, S. A review on thermal issues in Li-ion battery and recent advancements in battery thermal management system. Mater. Today Proc. 2020, 33, 116–128. [Google Scholar] [CrossRef]

| Model | Equations | Differences |
|---|---|---|
| 1. | Reference model. | |
| 2. | . | |
| 3. | term. | |
| 4. | . . | |
| 5. | . | |
| 6. | ||
| 7. | ||
| 8. |
| Model | Parameters | # Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Common | r | c | d | e | |||||||
| 1 | a b q | 5 | |||||||||
| 2 | ✓ | 6 | |||||||||
| 3 | ✓ | ✓ | 7 | ||||||||
| 4 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 11 | ||||
| 5 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 11 | ||||
| 6 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 11 | ||||
| 7 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 12 | |||
| 8 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 14 | |
| Model | Fitted Plot | ||||
|---|---|---|---|---|---|
| 1 | 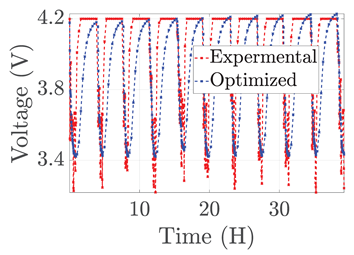 | 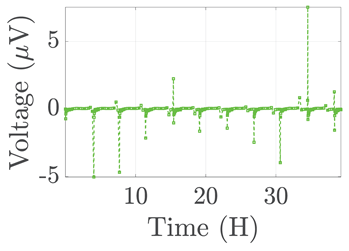 | 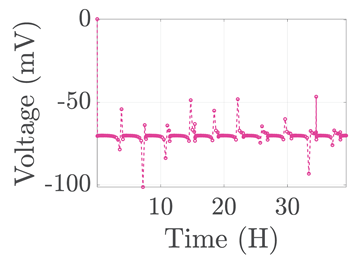 | ||
| 2 | 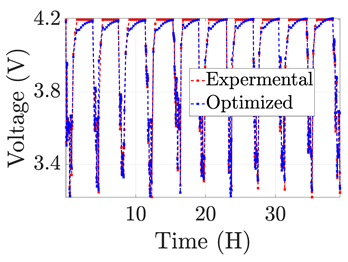 | 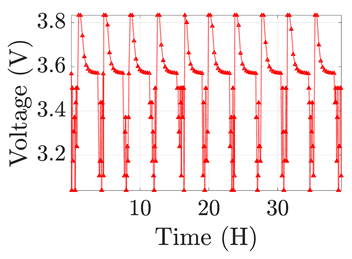 | 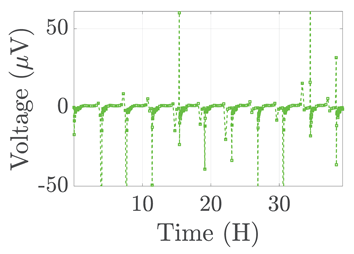 |  | |
| 3 | 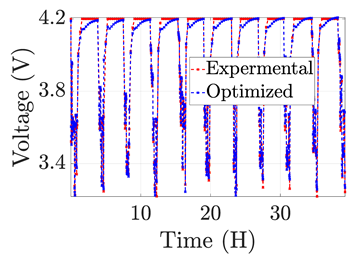 |  | 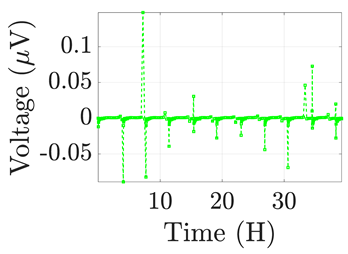 |  | |
| 4 | 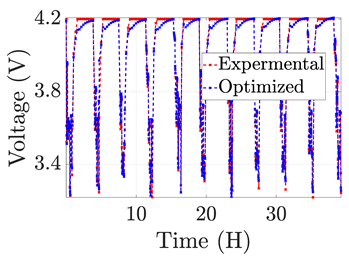 | 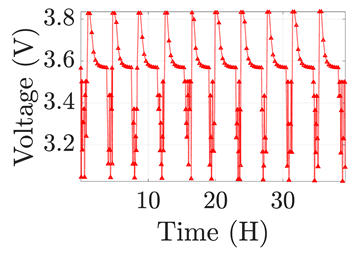 |  |  | |
| 5 | 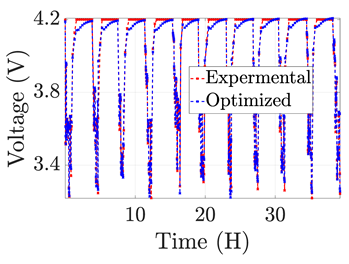 | 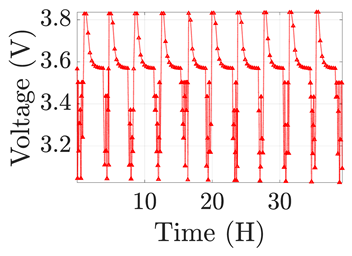 | 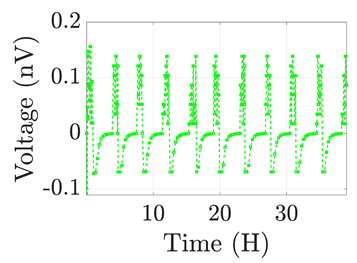 | 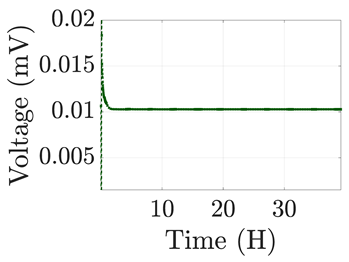 | 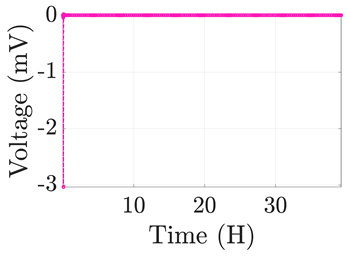 |
| 6 | 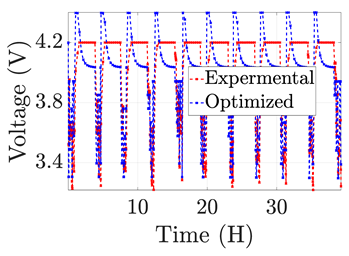 | 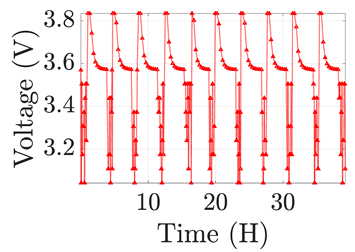 |  |  | 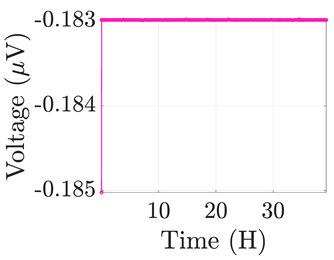 |
| 7 |  | 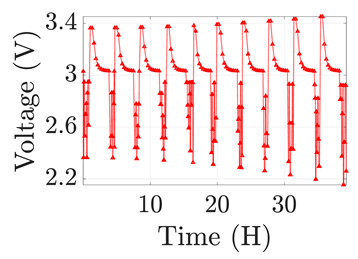 | 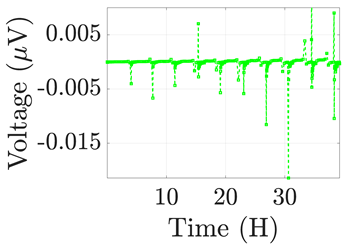 | 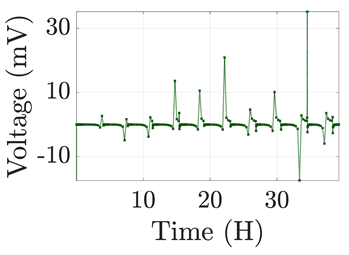 | 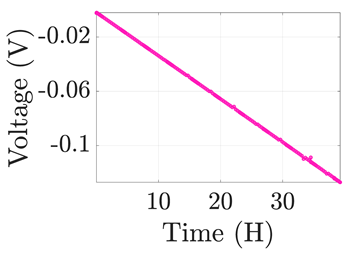 |
| 8 | 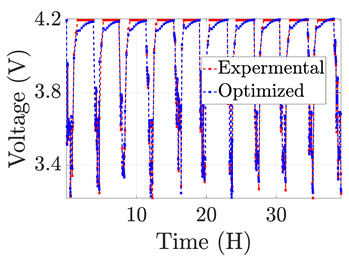 |  | 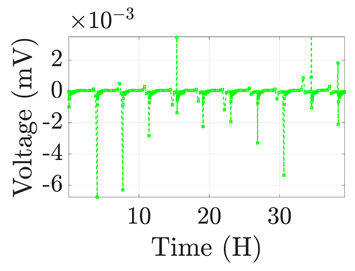 | 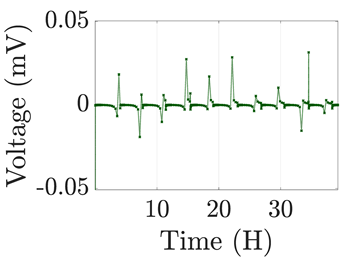 | 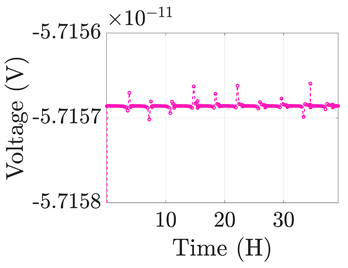 |
| Model | ||||
|---|---|---|---|---|
| 1 | 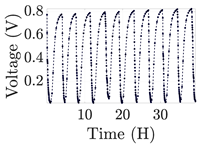 | |||
| 2 | 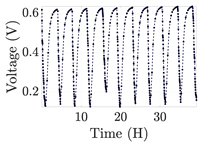 | |||
| 3 | 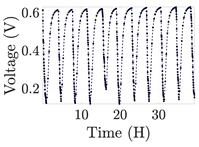 | |||
| 4 | 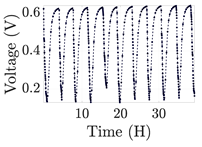 | |||
| 5 | 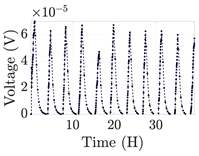 | |||
| 6 | 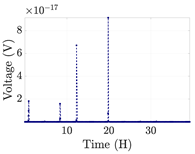 | |||
| 7 | 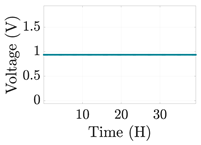 | |||
| 8 | 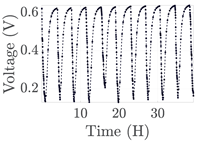 |  |
| Model | Fitted Plot | ||||
|---|---|---|---|---|---|
| 1 | 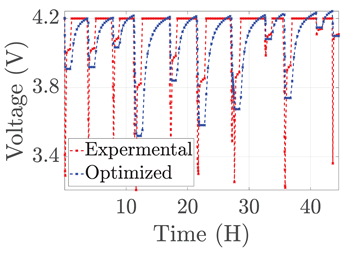 | 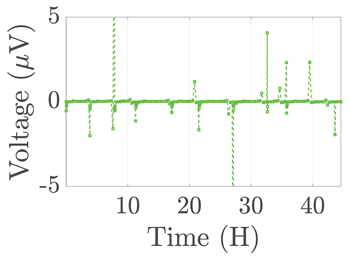 | 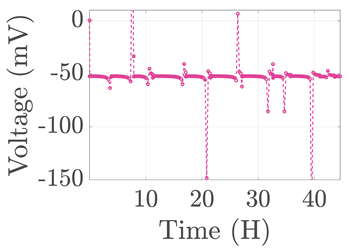 | ||
| 2 |  | 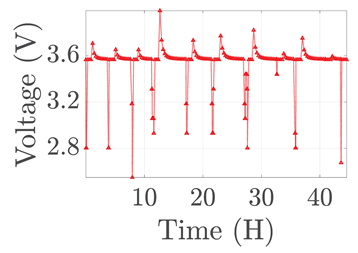 | 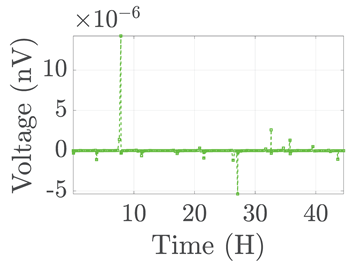 |  | |
| 3 |  | 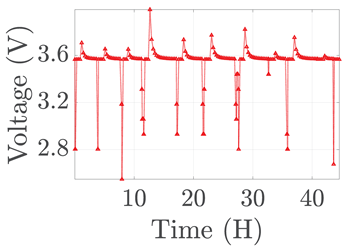 | 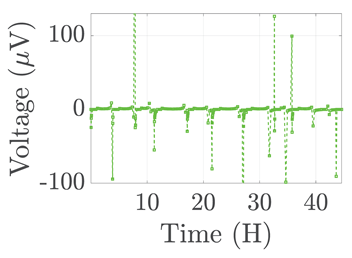 | 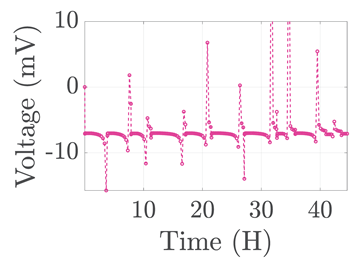 | |
| 4 |  | 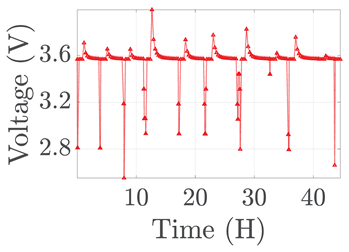 | 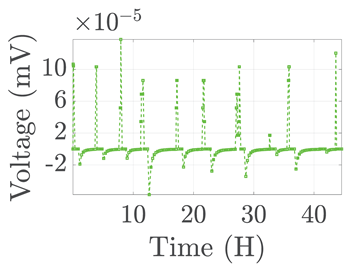 | 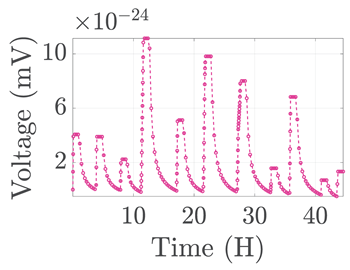 | |
| 5 | 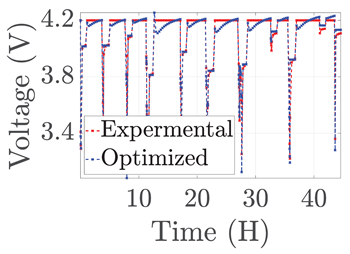 | 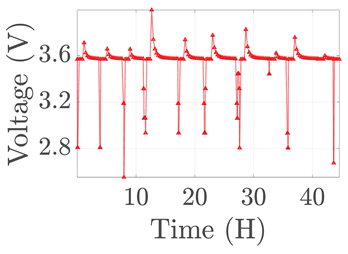 | 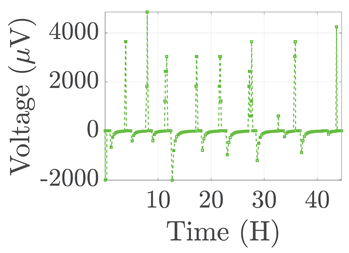 | 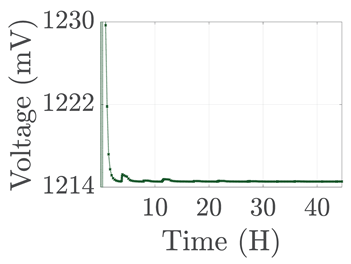 | 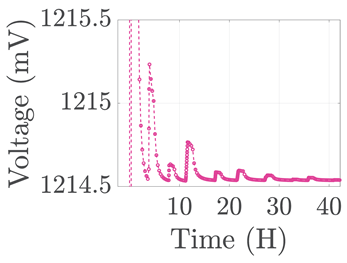 |
| 6 | 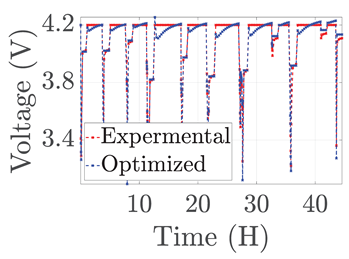 | 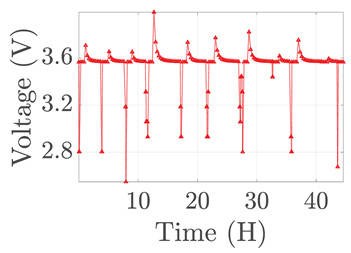 |  | 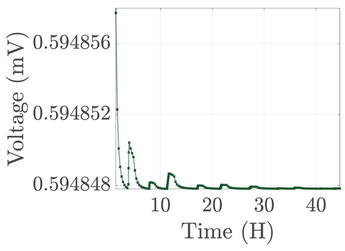 |  |
| 7 | 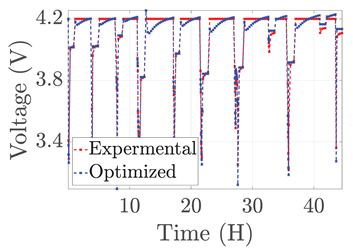 | 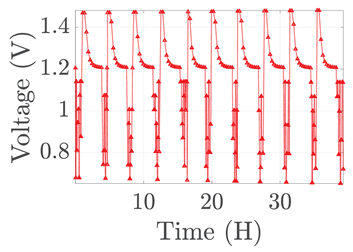 | 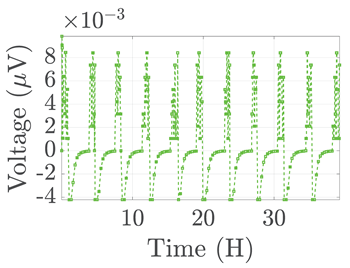 | 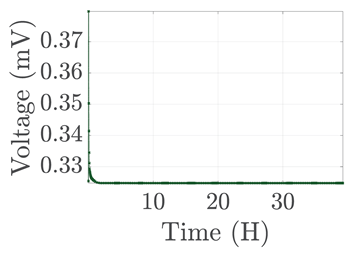 | 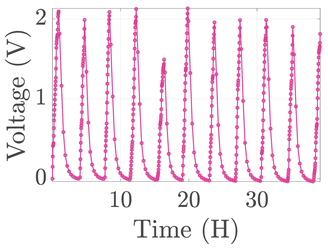 |
| 8 | 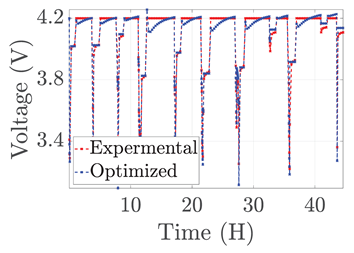 |  | 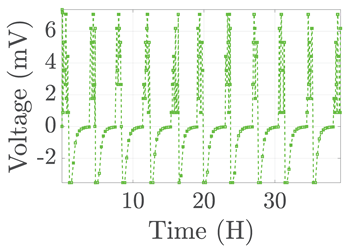 | 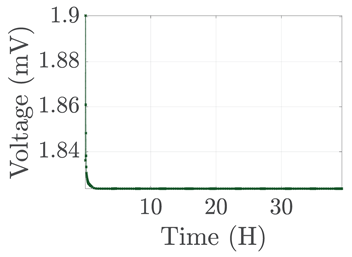 | 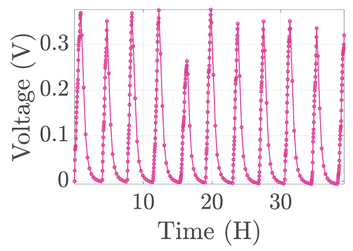 |
| Model | ||||
|---|---|---|---|---|
| 1 |  | |||
| 2 | 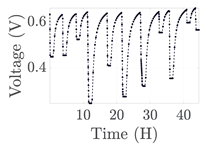 | |||
| 3 | 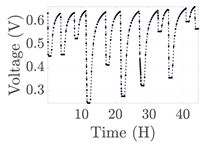 | |||
| 4 | 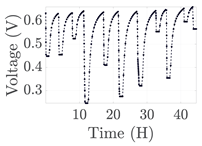 | |||
| 5 | 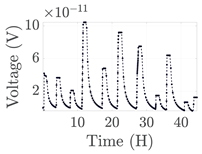 | |||
| 6 | 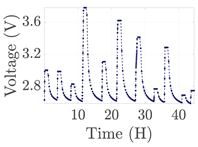 | |||
| 7 | 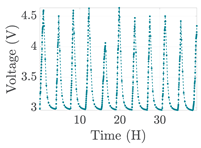 | |||
| 8 | 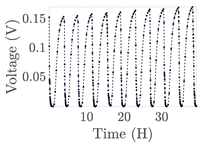 | 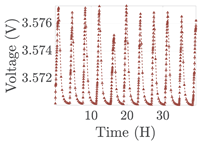 |
| Model Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Parameter | |||||||||
| (V) | |||||||||
| (V/Ah) | 4.49 | 2.38 | 0 | 4.73 | |||||
| () | 2.38 | 1.02 | 4.03 | ||||||
| a (Ah) | 0 | ||||||||
| b (V) | 5.76 | 2.43 | 2.4 | 2.4 | 0 | 2.4 | |||
| q (Ah) | 1.07 | 1.1 | 1.42 | ||||||
| r () | |||||||||
| 0 | 1 | 0 | 7.3 | 0 | |||||
| 0 | 0 | 0 | 0 | ||||||
| 2.55 | 2.05 | 0 | 0 | 2.56 | |||||
| 0 | 0 | 0 | 0 | 0 | |||||
| c | |||||||||
| d | |||||||||
| e | 0 | ||||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Parameter | |||||||||
| (V) | 5.73 | ||||||||
| (V/Ah) | 3.79 | 0 | 5.46 | 3.44 | 1.22 | 0 | 5.6 | 2.84 | |
| () | 1.62 | 0 | 0 | 5.95 | 4.16 | 2.28 | |||
| a (Ah) | |||||||||
| b (V) | 2.21 | 3.69 | 3.68 | 3.69 | 1.41 | 2.38 | 2.35 | ||
| q (Ah) | |||||||||
| r () | |||||||||
| 1 | 1 | 1 | |||||||
| 1 | 1 | 1 | |||||||
| 3.91 | 9.91 | 4.76 | 4.49 | 4.3 | |||||
| 0 | 0 | 0 | 0 | 0 | |||||
| c | |||||||||
| d | 5.4 | ||||||||
| e | 8.44 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelhafiz, S.M.; Fouda, M.E.; Radwan, A.G. Parameter Identification of Li-ion Batteries: A Comparative Study. Electronics 2023, 12, 1478. https://doi.org/10.3390/electronics12061478
Abdelhafiz SM, Fouda ME, Radwan AG. Parameter Identification of Li-ion Batteries: A Comparative Study. Electronics. 2023; 12(6):1478. https://doi.org/10.3390/electronics12061478
Chicago/Turabian StyleAbdelhafiz, Shahenda M., Mohammed E. Fouda, and Ahmed G. Radwan. 2023. "Parameter Identification of Li-ion Batteries: A Comparative Study" Electronics 12, no. 6: 1478. https://doi.org/10.3390/electronics12061478
APA StyleAbdelhafiz, S. M., Fouda, M. E., & Radwan, A. G. (2023). Parameter Identification of Li-ion Batteries: A Comparative Study. Electronics, 12(6), 1478. https://doi.org/10.3390/electronics12061478







