Electromagnetic Characteristics and Capacity Analysis of a Radial–Axial Hybrid Magnetic Bearing with Two Different Radial Stators
Abstract
:1. Introduction
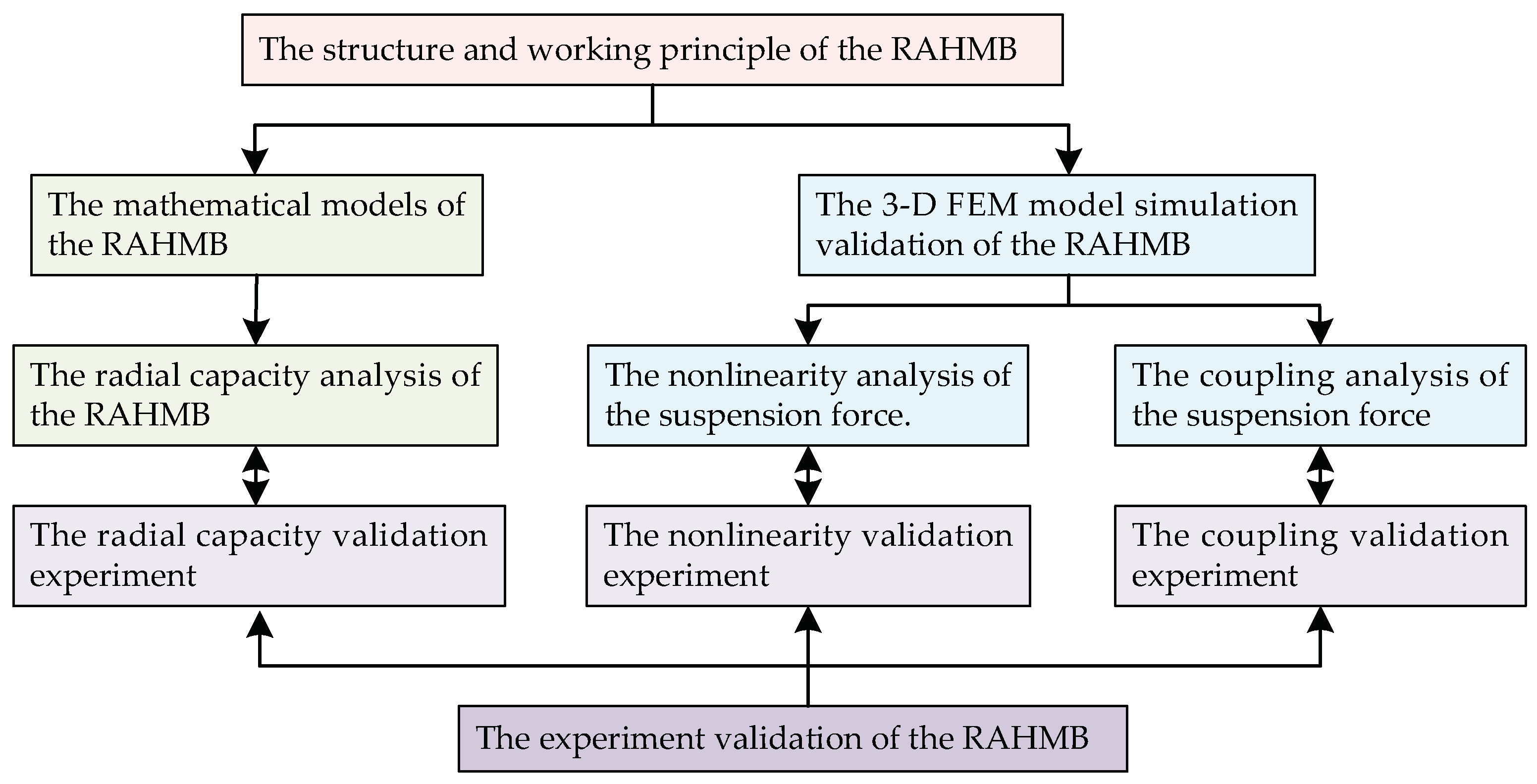
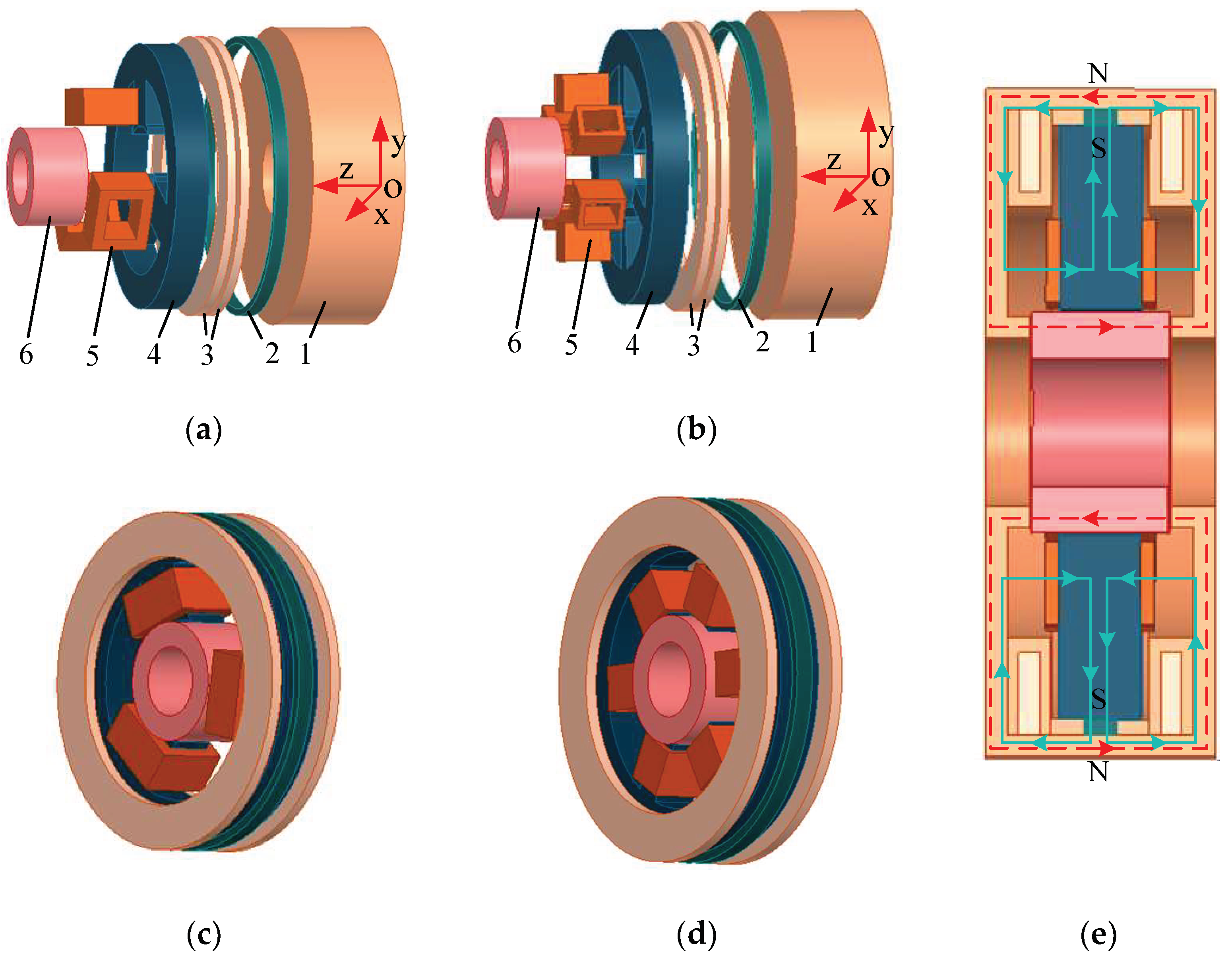
2. Structure and Working Principle of the RAHMBs
3. Mathematical Model and Capacity Analysis of the RAHMBs
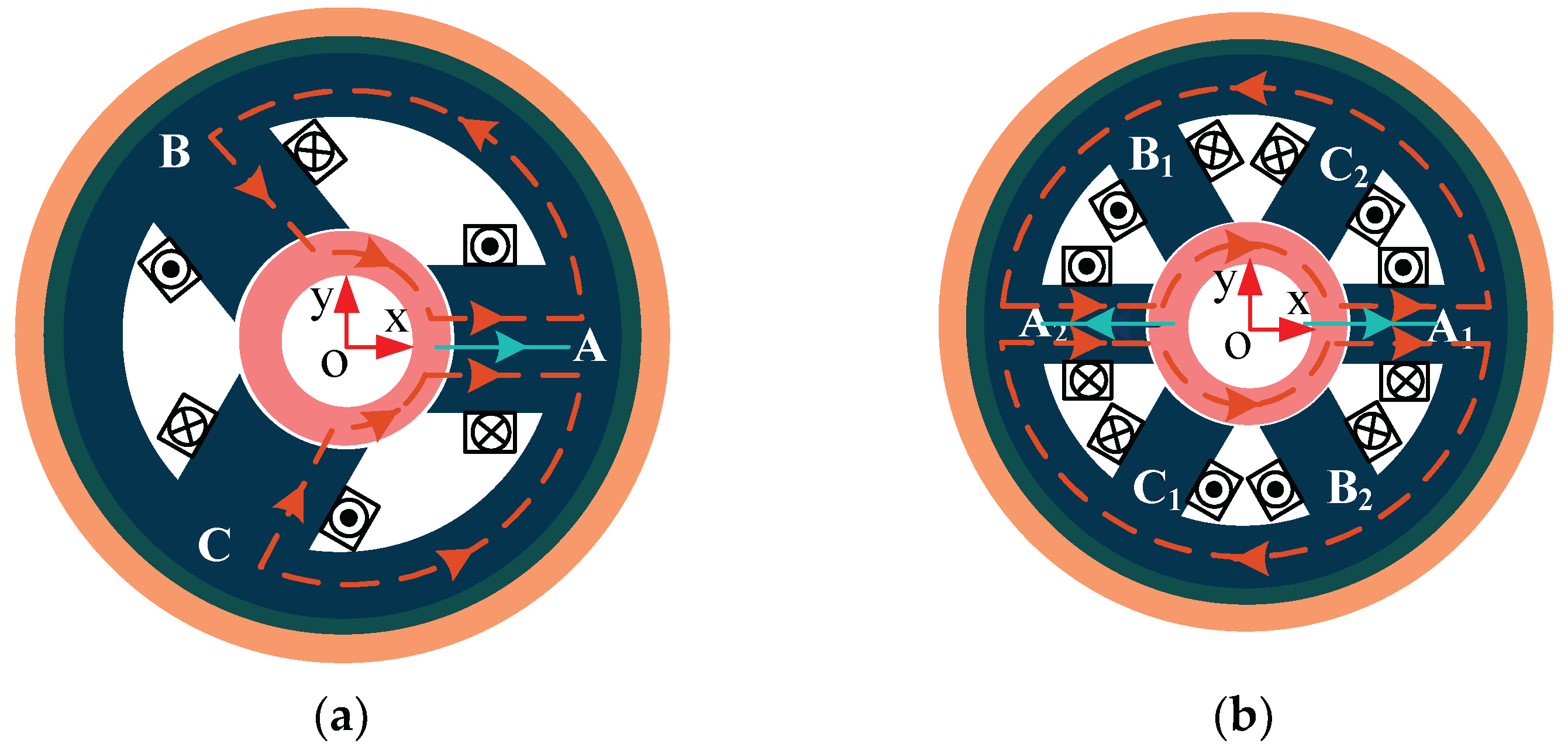
3.1. Magnetic Circuit Analysis
3.1.1. Mathematical Model of the Three-Pole RAHMB
3.1.2. Mathematical Model of the Six-Pole RAHMB
3.2. Analysis of the Radial Capacity
3.2.1. The Maximum Radial Capacity of the Three-Pole RAHMB
3.2.2. The Maximum Radial Capacity of the Six-Pole RAHMB
4. Simulation Validations
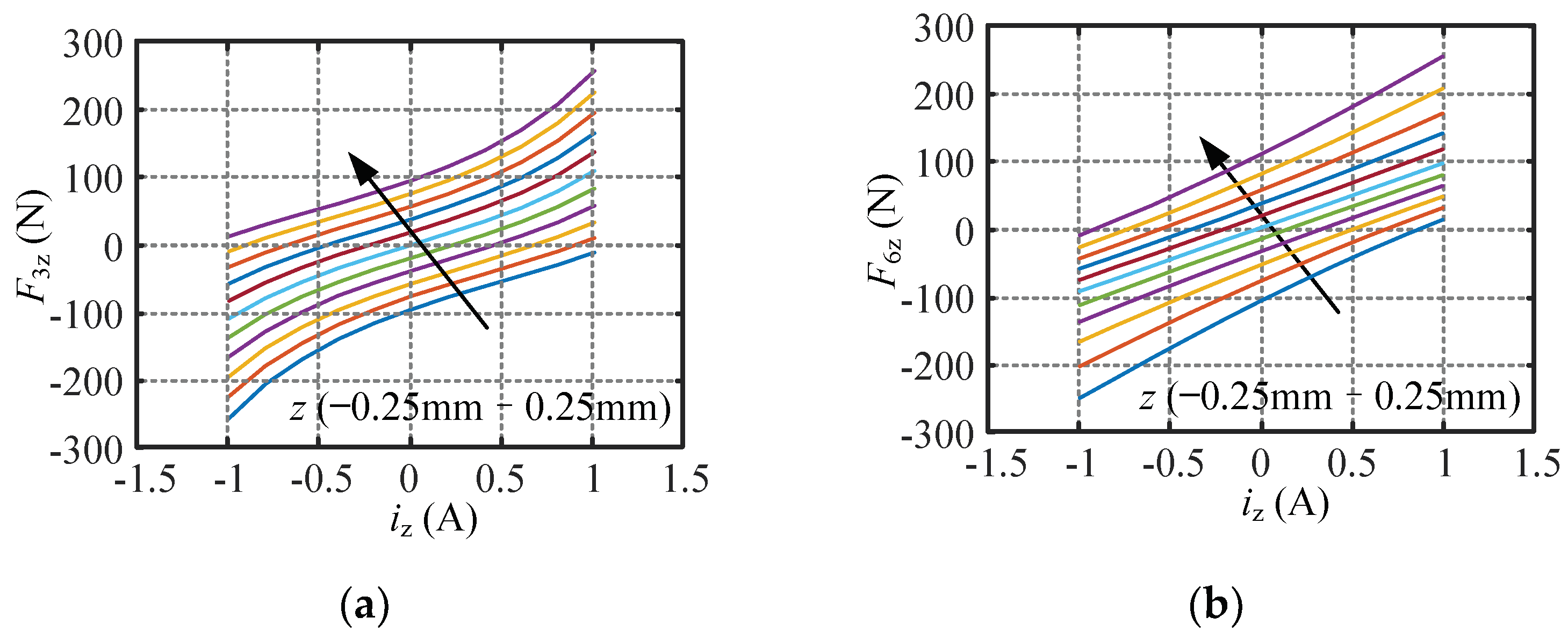
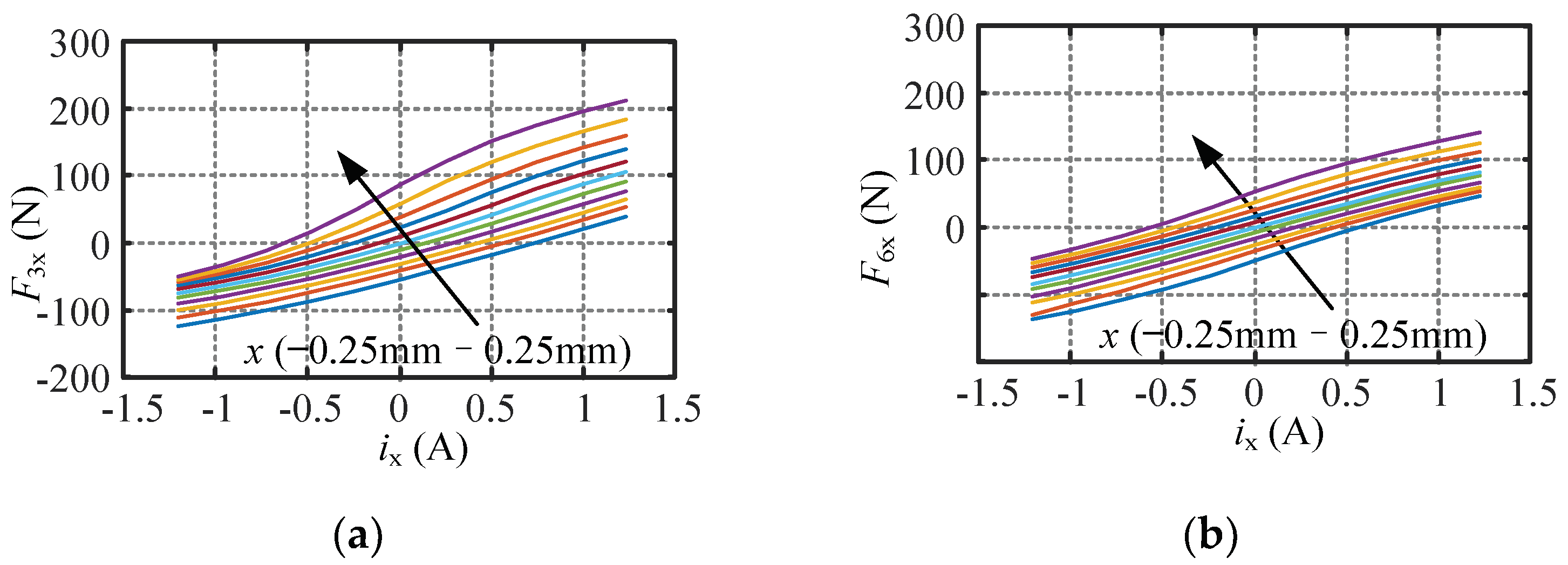
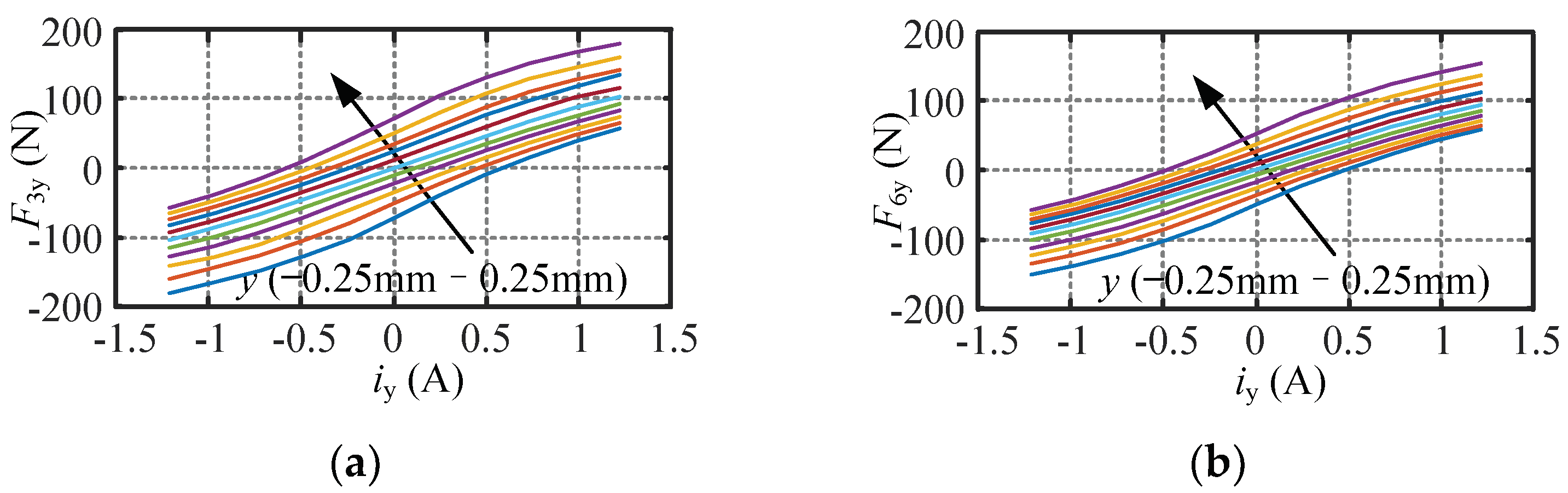
4.1. Nonlinearity Analysis of the Suspension Force
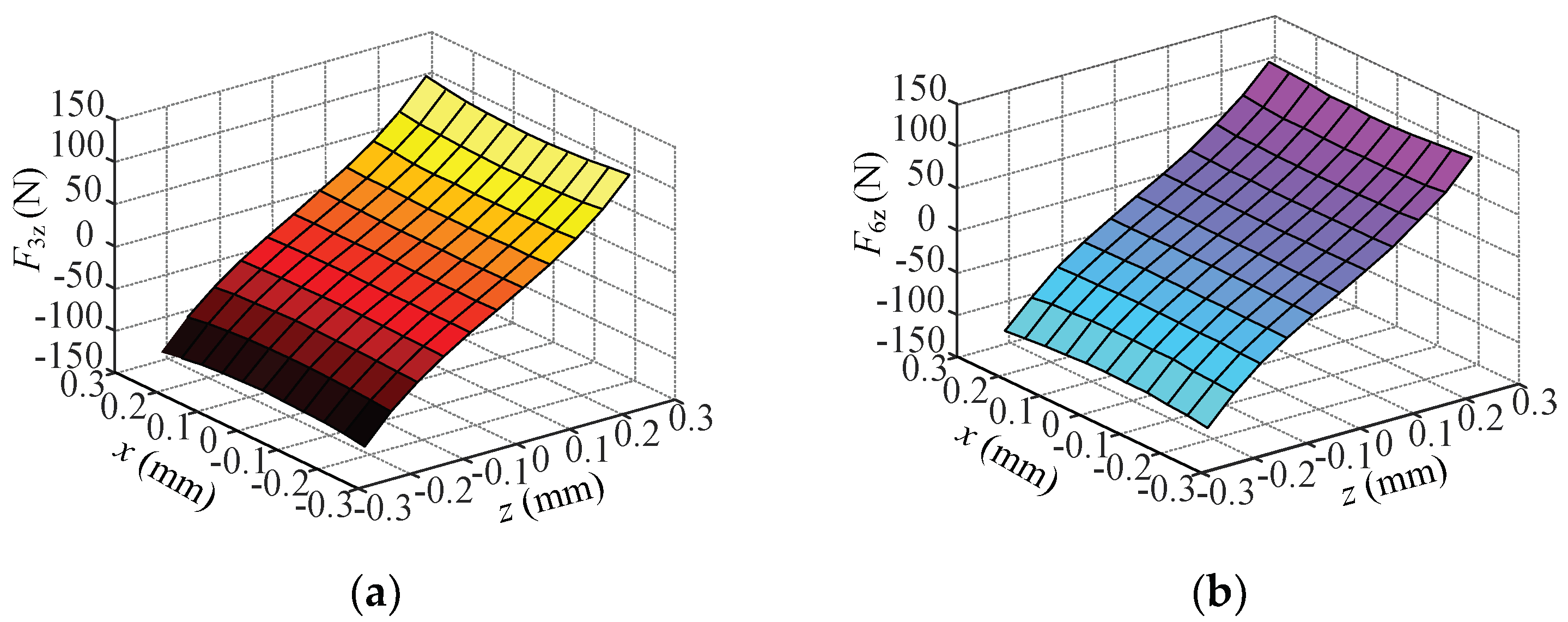
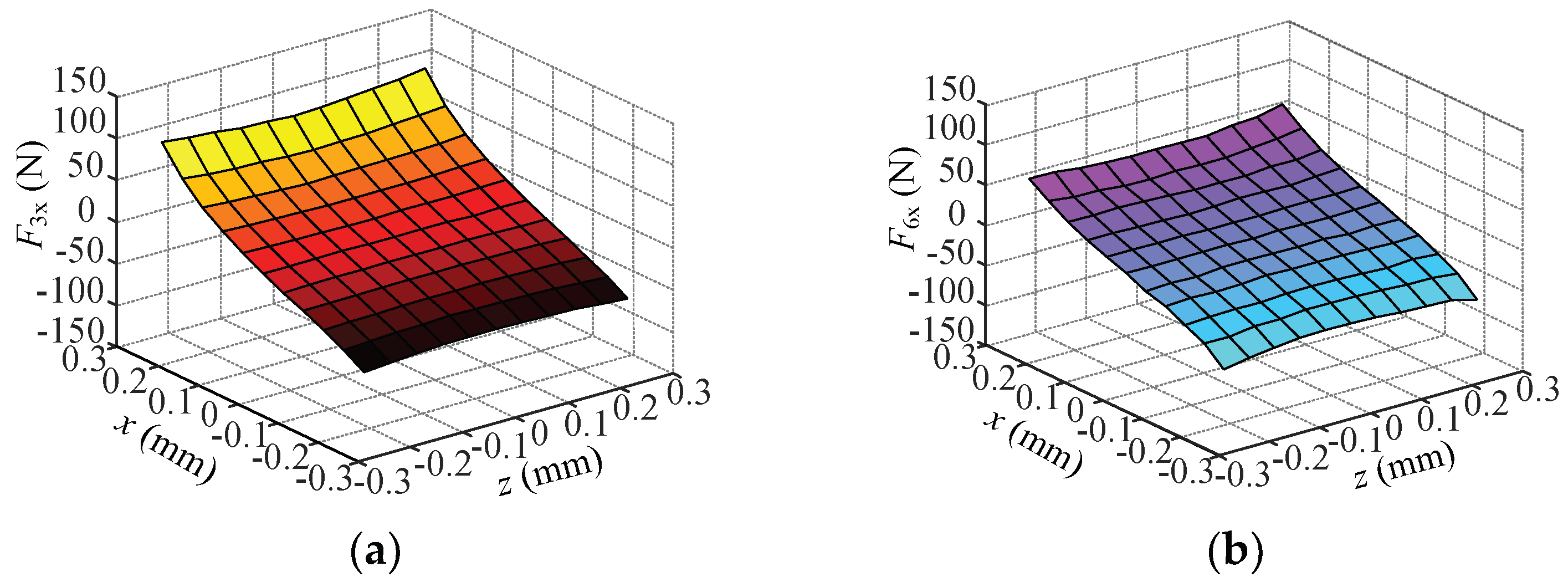
4.2. Coupling Analysis of the Suspension Force
5. Experiment Validations
5.1. Radial Capacity Validation Experiment
5.2. Nonlinearity Validation Experiment
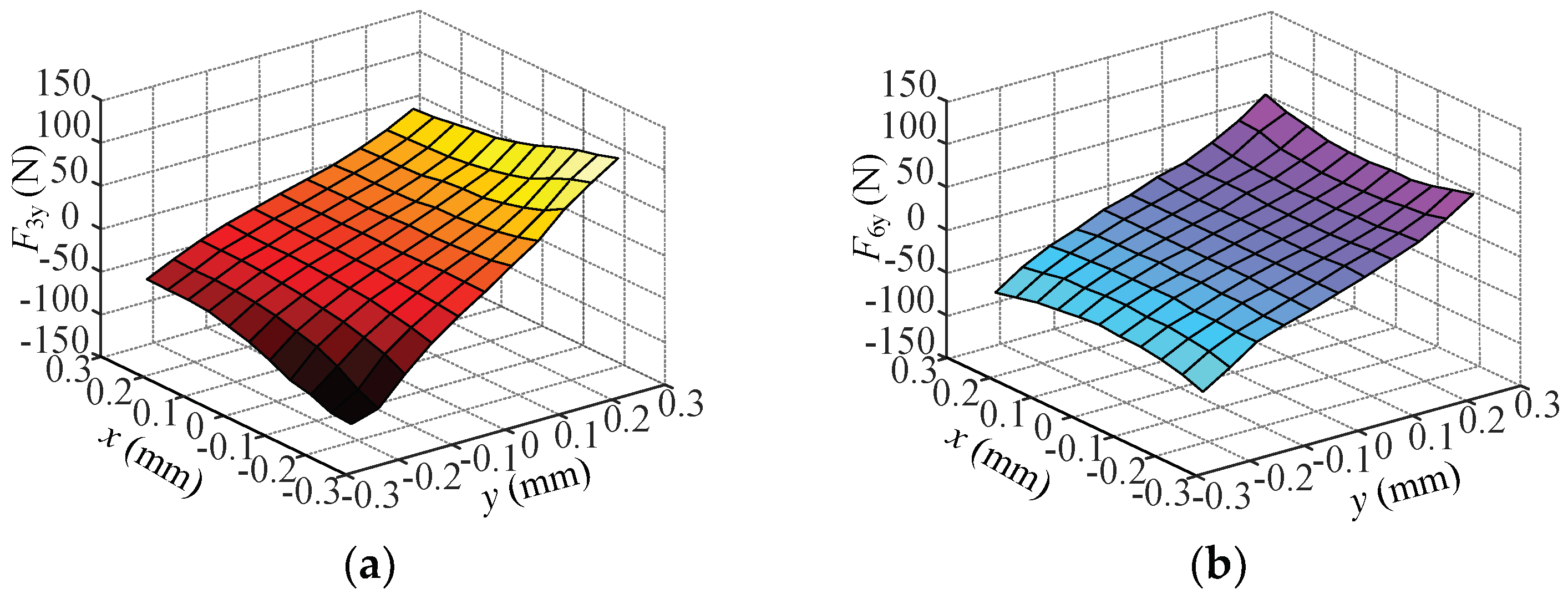
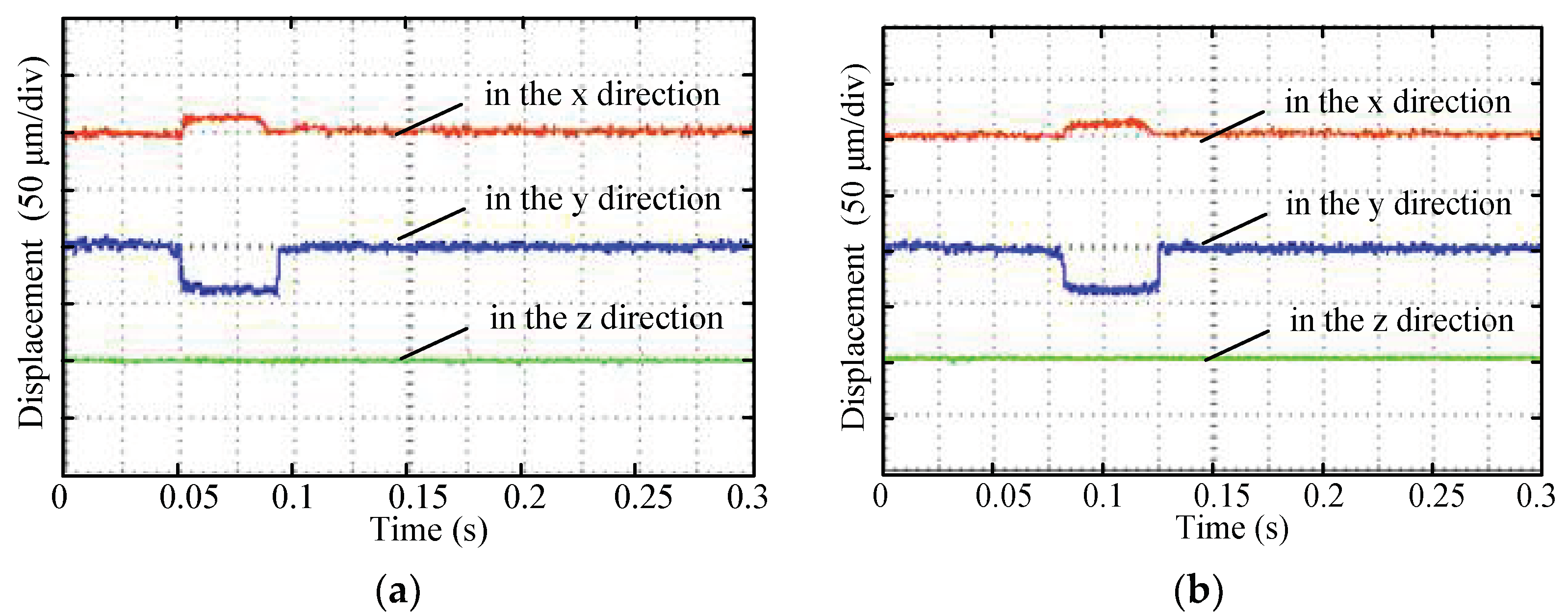
5.3. Coupling Validation Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, X.; Liu, G.; Le, Y.; Dong, B.; Zheng, S. Unbalanced Magnetic Pull Disturbance Compensation of Magnetic Bearing Systems in MSCCs. IEEE Trans. Ind. Electron. 2023, 70, 4088–4097. [Google Scholar] [CrossRef]
- Le, Y.; Wang, D.; Zheng, S. Design and Optimization of a Radial Magnetic Bearing Considering Unbalanced Magnetic Pull Effects for Magnetically Suspended Compressor. IEEE/ASME Trans. Mechatron. 2022, 27, 5760–5770. [Google Scholar] [CrossRef]
- Wang, C.; Le, Y.; Zheng, S.; Han, B.; Dong, B.; Chen, Q. Suppression of Gyroscopic Torque Disturbance in High Speed Magnetically Levitated Rigid Rotor Systems Based on Extended State Observer. IEEE/ASME Trans. Mechatron. 2022, 1–11. [Google Scholar] [CrossRef]
- Hu, H.; Liu, K.; Wang, H.; Wei, J.A. Wide Bandwidth GaN Switching Power Amplifier of Active Magnetic Bearing for a Flywheel Energy Storage System. IEEE Tran. Power Electron. 2023, 38, 2589–2605. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Zhu, P.; Yu, J. A Novel Vehicle-Mounted Magnetic Suspension Flywheel Battery With a Virtual Inertia Spindle. IEEE Trans. Ind. Electron. 2022, 69, 5973–5983. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, H.; Cheng, L.; Zhu, H. Modeling Based on Exact Segmentation of Magnetic Field for a Centripetal Force Type-Magnetic Bearing. IEEE Trans. Ind. Electron. 2020, 67, 7691–7701. [Google Scholar] [CrossRef]
- Liu, X.; Ma, X.; Feng, R.; Chen, Y.; Shi, Y.; Zheng, S. Model Reference Adaptive Compensation and Robust Controller for Magnetic Bearing Systems With Strong Persistent Disturbances. IEEE Trans. Ind. Electron. 2022, 1–10. [Google Scholar] [CrossRef]
- Li, J.; Liu, G.; Zheng, S.; Cui, P.; Chen, Q. Micro-Jitter Control of Magnetically Suspended Control Moment Gyro Using Adaptive LMS Algorithm. IEEE/ASME Trans. Mechatron. 2022, 27, 327–335. [Google Scholar] [CrossRef]
- Han, B.; Chen, Y.; Zheng, S.; Li, M.; Xie, J. Whirl Mode Suppression for AMB-Rotor Systems in Control Moment Gyros Considering Significant Gyroscopic Effects. IEEE Trans. Ind. Electron. 2021, 68, 4249–4258. [Google Scholar] [CrossRef]
- Sun, M.; Xu, Y.; Chen, S. Research on Electromagnetic System of Large Capacity Energy Storage Flywheel. IEEE Trans. Magn. 2023, 1. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, S. Decoupling Control Based on Linear/Non-Linear Active Disturbance Rejection Switching for Three-Degree-of-Freedom Six-Pole Active Magnetic Bearing. IET Electr. Power App. 2020, 14, 1818–1827. [Google Scholar] [CrossRef]
- Wu, M.; Zhu, H. Backstepping Control of Three-Pole Radial Hybrid Magnetic Bearing. IET Electr. Power App. 2020, 14, 1480–1487. [Google Scholar] [CrossRef]
- Yu, C.; Deng, Z.Q.; Mei, L.; Peng, C.; Cao, X.; Chen, S.; Ding, Q. Evaluation Criteria of Material Selection on 3-DOF Hybrid Magnetic Bearing. IEEE Tran. Ind. App. 2021, 57, 4733–4744. [Google Scholar] [CrossRef]
- Hemenway, R.; Gjemdal, H.; Severson, L. New Three-Pole Combined Radial–Axial Magnetic Bearing for Industrial Bearingless Motor Systems. IEEE Tran. Ind. App. 2021, 57, 6754–6764. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Wu, S. Suspension Force Analysis of Four-Pole Hybrid Magnetic Bearing with Large Radial Bearing Capacity. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Schmidt, E.; Hofer, M. Static and Transient Voltage Driven Finite Element Analysis for the Sensorless Control of a Hybrid Radial Active Magnetic Bearing. In Proceedings of the 2009 International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Matsuda, K.; Kanemitsu, Y.; Kijimoto, S. Optimal Number of Stator Poles for Compact Active Radial Magnetic Bearings. IEEE Trans. Magn. 2007, 43, 3420–3427. [Google Scholar] [CrossRef]
- Chen, S.; Hsu, C. Optimal Design of a Three-Pole Active Magnetic Bearing. IEEE Trans. Magn. 2002, 38, 3458–3466. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, H.; Yang, Z.; Sun, X.; Yuan, Y. Nonlinear Model Analysis and “Switching Model” of AC–DC Three-Degree-of-Freedom Hybrid Magnetic Bearing. IEEE ASME Trans. Mechatron. 2016, 21, 1102–1115. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, H. Control System Design for a Five-Degree-of-Freedom Electrospindle Supported with AC Hybrid Magnetic Bearings. IEEE ASME Trans. Mechatron. 2015, 20, 2525–2537. [Google Scholar] [CrossRef]
- Chen, S. Nonlinear Smooth Feedback Control of a Three-Pole Active Magnetic Bearing System. IEEE Trans. Control Syst. Technol. 2011, 19, 615–621. [Google Scholar] [CrossRef]
- Darbandi, S.M.; Behzad, M.; Salarieh, H.; Mehdigholi, H. Linear Output Feedback Control of a Three-Pole Magnetic Bearing. IEEE/ASME Trans. Mechatron. 2014, 19, 1323–1330. [Google Scholar] [CrossRef]
- Han, B.; Zheng, S.; Le, Y.; Xu, S. Modeling and Analysis of Coupling Performance Between Passive Magnetic Bearing and Hybrid Magnetic Radial Bearing for Magnetically Suspended Flywheel. IEEE Trans. Magn. 2013, 49, 5356–5370. [Google Scholar] [CrossRef]
- Zhong, Y.; Wu, L.; Huang, X.; Fang, Y.; Zhang, J. An Improved Magnetic Circuit Model of a 3-DOF Magnetic Bearing Considering Leakage and Cross-Coupling Effects. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, T. Rotor Displacement Self-Sensing Modeling of Six-Pole Radial Hybrid Magnetic Bearing Using Improved Particle Swarm Optimization Support Vector Machine. IEEE Trans. Power Electron. 2020, 35, 12296–12306. [Google Scholar] [CrossRef]
- Zhong, Y.; Fang, L.; Huang, X. Investigation of cross-coupling effect of a 3-DOF magnetic bearing using magnetic circuit method. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017. [Google Scholar] [CrossRef]

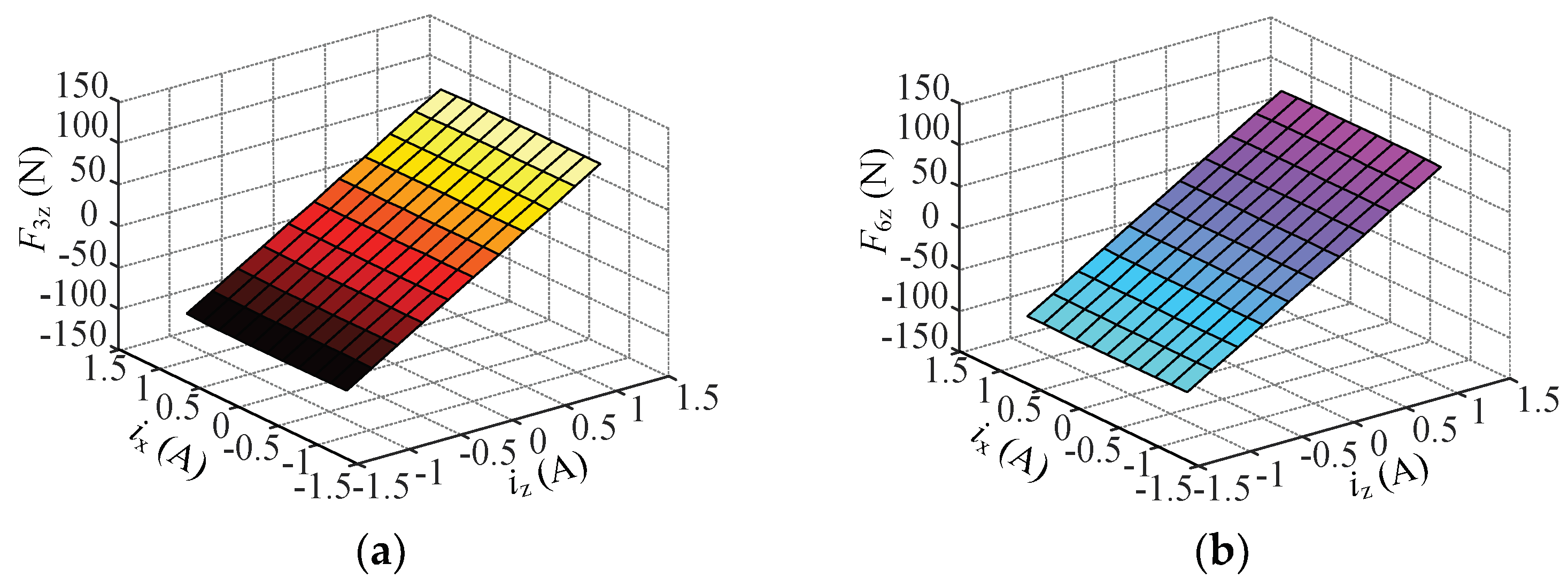
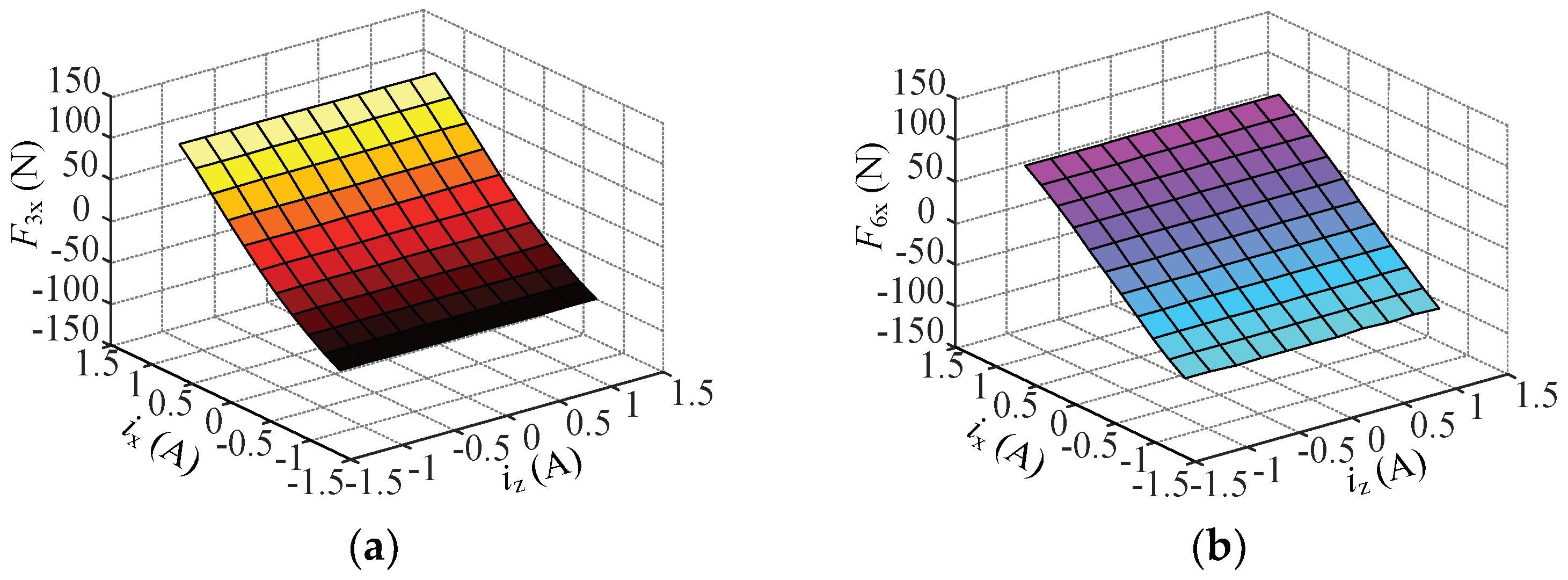
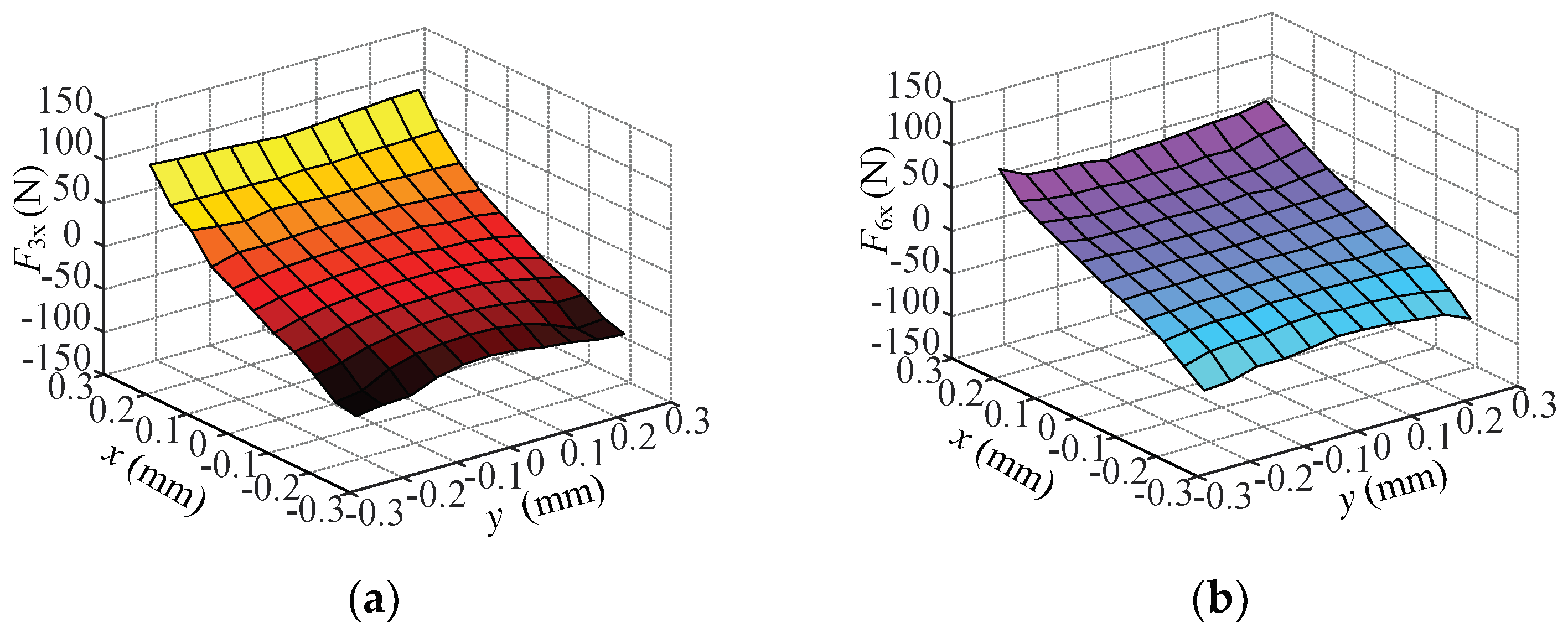



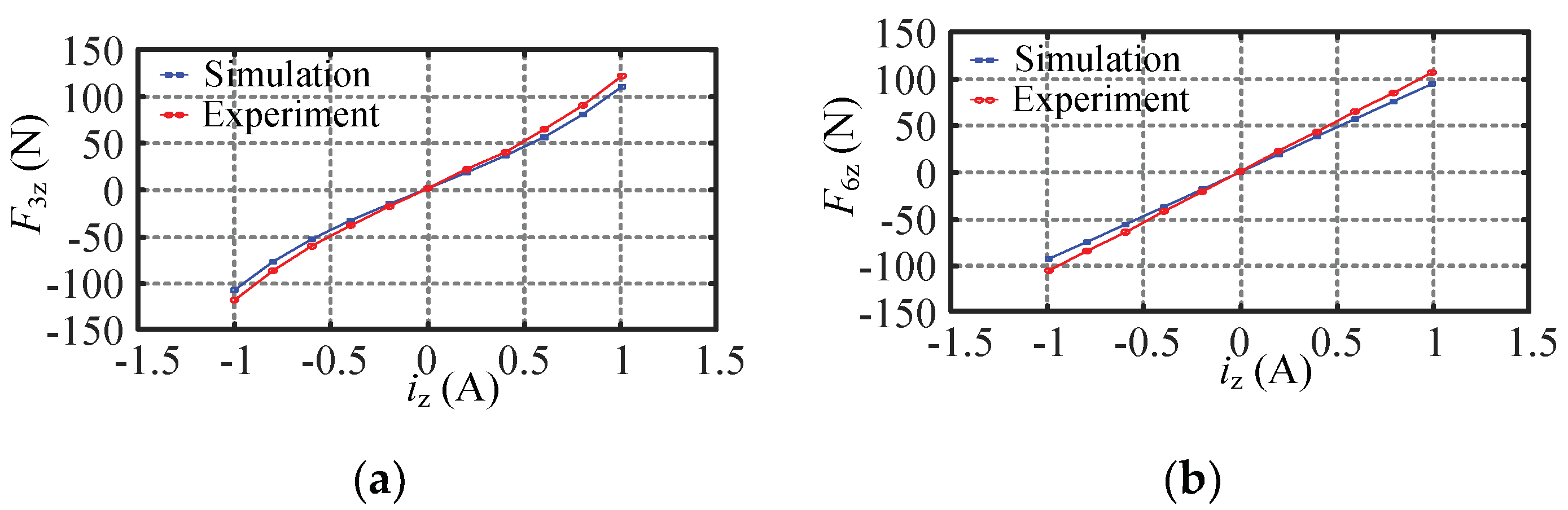
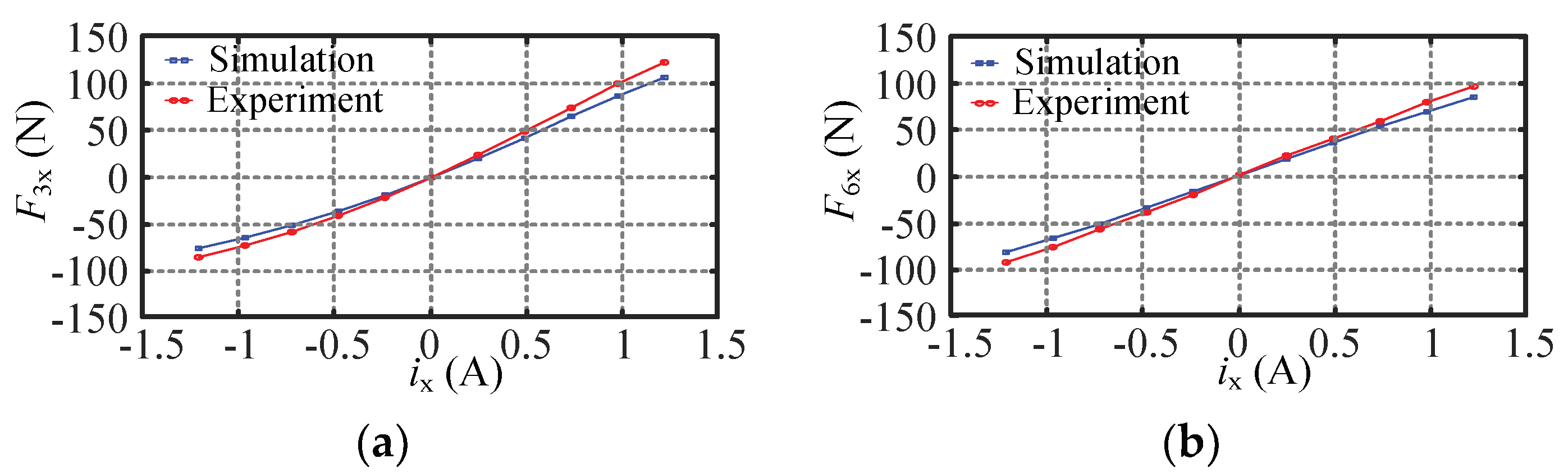

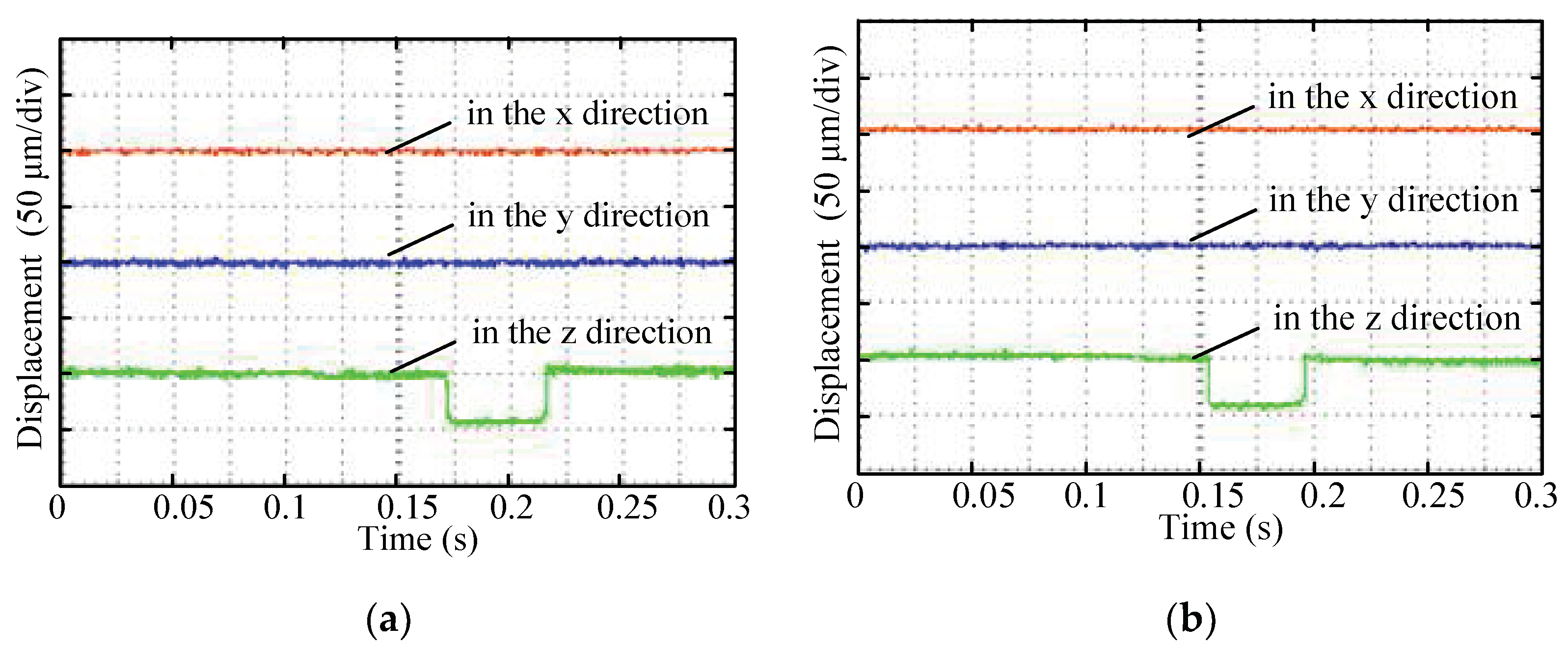
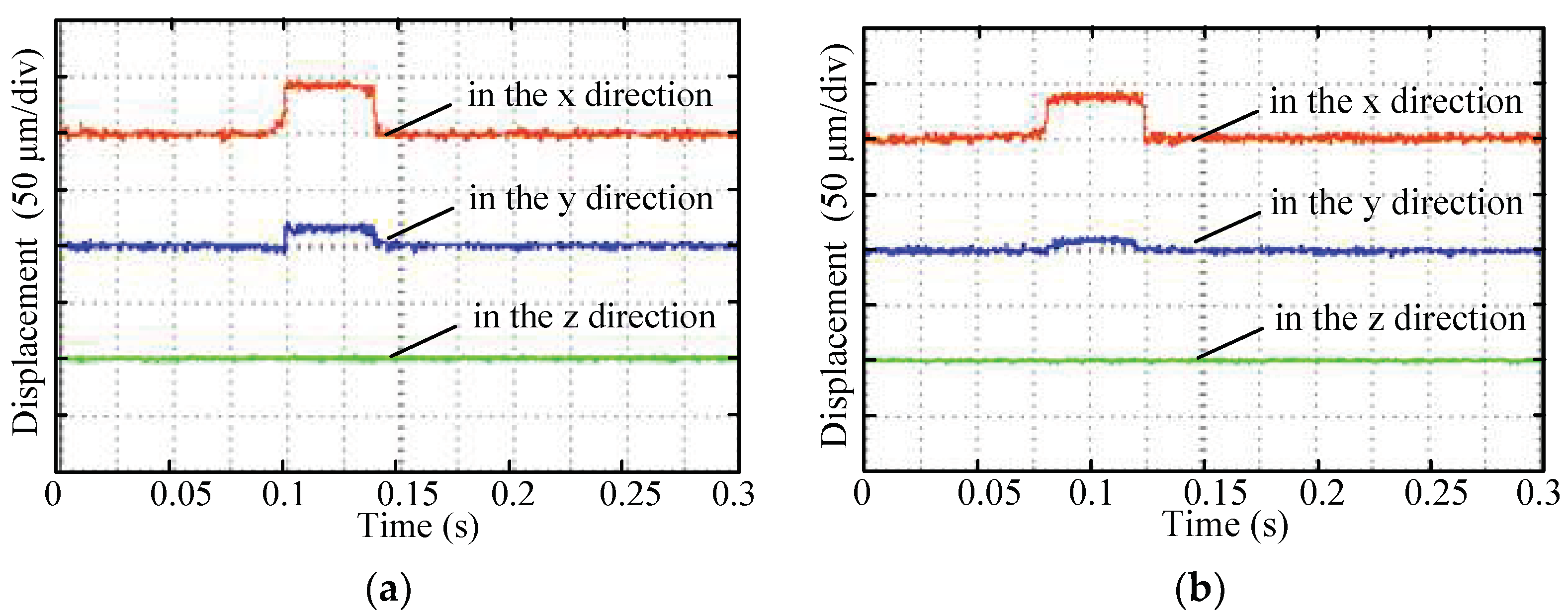
| Direction | Three-Pole Maximum Suspension Force (N) | Six-Pole Maximum Suspension Force (N) | ||
|---|---|---|---|---|
| Simulation | Experiment | Simulation | Experiment | |
| Positive x | 105.7 | 121.3 | 83.8 | 95.4 |
| Negative x | 74.6 | 84.1 | 83.6 | 94.8 |
| y | 101.8 | 114.7 | 92.1 | 104.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Zhu, H. Electromagnetic Characteristics and Capacity Analysis of a Radial–Axial Hybrid Magnetic Bearing with Two Different Radial Stators. Electronics 2023, 12, 1493. https://doi.org/10.3390/electronics12061493
Wu M, Zhu H. Electromagnetic Characteristics and Capacity Analysis of a Radial–Axial Hybrid Magnetic Bearing with Two Different Radial Stators. Electronics. 2023; 12(6):1493. https://doi.org/10.3390/electronics12061493
Chicago/Turabian StyleWu, Mengyao, and Huangqiu Zhu. 2023. "Electromagnetic Characteristics and Capacity Analysis of a Radial–Axial Hybrid Magnetic Bearing with Two Different Radial Stators" Electronics 12, no. 6: 1493. https://doi.org/10.3390/electronics12061493
APA StyleWu, M., & Zhu, H. (2023). Electromagnetic Characteristics and Capacity Analysis of a Radial–Axial Hybrid Magnetic Bearing with Two Different Radial Stators. Electronics, 12(6), 1493. https://doi.org/10.3390/electronics12061493





