Seismoelectric Coupling Equations of Oil-Wetted Porous Medium Containing Oil and Water
Abstract
:1. Introduction
2. Methods
2.1. Seismoelectric Coupling Equations
2.2. Coupling Functions of the Oil-Wetted Porous Medium with Oil–water Dual Phase Fluid
2.3. Seismoelectric Logging While Drilling
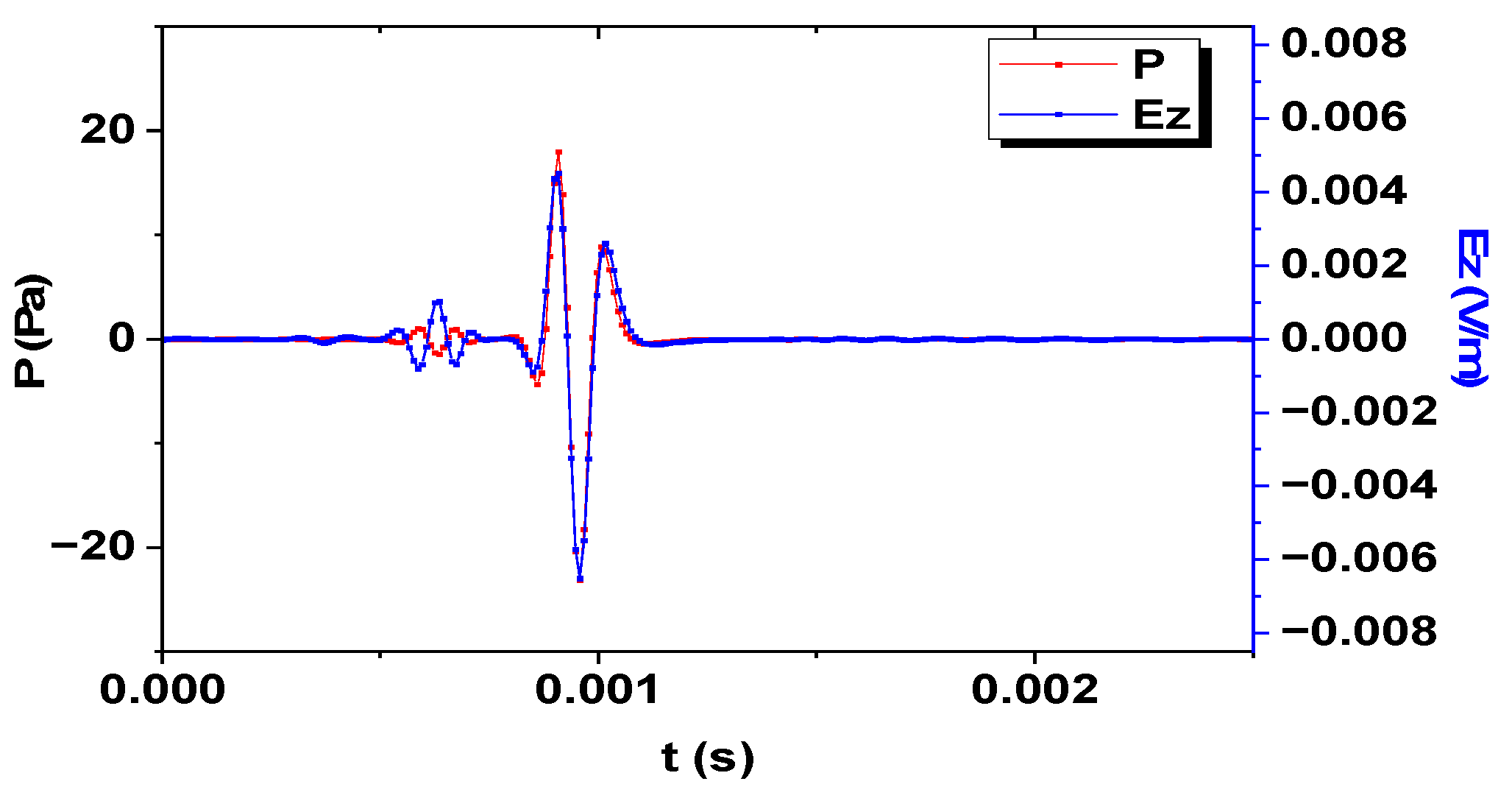
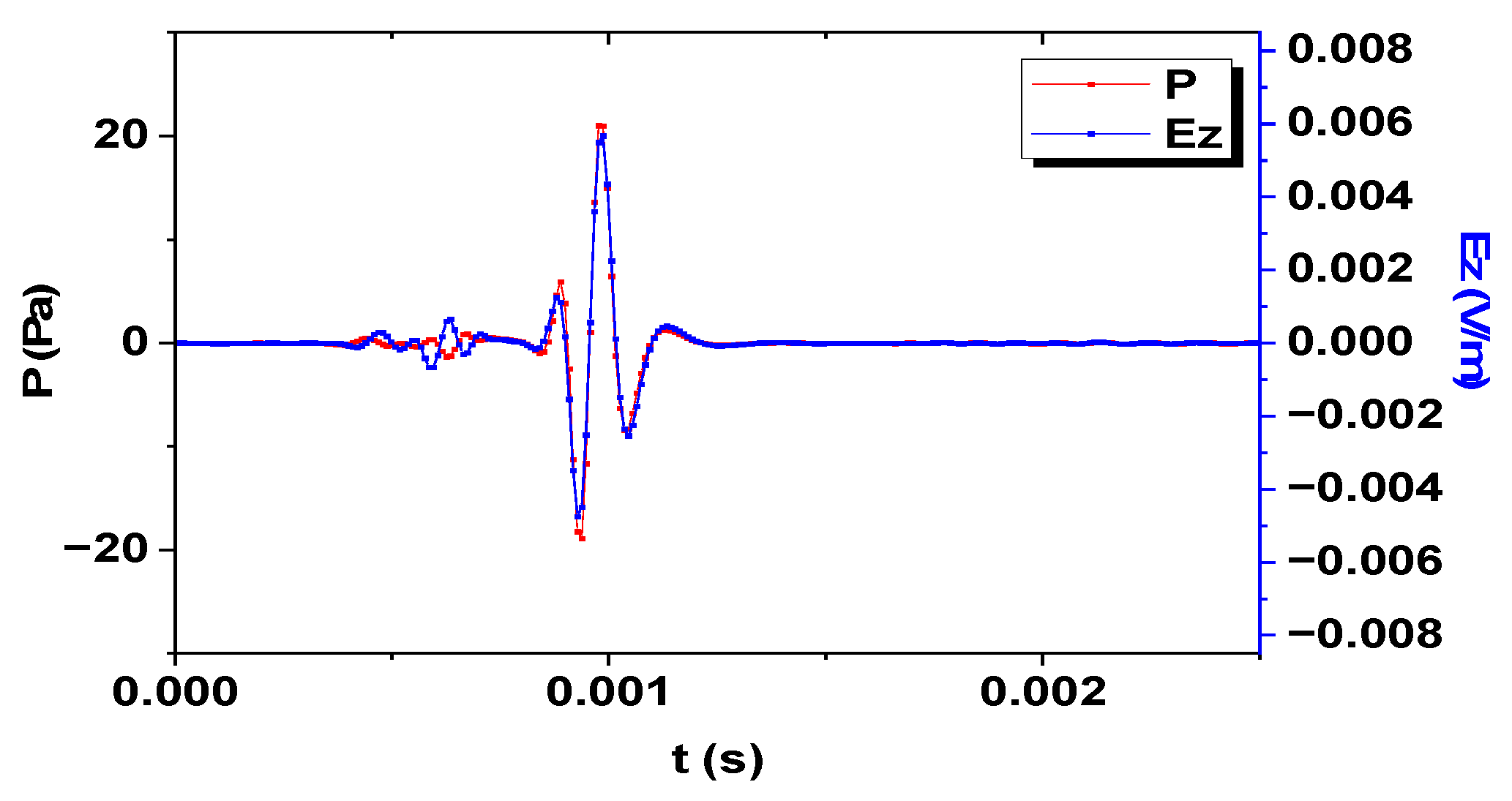
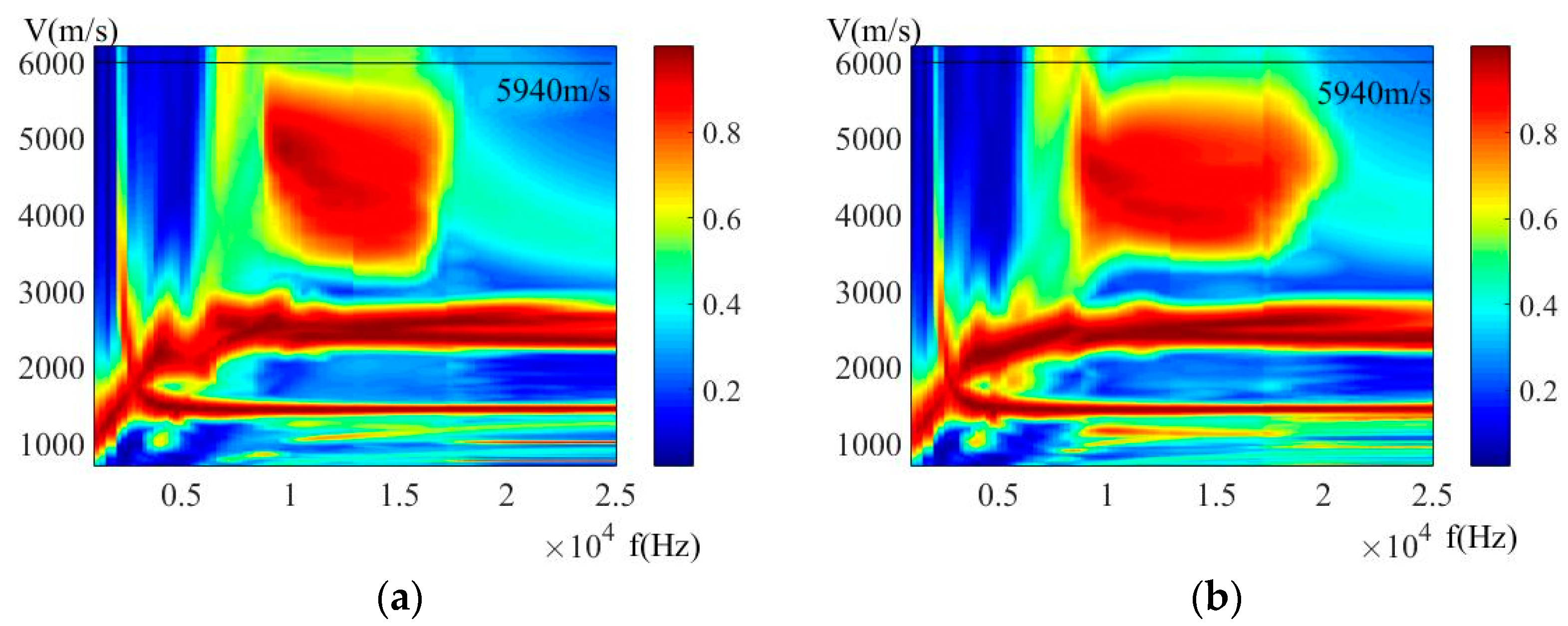
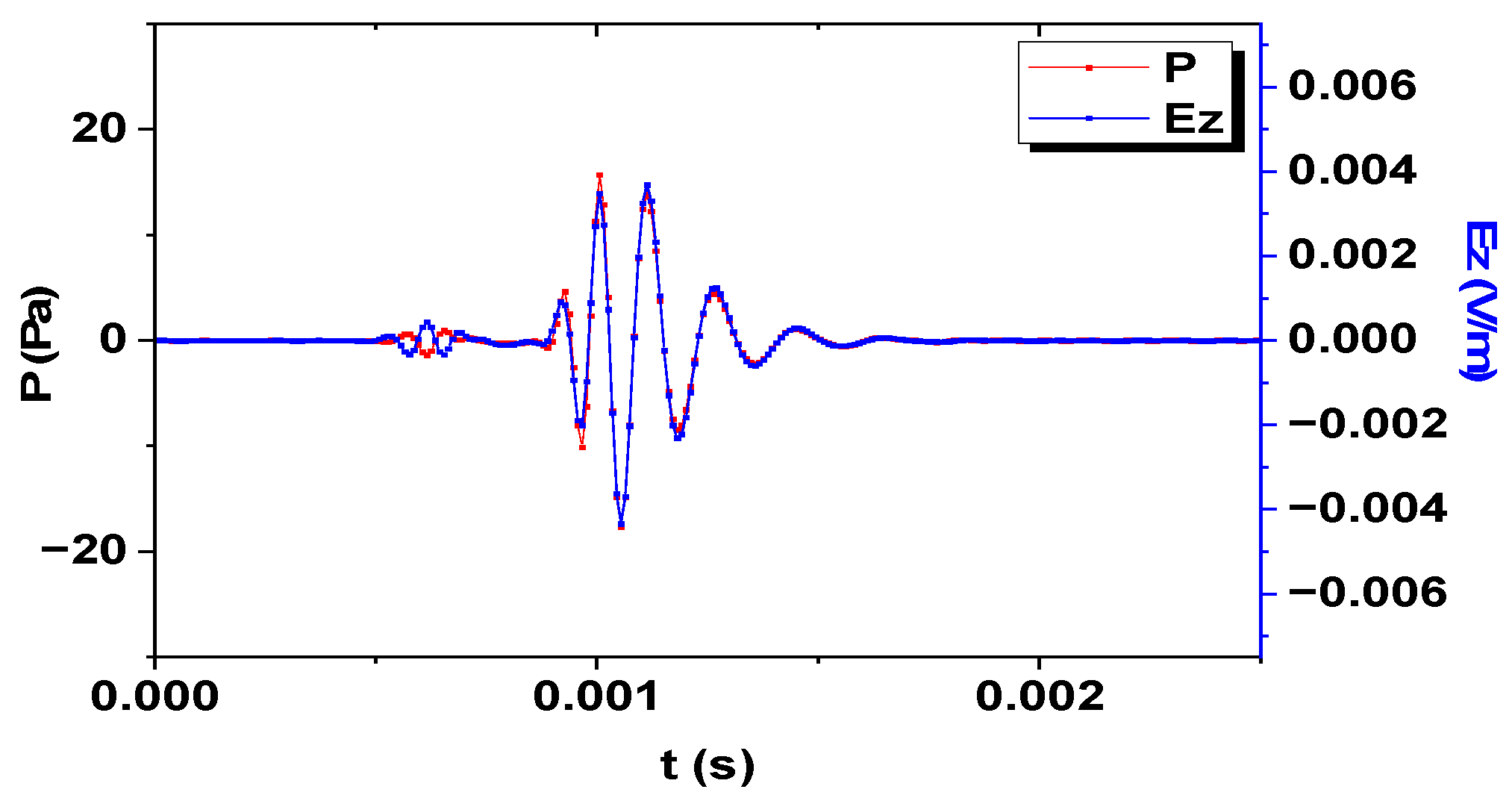
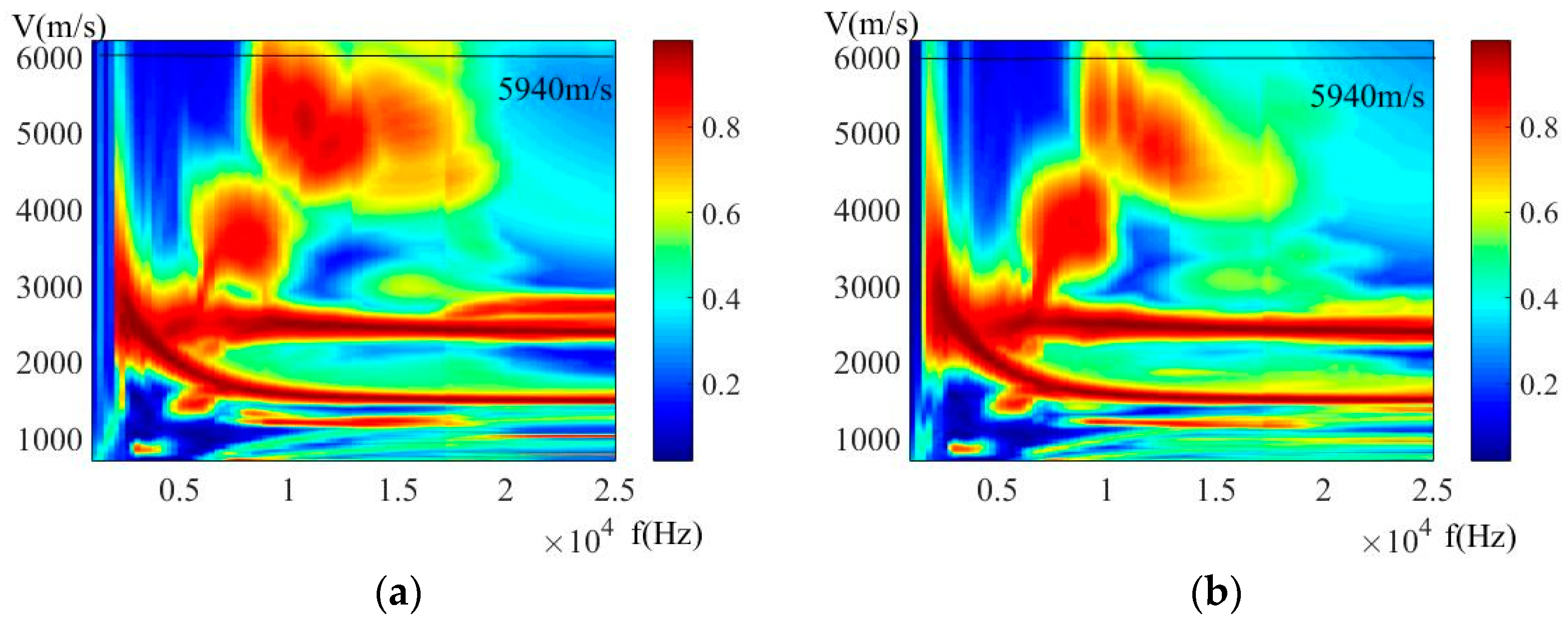
3. Simulation and Analysis
4. Discussion
5. Conclusions
- (1)
- The polarization direction of the electric field generated by the electrokinetic conversion in the oil-wetted porous medium with dual phase fluid is determined by the acoustic field. For the longitudinal wave part, the direction of the electric field is opposite to the sound field, while for other mode waves, the direction of the electric field is the same as the sound field.
- (2)
- The electrokinetic conversion in the oil-wetted porous medium with dual phase fluid will stimulate the electric field that accompanies each mode wave of the acoustic field; therefore, the electrokinetic logging can measure the acoustic velocity in the formation.
- (3)
- In the electrokinetic logging, the electrokinetic conversion efficiency of fast longitudinal wave is higher than that of other mode waves.
- (4)
- In electrokinetic logging while drilling, the electric field is less affected by the drill collar wave than the acoustic field, which is the advantage of electrokinetic logging.
- (5)
- In electrokinetic logging, while drilling in the oil-wetted porous formation with dual phase fluid, using dipole source excitation can effectively avoid the influence of drill collar wave.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Revil, A.; Jardani, A.; Sava, P.; Haas, A. The Seismoelectric Method: Theory and Applications, 1st ed.; John Wiley & Sons: The Atrium, UK, 2015; pp. 258–259. [Google Scholar]
- Pride, S. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B 1994, 50, 15678. [Google Scholar] [CrossRef] [PubMed]
- Pride, S.R.; Haartsen, M.W. Electroseismic wave properties. J. Acoust. Soc. Am. 1996, 100, 1301–1315. [Google Scholar] [CrossRef]
- Warden, S.; Garambois, S.; Jouniaux, L.; Brito, D.; Sailhac, P.; Bordes, C. Seismoelectric wave propagation numerical modelling in partially saturated materials. Geophys. J. Int. 2013, 3, 1498–1513. [Google Scholar] [CrossRef]
- Zyserman, I.; Monachesi, L.B.; Jouniaux, L. Dependence of shear wave seismoelectrics on soil textures: A numerical study in the vadose zone. Geophys. J. Int. 2017, 3, 918–935. [Google Scholar] [CrossRef]
- Alkafeef, S.; Gochin, R.J.; Smith, A.L. The effect of double layer overlap on measured streaming currents for toluene flowing through sandstone cores. Colloids Surf. A Physicochem. Eng. Asp. 2001, 195, 77–80. [Google Scholar] [CrossRef]
- Dullien, F. Porous Media: Fluid Transport and Pore Structure; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Jackson, M.D. Characterization of multiphase electrokinetic coupling using a bundle of capillary tubes model. J. Geophys. Res. Solid Earth 2008, 113, B04201. [Google Scholar] [CrossRef]
- Jackson, M.D. Multiphase electrokinetic coupling: Insights into the impact of fluid and charge distribution at the pore scale from a bundle of capillary tubes model. J. Geophys. Res. Solid Earth 2010, 115, B07206. [Google Scholar] [CrossRef]
- Zhan, X.; Chi, S.; Toksöz, M.N. Simulation of the converted electric field during multipole logging while drilling (LWD). In Proceedings of the 2006 SEG Annual Meeting, New Orleans, LA, USA, 1–6 October 2006. [Google Scholar]
- Zhu, Z.; Chi, S.; Toksoz, M.N. Experimental and theoretical studies of seismoelectric effects in boreholes. Commun. Comput. Phys. 2008, 3, 109–120. [Google Scholar]
- Gao, Y.; Huang, F.; Hu, H. Comparison of full and quasi-static seismoelectric analytically-based modeling. J. Geophys. Res. Solid Earth 2017, 122, 8066–8106. [Google Scholar] [CrossRef]
- Ren, H.; Chen, X.; Huang, Q. Numerical simulation of coseismic electromagnetic fields associated with seismic waves due to finite faulting in porous media. Geophys. J. Int. 2012, 3, 925–944. [Google Scholar] [CrossRef]
- Guan, W.; Hu, H.; Zheng, X. Theoretical simulation of the multipole seismoelectric logging while drilling. Geophys. J. Int. 2013, 195, 1239–1250. [Google Scholar] [CrossRef]
- Zheng, X.; Hu, H.; Guan, W.; Wang, J. Simulation of the borehole quasistatic electric field excited by the acoustic wave during logging while drilling due to electrokinetic effect. Geophysics 2015, 80, D417–D427. [Google Scholar] [CrossRef]
- Batzle, M.L.; Wang, Z. Seismic properties of pore fluids. Geophysics 1992, 57, 1396–1408. [Google Scholar] [CrossRef]
- Teja, A.S.; Rice, P. Generalized corresponding states method for the viscosities of liquid mixtures. Ind. Eng. Chem. Fundam. 1981, 20, 77–81. [Google Scholar] [CrossRef]
- Carcione, J.M.; Picotti, S.; Gei, D.; Rossi, G. Physics and Seismic Modeling for Monitoring CO2 Storag. Pure Appl. Geophys. 2006, 163, 175–207. [Google Scholar] [CrossRef]
- Liu, G.; Butler, J.J.; Knobbe, R.S. Hydraulic conductivity profiling with direct push methods. Grundwasser 2012, 17, 19–29. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. Aime 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Birchak, J.R.; Gardner, C.G.; Hipp, J.E.; Victor, J.M. High dielectric constant microwave probes for sensing soil moisture. Proc. IEEE 1974, 62, 93–98. [Google Scholar] [CrossRef]
- Revil, A.; Linde, N.; Cerepi, A.; Jougnot, D.; Matthäi, S.; Finsterle, S. Electrokinetic coupling in unsaturated porous media. J. Colloid Interface Sci. 2007, 313, 315–327. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, X.; Nie, Z. Seismoelectric Effect of Oil-Wetted Porous Media Containing Two-Phase Flow. Electronics 2023, 12, 346. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A.; Slob, E.; Söllner, W. Stochastic joint inversion of 2D seismic and seismoelectric signals in linear poroelastic materials: A numerical investigation. Geophysics 2010, 75, N19. [Google Scholar] [CrossRef]
- Garambois, S.; Dietrich, M. Seismoelectric wave conversions in porous media: Field measurements and transfer function analysis. Geophysics 2001, 66, 1417–1430. [Google Scholar] [CrossRef]
- Dziewonski, A.; Bloch, S.; Landisman, M.A. technique for the analysis of transient seismic signals. Bull. Seismol. Soc. Am. 1969, 59, 427–444. [Google Scholar] [CrossRef]

| Effective Parameters | |
|---|---|
| Effective density [16] | |
| Effective viscosity [17] | |
| Effective fluid bulk modulus [18] | |
| Effective critical frequency [19] | |
| Conductivity [20] | |
| Dielectric constant [21] | |
| Parameter | Value | Unit |
|---|---|---|
| Static permeability | ||
| Porosity | 0.2 | Dimensionless |
| Water phase viscosity | 0.001 | |
| Oil phase viscosity | 0.1 | |
| Water phase density | 1000 | |
| Oil phase density | 776 | |
| Solid matrix density | 2650 | |
| Skeleton shear modulus | 13.99 | |
| Skeleton bulk modulus | 14.4 | |
| Elastic modulus of skeleton | 35.73 | |
| Bulk modulus of water | 2.25 | |
| Bulk modulus of oil | 1.29 | |
| Water saturation | 0.9 | Dimensionless |
| Tortuosity | 2 | Dimensionless |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Sun, X.; Nie, Z. Seismoelectric Coupling Equations of Oil-Wetted Porous Medium Containing Oil and Water. Electronics 2023, 12, 2003. https://doi.org/10.3390/electronics12092003
Zhao Y, Sun X, Nie Z. Seismoelectric Coupling Equations of Oil-Wetted Porous Medium Containing Oil and Water. Electronics. 2023; 12(9):2003. https://doi.org/10.3390/electronics12092003
Chicago/Turabian StyleZhao, Yongpeng, Xiangyang Sun, and Zaiping Nie. 2023. "Seismoelectric Coupling Equations of Oil-Wetted Porous Medium Containing Oil and Water" Electronics 12, no. 9: 2003. https://doi.org/10.3390/electronics12092003
APA StyleZhao, Y., Sun, X., & Nie, Z. (2023). Seismoelectric Coupling Equations of Oil-Wetted Porous Medium Containing Oil and Water. Electronics, 12(9), 2003. https://doi.org/10.3390/electronics12092003






