Memory-Based Sand Cat Swarm Optimization for Feature Selection in Medical Diagnosis

Abstract

The rapid expansion of medical data poses numerous challenges for Machine Learning (ML) tasks due to their potential to include excessive noisy, irrelevant, and redundant features. As a result, it is critical to pick the most pertinent features for the classification task, which is referred to as Feature Selection (FS). Among the FS approaches, wrapper methods are designed to select the most appropriate subset of features. In this study, two intelligent wrapper FS approaches are implemented using a new meta-heuristic algorithm called Sand Cat Swarm Optimizer (SCSO). First, the binary version of SCSO, known as BSCSO, is constructed by utilizing the S-shaped transform function to effectively manage the binary nature in the FS domain. However, the BSCSO suffers from a poor search strategy because it has no internal memory to maintain the best location. Thus, it will converge very quickly to the local optimum. Therefore, the second proposed FS method is devoted to formulating an enhanced BSCSO called Binary Memory-based SCSO (BMSCSO). It has integrated a memory-based strategy into the position updating process of the SCSO to exploit and further preserve the best solutions. Twenty one benchmark disease datasets were used to implement and evaluate the two improved FS methods, BSCSO and BMSCSO. As per the results, BMSCSO acted better than BSCSO in terms of fitness values, accuracy, and number of selected features. Based on the obtained results, BMSCSO as a FS method can efficiently explore the feature domain for the optimal feature set.

1. Introduction

Features Selection (FS) is an effective data mining method to reduce the dimensionality of a feature space. Instead of generating all possible features subsets for large datasets, FS is applied to select the most informative features in the dataset and exclude redundant and irrelevant features. Redundant features are those features that are closely correlated with each other and eliminating any of them does not affect the classification results badly [1]. On the other hand, related features are those features that are closely related to class labels. Therefore, they have a great impact on the classification process and should be kept to train the model [2]. There are two commonly used FS methods: filter-based and wrapper-based. The filter methods use the characteristics of the dataset to score features without performing a learning process [3]. In contrast, wrapper methods are driven by a learning algorithm that determines the quality of each subset of features depending on the learning process [4]. This may yield more accurate results, but it takes more time compared to quick filter methods. Wrapper-based FS methods consist of search and evaluation processes. In the search process, a search algorithm is implemented to search the feature space to get a feature subset that achieves two goals simultaneously: The minimum number of features selected and the maximum classification performance. In designing a FS method, finding the optimal or near-optimal feature set is crucial. It is broadly known that FS can be considered as an NP-hard problem. In this regard, the exact search algorithms are less productive than the FS algorithms [5]. Hence, in the exact search methodology, all possible combinations of features are generated to choose the best solution from them. Thus, the exact search method is computationally expensive. For instance, consider a dataset of a feature selection task with N features. Then, when employing a wrapper FS method, a subset of $2^N$ features will be produced and evaluated using a learning model (i.e., the classifier). While the primary goal of FS is to find a minimum dimensional subset of features while augmenting classification accuracy, this method can be considered an optimization task. To make the best decision, it is usually necessary to make a trade-off between these two objectives. On this account, instead of viewing the feature selection problem as a single-objective problem [6], it should be viewed as a multi-objective problem. Thus, Sand Cat Swarm Optimization (SCSO) [7] as a meta-heuristic optimization could be very effective in handling FS tasks.

Many multi-objective meta-heuristic methods, such as Binary Snake Optimizer (BSO) [8], Binary Rat Swarm Optimizer (BRSO) [9], and Binary Ali Baba and the Forty Thieves (BAFT) algorithm [10], have recently been used for FS tasks in a wrapper-based technique. However, there is no single method can address the curse of dimensionality in the original dataset [6]. The No-Free-Lunch (NFL) theorem [11] states that no single optimization technique can solve all optimization problems with a higher level of performance than all other optimization techniques. For many years, this has encouraged many researchers to present new algorithms with improved performance and exploration and exploitation actions.

The demanding need for FS in various domains, as well as the stunning capabilities of meta-heuristics, fueled the desire to utilize a newly designed meta-heuristic algorithm to tackle a wide range of FS tasks. In this work, a newly proposed method, referred to as Sand Cat Swarm Optimization (SCSO) [7], was adopted to handle FS problems. At outset, this algorithm along with an appropriate transfer function was integrated to develop a binary algorithm, known as a Binary SCSO (BSCSO), from the parent continuous version of SCSO. This is to handle FS problems as the nature of these problems requires binary algorithms.

The SCSO algorithm is a recent developed swarm-based algorithm [7] that mimics the behavior of sand cats in nature. The main features of sand cats are the ability to search and attack prey. Sand cats can detect even low-frequency noises so they can capture prey on the ground or underground. The stages of the search attack are inspired by the SCSO as two major components of the search process. The main features of SCSO that prompted us to use it for tackling FS problems is that it has a high capability to control the exploration and exploitation balance of the search process with few parameters and operators used. Although the standard SCSO was improved and applied to address a variety of real-world optimization problems, including inverse robot arm kinematics [12], intrusion detection [13], and transformer defect diagnostics [14], it still suffers from many issues. These issues include premature convergence and cadence of solutions in local minima. Second, the standard SCSO was designed for continuous optimization problems, while the FS tasks are binary optimization problems. Third, the SCSO algorithm does not keep a record of its best positions from earlier iterations, which limits its potential for exploitation and results in early convergence with local optima. With randomization and static swarm behavior, SCSO’s global search ability is strong, but its local search ability is modest, which may lead solutions to fall into the local optimums [15]. All of the above gaps motivate this work to produce two new Binary versions of the standard SCSO, namely BSCSO and Binary Memory-based SCSO (BMSCSO), to handle FS tasks.

The proposed BSCSO utilizes the binary version of the basic SCSO, which employs the S-shaped transfer function to convert the continuous search space of this algorithm into a binary one. In more detail, the obtained solution using BSCSO is represented by binary values (i.e., 1 or 0) depending on whether the features are selected or not. The selected features are represented by one, while non-selected features are denoted by zero. While the proposed BMSCSO integrates the memory-based strategy [16,17] into the positioning updating process of SCSO with the best solutions for further exploitation. More particularly, BMSCSO utilizes two main phases at the core of BSCSO: in the first phase, a new random operator is added to the SCSO for additional exploration. In the second phase, a memory component is incorporated into the SCSO algorithm to keep the coordinates in the solution space connected to the best solution (i.e., fitness score) that the sand cat has realized so far. Thus, this inclusion approach ensures early-stage exploration and later-stage exploitation capability and ensures global optimum achievement with enhanced performance level.

The performance of the proposed FS methods was assessed on many low and high-dimensional medical datasets, where the efficiency of these algorithms was compared with other algorithms. The relevance of the experimental outcomes was demonstrated by statistical analysis using Friedman’s and Holm’s test methods [18]. These methods were applied to evaluate the significance of the obtained results compared to other feature selection methods derived from other meta-heuristic algorithms.

As a result of this work, the following contributions have been made:

• Investigation of the impact of the binary SCSO, as a wrapper- based FS method, to tack FS tasks in the medical domain.
• Investigation of the memory-based technique’s influence on the BSCSO, called BMSCSO, to form a new wrapper-based FS method. This new BMSCSO was designed to improve the exploitation potential of BSCSO in addressing FS problems.
• Examination of the performance of BMSCSO on medical FS problems compared to other popular wrapper FS methods.

The rest the paper is arranged as follows: In Section 2, a literature review is presented. The SCSO algorithm is described in Section 3. In Section 4, the proposed memory based SCSO is presented. While in Section 5, the proposed binary methods for features selection are presented. The performance of BMSCSO is evaluated and compared with other meta-heuristic algorithms in Section 6, and finally, conclusion and future works are given in Section 7.

2. Literature Review

The use of meta-heuristic algorithms to solve NP-complete and multimodal problems in real-world optimization has shown promising results. In recent years, several meta-heuristic types are adapted by scholar for solving optimization problems, which can be categorized into nature-inspired and non-nature inspired methods [19]. blueSeveral nature-inspired methods have been introduced in the literature, including the Whale Optimization Algorithm (WOA) [20] and its improvements in [21], wrapper-based binary Sine Cosine method [22], Discrete moth-flame optimization algorithms [23], which was developed using the moth’s navigation method, and the multi-trial vector-based differential evolution(MTDE) [24]. In recent studies, a sand cat optimization algorithm [7] has been developed based on desert cats’ lifestyle, and it is designed with artificial intelligence to solve continuous optimization problems. Table 1 shows most of the modifications made to the standard SCSO. Because feature selection is an NP-complete problem [10], swarm intelligence methods are frequently used to tackle it.

The main goal of FS is to investigate the characteristics of the data features and then pick the smallest number of essential and significant features capable of describing the original data [9,10,25]. Generally, FS can be accomplished using wrapper or filter approaches. The FS method described in this work is a wrapper-based approach. As a result, filter-based FS and hybridization of the filter and wrapper-based FS approaches are outside the scope of this study. The wrapper FS methods utilize a search algorithm to generate a subset of features that can accurately represent the entire set. After that, the selected subset is evaluated using a specific classifier model (e.g., k-Nearest Neighbor (k-NN) or Support Vector Machine (SVM)). One of the best well-known methods to create feature subsets is meta-heuristic algorithms. The latter is utilized to minimize the time required to generate subsets of features.

Wrapper feature selection based on meta-heuristic methods has been used in many real-life applications, including intrusion detection [26], image processing [27,28], sentiment analysis [29], and many other fields [30,31]. Nevertheless, one of the remaining challenges in using the FS process is its application in medical data diagnosis, which is the focus of this study. Thus, most of the work relevant to the use of FS in the diagnosis of medical data is reviewed in this section.

Table 1. A summary of the most adaptation methods of SCSO in the literature.

Citation	Evolution of SCSO	Domain
Iraji et al. [32]	Hybrid chaotic SCSO and pattern search approach	Safety factors of the earth slope exposed
Wu et al. [33]	Hybrid of SCSO with a wandering strategy	Engineering optimization problems
Li and Wang [34]	Hybrid of stochastic variation and elite collaboration with SCSO	Engineering optimization problems
Kiani et al. [35]	Updates SCSO positions by the political system	Engineering optimization problems
Arasteh et al. [36]	Discredited sand cat swarm optimization	Software clustering

Table 1. A summary of the most adaptation methods of SCSO in the literature.

Citation	Evolution of SCSO	Domain
Iraji et al. [32]	Hybrid chaotic SCSO and pattern search approach	Safety factors of the earth slope exposed
Wu et al. [33]	Hybrid of SCSO with a wandering strategy	Engineering optimization problems
Li and Wang [34]	Hybrid of stochastic variation and elite collaboration with SCSO	Engineering optimization problems
Kiani et al. [35]	Updates SCSO positions by the political system	Engineering optimization problems
Arasteh et al. [36]	Discredited sand cat swarm optimization	Software clustering

In a promising study, Alweshah et al. [37] designed a wrapper FS method based on the Greedy Crossover (GC) operator using a binary Coronavirus Herd Immunity Optimizer (BCHIO) to improve the exploration of BCHIO. The proposed algorithm was evaluated on 24 benchmark medical datasets. Experimental results show that BCHIO surpassed state-of-the-art wrapper FS methods in terms of average fitness and accuracy. In [38], the authors presented an improved binary version of the flamingo search algorithm, referred to as IBFSA, by incorporating the Levy flight technique to increase the diversity and provide a high level of randomization. The proposed IBFSA is employed to select the most vital features in the COVID-19 datasets. The proposed method is evaluated on two benchmark sets of COVID-19 text data. The results show that the IBFSA can select essential features to improve diagnostic performance. However, the algorithm’s improvement focused on the exploration phase while ignoring the exploitation phase, resulting in an imbalance between these two phases [39]. Nadimi-Shahraki et al. [40] developed a feature selection method for medical data classification and diagnosis based on improving the binary whale optimization method (BE-WOA). The main goal of the E-WOA was to enhance the WOA by utilizing three search techniques: encircling prey, migrating, and preferential selection. The suggested E-WOA aimed to fill the gap of suffering from the poor search strategy and low population diversity. The BE-WOA outperformed other methods regarding the accuracy and average fitness values when tested on COVID-19 numerical data. In [41], the author utilized Sine Cosine Algorithm (SCA) to solve the FS task for medical datasets. The authors used various transfer functions (S-shaped and V-shaped) to represent the solution in the binary format. The proposed Binary SCA was tested on five medical datasets, and the results showed the effectiveness of the BSCA method. However, the benchmark dataset is relatively small compared to most related studies. In another [42], the authors proposed two binary versions from the Aquila optimizer (AO) algorithm for handling the FS task in the medical domain. The first version of the AO was based on the S-shaped transfer function. In contrast, the second version was based on the V-shaped transfer function. The proposed methods were tested on seven medical datasets. The results showed the S-shaped version outperformed the V-shaped version in most of the datasets.

In a recent study, the author in [43] recently introduced the Binary version of the Starling Murmuration Optimization (BSMO) algorithm for feature selection tasks. The BSMO was developed to select the best feature subset from large medical datasets. Using S- and V-shaped transfer functions, the proposed BSMO was converted to a binary version. The reported experimental results show that the BSMO can dominate all competing methods on medical Nevertheless, the authors should have paid more attention to the balance between exploration and exploitation search in the BSMO. The authors in [44] introduced several binary versions of the quantum-based avian navigation optimizer algorithm (BQANA) [45] to assist in solving the feature selection tasks based on variant transfer functions. The proposed BQANA was applied to ten medical benchmark datasets to select the essential features for the diagnosis tasks. The results exhibit that the BQANA has merit for medical feature selection tasks. However, the authors ignored the balance between the exploration and exploitation phases in the binary version of QANA. The study presented in [46] adapted Binary Particle Swarm Optimization (BPSO) for feature selection tasks using the inertia weight operator. This was used to update the velocity of the BPSO while also balancing the exploitation and exploration features of BPSO. On known heart disease datasets, the proposed BPSO was tested. The findings of this study showed that the proposed technique generates superior outcomes in terms of classification accuracy as well as convergence rate with a smaller feature set.

The primary contribution of this study lies in the development of an effective wrapper FS method for various medical datasets used in diagnosis. According to the literature, wrapper FS methods have been successfully applied to select the most relevant features from a wide range of large datasets. However, due to the large number and variety of medical datasets, it is difficult to determine an appropriate FS cover method for a particular medical data set. In more detail, the key contributions of this study are to propose two wrapper FS methods based on the SCSO algorithm. First, a binary version of the basic SCSO was proposed to handle FS problems in the binary domain. Then, an improved version of SCSO was developed using a new random operator and memory-based technique. This is to increase the exploitation capability and balance the exploitation and exploration capabilities of the basic SCSO. Finally, a binary version of the memory-based SCSO was obtained to tackle FS problems.

3. Sand Cat Swarm Optimization Algorithm

The sand cat is a type of animal belongs to mammals that live in harsh environments such as deserts. It has different behavior in hunting and living. The mechanism of hunting sand cats is very interesting. These types of animals use their great sense of hearing and hear low-frequency noises. In this way, they can detect that prey is moving underground. The sand cat also has a peculiar ability to quickly dig if prey is underground. The SCSO algorithm consists of two stages in searching for and attacking the prey, as these stages were adopted to design the SCSO algorithm [7].

3.1. Initialization of the Population

The SCSO solutions are created by assigning initial random values to the sand cats. These initial values represent the task’s positions in the search space. Each solution is depicted by a one-dimensional vector that includes multidimensional variables (d) corresponding to the number of features in the original dataset. In SCSO, each feature in the solution (sand cat) has a value $X_i^d\in [L,U]$, where U and L are the upper and lower bounds of the feature, respectively. Based on the set of solutions, the population in the SCSO is represented by a matrix x, which has the shape of ($N\times d$), where (N) is the number of sand cats and d is the number of features in the handling problem. The SCSO is an iterative method like other swarm-based methods. In each iteration, the fitness value is computed for each solution. The initial position of the SCSO in the search space is determined at random as given in Equation (1).

$$X_i\left(k\right)=l_i+r·\left(u_i-l_i\right)$$

(1)

where $X_i\left(k\right)$ denotes the position of the ith population of sand cats in the search space at iteration k, r denotes a random value in the range $[0,1]$, and $l_i$ and $u_i$ represent the lower and upper bounds of the decision variables at the ith dimension in the search space.

The basic SCSO stated that the most appropriate solution is one that is very close to the prey. In addition, the best “sand cats” (i.e., solutions) change positions in the next iteration based on the suitability of the solutions. However, if a solution with good fitness is not found in the next iteration, it will not be saved to memory.

3.2. Exploration of the Search Space

The sand cat’s capability to hear low-frequency sounds is one of its most distinguishing characteristics. The sensitivity range of the sound cat is between [2, 0] kHZ. It begins at 2 kHz and linearly reduces until it approximates 0 kHz. In SCSO, the sensitivity level is referred to as $S_p$. The $S_p$ value is represented by Equation (2).

$$S_p=s_M-\left(\frac{2s_M\times k}{K+K}\right)$$

(2)

A decrease in the value of $S_p$ was detected as the algorithm was iterated. Based on SCSO [7], the value of the constant $S_M$ was set to 2 based on the hearing characteristics of sand cats. It should be noted that k and K are the current and maximum iterations, respectively.

Besides, R is a switching or transition parameter that is responsible for controlling the switching between the exploration and exploitation phases.

$$R=2\times S_p\times random(0,1)-S_p$$

(3)

Equation (3) shows the R controller, where it utilizes the $S_p$ and randomizes the variables. During the search process, the sand cats use a random variable to change their positions. Thus, a new area is discovered based on this random variable.

SCSO uses the variable r as a sensitivity range for each solution (i.e., sand cat) to avoid trapping in local minima. The variable r in Equation (4) utilizes $S_p$ to generate a new value in the search space. Thus, r is the sensitivity parameter in SCSO.

$$r=S_p\times random(0,1)$$

(4)

In SCSO, the position update process for each sand cat is affected by the sensitivity parameter ($S_M$), the current location ($X_c$), and the best-candidate sand cat ($X_{bc}$). These three factors help the sand cat locate the next best possible location close to prey, as illustrated in Equation (5).

$$X(k+1)=r\times (X_{bc}\left(k\right)-random(0,1)\times X_c\left(k\right))$$

(5)

Equation (5) shows that different local optimums in the search space can be found. Thus, the computed location is between $X_c$ and the location of prey.

3.3. Exploitation of the Search Space

In the sand cat’s life, hunting is achieved by exploiting a local area. To mathematically measure the hunting phase in the SCSO algorithm, the distance between $X_c$ and $X_b$ is computed.

$$X_{rnd}=|rand\times X_b\left(k\right)-X_c\left(k\right)|$$

(6)

Equation (6) illustrates this computation. Moreover, the sensitivity range of the sand cat is assumed to be a circle. Based on the behavior of the circle shape, the direction of movement is obtained by an arbitrary angle ($\theta$), where this angle can span between 0 and 360, and its cosine value is between −1 and 1. SCSO selects a random $\theta$ for each solution in the population utilizing the famous Roulette Wheel selection method. Thus, $\theta$ will guide the sand cat to hunt the prey. $X_{rnd}$ in Equation (6) represents a random location that allows the sand cats to approach prey.

3.4. Exploration and Exploitation of the Search Space

During the SCSO search process, the parameters $S_p$ and R are in charge of ensuring a soft dynamic transition between the exploration and exploitation phases. In SCSO, the value of the parameter R depends on the value of $S_p$. Thus, the value of R will decrease as the value of $S_p$ decreases. In addition, when the distribution of the value of $S_p$ is balanced, the value of R will also be balanced. Thus, the chances of operations between the two phases will be sufficient based on the problem. The next position of the sand cat can be determined based on the value of R, which ranges from 1 and −1. When $R\le 1$, the SCSO method focuses on exploitation. Otherwise, the algorithm is forced to go exploring in search of food.

$$X(k+1)=|X_b\left(k\right)-r\times X_{rnd}\times cos\left(\theta \right)|$$

(7)

Equation (7) shows these two phases. The exploration and exploitation phases are based on the use of different radius values. In exploration, traps can be avoided in local optima. In contrast, exploitation is achieved by assisting in hunting prey. The balanced approach of the SCSO algorithm makes the convergence rate very accurate. Thus, it will be suitable for multi-objective tasks. The mathematical formula for positioning update of each sand cat in the exploration and exploitation stages of the basic SCSO can be summed up by Equation (8).

$$X(k+1)=\left\{\begin{array}{c}rcos\left(\theta \right)\left(X_b\left(k\right)-X_{rnd}\left(k\right)\right)\left|R\right|\le 1\hfill \\ r\left(X_{bc}\left(k\right)-rand\times X_c\left(k\right)\right)\left|R\right|>1\hfill \end{array}\right.$$

(8)

The flowchart and pseudo code describing the steps of the standard sand cat swarm optimization algorithm are presented Figure 1 and Algorithm 1, respectively.

Algorithm 1 A pseudo code showing the main steps of the basic sand cat swarm optimization algorithm.

1: Input parameters: K, and k 2: Outcome: The global best solution 3: Randomly initialize the population (i.e., sand cats) 4: Define and initialize $S_p$, r, and R 5: while $k\le K$do 6:    Assess each search agent (i.e., sand cat) 7:    for each search agent do 8:      Randomly obtain an angle $\theta$ with the Roulette wheel selection method in which $0^{\circ }\le \theta \le {360}^{\circ }$ 9:      if ($\left|R\right|\le 1$) then 10:         Update the positions of the search agents using $X_b\left(k\right)-X_{rnd}cos\left(\theta \right)\times r$ 11:      else 12:         Update the positions of the search agents using $r\times (X_{bc}\left(k\right)-random(0,1)\times X_c\left(k\right))$ 13:      end if 14:    end for 15:    $k=k+1$ 16: end while 17: Return the global best solution

4. Proposed Memory-Based Improved SCSO Algorithm

For any optimization method, the exploration and exploitation of the search space must be properly balanced to arrive at the global optimum solution. Exploration, also known as diversification, entails searching globally in the search space, whereas exploitation, also known as intensification, entails searching locally, based on the best solution currently available. Excessive exploration and exploitation negatively impacts algorithm’s performance by lengthening the algorithm’s convergence time and raising the likelihood to drop into a local optimum. The traditional SCSO uses a random initial group of sand cats, which fly around to scout the search area in a random manner. This procedure of random initialization broadens the variety of possible solutions and improves the algorithm’s capacity for exploration. Additionally, SCSO only needs to fine-tune a few parameters, and adaptive adjusting of these swarming elements aids in striking a proper balance between local and global search capacities. SCSO, however, is devoid of an internal memory that may store information of formerly got possible solutions. SCSO never maintains track of the prospective set of solutions that may converge to the global optimum during its iterative process and discards all fitness values that are better than the global best solution. The SCSO’s capacity to properly exploit the search space is reduced, and it tends to converge extremely slowly and may stall at local optimums. To beat this issue, a memory-based mechanism as detailed below was proposed to boost the exploration and exploitation behaviors of SCSO. The proposed Binary Memory-based Sand Cat Swarm Optimization (BMSCSO) as a FS method improves the standard BSCSO method in solving FS problems in three main features to boost its performance score, which can be described as follows:

• First, amendment of the initialization process.
• Second, iterative adaptation of the dominant parameters of BMSCSO during the positioning update process.
• Third, an internal memory to store potential solutions that may eventually converge to the global optimum.

These enhancements points to the basic BSCSO are explained in detail below:

4.1. Improved Initialization Process

In the proposed BMSCSO, the initial population is constructed using the chaotic variable ($y\left(k\right)$) with a uniform random initialization [47,48]. The initialization process employs the number of sand cats in the population and the dimensions of the problem of interest as given in Equation (9).

$$y_i(k+1)=\left|1-2{\left(y_i\left(k\right)\right)}^2\right|$$

(9)

where $y_i\left(k\right)\in [0,1]$ is a chaotic variable, $k\in [1,Dim]$, and $Dim$ is the dimension of the problem, $i\in [1,Num]$, where $Num$ is the number of sand cats in the population.

Thus, the initial vector of the ith sand cat can be defined as shown in Equation (10) after the improved initialization process is achieved.

$$X_i\left(k\right)=l_i+(u_i-l_i)\times y_i(k+1)$$

(10)

where $X_i\left(k\right)$ is the new position of the ith sand cat in the k dimension, $l_i$ and $u_i$ are the lower and upper bounds of the search space at dimension i, respectively.

4.2. Adaptive Positioning Update Process

The technique for amending the mathematical model of BSCSO is described in full in this section. The proposed adaptive positioning update process is then described as a way to enhance the algorithm’s performance score and convergence process.

The proposed BMSCSO tends to provide a new solution $X_i\left(k+1\right)$ at iteration $k+1$ for a given problem that outperforms the present solution $X_i\left(k+1\right)$ at iteration k through the position update process described in Equation (5). In BMSCSO, a slightly different mathematical formula than that employed in BSCSO is utilized to update the locations of the sand cats. Equation (11) provides the positioning updating method of the sand cats in BMSCSO [49].

$$X_i\left(k+1\right)=rand\times W_1\times X_{bc}\left(k\right)-rand\times W_2\times X_c\left(k\right)$$

(11)

where $W_1$ and $W_2$ are adaptive parameters over the iteration loops of the proposed BMSCSO which are computed according to Equations (12) and (13), respectively,

$$W_1=c_0{e}^{(-c_1{\left(\frac{k}{K}\right)}^2)}$$

(12)

$$W_2=d_0-2e^{(-d_1{\left(\frac{k}{K}\right)}^2)}$$

(13)

where k and K are the current and maximum number of iteration values, respectively, where $c0$ is the starting estimate of the duration of the sand cats’ search, $c1$ is the final estimate of the length of the search that could be attained. The parameters $d_0$ and $d_1$ at the conclusion of the iterative process of BMSCSO are the coefficients of the growth exponential function that represents the capacity of sand cats to seek prey.

During the iteration loops of BMSCSO, the exponential functions specified in Equations (12) and (13) are updated iteratively. These adaptive parameters are updated exponentially with regard to time k and lifetime, K, of the sand cats, respectively.

To estimate the parameters $c_0,c_1,d_0$ and $d_1$ for the exponential functions of $W_1$ and $W_2$, there are numerous conventional and intelligent conventional methods reported in the literature that employ meta-heuristics in the adjustment of the parameters of other meta-heuristic algorithms in solving optimization problems [50]. These techniques could need a lot of computational burdens. In this study, the parameters $c_0,c_1,d_0$ and $d_1$ of the models proposed for the adaptive parameters $W_1$ and $W_2$ of BMSCSO were determined using experimental design through the investigation of the proposed BMSCSO on a significant subset of benchmark feature selection problems. The coefficients $c_0,c_1,d_0$ and $d_1$ are all equivalent to 2.0 for all feature selection problems covered in this study. Yet, in the majority of test cases, only good values-and sometimes not even the finest ones-are acquired by experimentation. As a result, these control settings can be changed as needed for various optimization optimal. For each iteration loop of the BMSCSO, the values of the parameters $W_1$ and $W_2$ are updated exponentially.

The BMSCSO is presented with time-varying parameters, where a higher $c_0$ and a lower $d_0$ were originally set and subsequently reversed over the search process, in light of Equations (12) and (13). Hence, it is anticipated that BMSCSO would reveal superior overall performance than the standard SCSO. This may be as a result of the time-varying of $c_0$, $c_1$, $d_0$, and $d_1$, which can balance the capabilities of both local and global search. This indicates that the performance of SCSO may be improved by adapting these settings. The sand cats would group up and converge into a locally or globally optimum location as the iterative BMSCSO process continued. As a result, the population distribution data would differ from that from the early stage.

The adaptive parameters $W_1$ and $W_2$ are identified as function of iterations as displayed in Figure 2a,b, respectively.

The curve of $W_1$ of BMSCSO in Figure 2a demonstrates that the trend of this parameter is decreasing exponentially. The behavior of sand cats in the BMSCSO is impacted by this, and it may be steered towards greater exploration and exploitation, where the sand cats complete their quest by locating prey at the conclusion of their excursion. Moreover, it could cause local optimum solutions to be avoided. Similarly, Figure 2b for the parameter $W_2$ of BMSCSO shows that this parameter’s trend is expanding exponentially. This has an effect on sand cats’ behavior in the BMSCSO and may lead to more exploration and exploitation, as the sand cats finish their hunt by finding prey at the end of their expedition. In this way, the basic SCSO’s exploration and exploitation stages are improved, allowing the sand cats to finally discover prey and avoid becoming separated from their other group members while foraging.

4.3. Further Exploration Behavior

The exploration phase of the BCOS method is influenced by the random behavior of sand cats. As a result, finding a better location and moving toward the prey can become problematic, lowering the solution’s quality [34].

$$Sol(X_i\left(k+1\right),\varphi )=\left|tanh\left(\varphi \left(X_i\left(k+1\right)\right)\right)\right|$$

(14)

where $X_i\left(k+1\right)$ is the position of the ith sand cat in the ($k+1$) iteration, and $\varphi$ increases with the number of iterations as given by Equation (15).

$$\varphi =({\varphi }_{max}-{\varphi }_{min})\left(\frac{k}{K}\right)$$

(15)

where ${\varphi }_{max}$ is the maximum value of $\varphi$, and ${\varphi }_{min}$ is the minimum value of $\varphi$.

A binary matrix of size $Num\times Dim$ is used to initialize the population of sand cats, where $Dim$ is the number of features. When the feature of sand cat is set to 0, it means that this feature is excluded. However, when the dimension of sand cat is set to 1, it means that this feature is selected.

4.4. Implementation of the Interior Memory

With the inclusion of interior memory, each sand cat is given the ability to store its co-ordinates in the hyperspace problem associated with fitness value. This is comparable to locating the best local solutions in the proximity neighborhood. The fitness value of sand cats in the present population is compared to the best fitness value throughout each iteration during the iterative process of MSCSO. Better solutions are saved and the local best solutions got by SCSO are framed. Better solutions are stored, and SCSO frames the best local solutions it obtained. The sand cats of SCSO are also designed to keep track of the best fitness values got thus far by any sand cat in the vicinity, which is equivalent to finding the global best solution. The concepts of global and local best solutions in SCSO are highly effective for boosting the exploitation capacity of SCSO. This characteristic of interior memory in MSCSO offers the potential to get out from local optima and offers better performance than the traditional SCSO. In order to realize global optimum solutions, the MSCSO therefore combines the exploration features of SCSO in the early iterations and the exploitation capabilities of local and global solutions integrated with memory concept in the final iterations. So, in this work, the memory-based approach is employed to raise the quality of the potential solutions in BSCSO. Additionally, it is anticipated that these updating processes would significantly enhance BSCO’s exploratory and exploitative behavior, which in turn will assist BSCSO to find a better solution. The memory matrix is used to store the current position of each solution in order to employ it in the exploitation stage. In the initialization procedure, the memory can be represented by the current position of the sand cats. As per this, the memory can be represented for all sand cats as shown below, Equation (16):

$$m=\left[\begin{array}{cccc}{m}_1^1& m_2^1& \dots & m_d^1\\ m_1^2& m_2^2& \dots & m_d^2\\ ⋮& ⋮& ⋮& ⋮\\ m_1^n& m_2^n& \dots & m_d^n\end{array}\right]$$

(16)

where $m_j^i$ denotes the memory for each sand cat in the ith solution at the jth dimension.

The mathematical model for the new positioning of sand cats in the proposed MSCSO was amended over that of the basic SCSO. Accordingly, the new positions of the sand cats in the proposed MSCSO can be located as presented in Equation (17).

$$X(k+1)=\left\{\begin{array}{c}fb-\left|r_a\times fb-X\left(k\right)\right|·SB\left|R\right|\le 1.0\hfill \\ X\left(k\right)+r_g\times r_c\left(m\left(c\right(k\left)\right)-lb\left(k\right)\right)else\hfill \end{array}\right.$$

(17)

where $X(k+1)$ and $X\left(k\right)$ represent the new and present positions of sand cats at iterations $k+1$ and k, respectively, $fb$ represents the global best position ever obtained by any sand cat up until the kth iteration, $m\left(c\right(k\left)\right)$ represents the best solutions found and reserved so far at iteration k by the best sand cats where c denotes the memory component of the sand cats utilized at iteration k, $lb\left(k\right)$ stands for the best position so far reached by sand cats at iteration k, $SB=(r_b-0.5)$ and it presents either −1 or 1 to modify the orientation of the search process, $r_a$, $r_b$ and $r_c$ are random values formed with a uniform distribution in the rang $[0,1]$, R and $r_g$ are two adaptive parameters specified as functions of iterations as demonstrated in Equations (18) and (19), respectively.

$$r_g={\tau }_0-\left({\tau }_1\times k/K\right)$$

(18)

where k and K identify the present iteration value and maximum value of iterations, respectively, ${\tau }_0$ (${\tau }_0=2$) stands for the incipient estimate of the function $r_g$ at the initial iteration value and ${\tau }_1$ (${\tau }_1=2$) is a fixed value employed to control exploitation and exploration abilities. These parameters’ values were determined thorough investigation and application to a sizable portion of FS problems, where they reported the best outcomes and served as the basis for all succeeding findings.

$$R=2r_g\times r_k-r_g$$

(19)

where $r_k$ is a random value at the kth index which has a uniform distribution in the interval $[0,1]$.

Equation (19) demonstrates that R is repeatedly updated during the path of iterations of the MSCSO algorithm.

The parameter c in $m\left(c\right(k\left)\right)$ can be identified as presented in Equation (20).

$$c=(n-1)·rand(n,1)$$

(20)

where n is the total number of sand cats, and $rand(n,1)$ is a vector of random values produced with a uniform distribution in the interval $[0,1]$.

Sand cats update their memory at each iterative loop throughout the processing of MSOCS. In this, they can identify if the quality of the new solution the sand cats find is of higher quality than their prior position. In this regard, Equation (21) may be utilized to iteratively update the memory of sand cats.

$$m(c\left(k\right)=\left\{\begin{array}{cc}X\left(k\right)\hfill & iff\left(X\left(k\right)\right)\ge f\left(m\left(c\right(k\left)\right)\right)\hfill \\ m\left(c\right(k\left)\right)\hfill & iff\left(X\left(k\right)\right)<f\left(m\left(c\right(k\left)\right)\right)\hfill \end{array}\right.$$

(21)

where $f(·)$ denotes the fitness function’s score.

It is expected from the discussions and the mathematical model of MSCSO described above that the proposed MSCSO can be highly efficient in solving feature selection problems.

5. The Proposed Binary SCS Method for Feature Selection

The feature selection tasks are binary optimization processes where solutions are represented in binary values (i.e., ‘0’ or ‘1’). In a specific solution, the selected features are assigned a value of one; otherwise, (i.e., not selected) are assigned a value of zero. This indicates that any meta-heuristic strategy used to solve FS tasks requires generating a binary form of the solution. SCSO’s first version was created to deal with continuous domains. To generate a binary version of SCSO (BSCSO), a solution must be characterized using a binary vector. The solution elements can only have values of ‘0’ or ‘1’. Regarding the algorithm’s update strategy, the solutions shift their positions in the feature space. This necessitates using transfer functions to ensure that the solution’s elements are either ‘0’ or ‘1’.

As they produce results in the range [0, 1], logistic transformation functions, also referred to as the S-shaped family, are reliable for mapping operations. This is necessary to explain the probability of changing a binary solution element from ‘0’ to ‘1’ and conversely [51]. Furthermore, Mirjalili et al. presented the V-shaped as a family of potent transformation functions in the field of feature selection that performed the same purpose as the S-shaped family [52]. The slope of the transformation function can be used to distinguish between exploitation and exploration characteristics. However, when the curve of the transformation function is very steep, it contributes to bad exploration. Also, when the curve of the transformation function is flat or less steep, it leads to poor exploitation and readily slips into local minima [53,54]. In addition, a U-shaped transfer function was evolved in [55] with $\eta$ and $\rho$ serving as two control parameters that, respectively, set the slope and width of the U-shaped function’s basin. In practice, no transfer function has yet been shown to be the best for problems involving feature selection. Three alternative transfer functions from three categories, referred to as S-shaped, V-shaped, and U-shaped, were studied in this study, although only an S-shaped TF was looked at because it is the most effective TF used in this field and allowed for the creation of binary versions of the proposed MSCSO and basic SCSO. As a result, this study explains three different transfer functions, and Figure 3 illustrates the essential graphs of these transfer functions. These transfer functions define the likelihood of updating the elements of the binary solution from ‘0’ to ‘1’ and conversely.

Later in the experimental findings section, the effectiveness of the S-shaped transfer function depicted in Figure 3a will be observed. As an example of how to convert a continuous search space into a binary one to address feature selection problems, three distinct transfer function types from the S-shaped, V-shaped, and U-shaped families are discussed below.

• S−shaped transfer function: The sigmoid function from the S-shaped family, as stated in Equation (22) [51], and shown in Figure 3a, was used to transform the search space of the proposed and basic algorithms applied in this work from continuous to binary.

  $$S\left(x_{t+1}^{i,j}\right)=\frac{1}{1+e^{-x_t^{i,j}}}$$

  (22)

  where S is the transmutation vector, $S\left(x_{t+1}^{i,j}\right)$ indicates the probability value generated by this transfer function, $x_t^{i,j}$ and $x_{t+1}^{i,j}$ indicate the current and next positions of search agent i at dimension j and iterations t and $t+1$, respectively.
  Equation (22) is a stable S-shaped transformation function that converts an unbounded input into a limited output, which changes any interval’s domain to the range $[0,1]$. The probability value of changing the position value increases as the slope of the S-shaped transformation function lowers, as shown in Figure 3a, which may effectively update search agents’ locations and find the best solutions. The fact that the S-shaped transformation function’s speed is increasing makes it easier to calculate position values. In this, the search agent’s position is converted into a probability value using the transfer function presented in Equation (22), from which the search agent’s next position, $x_{t+1}^{i,j}$ is computed using the probability value of its present position. As a result, Equation (23) guarantees the binary value of a Sigmoid expression by using the commonly utilized stochastic threshold.

  $$x_{t+1}^{i,j}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}rand<S\left(x_{t+1}^{i,j}\right)\hfill \\ 0\hfill & \mathrm{if}rand\ge S\left(x_{t+1}^{i,j}\right)\hfill \end{array}\right.$$

  (23)

  where $rand$ stands for random number created utilizing a uniform distribution in the range $[0,1]$, $x_{t+1}^{i,j}$ implements the position of search agent i at iteration $t+1$ dimension j, and $S\left(x_t^{i,j}\right)$ produces a probability value as presented in Equation (22).
  Equation (23) states that the probability value of changing the search agents’ next positions is calculated using the present positions of the search agents. The sigmoid transfer function in Equation (23) makes it clear that the current version of this function might not provide a good balance between exploration and exploitation, where the exploration amount should be higher than the exploitation amount at the beginning of the optimization process. Therefore, it’s possible that some intriguing areas of the search space may go untouched. Thus, there is a chance that the proposed BMSCSO might become trapped in local optima. In spite of several attempts to fix this problem, no one was able to stop entrapment in local optima [55].
• V-shaped transfer function: The V-shaped transfer function shown in Equation (24) [56] and displayed in Figure 3b could be employed in further work of this study to calculate the probability of altering the search agents’ position from continuous to binary in the basic SCSO and developed BMSCSO as feature selection algorithms as illustrated in Figure 4.

  $$V\left(x_{t+1}^{i,j}\right)=\left|tanh\left(x_t^{i,j}\right)\right|$$

  (24)

  where V denotes the V-shaped transfer function, and $V\left(x_{t+1}^{i,j}\right)$ indicates the likelihood of this transfer function of the position, $x_{t+1}^{i,j}y$, for search agent i at iteration $t+1$ and dimension j.
  The V-shaped transfer function presented in Equation (24) varies from the S-shaped transfer function in Equation (22) in that this function has been updated with new rules. This is evident from Figure 3b compared to that shown in Figure 3a. Simply expressed, Equation (25) may be used to convert the continuous solution obtained from Equation (24) into a binary one depending on the recovered probability outcomes of the V-shaped transfer function.

  $$x_{t+1}^{i,j}=\left\{\begin{array}{cc}\neg x_t^{i,j}\hfill & \mathrm{if}rand<V\left(x_{t+1}^{i,j}\right)\hfill \\ x_t^{i,j}\hfill & \mathrm{if}rand\ge V\left(x_{t+1}^{i,j}\right)\hfill \end{array}\right.$$

  (25)

  where $\neg x_t^{i,j}$ signifies the complement of the solution $x_t^{i,j}$, $rand$ specifies a random value generated between 0 and 1 and $V\left(x_{t+1}^{i,j}\right)$ embodies the probability value of the V-shaped transfer function.
  Figure 3b illustrates that the V-shaped transfer function is symmetrical. Equation (25) may be used to observe that the position updating is also different since the search agents are reversed and are not required to accept values of ‘0’ or ‘1’. When the present position value is low during an iteration, the V-shaped transfer function encourages the search agents to stay in their current position. As an alternative, the search agents change to complement when the existing position value is high. Meta-heuristics may still struggle with the problem of falling into local optima as a result of this process, which may have an impact on how search agents update their positions and find the optimal solution. It is obvious that issues like the S-shaped transfer function may still lead a meta-heuristic algorithm to display biased stability between the exploration and exploitation phases. It could be essential to research additional transfer functions in an effort to better balance exploration and exploitation. Therefore, in addition to the transfer functions previously discussed, U-shaped transfer functions may be employed as alternatives to transform continuous algorithms into binary ones.
• U-shaped transfer function: The U-shaped transfer function presented in Equation (26) [55] and displayed in Figure 3c could be applied to calculate the probability of altering the search agents’ position from continuous to binary in the basic and proposed feature selection algorithms.

  $$U\left(x_{t+1}^{i,j}\right)=\eta \left|{\left(x_t^{i,j}\right)}^{\rho }\right|\eta =1,\rho =1.5,2.0,3.0,4.0$$

  (26)

  where $\eta$ and $\rho$ are two basic parameters, where $\eta$ determines the function’s slope and $\rho$ represents the width of the curve’s basin, and $U\left(x_{t+1}^{i,j}\right)$ denotes the probability of the position of search agent i.
  The U-shaped transfer function was produced using two control parameters, $\eta$ and $\rho$, where $\eta$ permits modifying the saturation point of this function and $\rho$ specifies the width of the transfer function’s trough. The pace at which the U-shaped function reaches the saturation point affects how likely it is that the bit will be flipped. This promotes exploration since variables can change fast, and the lower the exploratory behavior, the larger the U-shaped curve. Using Equation (26), the values for the continuous solution elements can be converted to binary values by using Equation (27).

  $$x_{t+1}^{i,j}=\left\{\begin{array}{cc}\neg x_t^{i,j}\hfill & \mathrm{if}rand<U\left(x_{t+1}^{i,j}\right)\hfill \\ x_t^{i,j}\hfill & \mathrm{if}rand\ge U\left(x_{t+1}^{i,j}\right)\hfill \end{array}\right.$$

  (27)

  where $U\left(x_{t+1}^{i,j}\right)$ forms the probability value of the U-shaped transfer function and $rand$ denotes a uniform random number generated between 0 to 1.
  Equation (27) shows how the search agent’s current position might vary based on the probability value $U\left(x_{t+1}^{i,j}\right)$ got by Equation (26). In order to establish if the value of the solution $x_t^{i,j}$ at the current iteration is flipped, the random values produced using $rand$ are essential. Exploration is an important stage in early rounds of exploring the full search space. The latter phase is therefore required in the last iterations to find better solutions after switching from the exploration stage to the exploitation step.

As mentioned earlier, there are a variety of transfer functions, including S-shaped, V-shaped, and U-shaped ones, which have been extensively used in the literature to convert continuous data into binary data. The authors explained in [52] that the S-shaped and V-shaped transfer functions provided outcomes in binary optimization feature selection approaches that were quite similar. In order to get binary variants of the native continuous algorithms of the proposed MSCSO and basic SCSO, this work applied the sigmoid S-shaped transfer function described in Equation (22) and displayed in Figure 3a. This transfer function was used in this work due to its simplicity and small number of parameters as reported extensively in [10,57,58].

In the FS task, the goal is to reduce the number of features while improving the performance of the classifier (i.e., the learning model) [37]. In this sense, the FS method is a multi-objective optimization method designed to obtain the global solution that maximizes model performance while preserving the minimum number of relevant features.

In the current study, the objective function (i.e., fitness) of the solution is determined by the classification error rate (i.e., an accuracy of one unit) of the k-NN on the validation dataset and the number of selected features. Optimizing the k-NN error rate while minimizing the number of selected features yields a multi-objective function. As a result, to achieve a balance between these two criteria, one fitness function is used to merge both, as shown in Equation (28):

$$fitness=\alpha {\zeta }_k+\beta \frac{\left|R\right|}{\left|N\right|}$$

(28)

where ${\zeta }_k$ represents the classification error rate arrived at by the k-NN classier, $\left|R\right|$ and $\left|N\right|$ stand for the number of selected and original features in the dataset, respectively, $\alpha$ and $\beta$ are two counteractive parameters in the interval from 0 to 1. They represent respectively the weights of the classification rate and the selection ratio of the selected features, where $\alpha \in [0,1]$ and $\beta$ is the complement of $\alpha$, i.e., $\beta =\left(1-\alpha \right)$ [59].

Complexity Analysis of BSCSO and BMSCSO

Big-O notation was utilized to estimate the time complexity of the proposed FS methods, namely BSCSO and BMSCSO. The time complexity analysis of these methods for feature selection tasks primarily depends on the dataset dimensions (d), initialization stage, number of iterations (K), fitness function cost (C), population size (n), and number of experiments (V). The S-shaped transfer function is also used to generate binary versions of BSCSO and BMSCSO. The overall computational complexity of BSCSO and BMSCSO can be represented using Big-O notation as presented below:

$$\begin{array}{ccc}\hfill \mathcal{O}\left(BSCSO\right)& =& \mathcal{O}\left(init.\right)+\mathcal{O}\left(K\left(pop.update\right)\right)\hfill \\ \hfill & +& \mathcal{O}\left(K\left(fitnesseval.\right)\right)+\mathcal{O}\left(K\left(selection\right)\right)\hfill \end{array}$$

(29)

By calculating the Big-O for each phase in Equation (30), the time complexity for BSCSO can be represented as the following:

$$\begin{array}{ccc}\hfill \mathcal{O}\left(BSCSO\right)& =& \mathcal{O}\left(nd\right)+\mathcal{O}\left(VKnd\right)\hfill \\ \hfill & +& \mathcal{O}\left(VKnc\right)+\mathcal{O}\left(VKnd\right)\hfill \end{array}$$

(30)

For BMSCSO, the time complexity is the same as for BSO except that memory-based and adaptive update of positions are added in each iteration. Since the memory update is evaluated for each search agent within each iteration, it will be computed as $\mathcal{O}\left(VKnd\right)$. The adaptive update of positions utilizes a discrete loop as shown in Algorithm 2. Thus, its time complexity is $\mathcal{O}\left(VKnd\right)$. Based on these two additional procedures, the time complexity of BMSCSO, as illustrated in Figure 4, can be given as shown below:

$$\begin{array}{ccc}\hfill \mathcal{O}\left(BMSCSO\right)& =& \mathcal{O}\left(nd\right)+\mathcal{O}\left(VKnd\right)\hfill \\ \hfill & +& \mathcal{O}\left(VKnc\right)+\mathcal{O}\left(2VKnd\right)+\mathcal{O}\left(2VKnd\right)\hfill \end{array}$$

(31)

Algorithm 2 A pseudo code showing the mains steps of the proposed binary memory-based sand cat swarm optimizer (BMSCSO).

1: Input parameters: $S_p$, r, R, K, k 2: Outcome: The global best solution 3: Initialize the population of the BMSCSO algorithm 4: Initialize the memory for the initial population 5: Define and initialize the input parameters 6: while$k\le K$do 7:    Assess each search agent (i.e., sand cat) 8:    for each search agent do 9:      if (the position of the sand cat is between the lower and upper limits) then 10:         initialize the memory with the current position using Equation (16) 11:      end if 12:      Randomly obtain an angle $\theta$ using the roulette wheel selection method for which $0^{\circ }\le \theta \le {360}^{\circ }$ 13:      if ($\left|R\right|\le 1$) then 14:         Update the positions of the search agents using $fb-\left|r_a\times fb-X\left(k\right)\right|·SB$ 15:      else 16:         Update the positions of the search agents using $X\left(k\right)+r_g\times r_c\left(m\left(c\right(k\left)\right)-lb\left(k\right)\right)$ which uses memory-based technique 17:      end if 18:    end for 19:    for each search agent do 20:      Adapt the solution using $X_i\left(k+1\right)=rand\times W_1\times X_{bc}\left(k\right)-rand\times W_2\times X_c\left(k\right)$ 21:    end for 22:    Assess each search agent 23:    Update the current solution 24:    Update the global and best solution 25:    $k++$ 26: end while 27: Return the global best solution

As indicated by Equation (31), the major criteria for the complexity issue are the iteration count and the size of the population. Moreover, because $ndllVKnd$ and $ndllVKcn$, the component $nd$ can be excluded from the time complexity given in Equation (31). As a consequence, the BMSCSO’s time complexity can be presented as:

$$\begin{array}{c}\hfill \mathcal{O}\left(BMSCSO\right)\cong \left(VK\right(nf+nM)d+VK(nf+nm\left)c\right)\end{array}$$

(32)

6. Experimental Results

6.1. Training and Testing Datasets

Table 2. Medical benchmark datasets.

Number	Dataset	Number of Features	Number of Instances	Number of Classes
1	Diagnostic	30	569	2
2	BreastEW	30	596	2
3	Prognostic	33	194	2
4	Coimbra	9	115	2
5	Retinopathy	19	1151	2
6	ILPD-Liver	10	583	2
7	Lymphography	18	148	4
8	Parkinsons	22	194	2
9	ParkinsonC	753	755	2
10	SPECT	22	267	2
11	Cleveland	13	297	5
12	HeartEW	13	270	2
13	Hepatitis	18	79	2
14	SAHeart	9	461	2
15	Spectfheart	43	266	2
16	Thyroid0387	21	7200	3
17	Heart	13	302	5
18	Pima-diabetes	9	768	2
19	Leukemia	7129	72	2
20	Colon	2000	62	2
21	Prostate_GE	5966	102	2

shows the datasets used in this study. 21 medical benchmark datasets are used in the experiments. For the benchmark datasets, nine of them were downloaded from the UCI (Diagnostic, Coimbra, BreastEW, Prognostic, Retinopathy, ILPD-Liver, Lymphography, Parkinsons, and ParkinsonC). Seven datasets were downloaded from KEEL (SPECT, Cleveland, HeartEW, Hepatitis, SAHear, Spectfheart, and Thyroid0387). Two datasets (Heart and Pima-diabetes) were downloaded from Kaggle. The remaining three datasets, namely Leukemia, Colon and Prostate_GE, were downloaded from different locations.

(Prostate_GE from https://jundongl.github.io/scikit-feature/datasets.html (accessed on 23 February 2023)), (Colon from https://jundongl.github.io/scikit-feature/datasets.html, (accessed on 23 February 2023)), and (Leukemia from https://jundongl.github.io/scikit-feature/datasets.html, (accessed on 23 February 2023)).

6.2. Experimental Setup

In our experiments, each dataset’s instances were randomly divided into training and testing partitions. The split was 80% for training and 20% for testing as in the previous closed memory-based FS method [16]. Furthermore, to assess the generalizability of the suggested techniques (i.e., BSCSO and BMSCSO), the selected subset of features was evaluated using a k-NN classifier with a Euclidean distance of 5 [31]. Furthermore, as shown in Equation (28), the objective function’s main parameters are set to a = 0.99 and b = 0.01. These values have frequently appeared in many related works [31,37,60]. The upper and lower bounds are set to 1 and 0, respectively. The population size was set to 30, and the maximum number of iterations was 100 for each algorithm to ensure a fair comparison of the contestant algorithms. The details of the parameter settings for the comparison algorithms in this study are shown in

Table 3. Parameter settings of the competing FS methods.

Algorithm	Parameter	Value
All algorithms	Population size, Number of iterations	30, 100
BBBO	Immigration probability bounds for each gene	$[0,1]$
	Habitat modification probability	1
	Immigration rates for each island and maximum migration	1
	Mutation probability	0
	Step size for numerical integration of probabilities	1
BMFO	Logarithmic spiral	0.75
	Convergence constant	[−1, −2]
BPSO	Cognitive factor, Social factor	1.8, 2.0
	Inertia weight	$[0.9,0.4]$
BTLBO	No particular parameters	Population size is 5 as this method has two phases
BAFT	${\alpha }_0$, ${\alpha }_1$, ${\beta }_0$, ${\beta }_1$	1.0, 2.0, 0.1, 2.0
	$T{d}_0$, s, L	2.0, 2.0, 100
BLSHADE	Scaling factor $M_F$	0.5
	$M_{CR}$	0.5
	$Pbest$	0.11
	Archive rate, memory size	1.4, 5
BHBA	($\beta$), C	6.0, 2.0
BMSCSO	Sensitivity range (rG)	[2, 0]
	Phases control range (R)	[−2rG, 2rG]
	Maximum Sensitivity range (S)	2

.

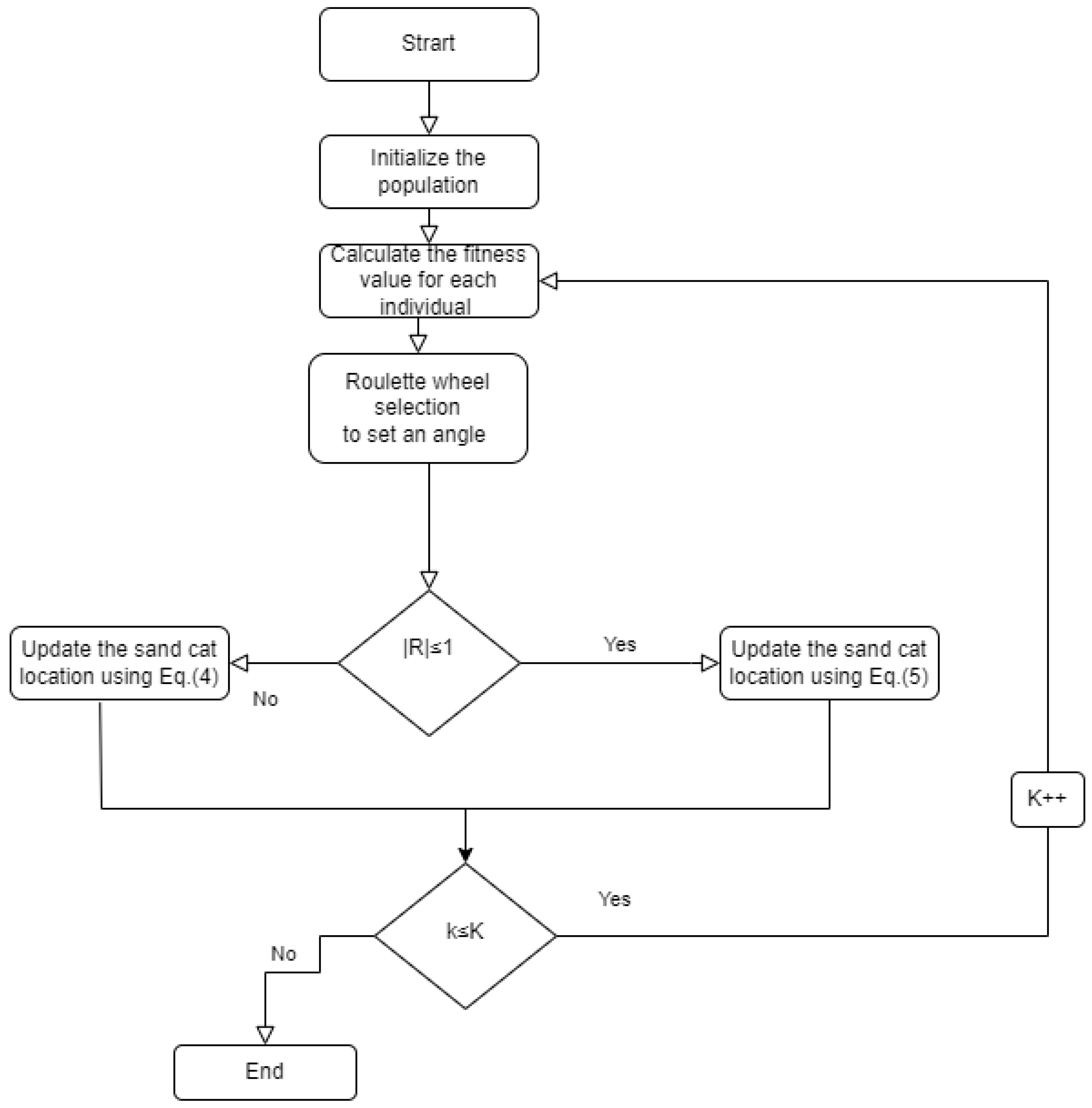
6.3. Performance Evaluation

To thoroughly examine the proposed BMSCSO’s performance, its results on FS problems were compared to those of the standard BSCSO and another seven FS methods that were published in the literature: Binary Biogeography-Based Optimization (BBBO) [61], Binary Moth-Flame Optimization (BMFO) algorithm [62], Binary Particle Swarm Optimization (BPSO) [63], Binary Teaching-Learning-Based Optimization (BTLBO) [64], Binary Ali Baba and the Forty Thieves (BAFT) algorithm [10], Binary Honey Badger Algorithm (BHBA) [65] and Binary Success-History based Adaptive Differential Evolution with Linear population size reduction (BLSHADE) [66]. In this comparison, not only were the specifics of the experimental findings provided, but also a thorough and meticulous comparison with those comparative optimization techniques was made. In order to fairly compare the proposed BMSCSO with the comparative optimization techniques, the same experimental settings, including population size and number of iterations, were used to all of the competing algorithms. The parameter settings for each of the contending methods are listed in Table 3.

The experiments were conducted 30 separate runs in order to get results that were statistically significant. The outcomes of the statistical analysis were then obtained based on the general capabilities and conclusions gained during these runs. Each dataset has the same amount of features as it has in terms of dimension. The proposed BMSCSO’s performance was assessed using classification accuracy, sensitivity, specificity, fitness values, and the average amount of selected features during the independent runs. This performance was then compared to the performance of other FS methods using all of the aforementioned rendering criteria. In all comparison tables, the best results are emboldened to give them more prominence over the other results.

The average classification accuracy scores for the standard BSCSO, the proposed BMSCSO, and other competing methods are presented in

Table 4. Comparison results between the proposed BMSCSO and other FS methods based on classification accuracy.

Dataset	Measure	BSCSO	BMSCSO	BBBO	BMFO	BPSO	BTLBO	BAFT	BLSHADE	BHBA
Diagnostic	AV	0.9439	0.9825	0.9634	0.9431	0.8575	0.8044	0.9540	0.9699	0.9823
	SD	0.0863	0.0000	0.0086	0.0731	0.1112	0.1044	0.0074	0.0101	0.0000
Breast	AV	0.9857	0.9931	0.9730	0.9191	0.8502	0.7331	0.9824	0.9868	0.9926
	SD	0.0000	0.0064	0.0035	0.1213	0.1558	0.1661	0.0066	0.0033	0.0000
Prognostic	AV	0.8737	0.8947	0.8184	0.7754	0.7211	0.7018	0.8895	0.8947	0.8947
	SD	0.0372	0.0471	0.0144	0.0669	0.0506	0.0348	0.0118	0.0000	0.0000
Coimbra	AV	0.8939	1.0000	0.8783	0.7971	0.6522	0.6014	0.8174	0.8261	0.8261
	SD	0.1611	0.0000	0.0289	0.1258	0.2157	0.1827	0.0194	0.0000	0.0000
Retinopathy	AV	0.7391	0.7391	0.7077	0.7236	0.6306	0.6225	0.6939	0.7139	0.7417
	SD	0.0000	0.0000	0.0108	0.0359	0.0511	0.0236	0.0196	0.0200	0.0024
ILPD	AV	0.7490	0.7492	0.7371	0.7130	0.6899	0.6896	0.7374	0.7461	0.7739
	SD	0.0171	0.0151	0.0118	0.0549	0.0266	0.0284	0.0167	0.0113	0.0000
Lymphography	AV	0.9333	0.9467	0.8575	0.7908	0.7333	0.7310	0.5389	0.5594	0.6402
	SD	0.0298	0.0471	0.0150	0.0646	0.0701	0.0668	0.0415	0.0437	0.0208
Parkinsons	AV	0.9900	0.9900	0.9974	0.9718	0.9231	0.9094	0.9744	0.9744	0.9744
	SD	0.0224	0.0224	0.0103	0.0483	0.0476	0.0385	0.0000	0.0000	0.0000
ParkinsonC	AV	0.7973	0.8271	0.6956	0.6916	0.6826	0.6770	0.7483	0.7550	0.7550
	SD	0.0304	0.0102	0.0021	0.0118	0.0087	0.0057	0.0094	0.0000	0.0000
SPECT	AV	0.8060	0.8496	0.7377	0.7006	0.6252	0.6088	0.7585	0.7849	0.8377
	SD	0.0921	0.0379	0.0181	0.0445	0.0573	0.0615	0.0207	0.0215	0.0169
Cleveland	AV	0.8067	0.8200	0.6808	0.6661	0.6113	0.5910	0.5729	0.5763	0.5763
	SD	0.0506	0.0548	0.0100	0.0500	0.0477	0.0419	0.0076	0.0000	0.0000
HeartEW	AV	0.8889	0.9259	0.8395	0.8463	0.7414	0.6796	0.8667	0.8741	0.9630
	SD	0.0370	0.0000	0.0301	0.0567	0.1028	0.0672	0.0275	0.0304	0.0000
Hepatitis	AV	1.0000	1.0000	1.0000	0.9708	0.9208	0.8792	0.8750	0.8750	0.9250
	SD	0.0000	0.0000	0.0000	0.0426	0.0769	0.0675	0.0000	0.0000	0.0280
Saheart	AV	0.7826	0.7957	0.7246	0.6953	0.6054	0.6022	0.7109	0.7304	0.7609
	SD	0.0000	0.0424	0.0096	0.0491	0.0476	0.0531	0.0182	0.0179	0.0000
Spectfheart	AV	0.8584	0.8875	0.8516	0.8063	0.7597	0.7497	0.8679	0.8717	0.9094
	SD	0.0252	0.0300	0.0155	0.0470	0.0547	0.0364	0.0267	0.0207	0.0084
Thyroid	AV	0.9797	0.9686	0.9751	0.9737	0.9542	0.9401	0.9800	0.9836	0.9875
	SD	0.0182	0.0214	0.0036	0.0171	0.0192	0.0105	0.0023	0.0008	0.0010
Heart	AV	0.8963	0.9037	0.8233	0.8222	0.7161	0.6633	0.7867	0.8067	0.8500
	SD	0.0310	0.0203	0.0230	0.0552	0.0864	0.0683	0.0361	0.0190	0.0000
PimaDiabetes	AV	0.8156	0.8260	0.7712	0.7495	0.7004	0.7192	0.7765	0.7974	0.7974
	SD	0.0116	0.0531	0.0000	0.0300	0.0679	0.0490	0.0286	0.0000	0.0000
Leukemia	AV	1.0000	1.0000	0.9952	0.9524	0.9238	0.9262	0.9286	0.9429	0.9857
	SD	0.0000	0.0000	0.0181	0.0433	0.0261	0.0130	0.0000	0.0319	0.0319
Colon	AV	0.8714	0.9333	0.7222	0.7222	0.6139	0.5500	0.8333	0.8667	0.9167
	SD	0.0726	0.0913	0.0505	0.0911	0.0742	0.0603	0.0000	0.0456	0.0000
ProstateGE	AV	1.0000	1.0000	0.8517	0.8117	0.7700	0.7517	0.9000	0.9000	0.9000
	SD	0.0000	0.0000	0.0091	0.0468	0.0466	0.0404	0.0000	0.0000	0.0000

along with their associated standard derivation findings.

Greater accuracy results indicate superior robustness, while lower SD values indicate algorithmic stability. Table 4 shows that the proposed BMSCSO obtained the maximum accuracy in a total of 14 datasets and was rated first solely based on having the best accuracy results in 10 datasets. BSCSO was able to acquire the optimal accuracy results in 3 datasets, namely Hepatitis, Leukemia and ProstateGE. BHBA came in second place by exclusively achieving the best results in 5 datasets and realized the best accuracy score in a total of 6 datasets. BBBO ranked third by getting the best accuracy results exclusively in 1 dataset, namely Parkinsons, and also got the best result in the Parkinsons dataset. Outstandingly, both BSCSO and BMSCSO obtained 100% accuracy in the Hepatitis, Leukemia and ProstateGE datasets. When reading Table 4, one can notice that the proposed BMSCSO was more reliable than its competitors, having the lowest SD values in several datasets and much better than many other rival methods.

Table 5. Comparison results between the proposed BMSCSO and other methods based on fitness values.

Dataset	Measure	BSCSO	BMSCSO	BBBO	BMFO	BPSO	BTLBO	BAFT	BLSHADE	BHBA
Diagnostic	AV	0.0802	0.0134	0.0413	0.0599	0.1446	0.0926	0.0512	0.0354	0.0217
	SD	0.1494	0.0006	0.0088	0.0725	0.1102	0.0049	0.0080	0.0103	0.0004
Breast	AV	0.0182	0.0176	0.0308	0.0832	0.1524	0.0494	0.0217	0.0179	0.0107
	SD	0.0000	0.0015	0.0033	0.1204	0.1542	0.0034	0.0073	0.0039	0.0005
Prognostic	AV	0.1495	0.1399	0.1848	0.2266	0.2802	0.1895	0.1148	0.1089	0.1080
	SD	0.0110	0.0138	0.0141	0.0661	0.0500	0.0143	0.0118	0.0004	0.0006
Coimbra	AV	0.2373	0.1347	0.1253	0.2049	0.3492	0.1234	0.1879	0.1797	0.1762
	SD	0.1439	0.0000	0.0282	0.1242	0.2137	0.0289	0.0190	0.0009	0.0015
Retinopathy	AV	0.2749	0.2745	0.2951	0.2777	0.3700	0.2953	0.3083	0.2884	0.2606
	SD	0.0059	0.0062	0.0110	0.0359	0.0503	0.0219	0.0194	0.0198	0.0027
ILPD	AV	0.2733	0.2650	0.2651	0.2870	0.3115	0.2614	0.2640	0.2556	0.2268
	SD	0.0132	0.0159	0.0123	0.0542	0.0263	0.0156	0.0174	0.0113	0.0000
Lymphography	AV	0.1401	0.1343	0.1465	0.2108	0.2680	0.1439	0.4621	0.4409	0.3613
	SD	0.0242	0.0160	0.0144	0.0639	0.0694	0.0083	0.0418	0.0432	0.0204
Parkinsons	AV	0.1160	0.1109	0.0078	0.0313	0.0798	0.0056	0.0305	0.0296	0.0280
	SD	0.0133	0.0108	0.0098	0.0475	0.0467	0.0048	0.0005	0.0010	0.0006
ParkinsonC	AV	0.2448	0.2415	0.3068	0.3108	0.3191	0.3049	0.2554	0.2484	0.2476
	SD	0.0049	0.0087	0.0021	0.0116	0.0086	0.0027	0.0091	0.0009	0.0005
SPECT	AV	0.1960	0.1810	0.2656	0.3012	0.3760	0.2558	0.2453	0.2187	0.1662
	SD	0.0337	0.0158	0.0179	0.0438	0.0566	0.0151	0.0201	0.0203	0.0173
Cleveland	AV	0.3514	0.3337	0.3211	0.3342	0.3894	0.3059	0.4287	0.4243	0.4226
	SD	0.0506	0.0551	0.0100	0.0493	0.0476	0.0238	0.0078	0.0015	0.0008
HeartEW	AV	0.1006	0.1077	0.1631	0.1562	0.2601	0.1457	0.1366	0.1288	0.0411
	SD	0.0159	0.0374	0.0295	0.0563	0.1018	0.0273	0.0279	0.0306	0.0006
Hepatitis	AV	0.0638	0.0772	0.0036	0.0313	0.0818	0.0033	0.1289	0.1270	0.0778
	SD	0.0005	0.0285	0.0007	0.0420	0.0757	0.0006	0.0004	0.0007	0.0268
Saheart	AV	0.2524	0.2840	0.2792	0.3068	0.3958	0.2812	0.2911	0.2709	0.2401
	SD	0.0024	0.0490	0.0093	0.0481	0.0470	0.0130	0.0177	0.0181	0.0000
Spectfheart	AV	0.1404	0.1367	0.1526	0.1969	0.2425	0.1439	0.1373	0.1321	0.0959
	SD	0.0647	0.0298	0.0150	0.0466	0.0542	0.0166	0.0263	0.0195	0.0078
Thyroid	AV	0.0324	0.0475	0.0297	0.0299	0.0493	0.0252	0.0152	0.0144	0.0144
	SD	0.0198	0.0243	0.0039	0.0168	0.0187	0.0038	0.0030	0.0015	0.0008
Heart	AV	0.1180	0.0915	0.1793	0.1791	0.2855	0.1656	0.2174	0.1974	0.1531
	SD	0.0410	0.0078	0.0229	0.0543	0.0857	0.0217	0.0362	0.0182	0.0000
PimaDiabetes	AV	0.2972	0.2589	0.2320	0.2526	0.3011	0.2320	0.2283	0.2058	0.2056
	SD	0.0150	0.0458	0.0007	0.0289	0.0665	0.0006	0.0294	0.0006	0.0000
Leukemia	AV	0.1040	0.0756	0.0101	0.0527	0.0803	0.0095	0.0771	0.0615	0.0182
	SD	0.0001	0.0387	0.0178	0.0429	0.0258	0.0129	0.0001	0.0316	0.0308
Colon	AV	0.3679	0.3845	0.2803	0.2806	0.3871	0.2498	0.1712	0.1369	0.0878
	SD	0.0452	0.0452	0.0498	0.0902	0.0734	0.0380	0.0001	0.0451	0.0005
ProstateGE	AV	0.1836	0.1840	0.1522	0.1919	0.2326	0.1981	0.1052	0.1039	0.1015
	SD	0.0439	0.0657	0.0091	0.0463	0.0461	0.0125	0.0000	0.0000	0.0000

shows the average fitness value and standard deviation of all competitors in each dataset.

It should be understood that the lowest fitness scores divulge better performance degrees for the optimization techniques. From Table 5, it can be observed that BHBA and BMSCSO ranked first and second, where each exclusively got the minimum fitness values in an overall of 11 and 4 datasets, respectively. BTLBO ranked third by exclusively obtaining the minimal fitness scores in 4 datasets, namely, Coimbra, Parkinsons, Cleveland and Hepatitis. BBBO exclusively obtained the minimum fitness value in one dataset, namely the Leukemia dataset. BLSHADE and BHBA shared the same minimum fitness value of 0.0144 in the Thyroid dataset. Finally, BAFT, BMFO, BSCSO and BPSO did not disclose any lowest fitness values in any of the datasets investigated in this study. A second reading of the standard derivation findings listed in Table 5 shows that BHBA’s and BMSCSO’s performance are superior to those of their rivals by achieving the lowest SD results across the majority of the datasets.

Table 6. Comparison results between the proposed BMSCSO and other methods based on sensitivity results.

Dataset	Measure	BSCSO	BMSCSO	BBBO	BMFO	BPSO	BTLBO	BAFT	BLSHADE	BHBA
Diagnostic	AV	0.9541	0.9667	0.8916	0.8728	0.7251	0.6186	0.8654	0.8900	0.8821
	SD	0.0574	0.0254	0.0522	0.1332	0.1973	0.2016	0.0352	0.0302	0.0425
Breast	AV	0.9863	0.9919	0.9680	0.9294	0.8796	0.7830	0.9574	0.9630	0.9684
	SD	0.0074	0.0090	0.0157	0.0982	0.1190	0.1305	0.0100	0.0074	0.0055
Prognostic	AV	0.1044	0.1200	0.1648	0.1855	0.1843	0.1024	0.8441	0.9027	0.8675
	SD	0.1005	0.1255	0.1457	0.1541	0.1996	0.1079	0.1584	0.1636	0.1244
Coimbra	AV	0.5924	0.7390	0.6909	0.6764	0.6275	0.5525	0.7123	0.6504	0.5610
	SD	0.2239	0.1020	0.1006	0.1669	0.2032	0.1849	0.1610	0.0532	0.1652
Retinopathy	AV	0.5998	0.6308	0.6336	0.6654	0.6189	0.6315	0.5936	0.5978	0.5546
	SD	0.0534	0.0520	0.0396	0.0402	0.0692	0.0456	0.0412	0.0510	0.0635
ILPD	AV	0.8176	0.8144	0.8178	0.8423	0.8272	0.8148	0.7736	0.8247	0.8083
	SD	0.0460	0.0444	0.0563	0.0593	0.0444	0.0398	0.0470	0.0564	0.0558
Lymphography	AV	0.7312	0.8938	0.6368	0.4850	0.4678	0.4644	0.6351	0.7109	0.6299
	SD	0.0853	0.4123	0.4262	0.4370	0.4217	0.4200	0.1329	0.1093	0.1989
Parkinsons	AV	0.8905	0.8886	0.9532	0.9536	0.9418	0.9397	0.9202	0.9018	0.9152
	SD	0.0281	0.0306	0.0327	0.0384	0.0514	0.0549	0.0468	0.0304	0.0415
ParkinsonC	AV	0.8766	0.8723	0.8829	0.8753	0.8941	0.8786	0.8228	0.8692	0.8325
	SD	0.0260	0.0349	0.0310	0.0265	0.0254	0.0405	0.0588	0.0488	0.0320
SPECT	AV	0.5553	0.6457	0.5240	0.5479	0.5370	0.5332	0.5868	0.6298	0.5478
	SD	0.1781	0.0908	0.1500	0.1135	0.1160	0.1149	0.0932	0.1735	0.0550
Cleveland	AV	0.2808	0.1225	0.1532	0.1423	0.1361	0.1076	0.6028	0.6554	0.6196
	SD	0.1017	0.1034	0.1304	0.1482	0.1159	0.0845	0.0358	0.0609	0.0524
HeartEW	AV	0.8138	0.8423	0.8115	0.8458	0.7613	0.7134	0.7699	0.9172	0.8189
	SD	0.0810	0.0547	0.0776	0.0789	0.1014	0.1084	0.0571	0.0400	0.0548
Hepatitis	AV	0.5000	0.4867	0.3428	0.4067	0.3428	0.2613	0.8155	0.8997	0.8795
	SD	0.5000	0.2805	0.3961	0.3533	0.3857	0.3748	0.4183	0.3419	0.2236
Saheart	AV	0.3126	0.3574	0.2988	0.2959	0.3094	0.3151	0.7174	0.7461	0.7296
	SD	0.0578	0.0564	0.0687	0.0740	0.0841	0.1016	0.1262	0.1126	0.1299
Spectfheart	AV	0.8472	0.8724	0.8686	0.8516	0.8573	0.8541	0.8622	0.8520	0.8661
	SD	0.0413	0.0433	0.0661	0.0640	0.0507	0.0676	0.0610	0.0650	0.0683
Thyroid	AV	0.7437	0.7433	0.7313	0.7663	0.6516	0.5339	0.9264	0.9594	0.9508
	SD	0.1370	0.1287	0.0987	0.1167	0.2175	0.2018	0.0490	0.0500	0.0491
Heart	AV	0.8558	0.8911	0.9161	0.9210	0.7931	0.6613	0.7336	0.7908	0.8146
	SD	0.0458	0.0343	0.0643	0.0531	0.1258	0.1071	0.0578	0.0361	0.0692
PimaDiabetes	AV	0.4932	0.5172	0.5713	0.5385	0.4867	0.5499	0.7224	0.7524	0.7467
	SD	0.0517	0.1006	0.0648	0.0760	0.1191	0.0768	0.0856	0.0504	0.0633
Leukemia	AV	0.7343	0.7371	0.6652	0.6947	0.7117	0.6912	0.8719	0.9514	0.9459
	SD	0.2453	0.1731	0.2172	0.1998	0.2443	0.2167	0.1404	0.2191	0.2453
Colon	AV	0.5990	0.4200	0.5695	0.6211	0.5490	0.6391	0.8284	0.8349	0.8284
	SD	0.2469	0.2387	0.2815	0.2605	0.2224	0.2160	0.3140	0.2033	0.1394
ProstateGE	AV	0.8616	0.8588	0.8947	0.8704	0.8365	0.8605	0.8497	0.8845	0.8793
	SD	0.0529	0.0578	0.1002	0.1351	0.1433	0.1080	0.0806	0.1019	0.0966

provides the sensitivity findings of the proposed BMSCSO compared to BSCSO and the other competitors.

Next, we evaluate the proposed BMSCSO with the other competing algorithms in terms of the sensitivity findings that the FS algorithms aim to improve. It should be mentioned that better performance level corresponds to higher sensitivity outcomes. Table 6 summarizes the outcomes of these opposing algorithms in terms of the average sensitivity findings correlated with their standard derivation values. Regarding the outcomes shown in this table, there is no doubt that BLSHADE has the highest sensitivity values when compared to all of its competitors. In particular, 9 out of 21 datasets, BLSHADE alone, obtained the greatest sensitivity values. By having the greatest sensitivity findings across 6 out of 21 datasets, the proposed BMSCSO clearly came in second place. BMFO has the best exclusive sensitivity results in 4 datasets, namely, Retinopathy, ILPD, Parkinsons and Heart, whereas BHBA placed next despite not achieving the best sensitivity values compared to all other competing algorithms. BBBO came in the next place with the best sensitivity findings only in the ParkinsonC and ProstateGE datasets with values of 0.8829 and 0.8947, respectively. Finally, BAFT, BPSO, and BTLBO did not disclose any distinguished sensitivity results. The proposed BMSCSO’s standard deviation values are low, which shows that the proposed BMSCSO is stable and well-established.

Similar to this,

Table 7. Comparison results between the proposed BMSCSO and other methods based on specificity results.

Dataset	Measure	BSCSO	BMSCSO	BBBO	BMFO	BPSO	BTLBO	BAFT	BLSHADE	BHBA
Diagnostic	AV	0.8289	0.8811	0.9685	0.9515	0.9279	0.9233	0.9288	0.9257	0.9361
	SD	0.0574	0.0256	0.0251	0.0453	0.0652	0.0538	0.0209	0.0259	0.0147
Breast	AV	0.9792	0.9876	0.9792	0.9070	0.8194	0.6768	0.9485	0.9649	0.9578
	SD	0.0074	0.0073	0.0168	0.1493	0.2046	0.2120	0.0153	0.0083	0.0078
Prognostic	AV	0.9307	0.9361	0.8936	0.9132	0.9144	0.9145	0.8736	0.8739	0.8879
	SD	0.1005	0.0267	0.0629	0.0613	0.0545	0.0461	0.0472	0.0652	0.0718
Coimbra	AV	0.7985	0.9305	0.7138	0.6919	0.6906	0.6575	0.7918	0.7942	0.7355
	SD	0.2239	0.0875	0.1458	0.1589	0.1546	0.1644	0.0708	0.2436	0.0517
Retinopathy	AV	0.6816	0.6921	0.7056	0.7036	0.6521	0.6562	0.6886	0.7106	0.7210
	SD	0.0534	0.0200	0.0507	0.0446	0.0767	0.0466	0.0236	0.0241	0.0570
ILPD	AV	0.3155	0.3637	0.3159	0.3018	0.3173	0.3084	0.7084	0.7518	0.7307
	SD	0.0460	0.1307	0.0807	0.0951	0.0781	0.0849	0.0739	0.0887	0.0659
Lymphography	AV	0.7726	0.8019	0.7888	0.7302	0.7244	0.7021	0.5795	0.6132	0.6111
	SD	0.0853	0.0691	0.0606	0.0739	0.0917	0.0863	0.1025	0.0357	0.1065
Parkinsons	AV	0.6738	0.8181	0.6713	0.7042	0.5804	0.5687	0.9243	0.9353	0.9313
	SD	0.0281	0.1476	0.1233	0.1438	0.1764	0.1812	0.2560	0.1006	0.1495
ParkinsonC	AV	0.2897	0.3670	0.2928	0.2861	0.2457	0.2878	0.7138	0.7569	0.7399
	SD	0.0260	0.1372	0.0729	0.0710	0.0697	0.0734	0.0829	0.0819	0.0455
SPECT	AV	0.6458	0.6926	0.7533	0.7093	0.7328	0.7322	0.7794	0.8036	0.7645
	SD	0.1781	0.0525	0.1296	0.1181	0.1362	0.1270	0.0494	0.0186	0.1047
Cleveland	AV	0.6426	0.6398	0.6235	0.6421	0.5891	0.5693	0.6164	0.6433	0.6258
	SD	0.1017	0.0634	0.0841	0.0575	0.0944	0.0685	0.0307	0.0722	0.0508
HeartEW	AV	0.7669	0.8253	0.7012	0.7096	0.6334	0.5675	0.7831	0.8037	0.7867
	SD	0.0810	0.0601	0.0847	0.1002	0.1465	0.0897	0.0797	0.0764	0.0847
Hepatitis	AV	0.9571	0.9004	0.9582	0.9060	0.9168	0.9039	0.7960	0.7480	0.7932
	SD	0.5000	0.1157	0.0497	0.1989	0.1876	0.2496	0.0654	0.2000	0.0000
Saheart	AV	0.8259	0.7961	0.8285	0.8205	0.7908	0.7817	0.9269	0.9243	0.9126
	SD	0.0578	0.0570	0.0595	0.0576	0.0612	0.0527	0.0747	0.0579	0.0544
Spectfheart	AV	0.4639	0.5331	0.3894	0.4133	0.3614	0.3972	0.7921	0.8238	0.8448
	SD	0.0413	0.1231	0.1665	0.1698	0.1359	0.1965	0.1433	0.2457	0.1828
Thyroid	AV	0.9703	0.9644	0.9821	0.9769	0.9614	0.9493	0.9513	0.9617	0.9621
	SD	0.1370	0.0225	0.0049	0.0170	0.0188	0.0126	0.0054	0.0055	0.0028
Heart	AV	0.6959	0.7730	0.6317	0.5990	0.5956	0.5728	0.7662	0.7615	0.7524
	SD	0.0458	0.0483	0.1095	0.1788	0.1342	0.0971	0.2024	0.0612	0.1418
PimaDiabetes	AV	0.7957	0.8329	0.8223	0.8233	0.8015	0.8087	0.7843	0.8148	0.7796
	SD	0.0517	0.0849	0.0456	0.0326	0.0477	0.0489	0.0824	0.0526	0.0431
Leukemia	AV	0.9560	0.9556	0.9776	0.9661	0.9459	0.9880	0.9546	0.9665	0.9653
	SD	0.2453	0.0609	0.0458	0.0491	0.0736	0.0368	0.0373	0.0994	0.0000
Colon	AV	0.7631	0.7451	0.8553	0.8610	0.8504	0.8956	0.8657	0.9168	0.8478
	SD	0.2469	0.1518	0.1472	0.1281	0.1323	0.1210	0.1087	0.0786	0.1337
ProstateGE	AV	0.8588	0.8891	0.8273	0.8556	0.8287	0.8385	0.8659	0.8643	0.8683
	SD	0.0529	0.0578	0.0966	0.0991	0.1323	0.1061	0.1251	0.1911	0.1218

provides an overview of the average and standard deviations of the specificity findings for BMSCSO, BSCSO, and all other competing methods.

Reading the specificity findings mentioned in Table 7 reveals that BMSCSO and BLSHADE came in first and second, respectively, with each having the greatest specificity values over a total of 8 and 6 datasets out of 21, respectively. By achieving the highest specificity outcomes across four datasets, BBBO came in third. BHBA alone had the greatest specificity values in Retinopathy and Spectfheart datasets with values of 0.7210 and 0.8448, respectively. The results produced by BMFO and BPSO are respectable and superior to those of other competing algorithms like BTLBO and BAFT, even if they did not attain the best specificity results in any of the datasets. In compared to other competitors, the proposed BMSCSO has relatively low standard deviation values throughout the majority of test datasets. These results demonstrate the stability of BMSCSO’s advantage.

As demonstrated in

Table 8. Comparison results between the proposed BMSCSO and other methods based on the average number of selected features.

Dataset	Measure	BSCSO	BMSCSO	BBBO	BMFO	BPSO	BTLBO	BAFT	BLSHADE	BHBA
Diagnostic	AV	15.20	14.400	15.70	11.03	11.00	19.43	17.40	17.40	13.00
	SD	2.59	1.82	3.80	1.61	2.42	2.93	3.21	2.51	1.22
Breast	AV	3.60	3.00	4.07	3.17	4.17	6.23	4.20	4.80	3.40
	SD	0.00	1.34	0.78	0.91	1.18	1.52	1.31	1.30	0.55
Prognostic	AV	15.20	12.20	17.17	14.53	13.90	21.63	18.40	16.00	12.80
	SD	2.59	1.79	2.96	2.21	2.80	2.13	2.88	1.41	1.92
Coimbra	AV	4.40	5.00	4.27	3.67	4.37	5.77	6.40	6.80	3.60
	SD	0.89	0.00	0.74	0.76	1.27	1.41	0.89	0.84	1.34
Retinopathy	AV	8.80	9.60	10.83	7.73	8.03	12.77	10.00	9.80	9.40
	SD	1.79	1.14	2.60	1.31	2.14	1.94	2.65	1.30	1.14
ILPD	AV	3.80	3.60	4.87	2.93	4.47	6.10	4.00	4.20	3.00
	SD	1.79	0.55	1.43	0.78	1.07	1.69	1.41	1.30	0.00
Lymphography	AV	6.40	8.20	9.73	6.60	7.17	11.43	10.20	8.40	9.20
	SD	2.19	2.86	1.72	1.35	2.07	1.79	2.28	0.55	1.30
Parkinsons	AV	9.40	9.40	11.67	7.50	8.00	13.87	11.20	9.20	5.80
	SD	1.52	1.82	2.43	1.36	1.98	1.93	1.10	2.17	1.30
ParkinsonC	AV	412.80	463.40	409.03	413.43	365.07	490.30	471.20	439.80	379.00
	SD	41.88	11.04	57.48	14.45	14.21	14.24	13.86	64.52	34.38
SPECT	AV	12.00	12.00	13.07	10.70	10.80	13.67	13.60	12.60	9.20
	SD	2.00	2.12	1.46	2.35	2.52	2.71	1.95	2.30	2.28
Cleveland	AV	6.20	7.40	6.67	4.73	5.90	8.90	7.60	6.20	4.00
	SD	0.84	2.30	1.75	1.14	1.58	1.47	1.52	1.92	1.00
HeartEW	AV	6.80	6.60	5.53	5.23	5.30	8.17	6.00	5.40	5.80
	SD	1.48	2.61	1.41	1.52	1.49	2.05	9.80	6.20	6.80
Hepatitis	AV	3.40	5.40	6.87	4.60	6.47	12.27	1.73	0.89	0.84
	SD	0.89	1.67	1.33	1.00	2.75	2.53	0.84	1.30	1.64
Saheart	AV	4.40	3.80	5.90	4.63	4.70	5.80	4.40	3.60	3.00
	SD	2.19	1.79	0.71	0.72	1.18	1.06	0.89	1.82	0.00
Spectfheart	AV	26.00	20.59	24.80	22.70	20.67	28.73	29.00	22.40	27.40
	SD	2.24	5.10	4.15	3.21	2.40	3.06	1.41	7.70	2.79
Thyroid	AV	10.60	8.00	10.53	8.10	8.27	13.37	12.40	10.20	8.40
	SD	1.87	2.30	1.96	1.60	2.05	1.71	1.95	1.79	0.55
Heart	AV	5.20	4.20	5.70	4.03	5.73	8.57	8.00	7.80	6.00
	SD	1.64	0.84	1.49	0.96	1.36	1.77	1.58	3.27	0.00
PimaDiabetes	AV	5.20	4.80	4.40	3.63	3.60	5.03	5.60	4.20	4.00
	SD	0.45	1.64	0.56	0.96	1.07	1.40	0.89	0.45	0.00
Leukemia	AV	3498.60	3586.00	3789.33	3898.57	3462.80	4588.53	4487.20	3500.00	2899.80
	SD	76.31	51.43	487.92	35.00	40.27	52.02	49.09	17.68	1157.29
Colon	AV	988.20	997.80	1064.47	1119.33	971.37	1300.20	1249.40	985.00	1051.80
	SD	21.42	9.23	140.25	26.95	20.16	20.23	11.72	23.72	98.62
ProstateGE	AV	3210.60	3442.40	3195.90	3267.93	2935.20	3889.83	3728.00	2904.40	1512.20
	SD	301.29	411.16	390.89	59.76	33.83	26.71	19.66	7.37	23.73

, the number of selected features is also taken into account when comparing the performance of the proposed BMSCSO to that of BSCSO and all other FS methods described above.

When evaluating any feature selection technique, the quantity of features selected during the classification process is just as crucial as the classification accuracy. There are many different outcomes when comparing the proposed method to the eight competing algorithms, as shown in Table 8. The nine competing algorithms can be divided into the following groups based on the results in the average number of features: By solely accumulating the fewest amount of selected features across a total of 8 out of 21 datasets, BHBA beat its competitors. BMSCSO came in second place, receiving the minimal number of features in 6 datasets entirely. Whereas BSCSO merely decreased the amount of features in the Lymphography dataset, BMFO had the fewest features in the Retinopathy, ILPD and HeartEW datasets, and BPSO reported its superiority against these two methods by having the fewest number of selected features in the Diagnostic, ParkinsonC, PimaDiabetes and Colon datasets. In every dataset taken into consideration, the BAFT, BLSHADE, BTLBO and BBBO algorithms failed to meet any minimal number of features. A second reading of the results in Table 8 may be used to infer that the BMSCSO outperformed its competitors since it had very small results across the majority of the datasets. This alludes that BMSCSO was able to choose around the same number of features by running the algorithm 30 separate times.

The comparisons between the proposed BMSCSO and other state-of-the-art feature selection algorithms found in the literature demonstrate the robustness of the proposed BMSCSO as noted from the results presented in Table 4, Table 5, Table 6, Table 7 and Table 8. One can observe that algorithms like BTLBO, BBBO, and BPSO behind BMSCSO by examining these outcomes in further detail and comparing the margins between BMSCSO and its rivals. Additionally, the proposed BMSCSO’s standard divisions are small and inferior to those of other rival algorithms.

This demonstrates that the proposed algorithm’s advantage is unquestionably strong. The key to BMSCSO’s acceptable level of performance is the algorithm’s sought-after balance between its exploration and exploitation features, which is made possible by the use of both the proposed mathematical model for this algorithm and the FS process. In this, the search agents of the proposed BMSCSO were able to explore and utilize each potential location in the search space as per its mathematical model, restoring a reasonable balance between exploration and exploitation. In this regard, the search agents of BMSCSO have the option of leaving their immediate area if they find themselves trapped in local optimums.

6.4. Convergence Curves

Figure 5 exhibits the convergence curves of the proposed BMSCSO, the basic BSCSO, and the other comparative optimization algorithms for the 21 datasets based on the fitness metric measure.

In the convergence plots illustrated in Figure 5, the y-axis displays the fitness values and the x-axis the number of iterations. These plot curves show the average convergence behavior of the best solution for the basic BSCSO, the proposed BMSCSO, and the other competing algorithms produced over a total of 30 independent runs. The algorithm that achieves the lowest fitness outcomes with the fewest iterations while also avoiding local optima is selected as the best algorithm. When exploring the search space of each feature selection problem, the behavior of the proposed BMSCSO and the other competing algorithms diverge by significant margins, as shown in Figure 5. This is because the proposed BMSCSO algorithm successfully balances the capacities for exploitation and exploration. Re-examining the curves in Figure 5 reveals that the convergence patterns of the proposed BMSCSO, the basic BSCSO, and the other rival algorithms in the first 40 iterations in the Diagnostic, Breast, Prognostic, Coimbra, Retinopathy, and ILPD datasets are noticeably different. Distinctly, the convergence behavior of the proposed BMSCSO is somewhat better than that of some of its competitors, namely BMFO, BPSO, BBBO, BLSHADE. After two-thirds of the iterations in the SPECT, Cleveland, Saheart, PimaDiabetes, and ProstateGE datasets, the convergence behavior of the two proposed companions (i.e., BSCSO and BMSCSO) becomes nearly similar. Anyway, the convergence behavior of the proposed BMSCSO is slightly and sometimes much better than that of the rival algorithms, namely BMFO, BPSO, BBBO, BLSHADE, BAFT, BHBA, BTLBO. The convergence curves of the HeartEW, Leukemia, and Colon datasets demonstrate how the convergence behaviors of the two proposed FS methods (that is, BSCSO and BMSCSO) and the other competing algorithms, BMFO, BBBO, BLSHADE, BAFT, BTLBO, are not similar in most iterations and becomes indistinguishable in the final few iterations. In the ParkinsonC and Spectfheart datasets, the convergence behavior of the proposed BMSCSO, however, is clearly superior to that of the standard BSCSO, as well as other competing algorithms including BTLBO and BBBO. Finally, in the datasets for Thyroid, Heart, and Hepatitis, the convergence behavior of BMSCSO is superior to that of the basic BSCSO, BTLBO, BBBO, and BAFT. It should be noted that Table 5 shows that the proposed BMSCSO performs better than the basic BSCSO and other competing algorithms, namely BMFO, BPSO, BBBO, BLSHADE, BAFT, BHBA, BTLBO, in terms of the average fitness values in these datasets.

6.5. Exploration and Exploitation

The two most crucial characteristics of optimization algorithms are exploration and exploitation, which can help solve optimization problems more effectively [67]. Empirical studies have demonstrated a strong correlation between optimization algorithm’s capacity for exploration and exploitation and its rate of convergence with reference to these two conceptions. In particular, exploitation techniques are known to increase convergence rate toward the global optimum but also to increase the risk of being trapped in local optimal states [67]. On the other hand, search methods that prioritize exploration over exploitation are more likely to lead to the location of regions within the search space where the global optimum is more likely to exist. This comes at the expense of optimization algorithms’ declining convergence speed [68]. Although it may seem minor, the question of how exploration and exploitation of solutions are accomplished in optimizations has remained an open one in recent years and has continued to be a cause of disagreement among many researchers [69]. Although many ideas and beliefs may appear to be at odds with one another, there seems to be agreement among researchers that this sort of search techniques must have an appropriate balance between exploration and exploitation in order to function reasonably. In order to identify reasonable solutions to an optimization problem, optimizations employ a set of potential solutions to explore the search space. In general, the search process should be directed in their direction by the search agents with the best solutions. This attraction causes the gap between the search agents to widen while the effects of exploitation diminish. On the other hand, the impact of the exploration approach becomes more noticeable when the search agents’ separation widens. A diversity measurement is used to calculate the rise and decrease in distance between the search agents [70]. According to this approach, population variety can be defined as follows [67]:

$$Ex{p}_j=\frac{1}{N}\sum _{i=1}^N\left|median\left(x^j\right)-x_i^j\right|$$

(33)

$$Exp=\frac{1}{m}\sum _{j=1}^{m}Ex{p}_j$$

(34)

where n is the number of search agents, m identifies the dimension of the problem, $x_i^j$ stands for the dimension j of search agent i, and $median\left(x^j\right)$ stands for the median of dimension j in the total population.

The distance between the dimension j of each search agent and the dimension’s average median is referred to as the diversity in each dimension, or $Ex{p}_j$. The percentage of exploration and exploitation that a specific optimization algorithm uses is known as the complete balance response. The following formulas are used to compute these values at each iteration step [67]:

$$XPL\%=\left(\frac{Exp}{Ex{p}_{max}}\right)\times 100$$

(35)

$$XPT\%=\left(\frac{\left|Exp-Ex{p}_{max}\right|}{Ex{p}_{max}}\right)\times 100$$

(36)

where $Ex{p}_{max}$ denotes the highest diversity value that was found throughout the whole optimization process.

The link between the diversity at each iteration and the greatest diversity obtained is represented by the percentage of exploration (XPL%). The amount of exploitation is represented by the percentage of exploitation (XPT%) [67]. As can be seen, the factors XPL% and XPT% are complimentary and in conflict with one another. The use of the median value while evaluating the balancing response prevents inconsistencies by using a reference element. The $Ex{p}_{max}$ value discovered over the whole optimization process also has an impact on this balancing reaction. The rate of exploration and exploitation is estimated using this value as a reference.

Optimization of the BreastEW dataset is used as an example to illustrate the evaluation of the balance response of the proposed BMSCSO. Figure 6 depicts the performance conduct produced by the proposed BMSCSO in optimizing the BreastEW dataset over 100 iterations with respect to the balance assessment presented by Equations (35) and (36).

Five points, denoted as (A), (B), (C), (D), and (E), in Figure 6 have been selected to demonstrate the diversity of solutions and the balance evaluations of each of them. Point (A) denotes an early stage of the proposed BMSCSO, when XPL% and XPT% have balance evaluation values of 90 and 10, respectively. These percentages provide BMSCSO a clear direction to operate within while it explores the search space. This implies that the solutions maintain a significant amount of dispersion of the search space. Point (B) corresponds to 70 iterations, where the balance assessment at this point preserves a value of XPL% = 70 together with XPT% = 30. In this position, the proposed BMSCSO mostly engages in exploration with minimal exploitation. Points (C) and (D) correlate with 75 and 100 iterations, respectively, where the balancing assessments’ exploration and exploitation values are XPL% = 25, XPT% = 75, XPL% = 5, and XPT% = 95, respectively. When these percentages were reached, the proposed BMSCSO’s behavior changed to encourage more exploitation than exploration. These configurations cause the solutions to be dispersed among numerous bunches, which lessens the diversity overall. Finally, point (E) implements the BMSCSO’s final junction. The proposed BMSCSO maintains a subtle tendency toward the exploitation of the top solutions without taking into consideration any exploration approach in such a case.

6.6. Sensitivity Analysis

To pinpoint the ideal parameter values of the proposed BMSCSO FS with memory based, a detailed sensitivity analysis based on the Design of Experiment (DoE) approach was performed. The suggested technique employs k-NN as a classifier in DoE to investigate the sensitivity of critical control parameters (${\tau }_1$ and ${\tau }_0$). The essential control parameter ranges were initially created, and the values of these parameters were determined to determine whether the best values came within the scope or whether further tests were necessary. The FS experiments then used a parameter with one input of the generated DoE values in the desired range while retaining the remaining parameters at their beginning levels. These tests were carried out systematically to investigate the influence of input parameters on the accuracy values of the suggested BMSCSO and arrive at a reasonable answer. Here are the values of each parameter used in this experiment: ${\tau }_0$ = 0.5, 1.0, 1.5, 2.0 and ${\tau }_1$ = 0.5, 1.0, 1.5, 2.0.

The numerical findings in

Table 9. Classification accuracy of BMSCSO using different values of ${\tau }_1$ and ${\tau }_0$ with the k-NN classifier.

Dataset	Measure	${\mathit{\tau }}_0=0.5$	${\mathit{\tau }}_0=1.0$	${\mathit{\tau }}_0=1.5$	${\mathit{\tau }}_0=2.0$	${\mathit{\tau }}_1=0.5$	${\mathit{\tau }}_1=1.0$	${\mathit{\tau }}_1=1.5$	${\mathit{\tau }}_1=2.0$
Diagnostic	AV	0.78	0.81	0.80	0.94	0.73	0.95	0.87	0.65
	SD	0.002	0.002	0.007	0.003	0.003	0.003	0.002	0.003
Breast	AV	0.81	0.86	0.83	0.98	0.71	0.99	0.8414	0.64
	SD	0.003	0.003	0.003	0.001	0.004	0.007	0.003	0.003
Prognostic	AV	0.71	0.75	0.78	0.83	0.67	0.88	0.74	0.663
	SD	0.003	0.003	0.003	0.002	0.007	0.009	0.004	0.007
Coimbra	AV	0.74	0.706	0.744	0.921	0.60	0.940	0.81	0.6391
	SD	0.0037	0.0034	0.0035	0.0022	0.0043	0.0024	0.0029	0.0045
Retinopathy	AV	0.56	0.636	0.623	0.745	0.511	0.71	0.627	0.50
	SD	0.0038	0.0038	0.0032	0.0039	0.0038	0.0038	0.0032	0.0037
ILPD	AV	0.62	0.68	0.68	0.77	0.57	0.74	0.61	0.5
	SD	0.0121	0.0114	0.0114	0.0100	0.0219	0.0123	0.0201	0.0223
Lymphography	AV	0.67	0.80	0.87	0.94	0.72	0.912	0.88	0.6954
	SD	0.0209	0.0209	0.0174	0.0211	0.0207	0.0205	0.0174	0.0203
Parkinsons	AV	0.790	0.874	0.85	0.973	0.74	0.97	0.86	0.662
	SD	0.0132	0.0132	0.0110	0.0133	0.0131	0.0130	0.0110	0.0128
ParkinsonC	AV	0.674	0.678	0.781	0.82	0.66	0.869	0.75	0.55
	SD	0.0236	0.0236	0.0197	0.0239	0.0234	0.0232	0.0197	0.0230
SPECT	AV	0.78	0.74	0.75	0.87	0.69	0.899	0.71	0.650
	SD	0.0114	0.0114	0.0095	0.0115	0.0113	0.0112	0.0095	0.0111
Cleveland	AV	0.41	0.51	0.54	0.60	0.42	0.66	0.52	0.4267
	SD	0.0037	0.0037	0.0031	0.0038	0.0037	0.0037	0.0031	0.0036
HeartEW	AV	0.707	0.768	0.782	0.953	0.656	0.89	0.75	0.643
	SD	0.0056	0.0056	0.0047	0.0057	0.0056	0.0055	0.0047	0.0055
Hepatitis	AV	0.75	0.84	0.8	0.94	0.72	0.935	0.83	0.65
	SD	0.0284	0.0284	0.0238	0.0287	0.0281	0.0279	0.0237	0.0276
Saheart	AV	0.58	0.56	0.64	0.705	0.55	0.602	0.6902	0.50
	SD	0.0241	0.0238	0.0228	0.0198	0.0281	0.0198	0.0187	0.0309
Spectfheart	AV	0.734	0.78	0.73	0.98	0.67	0.92	0.802	0.69
	SD	0.0137	0.0137	0.0114	0.0138	0.0135	0.0134	0.0114	0.0133
Thyroid	AV	0.71	0.8322	0.86	0.99	0.79	0.98	0.86	0.66
	SD	0.0010	0.0010	0.0008	0.0010	0.0009	0.0009	0.0008	0.0009
Heart	AV	0.77	0.70	0.74	0.80	0.65	0.8	0.703	0.69
	SD	0.0192	0.0192	0.0160	0.0194	0.0190	0.0188	0.0160	0.0186
PimaDiabetes	AV	0.690	0.68	0.68	0.71	0.56	0.73	0.65	0.66
	SD	0.0238	0.0229	0.218	0.0187	0.0252	0.0189	0.0210	0.0278
Leukemia	AV	0.81	0.850	0.88	0.99	0.76	0.99	0.87	0.72
	SD	0.0045	0.0038	0.0030	0.0035	0.0009	0.0023	0.0013	0.0018
Colon	AV	0.76	0.77	0.79	0.91	0.69	0.97	0.88	0.64
	SD	0.0043	0.0040	0.0038	0.0012	0.0048	0.0015	0.0033	0.0056
ProstateGE	AV	0.73	0.766	0.79	0.89	0.69	0.8	0.79	0.620
	SD	0.006	0.003	0.003	0.0093	0.003	0.009	0.002	0.0066

reveal that BMSCSO performed best when the parameters ${\tau }_1$ and ${\tau }_0$ of BMSCSO are set to 2.0 and 2.0, respectively. This highlights the need of using a reasonable range of these critical parameters to improve BMSCSO’s resilience. These suggested approaches are nearly stable to changes in the necessary control parameters for BMSCSO when data sets have varying degrees of dimensionality, as shown by the standard deviation values of the classification accuracy of BMSCSO. To summarize, the results in Table 9 show that BMSCSO is often extremely sensitive to parameter choices of ${\tau }_1$ and ${\tau }_0$ and the best values are 2 for both of them.

6.7. Statistical Analysis

The accuracy of the proposed BSCSO and BMSCSO algorithms was assessed in the aforementioned subsections using a variety of performance indicators, and their performance on FS problems was compared with that of other optimization FS methods stated in the literature. Over the course of 30 separate runs, the optimal solutions (i.e., classification accuracy and fitness values) were calculated using the average and standard deviation as statistical metric measures. These measures provide a general overview of how well the proposed algorithms handle FS problems with varied complexity. The first metric shows an algorithm’s average performance, while the second one shows how stable the method is throughout all of the separate run times. These evaluation measures may show the overall effectiveness and power of the FS method under evaluation, but they could not compare each of the separate runs independently. In other words, they have demonstrated the potential exploitation and exploratory behaviors of the proposed FS methods, but they are unable to demonstrate the quality of these methods. To demonstrate the significance of the results and that they were not the result of chance, Friedman’s and Holm’s statistical test methods [18,71] were carried out. Using the null hypothesis that there is no difference in the accuracy of any of the compared FS methods, Friedman’s test is used to determine if there is a root difference in the results of the competing FS methods.

Always receiving the lowest rank is the method with the best performance, while always receiving the highest rank is the method with the poorest performance. For the findings of the FS problems being studied, the p-value of the Friedman’s test must be determined. If this value is equal to or less than the degree of significance, which in this study is $0.05$, the null hypothesis is rejected. Achieving this instance indicates that there are statistically significant differences in how well the comparison strategies function. Following this statistical test, a post-hoc test method-in this case, the Holm’s test procedure-is used to examine pairwise comparison of the comparative algorithms. For post-hoc analysis, the method with the lowest rank obtained by Friedman’s test is typically employed as the control method. The average fitness and classification accuracy results of the proposed BMSCSO algorithm presented in Table 4 and Table 5 are, therefore, statistically deserving of attention and do not statistically deviate from the results of other promising algorithms, according to Friedman’s and Holm’s statistical methods, which were used to make this revelation.

Table 10. Statistical comparison between the presented BMSCSO and other competing methods based on the mean accuracy results.

Algorithm	Rank
BSCSO	2.857142
BMSCSO	1.714285
BBBO	4.785714
BMFO	6.119047
BPSO	7.714285
BTLBO	8.523809
BAFT	5.690476
BLSHADE	4.500000
BHBA	3.095238

shows the ranking results of the Friedman’s method on the basis of the results presented in Table 4.

Friedman’s test method yielded a p-value of 9.442002E-11 based on the average classification accuracy results shown in Table 10. The existence of a statistically significant difference in the accuracy of the compared algorithms was shown by the rejection of the null hypothesis of similar performance. BMSCSO is statistically significant and the most successful FS method among all other FS ones, according to the statistical results shown in Table 10. As a result, BMSCSO gets the highest rank, 1.714285, with a significance level of 5%. In particular, BMSCSO was put in the first place, and was followed in order by BSCSO, BHBA, BLSHADE, BBBO, BAFT, BMFO, BPSO, and BTLBO.

Following Friedman’s test, Holm’s test method was used to assess if there are statistically significant differences between the competing methods indicated in Table 10 and the control algorithm with the lowest rank (i.e., BMSCSO). Table 4 and Table 10 reflect the collected results;

Table 11. Results of Holm’s test between the control algorithm (i.e., BMSCSO) and all other algorithms in accordance with the results of Friedman’s test.

i	Algorithm	$\mathit{z}=({\mathit{R}}_0-{\mathit{R}}^{\mathit{i}})/\mathbf{SE}$	p-Value	$\mathit{\alpha }$÷i	Hypothesis
8	BTLBO	8.057137	7.810195E-16	0.006250	Rejected
7	BPSO	7.099295	1.253942E-12	0.007142	Rejected
6	BMFO	5.211784	1.870326E-07	0.008333	Rejected
5	BAFT	4.704692	2.542494E-06	0.010000	Rejected
4	BBBO	3.634163	2.788841E-04	0.012500	Rejected
3	BLSHADE	3.296101	9.803655E-04	0.016666	Rejected
2	BHBA	1.633964	0.102266	0.025000	Not rejected
1	BSCSO	1.352246	0.176296	0.050000	Not rejected

presents the statistical findings produced by Holm’s test procedures based on those results. In this table, z stands for the statistical difference between the two FS methods being compared, $R_0$ for the Friedman’s rank assigned to the control method, $R^i$ for the Friedman’s rank assigned to method i, and ES for the amount of the control algorithm’s influence on algorithm i.

Using the Holm’s test, which is shown in Table 11 and excludes hypotheses with a p-value $\le 0.025000$, BMSCSO was compared to the other competing algorithms. BMSCSO is a potent FS approach for obtaining favorable results for the datasets under examination, as can be shown from the findings in Table 11, and it performs noticeably better than other skilled methods utilized to handle these FS problems. The p-values also divulges the BMSCSO’s level of performance on FS tasks and demonstrate the effectiveness of this approach. The results in Table 10 and Table 11 demonstrate, in brief, that BMSCSO has successfully avoided local optimal solutions and is regarded as statistically significant by achieving high classification accuracy scores in comparison to the obtained classification accuracy rates by the basic BSCSO and the other competing FS algorithms.

A secondary statistical comparison was done between the proposed BMSCSO and the other competing FS methods in regards to the mean fitness results where their obtained results are displayed in Table 5. The ranking results of the Friedman’s test-based statistical analysis based on fitness values are listed in

Table 12. Statistical comparison between the proposed BMSCSO and all other rivals in reference to the average fitness outcomes.

Method	Rank
BSCSO	5.142857
BMSCSO	4.095238
BBBO	4.976190
BMFO	6.380952
BPSO	8.476190
BTLBO	3.833333
BAFT	5.571428
BLSHADE	4.119047
BHBA	2.404761

.

As per the fitness scores exhibited in Table 5, the p-value determined by Friedman’s test is 6.380973E-11. Due to the outcomes presented in Table 12, the proposed BMSCSO algorithm is ranked among the top three FS methods among all other competing ones. The proposed BSCSO method gained the first rank with a value of 5.14, which means the two proposed methods earned the top ranking among all other competing FS methods due to the nature of their local and global search strategies. In more detail, the proposed BMSCSO method gained the second-rank algorithm with a value of 4.095 with a significance level of a = 5%. The BTLBO is the second best FS method in this comparison with a rank of 3.833333 with a little difference from the rank obtained by BMSCSO. In view of the results displayed in Table 12, BMSCSO acted much better than the other algorithms in the FS task, where it ranked first, followed successively by BHBA, BSCSO, BCMA-ES, BLSHADE, BAFT, BMFO, BPSO, and BTLBO.

Based on the fitness ratings shown in Table 5, Friedman’s test yielded a p-value of 6.380973E-11. According to the outcomes shown in Table 12, the proposed BMSCSO is one of the most effective FS method out of all those in competition. BHBA received the top position as noted from the ranking results presented in Table 12 with a value of 3.833333 and a degree of significance of $\alpha =5\%$. With an average ranking score of 3.833333, slightly better than the rank attained by BHBA, the BTLBO technique is the second-best approach. In sum and in light of the ranking results presented in Table 12, BMSCSO performed much better than the other algorithms in the FS problems, where it came in the third place, followed by BLSHADE, BBBO, BSCSO, BAFT, BMFO, and BPSO in the last rank.

These outcomes approximately match those that were previously shown in Table 10. The control algorithm (i.e., BHBA) and the other compared algorithms are then compared using Holm’s test procedure to see if there are statistically discernible differences. The outcomes obtained after performing Holm’s test with $\alpha =0.05$ to the results shown in Table 12 are provided in

Table 13. Holm’s test Results between the control method and all other methods in reference to Friedman’s test results.

i	Method	$\mathit{z}=({\mathit{R}}_0-{\mathit{R}}^{\mathit{i}})/\mathbf{SE}$	p-Value	$\mathit{\alpha }$ ÷ i	Hypothesis
8	BPSO	7.183811	6.779448E-13	0.00625	Rejected
7	BMFO	4.704692	2.542494E-06	0.007142	Rejected
6	BAFT	3.746850	1.790687E-04	0.008333	Rejected
5	BSCSO	3.239757	0.001196	0.010000	Rejected
4	BBBO	3.042555	0.002345	0.012500	Rejected
3	BLSHADE	2.028370	0.042522	0.016666	Rejected
2	BMSCSO	2.000198	0.045478	0.025000	Rejected
1	BTLBO	1.690308	0.090968	0.050000	Not rejected

.

For the outcomes in Table 13, Holm’s technique eliminated the hypotheses with a p-value $\le 016666$. These findings clearly manifest that BMSCSO outperformed many other binary algorithms in solving FS problems, as evidenced by its high performance score compared to those rival ones. These results demonstrate that BMSCSO has wonderfully avoided local solutions throughout the search space by undertaking sensible exploration and exploitation aspects. Table 10, Table 11, Table 12 and Table 13 show that the results of BMSCSO are statistically significant, demonstrating that this FS method is superior to many other FS methods with excellent results over other well-known established optimization algorithms. This ending demonstrates the excellent efficiency of the proposed BMSCSO, which is a binary extension of the SCSO method, in solving a wide range of well-known FS problems.

7. Conclusions and Future Works

This paper proposes a new effective Memory based Sand Cat Swarm Optimization (MSCSO) for addressing Feature Selection (FS) problems. The proposed MSCSO makes use of the exploration ability of SCSO to scout the search space efficiently and internal memory component for quicker convergence and to locate the global best solution. For this study, the basic SCSO and proposed MSCSO are converted to binary format, and given the names BSCSO and BMSCSO, respectively, to properly handle FS tasks. The goals of these FS algorithms include developing clear and non-redundant data, improving data mining performance, and producing straightforward and comprehensive models. In the interim, these proposed algorithms might be utilized to successfully reduce the dimensionality of data for machine learning applications. The performance level of the proposed methods was evaluated on 20 benchmark medical datasets using a number of evaluation criteria. For comparative assessments, the proposed BMSCSO and fundamental binary SCSO are compared with other well-known FS algorithms. According to analysis based on Friedman’s and Holm’s test methods, the proposed BMSCSO got the highest classification accuracy rate. This encourages the use of MSCSO in expert systems as a dependable and robust optimization method. Similar to SCSO, MSCSO has relatively few parameters that need to be adjusted, and because these variables are self-adaptive, it is simple to employ MSCSO to solve optimization problems. MSCSO has a great capacity to avoid local optima compared to other algorithms since it is a population-based algorithm. Additionally, by incorporating the internal memory idea into MSCSO, stagnation at local optima is avoided and the quality of the solution is improved during the iterative updating process. Further enhancements of this version might be done for further study as the proposed BMSCSO demonstrated appealing performance in solving FS problems. For instance, researchers working on multi-objective optimization problems could employ the proposed MSCSO. The applicability of the proposed methods may also be confirmed using a high-dimensional dataset like gene selection. Other types of transfer functions such as V-shaped, X-shaped and U-shaped could be applied to examine the impact of these transfer functions on the effectiveness of the developed FS algorithms.