Abstract
Currently, most recommendation algorithms only use a single type of user behavior information to predict the target behavior. However, when browsing and selecting items, users generate other types of behavior information, which is important, but often not analyzed or modeled by traditional recommendation algorithms. This study aims to design a multi-behavior recommendation algorithm based on graph neural networks by analyzing multiple types of behavior information in users’ product purchasing process, to fully utilize multiple types of user behavior information. The algorithm models users, items, and user behavior in multiple dimensions by incorporating attention mechanisms and multi-behavior learning into graph neural networks, and solves the problem of imbalanced user behavior weights from the perspective of multi-task loss optimization. After experimental verification, we proposed that the multi-behavior graph attention network (MGAT) algorithm has better performance compared to four other classical recommendation algorithms on the Beibei and Taobao datasets. The results demonstrate that the multi-behavior recommendation algorithm based on graph neural networks has practicality in fully utilizing multiple types of user information, and can solve the problem of imbalanced user behavior weights to some extent.
1. Introduction
With the rapid development of deep learning, excellent network models, such as convolutional neural network (CNN) [1] and recurrent neural network (RNN) [2], have been produced for Euclidean data, but there is no such model for non-Euclidean data. In recent years, the emergence of graph neural networks has given an excellent solution for non-Euclidean graph structure data. Graph neural networks have been widely used in recommendation systems [3,4,5,6,7,8,9,10,11,12,13], social networks [14], drug discovery [15,16], fraud detection [17,18], and other fields, because they can aggregate high-order neighbor features on graph structure data, enhance node representation, and enable it to better express node information.
Due to the powerful information aggregation ability of graph neural networks in graph structured data, and the relationship between users and products in the recommendation system being regarded as a standard user–product bipartite graph, multiple behavior types between users and products can be modeled as different types of edges between nodes, so graph neural networks are widely used in the field of recommendation systems [18].
With the development of the Internet and the increasing level of informatization, people have access to more and more information. Therefore, recommendation systems have transitioned from traditional matrix factorization [19] and context-based filtering [20,21], to deep-learning-based recommendation [22,23,24]. Due to the exceptional performance of graph neural networks on graph structure data, they have also flourished in the field of recommendation systems. In the context of graph neural networks, recommendation systems are roughly divided into social recommendation, sequence recommendation, session-based recommendation, bundle recommendation, cross-domain recommendation, and multi-behavior recommendation [25]. This study mainly focuses on multi-behavior recommendation.
Multi-behavior recommendation is an emerging branch in the field of recommender system research, which aims to utilize multiple user behavior data to improve the recommendation performance for target actions [7]. In the traditional recommendation model, only one kind of user-item interaction behavior is used, while the multi-behavior recommendation mainly utilizes multiple types of user behaviors to improve the recommendation performance of the target behavior [8]. For example, in Figure 1, when shopping, users will generate various user behaviors, such as searching for products, viewing products, adding to the shopping cart, purchasing products, and collecting products. However, traditional recommendation algorithms mostly only use purchase behavior information and do not fully utilize other user behavior information generated by users during the purchase process.

Figure 1.
Shopping flow chart.
There are two key issues for multi-behavior recommendation. One is how to model the relationship between multiple user behaviors and target behaviors. The second is how to model users and products under various user behaviors [26].
How can the relationship between various user behaviors and target behaviors be modeled? The most common method for modeling the relationship between multiple user behaviors and the target behavior is to treat them equally and not consider the differences between behaviors when modeling. Ignoring the differences between behaviors can lead to information loss [26]. For example, in the context of an e-commerce platform, compared with the behavior of viewing a product, adding the product to the shopping cart is clearly more effective for the target behavior of shopping, regardless of the differences in the number of user behaviors. In addition, the target behavior is not necessarily more influential than other behaviors. For example, after a customer purchases a product on an e-commerce platform, sharing the product or giving it a positive review may be more effective than the purchase behavior. In summary, the relationship between multiple user behaviors and the target behavior is not fixed and may vary in different datasets. Therefore, this study uses multi-task learning to train the model, and ultimately converts the relationship between other user behaviors and the target behavior into a problem of multi-task learning with multiple losses combined. Finally, by experimenting with existing classic loss combination algorithms and considering various factors, the best loss combination algorithm is selected.
How can users and items under various user behaviors be modeled?
When modeling users and products, their methods are also different. For example, Wang et al. [27] directly aggregate the products interacting with users under various behaviors through the gate control mechanism; Xia et al. [9] does so by using the knowledge of graphs to model the users; and Chen et al. [7] modeled users, commodities, and relationships, and then performed information fusion to obtain new node representations. However, most of them do not consider the relationship between users and products when modeling users and products. This study builds maps of user–product interaction relationships under different behaviors, and then uses the attention mechanism of graph attention networks (GATs) to analyze the relationship between users and products. The user–product relationship under each behavior is modeled, and the hard parameter sharing mechanism of multi-task learning is used to achieve parameter sharing and enhance the purpose of representation, and learn from the previous practice. At the same time, the relationship is modeled to obtain the user, modeling representation of goods and relationships.
Based on the above two problems, this paper proposes a recommendation model based on graph neural networks, to use user–product graphs under various behaviors to model users and products. Then, multi-task learning was conducted, followed by parameter sharing, to achieve the effect of information sharing and mutual complementation, so as to improve the recommendation performance. This paper then considers the weight of each behavior from the perspective of loss combination, and finally proposes a multi-behavior recommendation model based on graph neural networks.
In summary, the model designed in this paper has the following advantages: 1. Innovation: the GAT attention mechanism is integrated into the node information aggregation, so that it has attention characteristics when aggregating neighbors, and enhances the node representation ability; 2. Convenience: through experiments on various loss-combining algorithms, the problem of behavior weight is solved from the perspective of loss combining. There is no need to manually set behavior weights, nor design behavior weights from the perspective of network structure, so that the network structure and behavior weight structure are decoupled; 3. Efficiency: The model in this paper shows better results for the Beibei and Taobao datasets, compared with the single-behavior recommendation model and the multi-behavior recommendation model.
2. Related Works
2.1. Multi-Behavior Recommendation
Multi-behavior recommendation is an emerging branch in the field of recommender system research. Its research purpose is to use multiple user behavior data to improve the recommendation performance of the target behavior [7]. Nowadays, most recommendation algorithms use single-user behavior information to predict the target behavior, and when users choose products, they will generate other types of behavior information. Most of the traditional recommendation algorithms do not make the full use of these user behaviors [8]. Aiming at the problem of not making the full use of multi-behavior data, most of the existing researches solve this problem from three aspects.
One is to extend the matrix decomposition [19] of the early single behavior to the de-composition of multiple behavior matrices, which has achieved the learning of different behaviors. For example, Singh et al. [28] proposed an ensemble matrix factorization model in 2008, when an entity participates in multiple relationships, decomposes several matrices at the same time, and shares parameters between the matrices to use multi-behavioral data. When solving this problem in 2012, Krohn-Grimberghe et al. [29] proved that its effectiveness is higher than other methods by designing a multi-behavior recommendation model based on multi-behavior decomposition technology. Zhao et al. [30] have built a topic recommendation system under the Google+ framework using matrix decomposition technology. They modeled each user’s behavior as a separate example entry in the input user–topic matrix and predicted the users’ topic interests based on their behavior.
One is to introduce multi-behavioral data into the sampling process from the perspective of learning, and make full use of the multiple behavioral data by using auxiliary behaviors to expand the training set and changing the sampling strategy. For example, Loni et al. [31] proposed multiple-feedback Bayesian personalized ranking (MF-BPR) in 2016, which is a method to exploit the different types of user behaviors by using an expanded sampling method. In 2018, Qiu et al. [32] proposed a Bayesian personalized ranking method with heterogeneous implicit feedback, which improves recommendation performance by using auxiliary behaviors, and solves the gap between behaviors through an adaptive sampling strategy imbalance. Ding et al. [33] modeled the pairwise ranking relationship between purchase, viewing, and non-viewing interactions, and designed a learning algorithm based on an elementwise alternating least squares (eALS) learner. This algorithm can effectively learn model parameters from the entire user–item matrix and has a relatively low time complexity. In addition, Ding et al. [34] improved the performance of the recommendation model by proposing a simple and effective Bayesian personalized ranking (BPR) sampler and using additional view data for sampling. The third aspect attempts to capture complex and multi-type interactions between users and items by designing neural network models. For example, in 2019, Gao et al. [35] proposed a new neural network model, neural multi-task recommendation (NMTR), which can learn user preferences from multi-behavior data, and associate model predictions of each behavior type in a cascaded manner. In 2021, Jin et al. [26] proposed a new model, named a multiple-behavior graph convolutional network (MBGCN), to improve the recommendation effect of multi-behavior recommendation by constructing a unified graph to represent multi-behavior data. Lifeng et al. [10] proposed a recommendation model based on probabilistic matrix factorization. This model uses resource allocation in a bipartite graph and random walks on meta-paths in a heterogeneous network to determine the implicit association of items and the implicit similarity of users, respectively. The final item association and user similarity are obtained. The final item and user similarity relationships are integrated into the probabilistic matrix factorization model to obtain the predicted score of a user for a specific item.
2.2. Graph Neural Networks
In recent years, graph neural networks have achieved great success due to their powerful ability to represent learning from structured data, and have thus been widely used in recommender systems. For example, the graph convolutional matrix completion (GC-MC) framework, proposed by Berg et al. [3] in 2017, is a graph autoencoder framework for matrix completion tasks in recommendation systems. The encoder consists of a graph convolutional layer that constructs user and item embeddings by passing messages over the user–item graph. In 2018, Ying et al. [4] proposed and developed an efficient graph convolution network algorithm, PinSage, which combines efficient random walk and graph convolution to use graph structure information, and node feature information to generate user and product embeddings. In 2019, Wang et al. [36] designed a graph neural collaborative filtering (NGCF) framework, which obtains the embeddings of users and products under high-order connectivity by using the graph structure propagation embedding on the user–product graph, effectively combining collaborative signals that are explicitly injected into the embedding process. In 2020, He et al. [5] proposed a new model called LightGCN, which only includes the graph convolution network (GCN) neighborhood aggregation and uses it for collaborative filtering. This simple, linear, and tidy model is easier to implement and train.
There are more and more applications in multi-behavior learning based on graph neural networks. For example, in 2020, Jin et al. [26] proposed a new model called MBGCN, which constructs a unified graph for representing multi-behavior data, thus the user–item propagation layer learns the behavior intensity, and the behavior semantics are captured by the item–item propagation layer. In 2020, the multiplex graph neural network (MGNN) framework, proposed by Zhang et al. [6], was demonstrated to learn the shared embedding and specific behavior embedding of users and items by using the reuse network structure and graph representation learning technology. In 2021, Chen et al. [7] used the advantages of GCN to jointly embed the representation and relationship of nodes (users and items) into multi-relational prediction, and performed advanced and efficient non-sampling optimization. In a 2022 study by Yu et al. [11], the graph-neural-network-based hybrid model (GNNH) leveraged graph neural networks (GNNs) to capture items and feature representations, preserving global item–item and feature–feature relationships. Mingyu et al. [13] proposed a new hybrid graph network recommendation model called the user multi-behavior graph network (UMBGN), by integrating user–item multi-behavior interaction sequences, using a joint learning mechanism. This model extracts the long-term multi-behavior features of users through the user multi-behavior information perception layer, and learns the time-ordered user–item interaction information through BiGRU and AUGRU units. Zhang et al. [12] proposed a new fine-grained POI recommendation based on multi-graph convolutional networks (FP-MGCNs). A FP-MGCN uses multiple embedded propagation layers and models high-order connections of different POI-related relationships using an information propagation mechanism to enhance representation.
3. Methodology
The algorithm model in this paper is mainly divided into three parts: embedding acquisition based on graph neural networks, the parameter sharing based on multi-task learning, and the selection of a loss-merging algorithm. This paper will explain these three parts respectively.
3.1. Embedded Acquisition Based on Graph Neural Networks
Predecessors mainly rely on CNN [1] and RNN [2] for embedding acquisition. These two embedding acquisitions have two limitations. On top of space, data in non-Euclidean spaces cannot be processed. Second, it can only aggregate information from first-order neighbors, but cannot aggregate information from higher-order neighbors. The birth of the graph neural network has proposed a brand-new idea to solve these two problems. Therefore, this model intends to use the graph neural network to obtain embedding. The reason is that this model is mainly through the interaction between users and products. relationship, without considering the information of the user and the product itself. It seems that this article operates on the graph, so it is a better choice to choose the graph neural network.
For the classic GCN [37], the embedding of the node obtained by the single-layer GCN layer is expressed as (1):
where represents the embedding obtained by the l layer, is the normalized adjacency matrix, where A is the adjacency matrix, D is the angle matrix, , I is the identity matrix. is the parameter matrix of layer l, and is the activation function. is the initialization embedding matrix.
The problem with this classic GCN model is that it only aggregates node information (user nodes aggregate user node information, and commodity nodes aggregate commodity node information. In fact, it is meaningless under the current assumptions of this article, because this article does not consider the relationship between users for the time being. The connection or the relationship between the items (but only considering the relationship between users and items) and the model does not take into account a variety of behaviors, so this paper needs to improve it to meet the ideal requirements.
For the first question, this article wants to achieve the representation of the user aggregated through the related products, and also establishes a relationship through the relationship between the user and the product; therefore, taking the user as an example, the original GCN representation becomes (2):
In the graph neural network, it is mainly divided into two theoretical systems, the graph domain and the frequency domain, where (1) is the frequency domain implementation method of GCN, and (2) is actually a variant of the GCN graph domain implementation method, where represents the neighbors of user, u, under various behaviors, and is a standardized item.
The representation of the commodity is shown in (3):
After completing the previous work, this paper introduces the attention mechanism of GAT into the work of this paper.
First of all, this article calculates the attention coefficient, first looking at the attention coefficient calculation method in GAT [38].
For vertex u, the similarity coefficient between its neighbors, and itself, was calculated, as indicated in (4):
This formula was interpreted as (4): First, a linear map with a shared parameter, W, increases the dimension of the feature of the vertex. Of course, this is a common feature enhancement method; splicing, and finally, a(⋅) maps the spliced high-dimensional features to a real number. This is the calculation method of the similarity coefficient in the classic GAT. With the correlation coefficient, the distance from the attention coefficient is normalized. Here, the normalization method similar to GAT is directly used, as shown in Formula (5):
After getting the attention coefficient, this article can improve Formula (2) to (6):
and improve Formula (3) to (7):
After the attention mechanism is improved, it does not depend on the structure of the graph, has no pressure on the inductive task, and realizes the assignment of different learning weights to different neighbors. In the future, it can continue to be optimized and improved to a multi-head attention mechanism. After completing the above work, the first part of the model of this paper is completed.
3.2. Parameter Sharing Based on Multi-Tasking Learning
This paper obtains the embedded representation of users and products, but does not introduce the parameter sharing of multi-task learning, which leads to the fact that the multiple behaviors in this paper as the embedded representation between is only an independent representation, so this paper needs to find a way to solve the problem of parameter sharing [39]. Based on this idea, looking back at Formula (6), this paper finds that the parameter is actually , so it considers setting this parameter as a parameter common to multiple behaviors, and then improves (6) to:
After the improved Formula (8), this paper finds that the parameters represent the behavior disappearance, so this paper introduces an embedded representation, , for each behavior, and then improves Formula (8) to (9):
The update method is as follows (10):
In fact, here gives different weights to different behaviors, which is the non-shared layer in multi-behavior learning.
So far, this paper has solved the problem of the shared layer, and also obtained the embedded representation of users, products, and relationships.
The representations obtained from different layers emphasize the information delivered from different hops. For example, the first layer enforces the smoothing of interacting users and items, the second layer smooths overlapping users (items) on interacting items (users), and the higher layers capture higher-order proximity, thus combining them further to get the final representation. The attention mechanism is still used here, and the attention coefficient is (11):
The superimposed users, items, and relationship embeddings are expressed as (12):
Finally, this paper obtains the predicted value, which represents the probability of interaction between user, u, and product, v, under k behaviors (13):
where represents a diagonal matrix, of which the diagonal elements are equal .
At this point, the first two modules of this model in the article are solved, and the subsequent third module is to solve the problem of loss.
3.3. Introduction to the Algorithm of Loss Merging
Taking the single k-th behavior as an example for a batch of users, B, and the entire product set, V, the traditional weighted regression loss is:
It can be seen that the time complexity of calculating this loss is , which is generally unaffordable in practice. However, based on previous research [40], it can be optimized to . The work of this paper is not focused on this, but on the summation of the subsequent multi-behavior losses. Optimizing model operations, such as reducing model time complexity and optimal resource allocation, can be done according to [41,42].
For the traditional summation method, the losses of multiple tasks are directly added to obtain the overall loss. However, there are two problems. One is that the magnitude of the loss of different tasks is different, and there may be a phenomenon that the task with a larger loss dominates. The other is that the learning speed of different tasks is different; some are slow, and some are fast. This paper discusses three commonly used loss optimization algorithms: gradient normalization (GradNorm) [43], using uncertainty to weigh losses (UWL) [44], and dynamic weight average (DWA) [45], to conduct experiments to obtain an algorithm with better results in the current scenario. This is added to the model to improve the final effect of the model.
GradNorm proposes a new method which can automatically balance the different gradient levels of multitasks, improve the effect of multitask learning, and reduce overfitting.
The definition of total loss is still the weighted average of the loss of different tasks, as shown in (15):
GradNorm designed an additional loss to learn the weight, , of different task losses, but it does not participate in the reverse gradient update of the parameters of the network layer. The purpose is that the gradients of different tasks can become the same magnitude through regularization, so that different tasks can be achieved. The train at a close speed is as follows:
Among them, t represents the number of training steps, W generally takes the weight of the last shared layer, where represents the regularization gradient of the i-th task; that is, the gradient of loss to , and then L2-norm. represents the mean of multiple regularized gradients.
indicates the relative learning speed of the i-th task:
Among them, represents the loss ratio of the i-th task (step t) and the initial loss ratio, which is used to represent the learning speed:
The core of UWL is , where is a learnable parameter, and the paper regards it as the uncertainty (uncertainty) of the corresponding task modeling. It can be seen that the consequence of the total loss on the tasks is a large loss and a small , because for this kind of task, will be very large and SGD will optimize it to a small size, This represents a task with a large loss, which means that its uncertainty (uncertainty) is also high. In order to prevent the model from “big steps” in the wrong direction, smaller gradients should be used to update w. On the contrary, for tasks with smaller losses, its uncertainty is also lower, and w is updated with larger gradients. At the same time, this can also avoid the problem of letting tasks with larger losses dominate.
The DWA method is relatively simple and direct. Unlike GradNorm, it does not need to calculate the gradient, but only needs the loss of the task. The formula is expressed as (19):
is the weight of the task; that is, the total loss is still the weighted average of the loss of all tasks: . is the loss ratio of the previous round, representing learning rates for different tasks. T plays a role in smoothing task weights, and the larger the T is, the more uniform the weight distribution of different tasks is. If T is large enough, then , and the weight of each task is equal. K means that the weighted sum of all tasks is K. Because in general, if there is no special treatment the weight of each task is equal to 1, all tasks will be K after weighting.
In terms of experimental indicators, this paper selects the hit rate (HR) and the normalized discounted cumulative gain (NDCG) as the experimental indicators of the experiment. These two indicators are commonly used in recommendation systems. Both HR and precision indicators are indicators for evaluating the accuracy of the model predictions. The HR indicator focuses more on whether the model can include user demand items in the recommendation list, while the precision indicator focuses more on how many of the samples predicted by the model as positive are truly positive. The main difference is in the calculation method and focus. In this study, the final test set used is the product that the user finally purchased. The model is to predict whether it is correctly recommended, so using the HR indicator is more appropriate. Recall and F-ratio indicators are similar to precision and will not be repeated. In addition to the accuracy of the recommendations, it is also necessary to consider whether the recommended items are closer to the front and whether they are placed in a more conspicuous position. Precision, recall, F-ratio, and other indicators cannot be represented, but the NDCG can be represented. NDCG is an evaluation indicator that emphasizes orderliness. Its focus is on whether the recommended items are placed in a conspicuous position for users and assigns higher scores to items that are closer to the front.
HR indicates the users’ things and whether the recommendation system has recommended it, emphasizing the accuracy of the prediction as per the formula shown in (20):
Among them, N represents the users’ access weight, which is the number of real clicks by the user. If the recommendation system recommends product i, hit(i) is 1, otherwise it is 0.
NDCG concerns with whether the found products are placed in a prominent position for users; that is, it emphasizes the order, as per the formula shown in (21):
Among them, N represents the total number of user visits, which is the number of real clicks by users. indicates the position where the item appears in the recommendation results; if it does not appear, then is infinite.
4. Results
4.1. Experimental Settings
In terms of experimental datasets, this paper conducts experiments on two datasets, namely the Beibei and the Taobao datasets. The dataset structure information is shown in Table 1.

Table 1.
Dataset structure statistics.
The Beibei dataset comes from Beibei, the largest e-commerce platform for baby products in China. In this dataset, there are 21,716 users and 7977 entries with three behavior types, including click, add to cart, and purchase behavior.
The Taobao dataset comes from the Taobao e-commerce platform and is a Taobao user behavior dataset provided by Alibaba. In this dataset, there are 48,749 users and 39,493 entries with three behavior types, including click, add to cart, and purchase behaviors.
After that, the last purchase records of users are used as test data, the second last records are used as validation data, and the remaining records are used for training.
The experiments in this paper are compared with four models, including two single-behavior recommendation models and two multi-behavior recommendation models, among which BPR [46] and LightGCN [5] are single-behavior recommendation models, and MC-BPR [47] and NMTR [35] are multi-behavior recommendation models.
Among them, BPR is a Bayesian personalized ranking, which is a commonly used recommendation algorithm based on traditional machine learning in recommendation systems. It was proposed earlier, but is often cited as a baseline, so this study also uses it as one of the baselines. Different from other methods based on the user rating matrix, BPR mainly uses the users’ implicit feedback (such as click, favorite, etc.), and sorts the products through the maximum posterior probability obtained by Bayesian analysis of the problem, and then generates recommendations.
LightGCN is a light, but effective GCN network. This study is also based on graph neural networks, so it is necessary to use LightGCN as a baseline. It discards the feature transformation and nonlinear activation of traditional GCN, and it is verified by experiments that these two operations are invalid for collaborative filtering. At the same time, a lightweight GCN is proposed. The network construction model (LightGCN) is used for recommender systems. LightGCN only contains the most basic structure in GCN (neighborhood aggregation) for collaborative filtering. LightGCN learns user and item embeddings by performing a linear propagation on the user–item interaction matrix, and finally takes the weighted sum of the embeddings learned by all the layers as the final embedding.
BPR and LightGCN were selected as single-behavior models to demonstrate the advantages of multi-behavior models.
In MC-BPR, negative items are sampled in the item space reduced by BPR, and it is shown that sampling from all items is unnecessary. BPR was used as a baseline earlier, and MC-BPR will be used as a baseline later. The reason is that it can not only show the advantages of multi-behavior recommendations, but also serve as a comparison between traditional machine learning recommendation algorithms and deep learning algorithms. Additionally, a view-enhanced user-oriented BPR sampler is designed, which can effectively integrate user view data into an online shopping recommendation system, where the viewed interaction behavior is regarded as the difference between the purchased interaction and the unobserved interaction. The intermediate feedback of using multiple behaviors enhances the model performance.
NMTR is an advanced method that combines the latest developments in neural collaborative filtering (NCF) modeling with the effectiveness of multitask learning. It is mainly through research on deep learning algorithms and multi-behavior learning, while we set graph neural networks to carry out multi-behavior learning. Comparing with it can show the effectiveness of graph neural networks and traditional deep learning methods. NMTR is capable of learning user preferences from multi-behavioral data, where users (and items) have shared embeddings across multiple behavior types, and each behavior type learns a data-dependent interaction function. Furthermore, in order to integrate behavioral semantics, especially the sequential relationship between behavioral types, model predictions for each behavioral type are connected in a cascaded manner.
All parameters of the baseline methods are initialized as in the corresponding papers and then carefully tuned for the best performance. The MGAT algorithm related parameters are set as follows: epoch is 100, embed_size is 64, layer_size is 3, batch_size is 256, node_dropout is 0.5, mess_dropout is 0.2, and lr is 0.01.
All experiments are conducted in the same experimental environment. Experimental environment hardware parameters are set as follows: CPU is AMD EPYC 7543 32-Core Processor, memory is 30GB, graphics card is RTX A5000, and video memory is 24GB. For the experimental environment software parameters, the operating system is Ubuntu 18.04, using python 3.6 and TensorFlow-GPU version 1.12.
4.2. Recommended Algorithm Experiment Results
In this paper, five models are tested on the Beibei and Taobao datasets, and the experimental results are summarized in Table 2 and Table 3.

Table 2.
The comparison results of the Beibei dataset across four kinds of recommendation algorithms.

Table 3.
The comparison results of the Taobao dataset across four kinds of recommendation algorithms.
As shown in Table 2 and Table 3, we can intuitively see that the multi-behavior recommendation algorithm based on the graph neural network (MGAT) under HR and NDCG indicator experiments on Beibei and Taobao datasets, the effect is significantly better than other recommendation algorithms. For BPR and LightGCN, the single-behavior algorithms do not use other user behaviors, making them unable to capture the relationship between users and items through other behaviors. Therefore, the effects of these two algorithms are worse than other multi-behavior algorithms.
For MC-BPR, it is mainly BPR extended on multi-behavior data and its effect is better than single-behavior BPR, but it still uses a traditional recommendation algorithm. Therefore, the effect is relatively worse than NMTR and MGAT. NMTR is a method that uses multi-behavior data to complete recommendations, but this algorithm does not use multi-behavior data to adjust user and item embedding, nor does it mine complex relationships between behaviors. Our algorithm captures user–item relationships through attention mechanism and iteratively updates user, item, and relationship embedding through multiple graph neural network layers, making it able to update embedding, so its effect is better than that of other models.
Subsequently this paper carries out an ablation experiment to prove that multi-behavior recommendation indeed improves the model accuracy rate. It separately carries out only purchase behavior, purchase behavior plus shopping cart behavior, and purchase behavior plus view behavior, and the three kinds of behaviors are used for the experiment. The experimental results are shown in Table 4 and Table 5. In Table 4 and Table 5, Only-Buy refers to the experimental results of the MGAT algorithm using only purchase behavior, Buy-Cart refers to the experimental results of the MGAT algorithm using purchase behavior and add-to-cart behavior, Buy-Pv refers to the experimental results of the MGAT algorithm using purchase behavior and browsing behavior, and All refers to the experimental results of the MGAT algorithm using purchase behavior, add-to-cart behavior and browsing behavior. From Table 4, it can be seen that for the Beibei dataset, the experimental results using purchase behavior and add-to-cart behavior are the best. For the Taobao dataset, the experimental results using purchase behavior, add-to-cart behavior and browsing behavior are the best. The meaning of the horizontal axis in Figure 2a,b is the same as in Table 4 and Table 5.

Table 4.
The results of the ablation experiment under the Beibei dataset.

Table 5.
The results of the ablation experiment under the Taobao dataset.
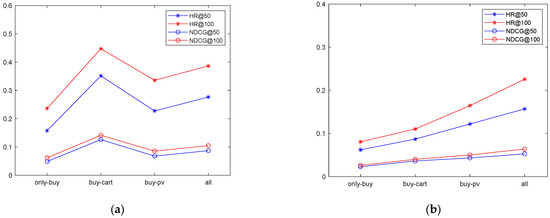
Figure 2.
(a) Comparison of the ablation results of the Beibei dataset; (b) comparison of the ablation results of the Taobao dataset.
From Figure 2a,b, we can intuitively see that adding user behavior can indeed improve the experimental results on both the Beibei and Taobao datasets. Moreover, different user behaviors have different impacts on the experimental results. From the Beibei dataset, it can be found that blindly increasing user behavior does not always improve the experimental results. On the Taobao dataset, increasing user behavior can improve the experimental results. In summary, it can be concluded that increasing user behavior can indeed improve the experimental results to a certain extent, but may not continue to improve. The reason may be related to the quality of the dataset.
From the above ablation experiment results, it can be seen that compared to a single behavior, adding multiple user behaviors can indeed improve the performance of the model. However, from the experimental results in this paper, it can be found that adding different user behaviors has different impacts on the model. From the Beibei dataset, it can be seen that the model with purchase behavior and add-to-cart behavior is better than adding all behaviors. Therefore, we can infer that the impact between behaviors is also different and some behaviors may have a negative impact on the model. This paper considers solving this problem from loss optimization. By merging multiple losses and assigning different weights to different behaviors to affect changes in model loss, and thus improve the recommendation effect of this paper’s model. In fact, this is precisely the second key issue of multi-behavior recommendation: how to model relationships between multiple behaviors. This paper starts from loss optimization and uses DWA, UWL, and GradNorm, three loss optimization algorithms on our basic model, respectively, to conduct experiments on the Beibei and Taobao datasets.
4.3. The Algorithm Loses the Experimental Results of Optimization
This article uses DWA, UWL, and GradNorm, three loss-merging algorithms on the basic model of this article, and conducts experiments on two datasets. The experimental results are shown in Table 6 and Table 7. Here, the baseline models all use the MGAT model proposed in this paper and use multiple loss optimization algorithms to submit experimental results. None represents the experimental results without using any loss optimization algorithm, DWA represents the experimental results using the DWA loss optimization algorithm, UWL represents the experimental results using the UWL loss optimization algorithm, and GradNorm represents the experimental results using the GradNorm loss optimization algorithm. The meaning of the vertical axis in Figure 3a,b is the same as in Table 6 and Table 7.

Table 6.
Comparison of the loss optimization experiment results of the Beibei dataset.

Table 7.
Comparison of the loss optimization experiment results of the Taobao dataset.
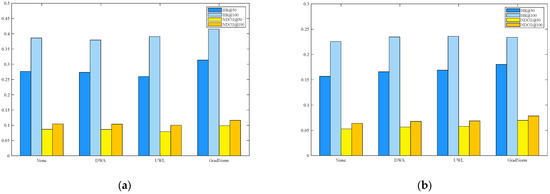
Figure 3.
(a) The results of multiple loss optimization algorithms are compared for the Beibei dataset; (b) the results of multiple loss optimization algorithms are compared for the Taobaodataset.
From Table 6 and Table 7, Figure 3a,b, it can be intuitively seen that in most cases, for the comparison of HR and NDCG indicators, the performance of GradNorm is better than other algorithms. Other loss optimization algorithms basically have no significant impact on the model’s performance in multi-behavior recommendation scenarios. Therefore, this paper reinforces that GradNorm algorithm is better than the DWA and UWL algorithms in multi-behavior recommendation scenarios. This paper uses GradNorm as the loss optimization algorithm for the model.
We conducted three experiments on the Beibei and Taobao datasets. First, we built a multi-behavioral recommendation model based on graph neural networks and compared it with BPR, LightGCN, MC-BPR, and NMTR. The results showed that our proposed MGAT algorithm performed better in the HR and NDCG metrics. Then, we conducted ablation experiments to prove that the addition of behavior can indeed improve the model performance. At the same time, according to the experimental results, we found that blindly increasing behavior data will not make the model performance continue to grow. Therefore, in order to solve the above problem, we started from the perspective of loss optimization and conducted experiments on the existing loss optimization algorithms, namely DWA, UWL, and GradNorm algorithms. Through the experiment, it was found that GradNorm algorithm had the best performance on the Beibei and Taobao datasets, so we used the GradNorm algorithm as the loss optimization algorithm of our model. Through the above experiments, it is proved that our proposed MGAT algorithm is better than the classical recommendation algorithm within HR and NDCG metrics, which proves that the MGAT algorithm has a certain superiority in multi-behavioral recommendation algorithms.
5. Conclusions
In this study, we propose a new multi-behavior recommendation model based on graph neural networks and attention mechanisms, that can effectively model users and items under multiple behaviors and achieve better results than existing recommendation models on two real-world datasets. In addition, we further improve the recommendation effect by considering the relationship between multiple user behaviors from the perspective of loss optimization. Future research can consider incorporating information contained within interaction behaviors into the model, and exploring the application of the MGAT model to other related tasks.
Author Contributions
Conceptualization, H.L., X.D. and J.L.; methodology, H.L.; software, H.L.; validation, H.L.; formal analysis, H.L. and X.D.; investigation, H.L.; resources, H.L.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, X.D. and J.L.; visualization, H.L. and X.D.; supervision, X.D. and J.L.; project administration, X.D. and J.L.; funding acquisition, X.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the 173 Basic Foundation Reinforcement Project of China in social network analysis grant number [No. JSLY-A12017] and the Key Technology Project of Shenzhen city with the name 2021 Research and development of key edge computing gateway technology based on 5G grant number [No. JSGG20201103092802010].
Data Availability Statement
Our training set Epinions dataset is publicly available.
Acknowledgments
The authors would like to thank the 173 Basic Foundation Reinforcement Project of China in social network analysis grant number [No. JSLY-A12017] and the Key Technology Project of Shenzhen city with the name 2021 Research and development of key edge computing gateway technology based on 5G grant number [No. JSGG20201103092802010].
Conflicts of Interest
The authors declare no conflict of interest.
References
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Berg, R.V.d.; Kipf, T.N.; Welling, M. Graph convolutional matrix completion. arXiv 2017, arXiv:1706.02263. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph Convolutional Neural Networks for Web-Scale Recommender Systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. Lightgcn: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; pp. 639–648. [Google Scholar]
- Zhang, W.; Mao, J.; Cao, Y.; Xu, C. Multiplex Graph neural Networks for Multi-Behavior Recommendation. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Virtual Event, Ireland, 19 October 2020; pp. 2313–2316. [Google Scholar]
- Chen, C.; Ma, W.; Zhang, M.; Wang, Z.; He, X.; Wang, C.; Liu, Y.; Ma, S. Graph Heterogeneous Multi-Relational Recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Palo Alto, CA, USA, 18 May 2021; pp. 3958–3966. [Google Scholar]
- Xia, L.; Huang, C.; Xu, Y.; Dai, P.; Lu, M.; Bo, L. Multi-Behavior Enhanced Recommendation With Cross-Interaction Collaborative Relation Modeling. In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering (ICDE), Chania, Greece, 19–22 April 2021; pp. 1931–1936. [Google Scholar]
- Xia, L.; Huang, C.; Xu, Y.; Dai, P.; Zhang, X.; Yang, H.; Pei, J.; Bo, L. Knowledge-Enhanced Hierarchical Graph Transformer Network for Multi-Behavior Recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 22 February–1 March 2022; pp. 4486–4493. [Google Scholar] [CrossRef]
- Han, L.; Chen, L.; Shi, X. Recommendation Model Based on Probabilistic Matrix Factorization and Rated Item Relevance. Electronics 2022, 11, 4160. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, R.; Chen, W.; Fang, J. Graph neural network based model for multi-behavior session-based recommendation. GeoInformatica 2022, 26, 429–447. [Google Scholar] [CrossRef]
- Zhang, S.; Bai, Z.; Li, P.; Chang, Y. Multi-Graph Convolutional Network for Fine-Grained and Personalized POI Recommendation. Electronics 2022, 11, 2966. [Google Scholar] [CrossRef]
- Jia, M.; Liu, F.A.; Li, X.; Zhuang, X. Hybrid Graph Neural Network Recommendation Based on Multi-Behavior Interaction and Time Sequence Awareness. Electronics 2023, 12, 1223. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, J.; Wang, H.; Li, S.; Kim, M.; Walker, M.; Xiao, Y.; Han, J. Relation Learning on Social Networks with Multi-modal Graph Edge Variational Autoencoders. In Proceedings of the 13th International Conference on Web Search and Data Mining, Houston, TX, USA, 3–7 February 2020; pp. 699–707. [Google Scholar]
- Sun, M.; Zhao, S.; Gilvary, C.; Elemento, O.; Zhou, J.; Wang, F. Graph convolutional networks for computational drug development and discovery. Brief. Bioinform. 2020, 21, 919–935. [Google Scholar] [CrossRef]
- Rong, Y.; Bian, Y.; Xu, T.; Xie, W.; Wei, Y.; Huang, W.; Huang, J. Self-supervised graph transformer on large-scale molecular data. Adv. Neural Inf. Process. Syst. 2020, 33, 12559–12571. [Google Scholar]
- Liu, Z.; Dou, Y.; Yu, P.S.; Deng, Y.; Peng, H. Alleviating the Inconsistency Problem of Applying Graph Neural Network to Fraud Detection. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; pp. 1569–1572. [Google Scholar]
- Zhang, Y.; Fan, Y.; Ye, Y.; Zhao, L.; Shi, C. Key Player Identification in Underground Forums over Attributed Heterogeneous Information Network Embedding Framework. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 549–558. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Medjahed, B.; Atif, Y. Context-based matching for web service composition. Distrib. Parallel Databases 2007, 21, 5–37. [Google Scholar] [CrossRef]
- Segev, A.; Toch, E. Context-based matching and ranking of web services for composition. IEEE Trans. Serv. Comput. 2009, 2, 210–222. [Google Scholar] [CrossRef]
- Huang, J.; Zhao, W.X.; Dou, H.; Wen, J.-R.; Chang, E.Y. Improving Sequential Recommendation with Knowledge-Enhanced Memory Networks. In Proceedings of the the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 505–514. [Google Scholar]
- Kim, D.; Park, C.; Oh, J.; Lee, S.; Yu, H. Convolutional Matrix Factorization for Document Context-Aware Recommendation. In Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; pp. 233–240. [Google Scholar]
- Zhang, Q.; Wang, J.; Huang, H.; Huang, X.; Gong, Y. Hashtag Recommendation for Multimodal Microblog Using Co-Attention Network. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, Australia, 19–25 August 2017; pp. 3420–3426. Available online: http://www.qizhang.info/paper/ijcai2017hashtag.pdf (accessed on 19 February 2023).
- Gao, C.; Zheng, Y.; Li, N.; Li, Y.; Qin, Y.; Piao, J.; Quan, Y.; Chang, J.; Jin, D.; He, X. A survey of graph neural networks for recommender systems: Challenges, methods, and directions. ACM Trans. Recomm. Syst. 2023, 1, 1–51. [Google Scholar] [CrossRef]
- Jin, B.; Gao, C.; He, X.; Jin, D.; Li, Y. Multi-Behavior Recommendation with Graph Convolutional Networks. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; pp. 659–668. [Google Scholar]
- Wang, W.; Zhang, W.; Liu, S.; Liu, Q.; Zhang, B.; Lin, L.; Zha, H. Incorporating link prediction into multi-relational item graph modeling for session-based recommendation. IEEE Trans. Knowl. Data Eng. 2021, 35, 2683–2696. [Google Scholar] [CrossRef]
- Singh, A.P.; Gordon, G.J. Relational Learning via Collective Matrix Factorization. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 650–658. [Google Scholar]
- Krohn-Grimberghe, A.; Drumond, L.; Freudenthaler, C.; Schmidt-Thieme, L. Multi-Relational Matrix Factorization Using Bayesian Personalized Ranking for Social Network Data. In Proceedings of the Fifth ACM International Conference on Web Search and Data Mining, Seattle, WA, USA, 8–12 February 2012; pp. 173–182. [Google Scholar]
- Zhao, Z.; Cheng, Z.; Hong, L.; Chi, E.H. Improving User Topic Interest Profiles by Behavior Factorization. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1406–1416. [Google Scholar]
- Loni, B.; Pagano, R.; Larson, M.; Hanjalic, A. Bayesian Personalized Ranking with Multi-Channel User Feedback. In Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; pp. 361–364. [Google Scholar]
- Qiu, H.; Liu, Y.; Guo, G.; Sun, Z.; Zhang, J.; Nguyen, H.T. BPRH: Bayesian personalized ranking for heterogeneous implicit feedback. Inf. Sci. 2018, 453, 80–98. [Google Scholar] [CrossRef]
- Ding, J.; Yu, G.; He, X.; Quan, Y.; Li, Y.; Chua, T.-S.; Jin, D.; Yu, J. Improving Implicit Recommender Systems with View Data. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18), Stockholm, Sweden, 13–19 July 2018; pp. 3343–3349. Available online: https://www.ijcai.org/proceedings/2018/0464.pdf (accessed on 19 February 2023).
- Ding, J.; Feng, F.; He, X.; Yu, G.; Li, Y.; Jin, D. An Improved Sampler for Bayesian Personalized Ranking by Leveraging View Data. In Proceedings of the Companion Proceedings of the The Web Conference 2018, Lyon, France, 23–27 April 2018; pp. 13–14. [Google Scholar]
- Gao, C.; He, X.; Gan, D.; Chen, X.; Feng, F.; Li, Y.; Chua, T.-S.; Jin, D. Neural Multi-Task Recommendation from Multi-Behavior Data. In Proceedings of the 2019 IEEE 35th International Conference on data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 1554–1557. [Google Scholar]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.-S. Neural Graph Collaborative Filtering. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; pp. 165–174. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Ruder, S. An overview of multi-task learning in deep neural networks. arXiv 2017, arXiv:1706.05098. [Google Scholar]
- Chen, C.; Zhang, M.; Zhang, Y.; Liu, Y.; Ma, S. Efficient neural matrix factorization without sampling for recommendation. ACM Trans. Inf. Syst. (TOIS) 2020, 38, 1–28. [Google Scholar] [CrossRef]
- Yeh, W.-C. A squeezed artificial neural network for the symbolic network reliability functions of binary-state networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2822–2825. [Google Scholar] [CrossRef]
- Yeh, W.-C.; Wei, S.-C. Economic-based resource allocation for reliable Grid-computing service based on Grid Bank. Future Gener. Comput. Syst. 2012, 28, 989–1002. [Google Scholar] [CrossRef]
- Chen, Z.; Badrinarayanan, V.; Lee, C.-Y.; Rabinovich, A. Gradnorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks. arXiv 2018, arXiv:1711.02257v4. [Google Scholar]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7482–7491. [Google Scholar]
- Liu, S.; Johns, E.; Davison, A.J. End-to-End Multi-Task Learning with Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–19 June 2019; pp. 1871–1880. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. arXiv 2012, arXiv:1205.2618. [Google Scholar]
- Ding, J.; Yu, G.; He, X.; Feng, F.; Li, Y.; Jin, D. Sampler design for bayesian personalized ranking by leveraging view data. IEEE Trans. Knowl. Data Eng. 2019, 33, 667–681. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).