Optimization and Design of Balanced BPF Based on Mixed Electric and Magnetic Couplings
Abstract
:1. Introduction
2. Analysis and Design
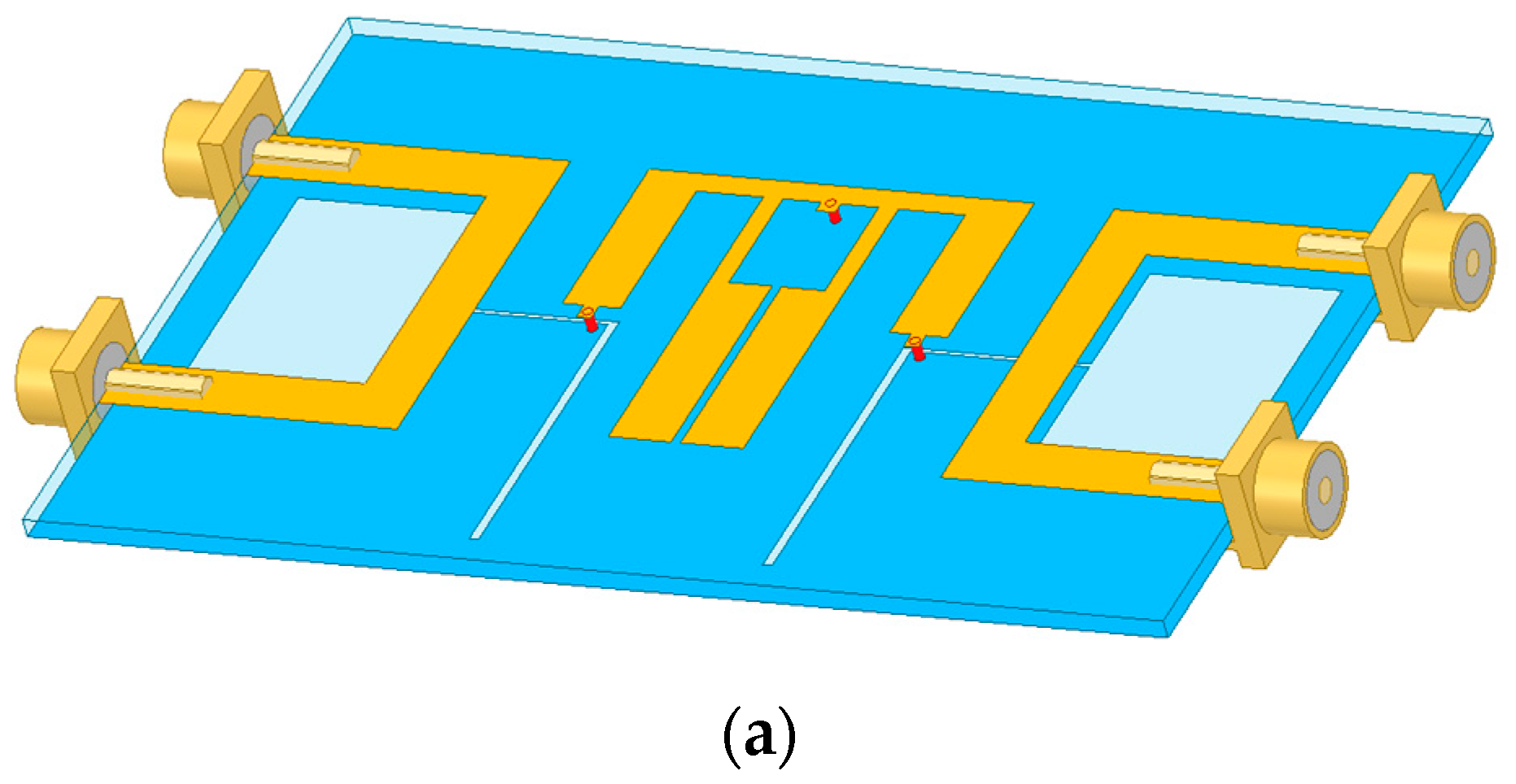
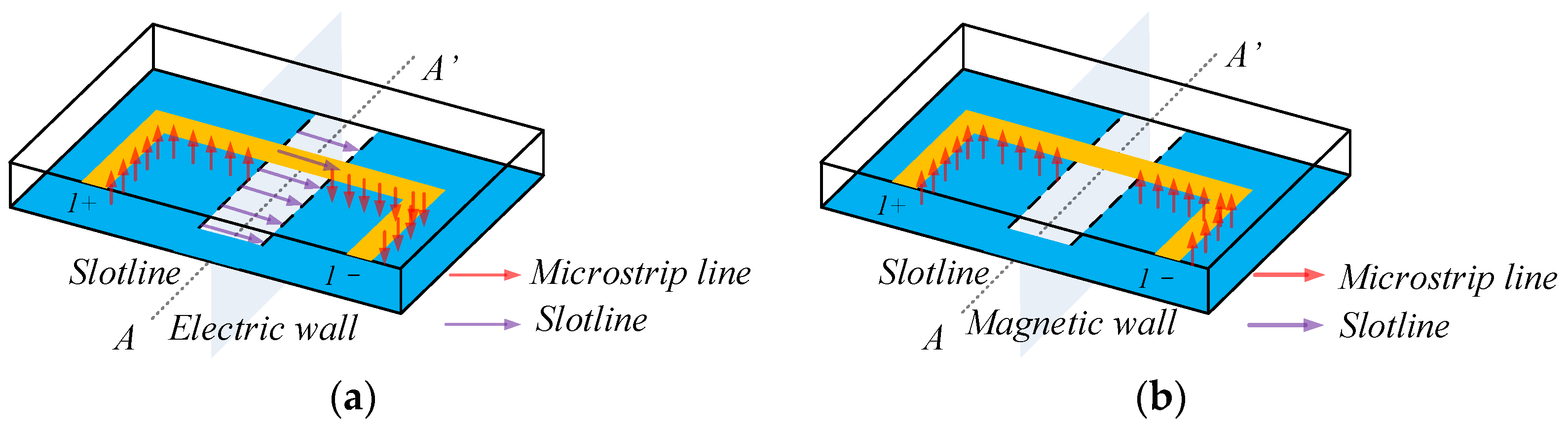
2.1. Configuration of Balanced BPF
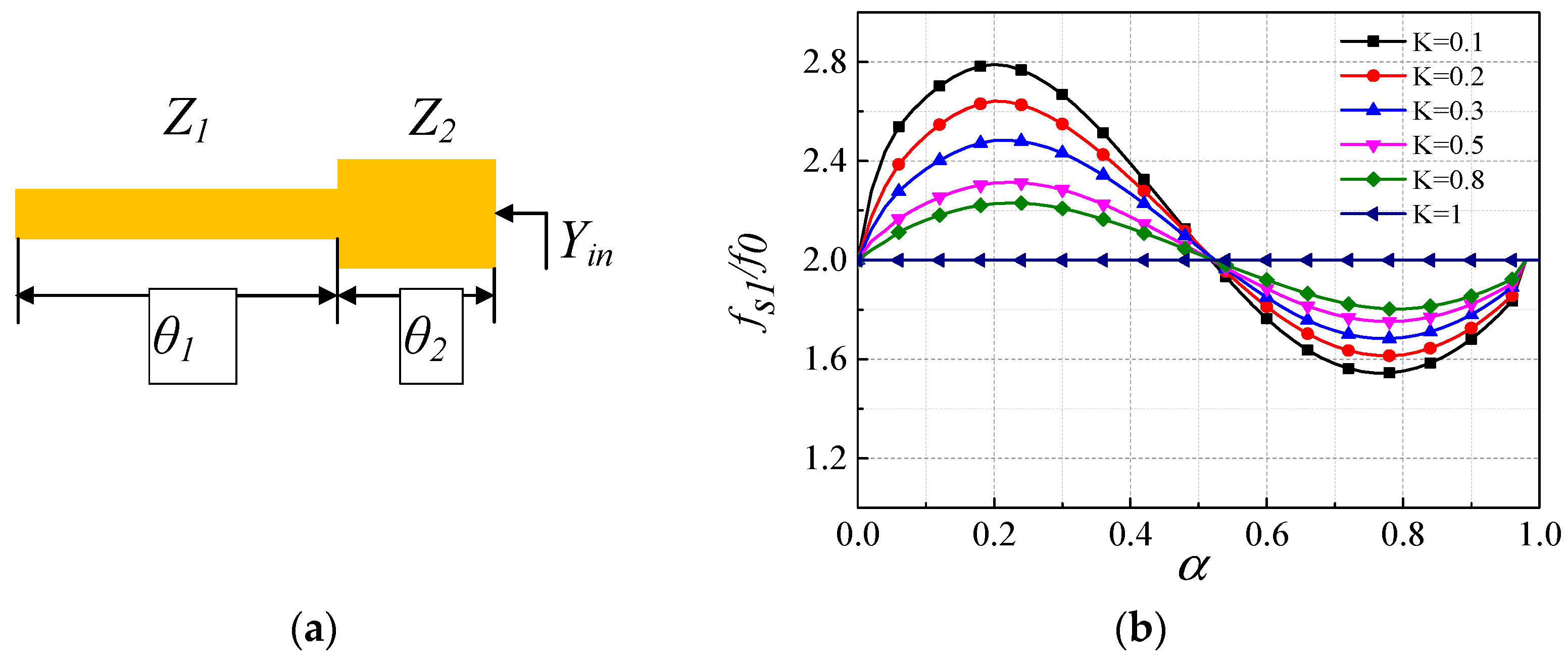
2.2. DM Response
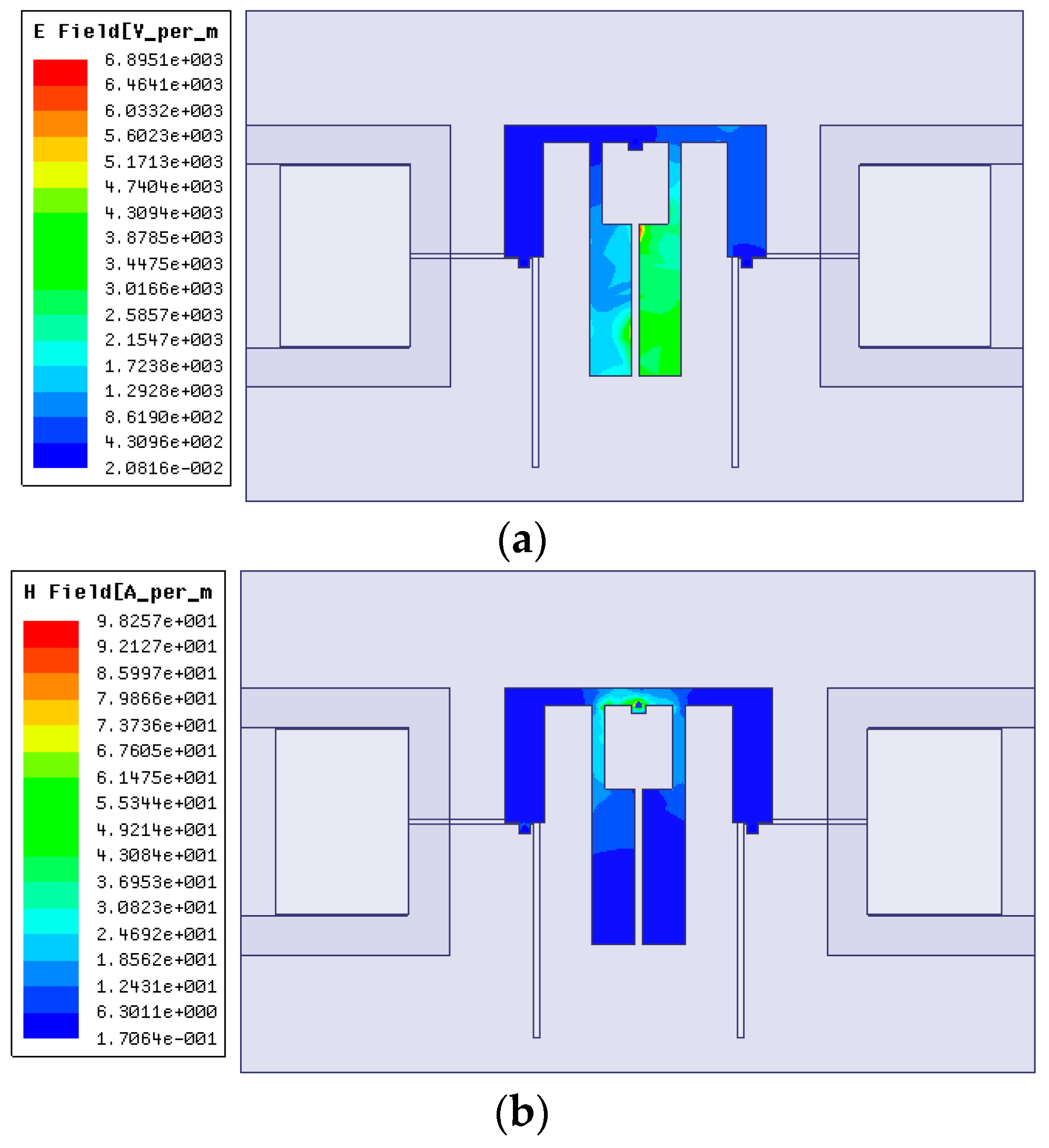
2.3. CM Suppression
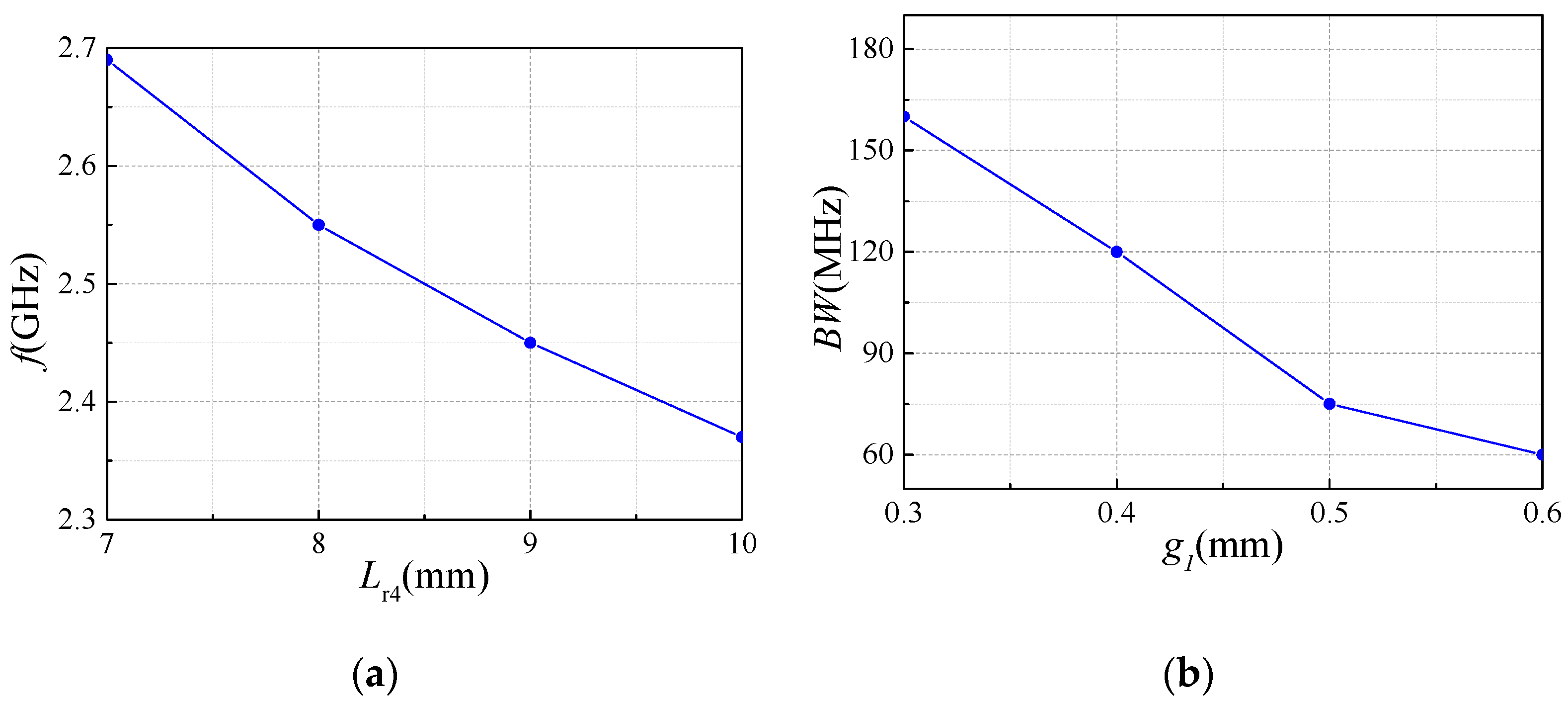
2.4. Design Procedure
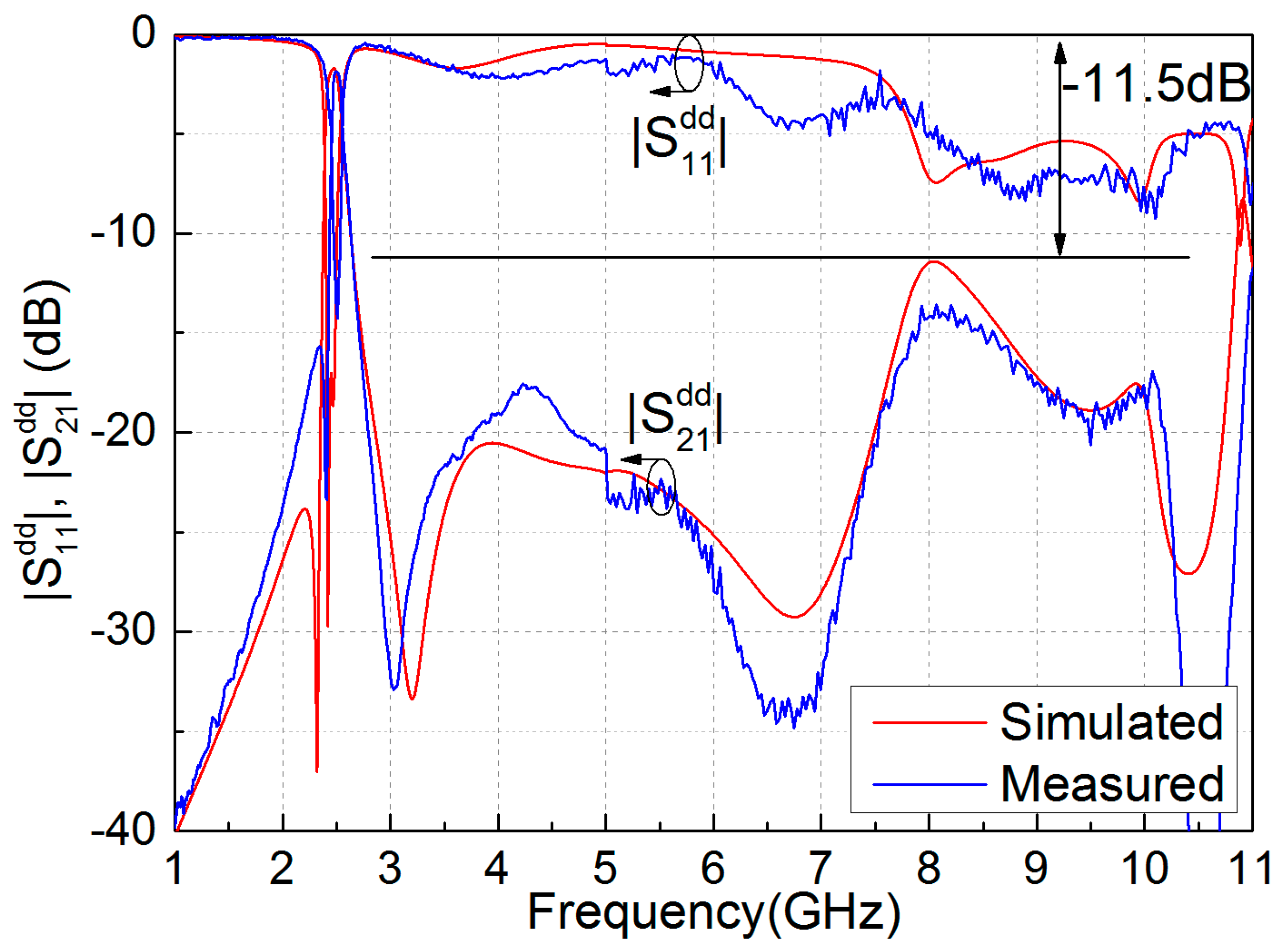
3. Simulation and Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, F.; Yang, Z.-J.; Qin, P.-Y.; Guo, Y.J.; Li, B.; Shi, X.-W. A Balanced-to-Balanced In-Phase Filtering Power Divider with High Selectivity and Isolation. IEEE Trans. Microw. Theory Tech. 2018, 67, 683–694. [Google Scholar] [CrossRef]
- Feng, W.; Che, W.; Xue, Q. New Balance-Applications for Dual-Mode Ring Resonators in Planar Balanced Circuits. IEEE Microw. Mag. 2019, 28, 15–23. [Google Scholar] [CrossRef]
- Shi, J.; Xue, Q. Balanced Bandpass Filters Using Center-Loaded Half-Wavelength Resonators. IEEE Trans. Microw. Theory Tech. 2010, 58, 970–977. [Google Scholar] [CrossRef]
- Shi, J.; Shao, C.; Chen, J.-X. Compact Low-Loss Wideband Differential Bandpass Filter With High Common-Mode Suppression. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 480–482. [Google Scholar] [CrossRef]
- Deng, H.; Zhao, Y.; He, Y.; Liu, H.; Wang, H. High selectivity and common-mode suppression wideband balanced bandpass filter using slotline resonator. IET Microw. Antennas Propag. 2015, 9, 508–516. [Google Scholar] [CrossRef]
- Deng, H.-W.; Zhang, T.; Liu, F.; Xu, T. High Selectivity and CM Suppression Frequency-Dependent Coupling Balanced BPF. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 413–415. [Google Scholar] [CrossRef]
- Sun, J.; Li, G.R. A balanced ultra-wideband bandpass filter based on H-type sandwich slotline. Int. J. RF Microw. Comput.-Aided Eng. 2021, 31, e22611. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, J.; Zhang, G.; Zhu, L.; Wu, W. A New Design Approach for Balanced Bandpass Filters on Right-Angled Isosceles Triangular Patch Resonator. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 5–7. [Google Scholar] [CrossRef]
- Zou, X.T.; Yang, Z.J.; Wei, F.; Li, B.; Shi, X.W. Compact Balanced Single-Band and Dual-Band BPFs with Controllable Bandwidth Using Folded S-Shaped Slotline Resonators (FSSRs). Frequenz 2018, 73, 13–18. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Chen, J.-X.; Xue, Q.; Li, S.-M. Dual-Band Bandpass Filters Using Stub-Loaded Resonators. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 583–585. [Google Scholar] [CrossRef]
- Aliqab, K.; Hong, J. Wideband Differential-Mode Bandpass Filters with Stopband and Common-Mode Suppression. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 233–236. [Google Scholar] [CrossRef]






| Refs. | f0(GHz)/3-dB FBW (%) | Number of TZs | CMS (dB) ※ | Upper Stopband (GHz) | Location of TZs (GHz) |
|---|---|---|---|---|---|
| [5] | 2.4/4 | 2 | 35 | 5.0 | 0/8.5 |
| [8] | 2/12.9 | 2 | 27.8 | 4.0 | 1.01/2.62 |
| Ref. [9] Design I | 1.2/20.1 | 1 | 55 | 2.0 | 0/1.75 |
| Ref. [11] Case 2 | 6.85 | 82 | 0 | 40 | None |
| This work | 2.47/6.4 | 2 | 45 | 10.8 | 2.4/3.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Fang, J.; Cao, W.; Sun, J.; Ding, J.; Tie, W.; Wei, F.; Zhai, C.; Wu, J. Optimization and Design of Balanced BPF Based on Mixed Electric and Magnetic Couplings. Electronics 2023, 12, 2125. https://doi.org/10.3390/electronics12092125
Li Q, Fang J, Cao W, Sun J, Ding J, Tie W, Wei F, Zhai C, Wu J. Optimization and Design of Balanced BPF Based on Mixed Electric and Magnetic Couplings. Electronics. 2023; 12(9):2125. https://doi.org/10.3390/electronics12092125
Chicago/Turabian StyleLi, Qiwei, Jinyong Fang, Wen Cao, Jing Sun, Jun Ding, Weihao Tie, Feng Wei, Chang Zhai, and Jiangniu Wu. 2023. "Optimization and Design of Balanced BPF Based on Mixed Electric and Magnetic Couplings" Electronics 12, no. 9: 2125. https://doi.org/10.3390/electronics12092125
APA StyleLi, Q., Fang, J., Cao, W., Sun, J., Ding, J., Tie, W., Wei, F., Zhai, C., & Wu, J. (2023). Optimization and Design of Balanced BPF Based on Mixed Electric and Magnetic Couplings. Electronics, 12(9), 2125. https://doi.org/10.3390/electronics12092125







