Assessing Impedance Analyzer Data Quality by Fractional Order Calculus: A QCM Sensor Case Study

Abstract

The paper presents the theoretical, simulation, and experimental results on the QCM sensor based on the Butterworth van Dyke (BVD) model with lumped reactive motional circuit elements of fractional order. The equation of the fractional order BVD model of the QCM sensor has been derived based on Caputo definitions and its behavior around the resonant frequencies has been simulated. The simulations confirm the ability of fractional order calculus to cover a wide range of behaviors beyond those found in experimental practice. The fractional order BVD model of the QCM sensor is considered from the perspective of impedance spectroscopy to give an idea of the advantages that fractional order calculus brings to its modeling. For the true values of the electrical parameters of the QCM sensor based on the standard BVD model, the experimental investigations confirm the equivalence of the measurements after the standard compensation of the virtual impedance analyzer (VIA) and the measurements without compensation by fitting with the fractional order BVD model. From an experimental point of view, using fractional order calculus brings a new dimension to impedance analyzer compensation procedures, as well as a new method for validating the compensation.

1. Introduction

Classical differential calculus in its modern form was discovered independently by Isaac Newton and Gottfried Wilhelm Leibnitz more than three centuries ago [1,2,3]. Leibnitz considered the existence of the half-order fractional derivative at the suggestion of l’Hopital, and consequently, several aspects of fractional calculus have been developed and studied over time [4,5]. There are different definitions for the fractional order derivative operator in the continuous time domain, such as the Riemann–Liouville and Caputo definitions, while in the discrete case, the Grunwald–Letnikov definition is used [6,7]. When modeling complex or nonlinear systems, fractional order calculus has become a common approach [8].

The intersection of other traditionally independent scientific fields with electronics and computer science involves modeling the behavior of intelligent systems or adaptive materials using an equivalent electrical circuit. Impedance spectroscopy measures the modulus of impedance and its phase as a function of frequency to obtain detailed information about the electrical behavior of the device under test (DUT). Advances in electrical circuit analysis based on impedance spectroscopy were the basis for this approach. The technological development of specific instruments has led to the complete automation of system analysis based on equivalent electrical circuits, thus contributing to the advancement of many fields such as mechatronics [9,10], piezotronics [11,12], and adaptronics [13,14], to name a few.

The impedance spectroscopy method for investigating complex behavior specific to adaptive materials or smart mechatronic structures may encounter difficulties in modeling based on ideal resistance, inductance, and capacitance (RLC) circuit elements [15,16]. This situation is well-known in electrochemistry and is the subject of extensive research [17,18,19]. These complex phenomena of a physical–chemical–biochemical nature encountered in electrochemistry or biological systems have led to the introduction of new circuit elements, such as constant phase element (CPE), Warburg impedance, T circuit element (Tanhyperbole), O circuit element (Cothyperbole), and Gerisher (G circuit element) [20], to list the most common circuit elements used in equivalent electrical models. Currently, the basis for a unified and general approach to this complex behavior is the use of fractional order calculus. As the impedance spectroscopy method is generalized, the use of fractional order calculus is required in the modeling of equivalent electrical circuits of complex or nonlinear phenomena [21,22,23]. The development of modern technologies such as supercapacitors [24], fuel cells [25], lithium-ion batteries [26], flyback converters [27], or nanosensors [28] could benefit from new approaches, such as fractional order calculus.

The use of the quartz crystal microbalance (QCM) sensor in liquid media [29,30,31] has brought great benefits in expanding the range of applications [32,33,34], especially in biological media [35]. A significant experimental effort was required to monitor the QCM sensor’s series resonance frequency and damping parameters using an active method (oscillator) [36,37,38] or passive interrogation, such as as ring-down methods [39,40,41] in high-viscosity liquid media.

Technological advances in digital electronics now offer substantial hardware support for extremely compact measuring instruments with outstanding performance. A powerful development direction with unprecedented flexibility in applications is virtual instruments [42,43]. Starting from a low-cost virtual instrument, it is possible to design an impedance analyzer with decent performance [44,45]. The advantages of impedance spectroscopy for monitoring QCM sensor behavior are (i) passive interrogation of the QCM sensor, (ii) determination of all electrical parameters of the Butterworth van Dyke (BVD) model, (iii) local processing of experimental data, (iv) an automatic self-compensation procedure, and (v) the evaluation of experimental data quality [46]. The impedance spectroscopy method, originally based on the vector network analyzer [47], was further developed by introducing the impedance analyzer in both its classical [48] and virtual versions [44]. The use of such instruments requires the application of laborious compensation methods. This stage of VIA compensation that precedes the measurements is critical to the correct measurement of the electrical parameters of the DUT. It is usually necessary to go through two stages: (i) an open-circuit measurement sequence followed by (ii) a measurement sequence under short-circuit conditions [44,46,49].

In this paper, an electrical model of the QCM sensor based on fractional order calculus (the fractional order BVD model) is proposed as an optimal compensation test. Knowing the true values of the electrical parameters of the QCM sensor using the fractional order BVD model, a reverse test can be performed by determining the fractional order of the circuit elements for an uncompensated VIA. These investigations applied to raw experimental data assess the quality of the data or the accuracy of the experimental setup. Measurements on the QCM sensor are performed in air so that the fractional order behavior of the reactive motional circuit elements is induced by using the VIA without optimal compensation. In this sense, the usefulness of the fractional order BVD model as a test of optimal VIA compensation should be understood.

The main contributions are summarized as follows: (i) the derivation of the equation for the fractional order BVD model of the QCM sensor, (ii) the simulation of the fractional order BVD model, (iii) a study of the fractional order BVD model as an optimal compensation test, and (iv) a study of the ability of the fractional order BVD model to generate a new compensation method.

This work is organized as follows. After a brief introduction, the VIA and fractional order BVD models are described. The simulation of the QCM sensor based on the fractional order BVD model concludes Section 2. The experimental results of the standard VIA compensation and the capabilities of fractional order calculus are presented in Section 3. Final discussions and conclusions are presented in Section 4 and Section 5.

2. Materials and Methods

2.1. Virtual Impedance Analyzer

Technological advances in electronics have generalized impedance analysis in many sensor applications [50,51,52]. In the case of the OCM sensor, the impedance analysis method is based on the passive interrogation of the QCM sensor to determine its response in the frequency domain. From the perspective of the BVD model of the QCM sensor, the impedance analysis method ensures the investigation of its behavior at a level that cannot be achieved by any other method [46].

The virtual impedance analyzer used in this paper, as well as its electrical characteristics and performance, have been presented in the literature [44,53]. Essentially, an Analog Discovery 2 (AD2) virtual instrument from Digilent Inc. (Pullman, WA, USA) is used along with an external shield of minimal complexity, as shown in Figure 1a. The AD2 virtual instrument shown in Figure 1b has remarkable performance for its technology class and provides the hardware resources needed to implement an impedance analyzer with decent performance.

Regarding the hardware resources of the AD2, it is worth mentioning the electrical performance of the ADC and DAC converters with a resolution of 14 bits at 100 MSPS. Two analog input channels and two analog output channels are available. They are digitally synchronized for phase measurements. Other hardware resources specific to virtual instruments are implemented in a Xilinx Spartan 6 FPGA (XC6SLX16-1L).

The analog input channels have an input impedance of 1 MΩ with 24 pF in parallel, with an absolute resolution of 0.32 mV for input voltages up to ±5 V. One of the output channels is used by the VIA application as an arbitrary wave generator (AWG) to provide the sine wave for passive interrogation of the QCM sensor. The sine wave interrogation is generated by direct digital synthesis and has an amplitude at the output of the DAC channel in the range of ±5 V.

Figure 1a shows the electrical circuit of the shield used by AD2 to passively measure the impedance of a QCM sensor. This configuration can provide a wide range of impedance measurements due to the high impedance of the input of the analog channels of the AD2 virtual instrument. The configuration shown in Figure 1a is a half-bridge that provides passive interrogation in the resonant frequency range of the QCM sensor. The analog input channels are digitally synchronized and measure two voltages, $V_{CH2}\left(j\omega \right)$ and $V_{CH1}\left(j\omega \right)$. The impedance of the QCM sensor $Z\left(j\omega \right)$ is given by the following equation:

$$Z\left(j\omega \right)=R\left(\frac{V_{CH2}}{V_{CH1}-V_{CH2}}\right)=R\frac{V_{CH2}}{V_R}$$

(1)

where R is the reference resistance equal to 1 KΩ.

The ability to build high-precision instruments with automatic data processing capabilities, ensuring automatic compensation procedures and advanced data communication capabilities through high-speed interfaces, is the main advantage of digital technology. In the first stage, the impedance analyzer measures the electrical impedance of the QCM sensor around the resonant frequencies, followed in the second stage by the complete characterization of its response by calculating the electrical parameters of the BVD model.

The performance of the impedance spectroscopy method depends largely on the compensation procedures of the impedance analyzer. The standard compensation procedure [44,46] includes (i) compensation for open-circuit parasitic impedance, Z_oc, followed by (ii) compensation for the short circuit parasitic impedance, Z_sc. The compensated value of the impedance (Z_Q) of the QCM sensor is calculated using the following equation:

$$Z_Q=\frac{Z_{rm}-Z_{sc}}{1-\left(Z_{rm}-Z_{sc}\right)/Z_{oc}}$$

(2)

where Z_rm is the QCM sensor raw measured impedance.

2.2. Impedance Spectroscopy of the QCM Sensor Based on the BVD Model

The response of the QCM sensor is determined by the interaction of the electrode exposed to the working medium and the interactions occurring on its surface. Effective monitoring of the QCM sensor is ensured by measuring electrical parameters for the circuit elements of the BVD model. The diagram of the VIA shield is shown in Figure 1a with the BVD model of the QCM sensor. By connecting the electrode exposed to the working medium to the ground (Figure 1a), the most favorable experimental situation is ensured.

The BVD model for the QCM sensor consists of a circuit with two parallel branches. The main branch, called motional, is a series circuit R_m, L_m, C_m, as shown in Figure 1a. The secondary branch consists of a single capacitance called the parallel capacitance C_p. The impedance of the QCM sensor is given by the relation:

$$Z\left(j\omega \right)=\frac{Z_s\left(j\omega \right)Z_p\left(j\omega \right)}{Z_s\left(j\omega \right)+Z_p\left(j\omega \right)}$$

(3)

where Z_s and Z_p are the series and parallel branch impedances. The impedance of the series branch of the BVD model is given by the following equation:

$$Z_s\left(j\omega \right)=R_m+j\mathsf{\omega }{L}_m+\frac{1}{j\mathsf{\omega }{C}_m}$$

(4)

The parallel capacitance branch has the impedance given by the following equation:

$$Z_p\left(j\omega \right)=\frac{1}{j\mathsf{\omega }{C}_p}$$

(5)

From the point of view of impedance spectroscopy, the parallel capacitance parasitizes the motional branch. It is determined by the inevitable existence of electrodes responsible for the application of the alternating electric field. The existence of parallel capacitance C_p is difficult to eliminate by compensation of the impedance analyzer. If the working environment of the QCM sensor has a high viscosity, then the motional resistance is in the KΩ range, and together with the parallel capacitance, they become the source of the difficulties of interpreting the experimental results. In the series branch of the BVD model, the reactance of the circuit elements, in a complex conjugate form, is responsible for energy storage and the series resonance frequency. At the series resonance of the QCM sensor, the complex conjugated motional reactance is canceled and, in this case, the absolute impedance is determined by the motional resistance in parallel with C_p or its residue to a compensated experimental setup [46]. The compensation can be applied in front-end electronics [44] or in the software procedure of data acquisition during the measurements, or it can be performed by software as a post-processing task [46].

2.3. Impedance Spectroscopy of the QCM Sensor Based on the Fractional Order BVD Model

Fractional order calculus can be successfully applied to describe a new level of complexity in the field of sensors of an electrochemical or biosensor nature mediated by the impedance spectroscopy method. In electrical circuits, fractional order calculus more accurately describes the behavior of materialized capacitors and inductors because there are no ideal elements of integer order. Since the fractional order of most materialized capacitors or inductors is usually close to 1 (almost ideal), these circuit elements are often treated as being of fractional order 1 by neglecting their fractional order characteristics. In reality, some capacitors and inductors are found to have distinct fractional order characteristics, such as supercapacitors and lossy coils [54,55].

For fractional order inductors, the dependence of the voltage $v_L\left(t\right)$ on the current $i_L\left(t\right)$ is described by the relation:

$$v_L\left(t\right)=L_{\alpha }\frac{d^{\alpha }}{d{t}^{\alpha }}{i}_L\left(t\right)$$

(6)

where α is the order of the fractional inductance denoted L_α and d^α/dt^α is the fractional order derivative operator [56]. In general, the fractional order inductor of the α order is in the range of 0 < α < 2, and the voltage leads the current by (1/2) πα degrees. For fractional order greater than 2, the voltage leads the current with more than π and the element will become capacitive. Similarly, considering $i_C\left(t\right)$ and $v_C\left(t\right)$, the current and the voltage in the case of the fractional order capacitor, its characteristics can be described by the following relationship:

$$i_C\left(t\right)=C_{\beta }\frac{d^{\beta }}{d{t}^{\beta }}{v}_C\left(t\right)$$

(7)

where β (0 < β < 2) is the order of the fractional capacitance denoted C_β [57].

Consider the current through the fractional order inductor and the voltage across the terminals of the fractional order capacitance in the s-domain, expressed by the following equations:

$$i_L\left(t\right)=i_0{e}^{st}$$

(8)

$$v_C\left(t\right)=v_0{e}^{st}$$

(9)

as exponential solutions of Equations (6) and (7). Provided there is an exponential solution in the particular case $Re\left(s\right)\ge 0$, there is a correspondence between the fractional order derivative operators [7] only in this case. Considering Caputo fractional derivative operator [27], Equations (6) and (7) can be rewritten as follows:

$$v_L\left(t\right)=L_{\alpha }\frac{d^{\alpha }}{d{t}^{\alpha }}{i}_L\left(t\right)=L_{\alpha }{s}^{\alpha }{i}_0{e}^{st}=s^{\alpha }{L}_{\alpha }{i}_L\left(t\right)$$

(10)

$$i_C\left(t\right)=C_{\beta }\frac{d^{\beta }}{d{t}^{\beta }} v_C\left(t\right)=C_{\beta }{s}^{\beta }{v}_0{e}^{st}=s^{\beta }{C}_{\beta }{v}_C\left(t\right)$$

(11)

The fractional order impedance of the inductor and the capacitor in the s-domain can be derived as follows:

$$Z_{L_{\alpha }}\left(s^{\alpha }\right)=\frac{v_L\left(t\right)}{i_L\left(t\right)}=s^{\alpha }{L}_{\alpha }$$

(12)

$$Z_{C_{\beta }}\left(s^{\beta }\right)=\frac{v_C\left(t\right)}{i_C\left(t\right)}=\frac{1}{s^{\beta }{C}_{\beta }}$$

(13)

The s-domain impedance of the fractional order BVD model is described by the following equation:

$$Z\left(s^{\alpha , \beta }\right)=\frac{Z_s\left(s^{\alpha , \beta }\right)Z_p\left(s\right)}{Z_s\left(s^{\alpha , \beta }\right)+Z_p\left(s\right)}$$

(14)

The fractional order BVD model of the QCM sensor is shown in Figure 2, and considering s = jw, the fractional order impedance of the motional branch is expressed as:

$$Z_s\left(j{\omega }^{\alpha ,\beta }\right)=R_m+{(j\mathsf{\omega })}^{\alpha }{L}_{\alpha m}+\frac{1}{{\left(j\mathsf{\omega }\right)}^{\beta }{C}_{\beta m}}$$

(15)

Only reactive motional circuit elements were considered to be of a fractional order. In this simplified approximation, the fractional order BVD model is defined in this study.

This choice is justified by the critical role of the reactive motional circuit elements in modeling the behavior of the QCM sensor. The motional resistance describes the dissipative processes associated with the QCM sensor, which are not of interest from the perspective of fractional order calculus.

2.4. Simulation of the QCM Sensor Based on the Fractional Order BVD Model

In a simulation for experimental validation, the parameters of the circuit elements of the fractional order BVD model were chosen to be close to the typical values of a QCM sensor. The simulation scripts developed in the Matlab^® environment have two objectives: (i) to obtain a global picture of the behavior of the fractional order BVD model and (ii) to adapt the simulation to the experimental reality. The first objective is achieved by evaluating Equation (14) in the range of resonant frequencies.

According to the Bode plot, which is commonly used to represent the behavior of the BVD model, in the resonant frequency range there is an (i) impedance at the series resonant frequencies and (ii) an impedance at the parallel resonant frequency. It should be noted that the existence of parallel resonance implies taking into account the parallel capacitance, $C_p>0$. Additionally, only for the series branch of the BVD model, $C_p=0$, the maximum impedance is always at the maximum frequency of the investigated range since after the series resonance the behavior of the QCM sensor is purely inductive.

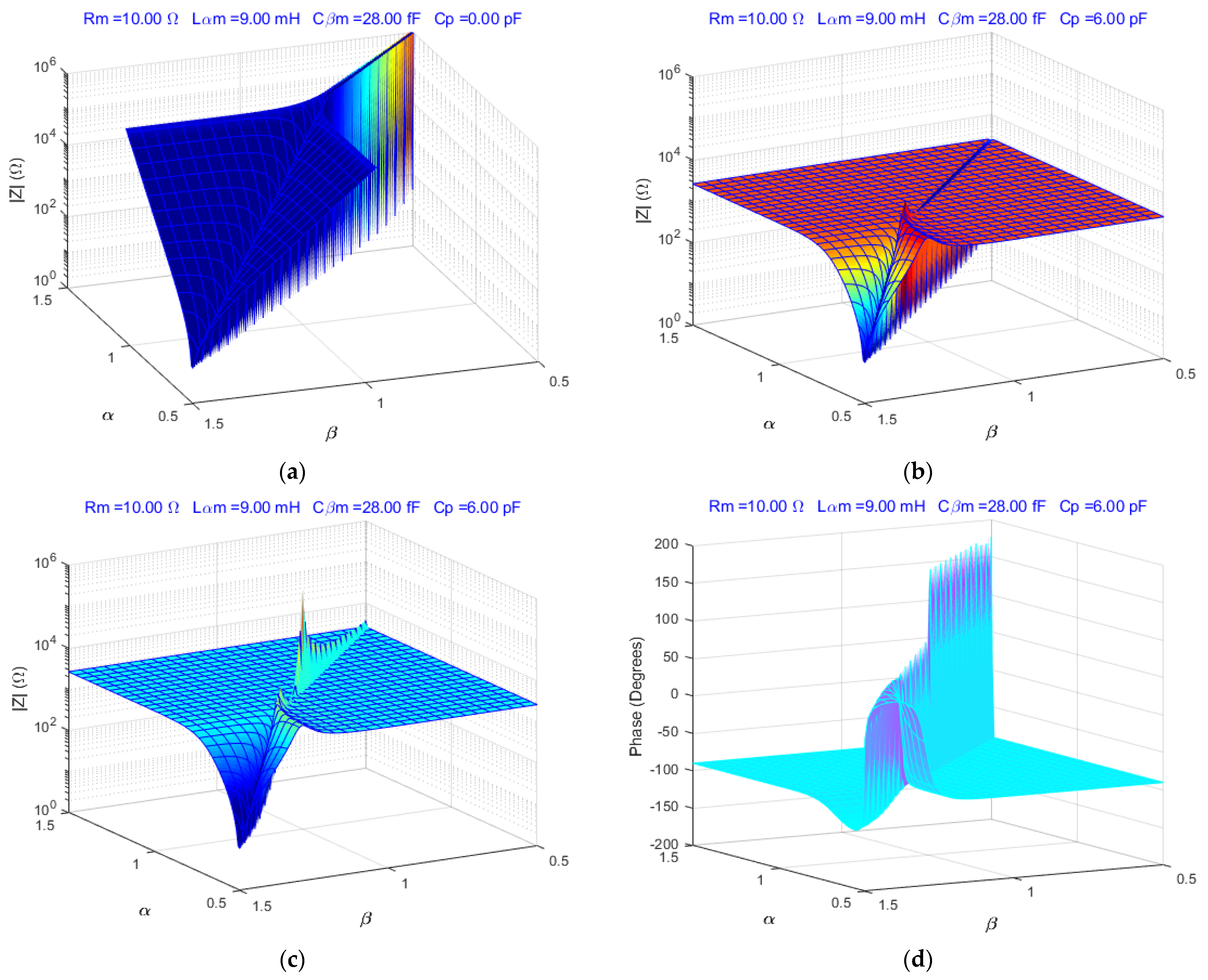
The fractional order BVD model is simulated for 0.5 < α < 1.5 and 1.5 > β > 0.5, respectively. The simulation results of the fractional order BVD model in the range of resonant frequencies (10,000,000 Hz to 10,070,000 Hz with 1 Hz step) are shown in Figure 3.

Figure 3a shows the response of the fractional order BVD model for the minimum impedance (C_p = 0 pF), respectively, in Figure 3b for C_p = 6 pF. Considering the parallel capacitance, C_p = 6 pF, the response at the parallel resonance of the fractional order BVD model changes significantly, as shown in Figure 3c,d. Fractional order calculus is impressive compared to integer order calculus where the above surfaces are reduced to a single point (α = β = 1).

To demonstrate the usefulness of the fractional order BVD model based on the results presented above, Equation (15) can be reduced to the following form:

$$Z_s\left(j{\omega }^{\left(1\pm \gamma \right)}\right)=R_m+{(j\mathsf{\omega })}^{\left(1+\gamma \right)}{L}_{\alpha m}+\frac{1}{{\left(j\mathsf{\omega }\right)}^{\left(1-\gamma \right)}{C}_{\beta m}}$$

(16)

where α = 1 + γ and β = 1 − γ consider the interval −0.5 < γ < 0.5. For this particular case, the fractional order BVD model is simulated, and the results are shown in Figure 4.

Figure 4a simulates the response of the fractional order BVD model for the QCM sensor considering the maximum ($Z_{max}$) and minimum ($Z_{min}$) impedance as a function of the γ parameter. Unlike the minimum impedance of the QCM sensor, which is modified for γ > 0.3, the maximum impedance is strongly influenced by the value of the γ parameter with a maximum value and a localization according to the value of the parallel capacitance, as shown in Figure 4c,d. Figure 4b simulates the evolution of the difference between the parallel and series resonance frequencies and the phase response of the QCM sensor as a function of the γ parameter. The minimum phase ($Phas{e}_{min}$) is before the series resonance and the maximum phase ($Phas{e}_{max}$) is before the parallel resonance. A simulation of the fractional order BVD model is not just a mathematical curiosity, it can be an extremely useful tool, as will be demonstrated below.

2.5. A Bode Plot of the Fractional Order BVD Model

In the case of experimental investigations on the QCM sensor by impedance spectroscopy, the most common representation of its response in the range of resonant frequencies is the Bode plot. The simulated results shown in Figure 5 as the Bode plot for γ = −0.05, γ = 0, γ = −0.02, and γ = 0.02 give a first impression of the experimental capabilities of the fractional order BVD model.

The Bode plot in Figure 5b shows the ideal case, and experimental results corresponding to this situation can be obtained with an optimally compensated VIA. The response of the QCM sensor is often inaccurate due to incorrect compensation of the VIA. A biased response is simulated in Figure 5a,c,d by the fractional order BVD model through the γ parameter. The usefulness of the fractional order BVD model addresses two situations: (i) testing the optimal compensation of the VIA and (ii) its ability to correctly determine the electrical parameters by fitting the experimental data with the α and β parameters determined in a previous step. From an application point of view, it is worth mentioning the ability of the fractional order BVD model to validate the optimal compensation of the VIA.

3. Results

In this section, a comparative analysis validates the fractional order BVD model of the QCM sensor against the standard compensation of the VIA. The experimental configuration shown in Figure 1 also includes a QCM sensor with a fundamental resonance frequency of 10 MHz (151225-10, International Crystal Manufacturing Co., Inc., Oklahoma City, OK, USA). During the measurements, the temperature in the laboratory was 21 ± 2 °C with a relative humidity of 50 ± 10%. The raw experimental data was obtained with the VIA configured as follows: (i) passive excitation with a sine wave of 1 V amplitude in the resonant frequency range and (ii) measurement of the impedance and phase of the QCM sensor at 50,001 points.

3.1. Standard Compensation of the Virtual Impedance Analyzer

The VIA algorithm is a Python application that uses the capabilities of the AD2 Software Development Kit (SDK) [58]. The Python application provides data acquisition of raw experimental data followed by real-time processing to compute the raw electrical parameters of the BVD model. The custom applications are based on the WaveForms software development kit (SDK), which provides access to a public application programming interface (API) [59].

Due to the distinct electrical characteristics of the QCM sensor measured in air, the experimental configuration must be carefully compensated to obtain experimental raw data according to the BVD model. Overcoming these difficulties of the impedance spectroscopy method is usually transparent to the users of professional instruments if they follow the compensation procedure recommended in the manual of the impedance analyzer. The procedure described below is specific to the VIA shown in Figure 1 but can be adapted for other impedance analyzers.

Since the resonant frequency range for the QCM sensor is narrow, the compensation procedure consists of determining four constants. These constants are the resistance and reactance for each of the two boundary conditions listed in Table 1.

The open-circuit condition is used for high-impedance compensation and the short-circuit condition is required for low-impedance compensation. The compensation procedure is carried out by software and the compensation constants are automatically updated in the VIA application. In Table 1, four compensation variants are proposed for the experimental evaluation of the QCM sensor response. In the first variant (a), the VIA is used without compensation. In the second variant (b), the VIA compensation is optimal. In the following two variants (c,d), the compensation impedance in open-circuit (Zoc) is modified by ±100 Ω compared to the optimal compensation variant (b). It is well-known and proven [46] that in the case of a QCM sensor in a liquid medium with high viscosity, a significant influence on its response is caused by compensation errors.

To validate the simulations in Figure 5, the experimental results obtained by the VIA compensation with the values in Table 1 are shown in Figure 6. There are two extreme situations of the QCM sensor response when using the VIA without compensation (Figure 6a) in contrast to its response with optimal compensation shown in Figure 6b. In Figure 6c, the VIA is compensated with a value greater than the optimal value for the open-circuit inductance. The experimental result for compensation with a value lower than optimal is shown in Figure 6d.

The Bode plots simulated in Figure 5 using the fractional order BVD model are effectively identical to those measured experimentally (Figure 6) by compensating the VIA with the variants in Table 1. Note that in the experimental study to validate the previously simulated results, only the open-circuit impedance was changed. Other effects of the QCM sensor response for an incorrectly compensated VIA can be obtained by acting on other parameters in Table 1. It is also possible to consider variations of compensation by modifying several parameters simultaneously. Figure 6a shows the QCM sensor response for an uncompensated VIA, and this case is the most atypical to fit with the BVD model.

Table 1. The compensation parameters used for experimental investigations.

Figure 6	Roc (Ω)	Zoc (Ω)	Rsc (Ω)	Zsc (Ω)
(a)	NaN 1	NaN	NaN	NaN
(b)	331.658	1375.878	−0.043	3.367
(c)	331.658	1475.878	−0.043	3.367
(d)	331.658	1275.878	−0.043	3.367

¹ NaN—not a number.

Table 1. The compensation parameters used for experimental investigations.

Figure 6	Roc (Ω)	Zoc (Ω)	Rsc (Ω)	Zsc (Ω)
(a)	NaN 1	NaN	NaN	NaN
(b)	331.658	1375.878	−0.043	3.367
(c)	331.658	1475.878	−0.043	3.367
(d)	331.658	1275.878	−0.043	3.367

¹ NaN—not a number.

3.2. The VIA Optimal Compensation Test Based on the Fractional Order BVD Model

To rigorously demonstrate the VIA optimal compensation test based on the fractional order BVD model, the raw data was fitted, and the result is shown in Figure 7.

As shown in Figure 7, the fractional order BVD model is satisfied by the ideal condition α = β = 1, which is a very good tool for testing optimal VIA compensation. Figure 8a,b show the response of the QCM sensor for two wrong compensation variants.

This situation is indicated by the value of the α and β parameters of the fractional order BVD model. The values of parameters α and β are close in the two situations because in both cases the adjustment is made for impedance that does not differ significantly; the major difference is for the phase response. The test can be reduced to a fit with Equation (16) using only one parameter, in which case the optimal compensation will be γ = 0.

The fitting algorithm used as an optimal compensation test is based on the “curve_fit” function in the Python library scipy.optimize, which basically implements the standard nonlinear least squares method. The existence of a numerical method that confirms optimal compensation with high accuracy is an important step toward automating compensation procedures, as well as refining the classical VIA compensation method.

3.3. VIA without Compensation Based on the Fractional Order BVD Model

Another experimental result demonstrating the usefulness of the fractional order BVD model is shown in Figure 9. In this case, in the first step, the true parameters of the circuit elements of the BVD model were calculated based on the raw experimental data measured with the optimally compensated VIA. Keeping the values of the circuit element parameters of the QCM sensor, its response was measured with the VIA without compensation. The raw experimental data from this stage were fitted with the fractional order BVD model to determine the parameters α and β. The value of the parameters α and β must be interpreted as a measure of the degree of compensation of the VIA. Alternatively, after determining them using the procedure described above, it is possible to use them as an alternative to the standard compensation method. In this case, using the determined value of the parameters α and β, the VIA can be used without compensation and the real parameters of the circuit elements are calculated using the fractional order BVD model.

It should be noted that this alternative is essentially a reverse procedure of the VIA optimal compensation test. The parameters α and β can only be calculated after going through the optimal compensation procedure mentioned above.

4. Discussion

Given the use of the QCM sensor in different working media, it can be argued that the fractional order BVD model approach is justified for impedance spectroscopy as a measure of the degree of VIA compensation [46,59,60,61]. Determining the correct value for the electrical parameters of the BVD model allows the calculation of the fractional order parameter of motional inductance and motional capacitance for an uncompensated VIA. It should be mentioned that motional inductance and motional capacitance is not actually of fractional order but they are measured as fractional order due to the VIA without compensation. After determining the fractional order parameter of the motional inductance and motional capacitance, correct measurements can be made by fitting the experimental data with the fractional BVD model in the case of a VIA without compensation.

This study validates the capability of the fractional order BVD model to test the optimum compensation of a VIA. Checking whether the standard compensation is optimal is the first consequence of modeling the QCM sensor with fractional order reactive motional circuit elements. Any deviation from the condition α = β = 1 requires a new VIA compensation or an automatic adjustment until the optimal condition is met. It has also been shown that the results obtained by an initial compensation of the VIA and fitting of the raw data with the BVD model are practically identical to those obtained by an uncompensated VIA and fit with the fractional order BVD model.

In future investigations on the fractional order BVD model for the QCM sensor, atypical working media in which experimental results are often difficult to interpret should be mentioned. In these cases, the usefulness of the fractional order BVD model should be investigated. In particular, in this paper, it has been shown that the fractional order BVD model is an extremely useful tool in testing the optimal compensation of the VIA and provides new insight into the QCM sensor response.

5. Conclusions

Extended simulations of the fractional order BVD model confirm the ability of fractional order calculus to cover a wide range of behavior. The possibility of checking the accuracy of the compensation of the VIA by evaluating parameters α and β of the fractional order BVD model brings an advantage to the experimental practice, which offers the possibility of evaluating the raw experimental data before their processing by advanced methods.

The experimental study confirms, in the particular case of the QCM sensor, the equivalence of measurements made with a standard compensated VIA, respectively, without compensation and with fractional order calculus. The use of fractional order parameters α and β as compensation procedures brings a new dimension to the standard compensation of a VIA, which is, in essence, a reverse method of verifying optimal compensation. Evaluation of the fractional order BVD model from the perspective of impedance spectroscopy provides insight into the advantages of fractional order calculus for modeling complex phenomena commonly encountered in experimental QCM practice.