An Electronic Jamming Method Based on a Distributed Information Sharing Mechanism
Abstract
:1. Introduction
2. Multi-Agent Cooperative Jamming Method
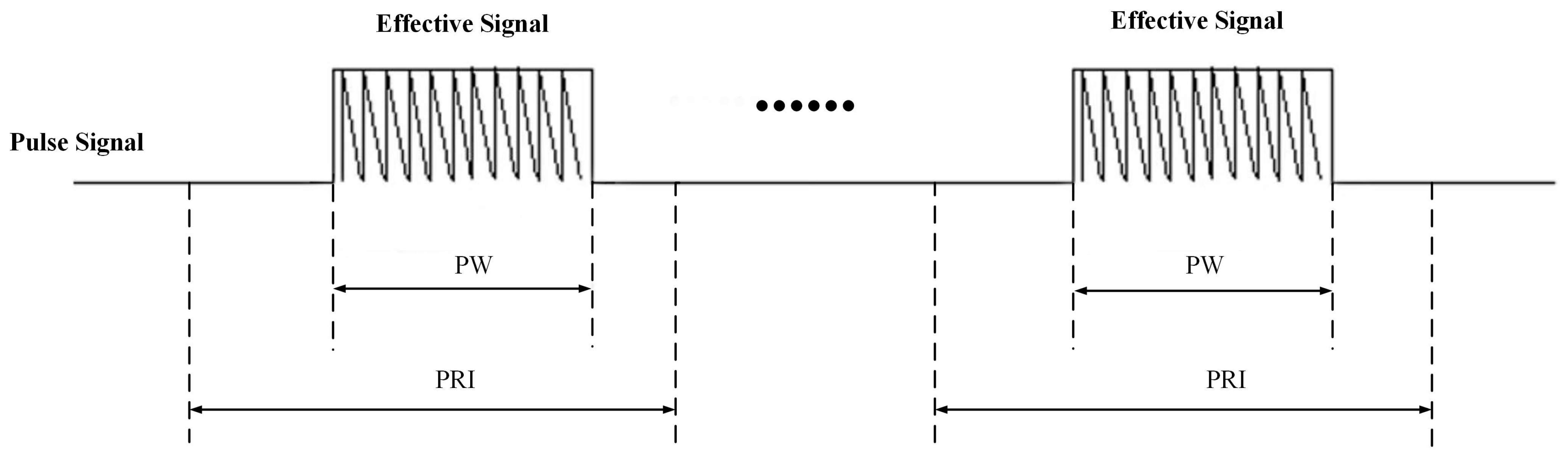
2.1. Range Gate Pull-Off Electronic Jamming Model
2.2. Balancing Parameters of the Multi-Agent Situation Information
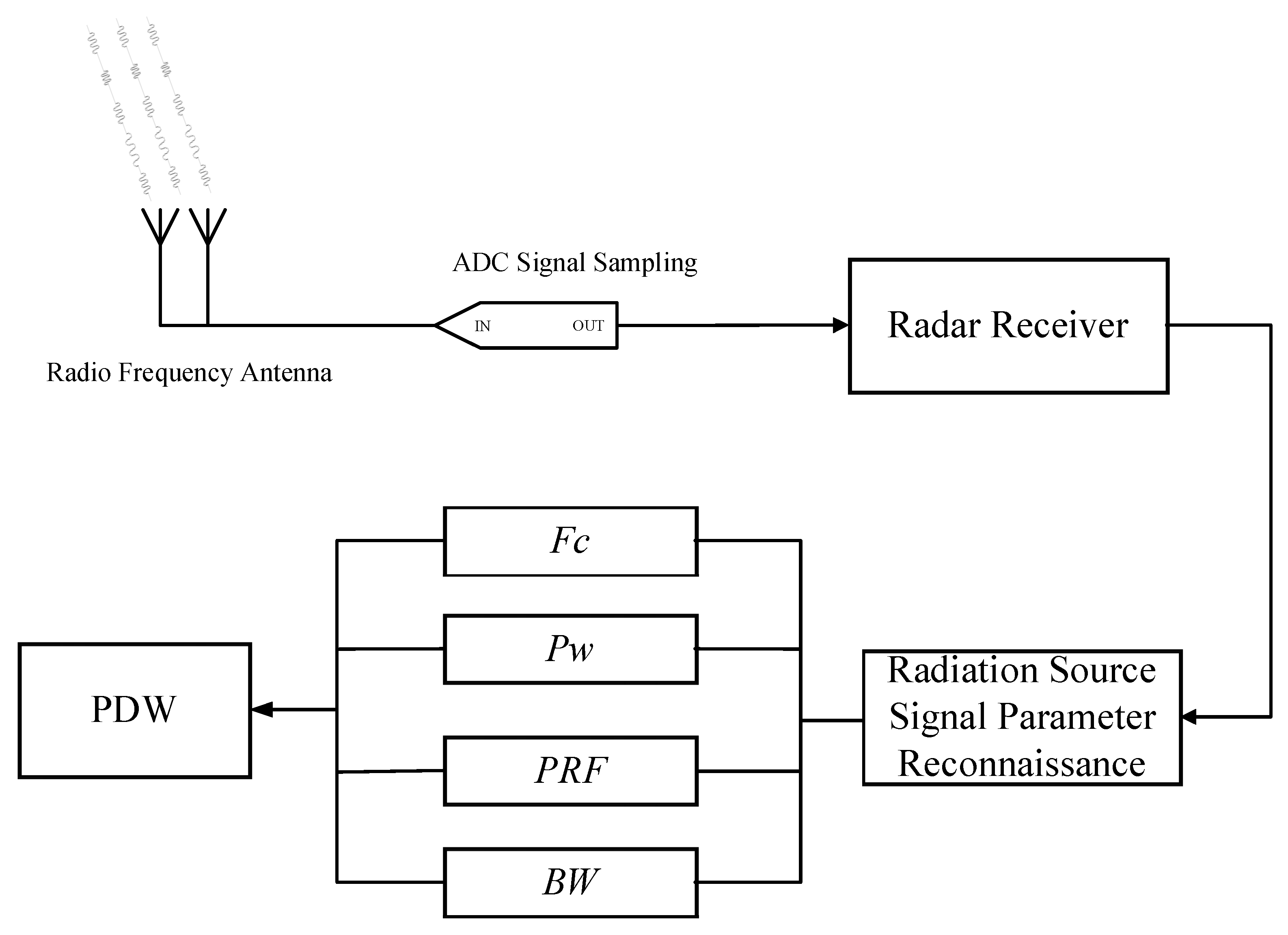
2.3. Autonomous Decision of Jammer Agent Parameters
3. Evaluation of Jamming Effectiveness
3.1. Jamming-to-Signal Ratio Definition
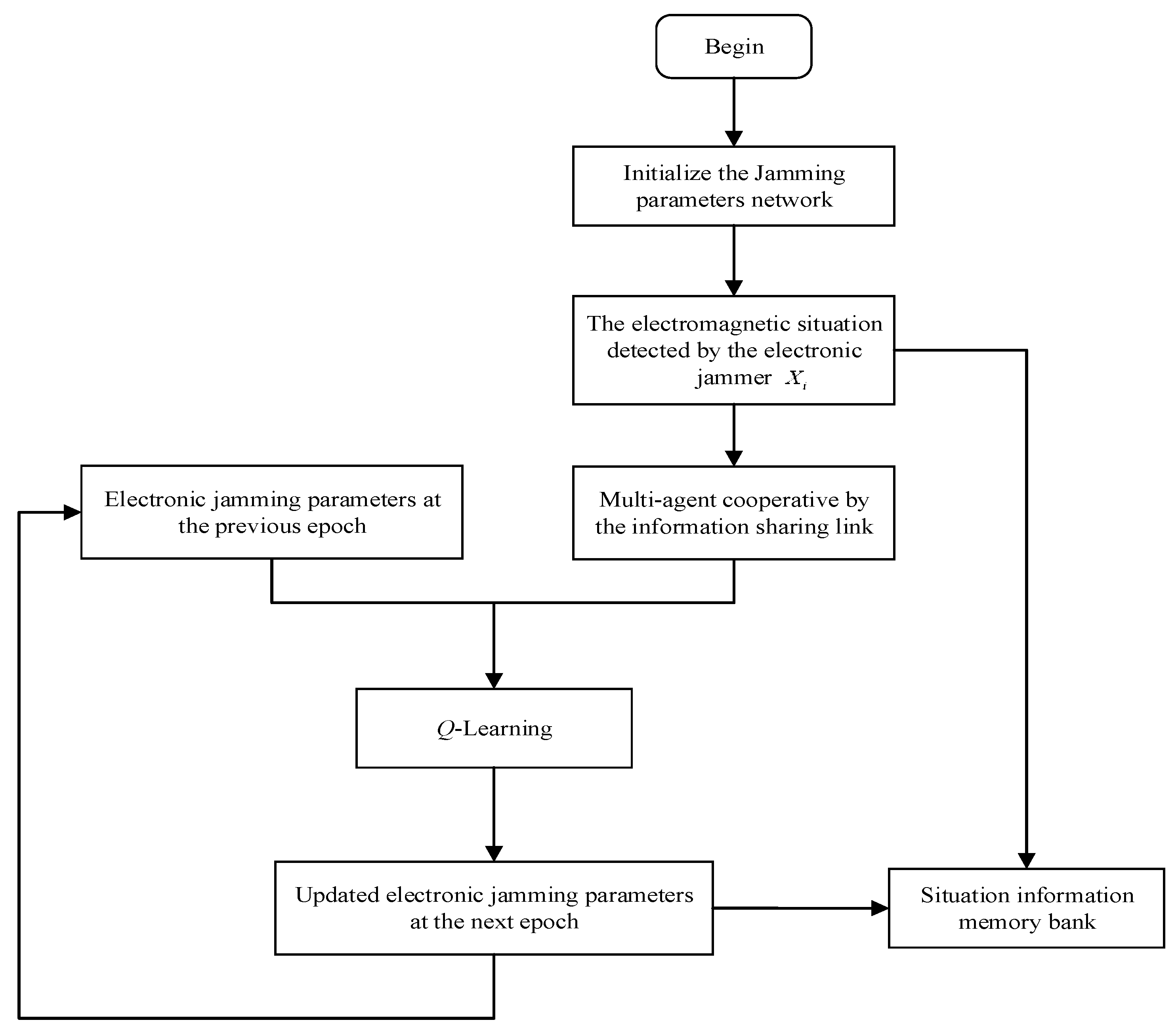
3.2. Q-Learning Method for Jamming Policy
4. Experiment and Analysis
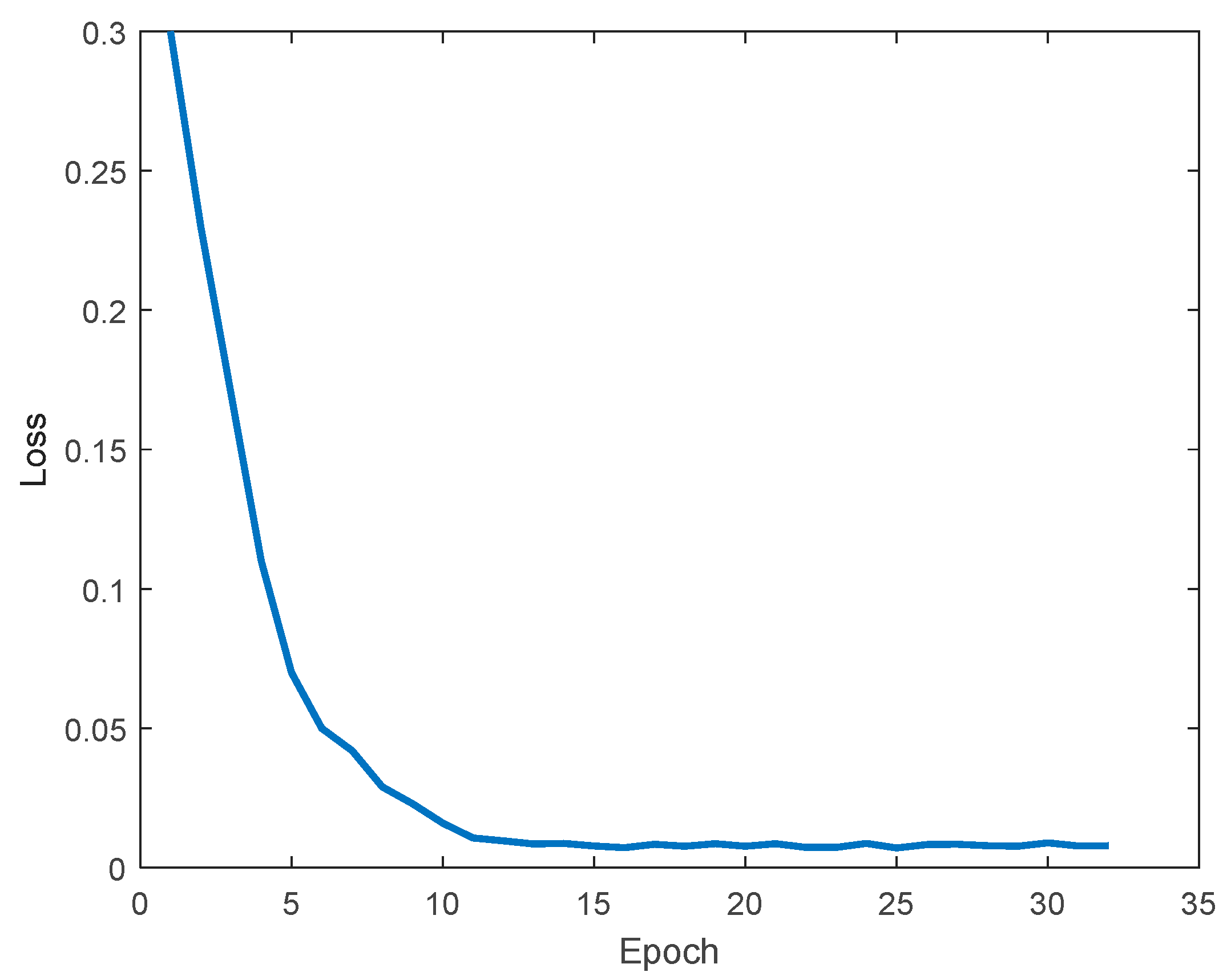
4.1. Situation Information Sharing
4.2. Optimization of the Jamming Parameters in Real Time
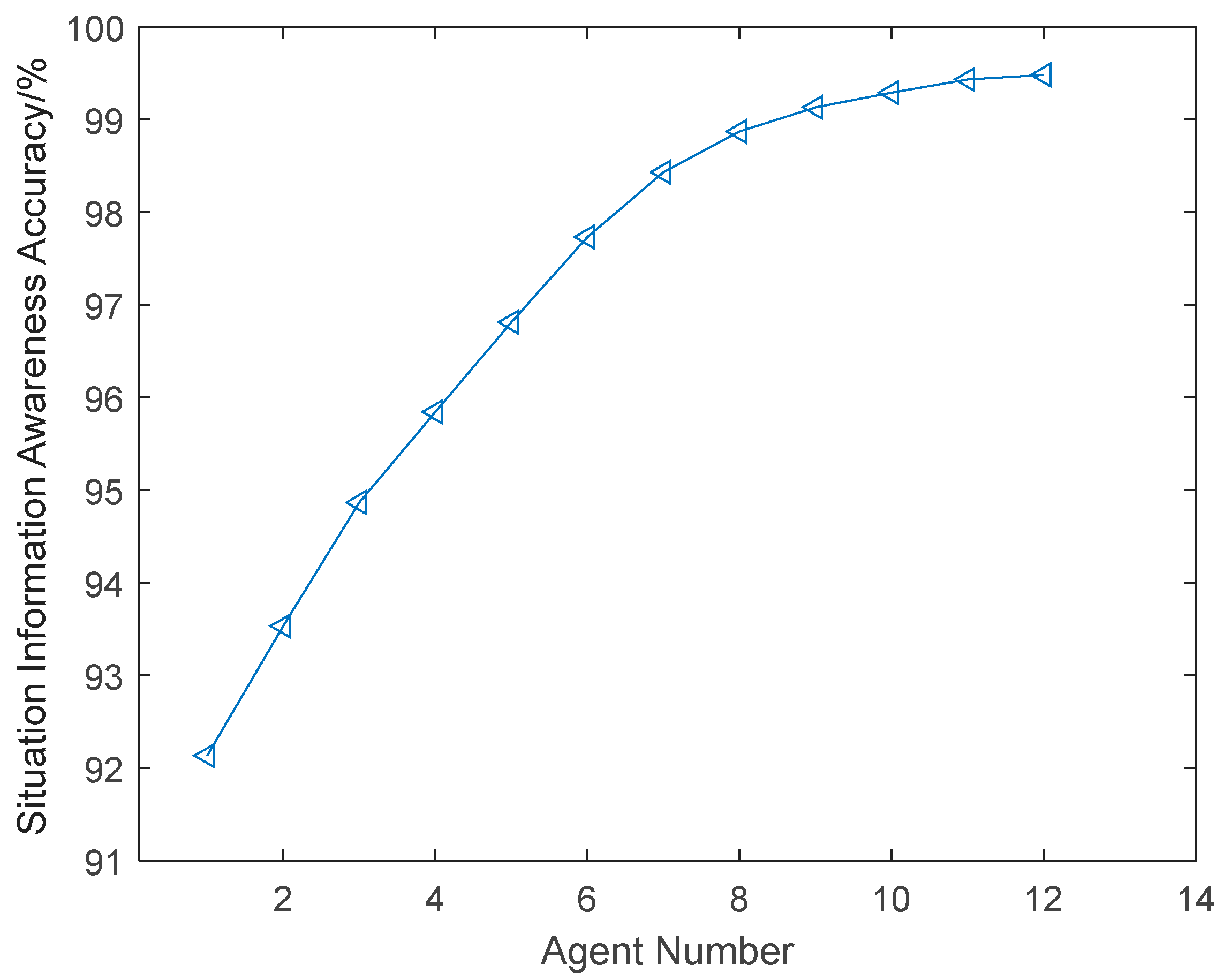
4.3. Effect of the Number of Jammers on Perception Accuracy
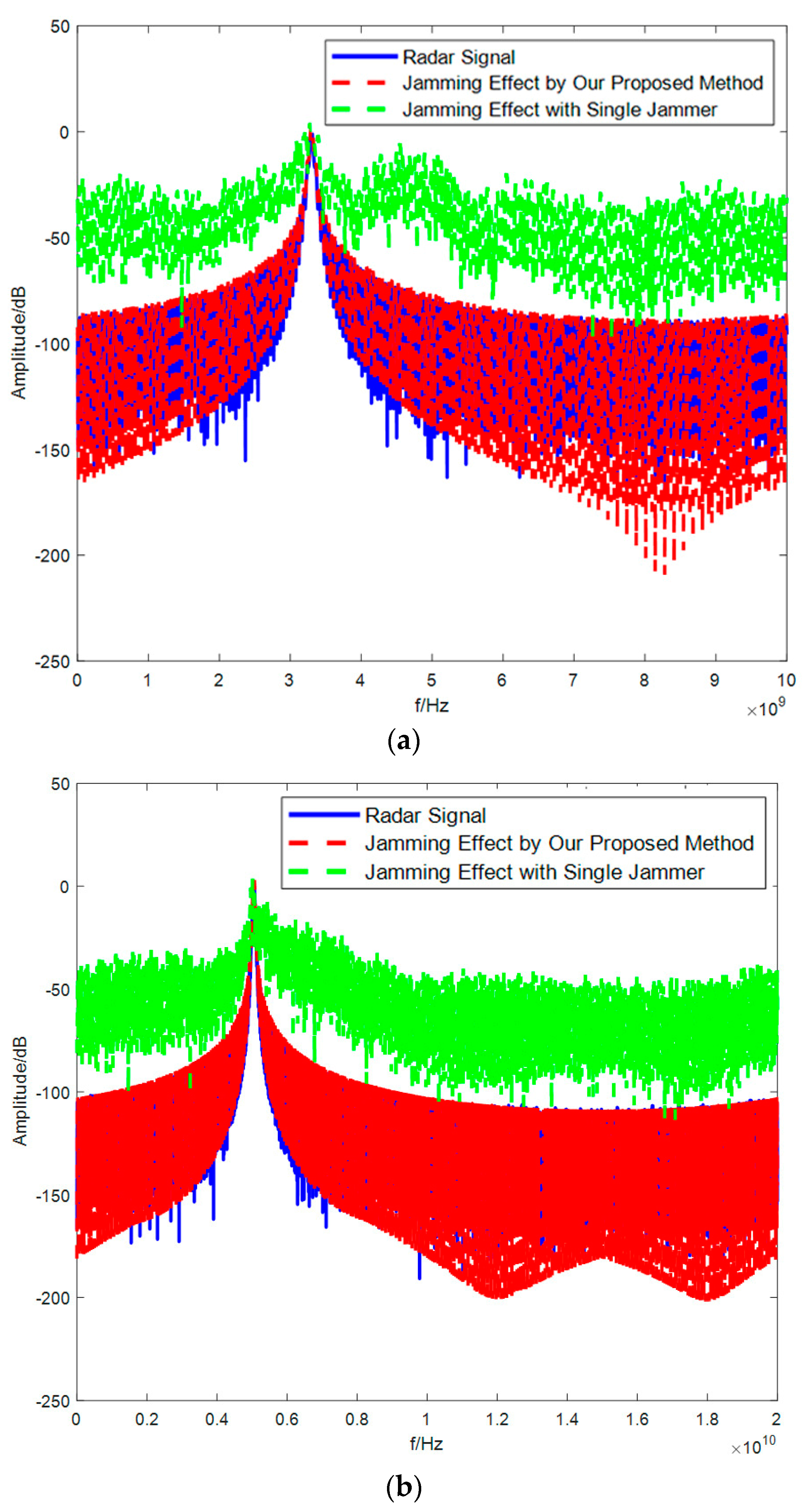
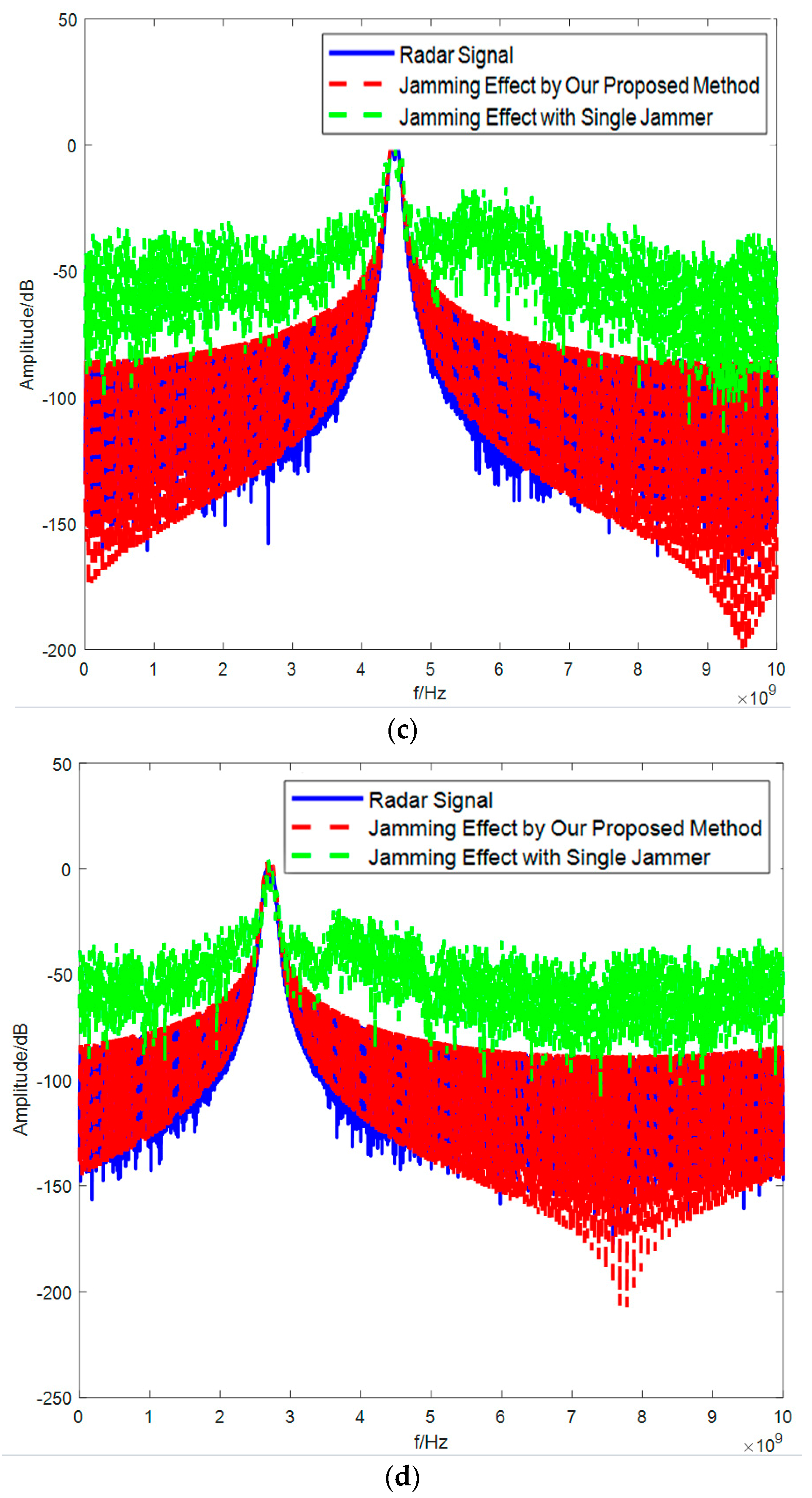
4.4. Analysis of Jamming Effectiveness Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cywiński, A.; Ostrowski, R.; Strzelec, M. Electronic warfare in the optical band: Main features, examples and selected measurement data. Def. Technol. 2020, 17, 1636–1649. [Google Scholar] [CrossRef]
- Smith, C.R.; Grasso, R.; Pledger, J.; Murarka, N. Trends in electro-optical electronic warfare. Proc. SPIE 2012, 8543, 854392. [Google Scholar] [CrossRef]
- Zhou, Y.; Rao, B.; Wang, W. UAV swarm intelligence: Recent advances and future trends. IEEE Access 2020, 8, 183856–183878. [Google Scholar] [CrossRef]
- Zhou, L.; Leng, S.; Liu, Q.; Wang, Q. Intelligent UAV swarm cooperation for multiple targets tracking. IEEE Internet Things J. 2021, 9, 743–754. [Google Scholar] [CrossRef]
- Wang, X.; Huang, T.; Liu, Y. Resource allocation for random selection of distributed jammer towards multistatic radar system. IEEE Access 2021, 9, 29048–29055. [Google Scholar] [CrossRef]
- Zhou, Z.; Rao, B.; Xie, X. The influence mechanism of UAV group on the detection performance of air defense radar. In Proceedings of the 2018 3rd International Conference on Automation, Mechanical Control and Computational Engineering (AMCCE 2018), Dalian, China, 12–13 May 2018; Atlantis Press: Beijing, China, 2018; pp. 338–343. [Google Scholar]
- DARPA. Behavior Learning for Adaptive Electronic Warfare. Available online: https://www.fbo.gov (accessed on 6 October 2010).
- Kingsley, N.; Guerci, J.R. Adaptive amplifier module technique to support cognitive RF architectures. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1329–1332. [Google Scholar]
- Fu, J.; Wan, Y.; Wen, G.; Huang, T. Distributed robust global containment control of second-order multiagent systems with input saturation. IEEE Trans. Control. Netw. Syst. 2019, 6, 1426–1437. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, J. Cooperative output regulation of discretetime linear time-delay multi-agent systems. IET Control. Theory Appl. 2016, 10, 2019–2026. [Google Scholar] [CrossRef]
- Wang, S.; Bao, Y.; Li, Y. The architecture and technology of cognitive electronic warfare. Sci. Sin. Inf. 2018, 48, 1603–1613. [Google Scholar] [CrossRef]
- Xing, Q.; Zhu, W.G.; Jia, X. Intelligent radar countermeasure based on Q-learning. Syst. Eng. Electron. 2018, 40, 1031–1035. [Google Scholar]
- He, J.-H. FPGA Software Design for Reconnaissance and Jamming Integration Processor; Harbin Engineering University: Harbin, China, 2017. [Google Scholar]
- Zuo, S.; Song, Y.; Lewis, F.L.; Davoudi, A. Output containment control of linear heterogeneous multi-agent systems using internal model principle. IEEE Trans. Cybern. 2017, 47, 2099–2109. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Distributed containment control of multi-agent systems with general linear dynamics in the presence of multiple leaders. Int. J. Robust Nonlinear Control. 2013, 23, 534–547. [Google Scholar] [CrossRef]
- Osner, N.R.; du Plessis, W.P. Threat evaluation and jamming allocation. IET Radar Sonar Navig. 2017, 11, 459–465. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Han, L.; Ning, Q.; Chen, B.; Lei, Y.; Zhou, X. Ground threat evaluation and jamming allocation model with markov chain for aircraft. IET Radar Sonar Navig. 2020, 14, 1039–1045. [Google Scholar] [CrossRef]
- Feng, H.Z.; Liu, H.W.; Yan, J.K.; Dai, F.Z.; Fang, M. A fast efficient power allocation algorithm for target localization in cognitive distributed multiple radar systems. Signal Process. 2016, 127, 100–116. [Google Scholar] [CrossRef]
- Bui, V.H.; Nguyen, T.T.; Kim, H.M. Distributed operation of wind farm for maximizing output power: A multi-agent deep reinforcement learning approach. Access IEEE 2020, 8, 173136–173146. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, L.; Xu, R.; Li, J. A distributed low-redundancy information sharing algorithm in ad hoc networks with directional antennas. Procedia Comput. Ence 2018, 131, 1142–1149. [Google Scholar] [CrossRef]
- Peng, T.; Leckie, C.; Ramamohanarao, K. Information sharing for distributed intrusion detection systems. J. Netw. Comput. Appl. 2007, 30, 877–899. [Google Scholar] [CrossRef]

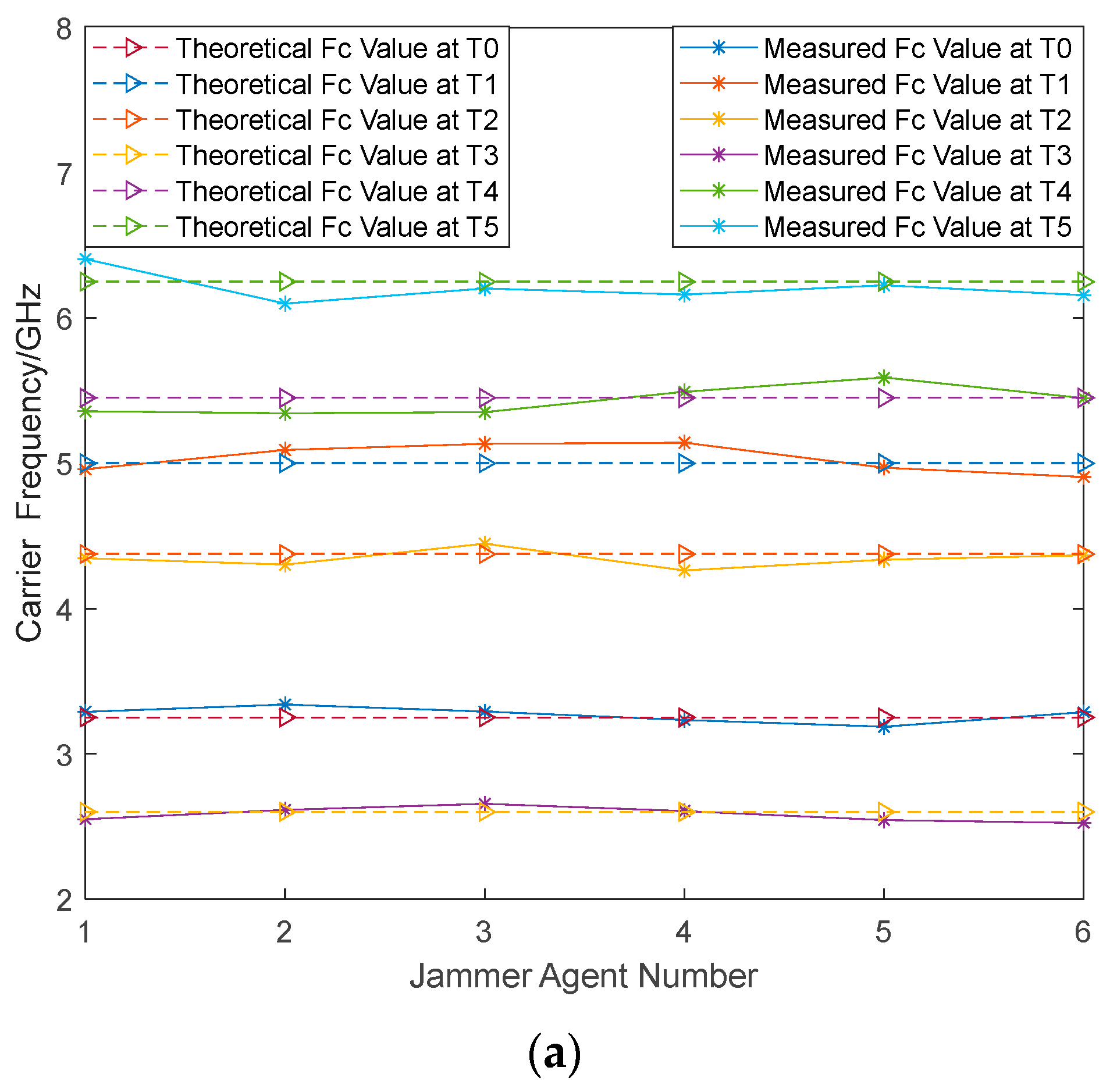


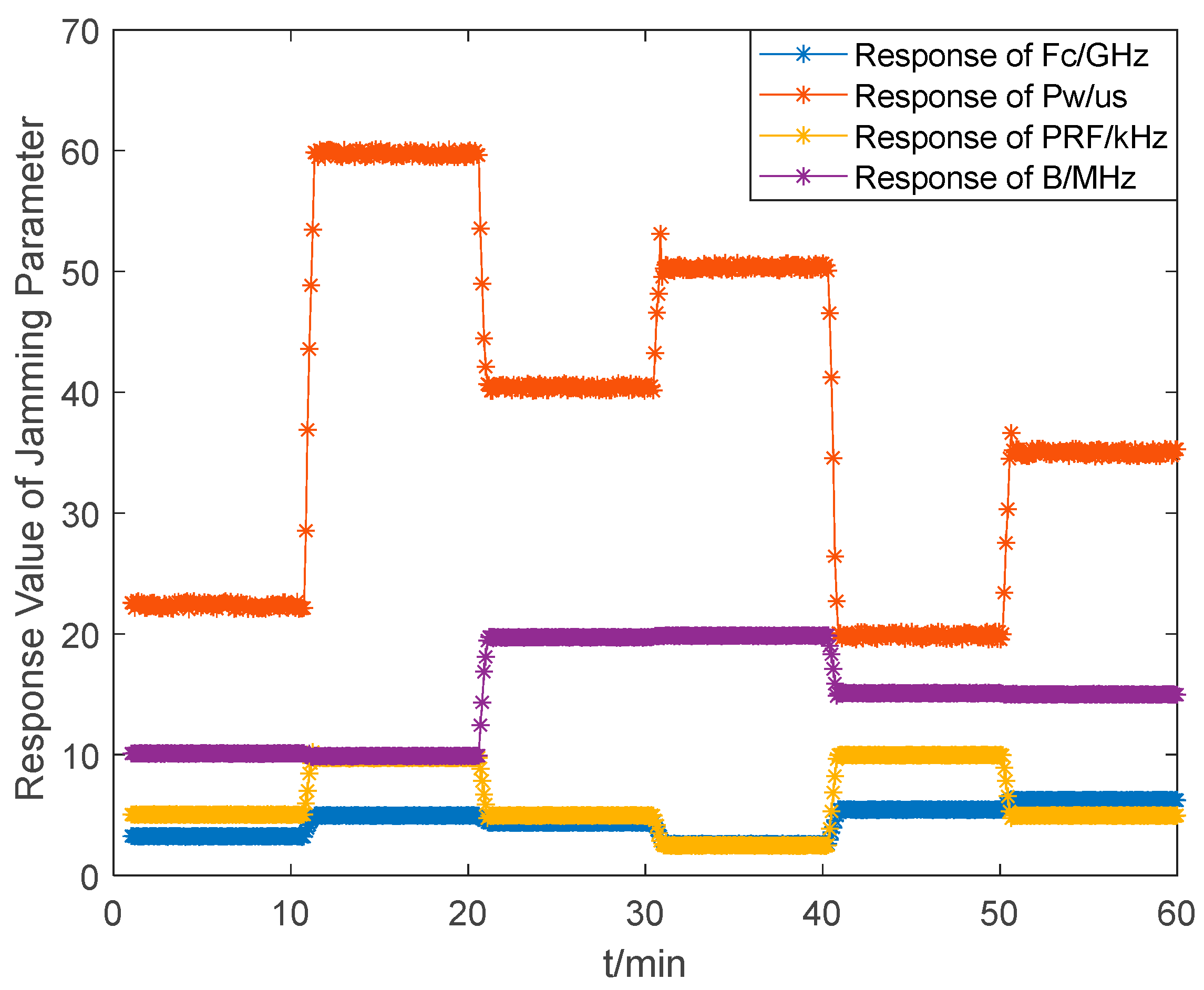

| Stage | Fc/GHz | Pw/us | PRF/Hz | BW/MHz |
|---|---|---|---|---|
| T0 | 3.25 | 22.5 | 5000 | 10 |
| T1 | 5 | 60 | 10,000 | 10 |
| T2 | 4.375 | 40 | 5000 | 20 |
| T3 | 2.6 | 50 | 2500 | 20 |
| T4 | 5.45 | 20 | 10,000 | 15 |
| T5 | 6.25 | 35 | 5000 | 15 |
| Stage | Fc/GHz | Pw/us | PRI/us | /Hz/s |
|---|---|---|---|---|
| T0 | 3.2539 | 22.367 | 198.3 | 4.492 × 1011 |
| T1 | 4.9758 | 59.76 | 102.76 | 1.634 × 1011 |
| T2 | 4.3863 | 40.432 | 200.843 | 4.9317 × 1011 |
| T3 | 2.6036 | 50.372 | 399.346 | 3.9705 × 1011 |
| T4 | 5.4620 | 19.874 | 100.264 | 7.5475 × 1011 |
| T5 | 6.2510 | 35.006 | 201.149 | 4.285 × 1011 |
| Method | JSR | |||||
|---|---|---|---|---|---|---|
| T0 | T1 | T2 | T3 | T4 | T5 | |
| Our algorithm | 1.0215 | 0.9987 | 1.0032 | 1.0386 | 1.0108 | 1.1250 |
| Jamming with a single jammer | 1.6732 | 1.7851 | 1.5738 | 1.6210 | 1.8327 | 1.5248 |
| NO. | Evaluation Indicator | Correlation with Evaluation Result |
|---|---|---|
| 1 | Fc | positive |
| 2 | Pw | positive |
| 3 | PRF | positive |
| 4 | BW | positive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Huang, Y.; Jin, Z. An Electronic Jamming Method Based on a Distributed Information Sharing Mechanism. Electronics 2023, 12, 2130. https://doi.org/10.3390/electronics12092130
Zhang P, Huang Y, Jin Z. An Electronic Jamming Method Based on a Distributed Information Sharing Mechanism. Electronics. 2023; 12(9):2130. https://doi.org/10.3390/electronics12092130
Chicago/Turabian StyleZhang, Pan, Yi Huang, and Zhonghe Jin. 2023. "An Electronic Jamming Method Based on a Distributed Information Sharing Mechanism" Electronics 12, no. 9: 2130. https://doi.org/10.3390/electronics12092130
APA StyleZhang, P., Huang, Y., & Jin, Z. (2023). An Electronic Jamming Method Based on a Distributed Information Sharing Mechanism. Electronics, 12(9), 2130. https://doi.org/10.3390/electronics12092130







