A Datasheet-Driven Electrothermal Averaged Model of a Diode–MOSFET Switch for Fast Simulations of DC–DC Converters
Abstract
:1. Introduction
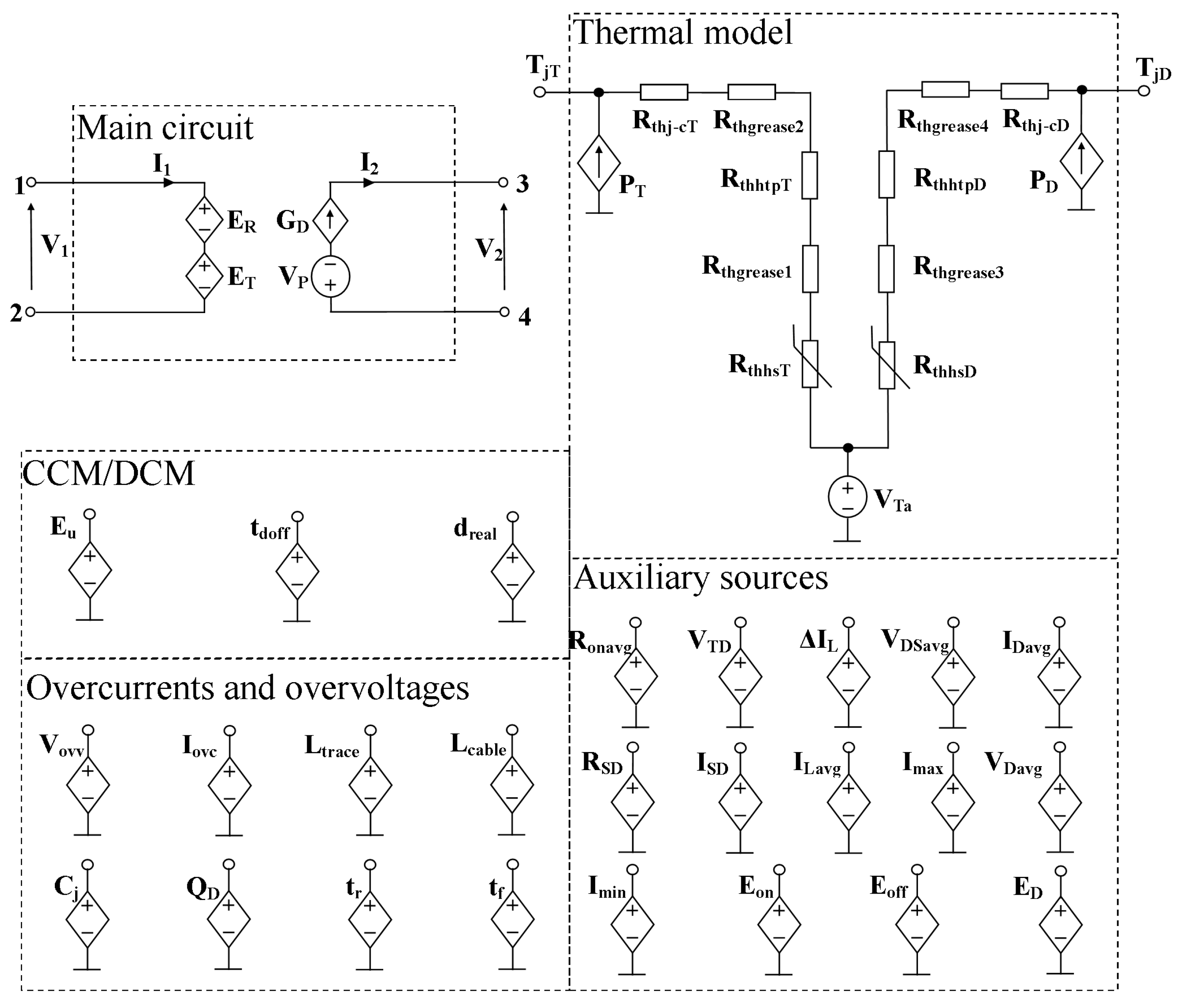
2. Model Form
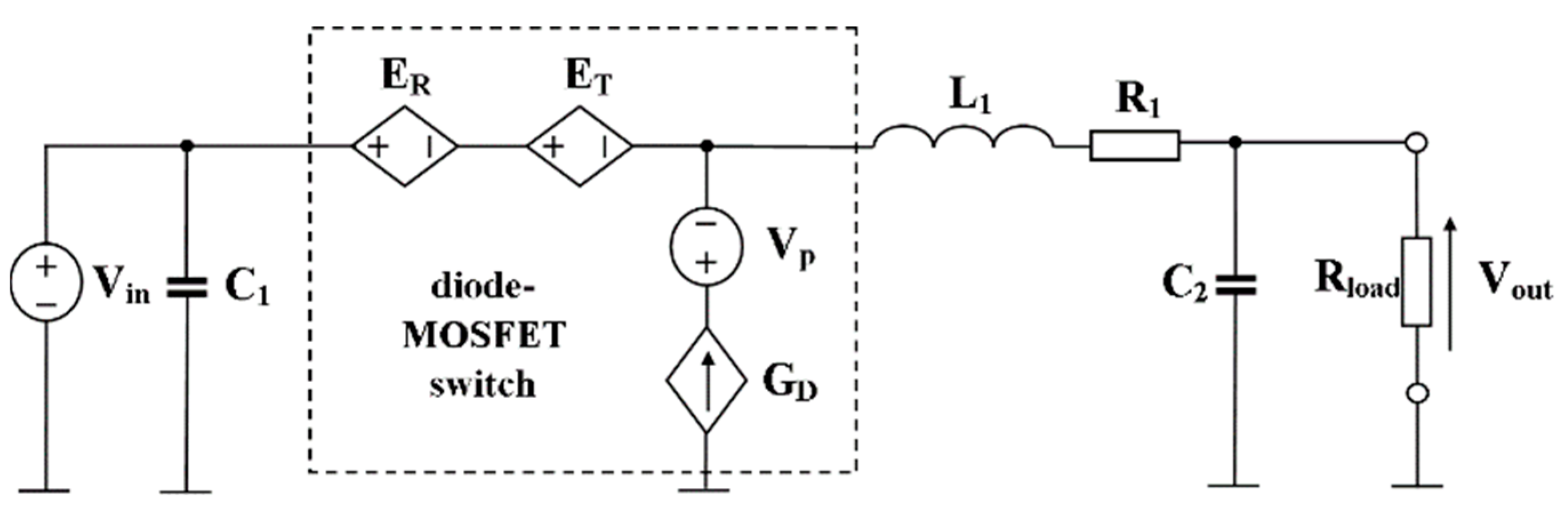
2.1. Main Circuit
2.2. CCM/DCM Block
2.3. Thermal Model
2.4. Overcurrents and Overvoltages Block
2.5. Auxiliary Sources
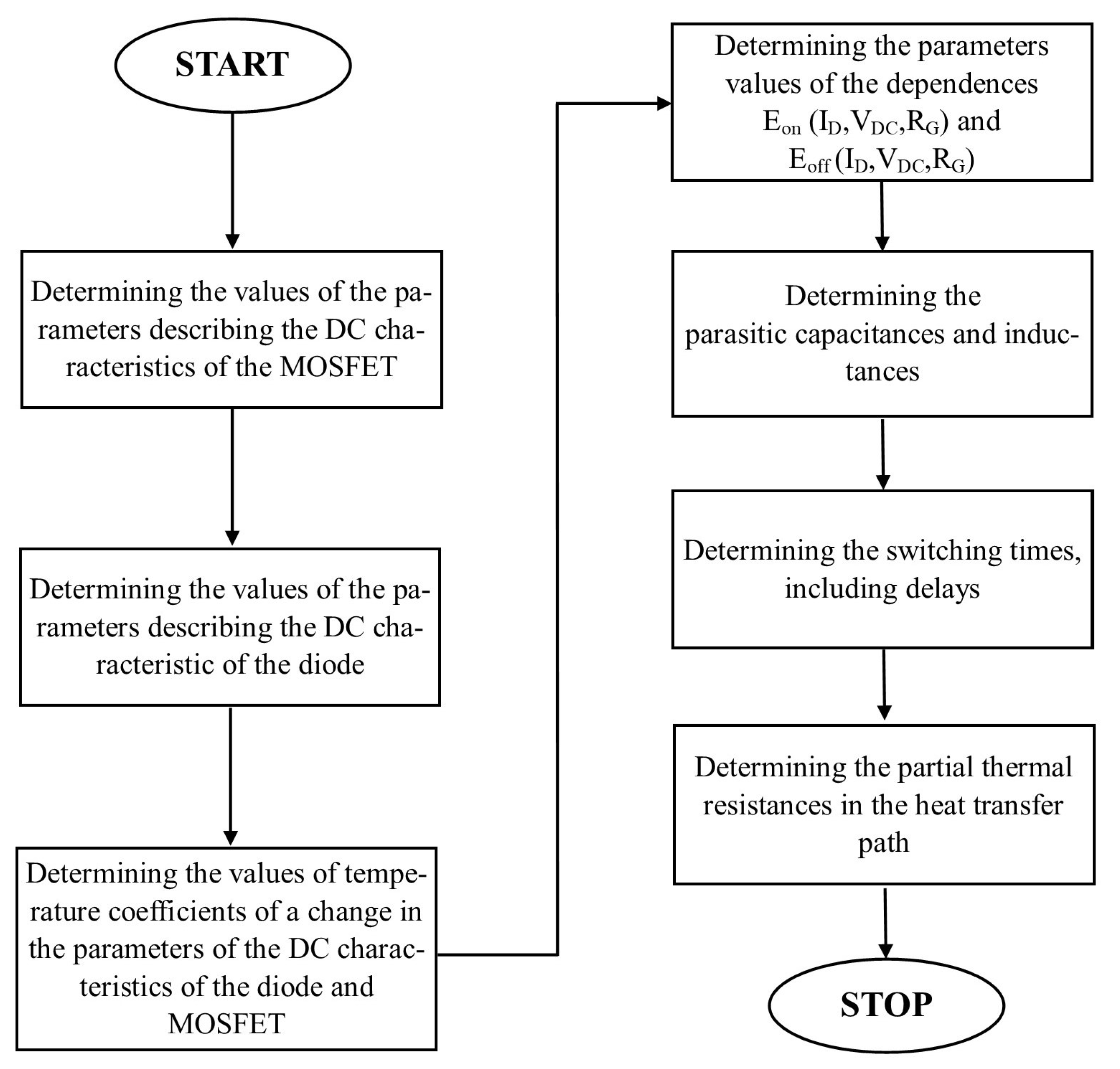
3. Estimation of Model Parameters
- Concerning the output characteristics of the MOSFET, parameters aRon, bRon, aVGS, bVGS, aID, bID are determined approximating the datasheet characteristics Ron(ID, VGS, Tj) of the MOSFET. Ronref in (19) is the value of Ron at the temperature T0 with ID = 0 and the maximum allowable voltage VGS.
- Concerning the output characteristics of the diode, parameters ISD, nD, and RSD are calibrated using the datasheet current-voltage characteristics of the diode measured at T0. Then, using the datasheet current-voltage characteristics for at least 3 temperatures, parameters KISD and nRSD are estimated.
- Using the datasheet characteristics Eon(ID, VDC, RG) and Eoff(ID, VDC, RG), the values of parameters aion1, aion2, aion3, aion4, bvdcon1, bvdcon2, cRGon, aioff1, aioff2, bvdcoff1, bvdcoff2, cRGoff in (22) and (23) are determined. These parameters are empirical and should be optimized by adjusting the computed characteristics to match the datasheet ones. VDCref and RGref have the values equal to the reference values of VDC and RG used in the Eoff and Eon characteristics available in the datasheet.
- Parameters related to the parasitic capacitance of the diode are calibrated on the basis of the datasheet characteristic Cj(VR). In (13), Vj is the built-in voltage determined by adjusting the computed characteristic to the datasheet one, and m is a factor characterizing the type of junction; for an abrupt junction, it is equal to 0.5.
- The parameters of the equations describe the parasitic inductances resulting from the structure of the circuit are the geometrical parameters of the printed circuit and the cables used.
- Parameters dtf1, dtf2, dtr1, dtr2 describing the dependence of switching times of the transistor on switched current in (14) and (18) are approximated from the datasheet characteristics tf(ID) and tr(ID).
- The parameters of the thermal model are estimated using the diode and the MOSFET datasheets, heatsink datasheet, and datasheet of the thermal interfaces between them. Rth0 is typically given by the producer, and Tx is a parameter dependent on heatsink geometry, which is equal to 26 K for a grilled heatsink [29]. kgrease and khtp are given by manufacturers of grease and pads on their packages. In turn, parameters agrease, tgrease, ahtp, and thp are related to the geometry of these interfaces. If measuring the thickness of thermal grease is a cumbersome task, one can use the value given by the manufacturer, or, in the case of its absence, the typical value indicated in the literature, i.e., 100 µm [30].
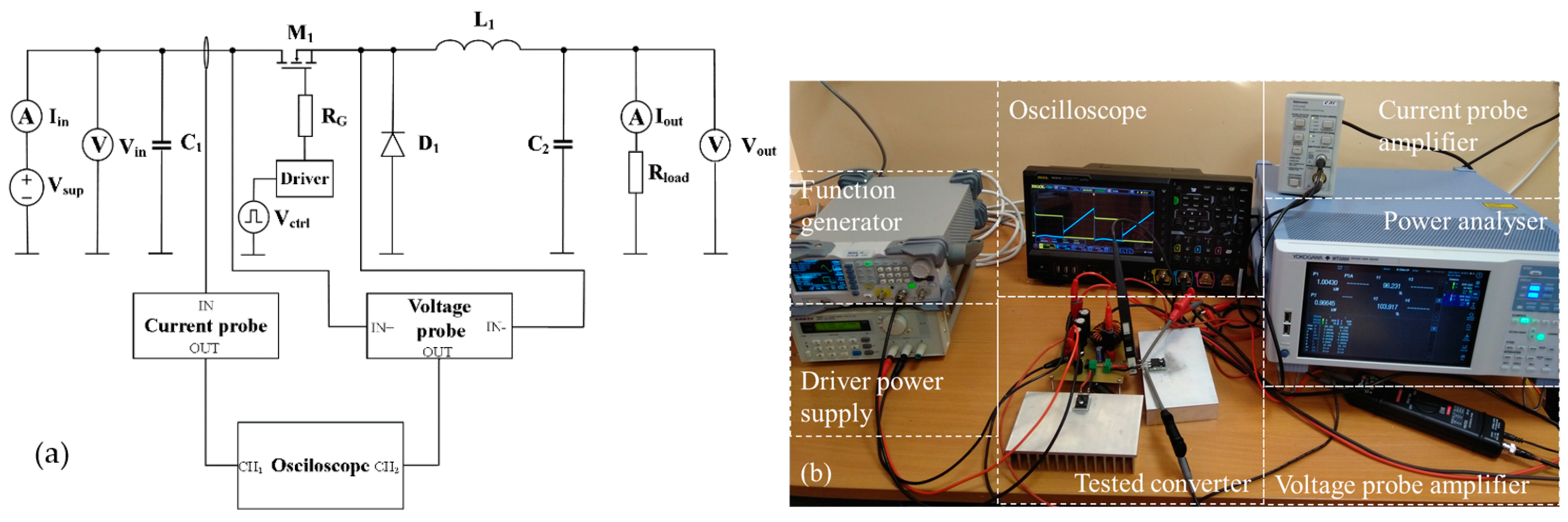
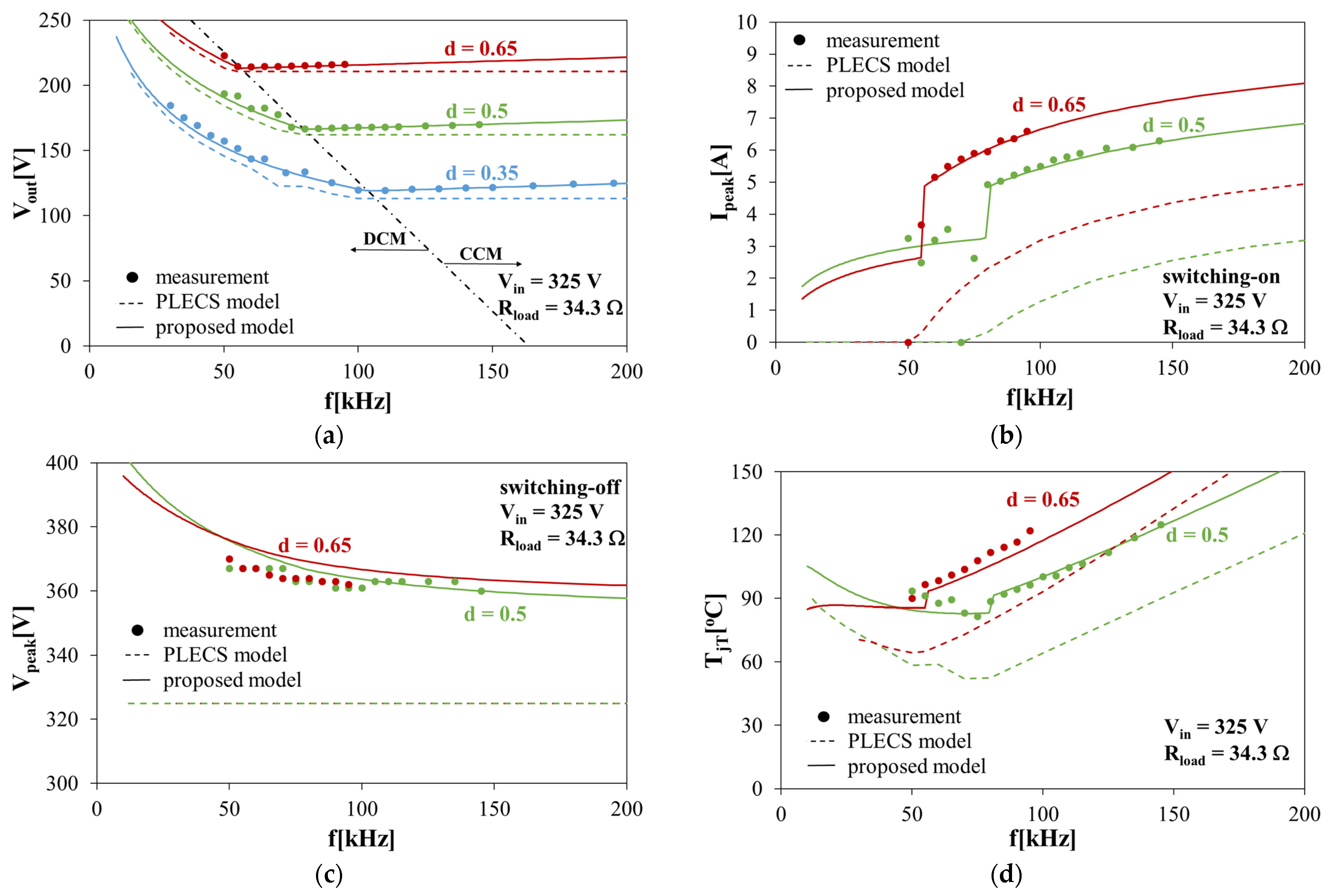
4. Experimental Verification
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kazimierczuk, M.K. Pulse-Width Modulated DC-DC Power Converters, 2nd ed.; Wiley: Chichester, UK, 2015. [Google Scholar]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Rashid, M.H. Spice for Power Electronics and Electric Power, 1st ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Allmeling, J.H.; Hammer, W.P. PLECS—Piece-wise Linear Electrical Circuit Simulation for Simulink. In Proceedings of the IEEE 1999 International Conference on Power Electron and Drive Systems PEDS’99, Hong Kong, China, 27–29 July 1999. [Google Scholar]
- Bryant, A.; Parker-Allotey, N.-A.; Hamilton, D.; Swan, I.; Mawby, P.A.; Ueta, T.; Nishijima, T.; Hamada, K. A Fast Loss and Temperature Simulation Method for Power Converters, Part I: Electrothermal Modeling and Validation. IEEE Trans. Power Electron. 2012, 27, 248–257. [Google Scholar] [CrossRef]
- Fu, H.; Chen, J.; Wang, H.; Liu, Z.; Sørensen, H.; Bahman, A.S. 3-D-Lumped Thermal Network Models for the Reliability Analysis of Fan-Cooled Plate-Fin Heatsink. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3480–3491. [Google Scholar] [CrossRef]
- Janicki, M.; Sarkany, Z.; Napieralski, A. Impact of nonlinearities on electronic device transient thermal responses. Microelectron. J. 2014, 45, 1721–1725. [Google Scholar] [CrossRef]
- Rezek, G. A Practical Method of Heat Computations in Electronic Equipment. IEEE Trans. Parts Mater. Packag. 1967, 3, 65–67. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Mayo-Maldonado, J.C.; Valdez-Resendiz, J.E.; Alejo-Reyes, A.; Beltran-Carbajal, F.; López-Santos, O. An Overview of Non-Isolated Hybrid Switched-Capacitor Step-Up DC–DC Converters. Appl. Sci. 2022, 12, 8554. [Google Scholar] [CrossRef]
- Górecki, P.; Górecki, K. Methods of fast analysis of DC–DC converters—A review. Electronics 2021, 10, 2920. [Google Scholar] [CrossRef]
- Codecasa, L.; d’Alessandro, V.; Magnani, A.; Irace, A. Circuit-Based Electrothermal Simulation of Power Devices by an Ultrafast Nonlinear MOR Approach. IEEE Trans. Power Electron. 2016, 31, 5906–5916. [Google Scholar] [CrossRef]
- Górecki, K.; Zarębski, J. The Method of a Fast Electrothermal Transient Analysis of Single-Inductance DC–DC Converters. IEEE Trans. Power Electron. 2012, 27, 4005–4012. [Google Scholar] [CrossRef]
- Azer, P.; Rodriguez, R.; Guo, J.; Gareau, J.; Bauman, J.; Ge, H.; Bilgin, B.; Emadi, A. Time-efficient integrated electrothermal model for a 60-kW three-phase bidirectional synchronous DC-DC converter. IEEE Trans. Ind. Appl. 2020, 56, 654–668. [Google Scholar] [CrossRef]
- Han, J.; Zhang, B.; Qiu, D. Bi-switching Status Modeling Method for DC–DC Converters in CCM and DCM Operations. IEEE Trans. Power Electron. 2017, 21, 2464–2472. [Google Scholar] [CrossRef]
- Azer, P.; Emadi, A. Generalized State Space Average Model for Multi-Phase Interleaved Buck, Boost and Buck-Boost DC-DC Converters: Transient, Steady-State and Switching Dynamics. IEEE Access 2020, 8, 77735–77745. [Google Scholar] [CrossRef]
- Vorperian, V. Simplified analysis of PWM converters using model of PWM switch. Continuous conduction mode. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 490–496. [Google Scholar] [CrossRef]
- Vorperian, V. Simplified analysis of PWM converters using model of PWM switch. II. Discontinuous conduction mode. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 497–505. [Google Scholar] [CrossRef]
- Kimhi, D.; Ben-Yaakov, S. A SPICE model for current mode PWM converters operating under continuous inductor current conditions. IEEE Trans. Power Electron. 1991, 6, 281–286. [Google Scholar] [CrossRef]
- Cheng, T.; Lu, D.D.-C.; Siwakoti, Y.P. A MOSFET SPICE Model with Integrated Electro-Thermal Averaged Modeling, Aging, and Lifetime Estimation. IEEE Access 2020, 9, 5545–5554. [Google Scholar] [CrossRef]
- Ayachit, A.; Kazimierczuk, M.K. Averaged Small-Signal Model of PWM DC-DC Converters in CCM Including Switching Power Loss. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 262–266. [Google Scholar] [CrossRef]
- Górecki, K.; Detka, K. Application of Average Electrothermal Models in the SPICE-Aided Analysis of Boost Converters. IEEE Trans. Ind. Electron. 2019, 66, 2746–2755. [Google Scholar] [CrossRef]
- Górecki, P. Electrothermal Averaged Model of a Diode–IGBT Switch for a Fast Analysis of DC–DC Converters. IEEE Trans. Power Electron. 2022, 37, 13003–13013. [Google Scholar] [CrossRef]
- Martínez-Caballero, L.; Kot, R.; Milczarek, A.; Malinowski, M. Converter Averaging Approach for Modeling a Residential Supply Subsystem. In Proceedings of the 17th IEEE International Conference on compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Tallinn, Estonia, 14–16 June 2023. [Google Scholar]
- Rashid, A.U.; Hossain, M.; Emon, A.I.; Mantooth, H.E.C.A. Datasheet-Driven Compact Model of Silicon Carbide Power MOSFET Including Third-Quadrant Behavior. IEEE Trans. Power Electron. 2021, 36, 11748–11762. [Google Scholar] [CrossRef]
- Górecki, K. A new electrothermal average model of the diode–transistor switch. Microelectron. Reliab. 2008, 48, 51–58. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Jaeger, R.C. Computerized Circuit Analysis Using SPICE Programs, 1st ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Grover, F.W. Inductance Calculations, 1st ed.; Dover Publications: Dover, DE, USA, 2004. [Google Scholar]
- Xiong, Y.; Sun, S.; Jia, H.; Shea, P.; Shen, Z.J. New Physical Insights on Power MOSFET Switching Losses. IEEE Trans. Power Electron. 2009, 24, 525–531. [Google Scholar] [CrossRef]
- Górecki, K.; Górecki, P. Nonlinear Compact Thermal Model of the IGBT Dedicated to SPICE. IEEE Trans. Power Electron. 2020, 35, 13420–13428. [Google Scholar] [CrossRef]
- Narumanchi, S.; Mihalic, M.; Kelly, K.; Eesley, G. Thermal interface materials for power electronics applications. In Proceedings of the 11th Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, Orlando, FL, USA, 28–31 May 2008. [Google Scholar]
- Zięba, D.; Rąbkowski, J. Problems related to the correct determination of switching power losses in high-speed SiC MOSFET power modules. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e140695. [Google Scholar] [CrossRef]
- Yun, C.-S.; Malberti, P.; Ciappa, M.; Fichtner, W. Thermal component model for electrothermal analysis of IGBT module systems. IEEE Trans. Adv. Packag. 2001, 24, 401–406. [Google Scholar] [CrossRef]
- Górecki, P.; Górecki, K.; Detka, K.; d’Alessandro, V. Influence of parasitics of components and circuit on switching losses of power SiC and GaN transistors in power converter applications. In Proceedings of the 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023. [Google Scholar]
- Anurag, A.; Acharya, S.; Bhattacharya, S. An Accurate Calorimetric Loss Measurement Method for SiC MOSFETs. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1644–1656. [Google Scholar] [CrossRef]
- SiC MOSFET Datasheet. Available online: https://fscdn.rohm.com/en/products/databook/datasheet/discrete/sic/mosfet/sct3060al-e.pdf (accessed on 16 November 2023).
- SiC Schottky Diode Datasheet. Available online: https://www.onsemi.com/pdf/datasheet/ffsh5065b-f085-d.pdf (accessed on 16 November 2023).
- Górecki, P.; Wojciechowski, D. Accurate Electrothermal Modeling of High Frequency DC–DC Converters with Discrete IGBTs in PLECS Software. IEEE Trans. Ind. Electron. 2023, 70, 5739–5746. [Google Scholar] [CrossRef]
- Kalker, S.; Ruppert, L.A.; van der Broeck, C.H.; Kuprat, J.; Andresen, M.; Polom, T.A.; Liserre, M.; De Doncker, R.W. Reviewing Thermal-Monitoring Techniques for Smart Power Modules. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1326–1341. [Google Scholar] [CrossRef]
- Optex PT-3S Datasheet. Available online: https://www.optex-fa.com/products/discontinue/pdf/pt_3s_catalog.pdf (accessed on 16 November 2023).
- Pintek Catalog. Available online: http://www.pintek.com.tw/customer/pintek/pdf/catalog-2020a.pdf (accessed on 16 November 2023).
- Tektronix TCPA300 Datasheet. Available online: https://www.tek.com/en/datasheet/ac-dc-current-measurement-systems (accessed on 16 November 2023).
- Wilson, P.; Ross, J.; Brown, A. Simulation of magnetic component models in electric circuits including dynamic thermal effects. IEEE Trans. Power Electron. 2002, 17, 55–65. [Google Scholar] [CrossRef]
- Xu, M.; Yang, X.; Li, J. C-RC Snubber Optimization Design for Improving Switching Characteristics of SiC MOSFET. IEEE Trans. Power Electron. 2022, 37, 12005–12016. [Google Scholar] [CrossRef]
- Górecki, P.; Górecki, K. Thermal limits of the maximum operating frequency of SiC MOSFETs. In Proceedings of the IEEE 16th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Birmingham, UK, 29 June–1 July 2022. [Google Scholar]
- Li, B.; Riaz, S.; Zhao, Y. Experimental Validation of Iterative Learning Control for DC/DC Power Converters. Energies 2023, 16, 6555. [Google Scholar] [CrossRef]


| T0 [K] | nD | ISD [fA] | RSD [mΩ] | VTref [mV] | tdoffref [ns] | tdon [ns] | tdoffdriver [ns] | tdondriver [ns] |
| 298 | 1.1 | 30 | 7.3 | 25.8 | 4 | 19 | 210 | 120 |
| aron [K−1] | NRSD [K−1] | kISD [K−1] | bron [K−1] | VGShigh [V] | aVGS [V] | bVGS [V] | aID [V/A3] | bID [V/A2] |
| 1.17 × 10−6 | 6 × 10−4 | 9.339 × 10−2 | −9 × 10−6 | 18 | 46 | 2.2 | 5 × 10−6 | 4 × 10−5 |
| aIon1 [pJ/A4] | aIon2 [nJ/A3] | aIon3 [nJ/A3] | aIon4 [μJ/A] | cRGon [mS] | aVD1 [pJ/V2] | aVD2 [nJ/V] | bVDCon1 [V−2] | bVDCon2 [V−1] |
| −550 | 393 | −712.3 | 9.1528 | 77.178 | 50 | 16.2 | 8.3 × 10−6 | 5.82 × 10−6 |
| bVDCoff1 [V−2] | bVDCoff2 [V−1] | cRgoff [mS] | aIoff1 [nJ/A2] | aIoff2 [nJ/A] | RGref [Ω] | RGin [Ω] | VDCref [V] | Cj0 [nF] |
| 1.7 × 10−5 | 6.353 × 10−3 | 575.7 | 64.5 | −210.4 | 0 | 12 | 300 | 2.5 |
| m | Vj [V] | dtr1 [ns/A] | dtr2 [ns] | dtf1 [ps/A] | dtf2 [ns] | lt [mm] | ht [mm] | wt [mm] |
| 0.5 | 1.5 | 1.6748 | 17 | 417.4 | 9.278 | 51 | 1.5 | 4 |
| tt [μm] | lc [mm] | dc [mm] | ref1 | ref2 | Ronref [mΩ] | tgrease [μm] | Rth0 [K/W] | agrease [mm2] |
| 35 | 179 | 18 | 0.9 | 0.1 | 48 | 100 | 2.75 | 321 |
| kgrease [W/m/K] | Rthj-cT [K/W] | Rthj-cD [K/W] | thtp [mm] | khtp [W/m/K] | ahtp [mm2] | |||
| 2.8 | 0.7 | 0.5 | 3 | 25 | 525 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Górecki, P.; d’Alessandro, V. A Datasheet-Driven Electrothermal Averaged Model of a Diode–MOSFET Switch for Fast Simulations of DC–DC Converters. Electronics 2024, 13, 154. https://doi.org/10.3390/electronics13010154
Górecki P, d’Alessandro V. A Datasheet-Driven Electrothermal Averaged Model of a Diode–MOSFET Switch for Fast Simulations of DC–DC Converters. Electronics. 2024; 13(1):154. https://doi.org/10.3390/electronics13010154
Chicago/Turabian StyleGórecki, Paweł, and Vincenzo d’Alessandro. 2024. "A Datasheet-Driven Electrothermal Averaged Model of a Diode–MOSFET Switch for Fast Simulations of DC–DC Converters" Electronics 13, no. 1: 154. https://doi.org/10.3390/electronics13010154
APA StyleGórecki, P., & d’Alessandro, V. (2024). A Datasheet-Driven Electrothermal Averaged Model of a Diode–MOSFET Switch for Fast Simulations of DC–DC Converters. Electronics, 13(1), 154. https://doi.org/10.3390/electronics13010154







