Integrating Sensor Systems and Signal Processing for Sustainable Production: Analysis of Cutting Tool Condition
Abstract
:1. Introduction
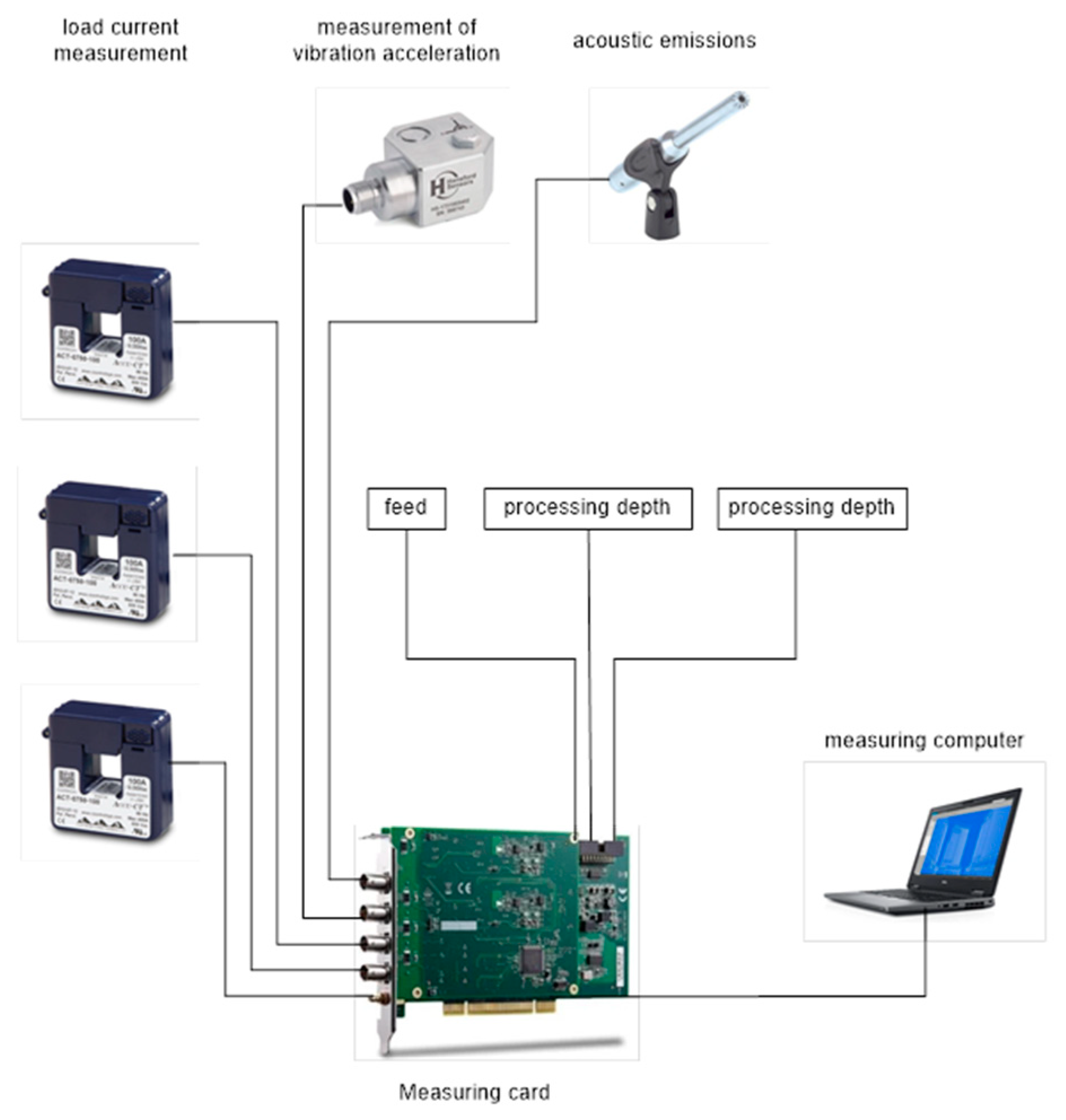
2. Materials and Methods
3. Results and Discussion
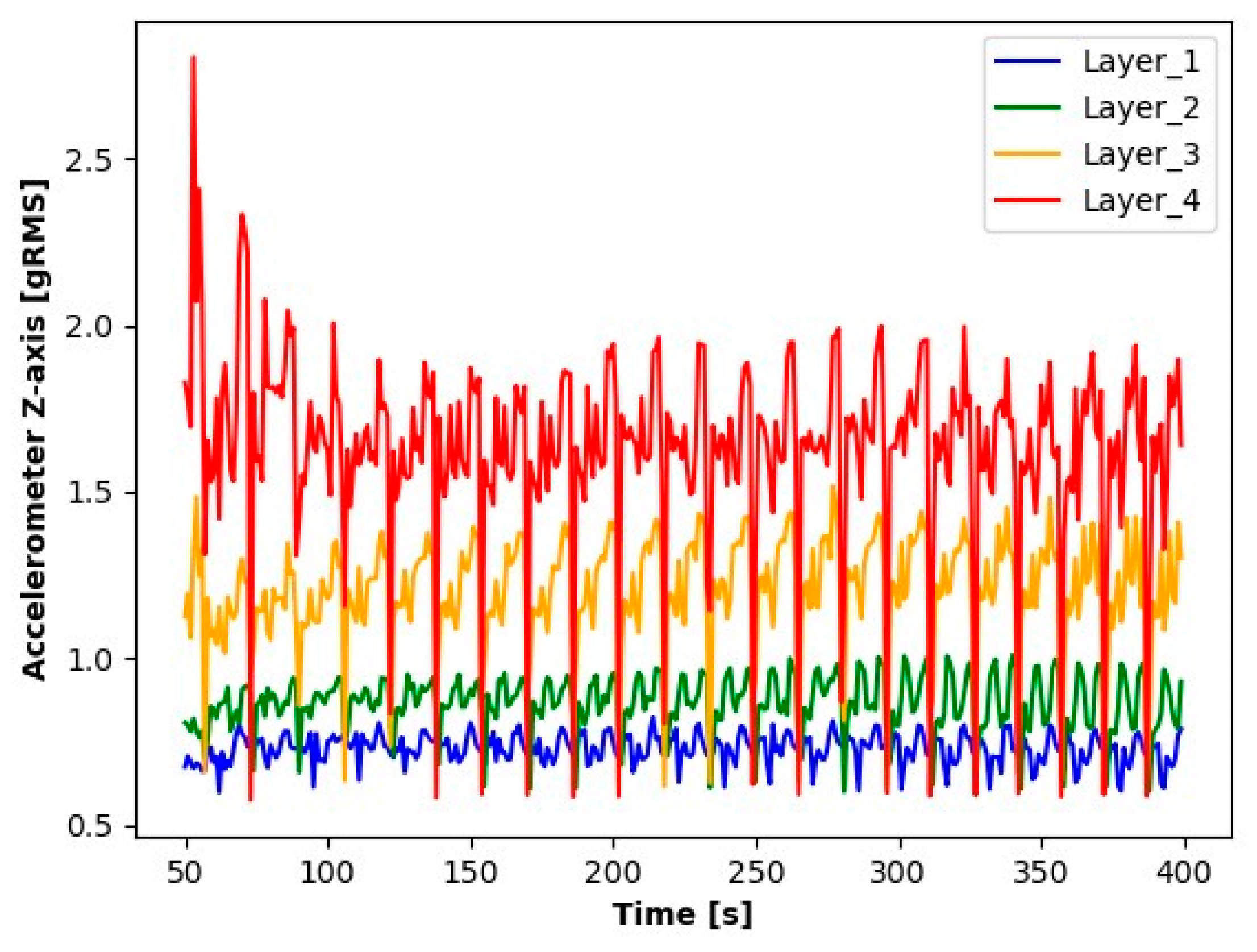
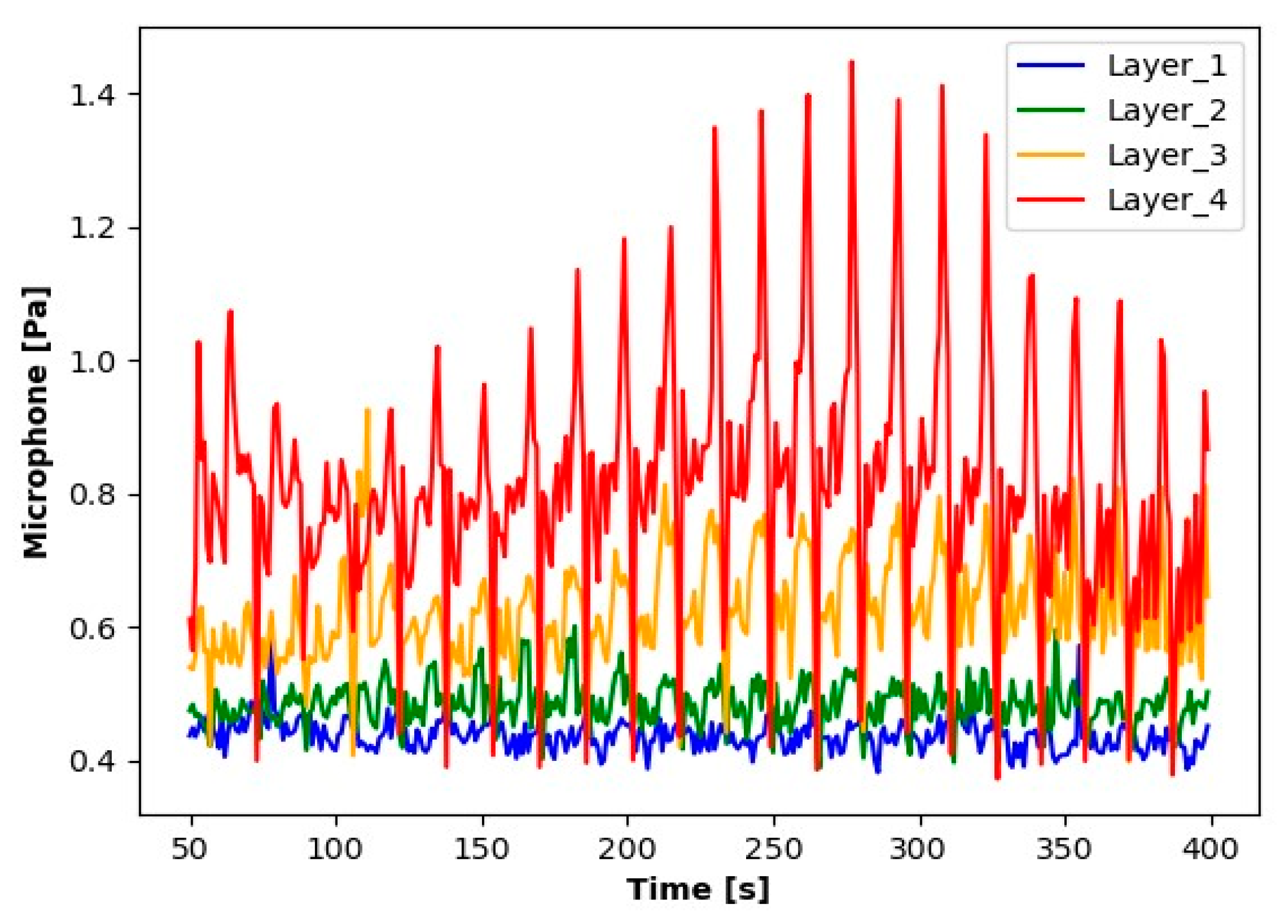
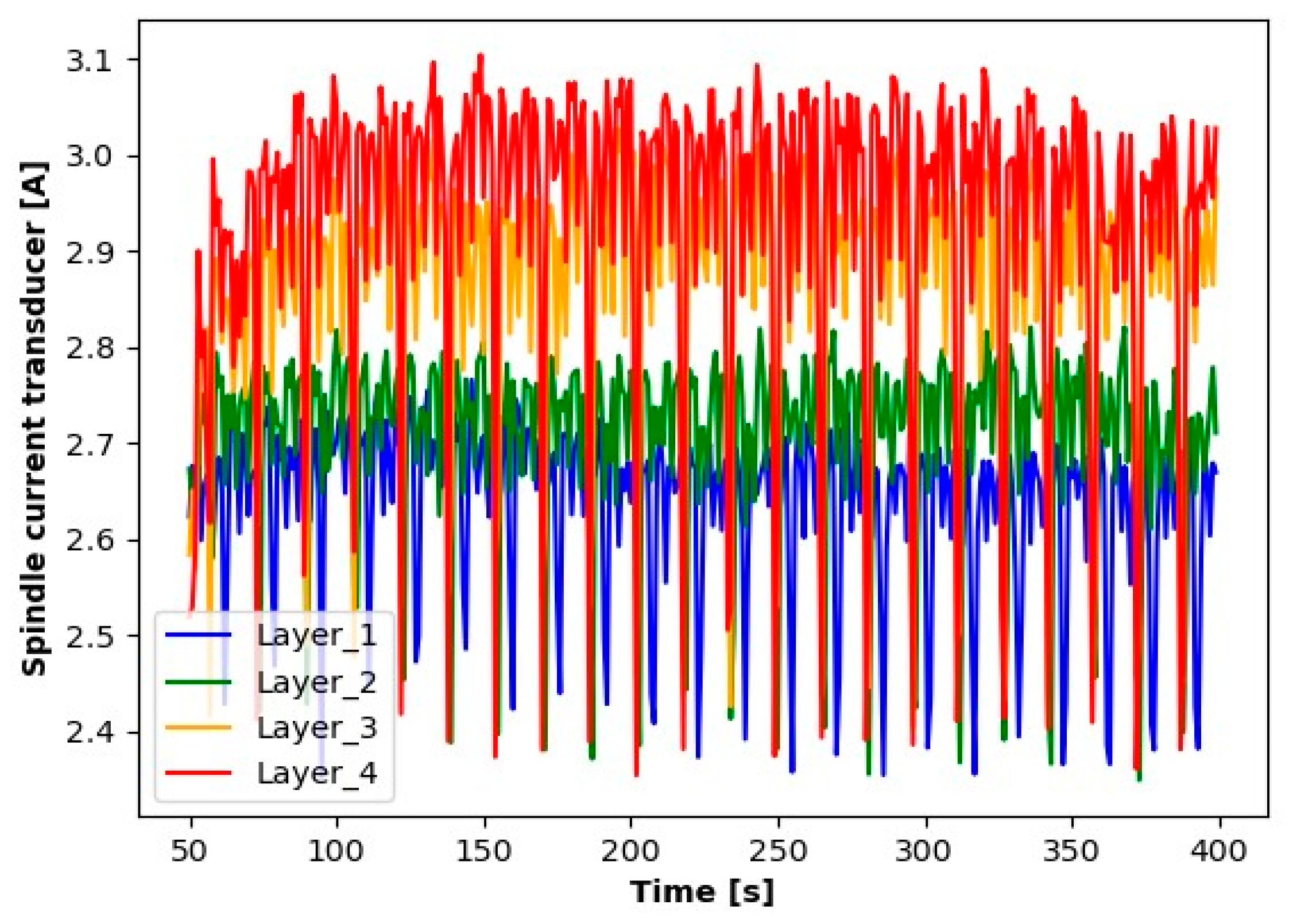
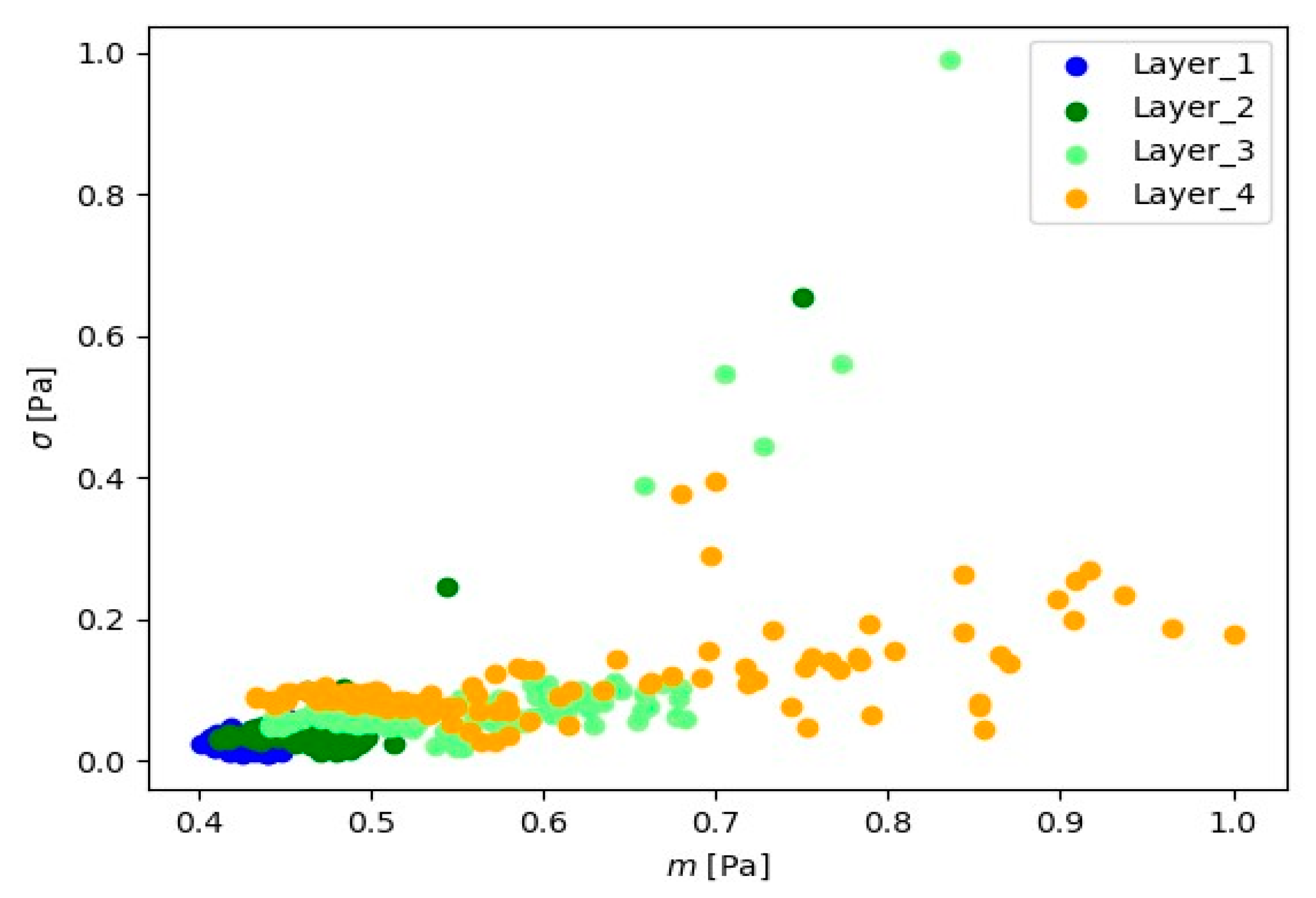
3.1. Preliminary Analysis of the Results Obtained
- Channel A0 included signals from the Z-axis sensor, associated with the machine’s movement along the Y-axis.
- Channel A1 recorded signals from the Y-axis sensor, associated with the machine’s movement along the Z-axis.
- Channel A2 was responsible for recording signals from the X-axis sensor, associated with the machine’s movement along the X-axis.
- Channel A3 encompassed signals from a microphone with a sensitivity of 50 mV/Pa, used for monitoring the noise generated during processing.
- Channel A4 recorded signals from the spindle current transducer, providing information about the current in that area.
- Channel A5 included signals from the milling machine’s current transducer, supplying information about the current in the milling area.
3.2. Construction of the Classifier
3.2.1. Creating a Database
- Logistic regression;
- Gradient boosting classifier.
3.2.2. Logistic Regression
3.2.3. Gradient Boosting Classifier
4. Conclusions
- Confirm the effectiveness of the applied predictive models, especially the gradient boosting classifier, which achieved high accuracy at 97.46%. The analysis of ROC curves and AUC values further confirmed the high quality of the classifiers, emphasizing their ability to precisely identify different material layers. It is worth noting that the analysis of sensor signals was comprehensive, covering various machine monitoring channels, which additionally enhances the credibility of the obtained results;
- Not only confirm the importance of monitoring tools in the milling process but also introduce innovative approaches that can significantly improve the effectiveness of this process in production conditions;
- Confirm that the implementation of the proposed models could play a crucial role in diminishing the occurrence of nonconforming products attributed to the condition of the cutting tool. These considerations are poised to curtail the consumption of raw materials, minimize production waste, and consequently alleviate the environmental impact of the company. This aligns seamlessly with the principles of sustainable production.
- The heavy reliance on machine-learning models, particularly methods like gradient boosting classifiers, poses its own set of challenges. Though these models have shown high accuracy, their performance is contingent on the availability of substantial and quality data. In situations with limited or noisy data, their applicability and effectiveness could be compromised.
- The research’s focus on specific materials and machining layers also raises questions about the generalizability of the findings. The models developed might require additional adjustments to be applicable to different materials or layers, limiting their immediate transferability to other manufacturing contexts.
- Despite being comprehensive and covering various machine monitoring channels, it is possible that not all aspects of tool wear are fully captured through these channels. There might be facets of tool wear or conditions that remain undetected, which could affect the overall accuracy and reliability of the predictive models.
- The practical implementation of these models in real-world production settings is another area of concern. Integrating these advanced systems with existing manufacturing processes, training personnel, and ensuring consistent performance under varying operational conditions could pose significant challenges, especially in less technologically advanced facilities.
5. Directions of Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Borucka, A.; Kozłowski, E.; Parczewski, R.; Antosz, K.; Gil, L.; Pieniak, D. Supply Sequence Modelling Using Hidden Markov Models. Appl. Sci. 2023, 13, 231. [Google Scholar] [CrossRef]
- Sayyad, S.; Kumar, S.; Bongale, A.; Kamat, P.; Patil, S.; Kotecha, K. Data-driven remaining useful life estimation for milling process: Sensors, algorithms, datasets, and fu-ture directions. IEEE Access 2021, 9, 110255–110286. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Gupta, M.K.; da Silva, L.R.; Kiran, M.; Khanna, N.; Krolczyk, G.M. Application of measurement systems in tool condition monitoring of Milling: A review of measurement science approach. Measurement 2022, 199, 111503. [Google Scholar] [CrossRef]
- Kozłowski, E.; Antosz, K.; Mazurkiewicz, D.; Sęp, J.; Żabiński, T. Integrating advanced measurement and signal processing for reliability decision-making. Eksploat. I Niezawodn.—Maint. Reliab. 2021, 23, 777–787. [Google Scholar] [CrossRef]
- Antosz, K.; Mazurkiewicz, D.; Kozłowski, E.; Sęp, J.; Żabiński, T. Machining Process Time Series Data Analysis with a Decision Support Tool. In Innovations in Mechanical Engineering, Lecture Notes in Mechanical Engineering; Machado, J., Soares, F., Trojanowska, J., Ottaviano, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 14–27. [Google Scholar]
- Li, X.; Yue, C.; Liu, X.; Zhou, J.; Wang, L. ACWGAN-GP for milling tool breakage monitoring with imbalanced data. Robot. Comput.–Integr. Manuf. 2024, 85, 102624. [Google Scholar] [CrossRef]
- Lu, X.; Jia, Z.; Wang, H.; Feng, Y.; Liang, S.Y. The effect of cutting parameters on micro-hardness and the prediction of Vickers hardness based on a response surface method-ology for micro-milling Inconel 718. Meas. J. Int. Meas. Confed. 2019, 140, 56–62. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.P.; Lu, Y.T.; Lin, Y.F.; Hsu, F.C.; Lin, C.F.; Lu, Y.C.; Lu, X.; Liang, S.Y. Inverse analysis of inconel 718 laser-assisted milling to achieve machined surface roughness. Int. J. Precis. Eng. Manuf. 2018, 19, 1611–1618. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Sun, J.; Zhang, H.; Feng, Y. The influence factors and prediction of curve surface roughness in micro-milling nickel based superalloy. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference, MSEC 2018, College Station, TX, USA, 18–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V004T03A010. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.P.; Lu, Y.T.; Lin, Y.F.; Hsu, F.C.; Lin, C.F.; Lu, Y.C.; Lu, X.; Liang, S.Y. In-verse analysis of the cutting force in laser-assisted milling on Inconel 718. Int. J. Adv. Manuf. Technol. 2018, 96, 905–914. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, W.; Ye, C.; Peng, B.; Fang, X.; Lin, C.; Wang, G.; Kumar, A.; Sun, W. Time-frequency Representation -enhanced Transfer Learning for Tool Condition Monitoring during milling of Inconel 718. Eksploat. I Niezawodn.—Maint. Reliab. 2023, 25, 165926. [Google Scholar] [CrossRef]
- Dutta, S.; Pal, S.K.; Mukhopadhyay, S.; Sen, R. Application of digital image processing in tool condition monitoring: A review. CIRP J. Manuf. Sci. Technol. 2013, 6, 212–232. [Google Scholar] [CrossRef]
- Kozłowski, E.; Mazurkiewicz, D.; Żabiński, T.; Prucnal, S.; Sęp, J. Machining sensor data management for operation-level predictive model. Expert. Syst. Appl. 2020, 159, 113600. [Google Scholar] [CrossRef]
- Tran, M.Q.; Doan, H.P.; Vu, V.Q.; Vu, L.T. Machine Learning and IoT-Based Approach for Tool Condition Monitoring: A Review and Future Prospects. Measurement 2022, 207, 112351. [Google Scholar] [CrossRef]
- Isavand, J.; Kasaei, A.; Peplow, A.; Wang, X.; Yan, J. A Reduced-Order Machine-Learning-Based Method for Fault Recognition in Tool Condition Monitoring. Measurement 2023, 224, 113906. [Google Scholar] [CrossRef]
- Salgado, D.R.; Alonso, F.J. Tool Wear Detection in Turning Operations Using Singular Spectrum Analysis. J. Mater. Process. Technol. 2006, 171, 451–458. [Google Scholar] [CrossRef]
- Kilundu, B.; Dehombreux, P.; Chiementin, X. Tool Wear Monitoring by Machine Learning Techniques and Singular Spectrum Analysis. Mech. Syst. Sig. Process. 2011, 25, 400–415. [Google Scholar] [CrossRef]
- He, M.; He, D. A New Hybrid Deep Signal Processing Approach for Bearing Fault Diagnosis Using Vibration Signals. Neurocomputing 2020, 396, 542–555. [Google Scholar] [CrossRef]
- Segreto, T.; Simeone, A.; Teti, R. Multiple Sensor Monitoring in Nickel Alloy Turning for Tool Wear Assessment via Sensor Fusion. Procedia CIRP 2013, 12, 85–90. [Google Scholar] [CrossRef]
- Seemuang, N.; McLeay, T.; Slatter, T. Using Spindle Noise to Monitor Tool Wear in a Turning Process. Int. J. Adv. Manuf. Technol. 2016, 86, 2781–2790. [Google Scholar] [CrossRef]
- Liu, M.-K.; Tseng, Y.-H.; Tran, M.-Q. Tool Wear Monitoring and Prediction Based on Sound Signal. Int. J. Adv. Manuf. Technol. 2019, 103, 3361–3373. [Google Scholar] [CrossRef]
- Tran, M.Q.; Liu, M.K.; Tran, Q.V. Milling Chatter Detection Using Scalogram and Deep Convolutional Neural Network. Int. J. Adv. Manuf. Technol. 2020, 107, 1505–1516. [Google Scholar] [CrossRef]
- Kothuru, A.; Nooka, S.P.; Liu, R. Application of Audible Sound Signals for Tool Wear Monitoring Using Machine Learning Techniques in End Milling. Int. J. Adv. Manuf. Technol. 2018, 95, 3797–3808. [Google Scholar] [CrossRef]
- Zhang, C.; Yao, X.; Zhang, J.; Jin, H. Tool Condition Monitoring and Remaining Useful Life Prognostic Based on a Wireless Sensor in Dry Milling Operations. Sensors 2016, 16, 795. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.-C.; Wan, B.-S. Study of High-Frequency Sound Signals for Tool Wear Monitoring in Micromilling. Int. J. Adv. Manuf. Technol. 2013, 66, 1785–1792. [Google Scholar] [CrossRef]
- Schueller, A.; Saldana, C. Generalizability Analysis of Tool Condition Monitoring Ensemble Machine Learning Models. J. Manuf. Process. 2022, 84, 1064–1075. [Google Scholar] [CrossRef]
- Soori, M.; Arezoo, B.; Dastres, R. Machine learning and artificial intelligence in CNC machine tools, A review. Sustain. Manuf. Serv. Econ. 2023, 2, 100009. [Google Scholar] [CrossRef]
- He, J.; Sun, Y.; Gao, H.; Guo, L.; Cao, A.; Chen, T. On-line milling tool wear monitoring under practical machining conditions. Measurement 2023, 222, 113621. [Google Scholar] [CrossRef]
- Xin, Y.; Xiaogang, S. Linear Regression Analysis; World Scientific Publishing Company: Singapore, 2009. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1994, 58, 267–288. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Hand, D.J.; Till, R.J. A Simple Generalization of the Area Under the ROC Curve for Multiple Class Classification Problems. Mach. Learn. 2001, 45, 171–186. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Inc.: New York, NY, USA, 2009. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Li, G.; Wang, Y.; He, J.; Hao, Q.; Yang, H.; Wei, J. Tool wear state recognition based on gradient boosting decision tree and hybrid classification RBM. Int. J. Adv. Manuf. Technol. 2020, 109, 2417–2428. [Google Scholar] [CrossRef]
- Alajmi, M.S.; Almeshal, A.M. Predicting the Tool Wear of a Drilling Process Using Novel Machine Learning XGBoost-SDA. Materials 2020, 13, 4952. [Google Scholar] [CrossRef] [PubMed]
- Riego, V.; Castejón-Limas, M.; Sánchez-González, L.; Fernández-Robles, L.; Pérez, H.; Díez-González, J.; Guerrero-Higueras, Á.M. Strong classification system for wear identification on milling processes using computer vision and ensemble learning. Neurocomputing 2021, 423, 643–654. [Google Scholar] [CrossRef]



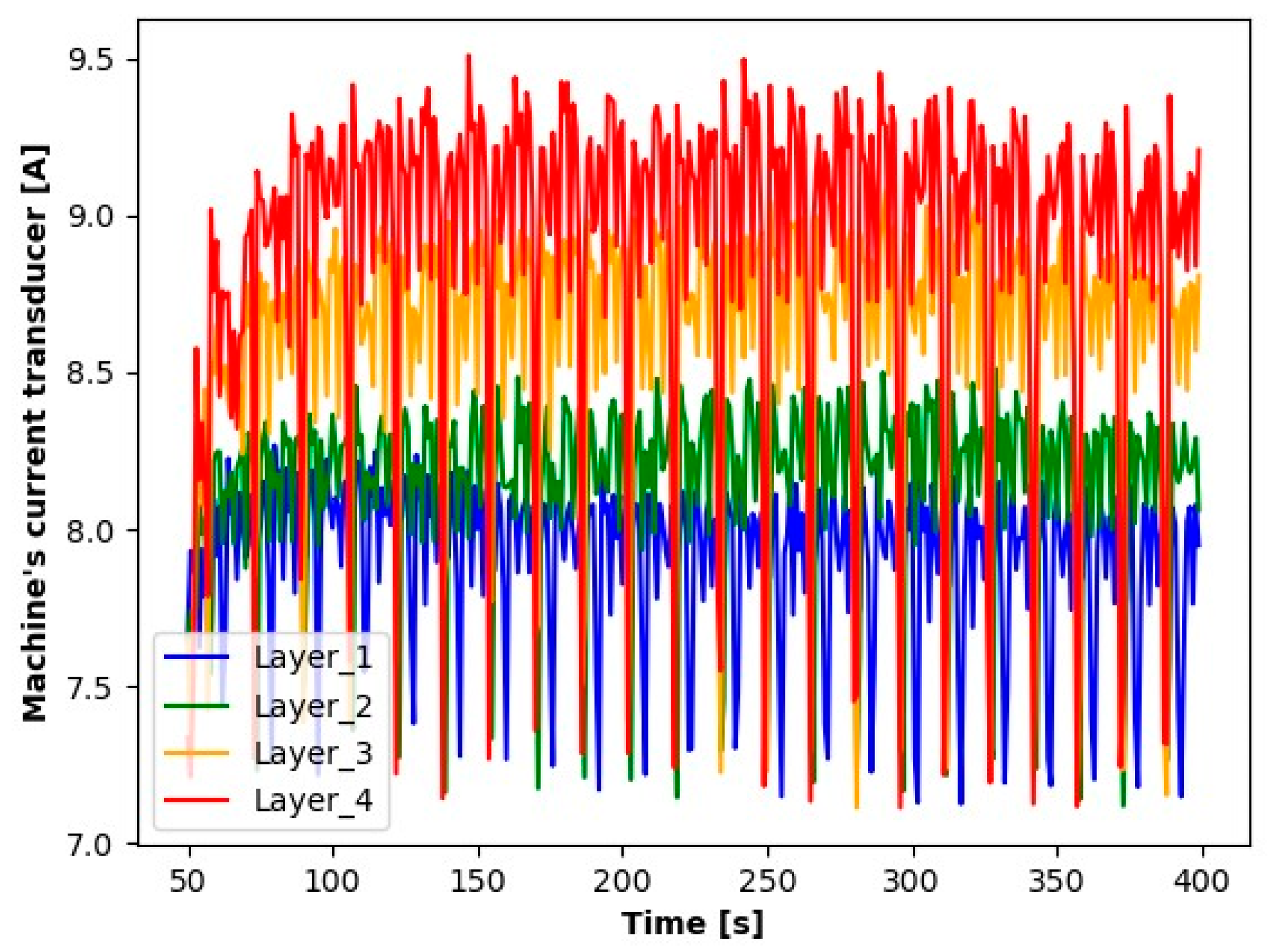
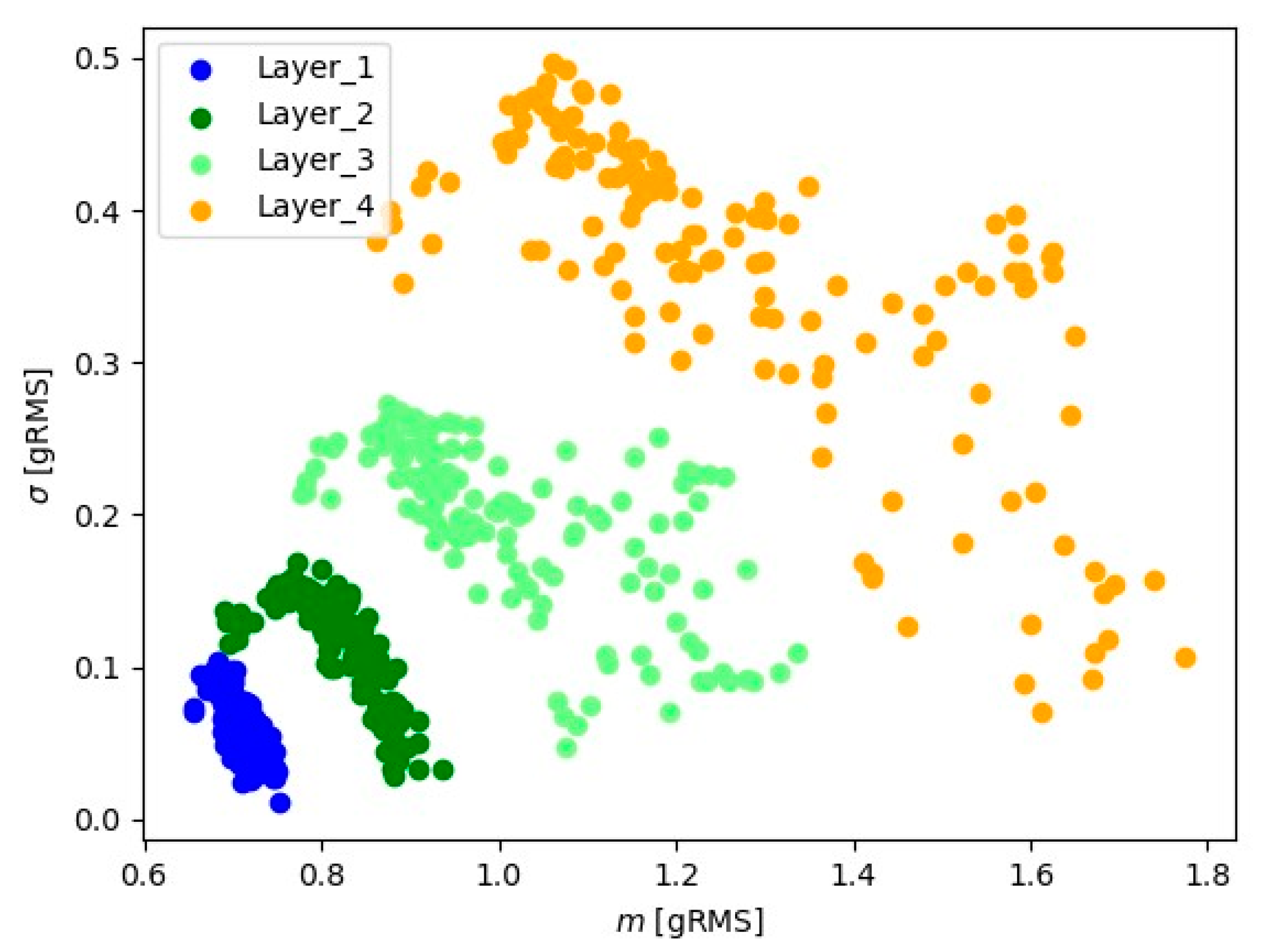
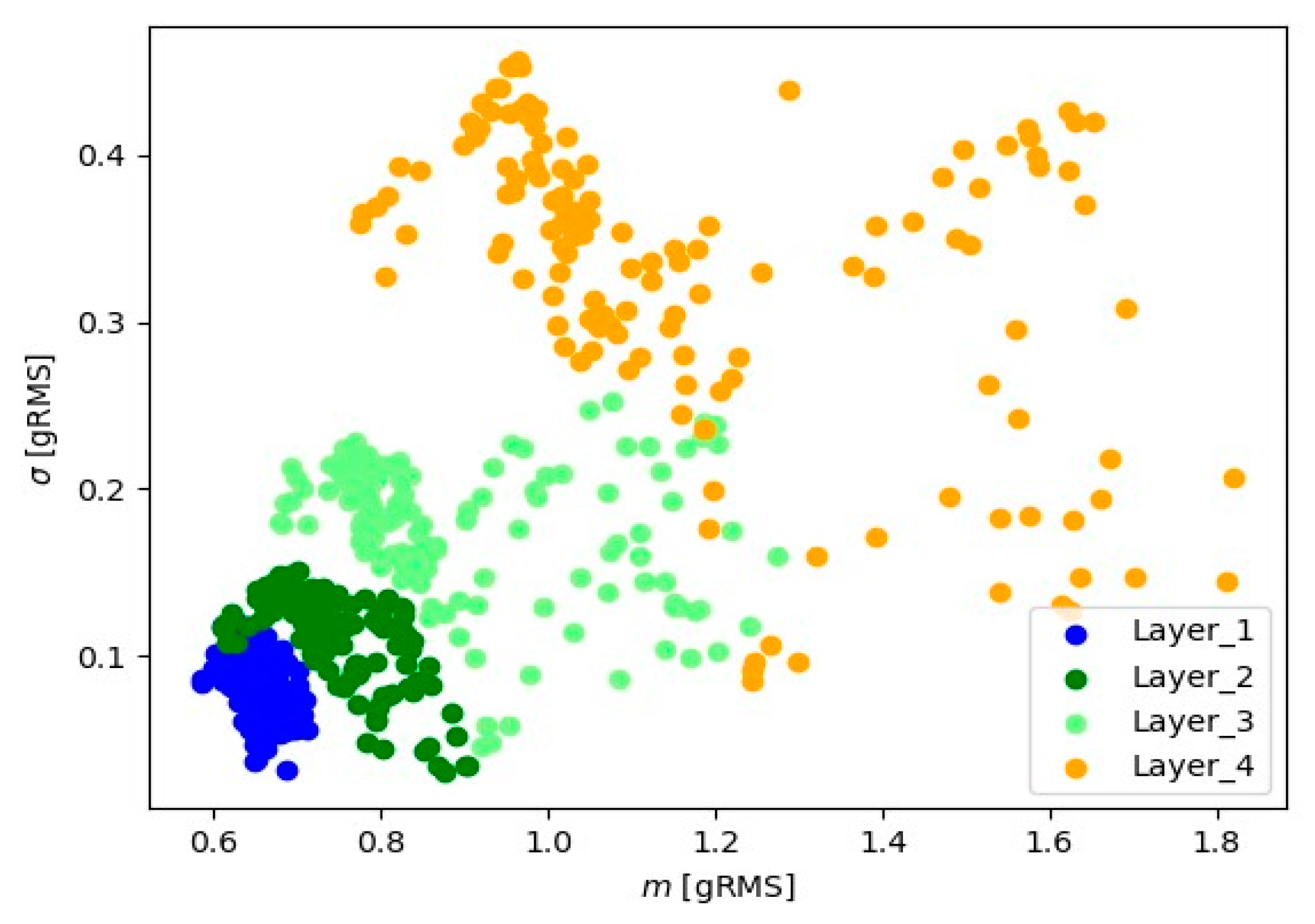
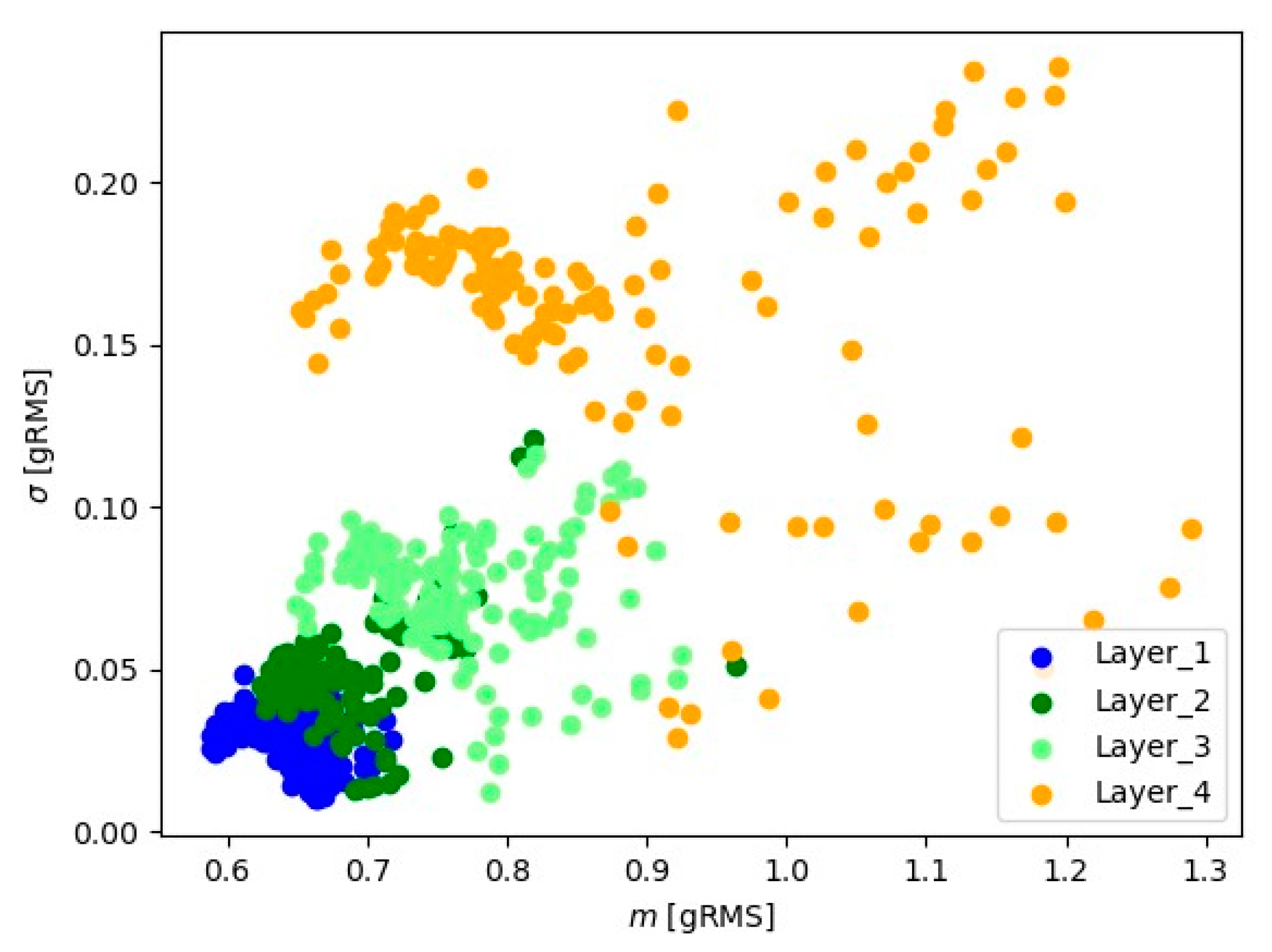




| Layer | Channel | ||||
|---|---|---|---|---|---|
| 7.3000 | 8.0840 | 0.0758 | 0.4098 | Layer_1 | A0 |
| 7.3959 | 8.2794 | 0.0811 | 0.5234 | Layer_2 | A0 |
| 7.5549 | 8.8139 | 0.0995 | 0.7058 | Layer_3 | A0 |
| 7.5939 | 9.1788 | 0.1018 | 0.8588 | Layer_4 | A0 |
| 7.3230 | 8.0840 | 0.0758 | 0.4098 | Layer_1 | A1 |
| 7.3959 | 8.2794 | 0.0811 | 0.5234 | Layer_2 | A1 |
| 7.5549 | 8.8139 | 0.0995 | 0.7058 | Layer_3 | A1 |
| 7.5939 | 9.1788 | 0.1018 | 0.8588 | Layer_4 | A1 |
| 7.3230 | 8.0840 | 0.0758 | 0.4098 | Layer_1 | A2 |
| 7.3959 | 8.2794 | 0.0811 | 0.5234 | Layer_2 | A2 |
| 7.5549 | 8.8139 | 0.0995 | 0.7058 | Layer_3 | A2 |
| 7.5939 | 9.1788 | 0.1018 | 0.8588 | Layer_4 | A2 |
| 7.3230 | 8.0840 | 0.0758 | 0.4098 | Layer_1 | A3 |
| 7.3959 | 8.2794 | 0.0811 | 0.5234 | Layer_2 | A3 |
| 7.5549 | 8.8139 | 0.0995 | 0.7058 | Layer_3 | A3 |
| 7.5939 | 9.1788 | 0.1018 | 0.8588 | Layer_4 | A3 |
| 7.3230 | 8.0840 | 0.0758 | 0.4098 | Layer_1 | A4 |
| 7.3959 | 8.2794 | 0.0811 | 0.5234 | Layer_2 | A4 |
| 7.5549 | 8.8139 | 0.0995 | 0.7058 | Layer_3 | A4 |
| 7.5939 | 9.1788 | 0.1018 | 0.8588 | Layer_4 | A4 |
| 7.3230 | 8.0840 | 0.0758 | 0.4098 | Layer_1 | A5 |
| 7.3959 | 8.2794 | 0.0811 | 0.5234 | Layer_2 | A5 |
| 7.5549 | 8.8139 | 0.0995 | 0.7058 | Layer_3 | A5 |
| 7.5939 | 9.1788 | 0.1018 | 0.8588 | Layer_4 | A5 |
| Layer | Number of Case |
|---|---|
| 1 | 1305 |
| 2 | 1305 |
| 3 | 955 |
| 4 | 173 |
| Predicted | |||||
|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | ||
| Real | Layer 1 | 254 | 7 | 0 | 0 |
| Layer 2 | 11 | 243 | 6 | 1 | |
| Layer 3 | 1 | 30 | 159 | 1 | |
| Layer 4 | 2 | 0 | 10 | 23 | |
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | |
|---|---|---|---|---|
| Specificity | 0.9854 | 0.9615 | 0.9442 | 0.9834 |
| Neg Pred Value | 0.9713 | 0.9240 | 0.9713 | 0.9972 |
| Precision | 0.9732 | 0.9310 | 0.8325 | 0.6571 |
| Recall | 0.9478 | 0.8679 | 0.9086 | 0.9200 |
| F1 | 0.9603 | 0.8983 | 0.8689 | 0.7667 |
| Prevalence | 0.3583 | 0.3743 | 0.2340 | 0.0334 |
| Balanced Accuracy | 0.9666 | 0.9147 | 0.9264 | 0.9517 |
| Predicted | |||||
|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | ||
| Real | Layer 1 | 261 | 0 | 0 | 0 |
| Layer 2 | 3 | 257 | 1 | 0 | |
| Layer 3 | 0 | 7 | 183 | 1 | |
| Layer 4 | 0 | 0 | 7 | 28 | |
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | |
|---|---|---|---|---|
| Specificity | 1.0000 | 0.9917 | 0.9856 | 0.9903 |
| Neg Pred Value | 0.9938 | 0.9856 | 0.9856 | 0.9986 |
| Precision | 1.0000 | 0.9847 | 0.9581 | 0.8000 |
| Recall | 0.9886 | 0.9735 | 0.9581 | 0.9655 |
| F1 | 0.9943 | 0.9790 | 0.9581 | 0.8750 |
| Prevalence | 0.3529 | 0.3529 | 0.2553 | 0.0388 |
| Balanced Accuracy | 0.9943 | 0.9826 | 0.9719 | 0.9779 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozłowski, E.; Antosz, K.; Sęp, J.; Prucnal, S. Integrating Sensor Systems and Signal Processing for Sustainable Production: Analysis of Cutting Tool Condition. Electronics 2024, 13, 185. https://doi.org/10.3390/electronics13010185
Kozłowski E, Antosz K, Sęp J, Prucnal S. Integrating Sensor Systems and Signal Processing for Sustainable Production: Analysis of Cutting Tool Condition. Electronics. 2024; 13(1):185. https://doi.org/10.3390/electronics13010185
Chicago/Turabian StyleKozłowski, Edward, Katarzyna Antosz, Jarosław Sęp, and Sławomir Prucnal. 2024. "Integrating Sensor Systems and Signal Processing for Sustainable Production: Analysis of Cutting Tool Condition" Electronics 13, no. 1: 185. https://doi.org/10.3390/electronics13010185
APA StyleKozłowski, E., Antosz, K., Sęp, J., & Prucnal, S. (2024). Integrating Sensor Systems and Signal Processing for Sustainable Production: Analysis of Cutting Tool Condition. Electronics, 13(1), 185. https://doi.org/10.3390/electronics13010185








