Compact and Hybrid Dual-Band Bandpass Filter Using Folded Multimode Resonators and Second-Mode Suppression
Abstract
:1. Introduction
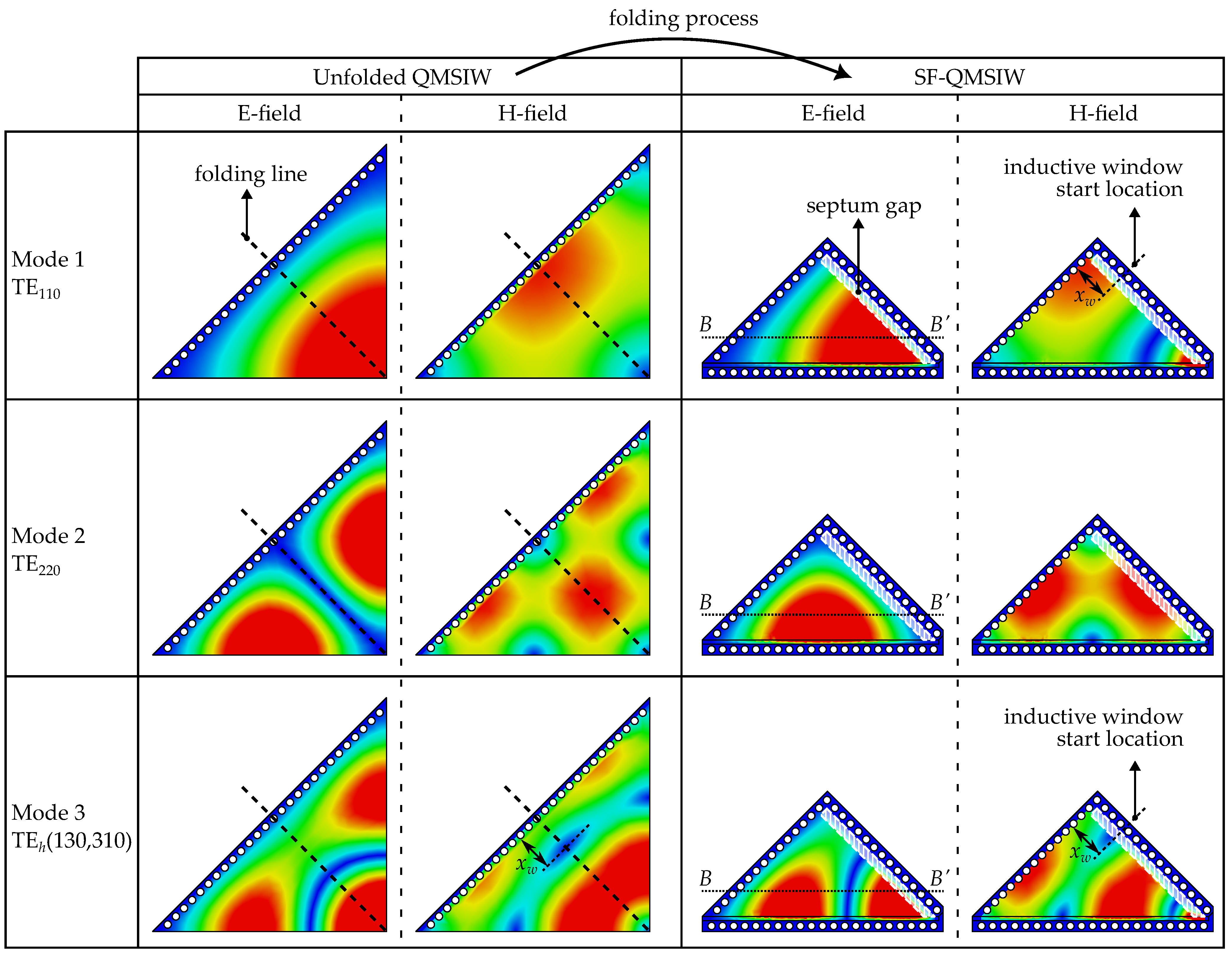
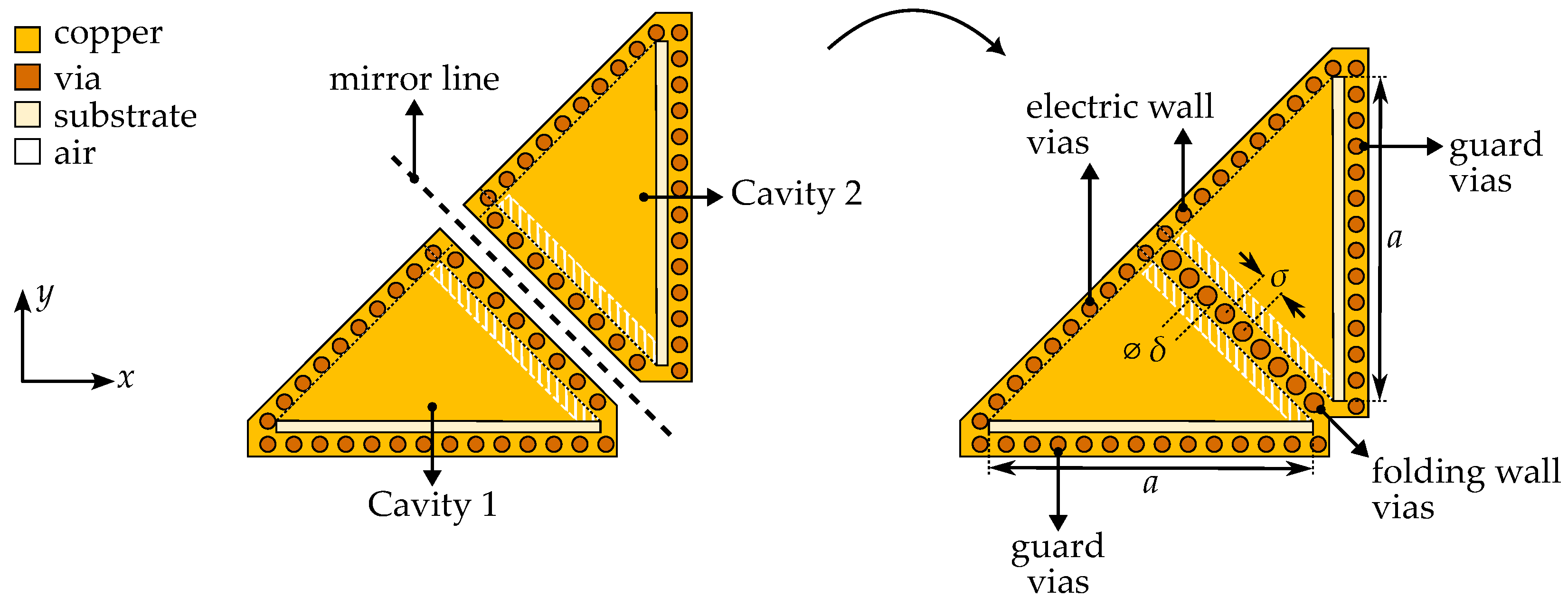
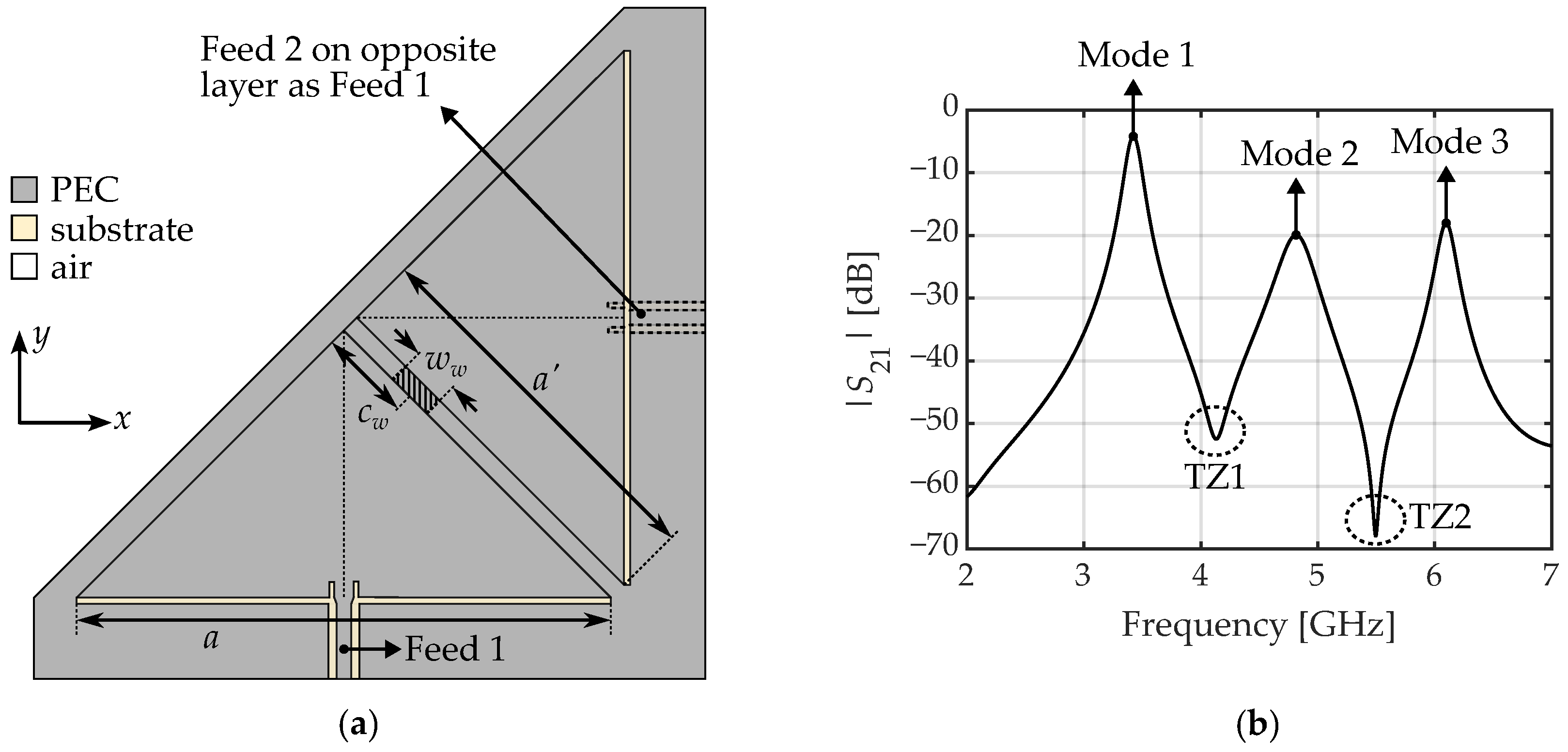
2. Shielded Folded QMSIW Cavity
3. Dual-Band Bandpass Filter
3.1. Design Requirements
3.2. Filter Topology and Implementation
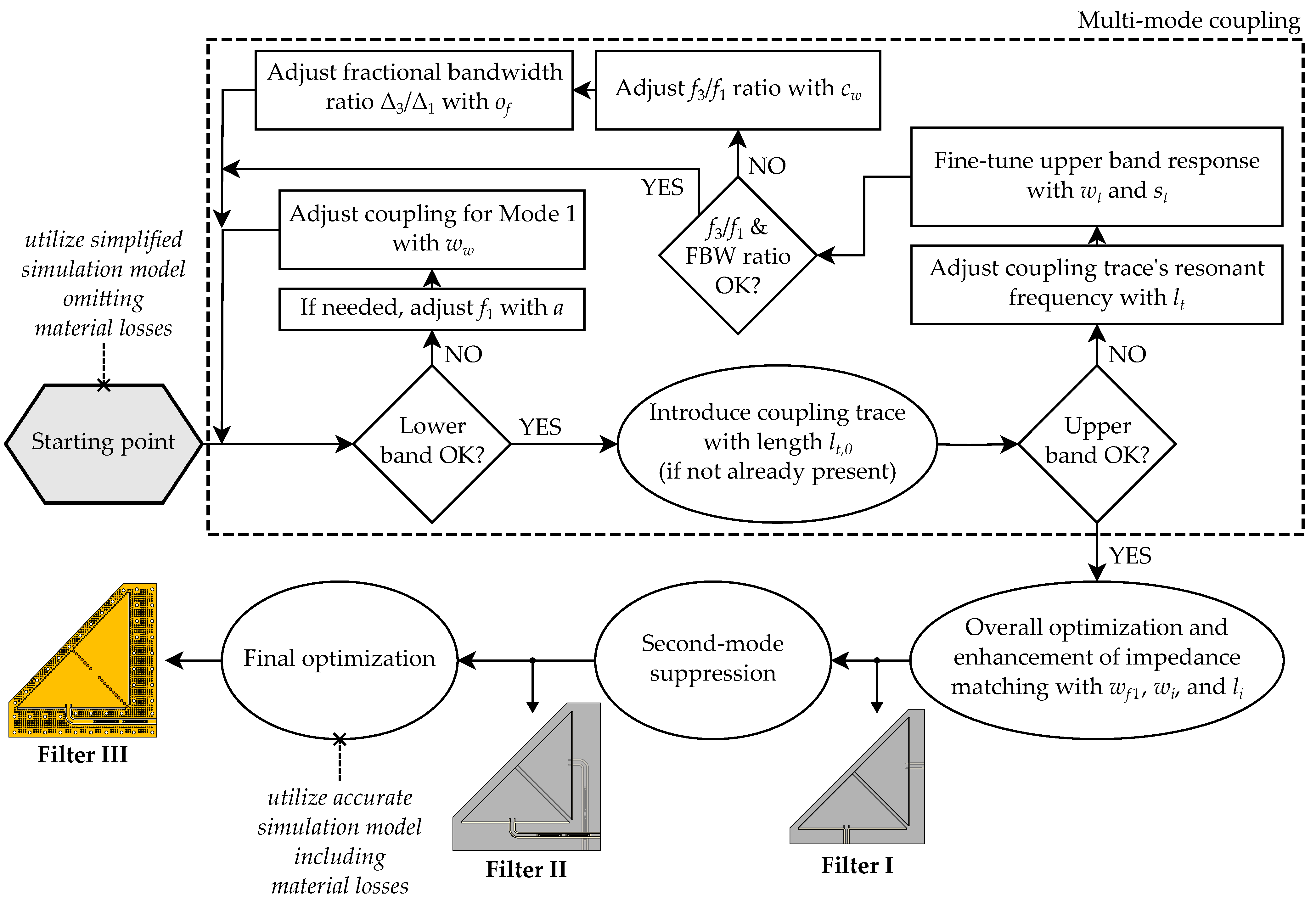
3.3. Design Methodology
3.3.1. Starting Point
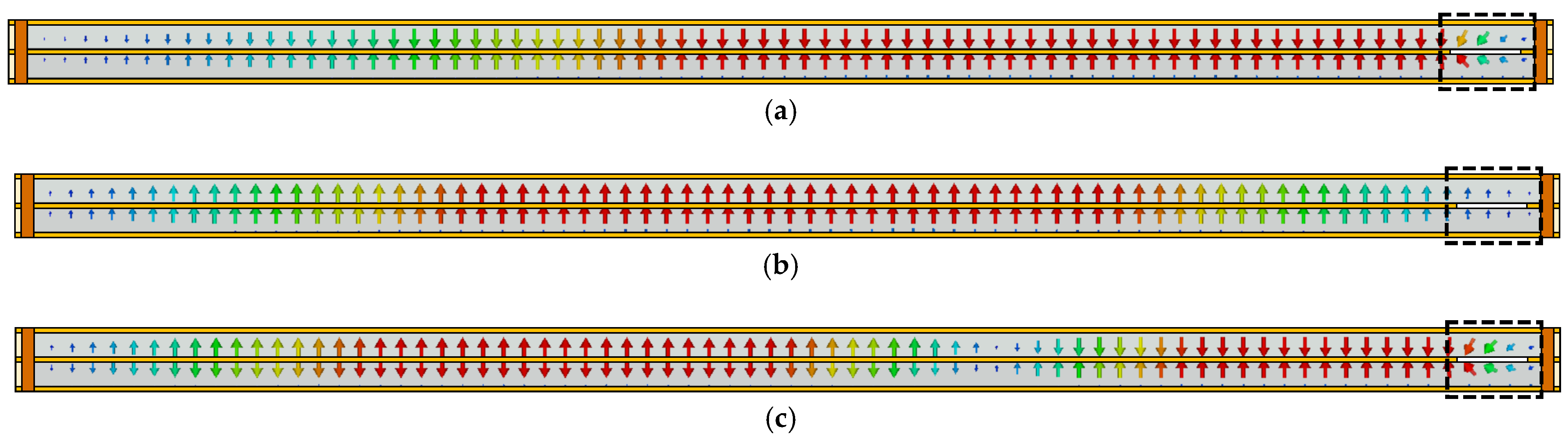
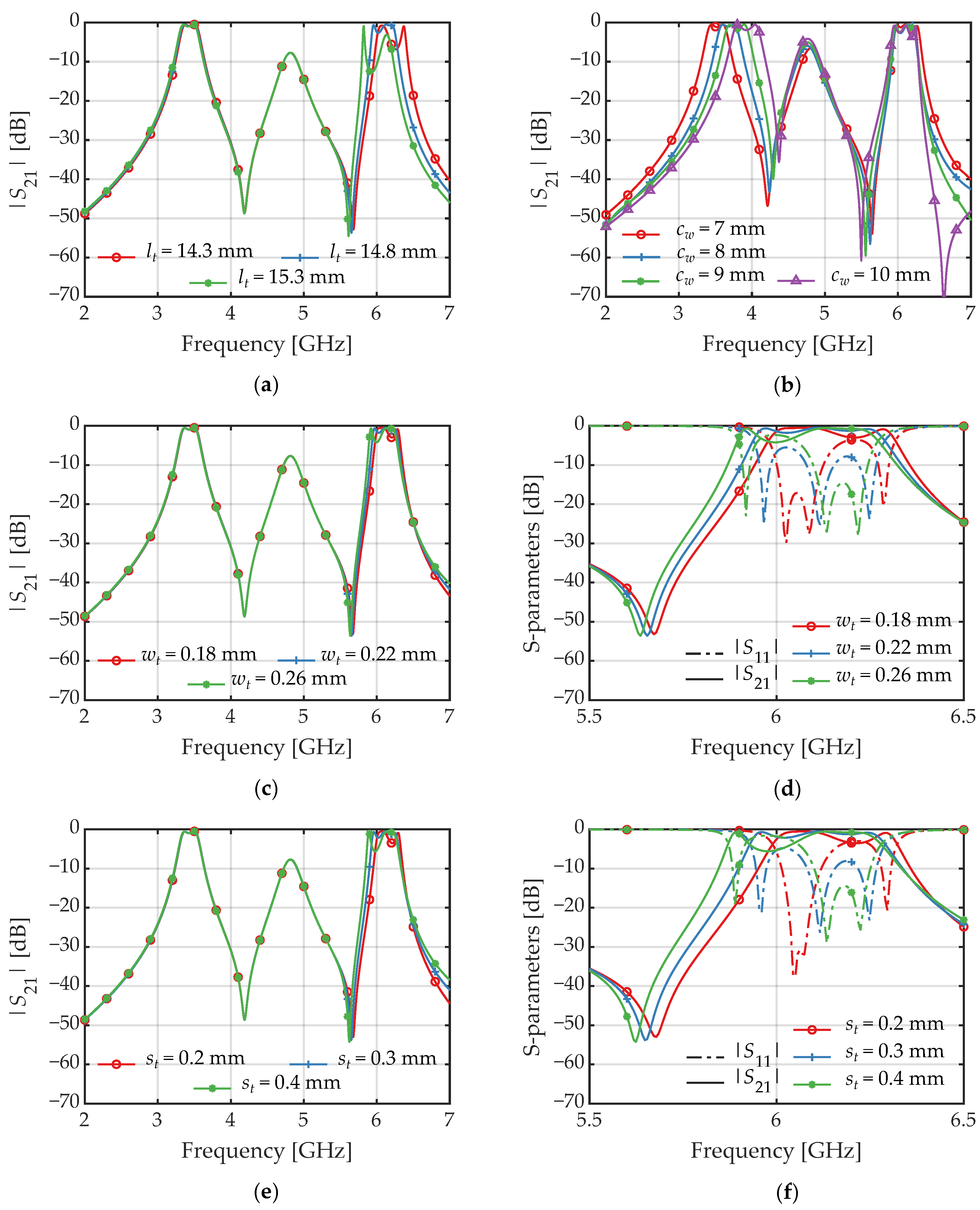
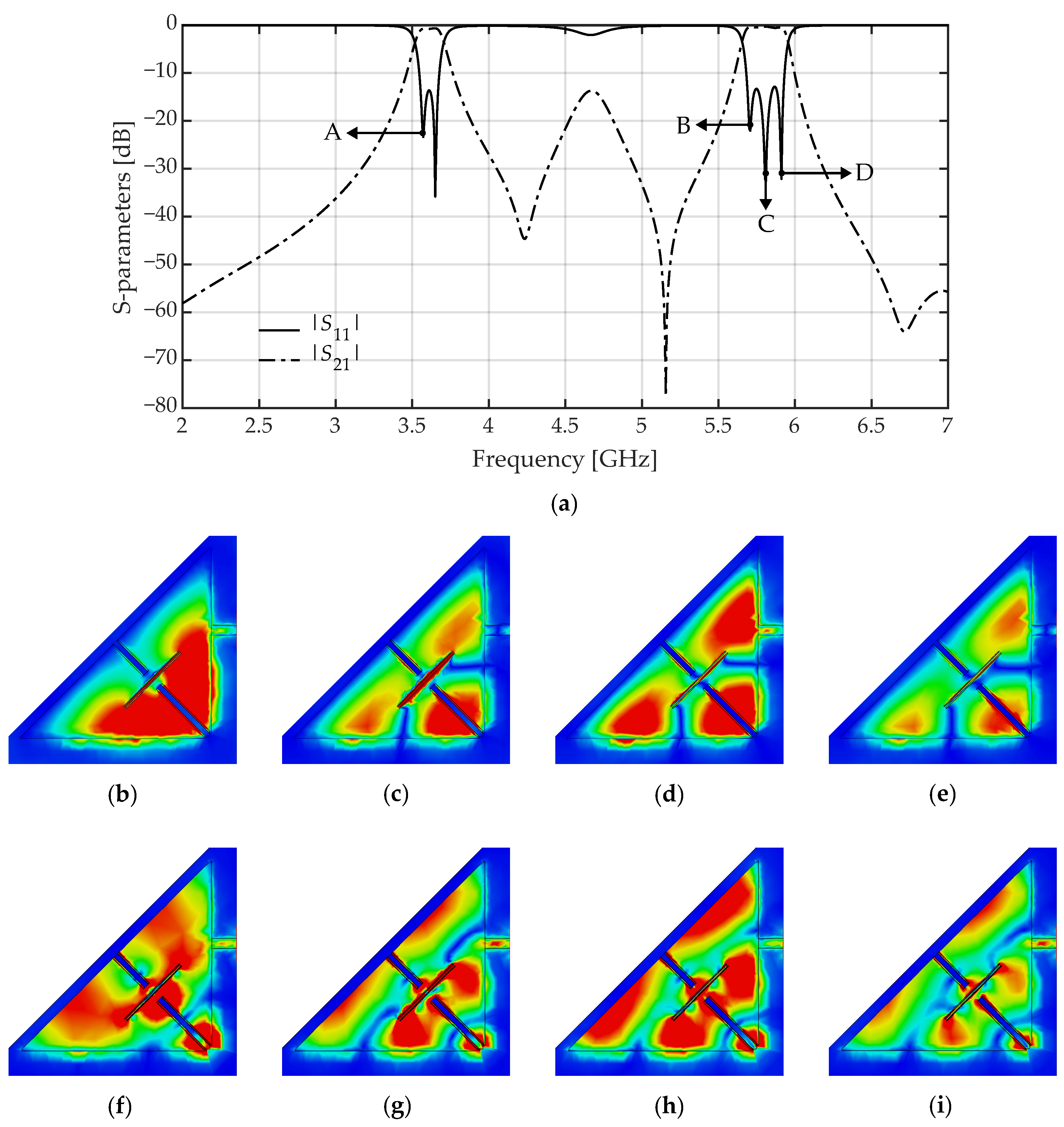
3.3.2. Multimode Coupling
3.3.3. Second-Mode Suppression
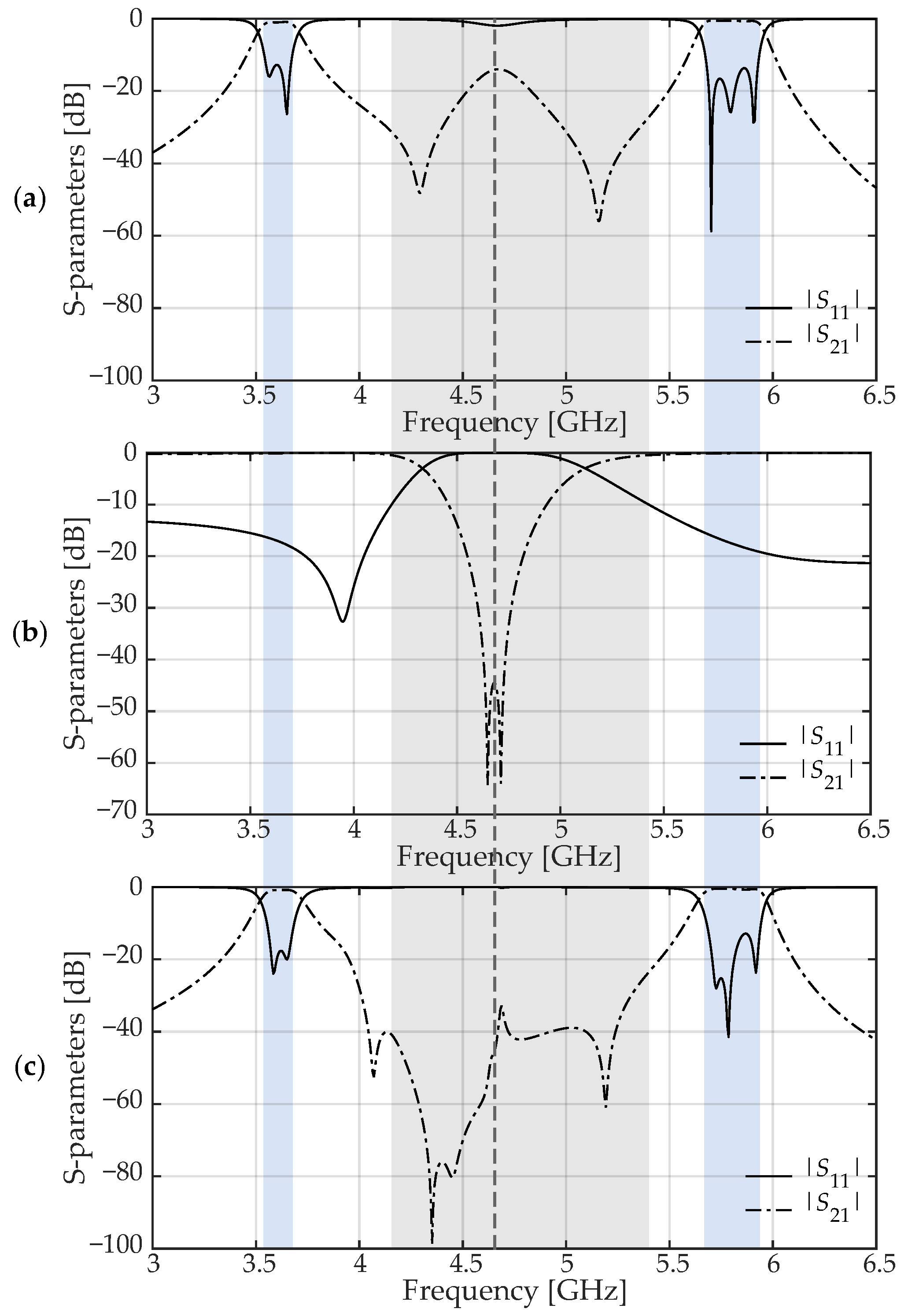
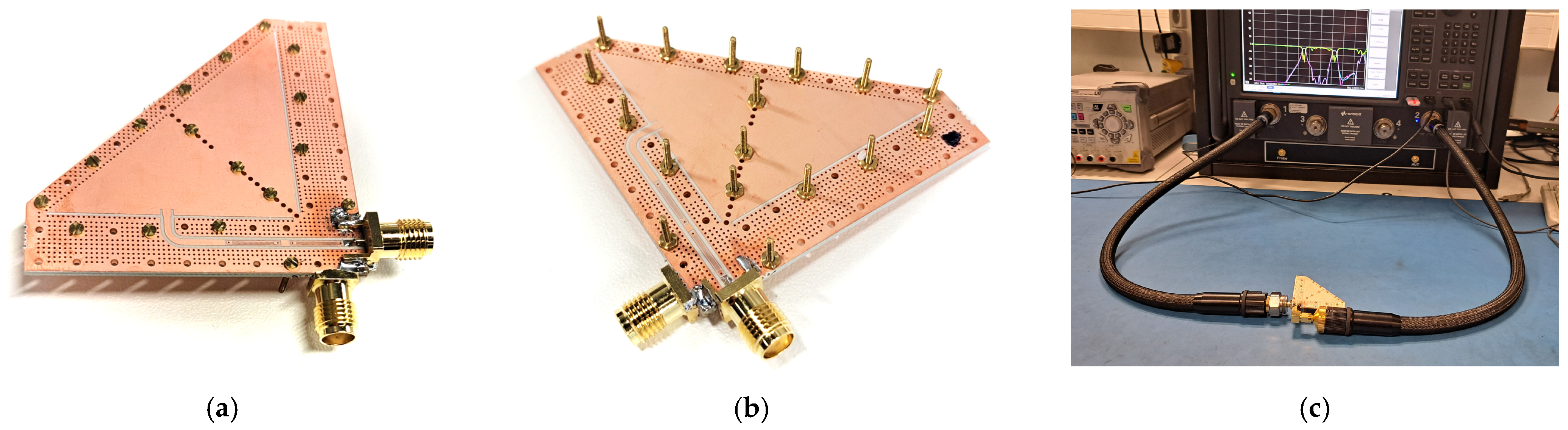
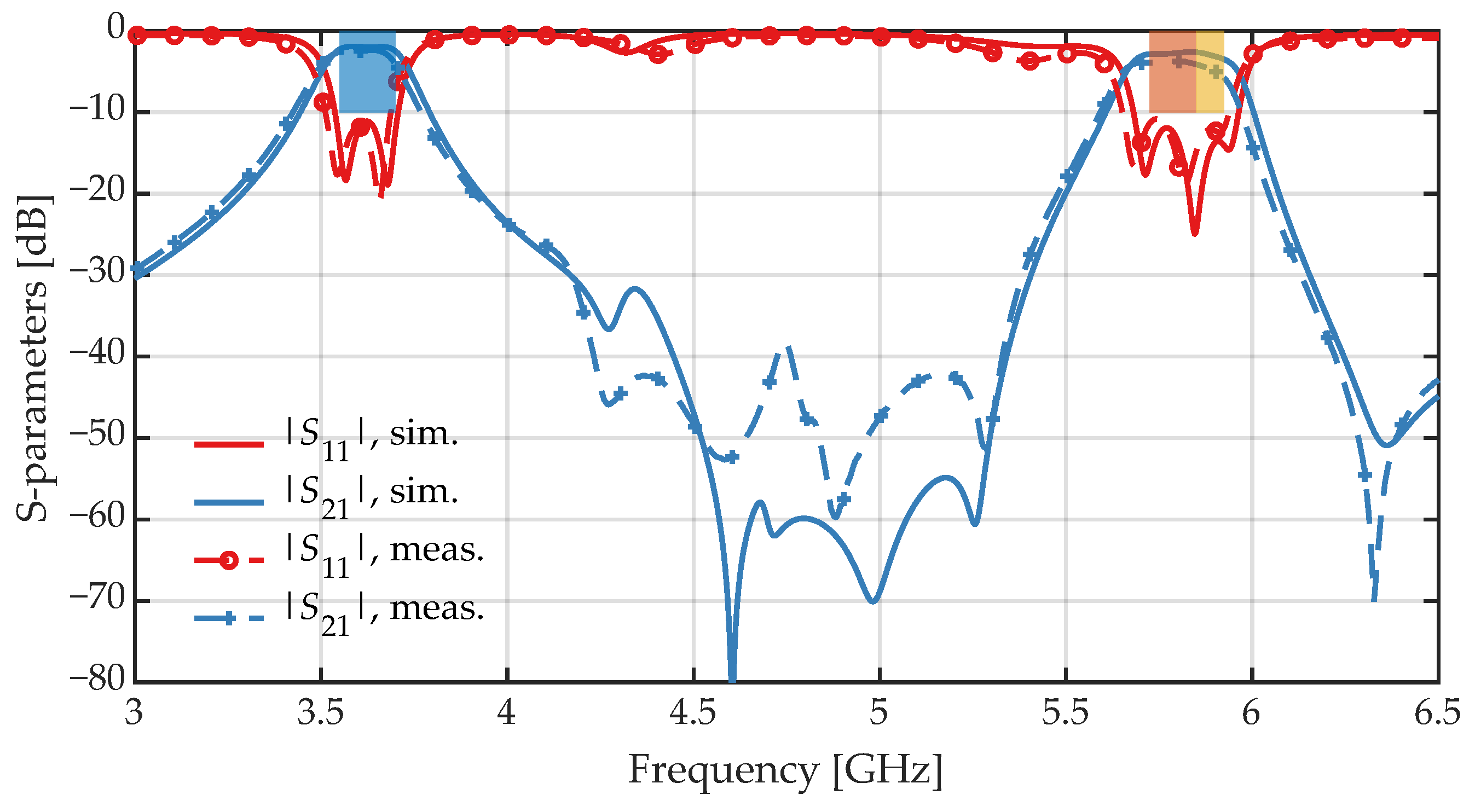
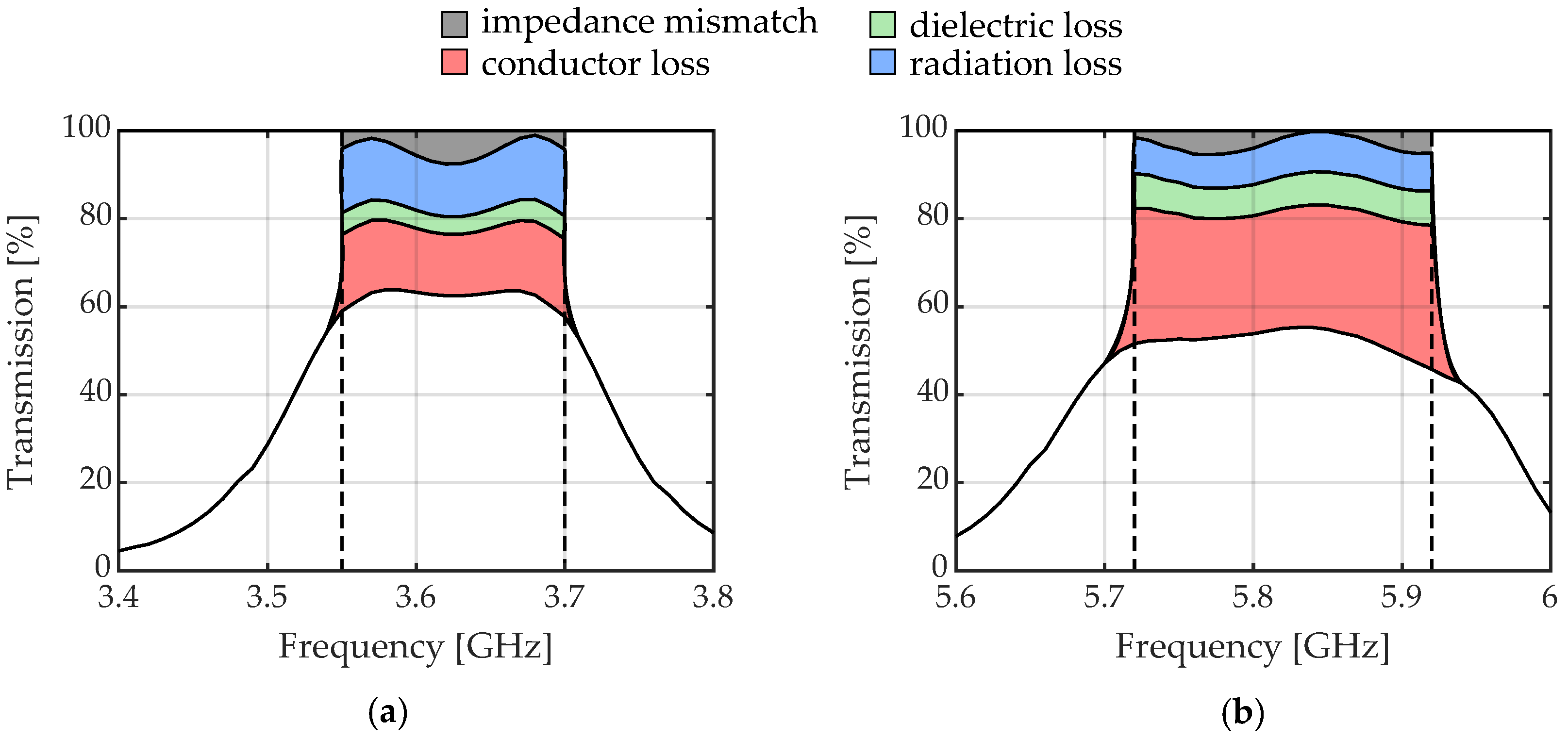
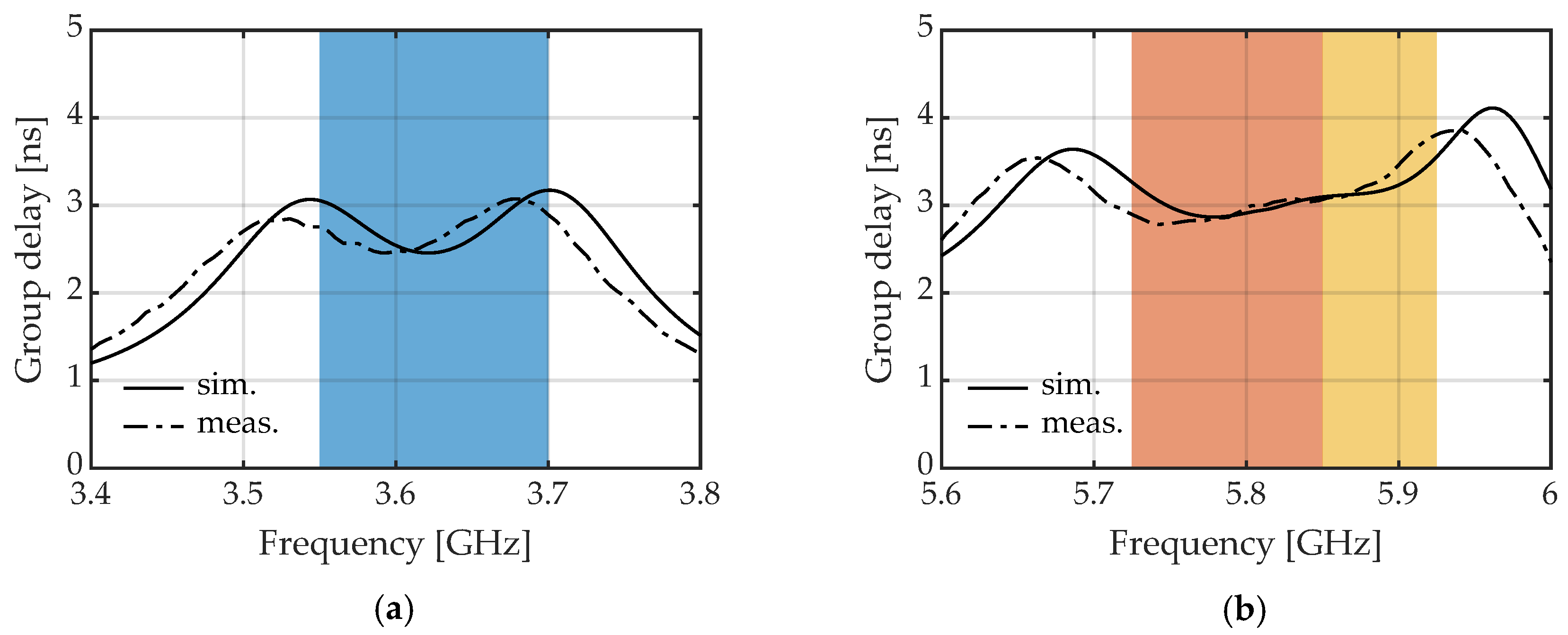
4. Experimental Results and Discussion
4.1. Optimized Dimensions and Fabrication Aspects
| Parameter | Value [mm] | Parameter | Value [mm] | Parameter | Value [mm] | Parameter | Value [mm] |
|---|---|---|---|---|---|---|---|
| a | 35.31 | 3.20 | 0.30 | 0.50 | |||
| d | 0.35 | 15.52 | 1.00 | 6.95 | |||
| s | 0.70 | 0.19 | 1.27 | 7.75 | |||
| 0.80 | 0.26 | * | 0.30 | ||||
| 1.30 | 9.00 | 1.00 | 1.20 | ||||
| 1.00 | 3.00 | 0.50 | 3.10 | ||||
| 1.20 | 3.00 | r | 2.00 | 0.10 | |||
| 10.30 | 0.31 | 0.80 | 6.05 | ||||
| 8.70 | 0.40 | 8.25 | 0.10 |
4.2. Measurement Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A Survey on Enabling Technologies, Protocols, and Applications. IEEE Commun. Surv. Tutorials 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Ejaz, W.; Anpalagan, A.; Imran, M.A.; Jo, M.; Naeem, M.; Qaisar, S.B.; Wang, W. Internet of Things (IoT) in 5G Wireless Communications. IEEE Access 2016, 4, 10310–10314. [Google Scholar] [CrossRef]
- Qadir, Z.; Le, K.N.; Saeed, N.; Munawar, H.S. Towards 6G Internet of Things: Recent Advances, Use Cases, and Open Challenges. ICT Express 2023, 9, 296–312. [Google Scholar] [CrossRef]
- Vaezi, M.; Azari, A.; Khosravirad, S.R.; Shirvanimoghaddam, M.; Azari, M.M.; Chasaki, D.; Popovski, P. Cellular, Wide-Area, and Non-Terrestrial IoT: A Survey on 5G Advances and the Road Toward 6G. IEEE Commun. Surv. Tutorials 2022, 24, 1117–1174. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Q.; Zhou, D.; Zhang, D. Single-and Triple-Band Bandpass Filters Using Novel Perturbed Isosceles Right-Angled Triangular SIW Cavities. IET Microwav. Antennas Propag. 2021, 15, 241–252. [Google Scholar] [CrossRef]
- Chu, P.; Hong, W.; Tuo, M.; Zheng, K.L.; Yang, W.W.; Xu, F.; Wu, K. Dual-Mode Substrate Integrated Waveguide Filter With Flexible Response. IEEE Trans. Microw. Theory Tech. 2016, 65, 824–830. [Google Scholar] [CrossRef]
- Basit, A.; Khattak, M.I.; Al-Hasan, M.; Nebhen, J.; Jan, A. Design and Analysis of a Compact GSM/GPS Dual-Band Bandpass Filter Using a T-Shaped Resonator. J. Electromagn. Eng. Sci. 2022, 22, 138–145. [Google Scholar] [CrossRef]
- Zhang, G.; Basit, A.; Khan, M.I.; Daraz, A.; Saqib, N.; Zubir, F. Multi Frequency Controllable In-Band Suppressions in a Broad Bandwidth Microstrip Filter Design for 5G Wi-Fi and Satellite Communication Systems Utilizing a Quad-Mode Stub-Loaded Resonator. Micromachines 2023, 14, 866. [Google Scholar] [CrossRef] [PubMed]
- Basit, A.; Daraz, A.; Khan, M.I.; Zubir, F.; AlQahtani, S.A.; Zhang, G. Design and Modelling of a Compact Triband Passband Filter for GPS, WiMAX, and Satellite Applications with Multiple Transmission Zero’s. Fractal Fract. 2023, 7, 511. [Google Scholar] [CrossRef]
- Nwajana, A.O.; Obi, E.R. A Review on SIW and Its Applications to Microwave Components. Electronics 2022, 11, 1160. [Google Scholar] [CrossRef]
- Li, P.; Chu, H.; Chen, R.S. Design of Compact Bandpass Filters Using Quarter-Mode and Eighth-Mode SIW Cavities. IEEE Trans. Components Packag. Manuf. Technol. 2017, 7, 956–963. [Google Scholar] [CrossRef]
- Azad, A.R.; Mohan, A. Single-and Dual-Band Bandpass Filters Using a Single Perturbed SIW Circular Cavity. IEEE Microw. Wirel. Components Lett. 2019, 29, 201–203. [Google Scholar] [CrossRef]
- Lai, Q.; Fumeaux, C.; Hong, W.; Vahldieck, R. Characterization of the Propagation Properties of the Half-Mode Substrate Integrated Waveguide. IEEE Trans. Microw. Theory Tech. 2009, 57, 1996–2004. [Google Scholar]
- Cheng, Y.; Hong, W.; Wu, K. Half Mode Substrate Integrated Waveguide (HMSIW) Directional Filter. IEEE Microw. Wirel. Components Lett. 2007, 17, 504–506. [Google Scholar] [CrossRef]
- Iqbal, A.; Tiang, J.J.; Lee, C.K.; Mallat, N.K.; Wong, S.W. Dual-Band Half Mode Substrate Integrated Waveguide Filter With Independently Tunable Bands. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 285–289. [Google Scholar] [CrossRef]
- Weng, M.H.; Tsai, C.Y.; Chen, D.L.; Chung, Y.C.; Yang, R.Y. A Bandpass Filter Using Half Mode SIW Structure With Step Impedance Resonator. Electronics 2020, 10, 51. [Google Scholar] [CrossRef]
- Iqbal, A.; Jiat Tiang, J.; Kin Wong, S.; Alibakhshikenari, M.; Falcone, F.; Limiti, E. Multimode HMSIW-Based Bandpass Filter With Improved Selectivity for Fifth-Generation (5G) RF Front-Ends. Sensors 2020, 20, 7320. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, A.; Zhang, P.; Zhang, Z. Triangular Cavity Multi-Passband HMSIW Filter Based on Odd-Even Mode Analysis. Electronics 2021, 10, 2927. [Google Scholar] [CrossRef]
- He, Z.; You, C.J.; Leng, S.; Li, X.; Huang, Y.M. Compact Bandpass Filter with High Selectivity Using Quarter-Mode Substrate Integrated Waveguide and Coplanar Waveguide. IEEE Microw. Wirel. Components Lett. 2017, 27, 809–811. [Google Scholar] [CrossRef]
- Eom, S.; Memon, M.U.; Lim, S. Frequency-Switchable Microfluidic CSRR-Loaded QMSIW Band-Pass Filter Using a Liquid Metal Alloy. Sensors 2017, 17, 699. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.W.; Jiang, Z.H.; Hao, Z.C.; Wu, Y.W.; Hong, W. Analysis of Eighth-Mode Substrate-Integrated Waveguide Cavity and Flexible Filter Design. IEEE Trans. Microw. Theory Tech. 2019, 67, 2701–2712. [Google Scholar] [CrossRef]
- Li, L.; Wu, Z.; Yang, K.; Lai, X.; Lei, Z. A Novel Miniature Single-Layer Eighth-Mode SIW Filter With Improved Out-of-Band Rejection. IEEE Microw. Wirel. Components Lett. 2018, 28, 407–409. [Google Scholar] [CrossRef]
- Weng, X.; Xu, K.D.; Fan, H. Wideband Bandpass Filters Based on Eighth-Mode Substrate Integrated Waveguide and Microstrip Resonators. In IEEE Transactions on Circuits and Systems II: Express Briefs; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Azad, A.R.; Mohan, A. A Compact Sixteenth-Mode Substrate Integrated Waveguide Bandpass Filter With Improved Out-of-Band Performance. Microw. Opt. Technol. Lett. 2017, 59, 1728–1733. [Google Scholar] [CrossRef]
- Azad, A.R.; Mohan, A. Sixteenth-Mode Substrate Integrated Waveguide Cavity Filters. Int. J. RF Microw. Comput.-Aided Eng. 2018, 28, e21603. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.W.; Tian, L.; Liu, P.; Hong, W.; Zhu, A. Design and Experiment of Filtering Power Divider Based on Shielded HMSIW/QMSIW Technology for 5G Wireless Applications. IEEE Access 2019, 7, 72411–72419. [Google Scholar] [CrossRef]
- Pradhan, N.C.; Subramanian, K.S.; Barik, R.K.; Cheng, Q.S. A Shielded-QMSIW-Based Self-Diplexing Antenna for Closely Spaced Bands and High Isolation. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 2382–2386. [Google Scholar] [CrossRef]
- Zheng, Z.; Tan, X.; Li, D.; Chen, Q. A Single-Layer Dual-Band Shielded HMSIW Bandpass Filter Using Single SIW Cavity. AEU-Int. J. Electron. Commun. 2022, 154, 154337. [Google Scholar] [CrossRef]
- Sieganschin, A.; Tegowski, B.; Jaschke, T.; Jacob, A.F. Compact Diplexers with Folded Circular SIW Cavity Filters. IEEE Trans. Microw. Theory Tech. 2020, 69, 111–118. [Google Scholar] [CrossRef]
- Che, W.; Geng, L.; Deng, K.; Chow, Y.L. Analysis and Experiments of Compact Folded Substrate-Integrated Waveguide. IEEE Trans. Microw. Theory Tech. 2008, 56, 88–93. [Google Scholar] [CrossRef]
- Huang, L.; Cha, H.; Zhang, S. Compact Wideband-Folded Ridge Substrate-Integrated Waveguide Filter. IEEE Microw. Wirel. Components Lett. 2020, 30, 241–244. [Google Scholar] [CrossRef]
- Jones, T.R.; Daneshmand, M. Miniaturized Folded Ridged Half-Mode and Quarter-Mode Substrate Integrated Waveguides for Filter Design. IEEE Trans. Microw. Theory Tech. 2019, 67, 3414–3426. [Google Scholar] [CrossRef]
- Jones, T.R.; Daneshmand, M. Miniaturized Folded Ridged Quarter-Mode Substrate Integrated Waveguide RF MEMS Tunable Bandpass Filter. IEEE Access 2020, 8, 115837–115847. [Google Scholar] [CrossRef]
- Dhwaj, K.; Li, X.; Shen, Z.; Qin, S. Cavity Resonators Do the Trick: A Packaged Substrate Integrated Waveguide, Dual-Band Filter. IEEE Microw. Mag. 2015, 17, 58–64. [Google Scholar] [CrossRef]
- Lee, B.; Koh, B.; Nam, S.; Lee, T.H.; Lee, J. Band-Switchable Substrate-Integrated Waveguide Resonator and Filter. IEEE Trans. Microw. Theory Tech. 2017, 66, 147–156. [Google Scholar] [CrossRef]
- Chen, X.P.; Wu, K.; Li, Z.L. Dual-Band and Triple-Band Substrate Integrated Waveguide Filters with Chebyshev and Quasi-Elliptic Responses. IEEE Trans. Microw. Theory Tech. 2007, 55, 2569–2578. [Google Scholar] [CrossRef]
- Esmaeili, M.; Bornemann, J. Substrate Integrated Waveguide Triple-Passband Dual-Stopband Filter Using Six Cascaded Singlets. IEEE Microw. Wirel. Components Lett. 2014, 24, 439–441. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C.X.; Xie, H.W.; Wu, W. Synthesis Design of SIW Multiband Bandpass Filters Based on Dual-Mode Resonances and Split-Type Dual-and Triple-Band Responses. IEEE Trans. Microw. Theory Tech. 2018, 67, 151–161. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, D.; Lv, D.; Zhang, D.; Zhang, J.; Zhang, Y. Multi-Layered Dual-Mode Substrate Integrated Waveguide Bandpass Filter With Input and Output Ports Located on Same Substrate Layer. IET Microwav. Antennas Propag. 2019, 13, 2641–2648. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C.X.; Wu, W. Substrate-Integrated Waveguide Dual-Mode Dual-Band Bandpass Filters With Widely Controllable Bandwidth Ratios. IEEE Trans. Microw. Theory Tech. 2017, 65, 3801–3812. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C.X.; Wu, W. Resonance Characteristics of Substrate-Integrated Rectangular Cavity and Their Applications to Dual-Band and Wide-Stopband Bandpass Filters Design. IEEE Trans. Microw. Theory Tech. 2017, 65, 1511–1524. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C.X.; Wu, W. Dual-Mode Characteristics of Half-Mode SIW Rectangular Cavity and Applications to Dual-Band Filters With Widely Separated Passbands. IEEE Trans. Microw. Theory Tech. 2018, 66, 4820–4829. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, C.X.; Wu, W. Substrate-Integrated Waveguide Dual-Band Filters with Closely Spaced Passbands and Flexibly Allocated Bandwidths. IEEE Trans. Components, Packag. Manuf. Technol. 2018, 8, 465–472. [Google Scholar] [CrossRef]
- Xie, H.W.; Zhou, K.; Zhou, C.X.; Wu, W. Substrate-Integrated Waveguide Triple-Band Bandpass Filters Using Triple-Mode Cavities. IEEE Trans. Microw. Theory Tech. 2018, 66, 2967–2977. [Google Scholar] [CrossRef]
- Xie, H.W.; Zhou, K.; Zhou, C.X.; Wu, W. Compact SIW Diplexers and Dual-Band Bandpass Filter With Wide-Stopband Performances. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2933–2937. [Google Scholar] [CrossRef]
- Han, Y.K.; Deng, H.W.; Zhu, J.M.; Xing, S.b.; Han, W. Compact Dual-Band Dual-Mode SIW Balanced BPF With Intrinsic Common-Mode Suppression. IEEE Microw. Wirel. Components Lett. 2021, 31, 101–104. [Google Scholar] [CrossRef]
- Yang, X.L.; Zhu, X.W.; Wang, X. Dual-Band Substrate Integrated Waveguide Filters Based on Multi-Mode Resonator Overlapping Mode Control. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Li, D.; Luo, W.; Chen, X.; Liu, Y.; Xu, K.D.; Chen, Q. Miniaturized Dual-/Tri-/Quad-Band Bandpass Filters Using Perturbed Multi-Mode SIW Cavity. IEEE Trans. Components Packag. Manuf. Technol. 2023, 13, 1685–1693. [Google Scholar] [CrossRef]
- Azad, A.R.; Mohan, A. Substrate Integrated Waveguide Dual-Band and Wide-Stopband Bandpass Filters. IEEE Microw. Wirel. Components Lett. 2018, 28, 660–662. [Google Scholar] [CrossRef]
- Zhang, H.; Kang, W.; Wu, W. Dual-Band Substrate Integrated Waveguide Bandpass Filter Utilising Complementary Split-Ring Resonators. Electron. Lett. 2018, 54, 85–87. [Google Scholar] [CrossRef]
- Liu, B.G.; Lyu, Y.P.; Zhu, L.; Cheng, C.H. Compact Single- and Dual-Band Filters on Hexa-Modes Half-Mode Substrate Integrated Waveguide Resonator With Loaded H-Shaped Slot. IEEE Microw. Wirel. Components Lett. 2020, 30, 1129–1132. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Y. Dual-Band, Dual-Mode, Microstrip Resonator Loaded, Compact Hybrid SIW Bandpass Filter. In Proceedings of the 2021 IEEE MTT-S International Microwave Symposium (IMS), Atlanta, GA, USA, 7–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 50–53. [Google Scholar]
- Zhu, Y.; Dong, Y. A Compact Dual-Band Quasi-Elliptic Filter Based on Hybrid SIW and Microstrip Technologies. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 719–723. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Z.; Dong, Y. Compact, Dual-Band, and Hybrid Filter Based on Combline and Substrate Integrated Waveguide Resonators. Int. J. RF Microw. Comput.-Aided Eng. 2022, 32, e22919. [Google Scholar] [CrossRef]
- Pradhan, N.C.; Koziel, S.; Barik, R.K.; Pietrenko-Dabrowska, A.; Karthikeyan, S.S. Miniaturized Dual-Band SIW-Based Bandpass Filters Using Open-Loop Ring Resonators. Electronics 2023, 12, 3974. [Google Scholar] [CrossRef]
- Farzami, F.; Khaledian, S.; Stutts, A.C.; Smida, B.; Erricolo, D. Embedded Split Ring Resonator Tunable Notch Band Filter in Microstrip Transmission Lines. IEEE Access 2022, 10, 37294–37304. [Google Scholar] [CrossRef]
- Bozzi, M.; Georgiadis, A.; Wu, K. Review of Substrate-Integrated Waveguide Circuits and Antennas. IET Microw. Antennas Propag. 2011, 5, 909–920. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Xu, F.; Wu, K. Guided-Wave and Leakage Characteristics of Substrate Integrated Waveguide. IEEE Trans. Microw. Theory Tech. 2005, 53, 66–73. [Google Scholar]
- Agneessens, S.; Rogier, H. Compact Half Diamond Dual-Band Textile HMSIW On-Body Antenna. IEEE Trans. Antennas Propag. 2014, 62, 2374–2381. [Google Scholar] [CrossRef]
- Agneessens, S. Coupled Eighth-Mode Substrate Integrated Waveguide Antenna: Small and Wideband With High-Body Antenna Isolation. IEEE Access 2017, 6, 1595–1602. [Google Scholar] [CrossRef]
- Han, W.; Yang, F.; Ouyang, J.; Yang, P. Low-Cost Wideband and High-Gain Slotted Cavity Antenna Using High-Order Modes for Millimeter-Wave Application. IEEE Trans. Antennas Propag. 2015, 63, 4624–4631. [Google Scholar] [CrossRef]
- Claus, N.; Verhaevert, J.; Rogier, H. High-Performance Air-Filled Multiband Antenna for Seamless Integration Into Smart Surfaces. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 2260–2264. [Google Scholar] [CrossRef]
- Ko, S.W.; Chae, H.; Han, K.; Lee, S.; Seo, D.W.; Huang, K. V2X-Based Vehicular Positioning: Opportunities, Challenges, and Future Directions. IEEE Wirel. Commun. 2021, 28, 144–151. [Google Scholar] [CrossRef]
- Noor-A-Rahim, M.; Liu, Z.; Lee, H.; Khyam, M.O.; He, J.; Pesch, D.; Moessner, K.; Saad, W.; Poor, H.V. 6G for Vehicle-to-Everything (V2X) Communications: Enabling Technologies, Challenges, and Opportunities. Proc. IEEE 2022, 110, 712–734. [Google Scholar] [CrossRef]
- Yang, X.L.; Zhu, X.W.; Wang, X. Dual-Band Substrate Integrated Waveguide Filters With Perturbed Circular Cavity. IEEE Microw. Wirel. Components Lett. 2021, 32, 293–296. [Google Scholar] [CrossRef]
- Rezaee, M.; Attari, A.R. Realisation of New Single-Layer Triple-Mode Substrate-Integrated Waveguide and Dual-Mode Half-Mode Substrate-Integrated Waveguide Filters Using a Circular Shape Perturbation. IET Microw. Antennas Propag. 2013, 7, 1120–1127. [Google Scholar] [CrossRef]
- Hong, J.S.G. Microstrip Filters for RF/Microwave Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004; Chapter 8. [Google Scholar]
- Hu, S.; Hu, Y.; Zheng, H.; Zhu, W.; Gao, Y.; Zhang, X. A Compact 3.3–3.5 GHz Filter Based on Modified Composite Right-/Left-Handed Resonator Units. Electronics 2019, 9, 1. [Google Scholar] [CrossRef]





| Ref. | Structure | No. of Cav. | No. of TZs | / [GHz] | * | Order I/II | FBW † I/II [%] | IL I/II [dB] | Rejection [dB]/‡ | Size [] § |
|---|---|---|---|---|---|---|---|---|---|---|
| [7] | Microstrip technology | - | 4 | 0.85/1.57 | 1.85 | 1/1 | 16.8/3.5 | 0.98/1.11 | >44/1.29–1.45 | 0.01 |
| [40] | Two-layer stacked PCB SIW + GCPW coupling line | 4 | 5 | 12.0/17.0 | 1.42 | 4/4 | 6.9/3.3 | 1.16/2.32 | >25/1.08–1.34 | 1.16 |
| [41] | Single-layer PCB SIW + microstrip coupling lines | 6 | 5 | 12.0/17.0 | 1.42 | 4/4 | 5.1/2.7 | 1.39/2.47 | >30/1.05–1.38 | 2.89 |
| [42] | Single-layer PCB HMSIW/QMSIW + IDC structure | 6 | 4 | 5.0/8.5 | 1.70 | 4/4 | 6.3/7.8 | 2.02/1.82 | >24/1.12–1.52 | 1.10 |
| [43] | Single-layer PCB SIW + GCPW coupling line | 6 | 4 | 20.0/21.5 | 1.08 | 4/4 | 2.4/2.5 | 2.84/2.03 | >18/1.03–1.06 | 5.66 |
| [48] | Single-layer PCB SIW + slotline perturbations | 1 | 2 | 8.3/10.9 | 1.31 | 2/2 | 2.4/4.7 | 1.90/1.71 | >30/1.04–1.18 | 1.06 |
| [49] | Single-layer PCB SIW + CPW coupling line | 2 | 1 | 10.1/13.7 | 1.36 | 2/2 | 2.9/4.8 # | 1.80/1.40 | >25/1.06–1.16 | 1.13 |
| [50] | Single-layer PCB SIW + CSRRs | 1 | 4 | 7.9/8.9 | 1.13 | 2/2 | 3.4/3.9 | 1.50/1.90 | >19/1.03–1.08 | 1.39 |
| [51] | Single-layer PCB HMSIW + H-slot resonator | 1 | 2 | 7.8/11.7 | 1.50 | 3/3 | 14.3/10.7 | 1.44/2.41 | >20/1.15–1.24 | 0.47 |
| [53] | Single-layer PCB SIW + microstrip resonators | 2 | 4 | 8.1/10.0 | 1.24 | 4/4 | 9.1/6.2 | 1.74/2.21 | >48/1.09–1.14 | 1.40 |
| [54] | Single-layer PCB SIW + combline resonators | 2 | 3 | 9.4/13.2 | 1.41 | 2/3 | 16.5/9.9 | 0.57/1.67 | >29/1.14–1.24 | 0.56 |
| This work | Two-layer stacked PCB Folded QMSIW + CPW coupling line | 2 | 5 | 3.6/5.8 | 1.61 | 2/3 | 6.4/5.3 | 2.37/3.74 | >38/1.17–1.48 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Claus, N.; Kapusuz, K.Y.; Verhaevert, J.; Rogier, H. Compact and Hybrid Dual-Band Bandpass Filter Using Folded Multimode Resonators and Second-Mode Suppression. Electronics 2024, 13, 1921. https://doi.org/10.3390/electronics13101921
Claus N, Kapusuz KY, Verhaevert J, Rogier H. Compact and Hybrid Dual-Band Bandpass Filter Using Folded Multimode Resonators and Second-Mode Suppression. Electronics. 2024; 13(10):1921. https://doi.org/10.3390/electronics13101921
Chicago/Turabian StyleClaus, Nicolas, Kamil Yavuz Kapusuz, Jo Verhaevert, and Hendrik Rogier. 2024. "Compact and Hybrid Dual-Band Bandpass Filter Using Folded Multimode Resonators and Second-Mode Suppression" Electronics 13, no. 10: 1921. https://doi.org/10.3390/electronics13101921
APA StyleClaus, N., Kapusuz, K. Y., Verhaevert, J., & Rogier, H. (2024). Compact and Hybrid Dual-Band Bandpass Filter Using Folded Multimode Resonators and Second-Mode Suppression. Electronics, 13(10), 1921. https://doi.org/10.3390/electronics13101921







