Using the Buckingham π Theorem for Multi-System Transfer Learning: A Case-Study with 3 Vehicles Sharing a Database
Abstract
1. Introduction
2. Background
3. Case-Study: Predicting the Braking Behaviour of Cars
4. Learning with Simulated Data
4.1. Simulator Presentation
4.2. Learning Model Types for the Simulation
4.2.1. Traditional Dimensionalized Learning Model
4.2.2. Buckingham Theorem-Based Model
4.2.3. Augmented Buckingham Theorem-Based Model
4.3. Results
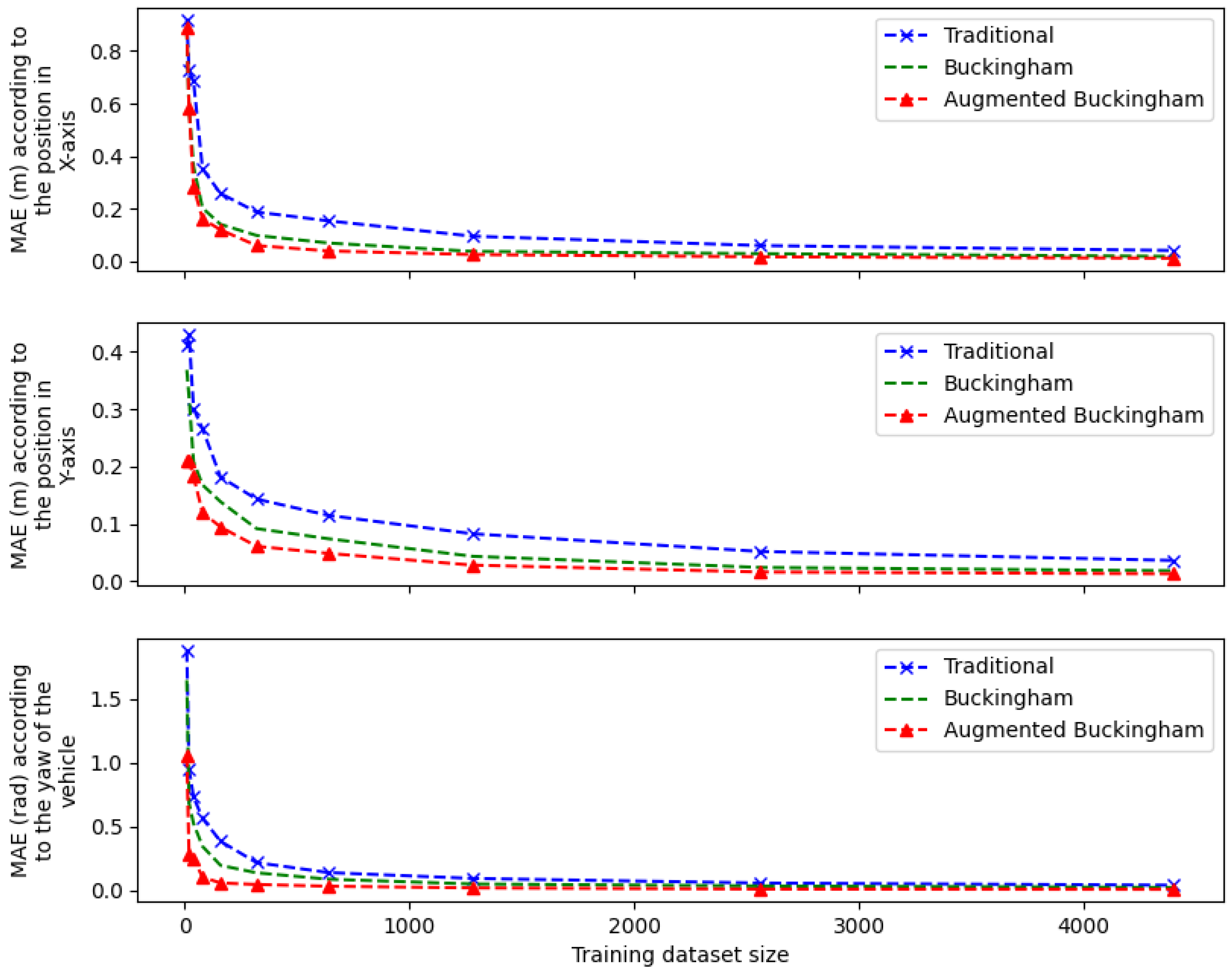
4.3.1. Mean Absolute Error
4.3.2. Learning Rate
4.3.3. Comparative Analysis
4.3.4. Discussion
5. Learning with Experimental Data
5.1. Methodology for Generating the Data
5.2. Model for the Dynamic Maneuvers
5.2.1. Traditional Baseline Model
5.2.2. Buckingham Theorem-Based Model
5.2.3. Augmented Buckingham Theorem-Based Model for Experimental Data
5.3. Results
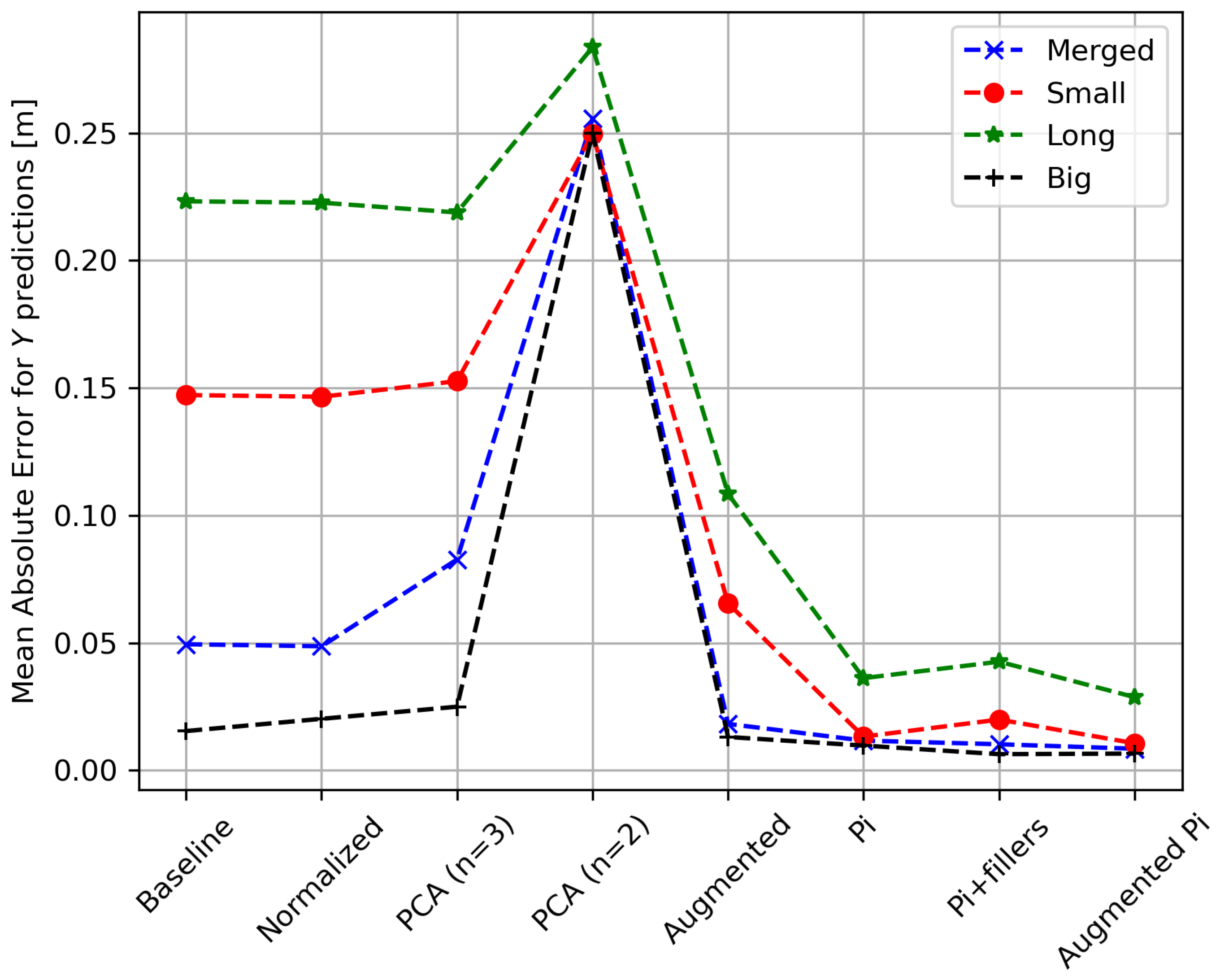
5.3.1. Mean Absolute Error
5.3.2. Learning Rate
5.3.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAS | Mean Absolute Error |
| PCA | Principal Component Analysis |
References
- Amer, N.H.; Zamzuri, H.; Hudha, K.; Kadir, Z.A. Modelling and Control Strategies in Path Tracking Control for Autonomous Ground Vehicles: A Review of State of the Art and Challenges. J. Intell. Robot. Syst. 2017, 86, 225–254. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Katrakazas, C.; Quddus, M.; Chen, W.H.; Deka, L. Real-time motion planning methods for autonomous on-road driving: State-of-the-art and future research directions. Transp. Res. Part C Emerg. Technol. 2015, 60, 416–442. [Google Scholar] [CrossRef]
- Aradi, S. Survey of Deep Reinforcement Learning for Motion Planning of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 23, 740–759. [Google Scholar] [CrossRef]
- Crites, R.H.; Barto, A.G. Improving Elevator Performance Using Reinforcement Learning. Adv. Neural Inf. Process. Syst. 1995, 8, 1017–1023. [Google Scholar]
- Di, X.; Shi, R. A survey on autonomous vehicle control in the era of mixed-autonomy: From physics-based to AI-guided driving policy learning. Transp. Res. Part C Emerg. Technol. 2021, 125, 103008. [Google Scholar] [CrossRef]
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building Machines That Learn and Think Like People; Cambridge University Press: Cambridge, UK, 2017; Volume 40. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, H.; Liu, D.; Wang, L. A digital twin-based sim-to-real transfer for deep reinforcement learning-enabled industrial robot grasping. Robot. Comput.-Integr. Manuf. 2022, 78, 102365. [Google Scholar] [CrossRef]
- Dey, S.; Boughorbel, S.; Schilling, A.F. Learning a Shared Model for Motorized Prosthetic Joints to Predict Ankle-Joint Motion. arXiv 2021, arXiv:2111.07419. [Google Scholar]
- Andrychowicz, O.M.; Baker, B.; Chociej, M.; Józefowicz, R.; McGrew, B.; Pachocki, J.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning dexterous in-hand manipulation. Int. J. Robot. Res. 2020, 39, 3–20. [Google Scholar] [CrossRef]
- Nagabandi, A.; Clavera, I.; Liu, S.; Fearing, R.S.; Abbeel, P.; Levine, S.; Finn, C. Learning to Adapt in Dynamic, Real-World Environments Through Meta-Reinforcement Learning. arXiv 2019, arXiv:1803.11347. [Google Scholar]
- Dasari, S.; Ebert, F.; Tian, S.; Nair, S.; Bucher, B.; Schmeckpeper, K.; Singh, S.; Levine, S.; Finn, C. RoboNet: Large-Scale Multi-Robot Learning. arXiv 2020, arXiv:1910.11215. [Google Scholar]
- Sorocky, M.J.; Zhou, S.; Schoellig, A.P. Experience Selection Using Dynamics Similarity for Efficient Multi-Source Transfer Learning Between Robots. arXiv 2020, arXiv:2003.13150. [Google Scholar]
- Chen, T.; Murali, A.; Gupta, A. Hardware Conditioned Policies for Multi-Robot Transfer Learning. Adv. Neural Inf. Process. Syst. 2018, 31, 9355–9366. [Google Scholar]
- Bertrand, J. Sur l’homogénéité dans les formules de physique. Cah. Rech. l’Acad. Sci. 1878, 86, 916–920. [Google Scholar]
- Rayleigh, L. VIII. On the question of the stability of the flow of fluids. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1892, 34, 59–70. [Google Scholar] [CrossRef]
- Buckingham, M.E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Fukami, K.; Taira, K. Robust machine learning of turbulence through generalized Buckingham Pi-inspired pre-processing of training data. In Proceedings of the APS Division of Fluid Dynamics Meeting Abstracts, Phoenix, AZ, USA, 21–23 November 2021; p. A31.004. [Google Scholar]
- Fukami, K.; Goto, S.; Taira, K. Data-driven nonlinear turbulent flow scaling with Buckingham Pi variables. J. Fluid Mech. 2024, 984, R4. [Google Scholar] [CrossRef]
- Bakarji, J.; Callaham, J.; Brunton, S.L.; Kutz, J.N. Dimensionally consistent learning with Buckingham Pi. Nat. Comput. Sci. 2022, 2, 834–844. [Google Scholar] [CrossRef]
- Xie, X.; Samaei, A.; Guo, J.; Liu, W.K.; Gan, Z. Data-driven discovery of dimensionless numbers and governing laws from scarce measurements. Nat. Commun. 2022, 13, 7562. [Google Scholar] [CrossRef] [PubMed]
- Oppenheimer, M.W.; Doman, D.B.; Merrick, J.D. Multi-scale physics-informed machine learning using the Buckingham Pi theorem. J. Comput. Phys. 2023, 474, 111810. [Google Scholar] [CrossRef]
- Villar, S.; Yao, W.; Hogg, D.W.; Blum-Smith, B.; Dumitrascu, B. Dimensionless machine learning: Imposing exact units equivariance. arXiv 2022, arXiv:2204.00887. [Google Scholar]
- Zhang, L.; Xu, Z.; Wang, S.; He, G. Clustering dimensionless learning for multiple-physical-regime systems. Comput. Methods Appl. Mech. Eng. 2024, 420, 116728. [Google Scholar] [CrossRef]
- Singh, A.S.P.; Osamu, N. Nondimensionalized indices for collision avoidance based on optimal control theory. In Proceedings of the 36th FISITA World Automotive Congress, Busan, Republic of Korea, 26–30 September 2016. [Google Scholar]
- Luo, X.; Xie, F.; Liu, X.J.; Xie, Z. Kinematic calibration of a 5-axis parallel machining robot based on dimensionless error mapping matrix. Robot. Comput.-Integr. Manuf. 2021, 70, 102115. [Google Scholar] [CrossRef]
- Girard, A. Dimensionless Policies Based on the Buckingham Pi Theorem: Is This a Good Way to Generalize Numerical Results? Mathematics 2024, 12, 709. [Google Scholar] [CrossRef]
- Lecompte, O.; Therrien, W.; Girard, A. Experimental Investigation of a Maneuver Selection Algorithm for Vehicles in Low Adhesion Conditions. Trans. Intell. Veh. 2022, 7, 407–412. [Google Scholar] [CrossRef]
- Vicon. Available online: https://www.vicon.com/ (accessed on 20 May 2024).

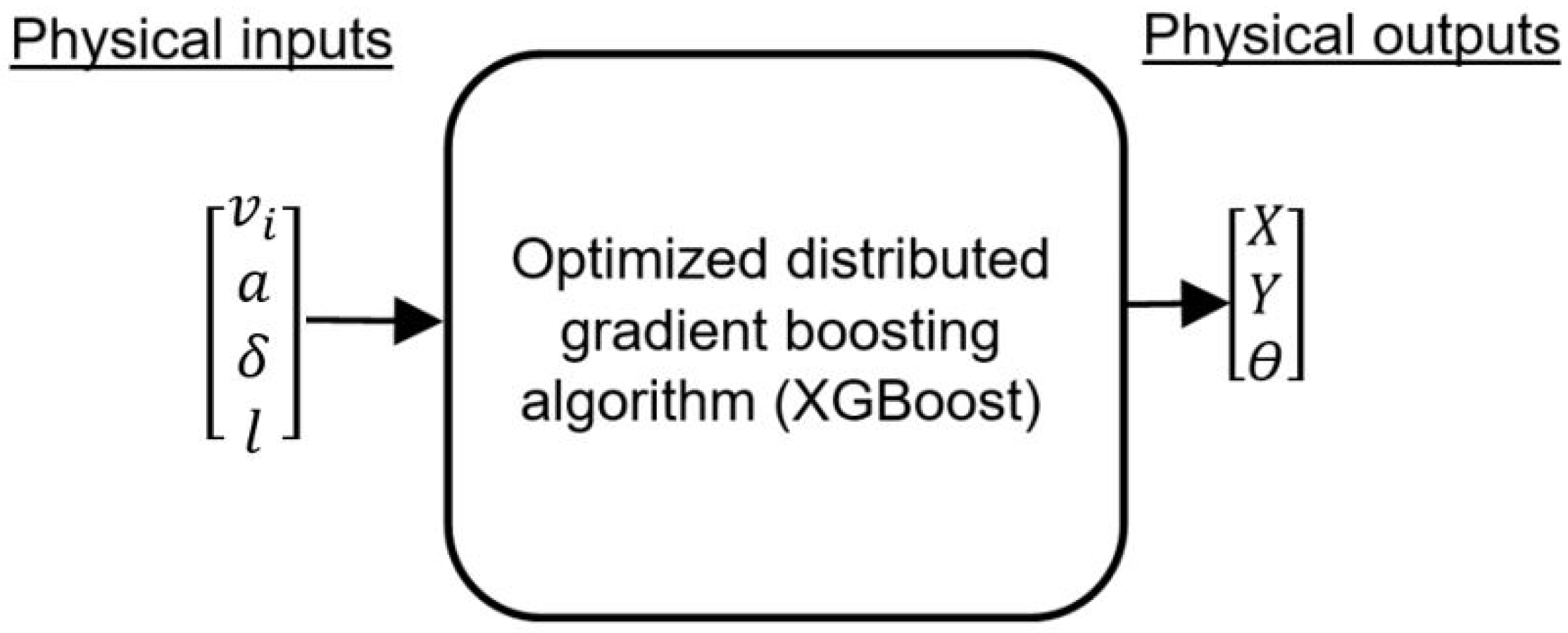






| Variables | Descriptions | Units [Dimensions] |
|---|---|---|
| State Variables | ||
| X | X-axis position of the vehicle in the world frame | m [L] |
| Y | Y-axis position of the vehicle in the world frame | m [L] |
| Yaw of the vehicle in the world frame | rad | |
| Environment related variables | ||
| Friction coefficient wheels/road | - | |
| v | Longitudinal velocity of the vehicle | m/s [] |
| g | Gravitational acceleration | m/s2 [] |
| Maneuvers related variables | ||
| a | Deceleration of the wheel | m/s2 [] |
| Steering angle of front wheels | rad | |
| Vehicles related variables | ||
| Normal force on front wheels | N [] | |
| Normal force on rear wheels | N [] | |
| l | Length between vehicle’s axles | m [L] |
| Wheel Base Length | Weight on Front Wheels (Static) | Weight on Back Wheels (Static) | |
|---|---|---|---|
| Vehicle | l [m] | [N] | [N] |
| Small | 0.345 | 37.77 | 28.84 |
| Long | 0.853 | 22.74 | 52.89 |
| Large | 0.475 | 71.12 | 71.12 |
| a | ||
|---|---|---|
| (m/s) | (m/s2) | (rad) |
| From 0.1 | From g | From 0.0000 |
| to 5.0 | to g | to 0.7854 |
| by 0.1 | by g | by 0.0785 |
| 50 values | 10 values | 11 values |
| Models | Data Vehicle 1 (Small) | Data Vehicle 2 (Long) | Data Vehicle 3 (Large) |
|---|---|---|---|
| Model | X: 0.0494 | X: 0.3703 | X: 0.1601 |
| Vehicle 1 | Y: 0.0466 | Y: 0.3071 | Y: 0.1459 |
| (Small) | : 0.0587 | : 0.9851 | : 0.4502 |
| Model | X: 0.3653 | X: 0.0316 | X: 0.2622 |
| Vehicle 2 | Y: 0.3032 | Y: 0.0257 | Y: 0.2061 |
| (Long) | : 0.9919 | : 0.0238 | : 0.5369 |
| Model | X: 0.1667 | X: 0.2679 | X: 0.0414 |
| Vehicle 3 | Y: 0.1440 | Y: 0.2125 | Y: 0.0362 |
| (Large) | : 0.4599 | : 0.5324 | : 0.0422 |
| Model | X: 0.0467 | X: 0.0433 | X: 0.0514 |
| Merged | Y: 0.0465 | Y: 0.0368 | Y: 0.0498 |
| (All 3) | : 0.0457 | : 0.0302 | : 0.0431 |
| Models | Data Vehicle 1 (Small) | Data Vehicle 2 (Long) | Data Vehicle 3 (Large) |
|---|---|---|---|
| Model | X: 0.0204 | X: 0.0144 | X: 0.0125 |
| Vehicle 1 | Y: 0.0261 | Y: 0.0102 | Y: 0.0099 |
| (Small) | : 0.0331 | : 0.0109 | : 0.0159 |
| Model | X: 0.0354 | X: 0.0145 | X: 0.0303 |
| Vehicle 2 | Y: 0.0394 | Y: 0.0176 | Y: 0.0262 |
| (Long) | : 0.2007 | : 0.0127 | : 0.0917 |
| Model | X: 0.0153 | X: 0.0103 | X: 0.0190 |
| Vehicle 3 | Y: 0.0162 | Y: 0.0095 | Y: 0.0182 |
| (Large) | : 0.0666 | : 0.0097 | : 0.0241 |
| Model | X: 0.0080 | X: 0.0087 | X: 0.0083 |
| Merged | Y: 0.0086 | Y: 0.0087 | Y: 0.0083 |
| (All 3) | : 0.0143 | : 0.0080 | : 0.0115 |
| Models | Data Vehicle 1 (Small) | Data Vehicle 2 (Long) | Data Vehicle 3 (Large) |
|---|---|---|---|
| Model | X: 0.0126 | X: 0.0117 | X: 0.0104 |
| Vehicle 1 | Y: 0.0121 | Y: 0.0090 | Y: 0.0077 |
| (Small) | : 0.0131 | : 0.0043 | : 0.0063 |
| Model | X: 0.0271 | X: 0.0103 | X: 0.0219 |
| Vehicle 2 | Y: 0.0286 | Y: 0.0134 | Y: 0.0222 |
| (Long) | : 0.1407 | : 0.0052 | : 0.0591 |
| Model | X: 0.0130 | X: 0.0090 | X: 0.0117 |
| Vehicle 3 | Y: 0.0133 | Y: 0.0091 | Y: 0.0129 |
| (Large) | : 0.0389 | : 0.0038 | : 0.0098 |
| Model | X: 0.0045 | X: 0.0055 | X: 0.0046 |
| Merged | Y: 0.0050 | Y: 0.0061 | Y: 0.0051 |
| (All 3) | : 0.0060 | : 0.0028 | : 0.0035 |
| Prediction Type | Traditional Dimensionalized Model | Buckingham Theorem Based Model | Augmented Buckingham Model |
|---|---|---|---|
| Self | X: 0.0408 | X: 0.0180 | X: 0.0115 |
| Predictions | Y: 0.0362 | Y: 0.0206 | Y: 0.0128 |
| : 0.0416 | : 0.0233 | : 0.0094 | |
| Cross | X: 0.2654 | X: 0.0197 | X: 0.0155 |
| Predictions | Y: 0.2198 | Y: 0.0186 | Y: 0.0128 |
| : 0.6594 | : 0.0659 | : 0.0422 | |
| Shared | X: 0.0471 | X: 0.0083 | X: 0.0049 |
| Predictions | Y: 0.0444 | Y: 0.0085 | Y: 0.0054 |
| : 0.0397 | : 0.0113 | : 0.0041 |
(m/s) | a g (9.81 m/s2) | (Rad) | |
|---|---|---|---|
| 0.2 | From 1.0 | From 0.1 | 0.0000 |
| 0.4 | to 3.5 | to 1.0 | 0.3927 |
| 0.9 | by 0.5 | by 0.1 | 0.7854 |
| 3 values | 6 values | 10 values | 3 values |
| Prediction Types | Traditional Dimensionalized Model | Buckingham Theorem Based Model | Augmented Buckingham Model |
|---|---|---|---|
| Self | X: 0.1229 | X: 0.1228 | X: 0.1197 |
| Predictions | Y: 0.0488 | Y: 0.0321 | Y: 0.0335 |
| : 0.0482 | : 0.0596 | : 0.0554 | |
| Cross | X: 0.3027 | X: 0.3752 | X: 0.3775 |
| Predictions | Y: 0.2198 | Y: 0.0186 | Y: 0.0128 |
| : 0.2007 | : 0.1494 | : 0.1454 | |
| Shared | X: 0.0539 | X: 0.0507 | X: 0.0400 |
| Predictions | Y: 0.0130 | Y: 0.0105 | Y: 0.0089 |
| : 0.0193 | : 0.0187 | : 0.0187 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Therrien, W.; Lecompte, O.; Girard, A. Using the Buckingham π Theorem for Multi-System Transfer Learning: A Case-Study with 3 Vehicles Sharing a Database. Electronics 2024, 13, 2041. https://doi.org/10.3390/electronics13112041
Therrien W, Lecompte O, Girard A. Using the Buckingham π Theorem for Multi-System Transfer Learning: A Case-Study with 3 Vehicles Sharing a Database. Electronics. 2024; 13(11):2041. https://doi.org/10.3390/electronics13112041
Chicago/Turabian StyleTherrien, William, Olivier Lecompte, and Alexandre Girard. 2024. "Using the Buckingham π Theorem for Multi-System Transfer Learning: A Case-Study with 3 Vehicles Sharing a Database" Electronics 13, no. 11: 2041. https://doi.org/10.3390/electronics13112041
APA StyleTherrien, W., Lecompte, O., & Girard, A. (2024). Using the Buckingham π Theorem for Multi-System Transfer Learning: A Case-Study with 3 Vehicles Sharing a Database. Electronics, 13(11), 2041. https://doi.org/10.3390/electronics13112041









