Current-Mode Active Filter Using EX-CCCII
Abstract
1. Introduction
2. Circuit Description
2.1. Second-Generation Current-Controlled Current Conveyor with Extra-X Terminal
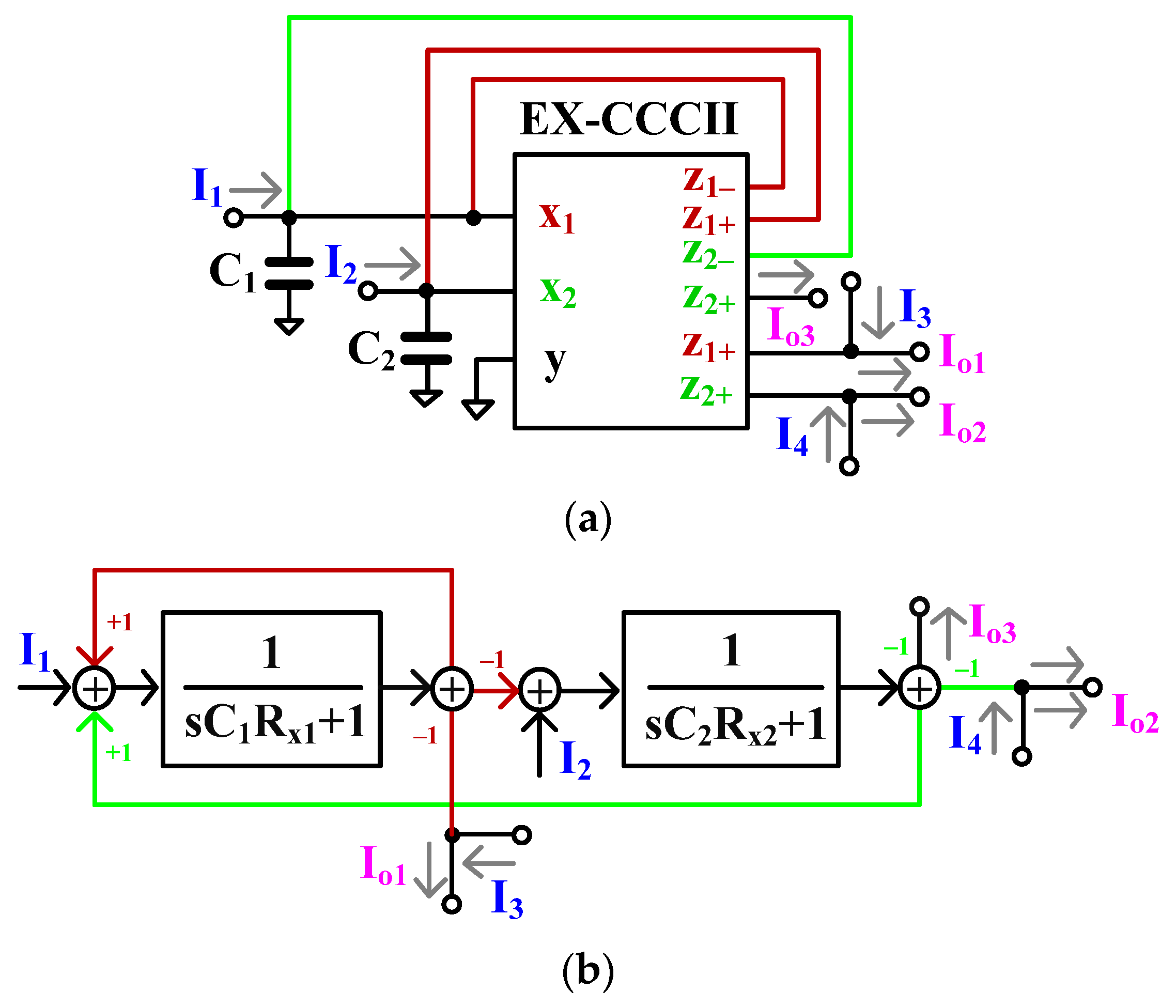
2.2. Current-Mode Universal Filter Using EX-CCCII
2.3. Non-Ideal Gain Analysis
2.4. Non-Ideal Parasitic Analysis
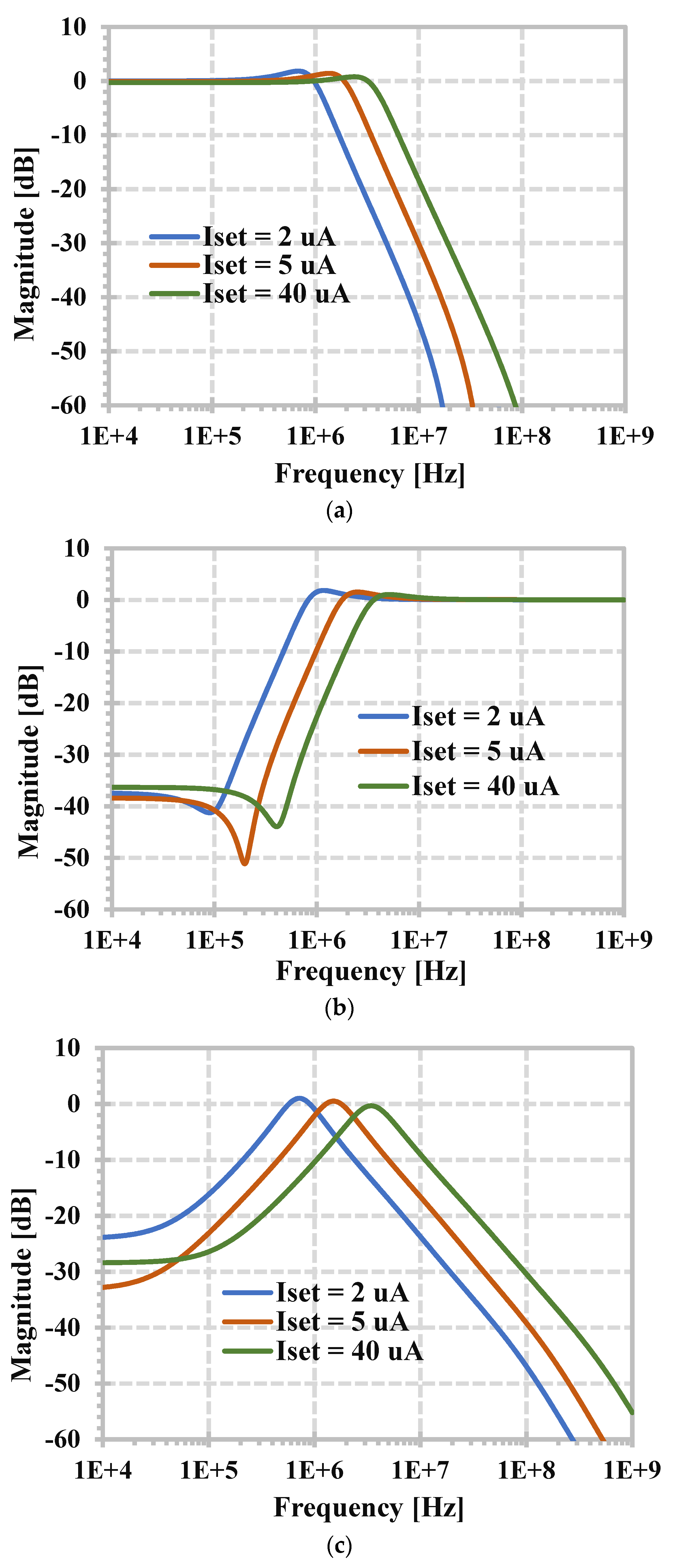
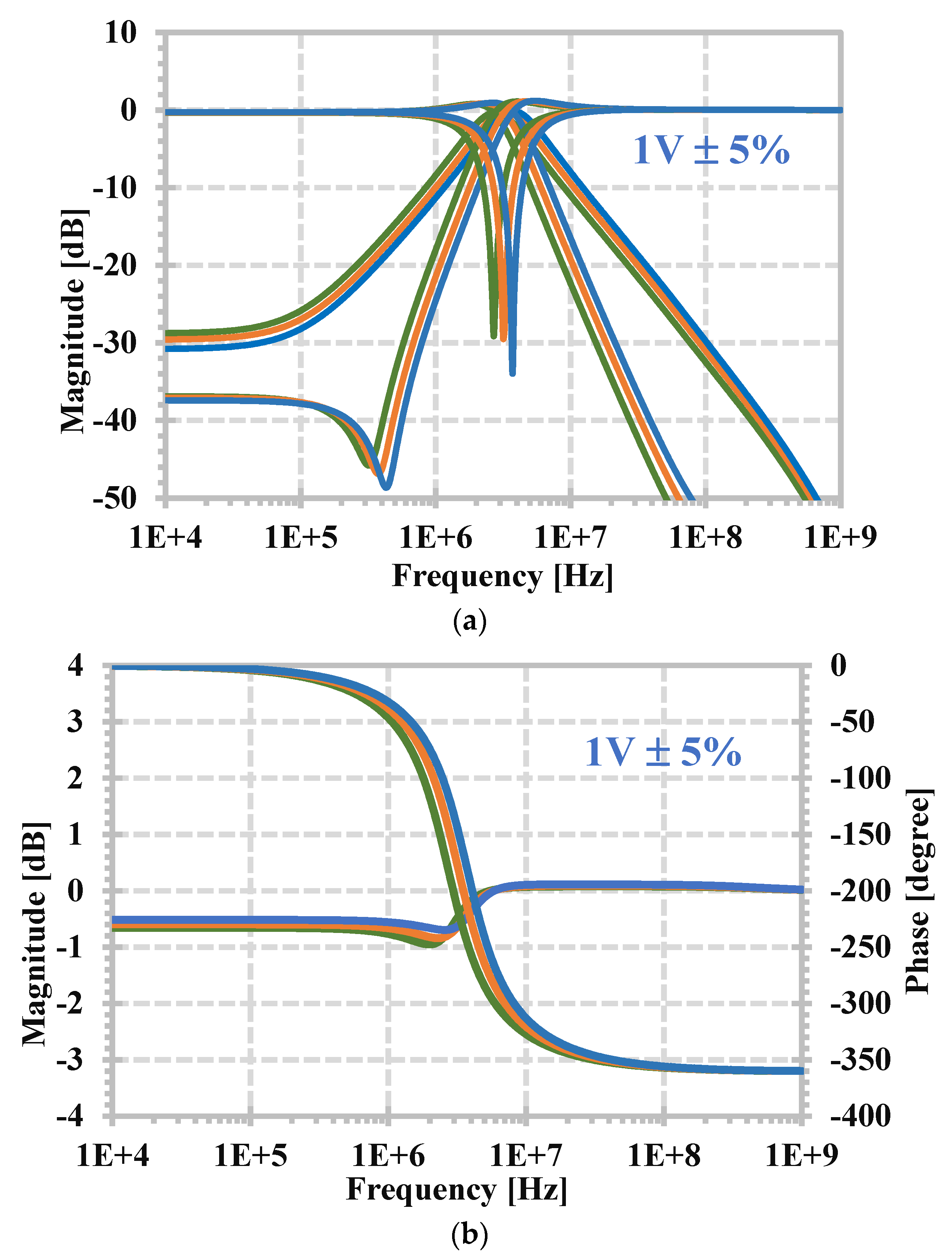
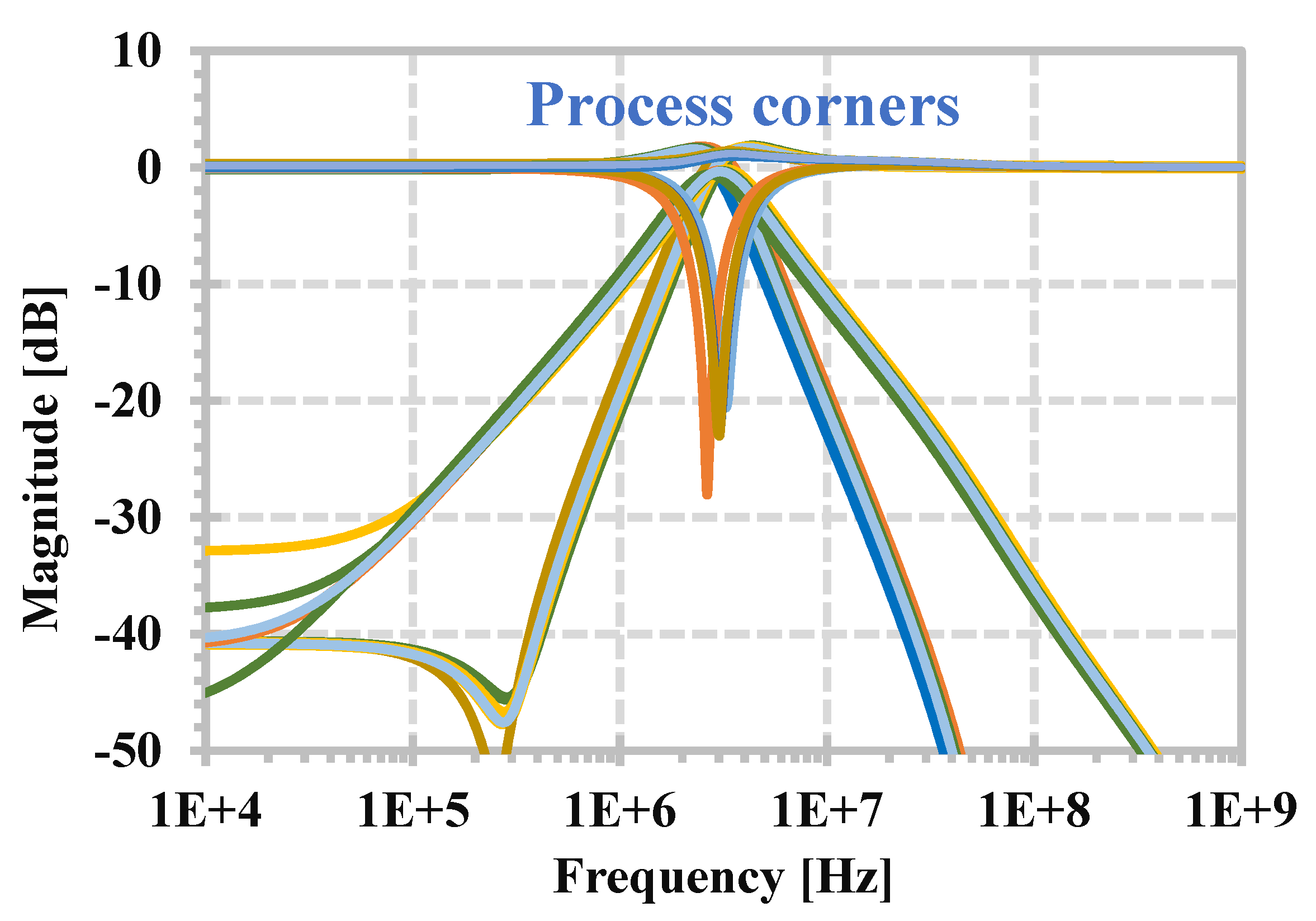
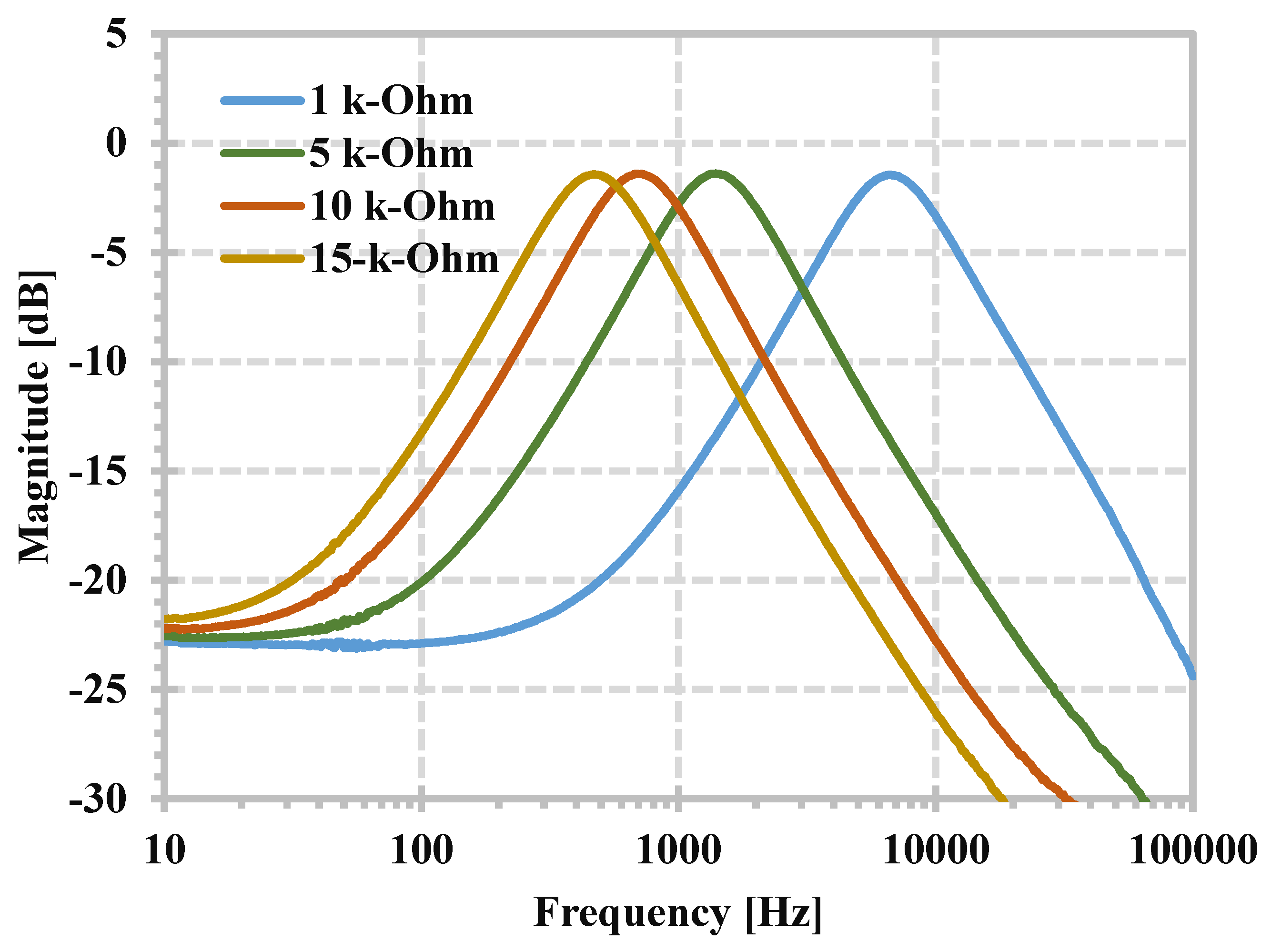
3. Simulation Results
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roberts, G.; Sedra, A. All current-mode frequency selective circuits. Electron. Lett. 1989, 25, 759–761. [Google Scholar] [CrossRef]
- Toumazou, C.; Lidgey, F.J.; Haig, D.G. Analogue IC Design: The Current-Mode Approach; Peter Peregrinus: London, UK, 1990. [Google Scholar]
- Sedra, A.; Smith, K. A second-generation current conveyor and its applications. IEEE Trans. Circuit Theory 1970, 17, 132–134. [Google Scholar] [CrossRef]
- Fabre, A.; Saaid, O.; Wiest, F.; Boucheron, C. Current controlled bandpass filter based on translinear conveyors. Electron. Lett. 1995, 31, 1727–1728. [Google Scholar] [CrossRef]
- Maheshwari, S. Current conveyor all-pass sections: Brief review and novel solution. Sci. World J. 2013, 2013, 429391. [Google Scholar] [CrossRef] [PubMed]
- Maheshwari, S. Voltage-mode full-wave precision rectifier and an extended application as ASK/BPSK Circuit Using a Single EXCCII. Int. J. Electron. Commun. 2018, 84, 234–241. [Google Scholar] [CrossRef]
- Maheshwari, S. Realization of simple electronic functions using EXCCII. J. Circuits Syst. Comput. 2017, 26, 1750171. [Google Scholar] [CrossRef]
- Agrawal, D.; Maheshwari, S. Current-mode precision full-wave rectifier circuits. Circuits Syst. Signal Process. 2017, 36, 4293–4308. [Google Scholar] [CrossRef]
- Das, R.; Paul, S.K. Resistorless current mode precision rectifier using EXCCII. Analog. Integr. Circuits Signal Process. 2020, 103, 511–522. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Single active element implementation of fractional-order differentiators and integrators. Int. J. Electron. Commun. 2018, 97, 6–15. [Google Scholar] [CrossRef]
- George, M.A.; Bhavani, I.V.L.D.; Kamath, D.V. EX-CCII Based FOPID controller for electric vehicle speed control. In Proceedings of the 2020 IEEE International Conference on Distributed Computing, VLSI, Electrical Circuits and Robotics (DISCOVER), Udupi, India, 30–31 October 2020; pp. 47–51. [Google Scholar]
- Joshana, R.; Singh, Y.S.; Ranjan, A. An electronically tunable fractional order inductor employing VD-EXCCII. Int. J. Electron. Commun. 2023, 174, 155055. [Google Scholar] [CrossRef]
- Agrawal, D.; Maheshwari, S. Design and implementation of current mode circuit for digital modulation. Integration 2021, 78, 118–123. [Google Scholar] [CrossRef]
- Kumar, A. Single EXCCII-based analog multiplier structure. J. Circuits Syst. Comput. 2021, 30, 2150107. [Google Scholar] [CrossRef]
- Chaturvedi, B.; Kumar, A. Single EXCCII based square/triangular wave generator for capacitive sensor interfacing and brief review. VLSI Post-CMOS Electron. Devices Circuits Interconnects 2019, 2, 329–349. [Google Scholar] [CrossRef]
- Maheshwari, S.; Agrawal, D. High performance voltage-mode tunable all-pass section. J. Circuits Syst. Comput. 2015, 24, 1550082. [Google Scholar] [CrossRef]
- Maheshwari, S. Tuning approach for first-order filters and new current-mode circuit example. IET Circuits Devices Syst. 2018, 12, 478–485. [Google Scholar] [CrossRef]
- Faseehuddin, M.; Herencsar, N.; Albrni, M.A.; Sampe, J. Electronically tunable mixed-mode universal filter employing a single active block and a minimum number of passive components. Appl. Sci. 2021, 11, 55. [Google Scholar] [CrossRef]
- Agrawal, D.; Maheshwari, S. Electronically tunable mixed-mode third-order universal filter using a single EX-CCCII. Aust. J. Electr. Electron. Eng. 2022, 19, 307–323. [Google Scholar] [CrossRef]
- Banerjee, K.; Joshi, M.; Sarkar, C.; Biring, S. Low-frequency resistorless electronically tunable quadrature oscillator based on an EX-CCCII. J. Electron. Mater. 2023, 52, 1–6. [Google Scholar] [CrossRef]
- Kumari, A.; Ranjan, A. Extra-X current controlled current conveyor based resistorless current mode quadrature sinusoidal oscillator. Int. J. Appl. Eng. Res. 2018, 13, 1–5. [Google Scholar]
- Bhatt, V.; Ranjan, A.; Singh, Y.S. Resistorless Chua’s diode implementation for chaotic oscillation employing single EXCCCII. Int. J. Electron. Commun. 2022, 156, 154398. [Google Scholar] [CrossRef]
- Li, Y.; Hou, J. Pathological models of EXCCCII and its applications in oscillator synthesis. Wuhan Univ. J. Nat. Sci. 2022, 26, 115–122. [Google Scholar] [CrossRef]
- Singh, P.; Nagaria, R.K. Single EX-CCCII based electronically tunable current mode instrumentation amplifier. Eng. Rev. 2022, 42, 1–16. [Google Scholar] [CrossRef]
- Agrawal, D.; Maheshwari, S. Cascadable current mode instrumentation amplifier. Int. J. Electron. Commun. 2018, 94, 91–101. [Google Scholar] [CrossRef]
- Agrawal, D. Electronically Tunable Grounded Immittance Simulators Using an EX-CCCII. Int. J. Electron. 2020, 107, 1625–1648. [Google Scholar] [CrossRef]
- Singh, P.; Nagaria, R. Low voltage EX-CCCII based on quasi-floating gate technique and its application as precision rectifier. Int. J. Electron. Commun. 2022, 155, 154378. [Google Scholar] [CrossRef]
- Singh, P.; Varshney, V.; Kumar, A.; Nagaria, R.K. DV-EXCCCII–based electronically tunable voltage mode all-pass filter. Lect. Notes Electr. Eng. 2021, 777, 485–494. [Google Scholar] [CrossRef] [PubMed]
- Maheshwari, S.; Agrawal, D. Cascadable and tunable analog building blocks using EX-CCCII. J. Circuits Syst. Comput. 2017, 26, 1750093. [Google Scholar] [CrossRef]
- Singh, P.; Varshney, V.; Kumar, A.; Nagaria, R.K. DV-EXCCCII–based electronically tunable current mode filter. Lect. Notes Electr. Eng. 2021, 777, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, D.; Maheshwari, S. Current mode filters with reduced complexity using a single EX-CCCII. Int. J. Electron. Commun. 2017, 80, 86–93. [Google Scholar] [CrossRef]
- Agrawal, D.; Maheshwari, S. High-performance electronically tunable analog filter using a single EX-CCCII. Circuits Syst. Signal Process. 2021, 40, 1127–1151. [Google Scholar] [CrossRef]
- Singh, P.; Nagaria, R.K. DV-EXCCCII based resistor-less current-mode universal biquadratic filter. Adv. Technol. Innov. 2023, 8, 12–28. [Google Scholar] [CrossRef]
- Singh, P.; Nagaria, R.K. Electronically tunable DV-EXCCCII-based universal filter. Int. J. Electron. Lett. 2020, 9, 301–317. [Google Scholar] [CrossRef]
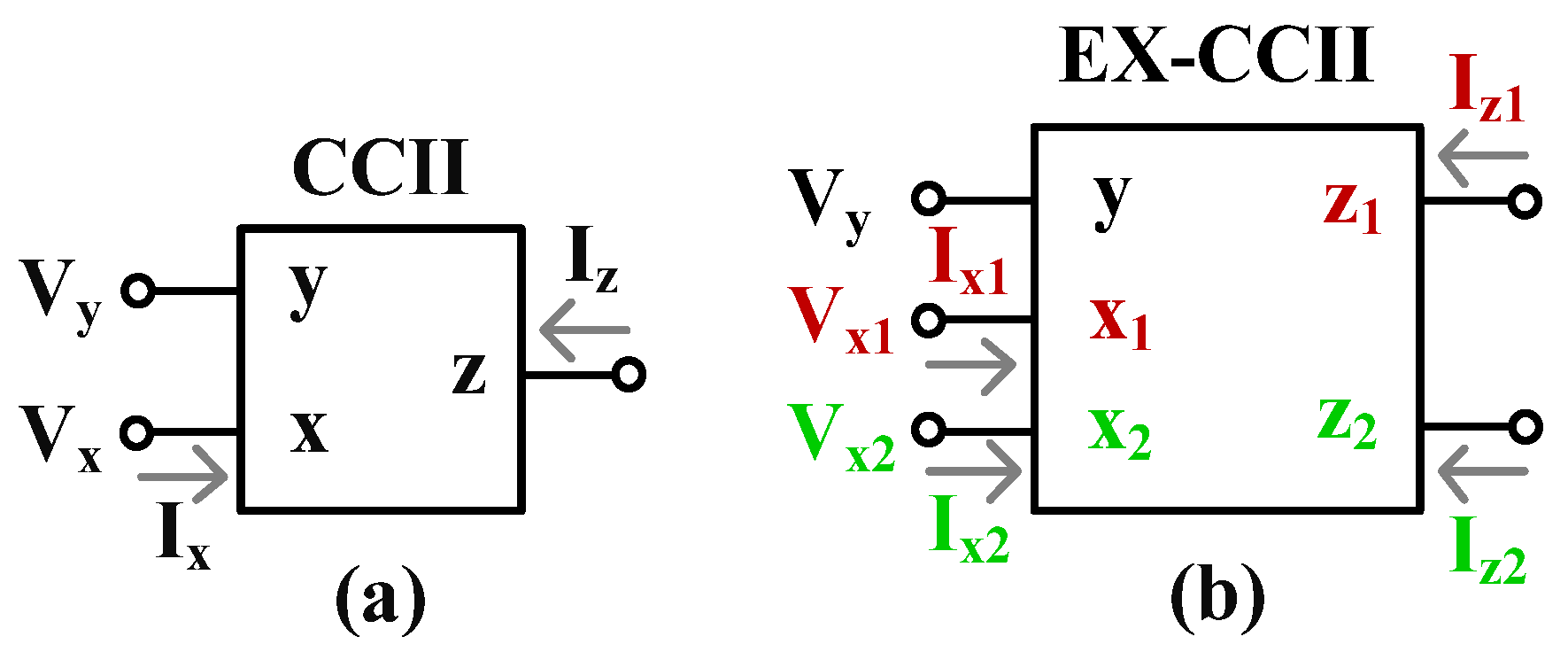


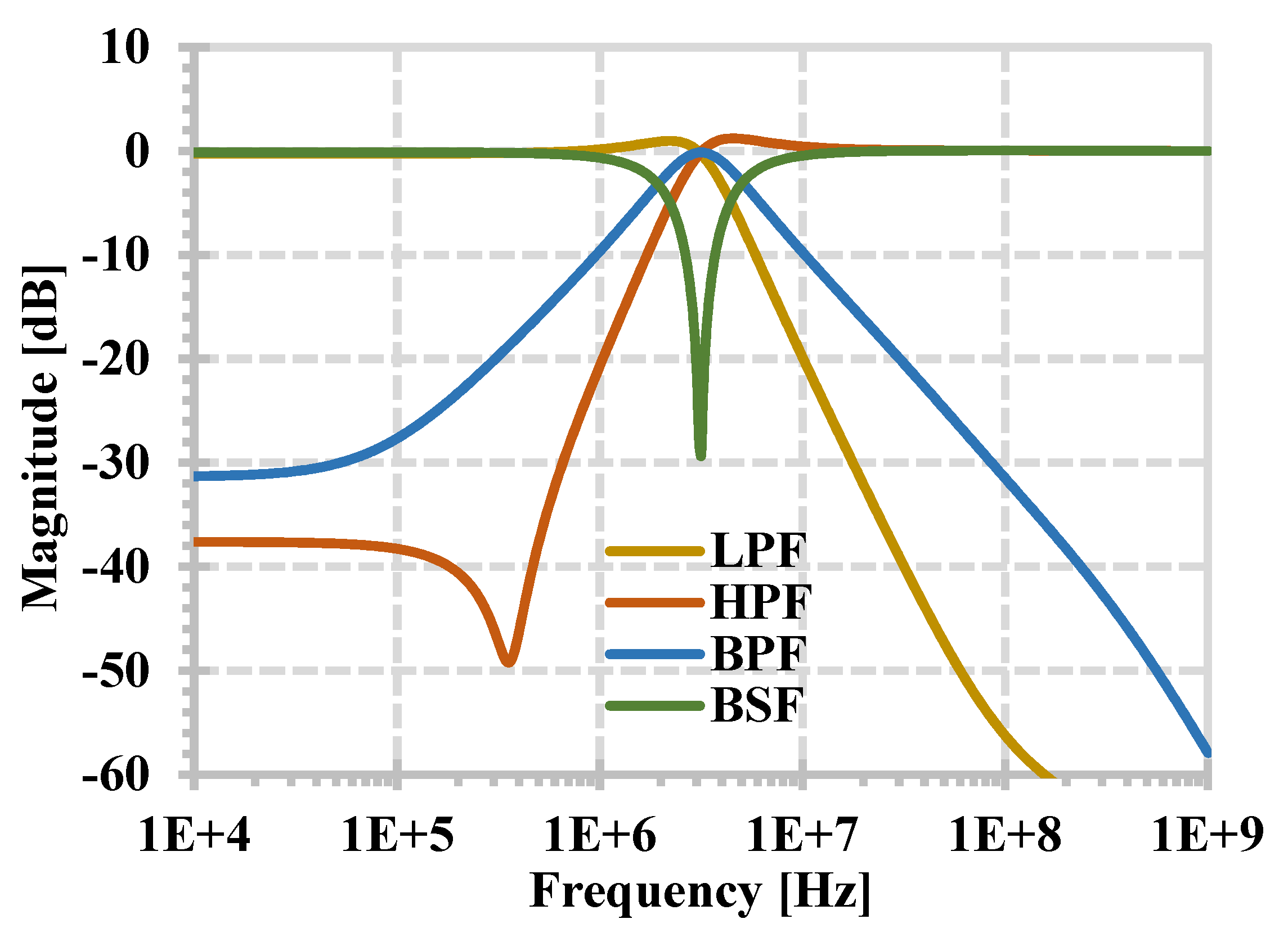








| Filtering Function | Input | Output | |
|---|---|---|---|
| LPF | Non-inverting | ||
| Non-inverting | |||
| BPF | Inverting | ||
| HPF | Non-inverting | ||
| BSP | Non-inverting | ||
| Non-inverting | |||
| APF | Non-inverting | ||
| Transistor | W/L (µm/µm) |
|---|---|
| M1, M2, M3 | 5/0.36 |
| M4, M5, M6 | 10/0.36 |
| Mb, M7–M18 | 3/0.36 |
| M19–M30 | 6/0.36 |
| Parameters | Value |
|---|---|
| Supply voltage | ±0.5 V |
| Technology | 0.18 μm |
| DC voltage range | −100 mV to 100 mV |
| Voltage gain | 0.953 |
| Current gain | |
| Iz+/Ix | 1.01 |
| Iz−/Ix | 1.04 |
| −3 dB bandwidth VF | 0.502 GHz |
| −3 dB bandwidth CF | |
| Iz+/Ix | 141.9 MHz |
| Iz−/Ix | 121.4 MHz |
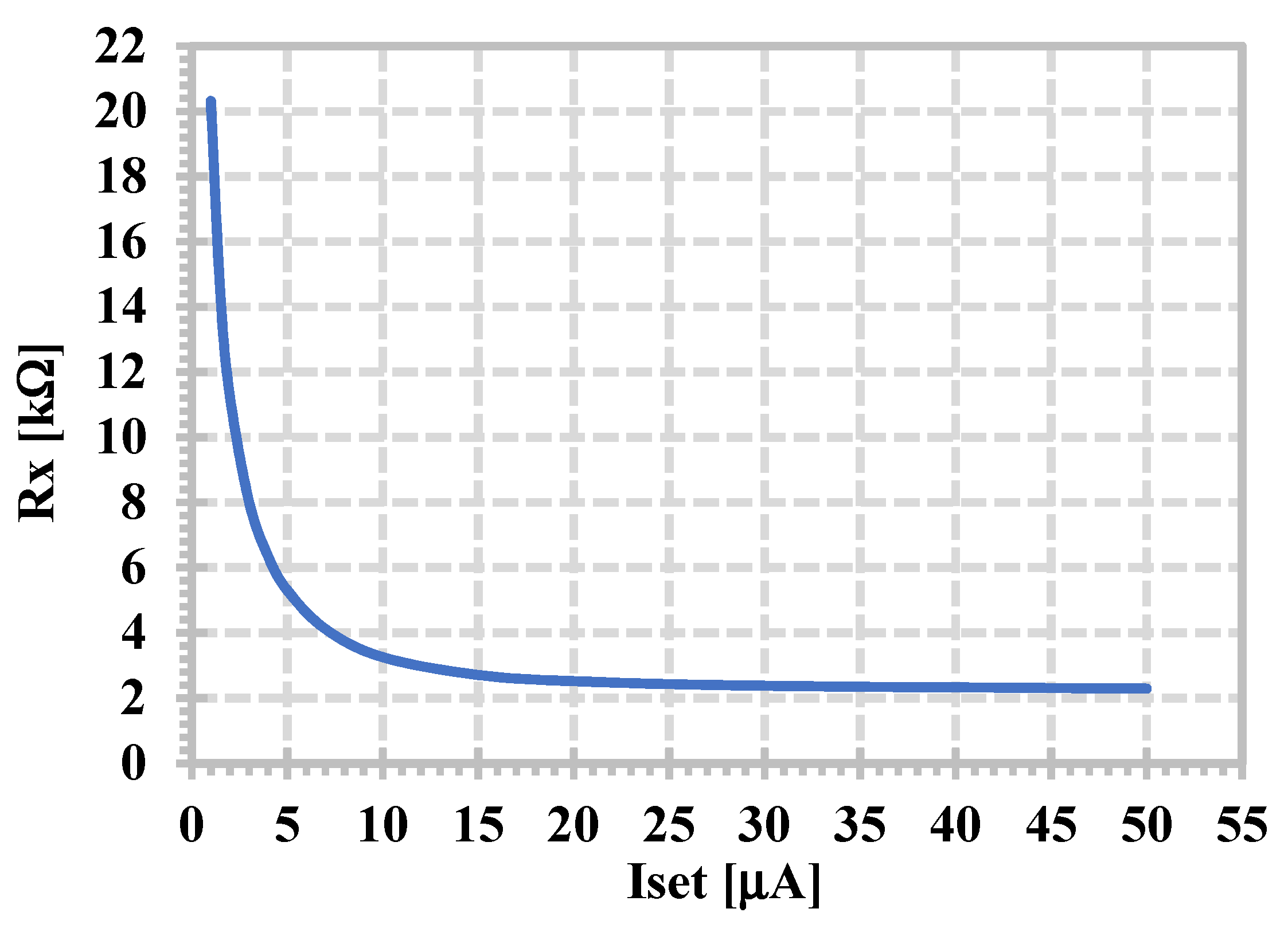
| Rx (Iset = 2–60 μA) | 20.3 kΩ–2.29 kΩ |
| Ry//Cy | 100 kΩ//0.251 pF |
| Rz//Cz | 462 kΩ//0.051 pF |
| Factor | Proposed | [18] | [31] | [32] | [33] | [34] |
|---|---|---|---|---|---|---|
| Number of active devices | 1-EX-CCCII | 1-VD-EXCCII (Figure 4) | 1-EX-CCCII (Figure 3) | 1-EX-CCCII | 1-DV-EXCCCII | 1-DV-EXCCCII |
| Realization | CMOS structure and commercial IC | CMOS structure | CMOS structure | CMOS structure and commercial IC | CMOS structure and commercial IC | CMOS structure |
| Number of passive elements | 2-C | 2-C, 2-R | 2-C | 2-C | 2-C | 2-C, 1-R |
| Type of filter | MIMO | SIMO | MISO | MIMO | MISO | MISO |
| Operation mode | CM | CM | CM | MM | CM | CM |
| Number of offered responses | 7 | 5 | 5 | 5 (CM) | 5 | 5 |
| All grounded capacitors | Yes | Yes | Yes | Yes (CM) | Yes | Yes |
| Without inverted/double input conditions | Yes | Yes | No | No | No | No |
| High output impedances | Yes | Yes | Yes | Yes | Yes | Yes |
| Electronic control of | Yes | Yes | Yes | Yes | Yes | Yes |
| Voltage supply (V) | ±0.5 | ±1.25 | ±1.25 | ±0.5 | ±0.9 | ±0.9 |
| Natural frequency (MHz) | 3.31 | 8.04 | 3.93 | 23 | 3.9 | ~3.5–4.2 |
| Power dissipation (mW) | 0.465 | 5.76 | 3.18 | 1.35 | 205 | 2.2 |
| Total harmonic distortion (%) | 1.038@140 µApp | 2.5%@360 µApp | 1.122%@100 µApp (BP) | 0.2%@200 µApp | <6%@200 µApp | 5%@120 µApp (BP) |
| Verification | Sim/Exp | Sim/Exp | Sim | Sim/Exp | Sim/Exp | Sim |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumngern, M.; Khateb, F.; Kulej, T.; Tooprakai, S. Current-Mode Active Filter Using EX-CCCII. Electronics 2024, 13, 2059. https://doi.org/10.3390/electronics13112059
Kumngern M, Khateb F, Kulej T, Tooprakai S. Current-Mode Active Filter Using EX-CCCII. Electronics. 2024; 13(11):2059. https://doi.org/10.3390/electronics13112059
Chicago/Turabian StyleKumngern, Montree, Fabian Khateb, Tomasz Kulej, and Siraphop Tooprakai. 2024. "Current-Mode Active Filter Using EX-CCCII" Electronics 13, no. 11: 2059. https://doi.org/10.3390/electronics13112059
APA StyleKumngern, M., Khateb, F., Kulej, T., & Tooprakai, S. (2024). Current-Mode Active Filter Using EX-CCCII. Electronics, 13(11), 2059. https://doi.org/10.3390/electronics13112059








