A Bayesian Deep Unfolded Network for the Off-Grid Direction-of-Arrival Estimation via a Minimum Hole Array
Abstract
:1. Introduction
- Based on the general signal model, real-valued SBL iterative formulas are rigorously derived and adjusted, and the corresponding Bayesian deep unfolded network is constructed according to each operation in the iterative formulas rather than an entire formula;
- Off-grid errors are directly modeled and estimated by the iterative formulas, and the corresponding network architecture is considered;
- MHA is adopted to maximize the DOF so that the estimation performance is improved.
2. Problem Formulation
3. Proposed Method
3.1. Bayesian Inference
3.2. Deep Unfolding
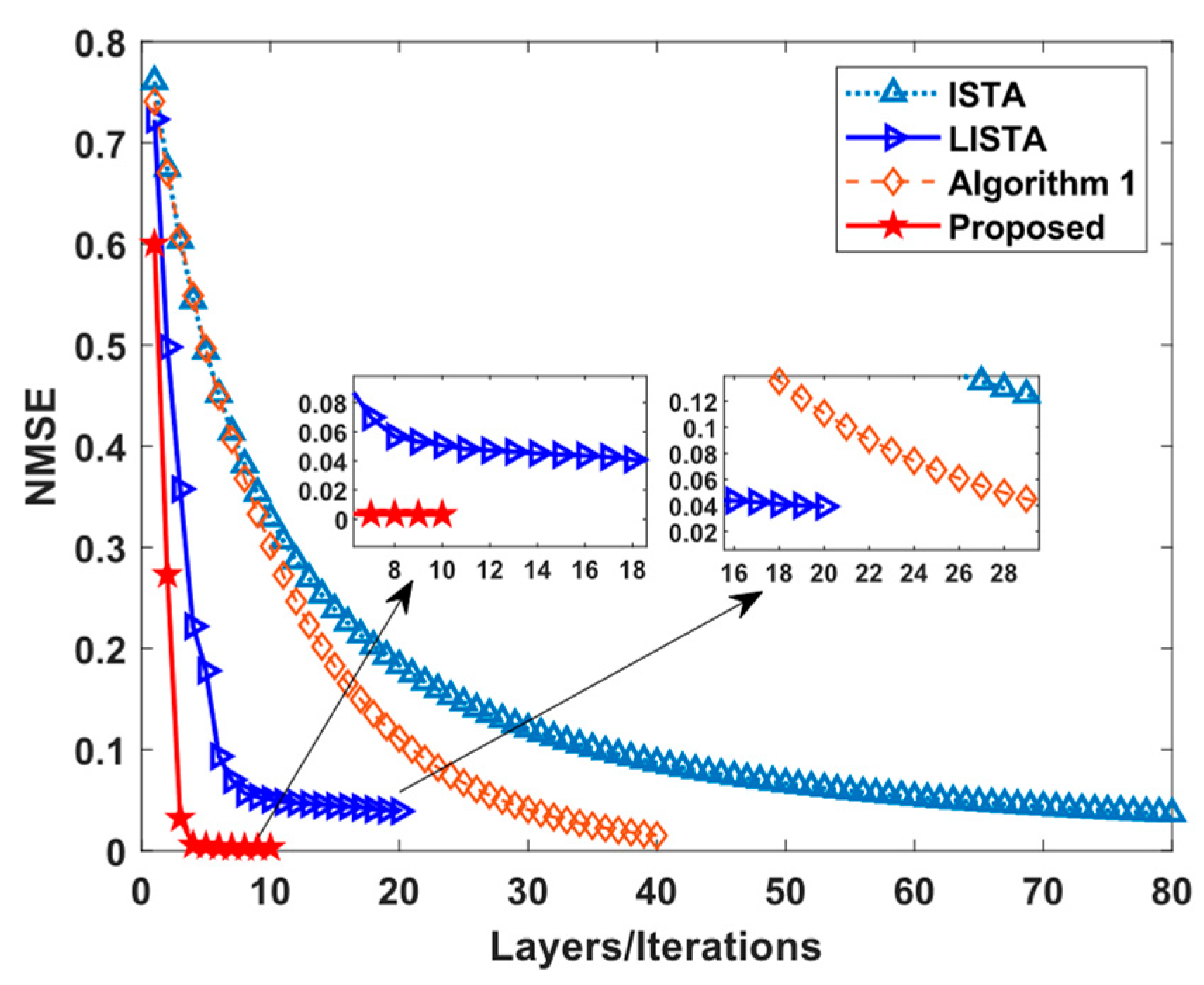
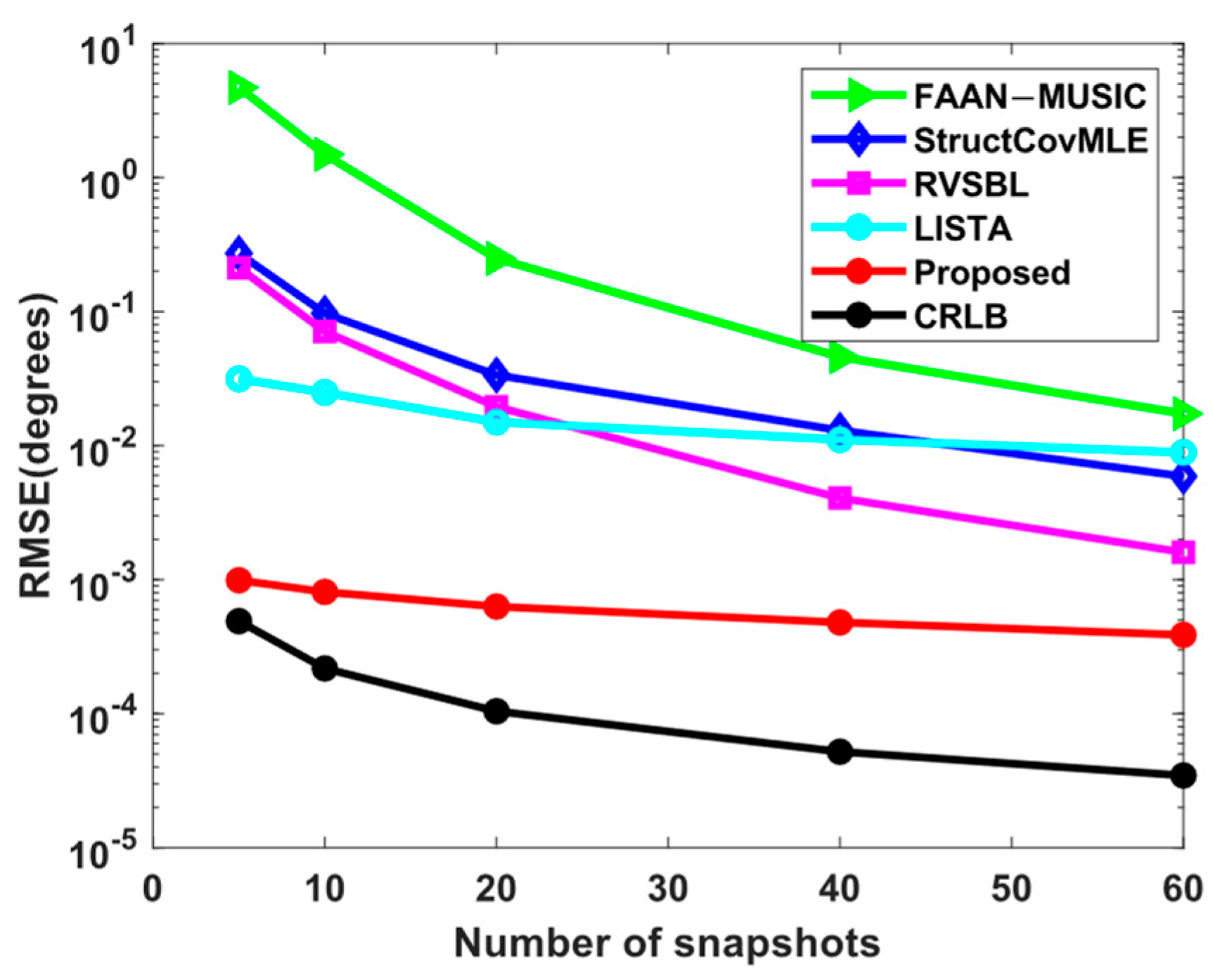
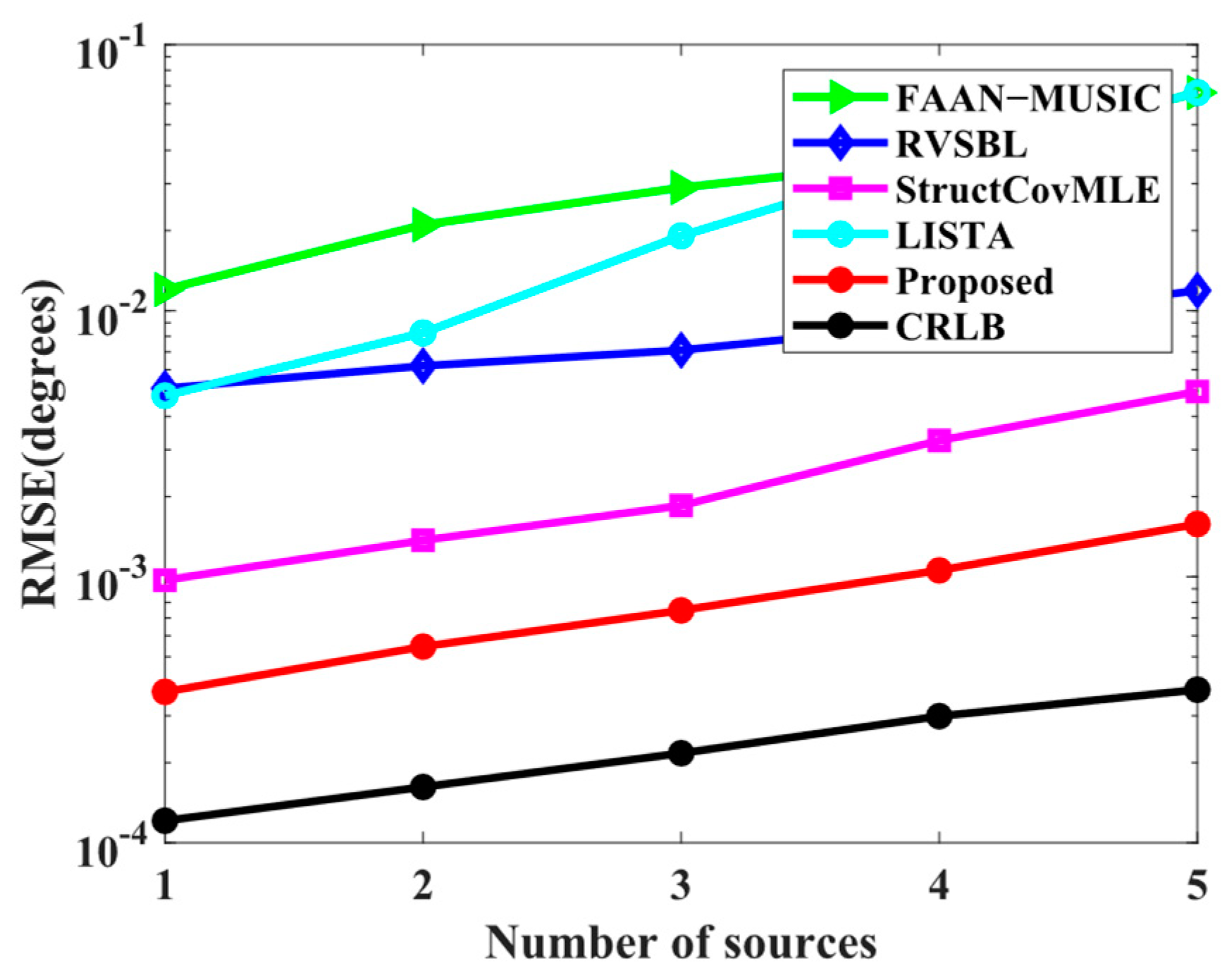
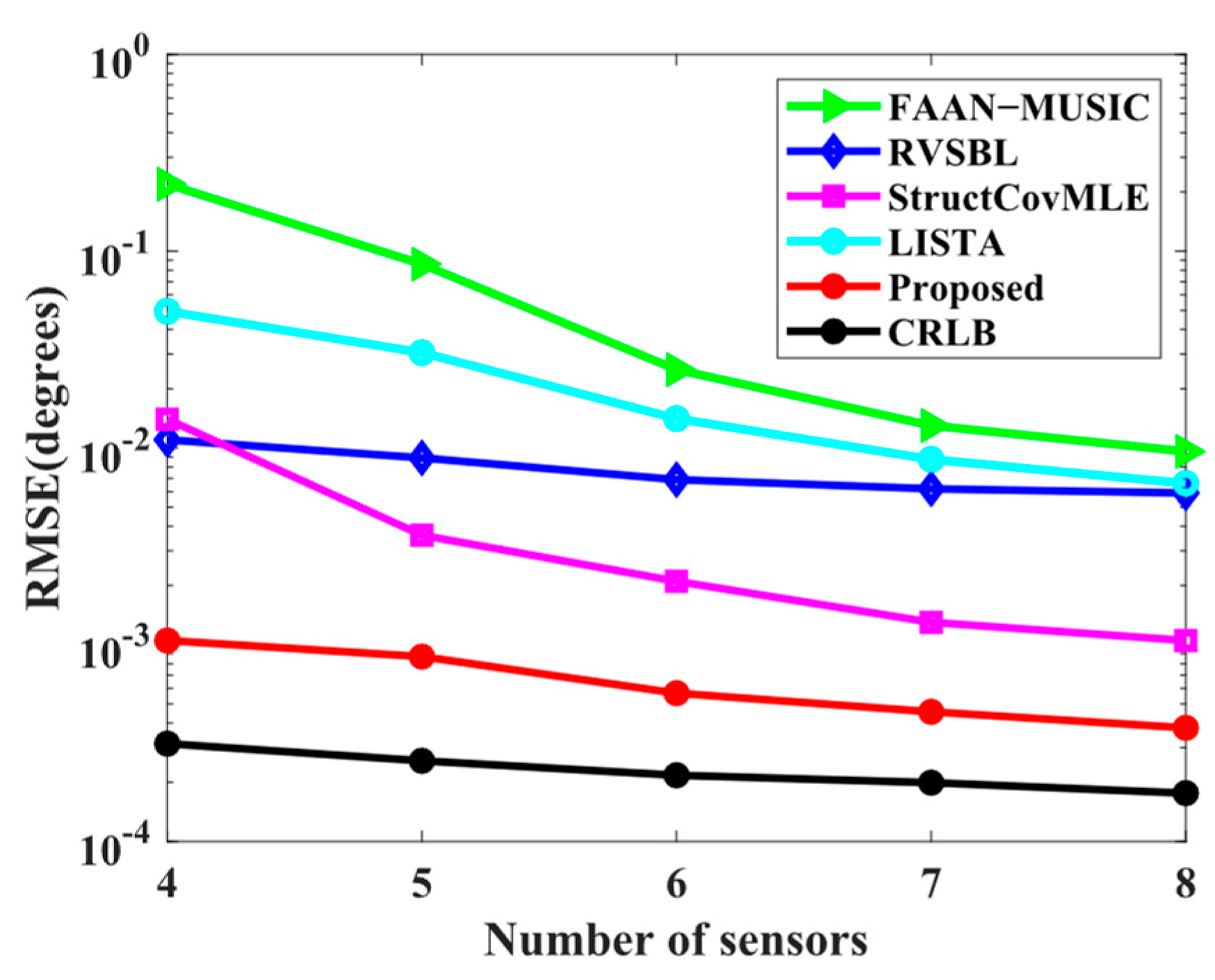
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Proc. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Pesavento, M.; Trinh-Hoang, M.; Viberg, M. Three More Decades in Array Signal Processing Research: An optimization and structure exploitation perspective. IEEE Signal Proc. Mag. 2023, 40, 92–106. [Google Scholar] [CrossRef]
- Liu, W.; Haardt, M.; Greco, M.S.; Mecklenbräuker, C.F.; Willett, P. Twenty-Five Years of Sensor Array and Multichannel Signal Processing: A review of progress to date and potential research directions. IEEE Signal Proc. Mag. 2023, 40, 80–91. [Google Scholar] [CrossRef]
- Purwins, H.; Li, B.; Virtanen, T.; Schlüter, J.; Chang, S.Y.; Sainath, T. Deep learning for audio signal processing. IEEE J. Sel. Top. Signal Process. 2019, 13, 206–219. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 84–90. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, I.E.; Dera, D.; Rasool, G.; Ramachandran, R.P.; Bouaynaya, N.C. Robust explainability: A tutorial on gradient-based attribution methods for deep neural networks. IEEE Signal Proc. Mag. 2022, 39, 73–84. [Google Scholar] [CrossRef]
- Monga, V.; Li, Y.; Eldar, Y.C. Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing. IEEE Signal Proc. Mag. 2021, 38, 18–44. [Google Scholar] [CrossRef]
- Gregor, K.; LeCun, Y. Learning fast approximations of sparse coding. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 399–406. [Google Scholar]
- Hershey, J.R.; Roux, J.L.; Weninger, F. Deep unfolding: Model-based inspiration of novel deep architectures. arXiv 2014, arXiv:1409.2574. [Google Scholar]
- Liu, J.; Chen, X. ALISTA: Analytic weights are as good as learned weights in LISTA. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Chen, X.; Liu, J.; Wang, Z.; Yin, W. Theoretical linear convergence of unfolded ISTA and its practical weights and thresholds. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1828–1837. [Google Scholar]
- Sun, J.; Li, H.; Xu, Z. Deep ADMM-Net for compressive sensing MRI. Adv. Neural Inf. Process. Syst. 2016, 29, 10–18. [Google Scholar]
- Su, X.; Liu, Z.; Shi, J.; Hu, P.; Liu, T.; Li, X. Real-valued deep unfolded networks for off-grid DOA estimation via nested array. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4049–4062. [Google Scholar] [CrossRef]
- Su, X.; Hu, P.; Liu, Z.; Shi, J.; Li, X. Deep alternating projection networks for gridless DOA estimation with nested array. IEEE Signal Proc. Let. 2022, 29, 1589–1593. [Google Scholar] [CrossRef]
- Wu, L.; Liu, Z.M.; Liao, J. DOA estimation using an unfolded deep network in the presence of array imperfections. In Proceedings of the 2022 7th International Conference on Signal and Image Processing (ICSIP), Suzhou, China, 20–22 July 2022; pp. 182–187. [Google Scholar]
- Tang, H.; Zhang, Y.; Luo, J.; Zhang, Y.; Huang, Y.; Yang, J. Sparse DOA Estimation Based on a Deep Unfolded Network for MIMO Radar. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 5547–5550. [Google Scholar]
- Li, Y.; Wang, X.; Olesen, R.L. Unfolded deep neural network (UDNN) for high mobility channel estimation. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Johnston, J.; Wang, X. Model-based deep learning for joint activity detection and channel estimation in massive and sporadic connectivity. IEEE Trans. Wirel. Commun. 2022, 21, 9806–9817. [Google Scholar] [CrossRef]
- Kang, K.; Hu, Q.; Cai, Y.; Yu, G.; Hoydis, J.; Eldar, Y.C. Mixed-timescale deep-unfolding for joint channel estimation and hybrid beamforming. IEEE J. Sel. Areas Commun. 2022, 40, 2510–2528. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Li, N.; Zhang, X.K.; Zong, B.; Lv, F.; Xu, J.; Wang, Z. An off-grid direction-of-arrival estimator based on sparse Bayesian learning with three-stage hierarchical Laplace priors. Signal Process. 2024, 218, 109371. [Google Scholar] [CrossRef]
- Gong, Z.; Su, X.; Hu, P.; Liu, S.; Liu, Z. Deep Unfolding Sparse Bayesian Learning Network for Off-Grid DOA Estimation with Nested Array. Remote Sens. 2023, 15, 5320. [Google Scholar] [CrossRef]
- Wan, Q.; Fang, J.; Huang, Y.; Duan, H.; Li, H. A variational Bayesian inference-inspired unrolled deep network for MIMO detection. IEEE Trans. Signal Process. 2022, 70, 423–437. [Google Scholar] [CrossRef]
- Hu, Q.; Shi, S.; Cai, Y.; Yu, G. DDPG-driven deep-unfolding with adaptive depth for channel estimation with sparse Bayesian learning. IEEE Trans. Signal Process. 2022, 70, 4665–4680. [Google Scholar] [CrossRef]
- Gao, J.; Cheng, X.; Li, G.Y. Deep Unfolding-Based Channel Estimation for Wideband TeraHertz Near-Field Massive MIMO Systems. arXiv 2023, arXiv:2308.13381. [Google Scholar]
- Linebarger, D.A.; Sudborough, I.H.; Tollis, I.G. Difference bases and sparse sensor arrays. IEEE Trans. Inf. Theory 1993, 39, 716–721. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Ottersten, B.; Stoica, P.; Roy, R. Covariance matching estimation techniques for array signal processing applications. Digit. Signal Process. 1998, 8, 185–210. [Google Scholar] [CrossRef]
- Yang, J.; Liao, G.; Li, J. An efficient off-grid DOA estimation approach for nested array signal processing by using sparse Bayesian learning strategies. Signal Process. 2016, 128, 110–122. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P. Low-rank covariance matrix estimation for factor analysis in anisotropic noise: Application to array processing and portfolio selection. IEEE Trans. Signal Process. 2023, 71, 1699–1713. [Google Scholar] [CrossRef]
- Das, A. Real-valued sparse Bayesian learning for off-grid direction-of-arrival (DOA) estimation in ocean acoustics. IEEE J. Ocean. Eng. 2020, 46, 172–182. [Google Scholar] [CrossRef]
- Pote, R.R.; Rao, B.D. Maximum likelihood-based gridless doa estimation using structured covariance matrix recovery and sbl with grid refinement. IEEE Trans. Signal Process. 2023, 71, 802–813. [Google Scholar] [CrossRef]
- Stoica, P.; Larsson, E.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 1448–1501. [Google Scholar] [CrossRef]



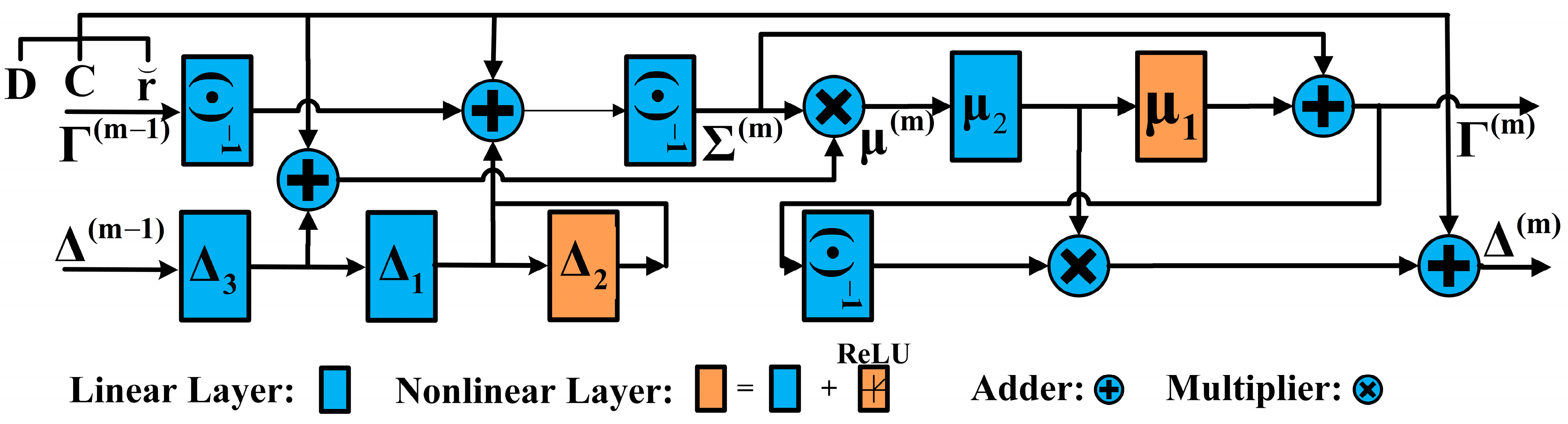

| Initialize , , , error tolerance , set elements in or as small and the same values. While do: compute and according to (20). compute and according to (22). . . End While Return and . Output refined DOAs. |
| Algorithms | Computational Time |
|---|---|
| FAAN-MUSIC | 1.223 s |
| RVSBL | 0.294 s |
| StructCovMLE | 0.537 s |
| LISTA | 0.00137 s |
| Proposed | 0.00472 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Zhang, X.; Lv, F.; Zong, B.; Feng, W. A Bayesian Deep Unfolded Network for the Off-Grid Direction-of-Arrival Estimation via a Minimum Hole Array. Electronics 2024, 13, 2139. https://doi.org/10.3390/electronics13112139
Li N, Zhang X, Lv F, Zong B, Feng W. A Bayesian Deep Unfolded Network for the Off-Grid Direction-of-Arrival Estimation via a Minimum Hole Array. Electronics. 2024; 13(11):2139. https://doi.org/10.3390/electronics13112139
Chicago/Turabian StyleLi, Ninghui, Xiaokuan Zhang, Fan Lv, Binfeng Zong, and Weike Feng. 2024. "A Bayesian Deep Unfolded Network for the Off-Grid Direction-of-Arrival Estimation via a Minimum Hole Array" Electronics 13, no. 11: 2139. https://doi.org/10.3390/electronics13112139





