Analysis and Construction of Hardware Accelerators for Calculating the Shortest Path in Real-Time Robot Route Planning

Abstract

This study introduces an optimization approach for calculating the shortest path in mobile robot route planning. The proposed solution targets real-time processing requirements by offering a high-performance alternative. This is achieved by embedding in the dedicated hardware an architecture which emphasizes parallelism. Through improvements in parallel exploration techniques, our solution aims to present not only a boost in performance but also a dynamic adaptation to graph changes, accommodating randomly occurring edge insertions or deletions as environmental conditions fluctuate. We present the developed architecture alongside its results. Our method efficiently updates obstacle matrices, resulting in a remarkable 120-fold improvement for 1024-node graphs. When utilizing a cost-effective device like the Cyclone IV E, it achieves approximately 12 times the performance of software applications.

1. Introduction

Efficient route planning is critical for enabling the autonomous and optimized navigation of mobile robots. Enhancing the energy efficiency of this task plays a crucial role in extending the operational duration of these robots. Consequently, optimizing the performance and efficiency of motion planning becomes pivotal in facilitating the integration of robotics into demanding environments and tasks. Although the expenses associated with high-degree-of-freedom (DOF) robots are diminishing, the existing primary obstacle to deploying autonomous robots with a high DOF lies in the latency of motion planning.

Calculating the shortest path is a fundamental aspect of route planning, allowing robots to navigate through complex environments while avoiding obstacles and optimizing their trajectory. However, since real-time processing of shortest-path calculations becomes increasingly challenging for robots with more than six degrees of freedom, innovative solutions are imperative to meet the stringent time constraints.

Studies such as [1,2] highlight the efficiency and potential improvements achievable with Field-Programmable Gate Array (FPGA) utilization in robotics. FPGAs offer distinct advantages, including a high parallelism, low latency, and reconfigurability, making them ideal for real-time route planning in mobile robots. Applications with low operational intensity and with greater processing of scalar values (as opposed to vectorization) struggle to fully exploit the peak performance offered by solutions based on Graphics Processing Unit (GPU), paving the way for FPGAs to deliver enhanced performance.

Through hardware acceleration and optimization, it is possible to achieve high processing frequencies and low execution times, meeting the stringent demands of real-time processing for high-degree-of-freedom mobile robots. Moreover, the specialized architecture for specific applications offered by FPGAs lead to a more efficient resource utilization and consequently, lower energy consumption.

The advantages of employing a Probabilistic Roadmap (PRM) to reduce the processing time required for route planning were demonstrated in [3,4]. In the pre-processing phase of the PRM, performed only once, the roadmap was built by only taking into account the permanent collisions in the environment and the robot self-collisions. In these cases, the FPGA reduced the time required for map creation and path calculation to a mere 650 microseconds at 125 MHz. However, the efficiency was compromised as the the shortest-path algorithm still consumed 425 microseconds of the total time. This was primarily due to the reliance on CPU-based PRM result processing and increased communication costs.

This work proposes a high-performance optimization solution for calculating the shortest path in route planning for robots, with a focus on real-time processing. The primary goal is to address the computational challenges associated with high-degree-of-freedom robots by leveraging parallelism and dedicated hardware, particularly FPGAs. Through the exploitation of parallelism and integration of key features from existing algorithms, the solution aims to improve performance while maintaining adaptability to changes in the analyzed graph. The proposed solution works together with an external component that runs a PRM, responsible for updating the graph as obstacles arise in the environment.

The optimization process comprises several critical stages that contribute to efficient route planning of mobile robots. Initially, a comprehensive graph representing the robot configuration space is constructed in an offline process (Figure 1A). This graph captures all possible configuration positions and their relationships, providing a comprehensive representation of the robot movement capabilities.

The PRM algorithm works by sampling valid configurations and connecting them through collision-free paths. It takes into account the presence of obstacles and efficiently captures the free space available for robot navigation. As obstacles are introduced into the environment during the robot operation (Figure 1B), the PRM algorithm dynamically updates the existing graph (Figure 1C). It removes the nodes compromised by the obstacle in order to create clear paths that facilitate seamless robot movement. This dynamic adaptation ensures obstacle-free navigation and optimizes the robot trajectory (Figure 1D).

To determine the optimal trajectory between the origin and destination points, shortest-path algorithms, such as the Dijkstra algorithm, are employed (Figure 1E). These algorithms meticulously analyze the dynamically evolving graph, taking into account its relationships and constraints. This process combined with the accountability of changes in the environment allows for robust and reliable path planning solutions to be achieved. This enables the robot to navigate from the initial to the destination configuration efficiently and safely (Figure 1F,G). The goal of this work is to act in steps E and F outlined in Figure 1 by optimizing the calculation of the shortest path.

One of the key distinctions of this application lies in its graph updating process (Figure 1F). Unlike conventional alternatives that regenerate the entire graph with each interaction, this application employs a novel approach by updating only a matrix containing obstacles. As a result, there is a remarkable 120-fold improvement in the updating process for graphs comprising 1024 nodes. Additionally, when utilizing a cost-effective FPGA such as the Cyclone IV E, this application achieves approximately 12 times the performance of its software counterparts.

In the following sections, a brief contextualization of the project is presented, followed by an explanation of the technique used and its evaluation. Then, the architecture of the proposed solution is presented in detail, along with a discussion of the simulation results obtained on FPGA hardware.

2. Background and Related Works

The utilization of parallelism techniques for route planning optimization has exhibited significant effectiveness, as demonstrated in studies like [5]. Works such as [6] further demonstrate the advantages of using a parallel approach to solve a Rapidly Exploring Random Tree (RRT) for computationally expensive planning approaches in real-time problems.

Works such as [7] apply a variant of the RRT* technique that adds a rewiring operation to improve the quality of solutions achieved. In addition, they use data compression techniques to reduce the impact of information transfers on a heterogeneous CPU/GPU platform. However, despite the favorable results, as their processing time is in the order of seconds, they are not suitable for real-time applications.

In [8], GPU utilization yields a notable 5× speedup on average compared to raw C++ implementations for motion prediction calculations. Furthermore, for robots with more than six degrees of freedom, many solutions that offer response times in the order of hundreds of milliseconds are implemented on GPUs, as shown by [9,10].

A promising alternative is the use of FPGAs, as highlighted in works like [11]. In that study, a route planner and a collision detector were built using an FPGA, resulting in a speed 25 times faster than the one achievable with a CPU.

Moreover, in [3,4], the path planning problem was addressed using dedicated hardware such as FPGAs, with the PRM construction as the foundation for the solution. The technique used was applied in a Kinova Jaco2 robot. These works presented an improvement in performance by three orders of magnitude and a reduction in energy consumption by more than one order when compared to other studies.

The main works cited in this section, along with their contributions, can be seen in

Table 1. Comparison of related works.

Technique	Reference(s)	Advantages	Hardware Type
Parallel RRT*	[6]	Enables real-time solutions for computationally expensive problems	CPU
RRT* with rewiring	[7]	Improves solution quality and reduces data transfer overhead (up to 10× over the RRT* algorithm)	CPU/GPU
Motion-predicted GPU acceleration	[8]	Speedup (5× ) compared to raw C++ implementations	GPU
High-DOF robot motion prediction	[9,10]	Offers response times in milliseconds for robots with a high DOF	GPU
FPGA-based route planning and collision detection	[11]	Achieves 25× faster speed compared to CPU	FPGA
PRM-based path planning with FPGA	[3,4]	Provides significant performance improvement (3 orders of magnitude) and energy reduction	FPGA

.

Shortest-Path Problem

As presented in [4], despite the promising results of the proposed solution, the final result ended up being impaired due to the non-optimization of the shortest-path calculation. In this case, the adequate solution for the shortest path should present, in addition to a performance improvement, a dynamic adaptation to fluctuations in the graph, since changes in the environment can cause edges to be randomly inserted or deleted. Therefore, it was imperative to explore other techniques.

The utilization of graph partitioning was first introduced by [12], while bidirectional processing was implemented as described in to [13]. Despite these advancements, both methodologies led to a significant increase in resource consumption, contrary to the primary goal of resource minimization on FPGAs.

The use of an obstacle-based genetic algorithm to address this issue was pioneered by [14]. This approach significantly reduced search spaces, resulting in shorter collision-free paths and quicker convergence compared to prior methods. However, the proposed solution assumed a static 2D environment.

In [15], the authors introduce a bi-level path planning algorithm that presents enhancements over the traditional A* algorithm. Particularly noteworthy is the fact that their approach outperforms both the classic Dijkstra and A* algorithms. However, it is crucial to acknowledge that this solution is tailored for a 2D environment; its applicability in a 3D environment remains untested and warrants further investigation.

The Dijkstra algorithm proposed by [16] is renowned for its capability to consistently discover the shortest optimal path, provided one exists. Since this is a widely used method, there are several works that seek to improve the performance of this type of algorithm. Studies such as [17] proposed enhancement solutions with the use of CPUs. In that case, it was possible to achieve up to 51% performance improvement using a multiprocessor strategy for a graph with ${10}^8$ nodes.

The study of the advantages of parallelizing Dijkstra’s base algorithm through the utilization of Open Multi-Processing (OpenMP) and Open Computing Language (OpenCL) on CPUs was presented in [18]. Despite achieving better results in the parallelized alternative, the study used the base structure of the algorithm, which is inherently sequential, thus impairing the performance of the parallelization. Nonetheless, the tests showed an average improvement of 10% in performance.

In addition, there are studies that explore the parallel nature of graphics cards, such as [19]. Based on the work conducted by [20,21], in which shortest-path search techniques were explored, [19] developed a solution for GPUs using the Message Passing Interface (MPI) and OpenCL. This solution yielded a performance enhancement ranging from 10 to 15 times when compared to the results obtained sequentially on CPU. However, the scope of that work was aimed at graphs with more than one hundred thousand nodes.

There are also works that perform optimizations using dedicated hardware, such as FPGAs. In [22], for example, a solution developed on an FPGA presented a performance approximately 67 times superior to the software version for an application with 64 nodes. However, the paper did not specify which clock frequency was used in the tests and made use of a Read-Only Memory (ROM) to store the graph, with no possibility of reconfiguration during execution.

A dedicated FPGA architecture to solve the routing table construction problem in Open Shortest Path First (OSPF) networks was proposed by [23]. The study achieved a performance improvement of up to 76 times over the standard Dijkstra implementation on a CPU for a graph with 128 nodes. However, the complexity of the architecture limited the solution applicability to a maximum of 28 nodes on the chosen device.

The work conducted by [24] introduces a hybrid matrix-multiply Floyd–Warshall algorithm technique, according to [25], an $O\left(n^3\right)$ algorithm designed specifically for addressing All-Pairs Shortest-Path (APSP) problems in graphs with more than 4096 nodes. The study presents favorable results when compared to similar solutions. However, it is important to note that the APSP problem entails greater complexity compared to the Single-Source Shortest-Path (SSSP) problem. This indicates that a project dedicated solely to the SSSP problem can potentially achieve even greater gains and optimizations.

In [26], an FPGA solution is presented which functions as a coprocessor for a C program running on a PowerPC-based computer. It involves loading the graph into the node processor memories. Despite yielding a remarkable 13.6-time performance boost, the process of transferring the graphs to the memories encounters a bottleneck. With each new iteration, the entire graph must be transferred, which adds overhead to the system. This limitation impacts the overall performance of the project despite the notable improvement achieved.

A variant of the Dijkstra algorithm called eager Dijkstra is presented in [27]. This version incorporates a constant factor which selects the nodes that will be processed in parallel. An FPGA-based adaptation of this approach developed by [28] addressed large graphs with more than 1 million nodes. Experimental results showed that the FPGA solution presented an improvement five times superior to the CPU implementation, with only one-fourth of the power consumption.

The solution proposed by [29], the PRAM algorithm, uses refined heuristics to increase the number of vertices removed at each iteration without causing any reinsertion. Unlike the eager algorithm, there are no parameters that need to be adjusted, as the removals are performed according to the distances and costs of neighbors. Recent works such as those presented in [17,30,31] validated the effectiveness of that approach in achieving efficient parallelism by partially or fully using the proposed method.

Moreover, the need to keep storing node distances in memory within the eager Dijkstra implementation, due to re-insertion possibilities, contributes to an increased memory usage. However, in the solution presented by [29], only the distances of the active nodes require storage in memory. Once these distances are established, they no longer necessitate any ongoing analysis, thereby liberating memory resources.

Table 2. Comparison of shortest-path algorithms.

Reference	Algorithm	Complexity
[24]	Floyd-Warshall	$O\left(n^3\right)$
[27]	Eager Dijkstra	$O\left(n^2\right)$
[16]	Dijkstra	$O\left(n^2\right)$
[23]	Enhanced Dijkstra	$O\left(n\right)$
[28]	Enhanced Eager Dijkstra	$O\left(n\right)$
[29]	PRAM	$O\left(n^{1/3}logn\right)$

shows a comparison with some shortest-path algorithms.

3. Proposal for the Shortest-Path Algorithm

Among the analyzed techniques, the solution proposed by [29] was the one that presented the greatest compatibility with the requirements of our proposal. Not only did it exhibit significant potential for parallelism, but it also had lower consumption of computational resources compared to other methods. Furthermore, we did not find implementations of that model on an FPGA, which highlights the innovative aspect of our work.

3.1. Construction of Reference Models

To facilitate the analysis and validation of the results from the developed system, an auxiliary tool was created. This tool simplified the construction of graphs with randomized weights in customizable ranges and relationships, an essential aspect for simulating diverse node interconnections. It allowed the configuration of the graph relationships according to the simulation requirements, including adjusting the maximum number of relations per node, their direction, and weights within a configurable range. These graphs were used to propagate the shortest path between a source and a destination.

Additionally, a base version of the Dijkstra algorithm was developed and tested using Python. This version served as a base model for validating the results obtained in the optimized versions. The results of the base version were extensively tested and validated. The tool generates images that represent the constructed graph and the shortest path found (as shown in Figure 2). These images are created using the matplotlib library [32] and serve as a support method in the process of validating the results.

3.2. Specification of the Optimized Shortest-Path Algorithm

The technique presented in [29] uses two criteria to select which nodes can be removed, namely, the IN and OUT criteria. Such criteria can be used separately or in conjunction (INOUT) in the node evaluation process.

Furthermore, the Dijkstra algorithm, as detailed in [29], was adapted to an FPGA approach. The updated flowchart can be seen in Figure 3. In this flow, graph nodes are categorized into five distinct classifications:

• Inactive: nodes awaiting analysis and processing;
• Stacked or active: former inactive nodes identified as neighbors of previously established nodes and undergoing classification;
• Approved: nodes that are stacked and have successfully passed the classification process;
• Established: approved nodes with identified shortest paths to the source, forwarded for expansion;
• Obstacle: nodes presenting a barrier or obstruction in the graph and that should be ignored.

The first step performed by the algorithm is to mark the source node (s) as stacked. Afterwards, it applies the criteria for identifying eligible nodes, resulting in a list of approved nodes. For each approved node (v), it expands to its not yet established neighbors that are not marked as obstacles. This step can be performed in parallel, as there are no dependencies between operations.

The expansion of a neighbor consists in comparing its current distance to the source ($L\left(w\right)$) with a potential new distance. The calculation of this new distance involves adding to the distance from the currently approved node to the source the cost between the approved node and its neighbor ($L\left(v\right)+c(v,w)$ ). If the new distance is shorter than the one currently stored, the neighbor’s distance is updated, along with its previous pointer ($w.previous$), thus becoming $L\left[w\right]=L\left[v\right]+c(v,w)$ and $w.previous=v$. In addition, each neighbor of the approved node that is not stacked, established, or part of an obstacle is marked as stacked ($stack\left(w\right)$). Finally, the approved nodes are removed from the stack and marked as established. The algorithm ends when there are no more stacked nodes. At that moment, the shortest path can be obtained by forming, from the destination node, the set of previous nodes to the source.

In order to ensure greater independence between these operations, each expansion outcome is stored in a structure of local vectors. Only after processing all neighboring nodes in the current iteration are their results inserted into global arrays. Moreover, given the possibility that a node may serve as neighbor to multiple others, thus being expanded more than once in the same iteration, the distance and the pointer to the previous node are updated in global memory solely when the new distance reached is smaller than the currently stored one.

During the analysis of this implementation, it was observed that it was not necessary to store the distance of all nodes, only of those marked as stacked. This was possible because in that approach, reading the distance to the source was only necessary in two scenarios: (i) during the expansion of an approved node—by that point, the node is already marked as stacked; and (ii) when a node is an inactive neighbor of an approved node during expansion, where the distance to non-stacked neighbors is always considered to be infinity.

3.3. Analysis of Removal Criteria

According to [29], the OUT removal criterion involves computing a weight for each stacked node based on its output edges. The lowest value obtained defines the removal threshold. Nodes with distances less than or equal to that threshold are considered approved, since their distance to the source can no longer decrease. In this case, it is necessary to use its current distance together with the cost of its lowest-cost neighbor that is stored in memory. To facilitate the collection of these data, the relations of each node are inserted in an adjacency list in an ordered way, according to the cost of the relation (see Figure 4). This arrangement ensures that the neighbor with the lowest cost always appears first, simplifying the search process.

As for the removal criterion of type IN, for each stacked node, a weight is calculated according to the input edges. The cutoff point is defined according to the shortest distance to the source among the stacked nodes. The calculation of the weight involves searching in memory for the current distance of each node and, among the neighbors that arrive at that node, the one with the lowest cost. This characteristic makes its implementation more complex than the OUT type, since it is necessary to search in the adjacency list all relations that affect the node under analysis. It would be possible to optimize this search by creating a second adjacency list, containing all incoming relations. However, such an approach would increase memory usage. Finally, the INOUT version applies both criteria simultaneously, thus expanding the nodes approved by both criteria.

4. Removal Criteria Evaluation

In order to compare the performance of the three selection criteria, several simulations were performed for each of them, varying the number of nodes in the graph and the number of obstacles.

For such simulations, it was considered that each iteration in the optimized Dijkstra algorithm corresponded to the steps of identifying approved nodes, expanding their neighbors and establishing these nodes. In contrast, in the standard implementation of the Dijkstra algorithm, as the number of approved nodes was always equal to one, the number of iterations was always equal to the number of nodes in the graph. This concept was used here as a comparison parameter between the selection criteria; the fewer the number of iterations, the greater the parallelization of the algorithm.

In every simulation, five metrics were extracted: (i) the number of necessary iterations; (ii) the efficiency gain compared to to the standard approach, generated by dividing the number of iterations of the standard model by the number of iterations of the criterion; (iii) the minimum number of approved nodes in each iteration; (iv) the maximum number of approved nodes in each iteration; and (v) the average number of approved nodes in each iteration.

In addition, to explore potential relationships between the approved nodes of the IN and OUT criteria, simulations using the IN criterion also executed the OUT criterion. In that case, the nodes approved by the OUT criterion were not included in the algorithm processing, being solely for comparison purposes. The same occurred, but in reverse, in the simulations of the OUT model. With these tests, it was possible to identify how many times the nodes approved by one criterion were contained in the nodes approved by the other. It is noteworthy that this analysis did not account for situations in which the two criteria had the same approved nodes, only when they had additional elements.

The simulation results for the IN criterion are presented in

Table 3. IN criteria simulation results.

Nodes	Iterations			Active Nodes		IN in OUT
	IN	Standard	Gain	Max.	Average
64	16	64	4.00	8	4	0
128	22	128	5.82	13	6	0
256	31	256	8.26	19	8	0
512	48	512	10.67	30	11	0
1024	73	1024	14.03	34	14	0
2048	103	2048	19.88	48	20	0
4096	147	4096	27.86	79	28	0

. From these results, it is possible to observe that there was no case in which the results of the IN criterion were contained in the set of results of the OUT criterion.

The results of the OUT criterion are detailed in

Table 4. OUT criteria simulation results.

Nodes	Iterations			Active Nodes		OUT in IN
	OUT	Standard	Gain	Max.	Average
64	17	64	3.76	10	4	12
128	23	128	5.57	11	6	18
256	32	256	8.00	20	8	27
512	50	512	10.24	24	10	42
1024	73	1024	14.03	39	14	61
2048	102	2048	20.08	55	20	94
4096	147	4096	27.86	83	28	141

. It was observed that a significant number of instances existed in which all nodes approved by the OUT criterion were also approved by the IN criterion.

Finally,

Table 5. INOUT criterion simulation results.

Nodes	Iterations			Active Nodes Per Iteration
	INOUT	Standart	Gain	Max.	Average
64	16	64	4.00	8	4
128	22	128	5.82	13	6
256	31	256	8.26	19	8
512	47	512	10.89	30	11
1024	72	1024	14.22	34	14
2048	102	2048	20.08	48	20
4096	147	4096	27.86	71	28

showcases the simulation results of the INOUT criterion. As it is the combination of the application of the two criteria, one might expect that the results of the INOUT criterion would stand out in relation to the others. However, this was not the case. The results were very close to those obtained when the IN and OUT criteria were applied independently.

Considering all the above results, it is possible to observe that the greater the number of nodes in the graph, the greater the gain in relation to the standard model, starting from a gain approximately 3 times greater with graphs of up to 64 nodes and reaching a gain 27 times higher for graphs with up to 4096 nodes. Furthermore, it is noteworthy that all criteria presented similar results.

5. Proposed Solution and Architecture

The goal of this project was to develop an embedded FPGA solution for the SSSP, enabling its integration into real-time operating robots. This solution considered that the robot’s movement graph was fixed and pre-established, with the simulation of obstacles being performed by removing or re-adding nodes during operation. The construction of the robot’s movement graph was performed offline and stored in the FPGA memory.

During robot execution, the system responsible for obstacle recognition and robot movement management acted as the master, communicating with the proposed module (slave) (see Figure 5). The master updated obstacle configurations and provided information about the current source and destination nodes, for which the shortest path needed to be identified. Once the shortest path was found, a flag was generated to indicate its availability. To enable this communication, the proposed solution connected to a communication bus shared with the master.

Internally, the slave implemented an adapted version of the solution proposed by [29]. The simulation results presented little difference between the IN, OUT, and INOUT selection criteria regarding the number of approved nodes by iteration. However, due to its classification method, the IN criterion needed a more complex structure with additional memory access, as previously explained. Thus, to reduce resource consumption, the architectural proposal outlined here employed solely the OUT criterion as the classification method.

The proposed architecture consisted of five primary modules:

• 1. The External Access Controller (EAC) controlled external communications flow;
• The Memory Access Controller (MAC) managed internal memory;
• The Active Node Manager (ANM) handled the management and storage of active nodes, including the identification of approved nodes;
• The Valid Neighborhood Locator (VNL) performed the procedure for expanding the approved nodes;
• The State Machine Controller (SMC) controlled the operation flow of the algorithm, overseeing the other modules.

Each of these modules played a different role in the process of finding the shortest path between the source and the destination node. Detailed explanations of each module’s contributions are provided in the subsequent subsections.

5.1. The External Access Controller

The External Access Controller is the module responsible for managing the project external communication. This module offers a reliable method for communication between the external interface and internal blocks, ensuring consistency across all systems. By utilizing it, there is no need to modify internal input and output signals to match external communication standards. This abstraction simplifies the development of the internal architecture, allowing for greater flexibility in the overall solution. Moreover, if a change in the communication protocol is required, the EAC can be easily adapted without affecting the rest of the system. It is responsible for receiving and updating information on obstacles in the Obstacle Memory Manager, as well as identifying the source and destination nodes. When a new path is to be formed, the EAC inserts the source node into the ANM as an active node and signals the SMC that the process of calculating a new path should be started.

5.2. The Memory Access Controller

For the correct operation of the proposed algorithm, it is necessary to allocate memory resources to store essential operational information. The management of these memories is performed by the MAC. Internally, it creates and manages four memories:

• The obstacle memory stores nodes identified as obstacles;
• The relationship memory stores the relationships of each node, along with their costs;
• The established memory stores nodes that have been established;
• The previous memory stores previous nodes, which are used to form the shortest path.

Both the obstacle memory and the established memory store 1 bit of data for each node in the graph. To create a more specialized solution, it was defined that each node could have up to eight relations. However, the system can support varying numbers of relationships through project customization if necessary. In order to increase parallelism during the expansion process (as explained in subsequent sections), both memories have eight reading ports. This configuration allows them to read information referring to eight neighbors of a node at once.

The relationship memory is responsible for storing all the relations of a node along with their costs. The word size depends on the number of bits needed to represent all the nodes of the graph and on the number of bits needed to represent the highest cost, both multiplied by the number of relations in the graph. For example, in a graph with 1024 nodes, 10 bits of data are required to identify each relation, and if a maximum cost of up to 31 is used, an additional 5 bits for the relation cost. Consequently, if each node had a maximum of eight relations, a total of (10 + 5) × 8 = 120 bits would be necessary per node, as shown in Figure 4. The relationship memory also has eight read ports.

To assemble the shortest path, it is necessary to store the previous node for each node. Starting from the destination node, the shortest path is formed by tracing back the previous nodes until the origin one. As each node only has one previous node, a graph with 1024 nodes, for example, only needs to store 5 bits per node.

The obstacle and relationship memory information is only updated by the master module. The other memories operate dynamically during the shortest-path calculation and are reinitialized at each new search. On the other hand, the relationship memory should preferably function as a ROM memory, with its content created before project execution.

5.3. The Active Node Manager

When an inactive node is identified as the neighbor of an approved node, provided it is not marked as an obstacle, it transitions to an active state and remains so until approved in the classification process. Active nodes are forwarded to the ANM, along with the following information to be stored: (i) the address; (ii) the current distance to the source; (iii) the neighbor address, which identifies its current previous node; and (iv) the non-obstacle neighbor with the lowest cost.

At each new iteration, active nodes undergo an evaluation process. This process compares their classification criterion, calculated by adding the lowest cost value of its neighbors to its current distance from the source, with a general classification criterion which is the minimum criterion among the existing active nodes. Active nodes whose current distance is less than or equal to the general criterion are considered approved and are forwarded to the Valid Neighborhood Locator for the expansion process.

To carry out these activities, the ANM is formed of three sub-blocks (see Figure 6):

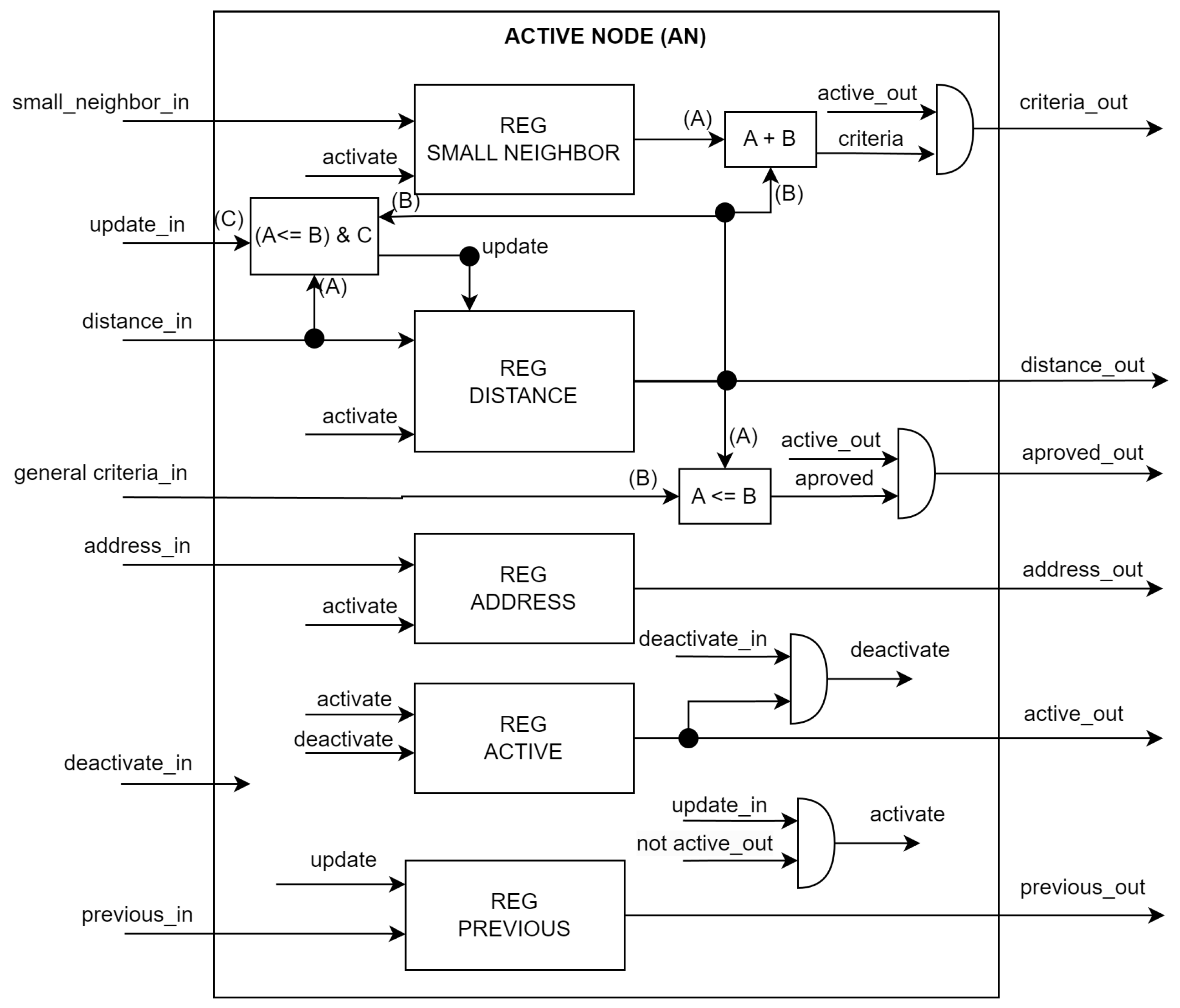
• The Active Node (AN) (Figure 7) stores critical information about each active node, such as its current distance, smallest neighbor, previous node, and address. It is also responsible for calculating the node classification criterion.
• The Active Classifier (AC) identifies the lowest classification criterion among the active nodes.
• The Active Manager (AM) manages the writing processes for active nodes and deactivates established nodes.

Approved nodes are established by marking their position in the established memory and recording the value of their previous node in the previous memory. Furthermore, their corresponding AN is marked as inactive in the ANM, freeing up space to receive new nodes. To determine the minimum criterion, the AC uses a comparator (CA) to receive criteria from active nodes and conduct comparisons. The purpose of this comparison process is to find the smallest criterion among all active nodes. In an ideal scenario, all these comparisons would be performed in a combinational way within a single clock cycle, thus enhancing the system performance. However, due to the number of nodes that must be compared, this is not feasible.

The maximum number of comparators that can be used in a combinational chain is related to the FPGA technology and clock period used. Thus, in order to achieve the best performance, this maximum number of combinational comparators must be configured according to the chosen FPGA. The results section presents some configurations to explore this functionality. As an example, in Figure 8, a structure is shown with eight combinational comparators. In this case, for a structure with sixteen active nodes, only two clock pulses are necessary to find the general criterion.

5.4. The Valid Neighborhood Locator

Each approved node must undergo an expansion process in the VNL (see Figure 9) to update the distances of its neighbors to the source. To accomplish this, the first step is to identify valid neighbors—nodes that are not obstacles and have not yet been established. Additionally, it finds the neighbor of the neighbor (sub-neighbor) with a lower cost, as this information is used in the calculation of the OUT criterion in the classification step. It is important to note that this lower-cost neighbor must also not be an obstacle, which requires a check with the obstacle memory. Thus, for each approved node, the following readings are performed in the memories, considering MAX_N as the maximum number of allowed neighbors per node:

• One x relationship memory—identifies node relationships;
• MAX_N x obstacle memory—identifies relationships that are obstacles;
• MAX_N x established memory—identifies established relationships;
• MAX_N x relationship memory—analyzes neighbor relationships to identify the smallest neighbor cost;
• MAX_N x MAX_N x obstacle memory—identifies the smallest neighbor obstacles.

After the expansion process, the distance from the approved node to the source is added to the cost of moving from the current approved node to its neighbor. This generates a potential distance from the neighbor to the source, which is then stored in ANM. This new distance is only stored in two situations: (i) when it is a new node being activated, as it does not yet have a valid distance; or (ii) when the new distance is smaller than the currently stored one. Whenever the distance value of a node is changed, the previous node address of that node is also updated to the address of the current approved node.

Each approved node has its expansion process carried out independently by multiple Aproved Node Expander (ANE) instances, enabling parallelism. External reads and writes are coordinated by the Writing Reading Manager (WRM). Upon activation, the Aproved Node Expander first performs a request to read the relations of its approved node. This request is received by the Writing Reading Manager and forwarded to the Memory Access Controller. Once the requested information becomes available, the relations are stored in internal registers. Subsequently, requests are made to read the obstacles and established node memories sequentially, in order to identify the valid neighbors.

Once the obstacle and established neighbors are identified, the expansion process of each neighbor is carried out. This involves identifying the neighbors of each neighbor, discarding sub-neighbors that are obstacles, and finding the cost of the smallest sub-neighbor. Then, the neighbor information is requested to be updated in the Active Node. This process is then repeated for each valid neighbor of a node until all neighbors have been analyzed. At this point, a signal is sent to the SMC, indicating that the expansion process has finished.

5.5. The State Machine Controller

The State Machine Controller plays a central role in overseeing the entire shortest path identification process. It sends activation and deactivation signals to the other modules, dictating which steps of the algorithm should be executed. It also monitors the process and determines when it is complete.

Upon receiving the start signal from the External Access Controller, it updates the general classification criterion in the Active Node Manager with the information from currently active nodes, in this case, the source node. Next, it checks if there are any approved nodes. If so, it stores the information of the approved nodes in a buffer. This step is necessary because the approved nodes are deactivated in the Active Node Manager at the beginning of the process, freeing up space for writing new nodes. However, the distance and address information of the approved node are still used during the expansion process. Then, it signals the VNL to begin the analysis of the approved nodes stored in the buffer. Once all approved nodes have been read and analyzed, the VNL and the State Machine Controller start a new classification criterion update. This cycle continues until there are no more approved nodes, indicating the completion of the node expansion process. At that moment, the path from the information stored in the MAC can be identified and made available to the master.

The SMC implements a Finite State Machine (FSM) with seven states (see Figure 10): (i) IDLE; (ii) UPDATE_CLASSIFICATION; (iii) EXPAND; (iv) UPDATE_BUFFER; (v) HAS_APPROVED; (vi) FORM_PATH; and (vii) READY.

The FSM of the State Machine Controller starts in the IDLE state and remains in that state until it receives the start signal from the External Access Controller to calculate a new shortest path. Upon receiving this signal, the FSM transitions to the UPDATE_CLASSIFICATION state, where it updates the general classification criterion in the Active Node Manager with the information from currently active nodes, in this case, the source node.

Subsequently, the FSM checks if there are any approved nodes. If so, it changes to the UPDATE_BUFFER state, where it stores the information of the approved nodes in a buffer. This step is necessary because the approved nodes are deactivated in the Active Node Manager at the beginning of the process, freeing up space for writing new nodes. However, the distance and address information of the approved node are still used during the expansion process. Then, the FSM transitions to the EXPAND state, where the VNL reads and analyzes the approved nodes stored in the buffer. Once all approved nodes have been read and analyzed, VNL activates the vnl_ready signal, and the FSM returns to the UPDATE_CLASSIFICATION state. This cycle continues until there are no more approved nodes, indicating the completion of the node expansion process.

When there are no more approved nodes, the FSM switches to the FORM_PATH state. In this state, it is ready to send the shortest path to the master application. Starting from the destination node, each subsequent read request from the master retrieves the next previous node from the previous memory stored in the MAC. This information is then transmitted through the External Access Controller. Once the source node has been reached, indicating the completion of the path formation process, the FSM returns to the IDLE state to await a new request.

6. Architecture Evaluation

In this section, we present the results obtained using the EP4CE115F29C7, an Altera FPGA from the Cyclone IV E family. This choice was based on the advantages offered by this family of devices, including its low cost and reduced energy consumption. The source and destination nodes chosen were the ones with the greatest spatial separation, thereby accounting for the worst-case scenario and the longest processing time. This relates to the fact that the algorithm ends when the source node is established, which implies that nearby nodes exhibit shorter execution time. As an example, Figure 2 depicts a situation with 30 nodes, where white nodes denote obstacles, and the red ones delineate the shortest path.

During the simulation and testing stage, it was observed that the maximum number of active nodes depended on certain graph characteristics, such as the total number of nodes, and the maximum number of connections per node. Since the active nodes are stored in the AN modules, an insufficient number of AN modules leads to errors. For instance, in situations where a neighboring node of an approved node cannot be stored due to space constraints, system crashes will occur. On the other hand, an excessive number of AN modules can result in a waste of resources. Therefore, it is necessary to use a value equal to the maximum number of simultaneously active nodes.

In this architecture proposal, a graph with 1024 nodes and up to eight relations was used in some of the tests we performed. Since the outcomes of the simulations indicated that the maximum number of active nodes was 88, this was the number of Active Node modules used. The same procedure was adopted for graphs of different sizes.

Tests were performed in order to measure the impact of using different numbers of comparators during the classification step in the Active Node Manager, as shown in

Table 6. Results obtained using varying numbers of comparators for a graph with 1024 nodes and up to 8 relations.

NUM CA	Best Clock (ns)	Clock Pulses	Time with Best Clock (ns)	Gain against Worst
1 CA	12.0	20,654	247,842	1.67
2 CA	12.0	16,784	201,402	2.06
3 CA (best)	12.0	15,434	185,202	2.24
4 CA	14.0	14,804	207,249	2.00
5 CA	20.0	14,444	288,870	1.43
6 CA	22.0	14,174	311,817	1.33
7 CA	25.5	13,994	356,834	1.16
8 CA (worst)	30.3	13,814	414,405	-

. The experiment demonstrated that increasing the number of comparators resulted in a decrease in necessary clock pulses for the shortest path calculation. However, the increasing complexity of comparators demanded a decrease in clock period in order to adhere to FPGA constraints. Therefore, when considering the simulation time based on the clock frequency achieved for each test, the configuration using three comparators emerged as the most efficient.

There were also tests carried out to analyze the impact of varying the number of ANEs. As shown in

Table 7. Results with different number of ANEs for a graph with 1024 nodes and up to 8 relations.

NUM ANE	Best Clock (ns)	Clock Pulses	Time with Best Clock (ns)	Gain against Worst
1 ANE (worst)	12.00	34,829	417,942	-
2 ANEs	12.00	23,367	280,398	1.491
4 ANEs	12.00	16,579	198,942	2.101
8 ANEs (best)	12.00	15,434	185,202	2.257
9 ANEs	12.00	15,437	185,238	2.256
10 ANEs	12.00	15,446	185,346	2.255
16 ANEs	12.00	15,691	188,286	2.220
32 ANEs	12.00	15,737	188,838	2.213

, there was a time stabilization when using eight ANEs. This occurred because the data buses were saturated, with no space for inserting more requests. On the other hand, a reduction in performance was observed due to the increased complexity in the process of managing these information exchanges. Moreover, there was a progressive rise in the use of FPGA resources as registers and LUTs. Thus, for the graph used, the ideal configuration was achieved when using eight ANEs.

Tests conducted using graphs of different sizes (see

Table 8. Synthesis results for various graphs on the EP4CE115F29C7 FPGA.

Nodes	Clock Pulses	Best Clock (ns)	Sim. Time (ns)	LUTs (%)	Registers (%)	Memory (%)
2048	27,102	15	406,523	51	18	58
1024	15,434	12	185,202	37	14	26
512	7859	12	94,302	34	13	13
256	4078	11	44,853	19	9	8
128	2212	11	24,327	15	7	8
64	1468	11	16,143	11	6	8

) demonstrated the possibility of embedding graphs with fewer than 2048 nodes in the EP4CE115F29C7 FPGA. In addition, it was observed that the processing time and resource consumption generally remained proportional to the increase in the number of nodes. For graphs with 1024 nodes, resource consumption was below 40%, which indicated the possibility of replacement by a lower-cost FPGA from the same family with reduced resources.

6.1. Impacts of Dedicated Obstacle Memory

One of the key features of this project was the implementation of separate memories for relationships and obstacles. This unique characteristic enabled easy modifications to the graph configuration by simply altering the obstacle memory. The effectiveness of this approach is illustrated in

Table 9. Transfer results with different data bus sizes.

	Results According to Bus Data Width
Bus data width	32	64	128	256	512
Number of transfers for 1024 bits	32	16	8	4	2
Number of transfers for 122,880 bits	3840	1920	960	480	240
Time to transfer 122,880 bits at 100 MHz (ns)	38,400	19,200	9600	4800	2400
Time to transfer 1024 bits at 100 MHz (ns)	320	160	80	40	20
Gain	120	120	120	120	120

, which demonstrates its application on a 1024-node graph with varying data bus sizes between this project and the master application.

The data requirements for a 1024-node graph with eight relations and a maximum cost of 31 units are demonstrated in Figure 4. To represent the relations of each node, 120 bits of storage per node were necessary, resulting in a total of 122,880 bits to represent the entire graph. In a conventional application, transferring 122,880 bits of data would be required for each new graph configuration. However, the use of the obstacle memory simplified that process significantly, as only 1 bit per node was needed. Consequently, the data to be transmitted were reduced to only 1024 bits.

This innovative approach reduces the time required for transferring a new configuration. For graphs with 1024 nodes, this improvement can reach up to 120 times when compared to the traditional approach, regardless of the data bus size. Moreover, the benefits extend to larger graphs, with gains of up to 480 times for graphs with 4096 nodes, for example.

When considering the contribution of this performance improvement relative to the total processing time, the advantages of this approach became clearer. As shown in

Table 10. Gain according to transfer type in a 32-bit data bus and the processing time for different graph sizes with a 125 MHz clock.

Nodes	Processing Time (ns)	Relations and Obstacles (ns)	Obstacles Only (ns)	Gain (%)
2048	406,523	472,059	407,035	15.98%
1024	185,202	215,922	185,458	16.43%
512	94,302	108,638	94,430	15.05%
256	44,853	51,509	44,917	14.68%
128	24,327	27,399	24,359	12.48%
64	16,143	17,551	16,159	8.61%

, the gain compared to the conventional model could reach 16% when using a 32-bit bus in both cases. Tests showed that smaller buses yielded greater gains. For example, 8-bit buses presented a gain of 63.66%. Conversely, larger buses, such as a 512-bit one, only achieved a 1% gain. This discrepancy occurred due to the greater transfer potential of larger buses, ultimately reducing the impact of the transfer process on the total processing time.

6.2. Comparison with Reference Models

To validate the obtained results, two reference models were created. The first model was an application developed in C, optimized to run on a computer equipped with an AMD Ryzen 5 3600 six-core processor running at a clock frequency of 3.59 GHz. The second reference model consisted of an application created using an Altera NIOS II processor and the EP4CE115F29C7 FPGA. In that application, the same C program used in the computer tests was executed.

The results obtained with the two reference models, along with the results achieved in the proposed solution with the best clock obtained for each graph size, can be seen in

Table 11. Comparison with reference models.

Nodes	Simulation Time (ns)			Gain
	Nios II 125 MHz	PC	This Solution	NIOS II	PC
2048	368,469,861	5,049,900.0	407,035	905.3	12.4
1024	166,728,444	3,776,000.0	185,458	899.0	20.4
512	75,204,452	2,003,100.0	94,430	796.4	21.2
256	33,799,636	1,711,600.0	44,917	752.5	38.1
128	15,597,804	758,900.0	24,359	640.3	31.2
64	7,548,676	672,700.0	16,159	467.2	41.6

. The last two columns of the table demonstrate the gains obtained. For all cases, the proposed application demonstrated superior performance. These gains are also shown in Figure 11.

6.3. Comparison with Other Solutions

A research effort was conducted to identify publications that most closely matched the specific context of the project, despite the differences. Factors such as the size of the graph, number of edges per node, FPGA selection, and project context influence the effectiveness of such comparisons. The result of this research can be seen in

Table 12. Runtime comparison with other solutions.

Solution	Nodes	Frequency	Time (ns)	This Solution (ns)	Gain
[23]	128	79 MHz	45,587	28,026	1.63
[26]	256	139 MHz	42,000	29,375	1.43
[4]	1024	125 MHz	425,000	123,724	3.44
[24]	4096	200 MHz	390,000	274,378	1.42

. To carry out the comparison, simulations of this project were conducted using the same clock frequency obtained in the cited papers and a 32-bit data transfer bus.

The research described in [23] introduces an FPGA-based solution for computing the shortest path in OSPF networks. This approach enhances the efficiency of the Dijkstra algorithm, reducing its processing time from $O\left(n^2\right)$ to $O\left(n\right)$. The proposed solution processes graphs with up to 128 nodes in 45,587 ns, a processing time 1.63x slower than our proposal.

In study [26], an FPGA solution is introduced as a coprocessor for software running on Linux. That solution achieves a maximum graph size of 256 nodes for the specific FPGA utilized, with a processing time of 42,000 nanoseconds, 1.43 times lower than that achieved by the model described in this paper. However, the performance of the project is compromised in [26] due to the need to load the entire graph into the FPGA for each new analysis. This approach proves to be particularly inefficient when larger graphs are employed, as illustrated in Table 9.

In [24], a heterogeneous CPU-FPGA solution is introduced to solve the All-Pairs Shortest-Path (APSP) problem. Although that solution shares some similarities with the approach presented here, such as performing graph generation outside the FPGA, it is specifically designed to handle larger graphs and addresses the more complex APSP problem. Notably, their results demonstrate a processing time 1.42 times smaller than the one reported in this paper for a graph containing 4096 nodes.

The primary emphasis of work [4] lies in optimizing the PRM using FPGA. However, since it lacks a dedicated solution for calculating the shortest path, its overall performance is negatively affected, requiring a substantial 425 $\mathsf{\mu }$s solely for that step. Table 12 illustrates that under similar conditions, adopting the solution proposed in this paper could potentially yield an approximate 3.44 times improvement in the shortest path calculation.

Based on the results presented, replacing the shortest-path algorithm used in [4] with our approach achieved a 47% reduction in the processing time of all the motion planning, from 650 $\mathsf{\mu }$s (225 $\mathsf{\mu }$s planning + 425 $\mathsf{\mu }$s pathfinding) to 349 $\mathsf{\mu }$s (225 $\mathsf{\mu }$s planning + 124 $\mathsf{\mu }$s pathfinding) on a 125 MHz FPGA.

Furthermore, the proposed solution demonstrated competitive performance against recent low-latency motion planning approaches. For instance, the RRT-based ASIC architecture presented in [33] achieved processing times between 350 $\mathsf{\mu }$s and 960 $\mathsf{\mu }$s at 1000 MHz. While operating at a lower clock frequency, our solution exhibited comparable processing times. Embedding both approaches in ASICs is expected to further improve the efficiency advantage of our proposal.

6.4. Improvement Points

One crucial aspect that can significantly impact performance is the number of memory reading ports. In the current proposal, the memories were equipped with eight reading channels, which restricted access to just one ANE at a time. Consequently, a pipeline of read requests had to be implemented. It was determined that eight ANEs would be optimal, but employing a larger number of ports, specifically multiples of eight, could potentially yield even better results. Further testing is required to verify this hypothesis.

Another aspect with the potential for significant improvement is the utilization of comparators for identifying the general selection criterion. In the current project, a structure resembling a comparator accumulator was employed. However, exploring alternative structures that can leverage parallelism more effectively during the comparison process could lead to better performance outcomes. Nonetheless, a dedicated study is essential to investigate which techniques could be employed, while also assessing the possible losses and benefits associated with each technique.

An important consideration regarding the selection of the relation memory structure is the consistent allocation of space for storing eight relations per node. However, it was noted that some nodes did not establish connections with all eight neighboring nodes, resulting in unused resources allocated for these unutilized connections. Despite this, maintaining a standardized structure is crucial for ensuring consistent operations. Introducing varying sizes in memory could add complexity, potentially outweighing any performance gains. Nonetheless, a comprehensive analysis is required to fully assess this possibility.

7. Conclusions

This work proposed solutions to the problem of identifying the shortest path between two nodes in a graph, which is crucial for guiding a robot in a configuration space. The proposed solution aimed to achieve low response times, enabling its use in real-time processing applications. The project anticipated dynamic changes in the environment, providing a simple and efficient method for inserting or removing obstacles. By incorporating dedicated memory for obstacle identification, the project achieved a remarkable 120× improvement in graph updating compared to traditional models for graphs with 1024 nodes. Tests also demonstrated significant gains in system efficiency, particularly when compared to reference software models, with a 20 times greater improvement for graphs consisting of 1024 nodes.

As part of our future work, we propose to develop a PRM application for FPGA and create an embedded solution capable of controlling a robot in real time, thus validating the entire process. For optimal performance, this solution should integrate the entire project onto a single FPGA, thereby eliminating communication bottlenecks.