Sliding-Mode Control of Linear Induction Motor Based on Exponential Reaching Law
Abstract
:1. Introduction
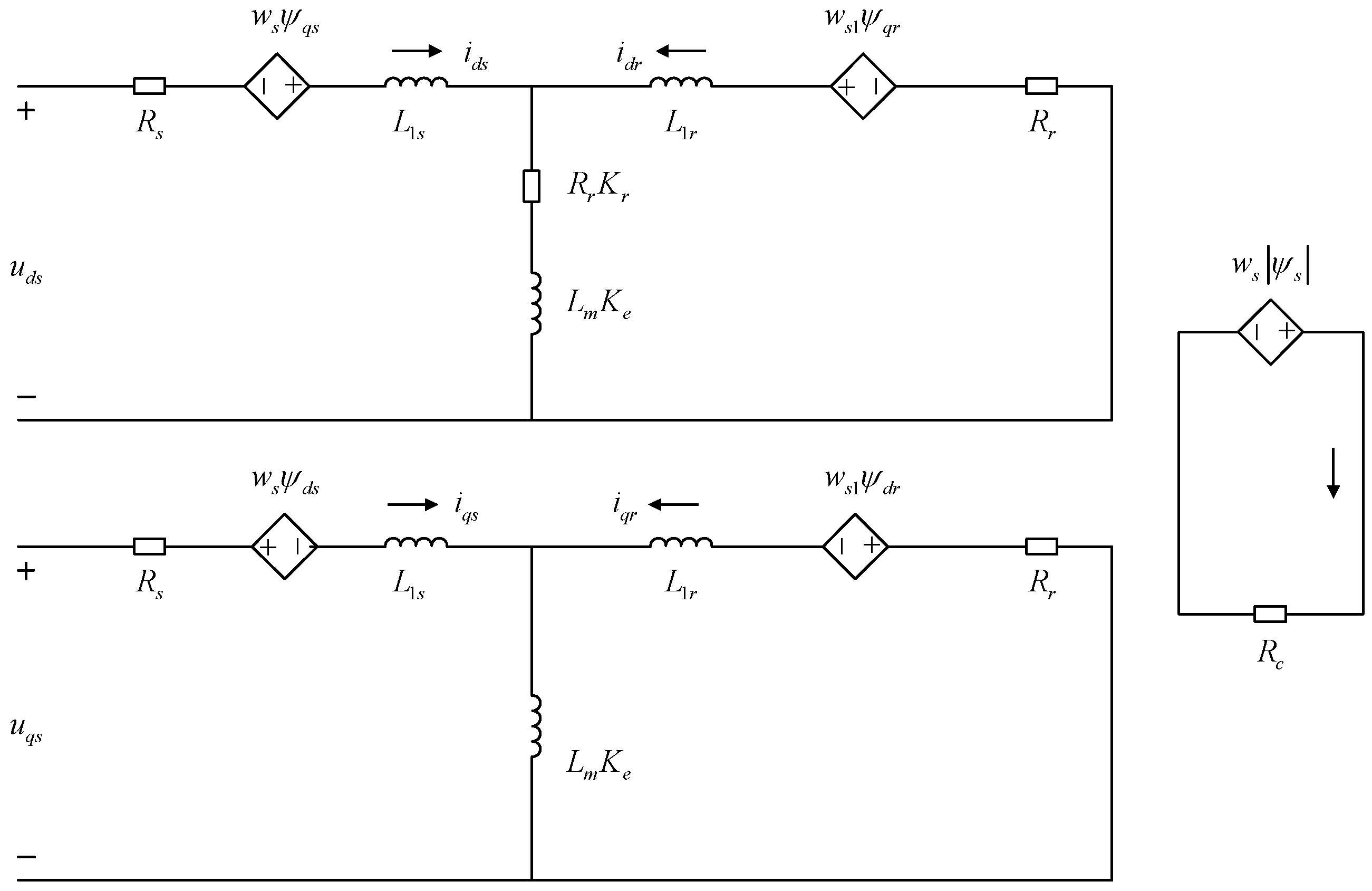
2. Mathematical Modeling of Linear Induction Motors
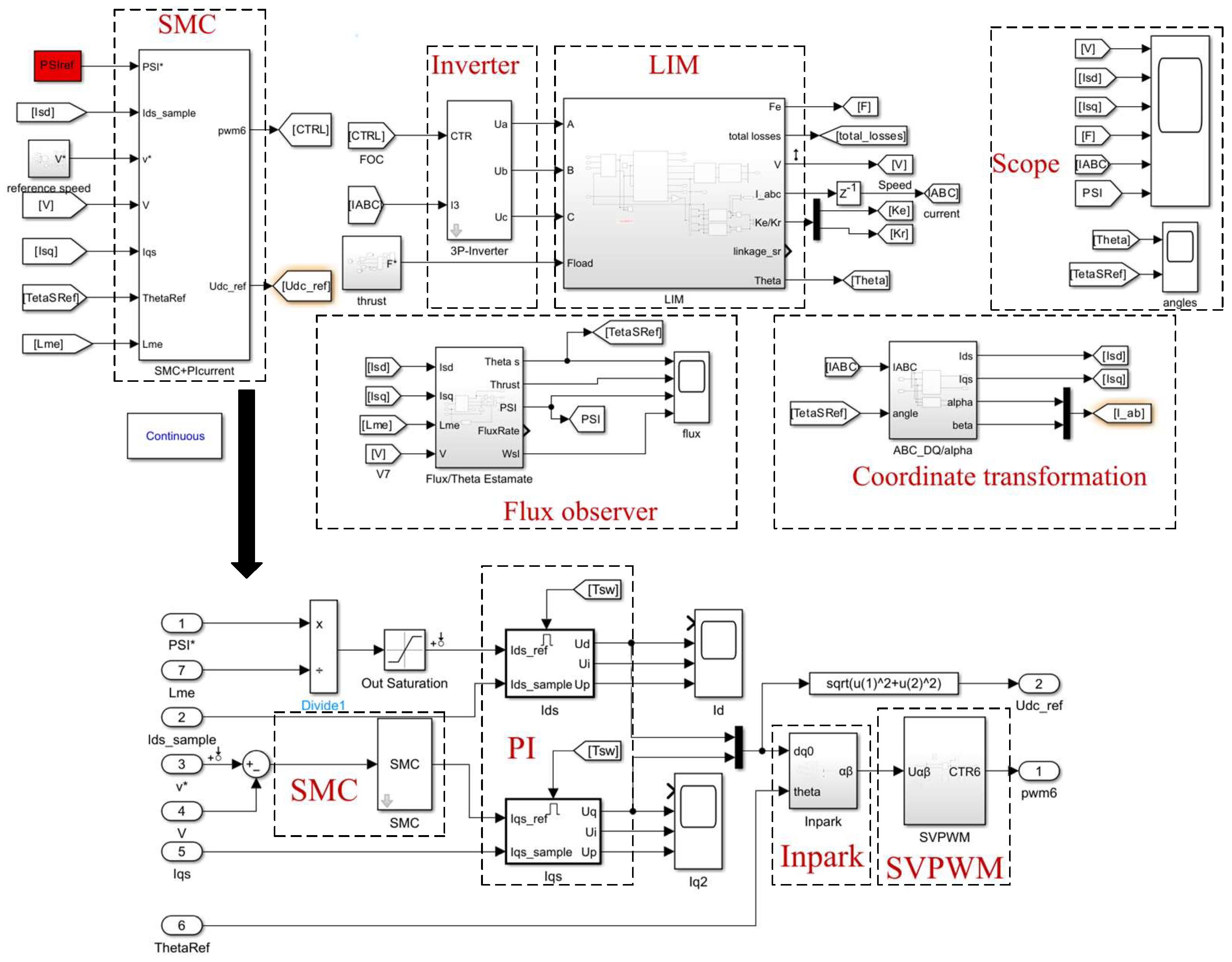
3. Sliding-Mode Controllers
3.1. Design for Reaching Law
3.2. Stabilization Analysis
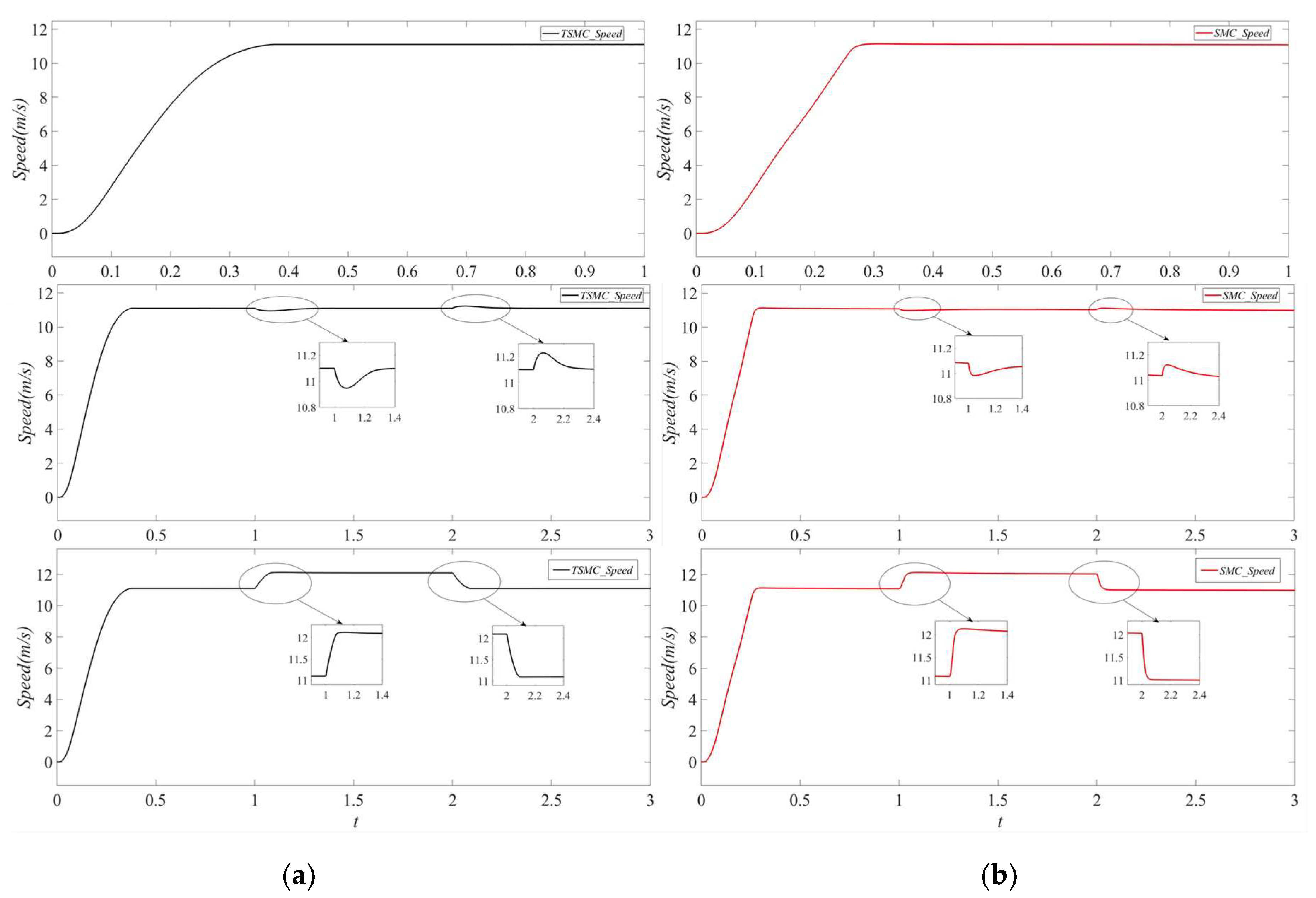
4. Simulation and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbols | Definition |
|---|---|
| Rs | Primary (stator) resistance |
| Rr | Secondary (rotor) resistance |
| Rc | Iron loss resistance |
| L1s | Primary (stator) leakage inductance |
| L1r | Secondary (rotor) leakage inductance |
| Ls | Primary (stator) Inductance |
| Lr | Secondary (rotor) inductance |
| Lm | Magnetizing inductance |
| ids, iqs | Primary d- and q-axis currents |
| Ψdr | Secondary d-axis flux |
| ωs | Primary angular frequency |
| ωr | Electric angular velocity of secondary |
| s | Slip |
| ωs1 | Slip angular frequencies |
| F | Thrust |
| T | Electromagnetic torque |
| τ | Pole pitch |
| LIM | Linear induction motors |
| SMC | Sliding-mode control |
| PID | Proportion integration differentiation |
| RIM | Rotary inductance motors |
| SVPWM | Space vector pulse width modulation |
| Parameters | Values | Unit |
|---|---|---|
| Pole-pair number | 6 | - |
| Pole pitch | 0.2808 | m |
| Rated flux | 6 | Wb |
| Primary resistance | 0.138 | Ω |
| Secondary resistance | 46.4 | Ω |
| Iron loss resistance | 167 | Ω |
| Magnetizing inductance | 0.026477 | H |
| Primary leakage inductance | 0.006688 | H |
| Secondary leakage inductance | 0.002091 | H |
| Secondary length | 2.476 | m |
References
- Li, J.Q.; Li, W.L.; Deng, G.Q.; Ming, Z. Continuous-Behavior and Discrete-Time Combined Control for Linear Induction Motor-Based Urban Rail Transit. IEEE Trans. Magn. 2016, 52, 8500104. [Google Scholar] [CrossRef]
- Boldea, I.; Pucci, M.; Xu, W. Design and Control for Linear Machines, Drives, and MAGLEVs—Part I. IEEE Trans. Ind. Electron. 2018, 65, 7423–7426. [Google Scholar] [CrossRef]
- Boldea, I.; Tutelea, L.N.; Xu, W.; Pucci, M. Linear Electric Machines, Drives, and MAGLEVs: An Overview. IEEE Trans. Ind. Electron. 2018, 65, 7504–7515. [Google Scholar] [CrossRef]
- Lai, C.K.; Shyu, K.K. A Novel Motor Drive Design for Incremental Motion System via Sliding-Mode Control Method. IEEE Trans. Ind. Electron. 2005, 52, 499–507. [Google Scholar] [CrossRef]
- Sun, Q.; Cheng, M.; Zhou, O. Variable-parameter PI control of a new biconvex permanent magnet motor speed control system. Chin. J. Electr. Eng. 2003, 7, 117–122. [Google Scholar]
- Oh, W.S.; Kim, Y.T.; Kim, C.S.; Kwon, T.S.; Kim, H.J. Speed control of induction motor using genetic algorithm based fuzzy controller. In Proceedings of the IECON’99. Conference Proceedings, 25th Annual Conference of the IEEE Industrial Electronics Society (Cat. No.99CH37029), San Jose, CA, USA, 29 November 1999–3 December 1999; IEEE: New York, NY, USA, 1999; Volume 2, pp. 625–629. [Google Scholar]
- Zhang, Z.; Wang, G.; Wang, Z.; Liu, Q.; Wang, K. Neural network based Q-MRAS method for speed estimation of linear induction motor. Measurement 2022, 205, 112203. [Google Scholar] [CrossRef]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Hung, J.Y.; Gao, W.; Hung, J.C. Variable structure control: A survey. IEEE Trans. Ind. Electron. 1993, 40, 2–22. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Z.X.; Pan, J.M.; Wang, J. Fixed boundary layer sliding mode control of permanent magnet linear synchronous motors. Chin. J. Electr. Eng. 2006, 26, 115–121. [Google Scholar]
- Yanfeng, T.; Qingding, G. Sliding mode-H∞ robust tracking control of permanent magnet linear synchronous motor. J. Electrotechnol. 2004, 2, 1060–1064. [Google Scholar]
- Chiang, H.H.; Hsu, K.C.; Li, I.H. Optimized Adaptive Motion Control Through an SoPC Implementation for Linear Induction Motor Drives. IEEE ASME Trans. Mechatron. 2015, 20, 348–360. [Google Scholar] [CrossRef]
- Levant, A. Chattering Analysis. IEEE Trans. Autom. Control 2010, 55, 1380–1389. [Google Scholar] [CrossRef]
- Utkin, V.I.; Poznyak, A.S. Adaptive sliding mode control with application to super-twist algorithm: Equivalent control method. Automatica 2013, 49, 39–47. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A New Reaching Law for Antidisturbance Sliding-Mode Control of PMSM Speed Regulation System. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Junejo, A.K.; Xu, W.; Mu, C.; Ismail, M.M.; Liu, Y. Adaptive Speed Control of PMSM Drive System Based a New Sliding-Mode Reaching Law. IEEE Trans. Power Electron. 2020, 35, 12110–12121. [Google Scholar] [CrossRef]
- Feng, L.; Sun, X.; Guo, D.; Yao, M.; Diao, K. Advanced Torque Sharing Function Strategy with Sliding Mode Control for Switched Reluctance Motors. IEEE Trans. Transp. Electrif. 2023, 10, 2302–2311. [Google Scholar] [CrossRef]
- Su, X.; Liu, X.; Song, Y.D. Event-Triggered Sliding-Mode Control for Multi-Area Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 6732–6741. [Google Scholar] [CrossRef]
- Kun, D. Active power factor correction using sliding mode control with reaching law. In Proceedings of the 2007 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007; IEEE: New York, NY, USA, 2007. [Google Scholar]
- Hou, Q.; Ding, S.; Yu, X. Composite Super-Twisting Sliding Mode Control Design for PMSM Speed Regulation Problem Based on a Novel Disturbance Observer. IEEE Trans. Energy Convers. 2021, 36, 2591–2599. [Google Scholar] [CrossRef]
- Ge, Y.; Yang, L.; Ma, X. Adaptive sliding mode control based on a combined state/disturbance observer for the disturbance rejection control of PMSM. Electr. Eng. 2020, 102, 1863–1879. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, Z.; Li, J.; Zhang, H.; Gerada, C. A Third-Order Super-Twisting Extended State Observer for Dynamic Performance Enhancement of Sensorless IPMSM Drives. IEEE Trans. Ind. Electron. 2020, 67, 5948–5958. [Google Scholar] [CrossRef]
- Qian, R.; Luo, M.; Sun, P. Improved nonlinear sliding mode control based on load disturbance observer for permanent magnet synchronous motor servo system. Adv. Mech. Eng. 2016, 8, 168781401664267. [Google Scholar] [CrossRef]
- Lim, S.; Nam, K. Loss-minimising control scheme for induction motors. IEE Proc. Electr. Power Appl. 2004, 151, 385. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T.A. Modeling and control of a multi-phase induction machine with structural unbalance. IEEE Trans. Energy Convers. 1996, 11, 570–577. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T.A. Space vector PWM control of dual three-phase induction machine using vector space decomposition. IEEE Trans. Ind. Appl. 1995, 31, 1100–1109. [Google Scholar] [CrossRef]
- Garcia, G.O.; Luis, J.C.M.; Stephan, R.M.; Watanabe, E.H. An efficient controller for an adjustable speed induction motor drive. IEEE Trans. Ind. Electron. 1994, 41, 533–539. [Google Scholar] [CrossRef]

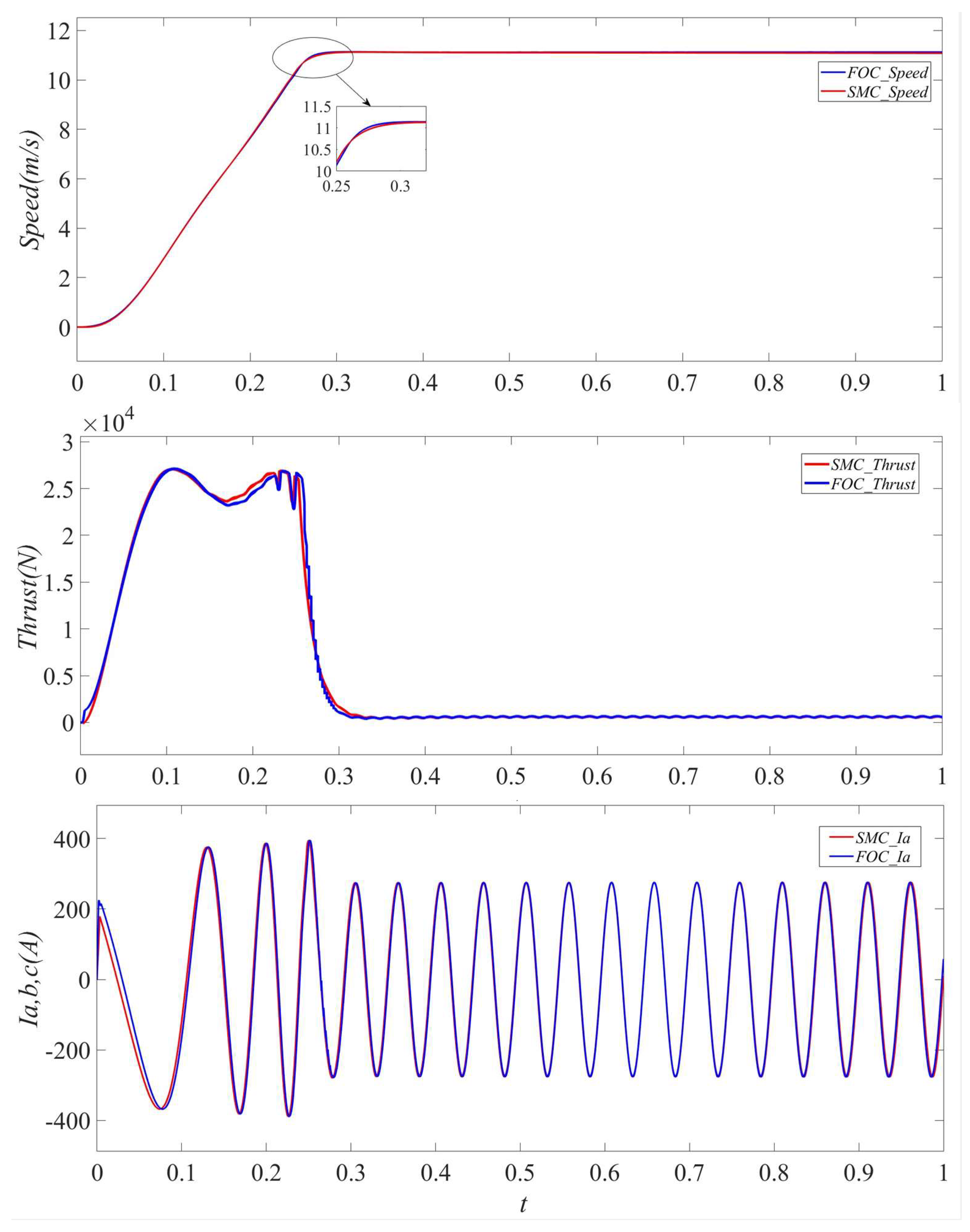
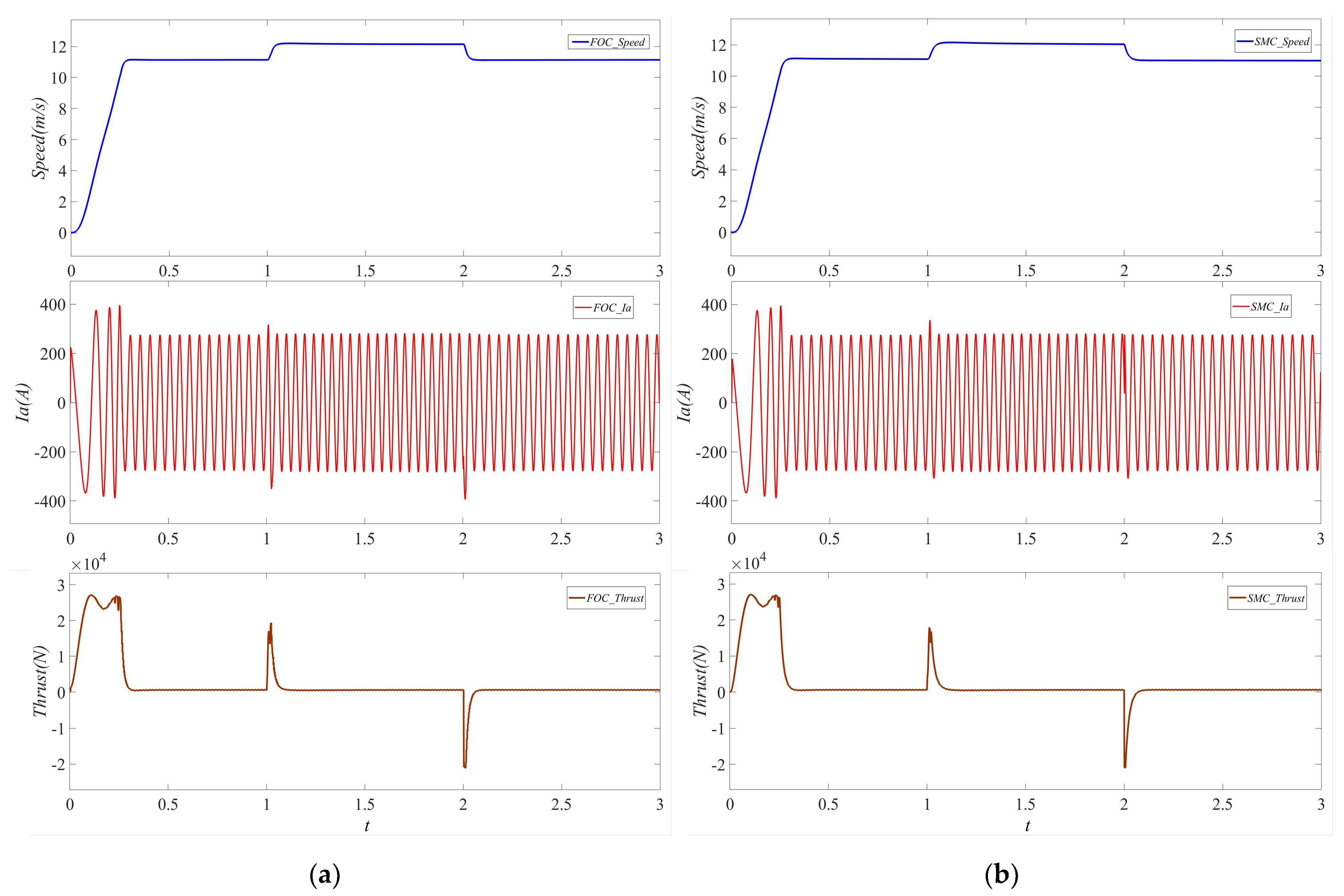

| ts(s) | |||||
|---|---|---|---|---|---|
| Constant Speed | Acceleration | Deceleration | Adding Loads | Subtracting Loads | |
| PI | 0.259 | 1.0455 | 2.0375 | 1.3195 | 2.3846 |
| SMC | 0.258 | 1.0366 | 2.0313 | 1.3011 | 2.3376 |
| ts(s) | ||
|---|---|---|
| Adding Loads | Subtracting Loads | |
| PI | 0.1001 | 0.0837 |
| SMC | 0.099 | 0.0829 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Zhao, J.; Xiong, Y.; Wang, H.; Yao, X. Sliding-Mode Control of Linear Induction Motor Based on Exponential Reaching Law. Electronics 2024, 13, 2352. https://doi.org/10.3390/electronics13122352
Ma S, Zhao J, Xiong Y, Wang H, Yao X. Sliding-Mode Control of Linear Induction Motor Based on Exponential Reaching Law. Electronics. 2024; 13(12):2352. https://doi.org/10.3390/electronics13122352
Chicago/Turabian StyleMa, Shuhang, Jinghong Zhao, Yiyong Xiong, Hanming Wang, and Xing Yao. 2024. "Sliding-Mode Control of Linear Induction Motor Based on Exponential Reaching Law" Electronics 13, no. 12: 2352. https://doi.org/10.3390/electronics13122352







