Adaptive Multi-Surface Sliding Mode Control with Radial Basis Function Neural Networks and Reinforcement Learning for Multirotor Slung Load Systems
Abstract
:1. Introduction
1.1. Background
1.2. Overview
- (i)
- Investigation of an RBFNN-MSSC applied to a thrust-vectored multirotor for trajectory tracking purposes;
- (ii)
- Application of a DQN-based RL agent to a slung load pendulum;
- (iii)
- Comparison of the performance of the combined control system with an RBFNN-MSSC applied to the entire multirotor slung load (MSL) system, based on the slung load oscillations.
2. Methodology
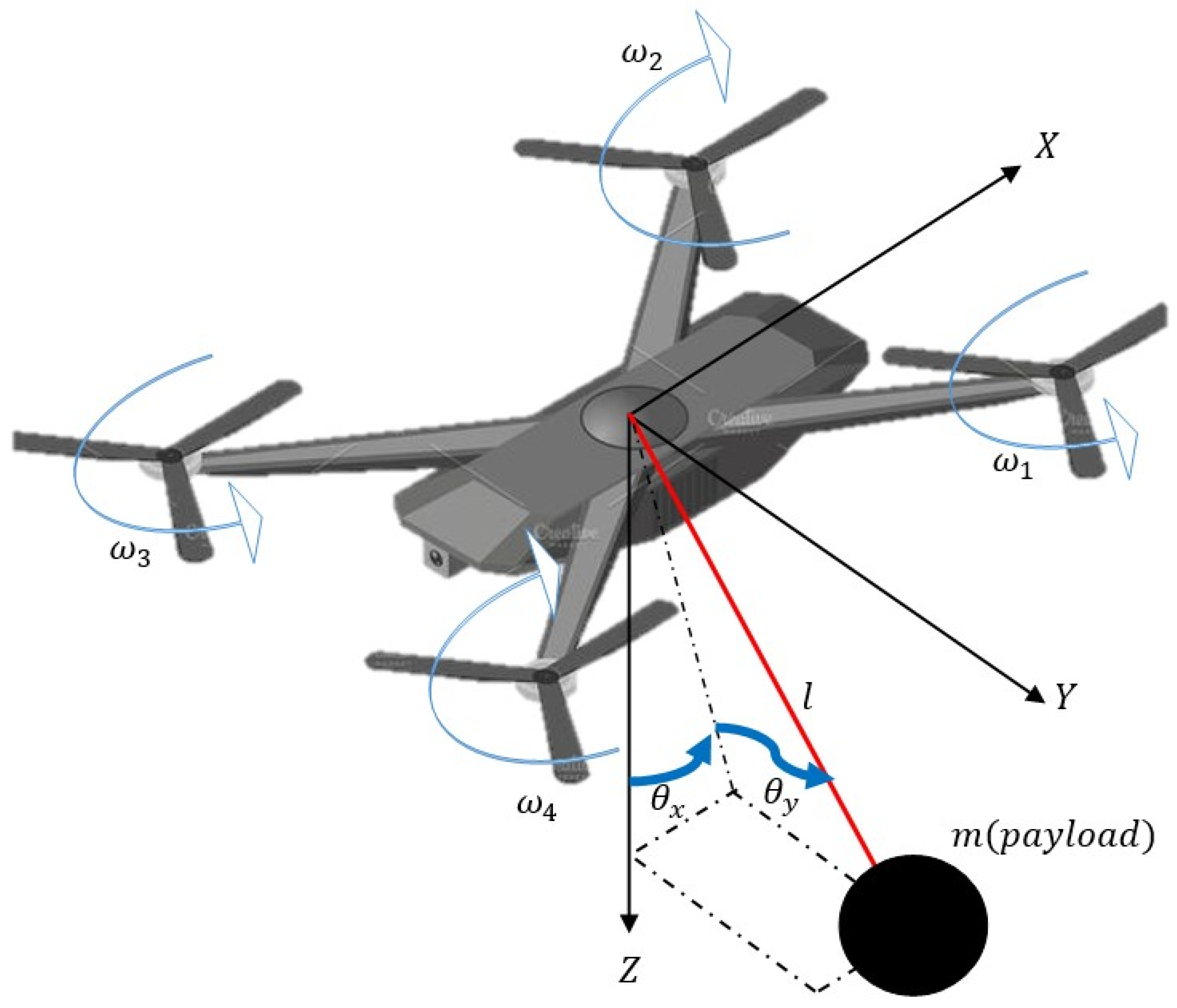
2.1. Dynamic Modeling
2.1.1. Multirotor Dynamics
2.1.2. Slung Load Dynamics
2.2. Multi-Surface Sliding Mode Control
2.3. Neural Network Approximation
2.4. RBFNN-Based MSSC
- (i)
- when , then , with , where .
- (ii)
- ; substituting into (65), we obtain
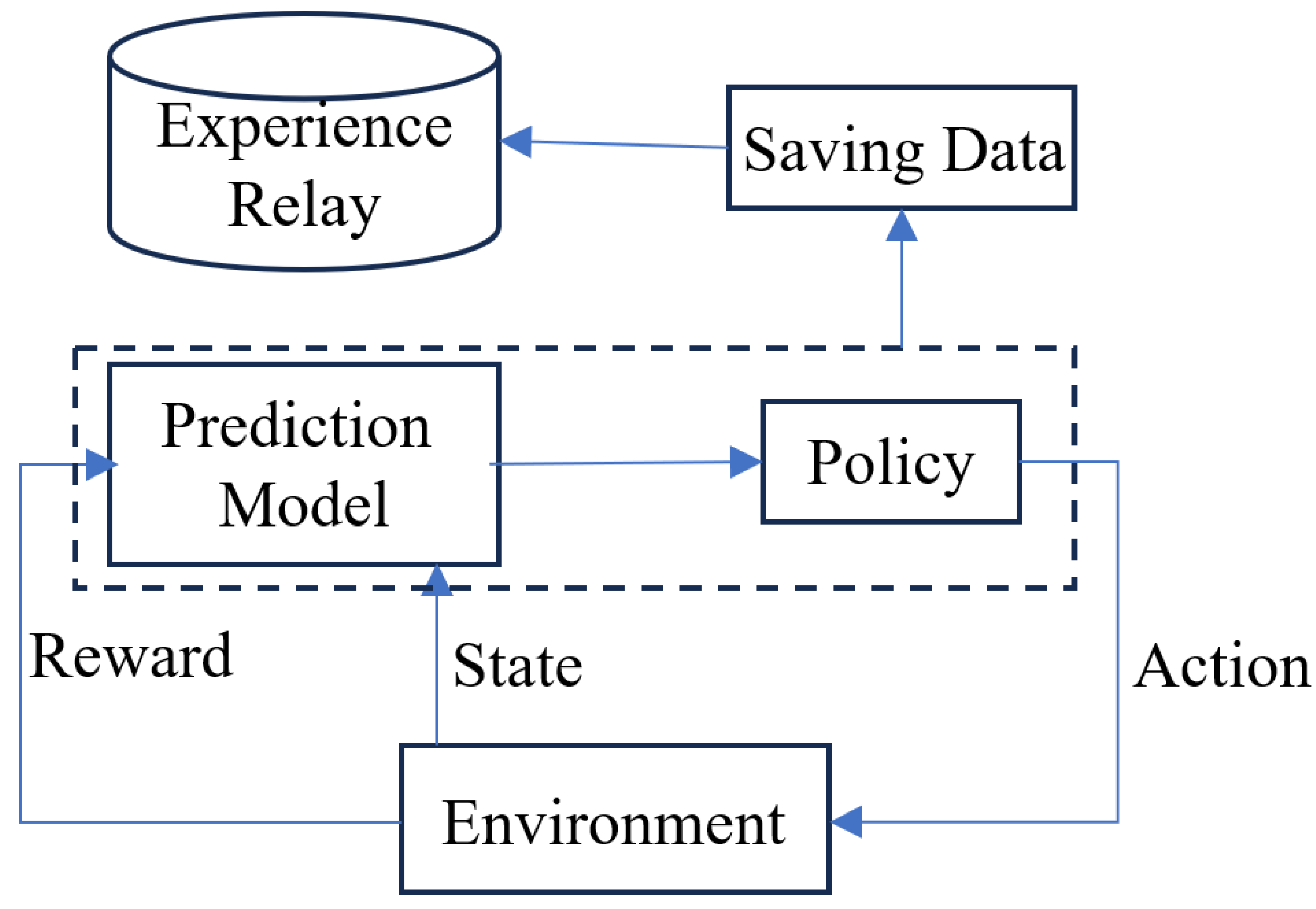
2.5. Deep Q-Network Reinforcement Learning
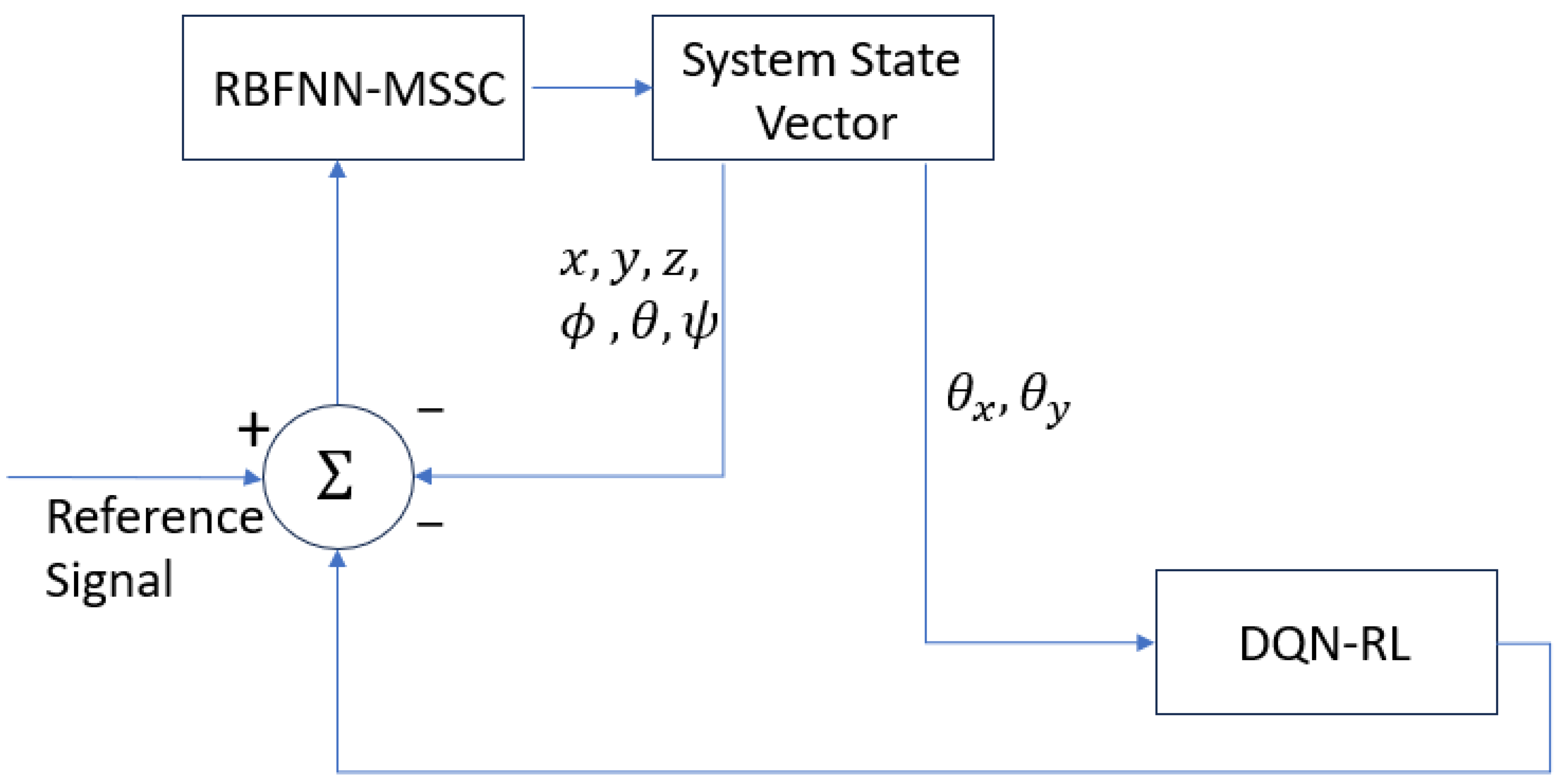
2.6. Control Architecture
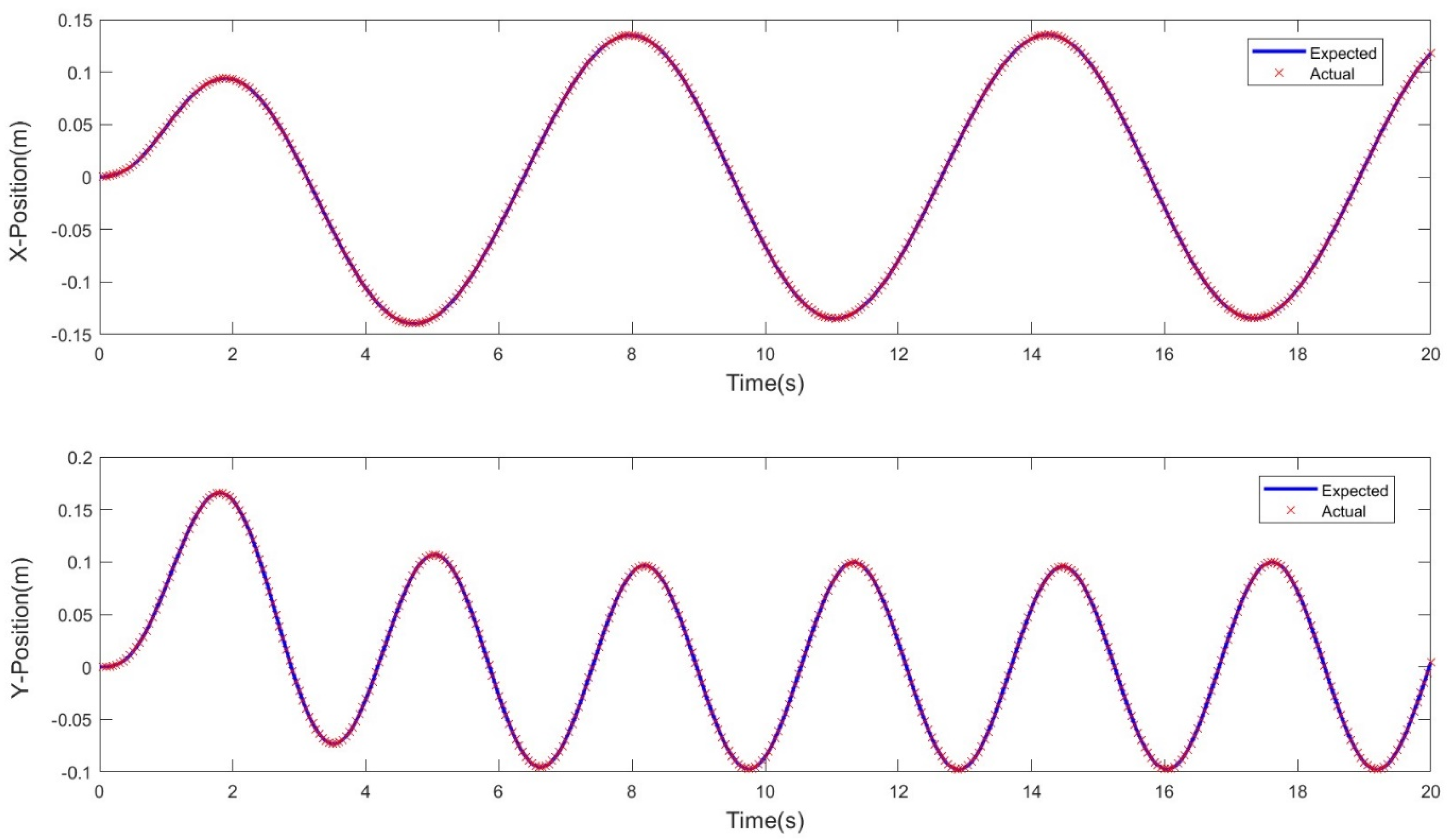
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nawaz, H.; Ali, H.M.; Massan, S. Applications of unmanned aerial vehicles: A review. Tecnol. Glosas Innovación Apl. Pyme. Spec. 2019, 2019, 85–105. [Google Scholar] [CrossRef]
- Emran, B.J.; Najjaran, H. A review of quadrotor: An underactuated mechanical system. Annu. Rev. Control. 2018, 46, 165–180. [Google Scholar] [CrossRef]
- Baraean, A.; Hamanah, W.M.; Bawazir, A.; Quama, M.M.; El Ferik, S.; Baraean, S.; Abido, M.A. Optimal Nonlinear backstepping controller design of a Quadrotor-Slung load system using particle Swarm Optimization. Alex. Eng. J. 2023, 68, 551–560. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M.; Al-Qahtani, F.M.; Elferik, S.; Saif, A.-W.A. Quadrotor robust fractional-order sliding mode control in unmanned aerial vehicles for eliminating external disturbances. Aerospace 2023, 10, 665. [Google Scholar] [CrossRef]
- Manalathody, A.; Krishnan, K.S.; Subramanian, J.A.; Thangavel, S.; Thangeswaran, R.S.K. Non-linear Controller for a Drone with Slung Load. In Proceedings of the International Conference on Modern Research in Aerospace Engineering, Noida, India, 21–22 September 2023; pp. 219–228. [Google Scholar]
- Li, B.; Li, Y.; Yang, P.; Zhu, X. Adaptive neural network-based fault-tolerant control for quadrotor-slung-load system under marine scene. IEEE Trans. Intell. Veh. 2023, 9, 681–691. [Google Scholar] [CrossRef]
- Wang, Z.; Qi, J.; Wu, C.; Wang, M.; Ping, Y.; Xin, J. Control of quadrotor slung load system based on double ADRC. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 6810–6815. [Google Scholar]
- Ren, Y.; Zhao, Z.; Ahn, C.K.; Li, H.-X. Adaptive fuzzy control for an uncertain axially moving slung-load cable system of a hovering helicopter with actuator fault. IEEE Trans. Fuzzy Syst. 2022, 30, 4915–4925. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Cabecinhas, D.; Silvestre, C.; Cunha, R. Geometric finite-time inner-outer loop trajectory tracking control strategy for quadrotor slung-load transportation. Nonlinear Dyn. 2022, 107, 2291–2308. [Google Scholar] [CrossRef]
- Tolba, M.; Shirinzadeh, B.; El-Bayoumi, G.; Mohamady, O. Adaptive optimal controller design for an unbalanced UAV with slung load. Auton. Robot. 2023, 47, 267–280. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, G.; Xie, W.; Zhang, W.; Silvestre, C. UDE-based Robust Control of a Quadrotor-Slung-Load System. IEEE Robot. Autom. Lett. 2023, 8, 6851–6858. [Google Scholar] [CrossRef]
- Kabzan, J.; Hewing, L.; Liniger, A.; Zeilinger, M.N. Learning-based model predictive control for autonomous racing. IEEE Robot. Autom. Lett. 2019, 4, 3363–3370. [Google Scholar] [CrossRef]
- Bag, A.; Subudhi, B.; Ray, P.K. A combined reinforcement learning and sliding mode control scheme for grid integration of a PV system. CSEE J. Power Energy Syst. 2019, 5, 498–506. [Google Scholar]
- Lee, D.; Lee, S.J.; Yim, S.C. Reinforcement learning-based adaptive PID controller for DPS. Ocean Eng. 2020, 216, 108053. [Google Scholar] [CrossRef]
- Rizvi, S.A.A.; Lin, Z. Reinforcement learning-based linear quadratic regulation of continuous-time systems using dynamic output feedback. IEEE Trans. Cybern. 2019, 50, 4670–4679. [Google Scholar] [CrossRef] [PubMed]
- Annaswamy, A.M. Adaptive control and intersections with reinforcement learning. Annu. Rev. Control Robot. Auton. Syst. 2023, 6, 65–93. [Google Scholar] [CrossRef]
- Du, B.; Lin, B.; Zhang, C.; Dong, B.; Zhang, W. Safe deep reinforcement learning-based adaptive control for USV interception mission. Ocean Eng. 2022, 246, 110477. [Google Scholar] [CrossRef]
- Wu, L.; Wang, C.; Zhang, P.; Wei, C. Deep reinforcement learning with corrective feedback for autonomous uav landing on a mobile platform. Drones 2022, 6, 238. [Google Scholar] [CrossRef]
- Liang, X.; Du, X.; Wang, G.; Han, Z. Deep reinforcement learning for traffic light control in vehicular networks. arXiv 2018, arXiv:1803.11115. [Google Scholar]
- Ma, S.; Lee, J.; Serban, N.; Yang, S. Deep Attention Q-Network for Personalized Treatment Recommendation. In Proceedings of the 2023 IEEE International Conference on Data Mining Workshops (ICDMW), Shanghai, China, 4 December 2023; IEEE: Piscataway, NJ, USA; pp. 329–337. [Google Scholar]
- Peng, B.; Sun, Q.; Li, S.E.; Kum, D.; Yin, Y.; Wei, J.; Gu, T. End-to-end autonomous driving through dueling double deep Q-network. Automot. Innov. 2021, 4, 328–337. [Google Scholar] [CrossRef]
- Fang, X.; Gong, G.; Li, G.; Chun, L.; Peng, P.; Li, W.; Shi, X.; Chen, X. Deep reinforcement learning optimal control strategy for temperature setpoint real-time reset in multi-zone building HVAC system. Appl. Therm. Eng. 2022, 212, 118552. [Google Scholar] [CrossRef]
- Kersandt, K.; Muñoz, G.; Barrado, C. Self-training by reinforcement learning for full-autonomous drones of the future. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–10. [Google Scholar]
- Muñoz, G.; Barrado, C.; Çetin, E.; Salami, E. Deep reinforcement learning for drone delivery. Drones 2019, 3, 72. [Google Scholar] [CrossRef]
- Raja, G.; Baskar, Y.; Dhanasekaran, P.; Nawaz, R.; Yu, K. An efficient formation control mechanism for multi-UAV navigation in remote surveillance. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Özalp, R.; Varol, N.K.; Taşci, B.; Uçar, A. A review of deep reinforcement learning algorithms and comparative results on inverted pendulum system. In Machine Learning Paradigms. Learning and Analytics in Intelligent Systems; Springer: Cham, Switzerland, 2020; pp. 237–256. [Google Scholar]
- Dang, K.N.; Van, L.V. Development of deep reinforcement learning for inverted pendulum. Int. J. Electr. Comput. Eng. 2023, 13, 3895–3902. [Google Scholar]
- Li, X.; Liu, H.; Wang, X. Solve the inverted pendulum problem base on DQN algorithm. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 5115–5120. [Google Scholar]
- Huang, H.; Yang, Y.; Wang, H.; Ding, Z.; Sari, H.; Adachi, F. Deep reinforcement learning for UAV navigation through massive MIMO technique. IEEE Trans. Veh. Technol. 2019, 69, 1117–1121. [Google Scholar] [CrossRef]
- Wang, S.; Qi, N.; Jiang, H.; Xiao, M.; Liu, H.; Jia, L.; Zhao, D. Trajectory Planning for UAV-Assisted Data Collection in IoT Network: A Double Deep Q Network Approach. Electronics 2024, 13, 1592. [Google Scholar] [CrossRef]
- Hedrick, J.K.; Yip, P.P. Multiple sliding surface control: Theory and application. J. Dyn. Sys. Meas. Control 2000, 122, 586–593. [Google Scholar] [CrossRef]
- Thanh, H.L.N.N.; Hong, S.K. An extended multi-surface sliding control for matched/mismatched uncertain nonlinear systems through a lumped disturbance estimator. IEEE Access 2020, 8, 91468–91475. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Mehmood, A.; Bhatti, A.I. Robust backstepping sliding mode control design for a class of underactuated electro–mechanical nonlinear systems. J. Electr. Eng. Technol. 2020, 15, 1821–1828. [Google Scholar] [CrossRef]
- Qu, X.; Zeng, Z.; Wang, K.; Wang, S. Replacing urban trucks via ground–air cooperation. Commun. Transp. Res. 2022, 2, 100080. [Google Scholar] [CrossRef]
- Nyaaba, A.A.; Ayamga, M. Intricacies of medical drones in healthcare delivery: Implications for Africa. Technol. Soc. 2021, 66, 101624. [Google Scholar] [CrossRef]
- Rejeb, A.; Abdollahi, A.; Rejeb, K.; Treiblmaier, H. Drones in agriculture: A review and bibliometric analysis. Comput. Electron. Agric. 2022, 198, 107017. [Google Scholar] [CrossRef]
- Zheng, C.; Yan, Y.; Liu, Y. Prospects of eVTOL and modular flying cars in China urban settings. J. Intell. Connect. Veh. 2023, 6, 187–189. [Google Scholar] [CrossRef]
- Khoo, S.; Norton, M.; Kumar, J.J.; Yin, J.; Yu, X.; Macpherson, T.; Dowling, D.; Kouzani, A. Robust control of novel thrust vectored 3D printed multicopter. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 1270–1275. [Google Scholar]
- Peris, C.; Norton, M.; Khoo, S.Y. Variations in Finite-Time Multi-Surface Sliding Mode Control for Multirotor Unmanned Aerial Vehicle Payload Delivery with Pendulum Swinging Effects. Machines 2023, 11, 899. [Google Scholar] [CrossRef]
- Peris, C.; Norton, M.; Khoo, S.Y. Multi-surface Sliding Mode Control of a Thrust Vectored Quadcopter with a Suspended Double Pendulum Weight. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Clevon Peris, M.N.; Khoo, S.Y. Adaptive Multi Surface Sliding Mode Control of a Quadrotor Slung Load System. In Proceedings of the IEEE 10th International Conference on Automation, Robotics and Application (ICARA 2024), Athens, Greece, 23 February 2024. [Google Scholar]
- Kuang, N.L.; Leung, C.H. Performance effectiveness of multimedia information search using the epsilon-greedy algorithm. In Proceedings of the 2019 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 929–936. [Google Scholar]









| Layer | Name | Definition |
|---|---|---|
| 1 | ‘observation’ | Feature Input |
| 2 | ‘CriticStateFC1’ | Fully Connected |
| 3 | ‘CriticStateFC2’ | Fully Connected |
| 4 | ‘CriticRelu1’ | Activation Function |
| 5 | ‘CriticCommonRelu’ | ReLU |
| 6 | ‘Output’ | Fully Connected |
| Parameters | Symbols | Values |
|---|---|---|
| Multirotor mass | M | 4 kg |
| Slung load mass | m | 0.5 kg |
| Slung load link length | l | 1 m |
| Rotor speed for hover | ωres | 29,700 m/s |
| UAV moment of inertia | I | 2.07 × 10−2 kg/m2 |
| Feedback control time step | Tc | 0.005 |
| Simulation run time | T | 10 s |
| Sampling rate | Ts | 0.01 s |
| Learning rate | γ | 5 × 10−3 |
| Parameter | Value | |||
|---|---|---|---|---|
| Butterfly Trajectory | Square Trajectory | |||
| MSSC | RL | MSSC | RL | |
| Rise time | 0.01 | 0.006 | 0.008 | 0.006 |
| Transient time | 27.08 | 22.6 | 25.35 | 22.21 |
| Settling time | 29.94 | 29.98 | 29.98 | 29.97 |
| Settling min | −0.12 | −0.12 | −2.55 | −3.26 |
| Settling max | 1.43 | 1.01 | 3.53 | 2.91 |
| Overshoot | 2.71 | 6.94 | 3.81 | 4.0 |
| Undershoot | 3.6 | 1.1 | 4.04 | 3.58 |
| Peak | 1.83 | 1.58 | 3.75 | 3.26 |
| Peak time | 1.01 | 0.37 | 1.02 | 0.38 |
| Parameter | Max | Mean | RMS | |
|---|---|---|---|---|
| Butterfly Trajectory | MSSC | 1.43 | −0.01 | 0.37 |
| RL | 1.01 | −0.01 | 0.26 | |
| Square Trajectory | MSSC | 3.53 | −1.22 × 10−4 | 0.98 |
| RL | 2.92 | −7.41 × 10−4 | 0.70 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peris, C.; Norton, M.; Khoo, S. Adaptive Multi-Surface Sliding Mode Control with Radial Basis Function Neural Networks and Reinforcement Learning for Multirotor Slung Load Systems. Electronics 2024, 13, 2424. https://doi.org/10.3390/electronics13122424
Peris C, Norton M, Khoo S. Adaptive Multi-Surface Sliding Mode Control with Radial Basis Function Neural Networks and Reinforcement Learning for Multirotor Slung Load Systems. Electronics. 2024; 13(12):2424. https://doi.org/10.3390/electronics13122424
Chicago/Turabian StylePeris, Clevon, Michael Norton, and Suiyang Khoo. 2024. "Adaptive Multi-Surface Sliding Mode Control with Radial Basis Function Neural Networks and Reinforcement Learning for Multirotor Slung Load Systems" Electronics 13, no. 12: 2424. https://doi.org/10.3390/electronics13122424
APA StylePeris, C., Norton, M., & Khoo, S. (2024). Adaptive Multi-Surface Sliding Mode Control with Radial Basis Function Neural Networks and Reinforcement Learning for Multirotor Slung Load Systems. Electronics, 13(12), 2424. https://doi.org/10.3390/electronics13122424







