Prediction of Nugget Diameter and Analysis of Process Parameters of RSW with Machine Learning Based on Feature Fusion
Abstract
:1. Introduction
2. Methodology
2.1. Data Preprocess
2.2. The Design of Dimensionality Reduction Algorithm Based on PCA
- In the original data class, the whole influencing factors are divided into two categories: a process parameter set and a material parameter set . Then, a set of mutually orthogonal coordinate axes are found in the corresponding data space, and the variables are projected onto these coordinate axes.
- The covariance difference is chosen to represent the distance between variables. The larger the covariance, the more information will be retained. Therefore, one group of m-dimensional original variables can be transformed into a group of -dimensional unrelated main variables.
- The covariance between and iswhere and are the mean of random variables, and is the element of vector . Then, the covariance matrix C of material can be calculated asThe pair covariance matrix is decomposed as:The eigenvalues of the covariance matrix are calculated as (arranged in descending order) and the corresponding unitized eigenvector . is the mth component of the jth eigenvector.where refers to the ith principal component. The contribution rate of the principal component is and the cumulative contribution rate is expressed by :
- The selection of principal components is determined according to several thresholds. In this study, two thresholds are chosen: the eigenvalue is greater than 1 and the cumulative contribution rate reaches 90%. Through many tests, this should guarantee that the selected main components can not only retain the original and complete amount of information, but also can reduce the required number of calculations, which can efficiently improve the performance of the model. For example, the main components and components selected for material characteristic parameters are recorded as
- After the above processing, three types of training data sets are obtained. The first type is the training set containing only process parameters:The second type is the training set of process parameters and material parameters:The third type is the training set for PCA fusion of process parameters and material parameters:
2.3. Feature Selection Methods
2.4. Multi-Model Machine Learning Algorithm Based on Bayesian
- Basic model selectionIn this study, two types of algorithms were selected as basic models: linear methods and integrated learning methods. The first type of basic model mainly includes multi-linear regression, k-nearest neighbor, and support vector machine regression (SVR) models. The second type mainly covers XGBoost, LightGBM, and CatBoost. SVR has strong fitting ability for data sets with small amounts of data. Extreme gradient enhancement (XGBoost) is an integrated machine learning model. LightGBM is an efficient gradient-lifting decision tree algorithm proposed by Microsoft. CatBoost is also an algorithm based on decision tree, with a low number of parameters and support for categorical variables.
- Model fusion and implementationIn practical application, it has been demonstrated many times that the general result of simply using the above algorithms leads to two extreme phenomena:
- (a)
- The effect is good in the modeling data set, but it is difficult to achieve the ideal effect in the test data set.
- (b)
- The machine learning algorithm lacks sufficient capacity to capture the underlying patterns and relationships in the data, resulting in poor performance.
During basic model training, the minimum variance and deviation are computed. Specifically, the variance is calculated according to the prediction data of the test set, and the deviation is calculated in accordance with the error of the training data. In order to avoid the overfitting phenomenon, this study combines the Bayesian optimization algorithm [17] to complete the parameter selection of the basic model, thus improving the model performance and reducing variance. Therefore, this study proposes a machine learning synthesis model based on Bayesian optimization:where x represents the hyperparameter to be optimized in the machine learning model, X represents the search space of super parameters, and denotes the objective function l, that is, the black-box model that inputs a set of hyperparameters and outputs the evaluation indices.In order to obtain the optimal x, the Bayesian optimization algorithm is further used to iteratively calculate the sampling function . is the objective function value of the current optimal x, and are the mean and variance of the objective function obtained by the Gaussian process—that is, the posterior distribution of —and is the trade-off coefficient to prevent obtaining the local optimal solution of . The implementation procedure of the Bayesian iterative optimization algorithm is given as Algorithm 1.Algorithm 1 Bayesian iterative optimization algorithm - 1:
- Input: , number of iterations T.
- 2:
- Calculate
- 3:
- for 1 to T do
- 4:
- 5:
- 6:
- 7:
- Rebuild Gaussian process model and calculate
- 8:
- end for
- 9:
- Output: X
- Model performance index selectionRegarding the utilization of machine learning to solve practical production problems, it is essential to select an evaluation index for model quality. This study uses several quantitative indicators to measure the uncertainty between measurement and calculation results in order to evaluate the model performance from different perspectives. These various quantitative indicators are defined as follows:where reflects the fitting accuracy of the model to the data. and take non-negative values. represents the proportion of data that can be interpreted by the data model. The average absolute relative deviation is used to judge the evaluation accuracy. denotes the percentage of accuracy and precision, which indicates the reliability of a model.
3. Experiments and Analysis
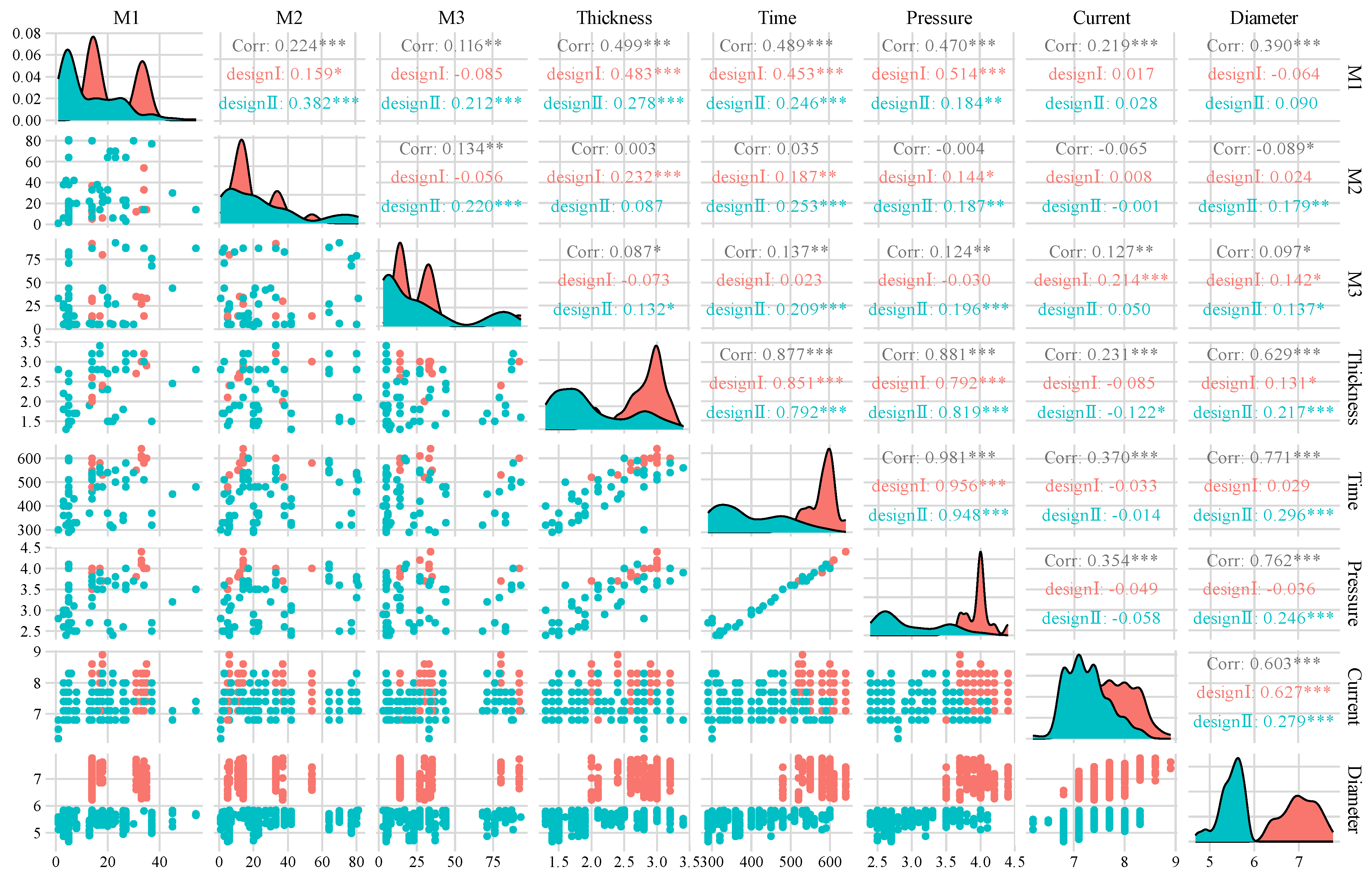
3.1. Data Sources
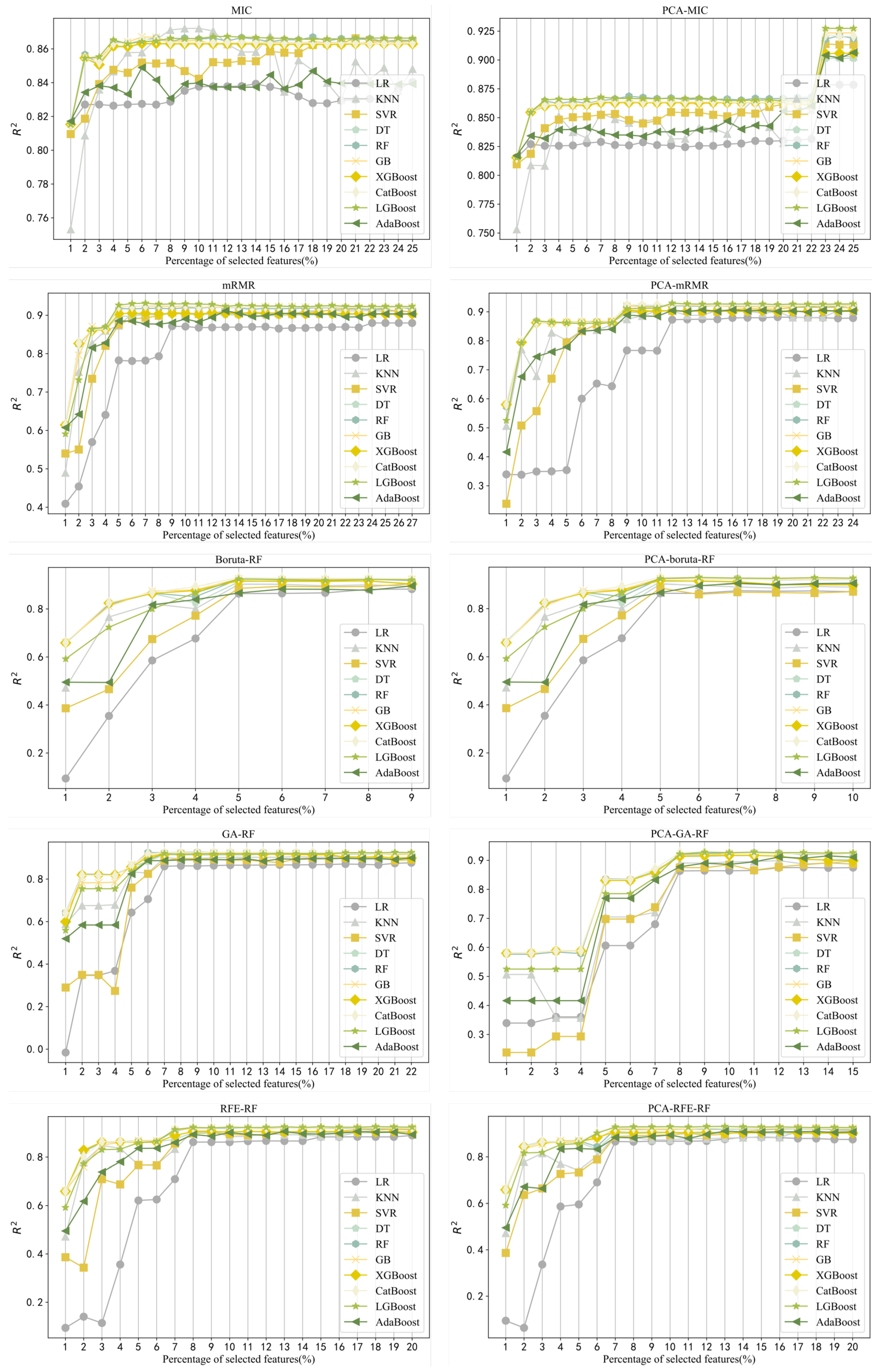
3.2. Feature Selection Experiment
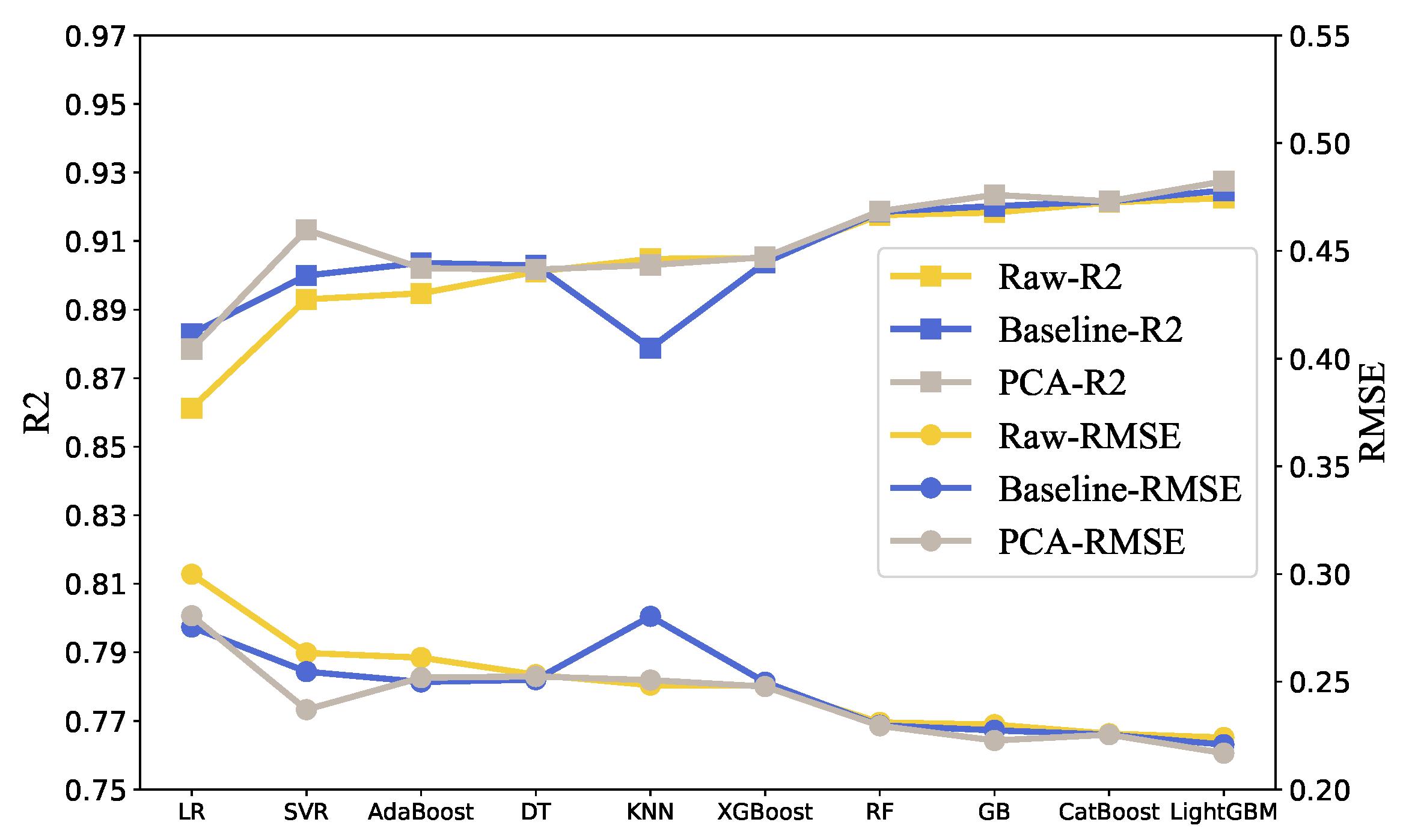
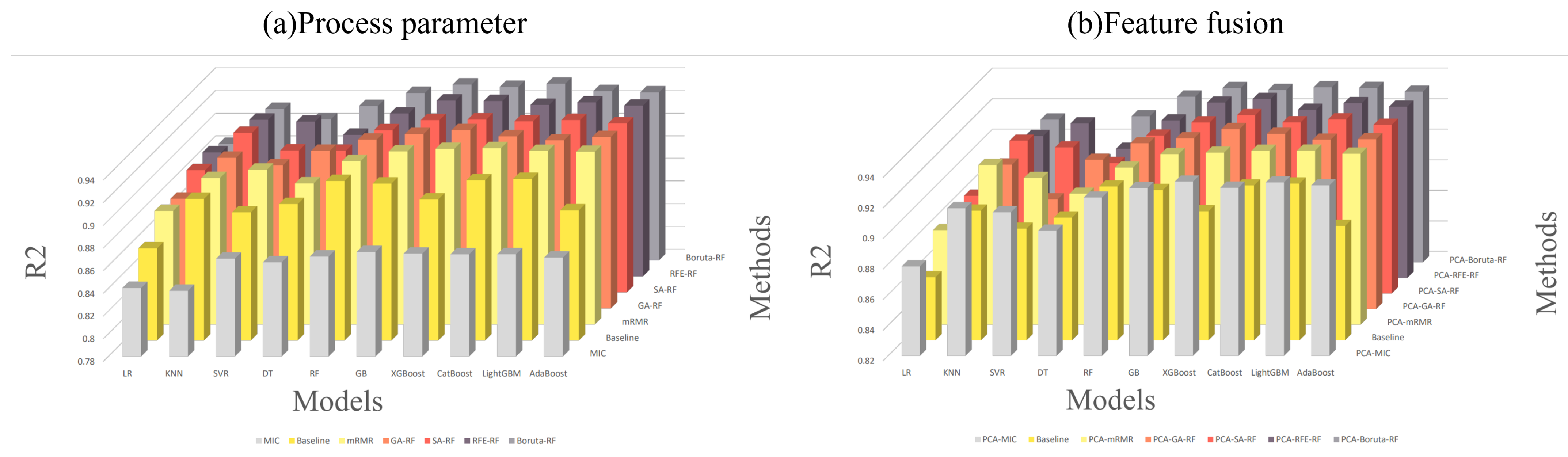
3.3. Hyperparameter Optimization and Quality Prediction
4. Conclusions
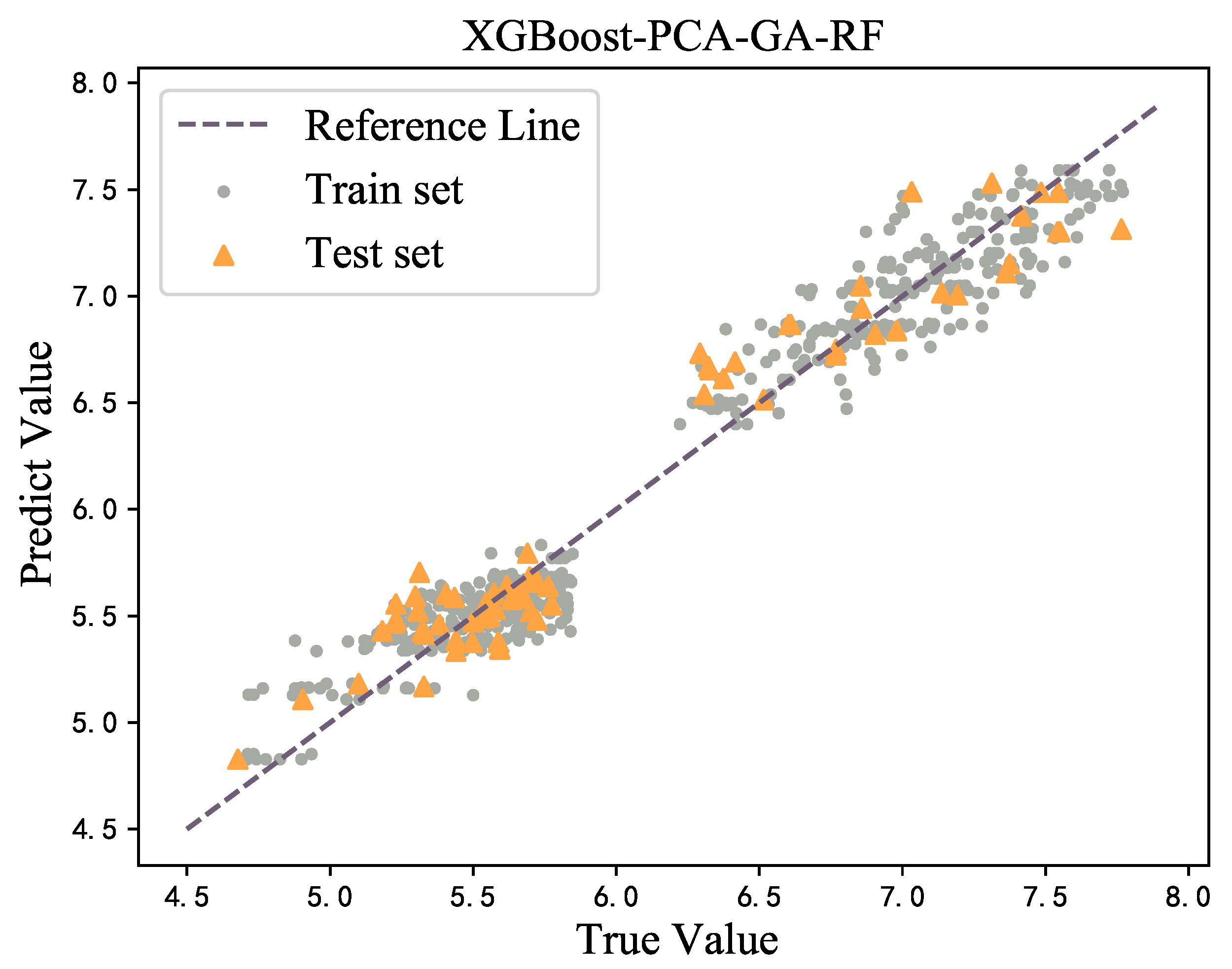
- The prediction model trained using a genetic algorithm combined with the Bayesian Optimization XGBoost algorithm can predict the size of nugget very accurately, and the complexity and inconsistency of data will not affect its prediction performance. Moreover, the Bayesian optimization method is completely effective for hyperparameter optimization and the regulation of overfitting.
- Through adding the mechanical properties and chemical element contents of materials into the feature set, and reducing its dimensionality using PCA to conduct feature fusion, the performance of the model can be effectively improved. For example, compared with the original data, the of the XGBoost model was enhanced by 3.2%.
- Material features impose a great impact on the prediction performance of the model. All feature selection methods added a certain proportion of material features to the feature subsets of the two data sets. In particular, electrode pressure, welding current, and welding time were included in all feature subsets. The three process parameters are of great importance for nugget formation, which is consistent with actual welding experience and theory.
- The PCA method can effectively remove redundant information of material characteristics. The four feature selection methods—consisting of maximum correlation minimum redundancy coefficient, Boruta, recursive feature elimination, and genetic algorithm—were applied to several machine learning models, and the performance of the machine learning algorithms was improved to varying degrees. Therefore, it is crucial to select and obtain the optimal feature subset using feature selection methods.
- The results revealed that the proportional increase or decrease in material features in different feature subsets is not stable. In fact, the heat generated during resistance spot-welding obeys Joule’s Law. Material characteristics are particularly critical for nugget formation, and the current has a greater impact on heat with an increase in time. While the disadvantage is that the dynamic resistance in the actual nugget formation process changes within a certain range, it is regarded as a fixed value for analysis in this paper. Therefore, there is a certain error with respect to the actual situation. In order to reduce this error, the maximum mutual information coefficient was adopted for feature selection, and the features were sorted and selected according to the size of the maximum mutual information coefficient. For the purpose of controlling the number of features selected with each feature selection method to be close to the same, it is sufficient to retain the first 20 dimensional features at most.
- This investigation was limited to the consideration of static process parameters and material properties, without real-time dynamic monitoring of the welding process. A promising avenue for future research is to exploit the wealth of data generated by internal sensors within the welding machine (e.g., current, voltage, and displacement sensors) and external environmental sensors (e.g., temperature and humidity sensors), and to integrate these data streams using advanced data fusion techniques to improve the accuracy of predictions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martin, O.; Ahedo, V.; Santos, J.I.; Galán, J.M. Comparative Study of Classification Algorithms for Quality Assessment of Resistance Spot Welding Joints From Pre-and Post-Welding Inputs. IEEE Access 2022, 10, 6518–6527. [Google Scholar] [CrossRef]
- Zhao, D.; Ivanov, M.; Wang, Y.; Liang, D.; Du, W. Multi-objective optimization of the resistance spot welding process using a hybrid approach. J. Intell. Manuf. 2021, 32, 2219–2234. [Google Scholar] [CrossRef]
- Vignesh, K.; Elaya Perumal, A.; Velmurugan, P. Resistance spot welding of AISI-316L SS and 2205 DSS for predicting parametric influences on weld strength—Experimental and FEM approach. Arch. Civ. Mech. Eng. 2019, 19, 1029–1042. [Google Scholar] [CrossRef]
- Bae, J.H.; Park, Y.D.; Lee, M. Optimization of Welding Parameters for Resistance Spot Welding of AA3003 to Galvanized DP780 Steel Using Response Surface Methodology. Int. J. Automot. Technol. 2021, 22, 585–593. [Google Scholar] [CrossRef]
- Vigneshkumar, M.; Varthanan, P.A. Comparison of RSM and ANN model in the prediction of the tensile shear failure load of spot welded AISI 304/316 L dissimilar sheets. Int. J. Comput. Mater. Sci. Surf. Eng. 2019, 8, 114–130. [Google Scholar] [CrossRef]
- Hoseini, H.T.; Farahani, M.; Sohrabian, M. Process analysis of resistance spot welding on the Inconel alloy 625 using artificial neural networks. Int. J. Manuf. Res. 2017, 12, 444–460. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Y.; Sun, S.; Ma, Z.; Huang, X. Multi-objective optimization of mechanical quality and stability during micro resistance spot welding. Int. J. Adv. Manuf. Technol. 2019, 101, 1903–1913. [Google Scholar] [CrossRef]
- Zamanzad Gavidel, S.; Lu, S.; Rickli, J.L. Performance analysis and comparison of machine learning algorithms for predicting nugget width of resistance spot welding joints. Int. J. Adv. Manuf. Technol. 2019, 105, 3779–3796. [Google Scholar] [CrossRef]
- Lee, S.; Kareem, A.B.; Hur, J.W. A Comparative Study of Deep-Learning Autoencoders (DLAEs) for Vibration Anomaly Detection in Manufacturing Equipment. Electronics 2024, 13, 1700. [Google Scholar] [CrossRef]
- Cheadle, C.; Vawter, M.P.; Freed, W.J.; Becker, K.G. Analysis of microarray data using Z score transformation. J. Mol. Diagn. 2003, 5, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Cai, L. Online nugget diameter control system for resistance spot welding. Int. J. Adv. Manuf. Technol. 2013, 68, 2571–2588. [Google Scholar] [CrossRef]
- Gomez, J.C.; Moens, M.F. PCA document reconstruction for email classification. Comput. Stat. Data Anal. 2012, 56, 741–751. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Kursa, M.B.; Jankowski, A.; Rudnicki, W.R. Boruta—A system for feature selection. Fundam. Informaticae 2010, 101, 271–285. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Hou, Y.; Yang, A.; Guo, W.; Zheng, E.; Xiao, Q.; Guo, Z.; Huang, Z. Bearing Fault Diagnosis Under Small Data Set Condition: A Bayesian Network Method With Transfer Learning for Parameter Estimation. IEEE Access 2022, 10, 35768–35783. [Google Scholar] [CrossRef]
- Wang, W.R.; Wang, W.L.; Wang, S.C.; Tsai, Y.C.; Lai, C.H.; Yeh, J.W. Effects of Al addition on the microstructure and mechanical property of AlxCoCrFeNi high-entropy alloys. Intermetallics 2012, 26, 44–51. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. The feature selection problem: Traditional methods and a new algorithm. In Proceedings of the Aaai, San Jose, CA, USA, 12–16 July 1992; Volume 2, pp. 129–134. [Google Scholar]
- Arunchai, T.; Sonthipermpoon, K.; Apichayakul, P.; Tamee, K. Resistance spot welding optimization based on artificial neural network. Int. J. Manuf. Eng. 2014, 2014, 154784. [Google Scholar] [CrossRef]


| Feature Names | Feature Types | Range |
|---|---|---|
| Design diameter | Design parameter | |
| Thickness | Design parameter | |
| Welding current | Process parameter | |
| Welding time | Process parameter | |
| Electrode pressure | Process parameter | |
| Electrode diameter | Process parameter | |
| Nugget diameter | Process parameter |
| Model | Metric | LR | SVR | AdaBoost | DT | KNN | XGBoost | RF | GB | CatBoost | LightGBM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.840 | 0.866 | 0.848 | 0.863 | 0.872 | 0.863 | 0.866 | 0.867 | 0.865 | 0.867 | ||
| MIC | 4 | 4 | 3 | 4 | 3 | 3 | 4 | 3 | 3 | 3 | |
| 21 | 16 | 3 | 18 | 6 | 4 | 14 | 3 | 3 | 9 | ||
| 0.880 | 0.916 | 0.911 | 0.904 | 0.912 | 0.907 | 0.921 | 0.924 | 0.926 | 0.931 | ||
| MRMR | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | |
| 19 | 18 | 9 | 6 | 17 | 8 | 22 | 4 | 5 | 4 | ||
| 0.882 | 0.904 | 0.895 | 0.916 | 0.902 | 0.916 | 0.923 | 0.924 | 0.930 | 0.924 | ||
| Boruta | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 5 | 5 | 5 | 3 | 1 | 1 | 4 | 1 | 1 | 1 | ||
| 0.889 | 0.915 | 0.905 | 0.904 | 0.914 | 0.906 | 0.921 | 0.921 | 0.921 | 0.925 | ||
| RFE | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 15 | 14 | 8 | 6 | 14 | 6 | 9 | 5 | 9 | 13 | ||
| 0.876 | 0.905 | 0.899 | 0.918 | 0.905 | 0.918 | 0.927 | 0.923 | 0.927 | 0.925 | ||
| GA | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| 16 | 14 | 16 | 10 | 12 | 6 | 3 | 6 | 5 | 15 | ||
| 0.878 | 0.913 | 0.906 | 0.901 | 0.902 | 0.905 | 0.921 | 0.923 | 0.921 | 0.927 | ||
| PCA-MIC | 6 | 5 | 6 | 6 | 5 | 6 | 6 | 5 | 5 | 5 | |
| 18 | 18 | 19 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | ||
| 0.881 | 0.915 | 0.906 | 0.905 | 0.907 | 0.905 | 0.922 | 0.924 | 0.924 | 0.929 | ||
| PCA-MRMR | 5 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 4 | 5 | |
| 14 | 16 | 9 | 9 | 11 | 18 | 18 | 17 | 7 | 7 | ||
| 0.874 | 0.885 | 0.904 | 0.914 | 0.902 | 0.916 | 0.925 | 0.924 | 0.930 | 0.929 | ||
| PCA-Boruta | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 3 | 1 | 3 | 2 | 1 | 1 | 2 | 1 | 1 | 2 | ||
| 0.884 | 0.921 | 0.910 | 0.904 | 0.912 | 0.908 | 0.921 | 0.923 | 0.925 | 0.931 | ||
| PCA-RFE | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 9 | 12 | 8 | 5 | 15 | 11 | 11 | 7 | 2 | 8 | ||
| 0.875 | 0.891 | 0.915 | 0.916 | 0.898 | 0.917 | 0.926 | 0.924 | 0.929 | 0.928 | ||
| PCA-GA | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | |
| 5 | 6 | 6 | 3 | 4 | 3 | 3 | 2 | 1 | 3 |
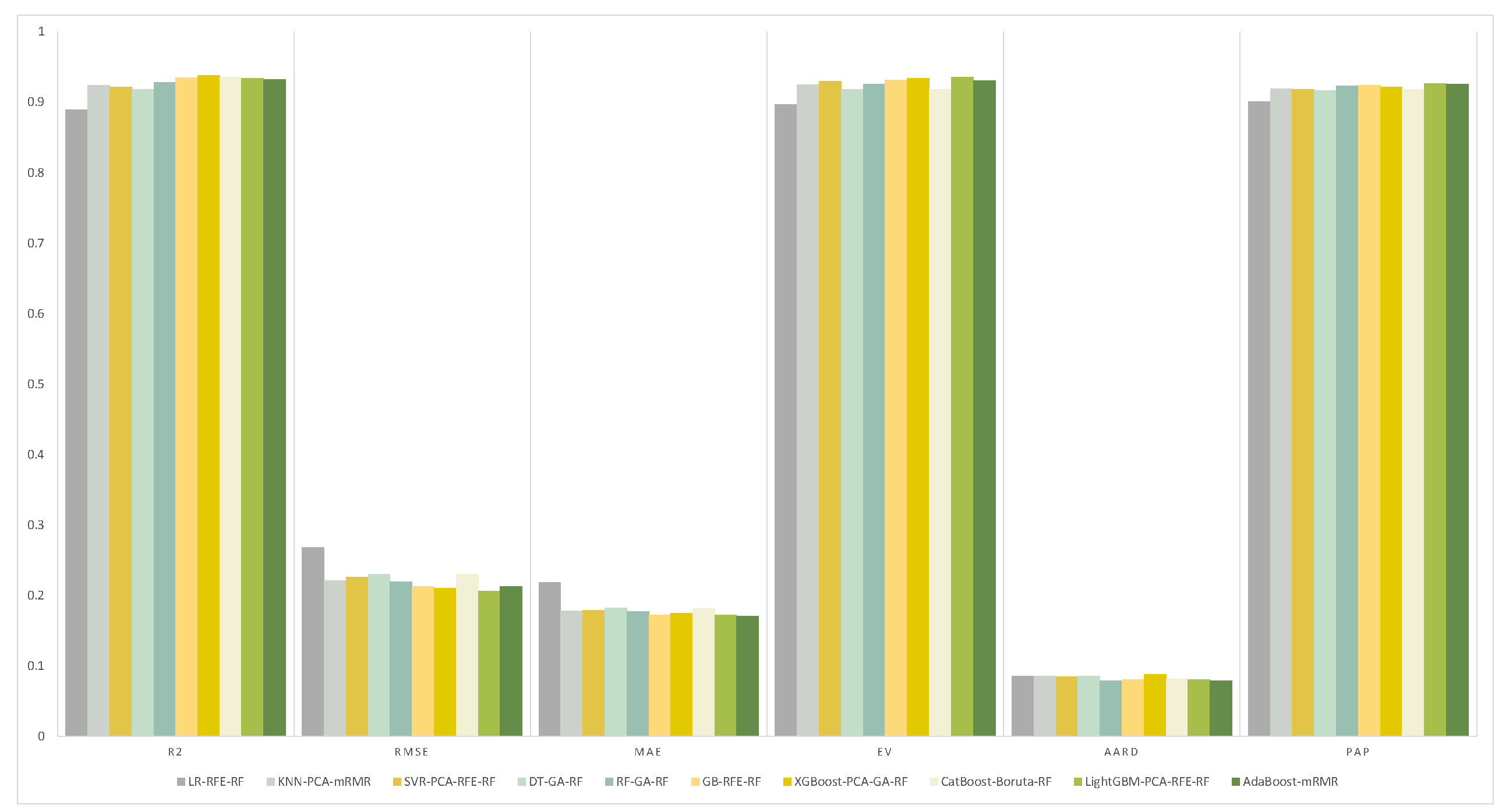
| Model | ||||||
|---|---|---|---|---|---|---|
| LR-RFE-RF | 0.889 | 0.267 | 0.218 | 0.896 | 0.085 | 0.901 |
| KNN-PCA-MRMR | 0.924 | 0.221 | 0.178 | 0.925 | 0.085 | 0.919 |
| SVR-PCA-RFE-RF | 0.921 | 0.226 | 0.179 | 0.930 | 0.084 | 0.918 |
| DT-GA-RF | 0.918 | 0.230 | 0.182 | 0.918 | 0.084 | 0.916 |
| RF-GA-RF | 0.925 | 0.219 | 0.177 | 0.925 | 0.078 | 0.923 |
| GB-RFE-RF | 0.931 | 0.211 | 0.170 | 0.932 | 0.079 | 0.925 |
| XGBoost-PCA-GA-RF | 0.937 | 0.200 | 0.164 | 0.939 | 0.084 | 0.925 |
| CatBoost-Boruta-RF | 0.935 | 0.204 | 0.160 | 0.935 | 0.085 | 0.924 |
| LightGBM-PCA-RFE-RF | 0.934 | 0.206 | 0.171 | 0.935 | 0.080 | 0.926 |
| AdaBoost-MRMR | 0.928 | 0.214 | 0.171 | 0.930 | 0.081 | 0.923 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Shen, H.; Zhu, X.; Wang, Y. Prediction of Nugget Diameter and Analysis of Process Parameters of RSW with Machine Learning Based on Feature Fusion. Electronics 2024, 13, 2484. https://doi.org/10.3390/electronics13132484
Zhu Q, Shen H, Zhu X, Wang Y. Prediction of Nugget Diameter and Analysis of Process Parameters of RSW with Machine Learning Based on Feature Fusion. Electronics. 2024; 13(13):2484. https://doi.org/10.3390/electronics13132484
Chicago/Turabian StyleZhu, Qinmiao, Huabo Shen, Xiaohui Zhu, and Yuhui Wang. 2024. "Prediction of Nugget Diameter and Analysis of Process Parameters of RSW with Machine Learning Based on Feature Fusion" Electronics 13, no. 13: 2484. https://doi.org/10.3390/electronics13132484
APA StyleZhu, Q., Shen, H., Zhu, X., & Wang, Y. (2024). Prediction of Nugget Diameter and Analysis of Process Parameters of RSW with Machine Learning Based on Feature Fusion. Electronics, 13(13), 2484. https://doi.org/10.3390/electronics13132484





