Influence of Post-Processing Techniques on Random Number Generation Using Chaotic Nanolasers
Abstract
:1. Introduction
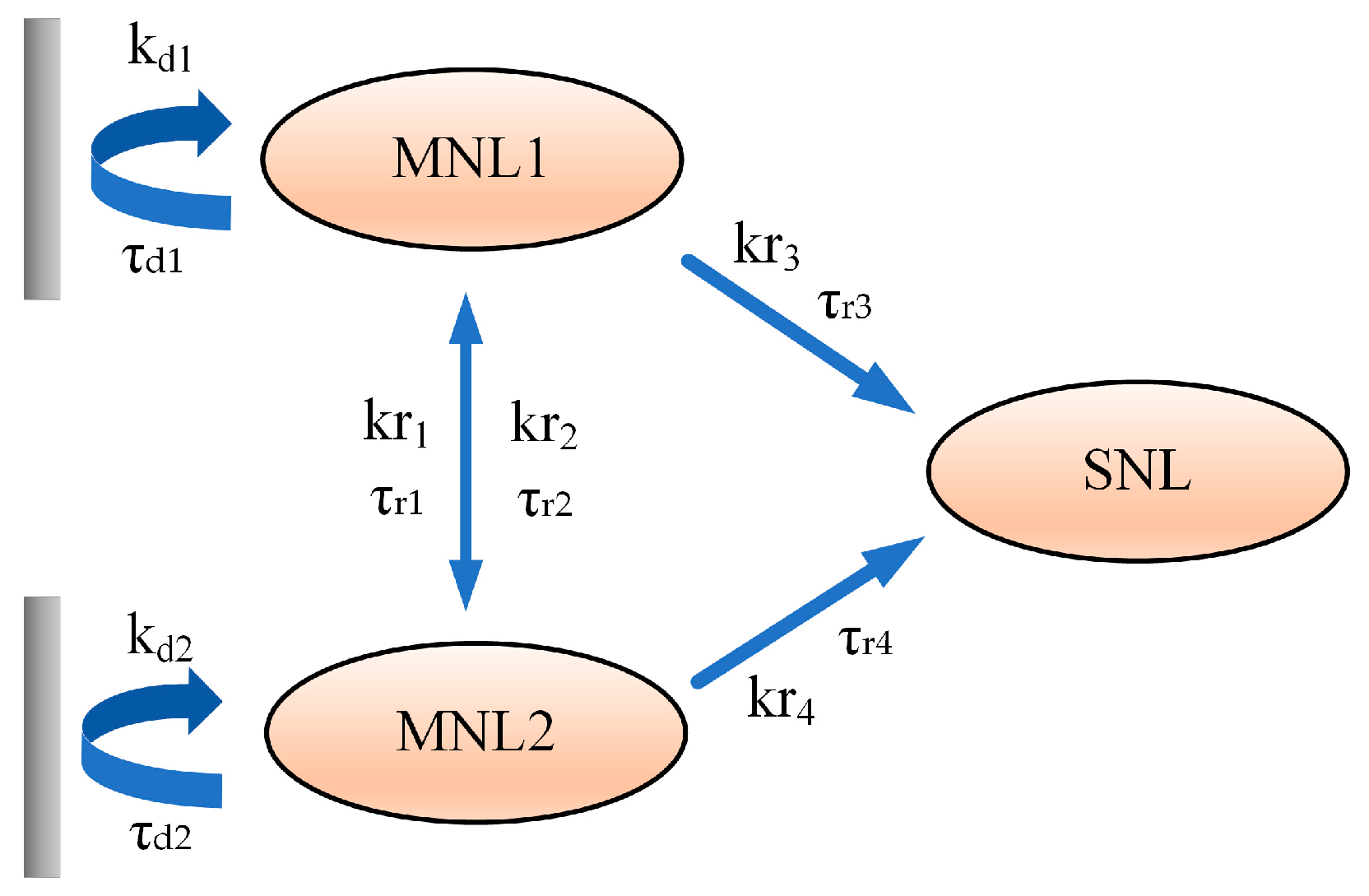
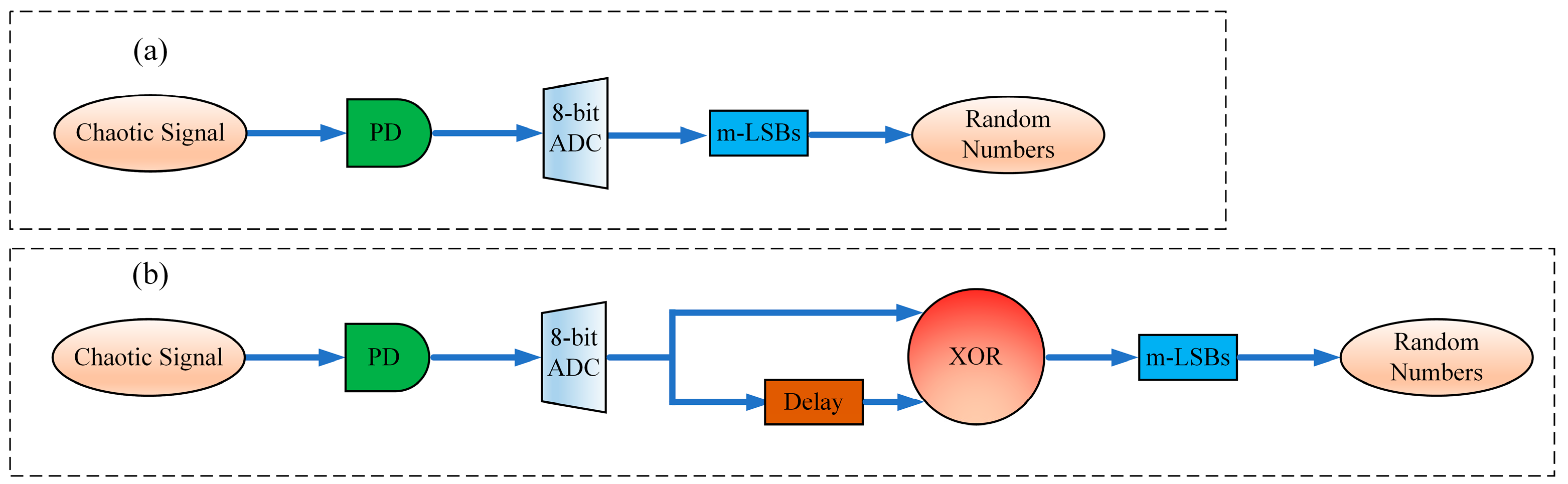
2. Theoretical Model
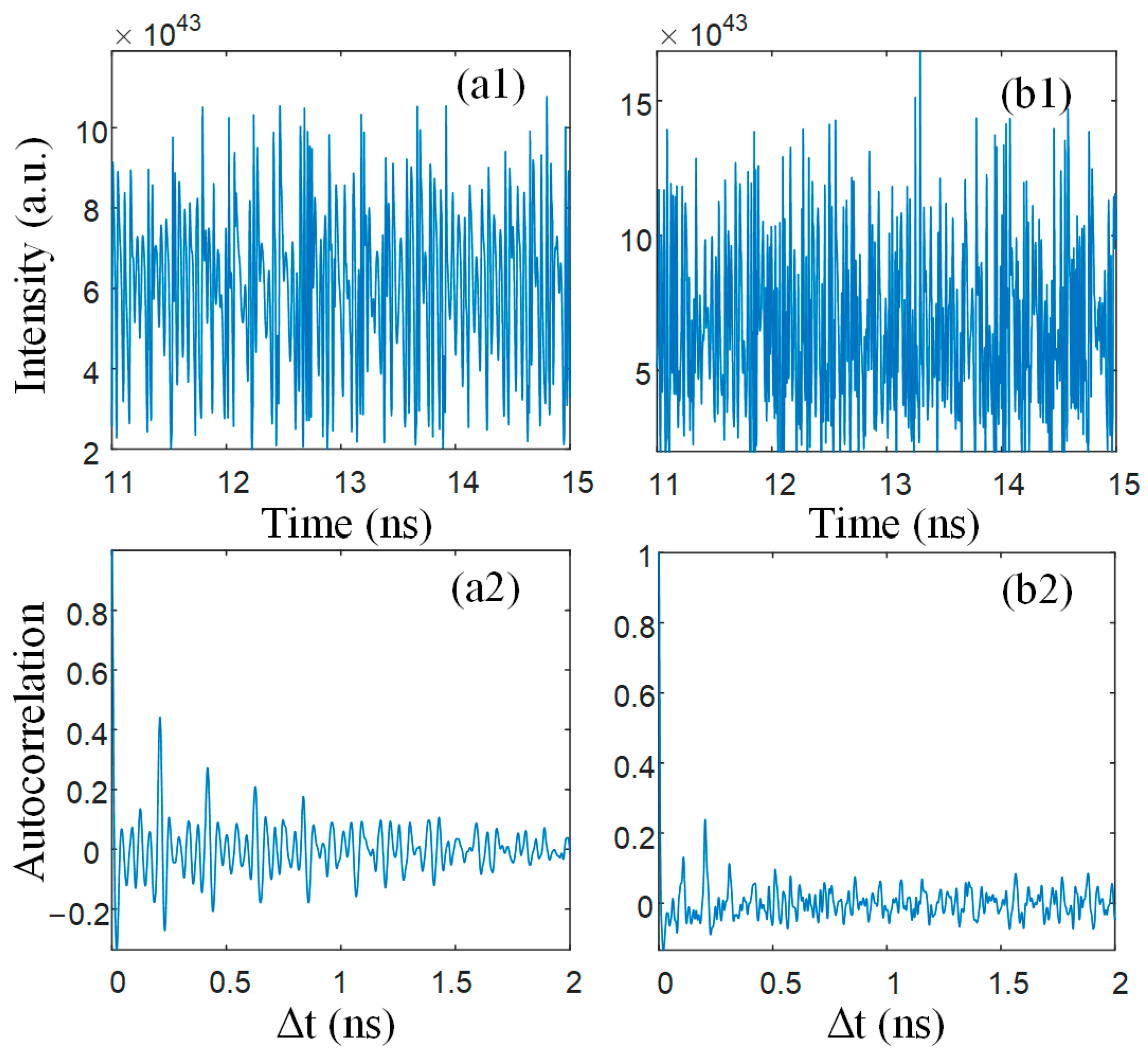
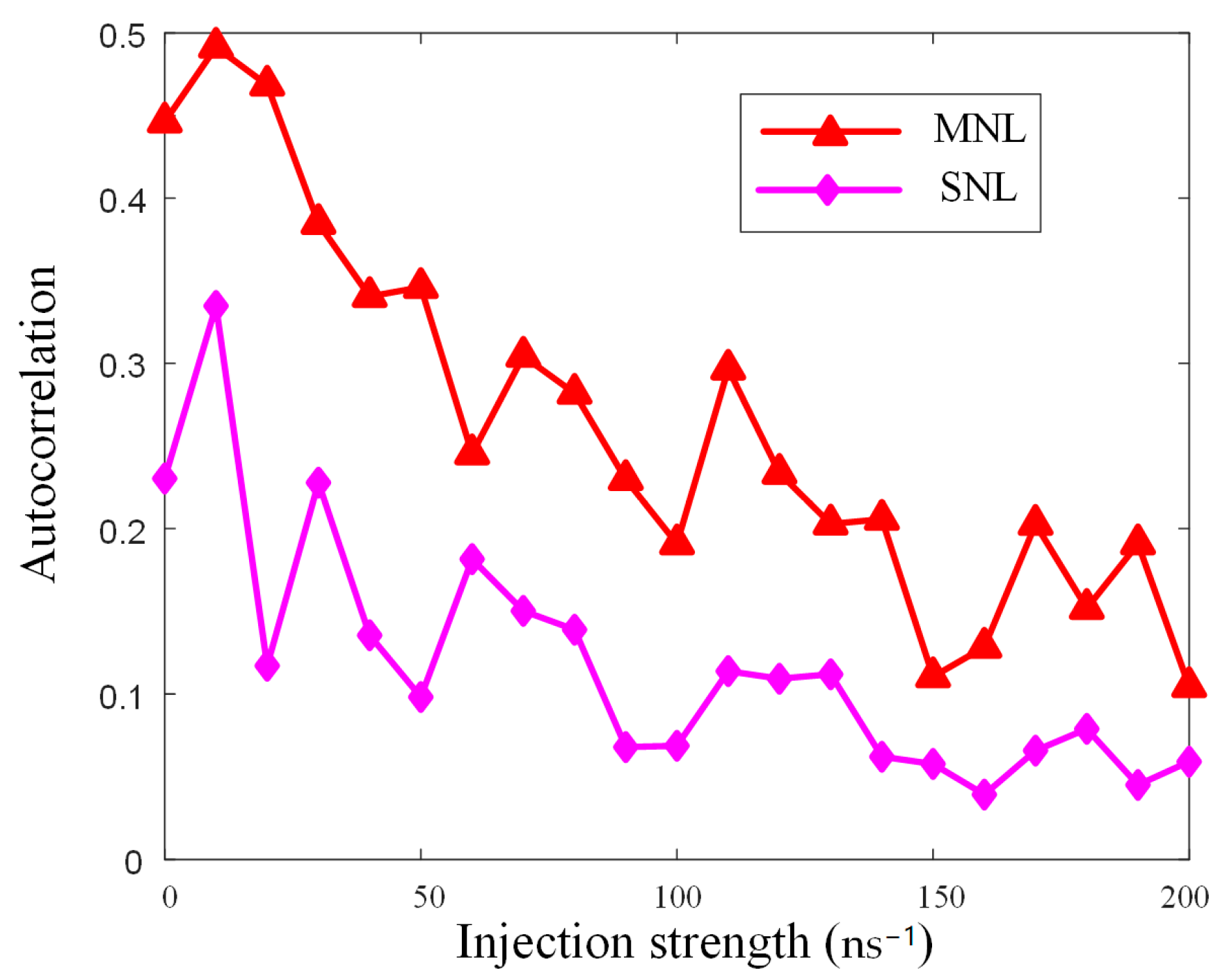
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum Cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, F.; Liu, B. Random Number Generators for Large-Scale Parallel Monte Carlo Simulations on FPGA. J. Comput. Phys. 2018, 360, 93–103. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, C.; Chen, H. A Novel Color Image Encryption Algorithm Based on Hyperchaotic System and Permutation-Diffusion Architecture. Int. J. Bifurc. Chaos 2019, 29, 1950115. [Google Scholar] [CrossRef]
- Zhou, L.; Tan, F.; Yu, F. A Robust Synchronization-Based Chaotic Secure Communication Scheme With Double-Layered and Multiple Hybrid Networks. IEEE Syst. J. 2020, 14, 2508–2519. [Google Scholar] [CrossRef]
- Yu, F.; Li, L.; Tang, Q.; Cai, S.; Song, Y.; Xu, Q. A Survey on True Random Number Generators Based on Chaos. Discret. Dyn. Nat. Soc. 2019, 2019, e2545123. [Google Scholar] [CrossRef]
- Peng, F.; Zhu, X.; Long, M. An ROI Privacy Protection Scheme for H.264 Video Based on FMO and Chaos. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1688–1699. [Google Scholar] [CrossRef]
- Datcu, O.; Macovei, C.; Hobincu, R. Chaos Based Cryptographic Pseudo-Random Number Generator Template with Dynamic State Change. Appl. Sci. 2020, 10, 451. [Google Scholar] [CrossRef]
- Gu, K.; Jia, W.; Wang, G.; Wen, S. Efficient and Secure Attribute-Based Signature for Monotone Predicates. Acta Inform. 2017, 54, 521–541. [Google Scholar] [CrossRef]
- Zhao, Q.; Yin, H. Gbits/s Physical-Layer Stream Ciphers Based on Chaotic Light. Optik 2013, 124, 2161–2164. [Google Scholar] [CrossRef]
- Abutaleb, M.M. A Novel True Random Number Generator Based on QCA Nanocomputing. Nano Commun. Netw. 2018, 17, 14–20. [Google Scholar] [CrossRef]
- Hasan, R.S.; Tawfeeq, S.K.; Mohammed, N.Q.; Khaleel, A.I. A True Random Number Generator Based on the Photon Arrival Time Registered in a Coincidence Window between Two Single-Photon Counting Modules. Chin. J. Phys. 2018, 56, 385–391. [Google Scholar] [CrossRef]
- Yu, F.; Wan, Q.; Jin, J.; Li, L.; He, B.; Liu, L.; Qian, S.; Huang, Y.; Cai, S.; Song, Y.; et al. Design and FPGA Implementation of a Pseudorandom Number Generator Based on a Four-Wing Memristive Hyperchaotic System and Bernoulli Map. IEEE Access 2019, 7, 181884–181898. [Google Scholar] [CrossRef]
- Rezk, A.A.; Madian, A.H.; Radwan, A.G.; Soliman, A.M. Reconfigurable Chaotic Pseudo Random Number Generator Based on FPGA. AEU-Int. J. Electron. Commun. 2019, 98, 174–180. [Google Scholar] [CrossRef]
- Li, N.; Kim, B.; Chizhevsky, V.N.; Locquet, A.; Bloch, M.; Citrin, D.S.; Pan, W. Two Approaches for Ultrafast Random Bit Generation Based on the Chaotic Dynamics of a Semiconductor Laser. Opt. Express OE 2014, 22, 6634–6646. [Google Scholar] [CrossRef] [PubMed]
- Bucci, M.; Germani, L.; Luzzi, R.; Trifiletti, A.; Varanonuovo, M. A High-Speed Oscillator-Based Truly Random Number Source for Cryptographic Applications on a Smart Card IC. IEEE Trans. Comput. 2003, 52, 403–409. [Google Scholar] [CrossRef]
- Cao, L.; Min, L.; Zang, H. A Chaos-Based Pseudorandom Number Generator and Performance Analysis. In Proceedings of the 2009 International Conference on Computational Intelligence and Security, Beijing, China, 11–14 December 2009; Volume 1, pp. 494–498. [Google Scholar]
- Kanter, I.; Aviad, Y.; Reidler, I.; Cohen, E.; Rosenbluh, M. An Optical Ultrafast Random Bit Generator. Nat. Photon 2010, 4, 58–61. [Google Scholar] [CrossRef]
- Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast Physical Random Bit Generation with Chaotic Semiconductor Lasers. Nat. Photon 2008, 2, 728–732. [Google Scholar] [CrossRef]
- Reidler, I.; Aviad, Y.; Rosenbluh, M.; Kanter, I. Ultrahigh-Speed Random Number Generation Based on a Chaotic Semiconductor Laser. Phys. Rev. Lett. 2009, 103, 024102. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-Z.; Li, S.-S.; Zhuang, J.-P.; Chan, S.-C. Random Bit Generation at Tunable Rates Using a Chaotic Semiconductor Laser under Distributed Feedback. Opt. Lett. OL 2015, 40, 3970–3973. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, B.; Wang, Y.; Han, Y.; Wen, A.; Hao, Y. 2.24-Tb/s Physical Random Bit Generation with Minimal Post-Processing Based on Chaotic Semiconductor Lasers Network. J. Light. Technol. JLT 2019, 37, 3987–3993. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, Y.; Ji, H. Sensing by Dynamics of Lasers with External Optical Feedback: A Review. Photonics 2022, 9, 450. [Google Scholar] [CrossRef]
- Wang, A.; Wang, Y.; He, H. Enhancing the Bandwidth of the Optical Chaotic Signal Generated by a Semiconductor Laser with Optical Feedback. IEEE Photonics Technol. Lett. 2008, 20, 1633–1635. [Google Scholar] [CrossRef]
- Komarov, A.; Komarov, K.; Niang, A.; Sanchez, F. Nature of Soliton Interaction in Fiber Lasers with Continuous External Optical Injection. Phys. Rev. A 2014, 89, 013833. [Google Scholar] [CrossRef]
- Yarunova, E.A.; Krents, A.A.; Molevich, N.E.; Anchikov, D.A. Suppression of Spatiotemporal Instabilities in Broad-Area Lasers with Pump Modulation by External Optical Injection. Bull. Lebedev Phys. Inst. 2021, 48, 55–58. [Google Scholar] [CrossRef]
- Tang, S.; Liu, J.M. Chaotic Pulsing and Quasi-Periodic Route to Chaos in a Semiconductor Laser with Delayed Opto-Electronic Feedback. IEEE J. Quantum Electron. 2001, 37, 329–336. [Google Scholar] [CrossRef]
- Priyadarshi, S.; Hong, Y.; Pierce, I.; Shore, K.K. Experimental Investigations of Time-Delay Signature Concealment in Chaotic External Cavity VCSELs Subject to Variable Optical Polarization Angle of Feedback. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1700707. [Google Scholar] [CrossRef]
- Wu, J.-G.; Wu, Z.-M.; Tang, X.; Lin, X.-D.; Deng, T.; Xia, G.-Q.; Feng, G.-Y. Simultaneous Generation of Two Sets of Time Delay Signature Eliminated Chaotic Signals by Using Mutually Coupled Semiconductor Lasers. IEEE Photon. Technol. Lett. 2011, 23, 759–761. [Google Scholar]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; Van Der Sande, G. Loss of Time-Delay Signature in Chaotic Semiconductor Ring Lasers. Opt. Lett. 2012, 37, 2541. [Google Scholar] [CrossRef]
- Mu, P.; He, P.; Li, N. Simultaneous Chaos Time-Delay Signature Cancellation and Bandwidth Enhancement in Cascade-Coupled Semiconductor Ring Lasers. IEEE Access 2019, 7, 11041–11048. [Google Scholar] [CrossRef]
- Lau, E.K.; Lakhani, A.; Tucker, R.S.; Wu, M.C. Enhanced Modulation Bandwidth of Nanocavity Light Emitting Devices. Opt. Express OE 2009, 17, 7790–7799. [Google Scholar] [CrossRef]
- Sattar, Z.A.; Shore, K.A. Dynamics of Nanolasers Subject to Optical Injection and Optical Feedback. In Proceedings of the Physics and Simulation of Optoelectronic Devices XXIV, San Francisco, CA, USA, 13–18 February 2016; SPIE: New York, NY, USA, 2016; Volume 9742, pp. 38–47. [Google Scholar]
- Abdul Sattar, Z.; Shore, K.A. External Optical Feedback Effects in Semiconductor Nanolasers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 500–505. [Google Scholar] [CrossRef]
- Abdul Sattar, Z.; Shore, K.A. Phase Conjugate Feedback Effects in Nano-Lasers. IEEE J. Quantum Electron. 2016, 52, 1–8. [Google Scholar] [CrossRef]
- Abdul Sattar, Z.; Ali Kamel, N.; Shore, K.A. Optical Injection Effects in Nanolasers. IEEE J. Quantum Electron. 2016, 52, 1–8. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Analysis of High-Frequency Oscillations in Mutually-Coupled Nano-Lasers. Opt. Express OE 2018, 26, 10013–10022. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Shore, K.A. Dynamical Characteristics of Nano-Lasers Subject to Optical Injection and Phase Conjugate Feedback. IET Optoelectron. 2018, 12, 25–29. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Modulated Mutually Coupled Nano-Lasers. IEEE J. Quantum Electron. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Qu, Y.; Xiang, S.; Wang, Y.; Lin, L.; Wen, A.J.; Hao, Y. Concealment of Time Delay Signature of Chaotic Semiconductor Nanolasers With Double Chaotic Optical Injections. IEEE J. Quantum Electron. 2019, 55, 1–7. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, G.; Liu, X.; Hu, G.; Wang, K.; Mu, P. Dynamics and Concealment of Time-Delay Signature in Mutually Coupled Nano-Laser Chaotic Systems. Photonics 2023, 10, 1196. [Google Scholar] [CrossRef]
- Zhang, X.; Mu, P.; Guo, G.; Liu, X.; He, P. Bidirectional Chaotic Synchronization Communication of Closed-Loop Mutually Coupled Nano-Lasers. Electronics 2024, 13, 239. [Google Scholar] [CrossRef]
- Liu, G.; Mu, P.; Wang, K.; Guo, G.; Liu, X.; He, P. Random Numbers Generated Based on Dual-Channel Chaotic Light. Electronics 2024, 13, 1603. [Google Scholar] [CrossRef]
- Liu, G.P.; Mu, P.H.; Guo, G.; Liu, X.T.; Hu, G.S. High-Quality Random Bit Generation Based on a Cascade-Coupled Nano-Laser System. Laser Phys. Lett. 2024, 21, 035206. [Google Scholar] [CrossRef]
- Xue, C.; Jiang, N.; Lv, Y.; Wang, C.; Li, G.; Lin, S.; Qiu, K. Security-Enhanced Chaos Communication with Time-Delay Signature Suppression and Phase Encryption. Opt. Lett., OL 2016, 41, 3690–3693. [Google Scholar] [CrossRef]
- Xiang, S.; Wen, A.; Pan, W.; Lin, L.; Zhang, H.; Zhang, H.; Guo, X.; Li, J. Suppression of Chaos Time Delay Signature in a Ring Network Consisting of Three Semiconductor Lasers Coupled with Heterogeneous Delays. J. Light. Technol. 2016, 34, 4221–4227. [Google Scholar] [CrossRef]
- Zhao, A.; Jiang, N.; Liu, S.; Xue, C.; Qiu, K. Wideband Time Delay Signature-Suppressed Chaos Generation Using Self-Phase-Modulated Feedback Semiconductor Laser Cascaded with Dispersive Component. J. Light. Technol. 2019, 37, 5132–5139. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. On the Implementation of the 0–1 Test for Chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]


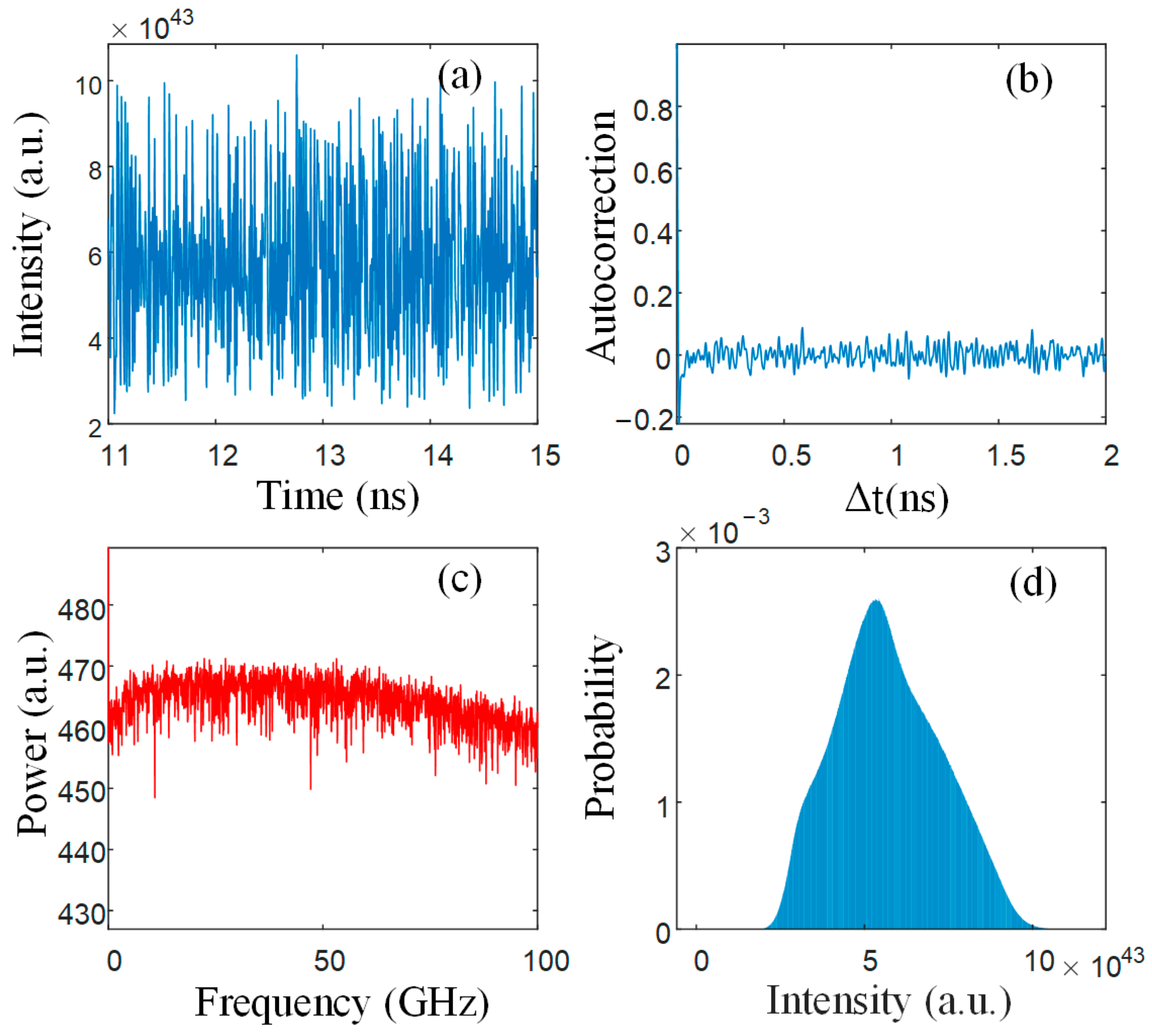
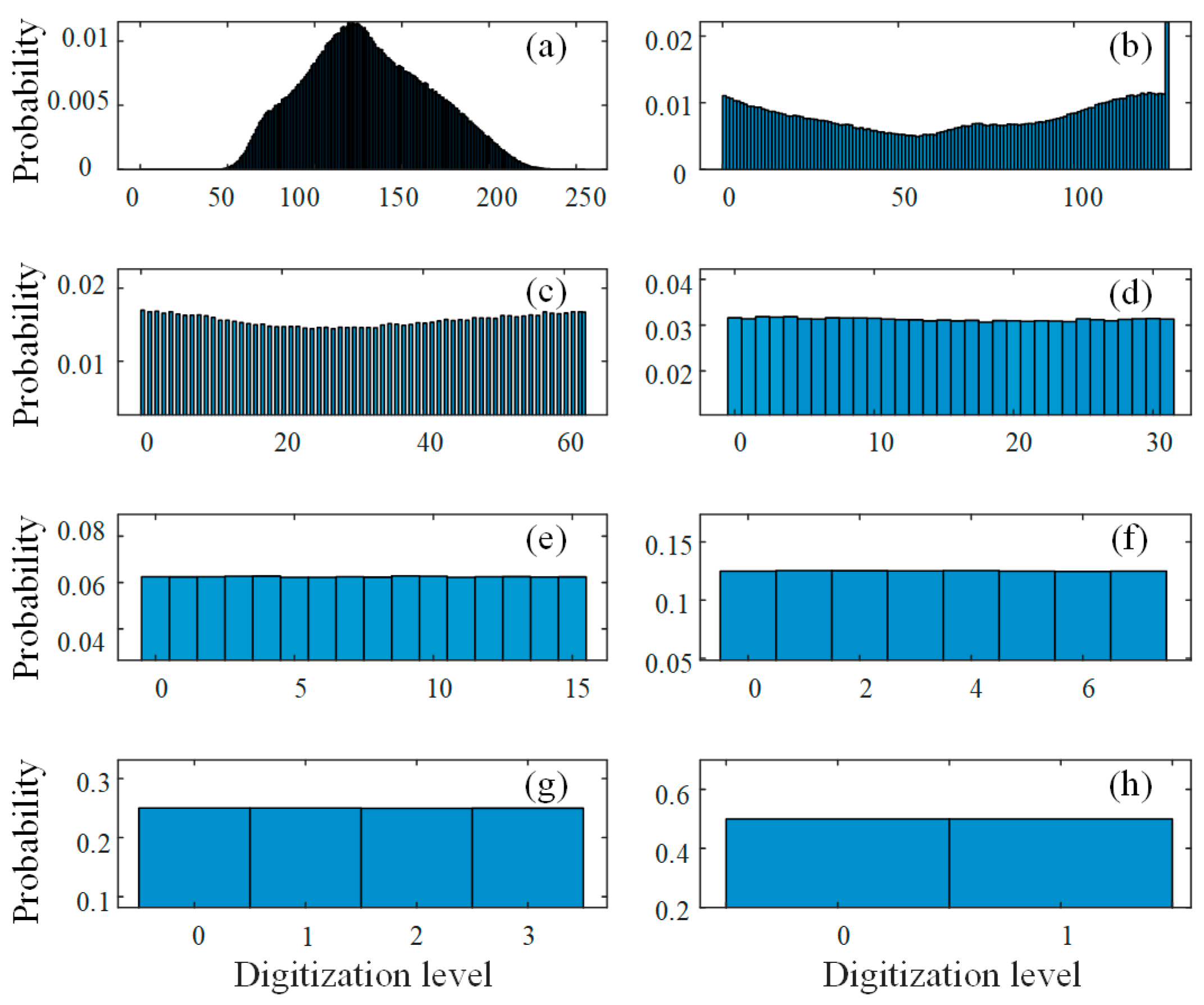
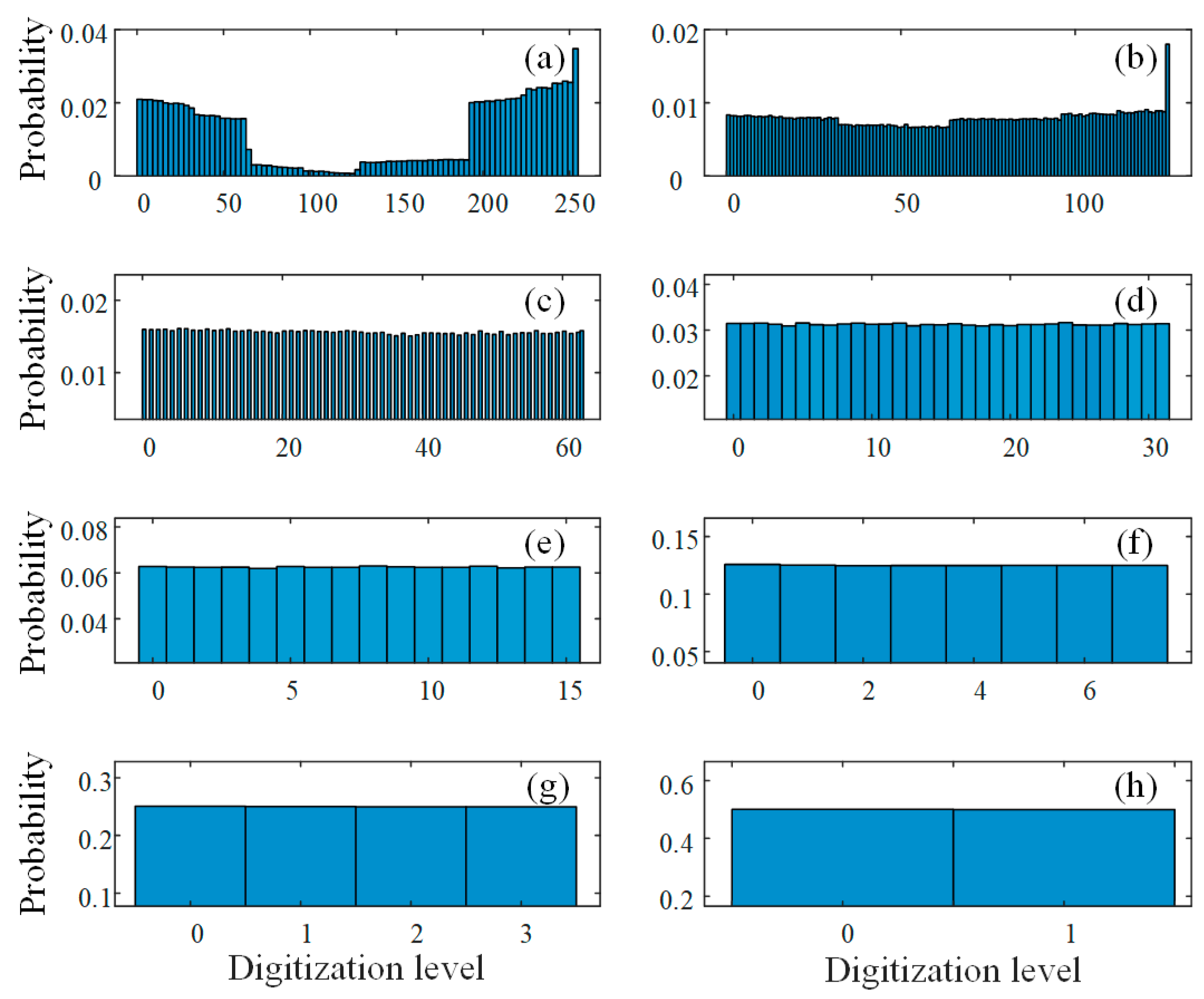
| Parameter | Description | Value |
|---|---|---|
| Wavelength of MNL | ||
| Cavity Length | ||
| Volume of Active Region | ||
| Mode Confinement | 0.645 | |
| Differential Gain | ||
| Photon Lifetime | ||
| Feedback Delay | ||
| Carrier Lifetime | ||
| Transparency Carrier Density | ||
| Gain Saturation Factor | ||
| Refractive Index | 3.4 | |
| Linewidth Enhancement Factor | 5 | |
| External Facet Power Reflectivity | 0.95 | |
| Laser Facet Reflectivity | 0.85 | |
| Speed of Light in Free Space | ||
| Injection Parameter | ||
| Feedback Coupling Fraction |
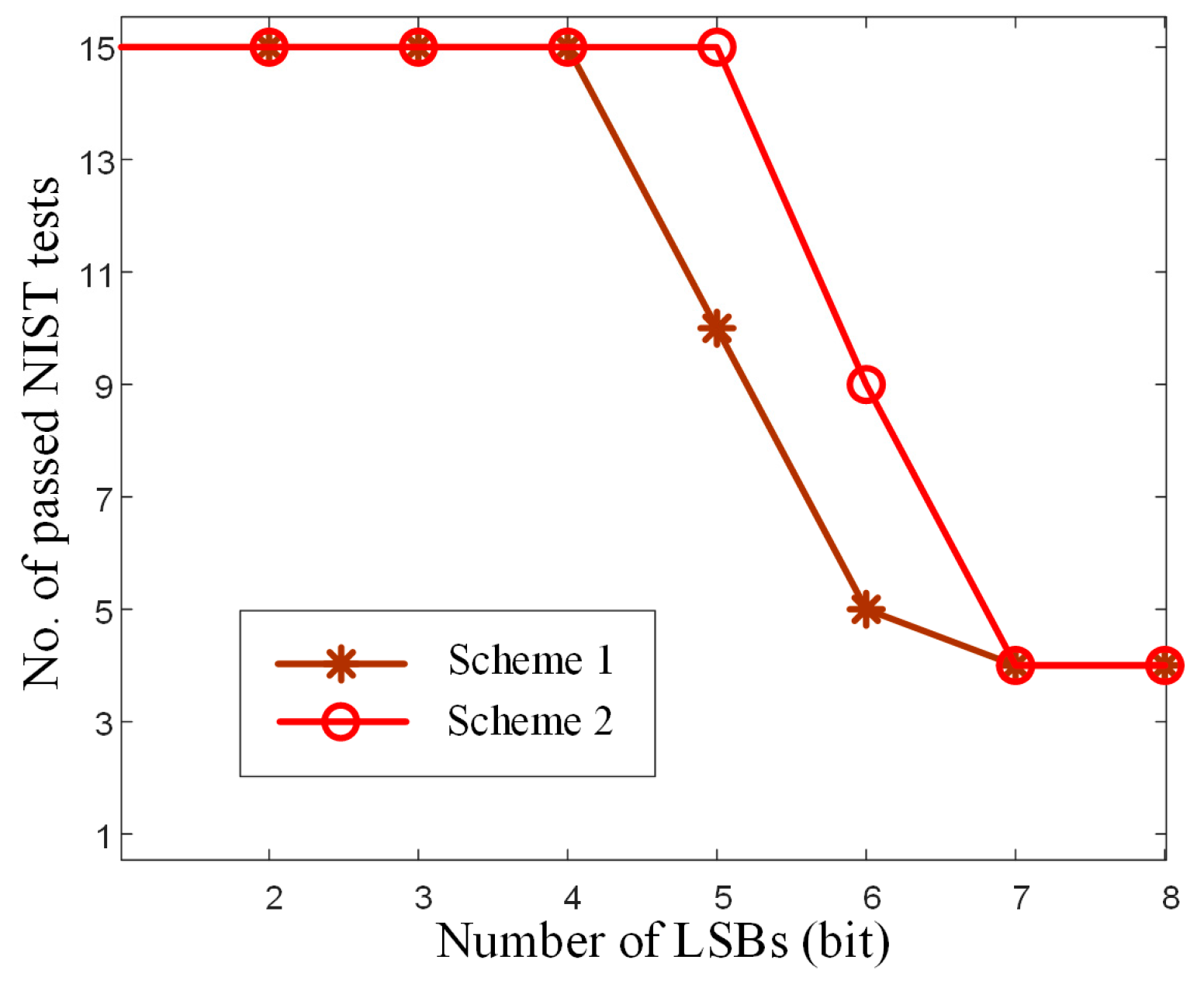
| Statistical Test | In Scheme 1, Four LSBs Are Retained. | In Scheme 2, Five LSBs Are Retained. | ||||
|---|---|---|---|---|---|---|
| p-Value | Proportion | Result | p-Value | Proportion | Result | |
| Frequency | 0.352107 | 0.994 | Success | 0.777265 | 0.987 | Success |
| Block frequency | 0.570792 | 0.990 | Success | 0.308561 | 0.990 | Success |
| Cumulative sums | 0.635037 | 0.992 | Success | 0.695200 | 0.987 | Success |
| Runs | 0.591409 | 0.986 | Success | 0.635037 | 0.994 | Success |
| Longest runs | 0.428095 | 0.992 | Success | 0.915317 | 0.989 | Success |
| Rank | 0.705466 | 0.993 | Success | 0.781106 | 0.994 | Success |
| Fast Fourier transform | 0.011875 | 0.993 | Success | 0.492436 | 0.990 | Success |
| Non-overlapping template | 0.664168 | 0.982 | Success | 0.007975 | 0.982 | Success |
| Overlapping template | 0.558502 | 0.988 | Success | 0.326749 | 0.994 | Success |
| Universal | 0.317565 | 0.989 | Success | 0.307077 | 0.986 | Success |
| Approximate entropy | 0.542228 | 0.991 | Success | 0.363593 | 0.985 | Success |
| Random excursions | 0.191505 | 0.984 | Success | 0.012181 | 0.982 | Success |
| Random excursions variant | 0.278122 | 0.986 | Success | 0.025588 | 0.982 | Success |
| Serial | 0.595549 | 0.990 | Success | 0.184549 | 0.984 | Success |
| Linear complexity | 0.469232 | 0.989 | Success | 0.373625 | 0.991 | Success |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Liu, G.; Li, R.; Mu, P. Influence of Post-Processing Techniques on Random Number Generation Using Chaotic Nanolasers. Electronics 2024, 13, 2712. https://doi.org/10.3390/electronics13142712
Zhao J, Liu G, Li R, Mu P. Influence of Post-Processing Techniques on Random Number Generation Using Chaotic Nanolasers. Electronics. 2024; 13(14):2712. https://doi.org/10.3390/electronics13142712
Chicago/Turabian StyleZhao, Jing, Guopeng Liu, Rongkang Li, and Penghua Mu. 2024. "Influence of Post-Processing Techniques on Random Number Generation Using Chaotic Nanolasers" Electronics 13, no. 14: 2712. https://doi.org/10.3390/electronics13142712
APA StyleZhao, J., Liu, G., Li, R., & Mu, P. (2024). Influence of Post-Processing Techniques on Random Number Generation Using Chaotic Nanolasers. Electronics, 13(14), 2712. https://doi.org/10.3390/electronics13142712









