User Scheduling and Path Planning for Reconfigurable Intelligent Surface Assisted MISO UAV Communication
Abstract
:1. Introduction
- We present an innovative multiple-input single-output (MISO) UAV communication model featuring a RIS integration. This advanced model equips the UAV with multiple transmitting antennas, considerably improving communication reliability. Our aim, focusing on equitable data transmission, is to increase the minimum reception rate for all ground users. Distinct from traditional methods that concentrate on optimizing UAV transmission power, our approach emphasizes the optimization of the UAV’s transmit beamforming, thereby introducing a new paradigm in UAV communication.
- We introduce a comprehensive framework that integrates the optimization of user scheduling, UAV trajectory, transmit beamforming, and RIS phase shift design. This intricate optimization task, formulated as a non-convex problem, is strategically decomposed into four distinct subproblems. We have derived closed-form expressions for both phase shift and transmit beamforming. Additionally, the UAV’s trajectory is determined through the application of the successive convex approximation (SCA) method, contributing to the advancements of UAV communication systems.
2. System Model and Problem Formulation
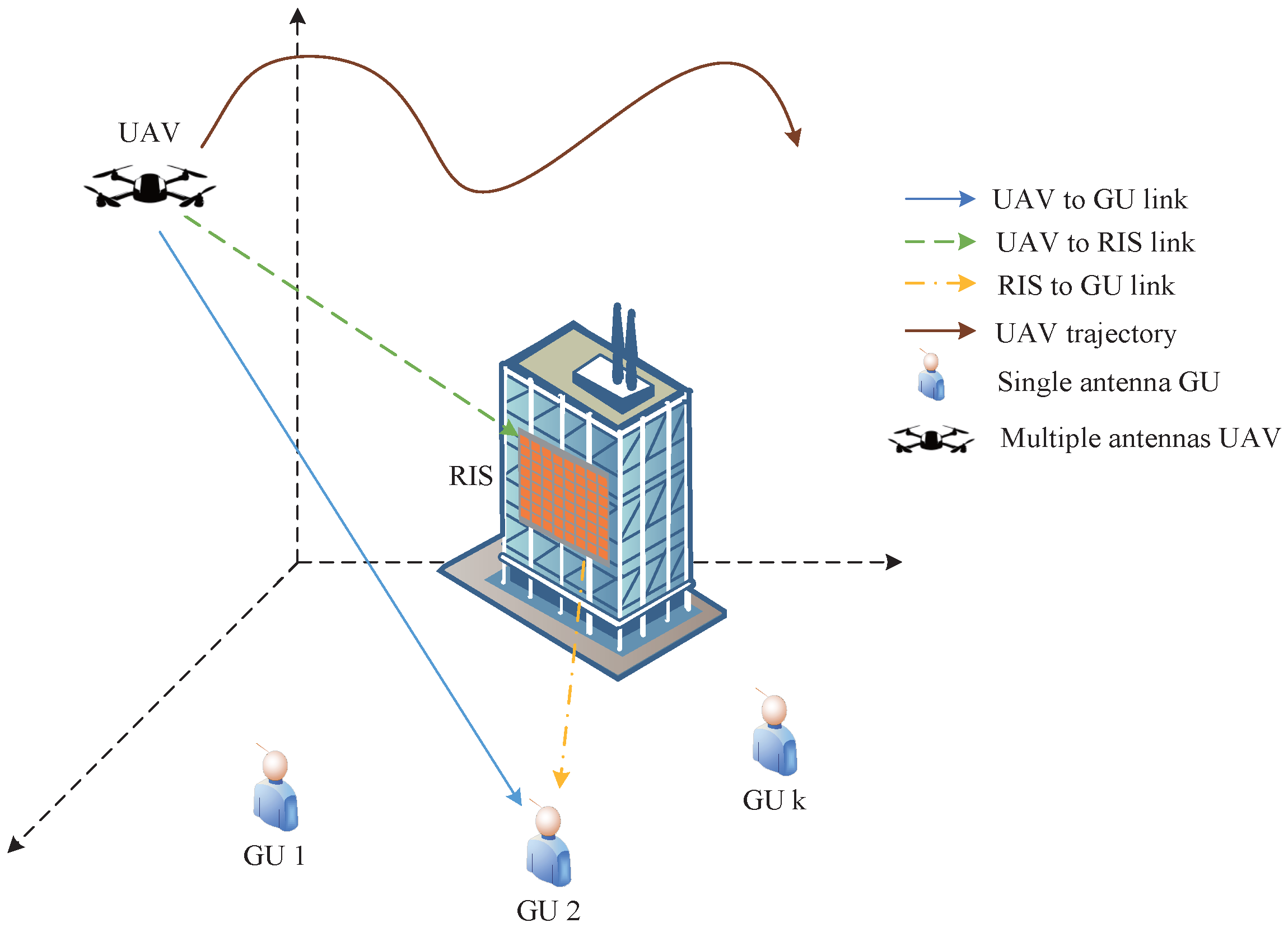
2.1. System Model
2.2. Problem Formulation
3. The Proposed Algorithm
3.1. User Scheduling Optimization
3.2. Transmit Beamforming Optimization
3.3. Phase Shift Optimization
3.4. Trajectory Optimization
3.5. Overall Algorithm
| Algorithm 1 Proposed Algorithm for Solving (13) | |
| 1: | Initialization: Set iteration number and tolerance error . Initialize and with the given |
| 2: | repeat |
| 3: | Solve problem (14) to find with given , and ; |
| 4: | Solve problem (19) to find with given , and ; |
| 5: | Solve problem (23) to find with given , and ; |
| 6: | Solve problem (31) to find with given , and ; |
| 7: | Set ; |
| 8: | Until:. |
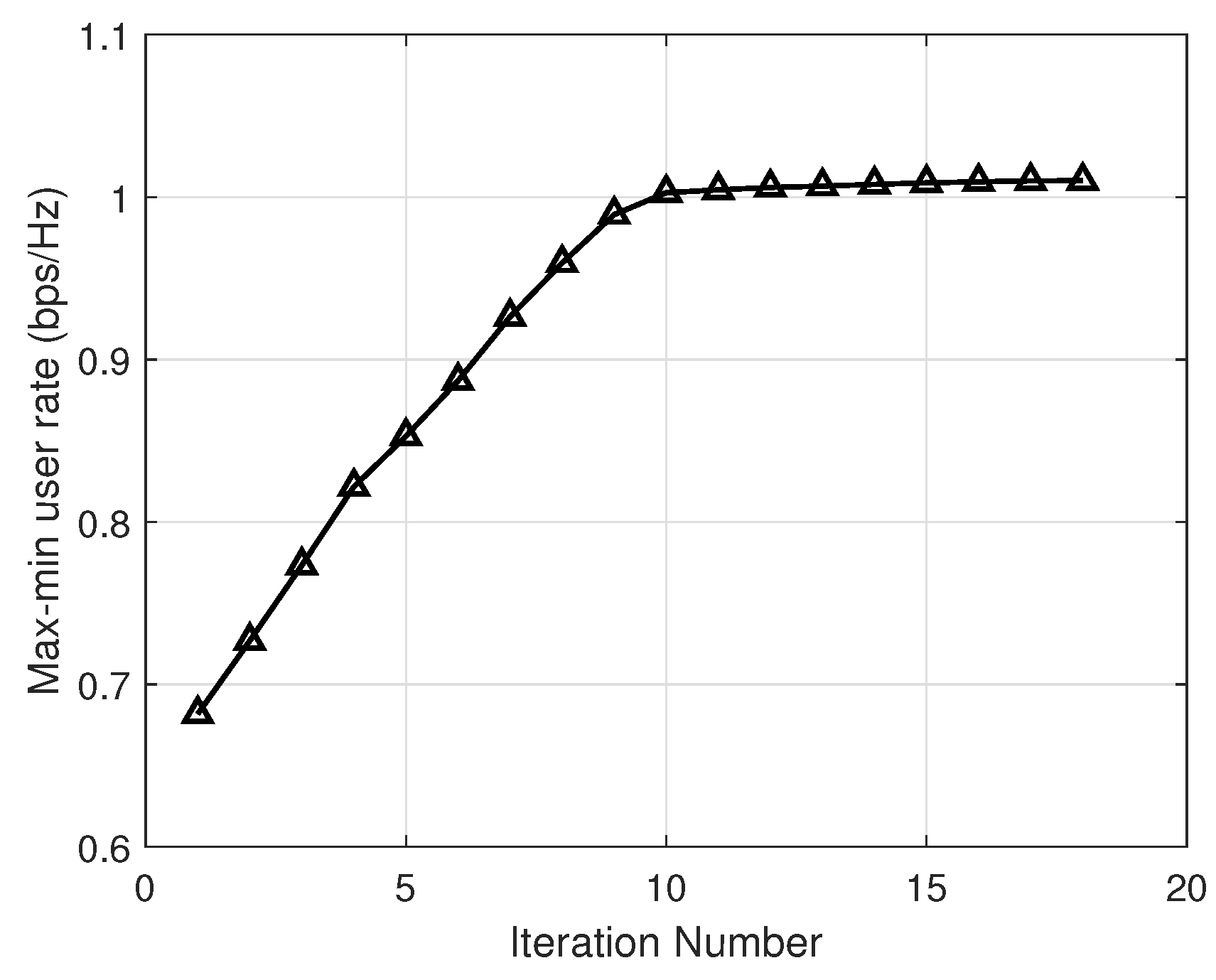
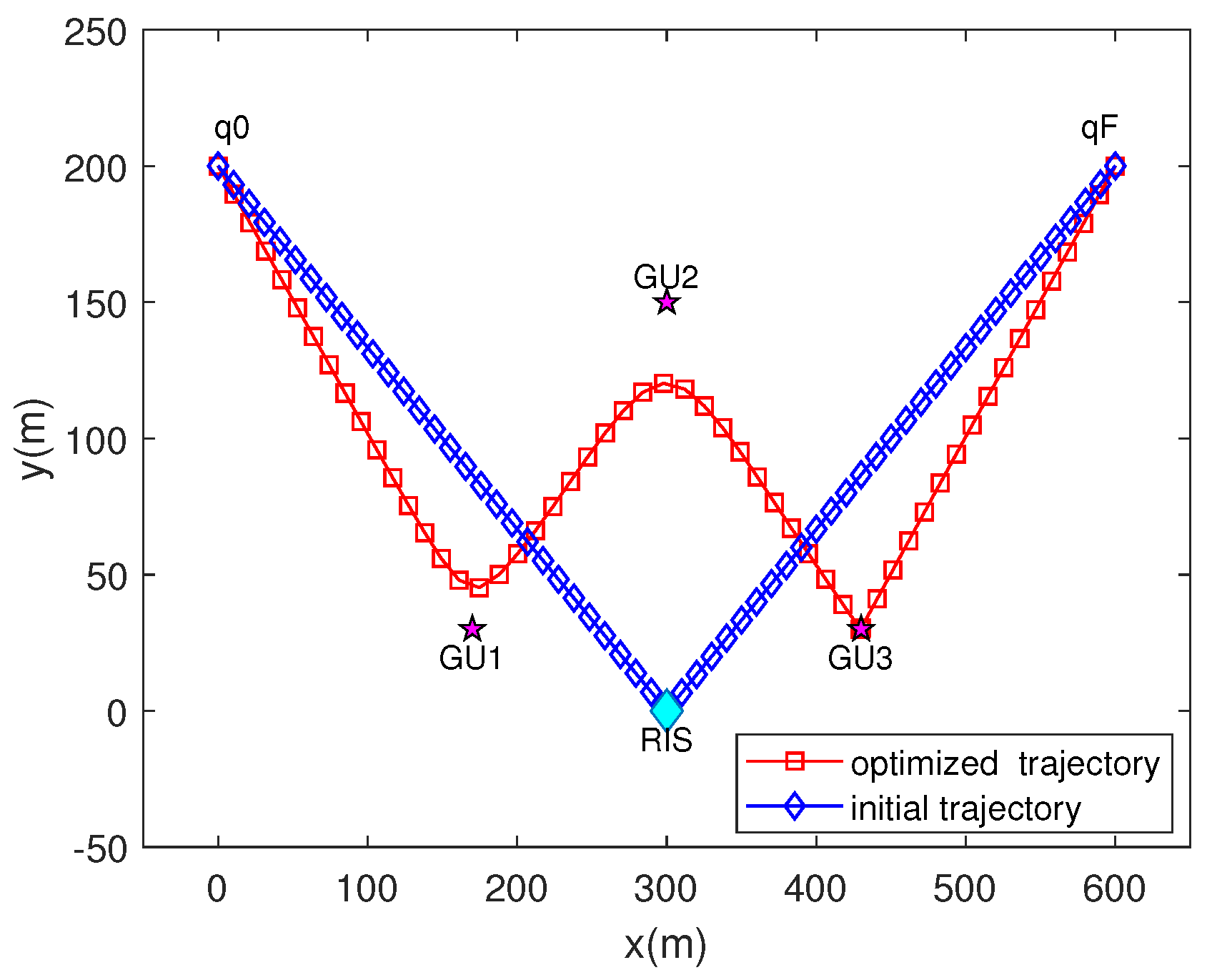
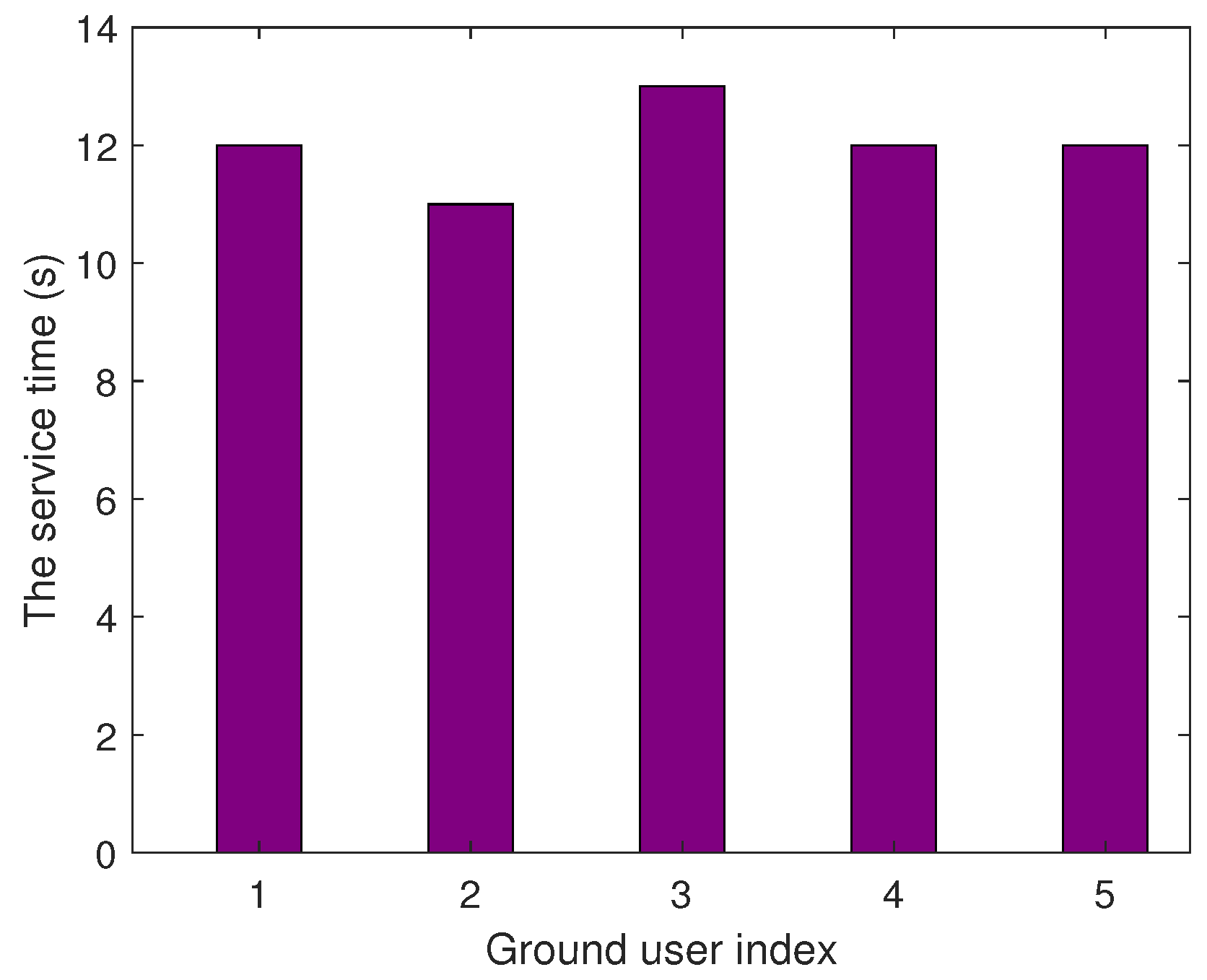
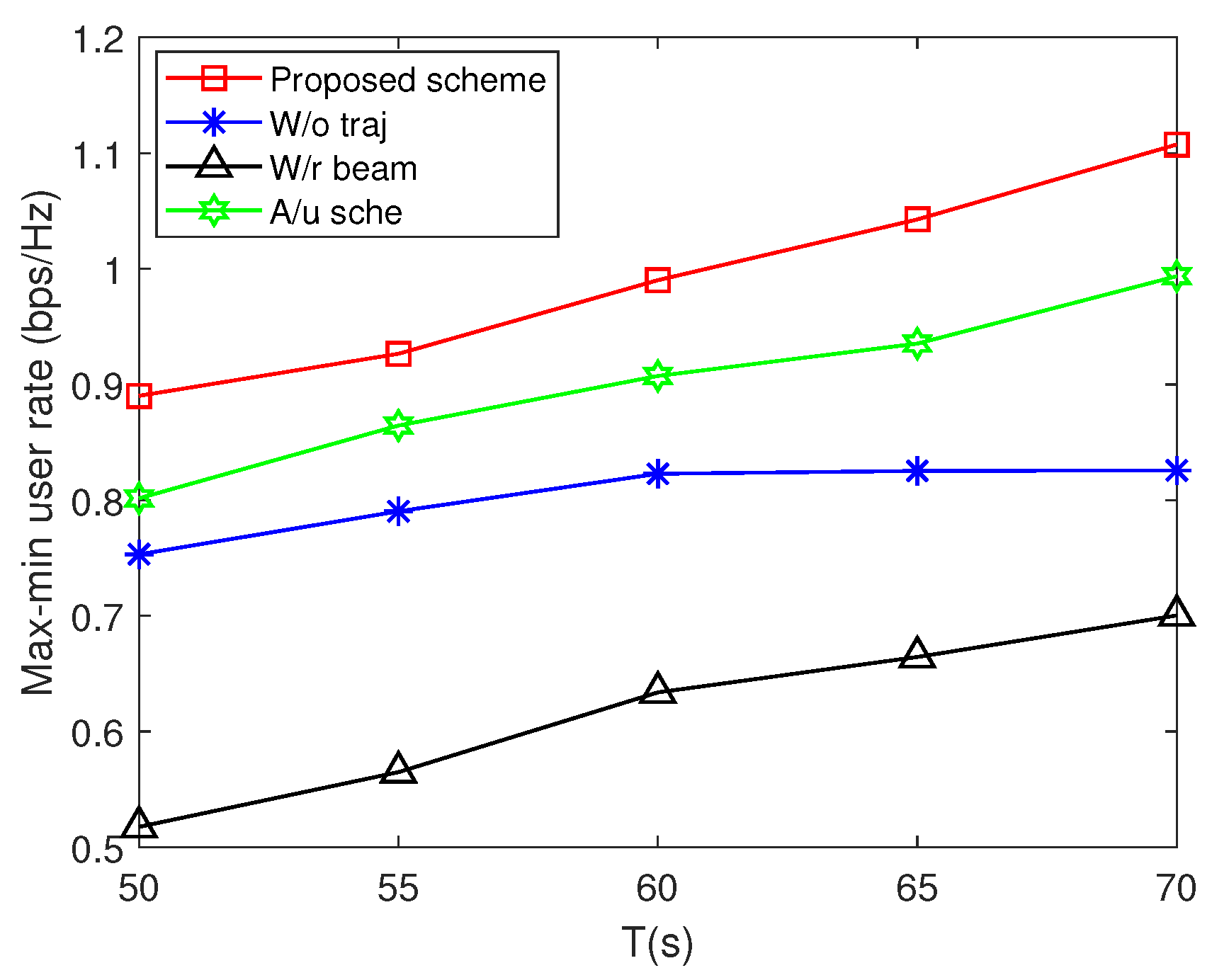
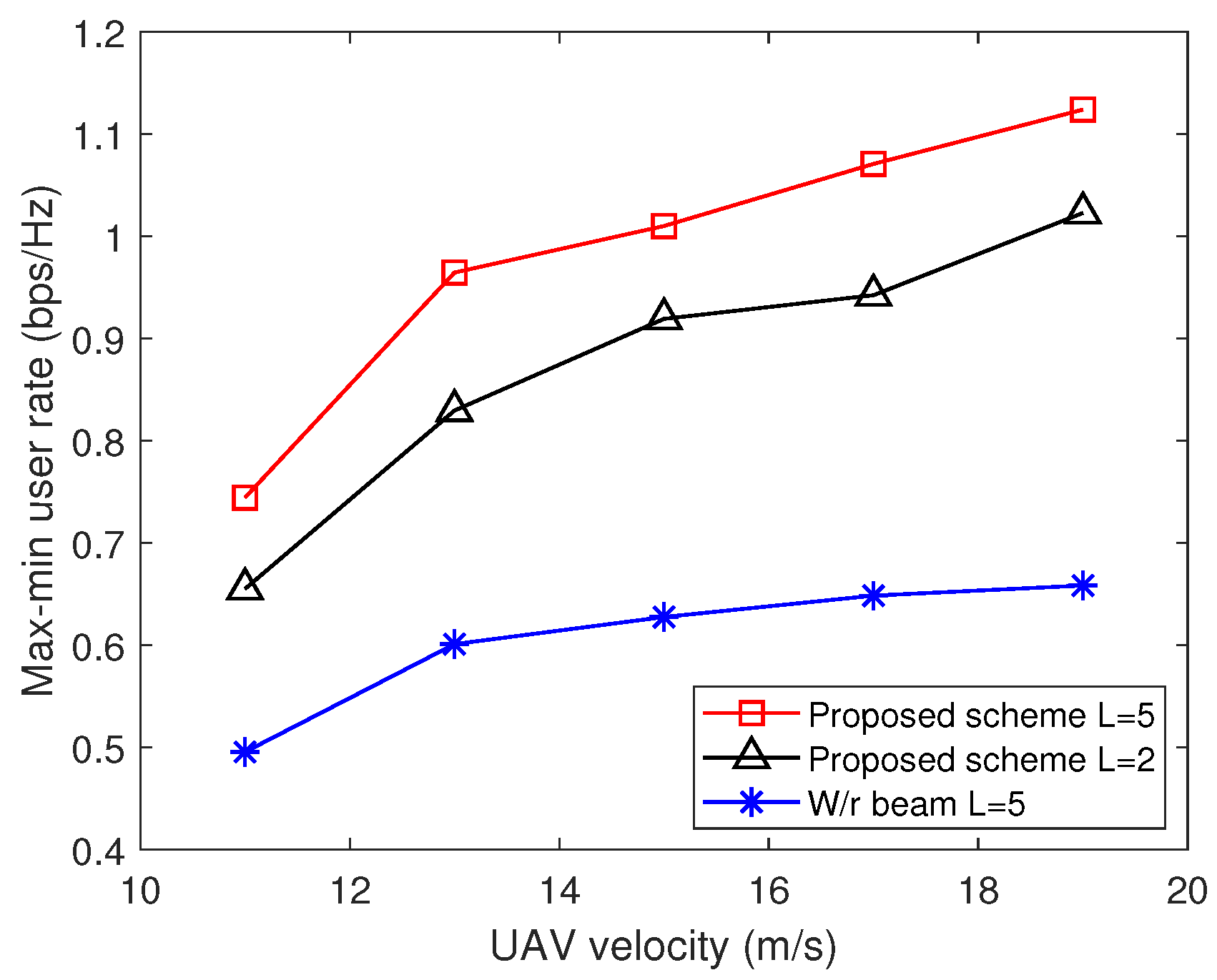
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSI | channel state information |
| CSCG | circularly symmetric complex gaussian |
| R2G link | link between the RIS and ground user |
| U2R link | link between the RIS and UAV |
| U2G link | link between UAV to ground user |
| MISO | multiple-input single-output |
| NLoS | non-line-of-sight |
| RIS | reconfigurable intelligent surface |
| SNR | signal-to-noise ratio |
| UPA | uniform planar array |
| UAV | unmanned aerial vehicle |
| LoS | line-of-sight |
References
- Liu, Y.; Xie, S.; Zhang, Y. Cooperative Offloading and Resource Management for UAV-Enabled Mobile Edge Computing in Power IoT System. IEEE Trans. Veh. Technol. 2020, 69, 12229–12239. [Google Scholar] [CrossRef]
- Tyrovolas, D.; Mekikis, P.-V.; Tegos, S.A.; Diamantoulakis, P.D.; Liaskos, C.K.; Karagiannidis, G.K. Energy-Aware Design of UAV-Mounted RIS Networks for IoT Data Collection. IEEE Trans. Commun. 2023, 71, 1168–1178. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, M.; Zhou, H.; Wang, X.; Wang, N.; Long, K. Capacity Maximization in RIS-UAV Networks: A DDQN-Based Trajectory and Phase Shift Optimization Approach. IEEE Trans. Wirel. Commun. 2023, 22, 2583–2591. [Google Scholar] [CrossRef]
- Qian, Y.; Wang, F.; Li, J.; Shi, L.; Cai, K.; Shu, F. User Association and Path Planning for UAV-Aided Mobile Edge Computing with Energy Restriction. IEEE Wirel. Commun. Lett. 2019, 8, 1312–1315. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H.; Dong, D. Path Planning for Cellular-Connected UAV: A DRL Solution with Quantum-Inspired Experience Replay. IEEE Trans. Wirel. Commun. 2022, 21, 7897–7912. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H. Radio Resource Management for Cellular-Connected UAV: A Learning Approach. IEEE Trans. Commun. 2023, 71, 2784–2800. [Google Scholar] [CrossRef]
- Hou, X.; Wang, J.; Jiang, C.; Zhang, X.; Ren, Y.; Debbah, M. UAV-Enabled Covert Federated Learning. IEEE Trans. Wirel. Commun. 2023, 22, 6793–6809. [Google Scholar] [CrossRef]
- Feng, W.; Wang, J.; Chen, Y.; Wang, X.; Ge, N.; Lu, J. UAV-Aided MIMO Communications for 5G Internet of Things. IEEE Internet Things J. 2019, 62, 1731–1740. [Google Scholar] [CrossRef]
- Lyu, L.; Zeng, F.; Xiao, Z.; Zhang, C.; Jiang, H.; Havyarimana, V. Computation Bits Maximization in UAV-Enabled Mobile-Edge Computing System. IEEE Internet Things J. 2022, 9, 10640–10651. [Google Scholar] [CrossRef]
- Yu, Z.; Gong, Y.; Gong, S.; Guo, Y. Joint Task Offloading and Resource Allocation in UAV-Enabled Mobile Edge Computing. IEEE Internet Things J. 2020, 7, 3147–3159. [Google Scholar] [CrossRef]
- Liu, B.; Wan, Y.; Zhou, F.; Wu, Q.; Hu, R.Q. Robust Trajectory and Beamforming Design for Cognitive MISO UAV Networks. IEEE Wirel. Commun. Lett. 2021, 10, 396–400. [Google Scholar]
- Khalili, A.; Monfared, E.M.; Zargari, S.; Javan, M.R.; Yamchi, N.M.; Jorswieck, E.A. Resource Management for Transmit Power Minimization in UAV-Assisted RIS HetNets Supported by Dual Connectivity. IEEE Trans. Wirel. Commun. 2022, 21, 1806–1822. [Google Scholar] [CrossRef]
- Zeng, S.; Zhang, H.; Di, B.; Han, Z.; Song, L. Reconfigurable Intelligent Surface (RIS) Assisted Wireless Coverage Extension: RIS Orientation and Location Optimization. IEEE Commun. Lett. 2021, 25, 269–273. [Google Scholar] [CrossRef]
- ElMossallamy, M.A.; Zhang, H.; Song, L.; Seddik, K.G.; Han, Z.; Li, G.Y. Reconfigurable Intelligent Surfaces for Wireless Communications: Principles, Challenges, and Opportunities. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 990–1002. [Google Scholar] [CrossRef]
- Yan, W.; Yuan, X.; He, Z.-Q.; Kuai, X. Passive Beamforming and Information Transfer Design for Reconfigurable Intelligent Surfaces Aided Multiuser MIMO Systems. IEEE J. Sel. Areas Commun. 2020, 38, 1793–1808. [Google Scholar] [CrossRef]
- He, Z.; Shen, H.; Xu, W.; Zhao, C. Low-Cost Passive Beamforming for RIS-Aided Wideband OFDM Systems. IEEE Wirel. Commun. Lett. 2022, 11, 318–322. [Google Scholar] [CrossRef]
- Yu, H.; Tuan, H.D.; Nasir, A.A.; Duong, T.Q.; Poor, H.V. Joint Design of Reconfigurable Intelligent Surfaces and Transmit Beamforming Under Proper and Improper Gaussian Signaling. IEEE J. Sel. Areas Commun. 2020, 38, 2589–2603. [Google Scholar] [CrossRef]
- Yu, H.; Tuan, H.D.; Dutkiewicz, E.; Poor, H.V.; Hanzo, L. Maximizing the Geometric Mean of User-Rates to Improve Rate-Fairness: Proper vs. Improper Gaussian Signaling. IEEE Trans. Wirel. Commun. 2022, 21, 295–309. [Google Scholar] [CrossRef]
- Liu, X.; Yu, Y.; Li, F.; Durrani, T.S. Throughput Maximization for RIS-UAV Relaying Communications. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19569–19574. [Google Scholar] [CrossRef]
- Byun, Y.; Kim, H.; Kim, S.; Shim, B. Channel Estimation and Phase Shift Control for UAV-Carried RIS Communication Systems. IEEE Trans. Veh. Technol. 2023, 72, 13695–13700. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Chen, Y.; Poor, H.V. RIS Enhanced Massive Non-Orthogonal Multiple Access Networks: Deployment and Passive Beamforming Design. IEEE J. Sel. Areas Commun. 2021, 39, 1057–1071. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, X.; Leung, V.C.M. Fair Downlink Communications for RIS-UAV Enabled Mobile Vehicles. IEEE Wirel. Commun. Lett. 2022, 11, 1042–1046. [Google Scholar] [CrossRef]
- Singh, S.K.; Agrawal, K.; Singh, K.; Li, C.-P.; Ding, Z. NOMA Enhanced Hybrid RIS-UAV-Assisted Full-Duplex Communication System with Imperfect SIC and CSI. IEEE Trans. Commun. 2022, 70, 7609–7627. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Yuan, X.; Liang, Y.-C.; Renzo, M.D. Reconfigurable Intelligent Surface Assisted UAV Communication: Joint Trajectory Design and Passive Beamforming. IEEE Wirel. Commun. Lett. 2020, 9, 716–720. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, K.; Pan, C.; Zhu, H.; Wang, J. UAV-Assisted and Intelligent Reflecting Surfaces-Supported Terahertz Communications. IEEE Wirel. Commun. Lett. 2021, 10, 1256–1260. [Google Scholar]
- Tian, K.; Duo, B.; Li, S.; Zuo, Y.; Yuan, X. Hybrid Uplink and Downlink Transmissions for Full-Duplex UAV Communication with RIS. IEEE Wirel. Commun. Lett. 2022, 11, 866–870. [Google Scholar] [CrossRef]
- Liu, B.; Wan, Y.; Zhou, F.; Wu, Q.; Hu, R.Q. Resource Allocation and Trajectory Design for MISO UAV-Assisted MEC Networks. IEEE Trans. Veh. Technol. 2022, 71, 4933–4948. [Google Scholar] [CrossRef]
- He, Z.-Q.; Yuan, X. Cascaded channel estimation for large intelligent metasurface assisted massive MIMO. IEEE Wirel. Commun. 2020, 9, 210–214. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Ground users | K = 5 |
| UAV antennas | L = 5 |
| Service time | T = 60 s |
| Reflecting elements | M = 200 |
| Maximum UAV velocity | = 15 m/s |
| UAV altitude | = 50 m |
| Transmit power constraint | P = 0.09 W |
| RIS altitude | = 25 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Y.; Huang, Z.; Gao, Y.; Fang, Y. User Scheduling and Path Planning for Reconfigurable Intelligent Surface Assisted MISO UAV Communication. Electronics 2024, 13, 2797. https://doi.org/10.3390/electronics13142797
Gu Y, Huang Z, Gao Y, Fang Y. User Scheduling and Path Planning for Reconfigurable Intelligent Surface Assisted MISO UAV Communication. Electronics. 2024; 13(14):2797. https://doi.org/10.3390/electronics13142797
Chicago/Turabian StyleGu, Yang, Zhiyu Huang, Yuan Gao, and Yong Fang. 2024. "User Scheduling and Path Planning for Reconfigurable Intelligent Surface Assisted MISO UAV Communication" Electronics 13, no. 14: 2797. https://doi.org/10.3390/electronics13142797
APA StyleGu, Y., Huang, Z., Gao, Y., & Fang, Y. (2024). User Scheduling and Path Planning for Reconfigurable Intelligent Surface Assisted MISO UAV Communication. Electronics, 13(14), 2797. https://doi.org/10.3390/electronics13142797






