Helicopter Turboshaft Engine Residual Life Determination by Neural Network Method
Abstract
1. Introduction
1.1. Relevance of the Research
1.2. State-of-the-Art
1.3. Main Attributes of the Research
- Development of a mathematical model for helicopter TE residual life determination.
- Development of a neural network model for helicopter TE residual life determination.
- Development of a neural network model training algorithm for helicopter TE residual life determination.
- Conducting a computational experiment to determine helicopter TE residual life (using the example of determining TE compressor turbine blade residual life).
- Conducting a comparative analysis of the results obtained for helicopter TE residual life determination with those obtained by classical methods, based on classical statistical methods for experimental data processing (for example, the least squares method).
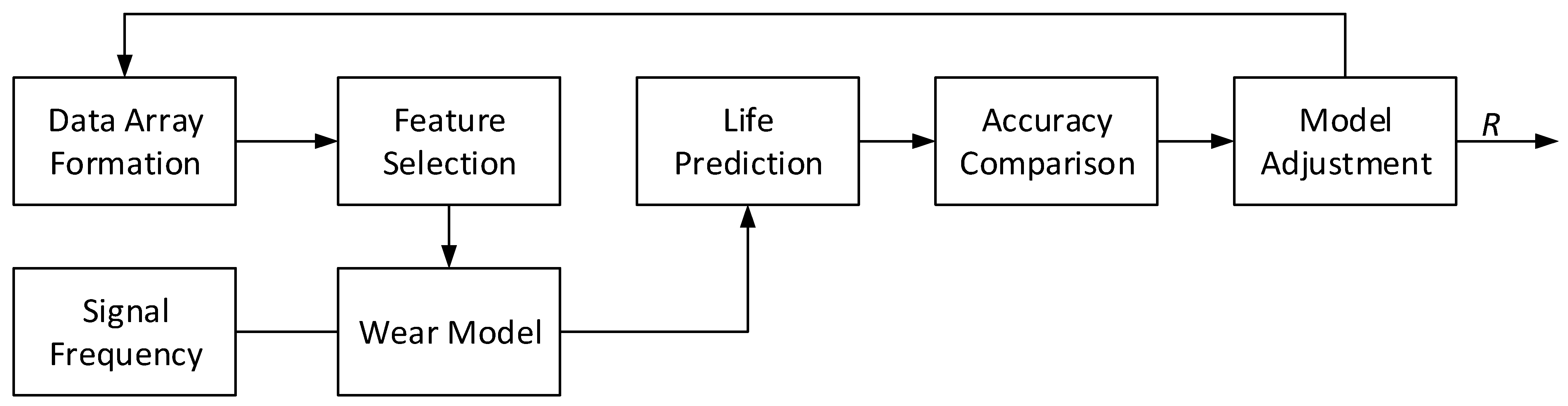
2. Materials and Methods
- The flexibility of including new factors (parameters) in the model allows you to integrate new factors that influence the operational status of the helicopter TE components using the function fi(Si). This makes it possible to take into account component degradation from various aspects, such as blade wear, compressor efficiency loss, and others, as they are researched and their impact on engine life is identified.
- The adaptability to changes in operating conditions indicates that the ΔTi coefficients in the model are adjusted for changes in operating conditions. For example, if the maintenance or operating conditions change, the factors may be revised to more accurately account for these factors.
- Neural networks allow you to customize a wear model for the specific characteristics of each engine.
- With increasing operating time, neural networks adjust parameter changes in the model until the limit value is reached, which makes it possible to adapt to the changing wear rate of components.
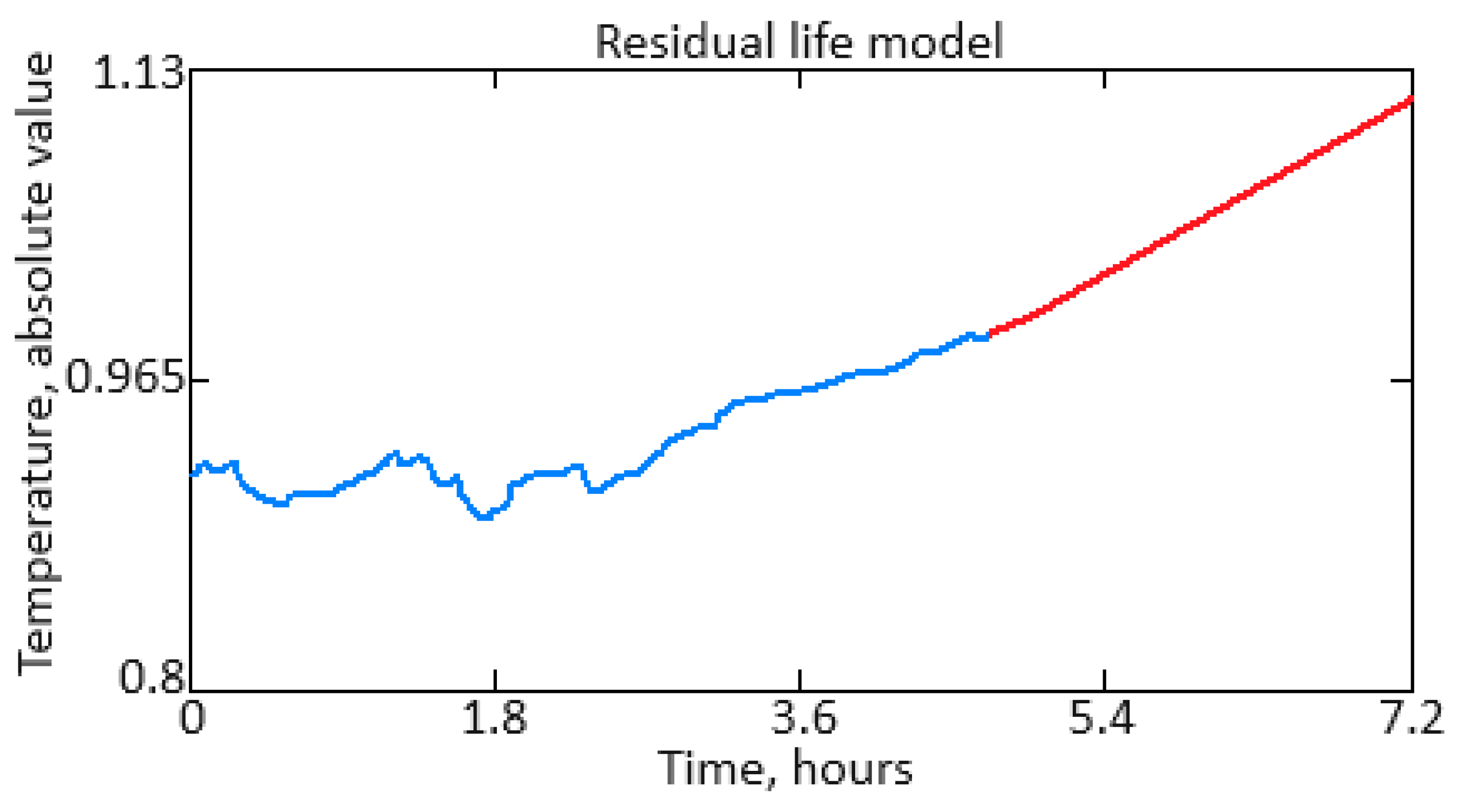
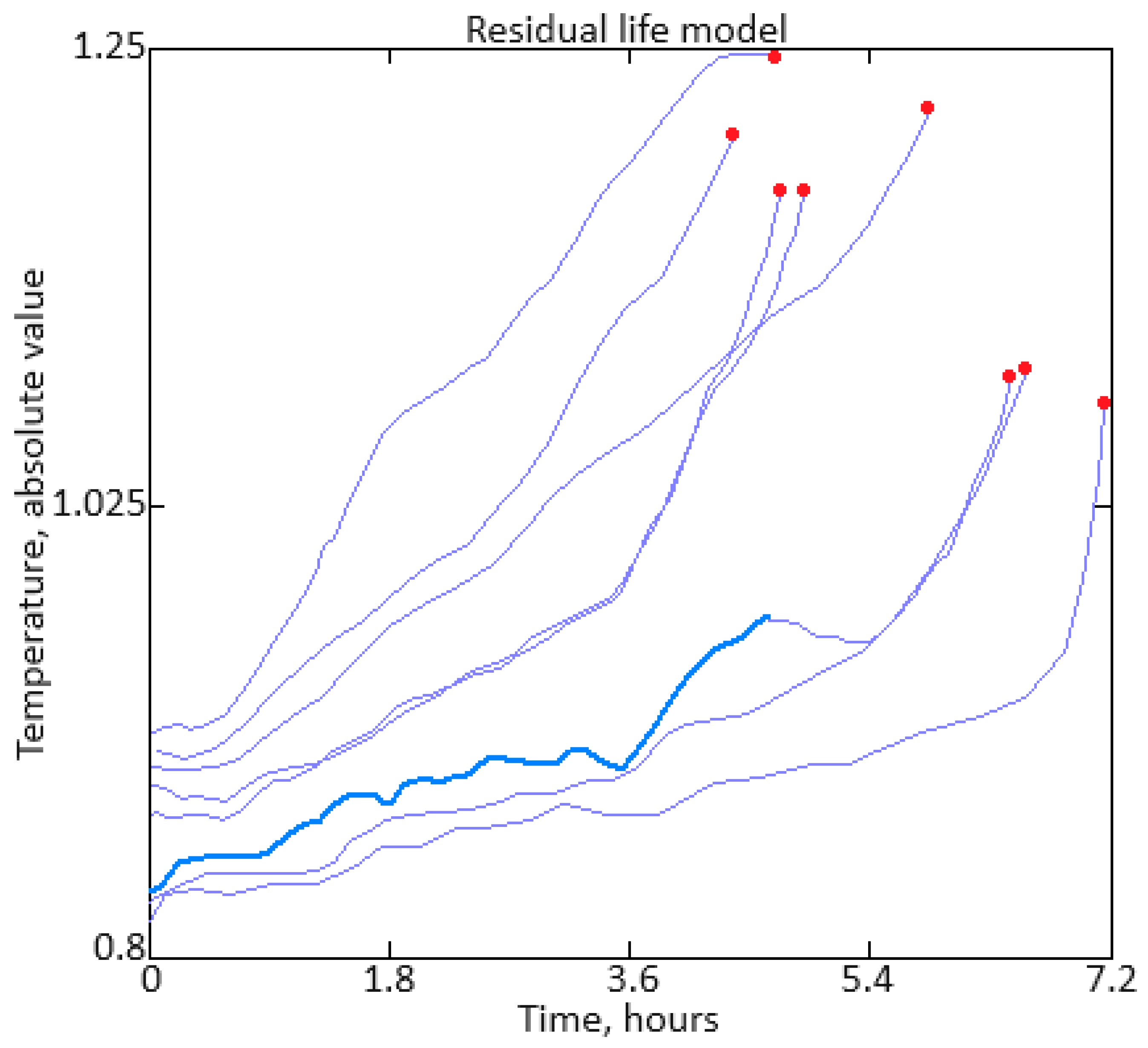
3. Results and Discussion
- The mean square error, as a model adequacy criterion, is a standard metric for assessing the predicted quality and models.
- Expression (19) takes into account degradation data at all available time points, which provides an overall model adequacy overview throughout its operation.
- Averaging the error over the entire sample allowed us to assess the overall adequacy of the model throughout the operation’s entire period.
- The model predicts the mean square error in real data and identifies deviations, which allows you to quickly detect and correct inaccuracies and inconsistencies.
- Expression (19) is a simple and understandable way to assess the model’s adequacy, which makes it convenient for use by engineers and equipment maintenance specialists.
- Zero expected value means that the average of all noise values is zero.
- Standard deviation σi = 0.025 means that it characterizes the spread of noise values relative to the average value. In this case, the standard deviation was 0.025, which indicated a small spread of values.
- A uniform distribution of the power spectral density means that the noise energy is equally distributed across all frequencies.
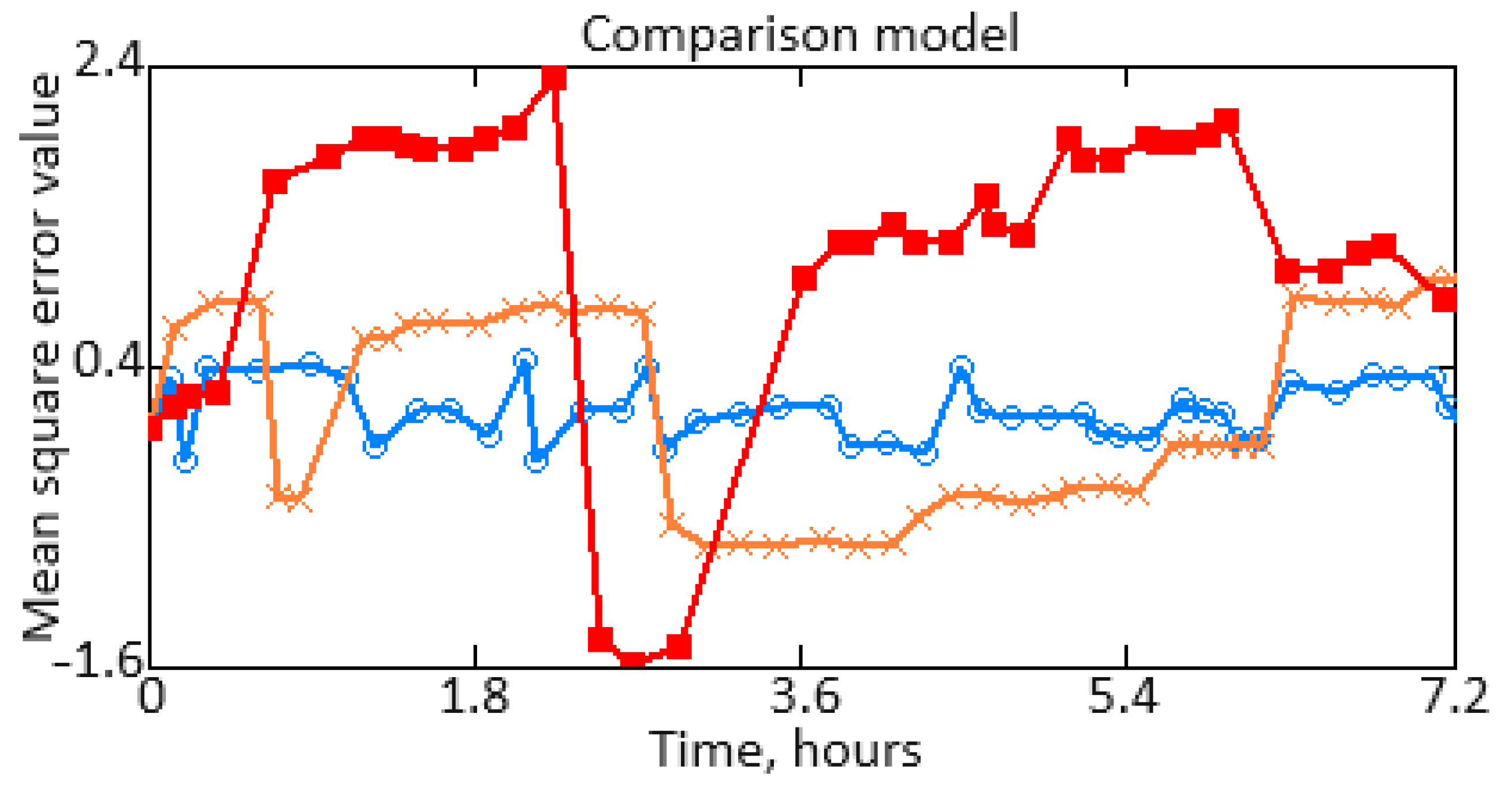
- Neural networks solve the helicopter TE compressor turbine blade residual service life determination task more accurately than traditional methods: the identification error at the output of the developed multilayer perceptron was 4.81 times lower than that of the regression model obtained using LSM.
- The error of solving the helicopter TE compressor turbine blade residual life determination task using the developed multilayer perceptron did not exceed 0.424%; for the classical RBF network, it was 1.079%, while for the LSM, it was 2.038%.
- Neural network methods are more robust to external disturbances: for a noise level σi = 0.025, the error in solving the helicopter TE compressor turbine blade residual life determination task when using the developed multilayer perceptron increased from 0.424 to 0.611%; for the classical RBF network—from 1.079 to 1.877%, and for the LSM—from 2.038 to 3.933%.
- The relevance of the helicopter turboshaft engine residual life determination method is substantiated, which lies in its critical role in ensuring flight reliability and safety, since timely assessment of engine conditions, taking into account many operating factors and environmental conditions, makes it possible to plan maintenance and component replacement, preventing emergencies, and increasing the resource prediction accuracy thanks to modern diagnostic systems.
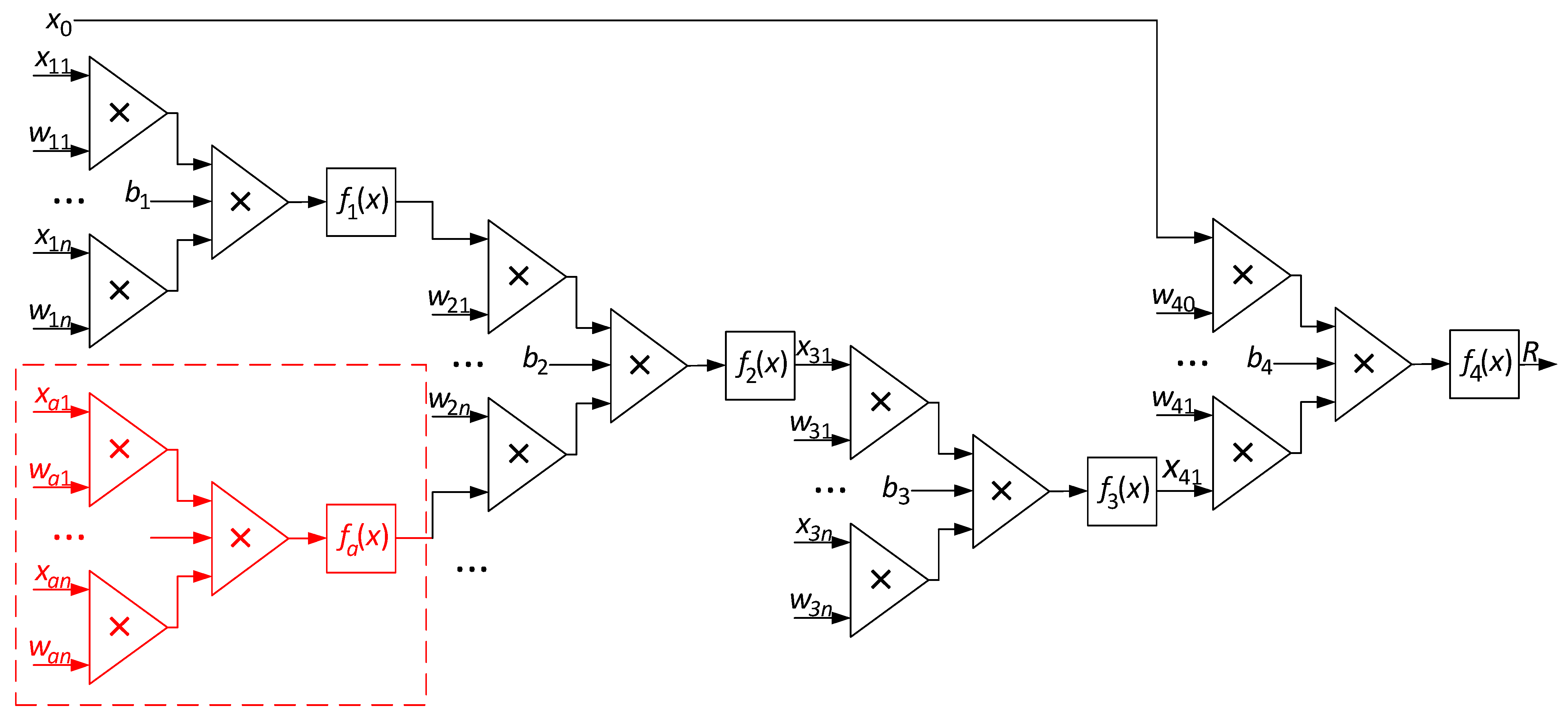
- A method for determining the residual life of helicopter turboshaft engines has been developed based on a hierarchical system utilizing neural network technologies. The experimental results showed that using a multilayer perceptron within this hierarchical system yielded a maximum root-mean-square error of no more than 0.424 when applied to solving the task of estimating the residual life of the compressor turbine blades of helicopter turboshaft engines.
- Based on the backpropagation algorithm, a multilayer perceptron training algorithm has been developed, which, by introducing the initial parameter x0 to the output layer, improved the helicopter turboshaft engine residual life prediction accuracy and use of the adaptive Adam training rate provided high accuracy (up to 99.3%) in solving the helicopter turboshaft engine compressor turbine blade residual life determination task. It has been experimentally proven that use of the developed multilayer perceptron training algorithm made it possible, with 160 training epochs, to ensure an accuracy of 99.3% and reduce losses to 0.5% in solving the helicopter turboshaft engine compressor turbine blade residual life determination task.
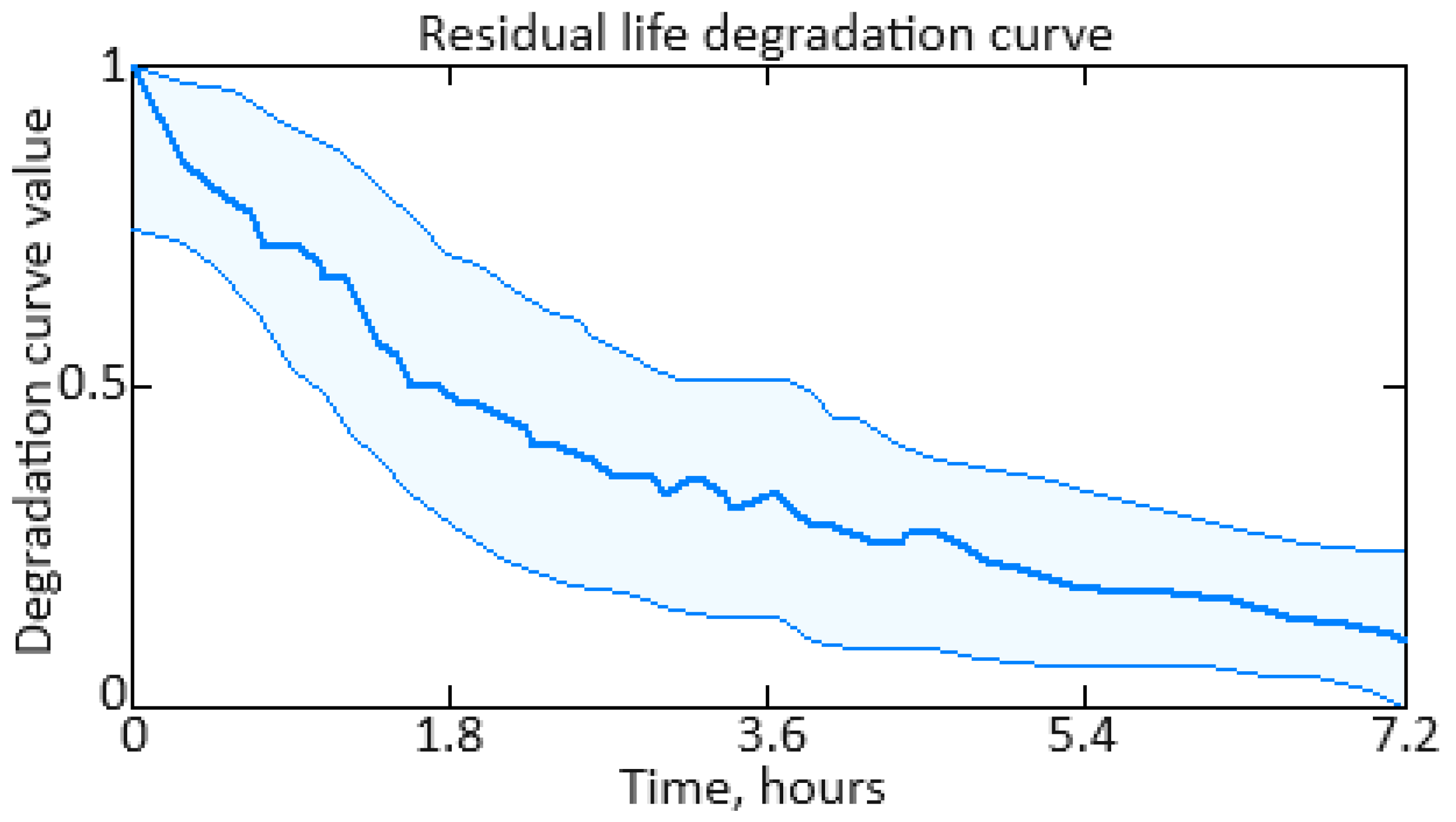
- Based on the helicopter turboshaft engine compressor turbine blade residual life assessment through parameter prediction and similarities with patterns from the past, a method for constructing a degradation curve has been developed. This method integrates parameter prediction and historical data analogies to enhance the accuracy of service life prediction and maintenance planning, thereby mitigating failures. Experimental validation showed that the mean square error between predicted and observed residual resource over the entire operational period did not exceed 0.0058 (0.58%), approaching zero, indicating the high adequacy of the constructed degradation curve.
- The results of solving the helicopter turboshaft engine compressor turbine blade residual life determination task using the developed multilayer perceptron as a hierarchical system were compared with the classical RBF network and the least squares method, which made it possible to reduce the first and second types of errors by 2.23 times compared with the use of the classical RBF networks, and by 4.74 times compared to using the least squares method.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aygun, H.; Turan, O. Exergetic sustainability off-design analysis of variable-cycle aero-engine in various bypass modes. Energy 2020, 195, 117008. [Google Scholar] [CrossRef]
- Balli, O. Exergetic, sustainability and environmental assessments of a turboshaft engine used on helicopter. Energy 2023, 276, 127593. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Huang, G.; Hu, Q.-K.; Li, B. An improved weighted one class support vector machine for turboshaft engine fault detection. Eng. Appl. Artif. Intell. 2020, 94, 103796. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, C.; Xi, Z.; Zhang, H.; Zhao, Q. An adaptive matching control method of multiple turboshaft engines. Eng. Appl. Artif. Intell. 2023, 123, 106496. [Google Scholar] [CrossRef]
- Sha, Y.; Zhao, J.; Luan, X.; Liu, X. Fault feature signal extraction method for rolling bearings in gas turbine engines based on threshold parameter decision screening. Measurement 2024, 231, 114567. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Q.; Xu, Z.; Zhang, H. A novel control method for turboshaft engine with variable rotor speed based on the Ngdot estimator through LQG/LTR and rotor predicted torque feedforward. Chin. J. Aeronaut. 2020, 33, 1867–1876. [Google Scholar] [CrossRef]
- Feng, K.; Xiao, Y.; Li, Z.; Jiang, Z.; Gu, F. Gas turbine blade fracturing fault diagnosis based on broadband casing vibration. Measurement 2023, 214, 112718. [Google Scholar] [CrossRef]
- Gu, N.; Wang, X.; Zhu, M. Multi-Parameter Quadratic Programming Explicit Model Predictive Based Real Time Turboshaft Engine Control. Energies 2021, 14, 5539. [Google Scholar] [CrossRef]
- Nan, G.; Yao, X.; Yang, S.; Yao, J.; Chen, X. Vibrational responses and fatigue life of dynamic blades for compressor in gas turbines. Eng. Fail. Anal. 2024, 156, 107827. [Google Scholar] [CrossRef]
- Bovsunovsky, A.; Nosal, O. Highly sensitive methods for vibration diagnostics of fatigue damage in structural elements of aircraft gas turbine engines. Procedia Struct. Integr. 2022, 35, 74–81. [Google Scholar] [CrossRef]
- Jin, M. The nonlinear dynamic characteristics of the aero-turboshaft engine rotor blade casing rubbing system with the curvic couplings considering the elastoplastic stage. Eng. Anal. Bound. Elem. 2024, 161, 78–102. [Google Scholar] [CrossRef]
- Abdalla, M.S.M.; Balli, O.; Adali, O.H.; Korba, P.; Kale, U. Thermodynamic, sustainability, environmental and damage cost analyses of jet fuel starter gas turbine engine. Energy 2023, 267, 126487. [Google Scholar] [CrossRef]
- Rabcan, J.; Levashenko, V.; Zaitseva, E.; Kvassay, M.; Subbotin, S. Non-destructive diagnostic of aircraft engine blades by Fuzzy Decision Tree. Eng. Struct. 2019, 197, 109396. [Google Scholar] [CrossRef]
- Gu, Z.; Pang, S.; Zhou, W.; Li, Y.; Li, Q. An Online Data-Driven LPV Modeling Method for Turbo-Shaft Engines. Energies 2022, 15, 1255. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, A.; Zhang, T.; Ge, N.; Huang, X. A Performance Simulation Methodology for a Whole Turboshaft Engine Based on Throughflow Modelling. Energies 2024, 17, 494. [Google Scholar] [CrossRef]
- Kim, S.; Im, J.H.; Kim, M.; Kim, J.; Kim, Y.I. Diagnostics using a physics-based engine model in aero gas turbine engine verification tests. Aerosp. Sci. Technol. 2023, 133, 108102. [Google Scholar] [CrossRef]
- Castiglione, T.; Perrone, D.; Strafella, L.; Ficarella, A.; Bova, S. Linear Model of a Turboshaft Aero-Engine Including Components Degradation for Control-Oriented Applications. Energies 2023, 16, 2634. [Google Scholar] [CrossRef]
- Baranovskyi, D.; Myamlin, S. The criterion of development of processes of the self organization of subsystems of the second level in tribosystems of diesel engine. Sci. Rep. 2023, 13, 5736. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Wang, Y.; Zhang, H. Research on adaptive feedforward control method for Tiltrotor Aircraft/Turboshaft engine system based on radial basis function neural network. Aerosp. Sci. Technol. 2024, 150, 109180. [Google Scholar] [CrossRef]
- Szrama, S.; Lodygowski, T. Aircraft Engine Remaining Useful Life Prediction using neural networks and real-life engine operational data. Adv. Eng. Softw. 2024, 192, 103645. [Google Scholar] [CrossRef]
- Li, B.; Zhao, Y.-P.; Chen, Y.-B. Unilateral alignment transfer neural network for fault diagnosis of aircraft engine. Aerosp. Sci. Technol. 2021, 119, 107031. [Google Scholar] [CrossRef]
- Yang, Q.; Tang, B.; Li, Q.; Liu, X.; Bao, L. Dual-frequency enhanced attention network for aircraft engine remaining useful life prediction. ISA Trans. 2023, 141, 167–183. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Li, J. A Framework of Dynamic Data Driven Digital Twin for Complex Engineering Products: The Example of Aircraft Engine Health Management. Procedia Manuf. 2021, 55, 139–146. [Google Scholar] [CrossRef]
- Li, B.; Zhao, Y.-P. Group reduced kernel extreme learning machine for fault diagnosis of aircraft engine. Eng. Appl. Artif. Intell. 2020, 96, 103968. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Hubachov, O.; Rud, J. Neuro-Fuzzy System for Detection Fuel Consumption of Helicopters Turboshaft Engines. CEUR Workshop Proc. 2024, 3628, 55–72. Available online: https://ceur-ws.org/Vol-3628/paper5.pdf (accessed on 22 April 2024).
- Talebi, S.S.; Madadi, A.; Tousi, A.M.; Kiaee, M. Micro Gas Turbine fault detection and isolation with a combination of Artificial Neural Network and off-design performance analysis. Eng. Appl. Artif. Intell. 2022, 113, 104900. [Google Scholar] [CrossRef]
- Andriushchenko, K.; Rudyk, V.; Riabchenko, O.; Kachynska, M.; Marynenko, N.; Shergina, L.; Kovtun, V.; Tepliuk, M.; Zhemba, A.; Kuchai, O. Processes of managing information infrastructure of a digital enterprise in the framework of the «Industry 4.0» concept. East.-Eur. J. Enterp. Technol. 2019, 1, 60–72. [Google Scholar] [CrossRef]
- Morozov, V.V.; Kalnichenko, O.V.; Mezentseva, O.O. The method of interaction modeling on basis of deep learning the neural networks in complex it-projects. Int. J. Comput. 2020, 19, 88–96. [Google Scholar] [CrossRef]
- Singh, R.; Maity, A.; Nataraj, P.S.V. Modeling, Simulation and Validation of Mini SR-30 Gas Turbine Engine. IFAC-Pap. 2018, 51, 554–559. [Google Scholar] [CrossRef]
- Pang, S.; Li, Q.; Ni, B. Improved nonlinear MPC for aircraft gas turbine engine based on semi-alternative optimization strategy. Aerosp. Sci. Technol. 2021, 118, 106983. [Google Scholar] [CrossRef]
- Catana, R.M.; Dediu, G. Analytical Calculation Model of the TV3-117 Turboshaft Working Regimes Based on Experimental Data. Appl. Sci. 2023, 13, 10720. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Hubachov, O.; Rud, J.; Stushchanskyi, Y. Neural Network Modeling of Helicopters Turboshaft Engines at Flight Modes Using an Approach Based on “Black Box” Models. CEUR Workshop Proc. 2024, 3624, 116–135. Available online: https://ceur-ws.org/Vol-3624/Paper_11.pdf (accessed on 7 May 2024).
- Pashaev, A.M.; Sadihov, R.A.; Samedov, A.S.; Ardil, D. Numerical modelijind of the temperuture fields in aviation gas turbine elements. Oper. Air Transp. Repair Aircr. Equipment. Flight Saf. 2005, 85, 109–120. [Google Scholar]
- Fatikov, V.S.; Kulikov, G.G.; Trushin, V.A.; Ganeev, A.A.; Abdulnagimov, A.I. The concept of intelligent monitoring of the condition of turbine blades during operation of aviation gas turbine engines. Bull. USATU 2013, 17, 11–17. [Google Scholar]
- Raspopov, E.V.; Kulikov, G.G.; Trushin, V.A.; Fatikov, V.S.; Andreeva, T.P.; Gubaidullin, I.T. Information technology integrated pyrometer intelligent module in the control, monitoring and diagnostics (FADEC) GTE. Bull. USATU 2010, 14, 101–110. [Google Scholar]
- Soltan, T.M.T.; Abdelrahman, M.M. Helicopter performance enhancement by alleviating retreating blade stall using active flow control. Sci. Afr. 2023, 21, e01888. [Google Scholar] [CrossRef]
- Suhankin, G.V.; Gertsen, N.T. Algorithm for creating a model of the residual life of an electric motor based on a trained neural network. Polzunovskiy Vestn. 2012, 4, 139–146. [Google Scholar]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Optimization of Helicopters Aircraft Engine Working Process Using Neural Networks Technologies. CEUR Workshop Proc. 2022, 3171, 1639–1656. Available online: https://ceur-ws.org/Vol-3171/paper117.pdf (accessed on 14 May 2024).
- Corotto, F.S. Appendix C—The method attributed to Neyman and Pearson. In Wise Use Null Hypothesis Tests; Academic Press: Cambridge, MA, USA, 2023; pp. 179–188. [Google Scholar] [CrossRef]
- Motsnyi, F.V. Analysis of Nonparametric and Parametric Criteria for Statistical Hypotheses Testing. Chapter 1. Agreement Criteria of Pearson and Kolmogorov. Stat. Ukr. 2018, 83, 14–24. [Google Scholar] [CrossRef]
- Babichev, S.; Krejci, J.; Bicanek, J.; Lytvynenko, V. Gene expression sequences clustering based on the internal and external clustering quality criteria. In Proceedings of the 2017 12th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 5–8 September 2017. [Google Scholar] [CrossRef]
- Hu, Z.; Kashyap, E.; Tyshchenko, O.K. GEOCLUS: A Fuzzy-Based Learning Algorithm for Clustering Expression Datasets. Lect. Notes Data Eng. Commun. Technol. 2022, 134, 337–349. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Bulakh, M.; Vysotska, V. Neural Network Approximation of Helicopter Turboshaft Engine Parameters for Improved Efficiency. Energies 2024, 17, 2233. [Google Scholar] [CrossRef]
- Vladov, S.; Scislo, L.; Sokurenko, V.; Muzychuk, O.; Vysotska, V.; Osadchy, S.; Sachenko, A. Neural Network Signals Integration from Thermogas-dynamic Parameters Sensors for Helicopters Turboshaft Engines at Flight Operation Conditions. Sensors 2024, 24, 4246. [Google Scholar] [CrossRef] [PubMed]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M.; Drozdova, S. Helicopters Turboshaft Engines Parameters Identification at Flight Modes Using Neural Networks. In Proceedings of the IEEE 17th International Conference on Computer Science and Information Technologies (CSIT), Lviv, Ukraine, 10–12 November 2022; pp. 5–8. [Google Scholar] [CrossRef]
- Li, Y.; Fan, C.; Li, Y.; Wu, Q.; Ming, Y. Improving deep neural network with Multiple Parametric Exponential Linear Units. Neurocomputing 2018, 301, 11–24. [Google Scholar] [CrossRef]
- Xu, M.; Wang, J.; Liu, J.; Li, M.; Geng, J.; Wu, Y.; Song, Z. An improved hybrid modeling method based on extreme learning machine for gas turbine engine. Aerosp. Sci. Technol. 2020, 107, 106333. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, K.; Wang, Y.; Yang, C.; Li, J.; Wang, Y. Research on gas turbine health assessment method based on physical prior knowledge and spatial-temporal graph neural network. Appl. Energy 2024, 367, 123419. [Google Scholar] [CrossRef]
- Sina Tayarani-Bathaie, S.; Sadough Vanini, Z.N.; Khorasani, K. Dynamic neural network-based fault diagnosis of gas turbine engines. Neurocomputing 2014, 125, 153–165. [Google Scholar] [CrossRef]
- Li, X.; Xu, S.; Yang, Y.; Lin, T.; Mba, D.; Li, C. Spherical-dynamic time warping—A new method for similarity-based remaining useful life prediction. Expert Syst. Appl. 2024, 238, 121913. [Google Scholar] [CrossRef]
- Dev, N.; Kumar, R.; Kumar Saha, R.; Babbar, A.; Simic, V.; Kumar, R.; Bacanin, N. Performance evaluation methodology for gas turbine power plants using graph theory and combinatorics. Int. J. Hydrogen Energy 2024, 57, 1286–1301. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M. Neural Network Method for Parametric Adaptation Helicopters Turboshaft Engines On-Board Automatic Control. CEUR Workshop Proc. 2023, 3403, 179–195. Available online: https://ceur-ws.org/Vol-3403/paper15.pdf (accessed on 29 May 2024).
- Hu, Z.; Shkurat, O.; Kasner, M. Grayscale Image Colorization Method Based on U-Net Network. Int. J. Image Graph. Signal Process. 2024, 16, 70–82. [Google Scholar] [CrossRef]
- Hu, Z.; Dychka, I.; Potapova, K.; Meliukh, V. Augmenting Sentiment Analysis Prediction in Binary Text Classification through Advanced Natural Language Processing Models and Classifiers. Int. J. Inf. Technol. Comput. Sci. 2024, 16, 16–31. [Google Scholar] [CrossRef]
- Gus’kov, S.Y.; Lyovin, V.V. Confidence interval estimation for quality factors of binary classifiers—ROC curves, AUC for small samples. Eng. J. Sci. Innov. 2015, 3, 1–15. Available online: http://engjournal.ru/catalog/mesc/idme/1376.html (accessed on 5 June 2024).
- Cherrat, E.M.; Alaoui, R.; Bouzahir, H. Score fusion of finger vein and face for human recognition based on convolutional neural network model. Int. J. Comput. 2020, 19, 11–19. [Google Scholar] [CrossRef]
- Marakhimov, A.R.; Khudaybergenov, K.K. Approach to the synthesis of neural network structure during classification. Int. J. Comput. 2020, 19, 20–26. [Google Scholar] [CrossRef]
- Pasieka, M.; Grzesik, N.; Kuźma, K. Simulation modeling of fuzzy logic controller for aircraft engines. Int. J. Comput. 2017, 16, 27–33. [Google Scholar] [CrossRef]
- Gromaszek, K.; Bykov, M.M.; Kovtun, V.V.; Raimy, A.; Smailova, S. Neural Network Modelling by Rank Configurations. In Proceedings of the Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments, Wilga, Poland, 26 May–4 June 2018. [Google Scholar] [CrossRef]
- Bisikalo, O.V.; Kovtun, V.V.; Kovtun, O.V. Modeling of the Estimation of the Time to Failure of the Information System for Critical Use. In Proceedings of the 2020 10th International Conference on Advanced Computer Information Technologies (ACIT), Deggendorf, Germany, 16–18 September 2020. [Google Scholar] [CrossRef]
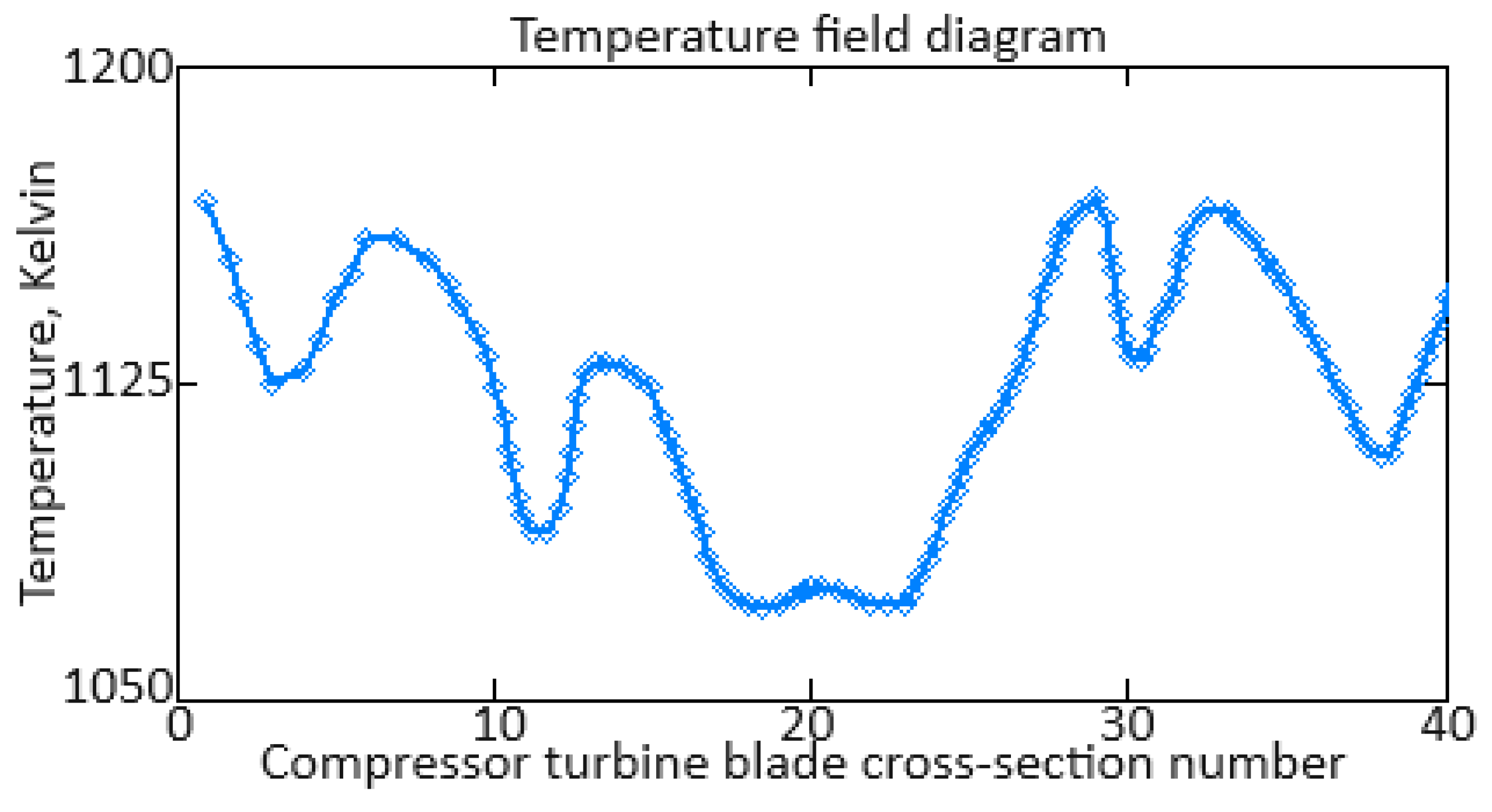
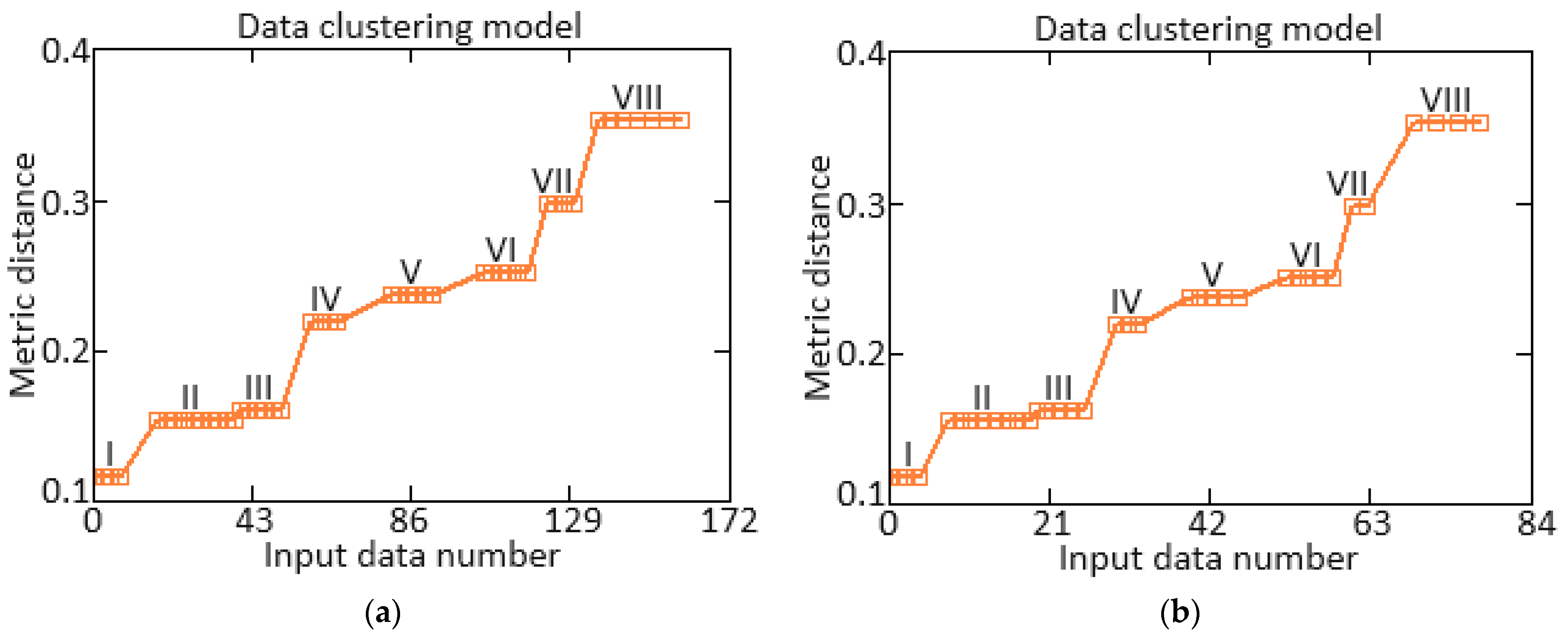
| Number | 1 | 2 | … | 72 | … | 133 | … | 205 | … | 256 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ti value | 0.973 | 0.962 | … | 0.936 | … | 0.951 | … | 0.925 | … | 0.973 |
| Metrics | Developed Multilayer Perceptron | Classical RBF Network | Least Squares Method |
|---|---|---|---|
| MSE | 0.611 | 1.877 | 3.933 |
| MAE | 0.781 | 1.369 | 1.983 |
| RMSE | 0.781 | 1.369 | 1.983 |
| MAPE | 1.03% | 2.05% | 4.84% |
| R2 | 0.993 | 0.971 | 0.837 |
| ME | 0.053 | 0.116 | 0.634 |
| MedAE | 0.068 | 0.132 | 0.311 |
| sMAPE | 1.03% | 2.05% | 4.80% |
| GMSE | 0.134 | 0.258 | 0.612 |
| r | 0.997 | 0.986 | 0.928 |
| RMSLE | 0.057 | 0.113 | 0.264 |
| Hit Rate | 70.3% | 36.7% | 17.2% |
| Max Error | 0.0385 | 0.0616 | 0.132 |
| Huber Loss | 4.17 × 10−5 | 0.000118 | 0.000334 |
| Metrics | Improvements When Using the Developed Multilayer Perceptron | |
|---|---|---|
| Classical RBF Network | Least Squares Method | |
| MSE | 3.07 | 6.44 |
| MAE | 1.75 | 2.54 |
| RMSE | 1.75 | 2.54 |
| MAPE | 2.00 | 4.70 |
| ME | 2.19 | 12.0 |
| MedAE | 1.94 | 4.60 |
| sMAPE | 2.00 | 4.70 |
| GMSE | 1.92 | 4.60 |
| RMSLE | 2.00 | 4.60 |
| Hit Rate | 1.92 | 4.10 |
| Max Error | 1.60 | 3.40 |
| Huber Loss | 2.80 | 8.00 |
| Error Type | Developed Multilayer Perceptron | Classical RBF Network | Least Squares Method |
|---|---|---|---|
| Type I error, % | 0.754 | 1.681 | 3.574 |
| Type II error, % | 0.447 | 1.063 | 2.119 |
| Actual\ Predicted | Developed Multilayer Perceptron | Classical RBF Network | Least Squares Method |
|---|---|---|---|
| True Positives | 97 | 3 | 0 |
| True Negatives | 3 | 88 | 2 |
| False Positives | 1 | 6 | 8 |
| False Negatives | 0 | 3 | 92 |
| Actual\ Predicted | Developed Multilayer Perceptron | Classical RBF Network | Least Squares Method |
|---|---|---|---|
| True Positives | 96 | 89 | 0 |
| True Negatives | 2 | 8 | 10 |
| False Positives | 275 | 260 | 290 |
| False Negatives | 25 | 41 | 100 |
| TPR | 0.79 | 0.64 | 0 |
| FPR | 0.010 | 0.029 | 0.31 |
| AUC | 0.862 | 0.717 | 0.295 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladov, S.; Kovtun, V.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. Helicopter Turboshaft Engine Residual Life Determination by Neural Network Method. Electronics 2024, 13, 2952. https://doi.org/10.3390/electronics13152952
Vladov S, Kovtun V, Sokurenko V, Muzychuk O, Vysotska V. Helicopter Turboshaft Engine Residual Life Determination by Neural Network Method. Electronics. 2024; 13(15):2952. https://doi.org/10.3390/electronics13152952
Chicago/Turabian StyleVladov, Serhii, Viacheslav Kovtun, Valerii Sokurenko, Oleksandr Muzychuk, and Victoria Vysotska. 2024. "Helicopter Turboshaft Engine Residual Life Determination by Neural Network Method" Electronics 13, no. 15: 2952. https://doi.org/10.3390/electronics13152952
APA StyleVladov, S., Kovtun, V., Sokurenko, V., Muzychuk, O., & Vysotska, V. (2024). Helicopter Turboshaft Engine Residual Life Determination by Neural Network Method. Electronics, 13(15), 2952. https://doi.org/10.3390/electronics13152952








