A Broadband Meta-Absorber for Curved Terahertz Stealth Applications
Abstract
:1. Introduction
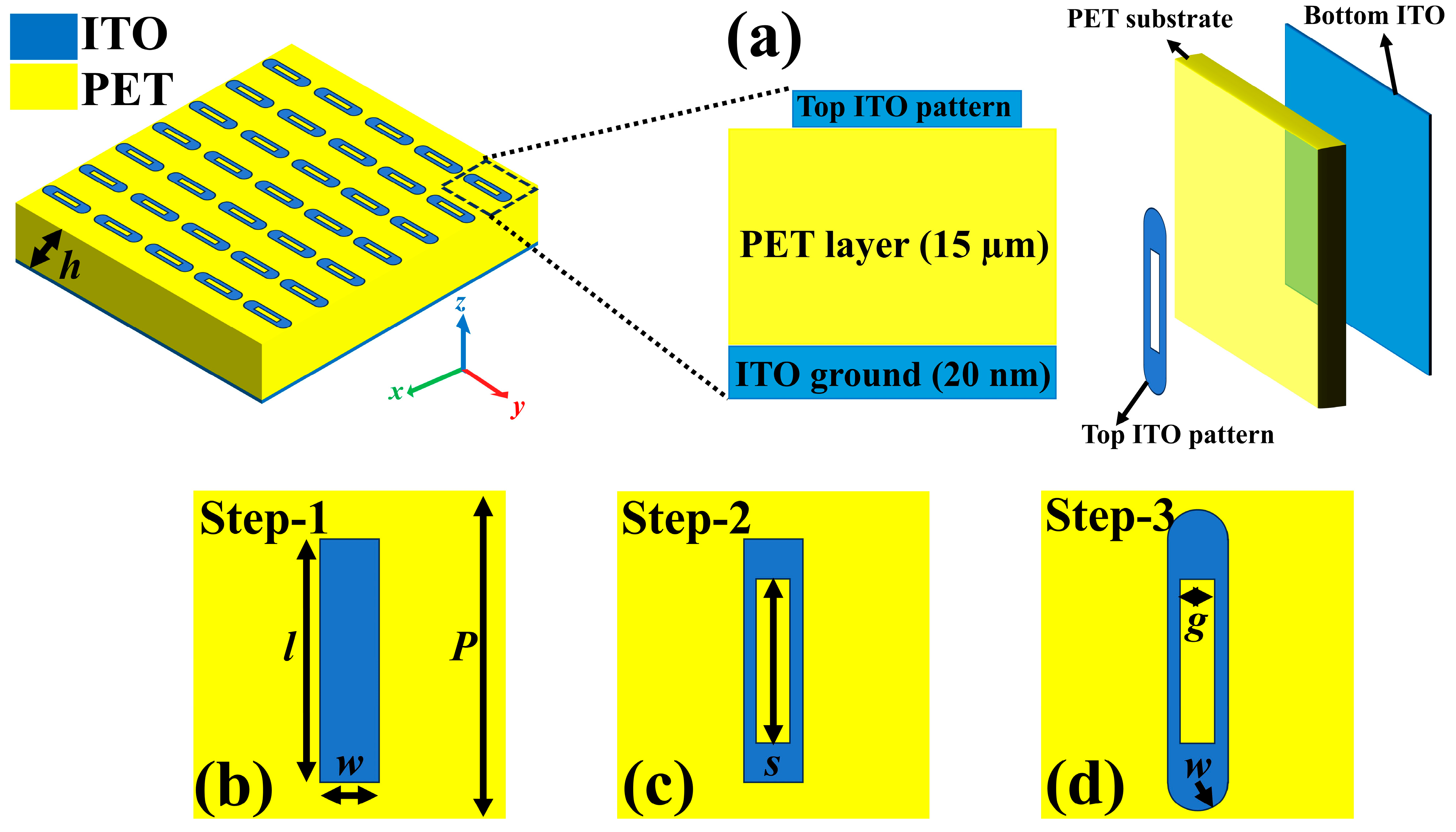
2. Design and Simulation Setup
3. Results and Analysis
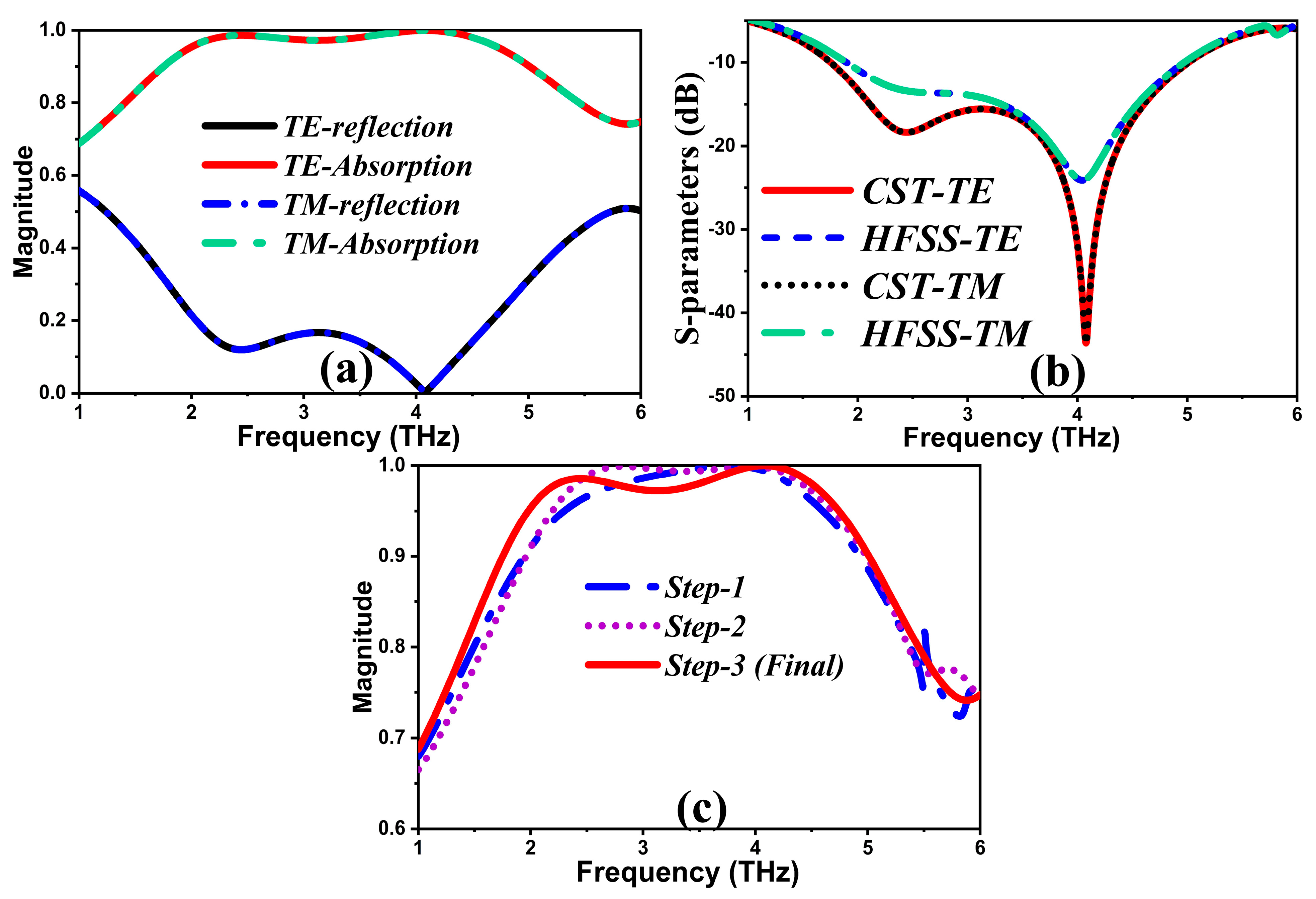
3.1. Absorption Characteristics
3.2. Absorption Characteristics
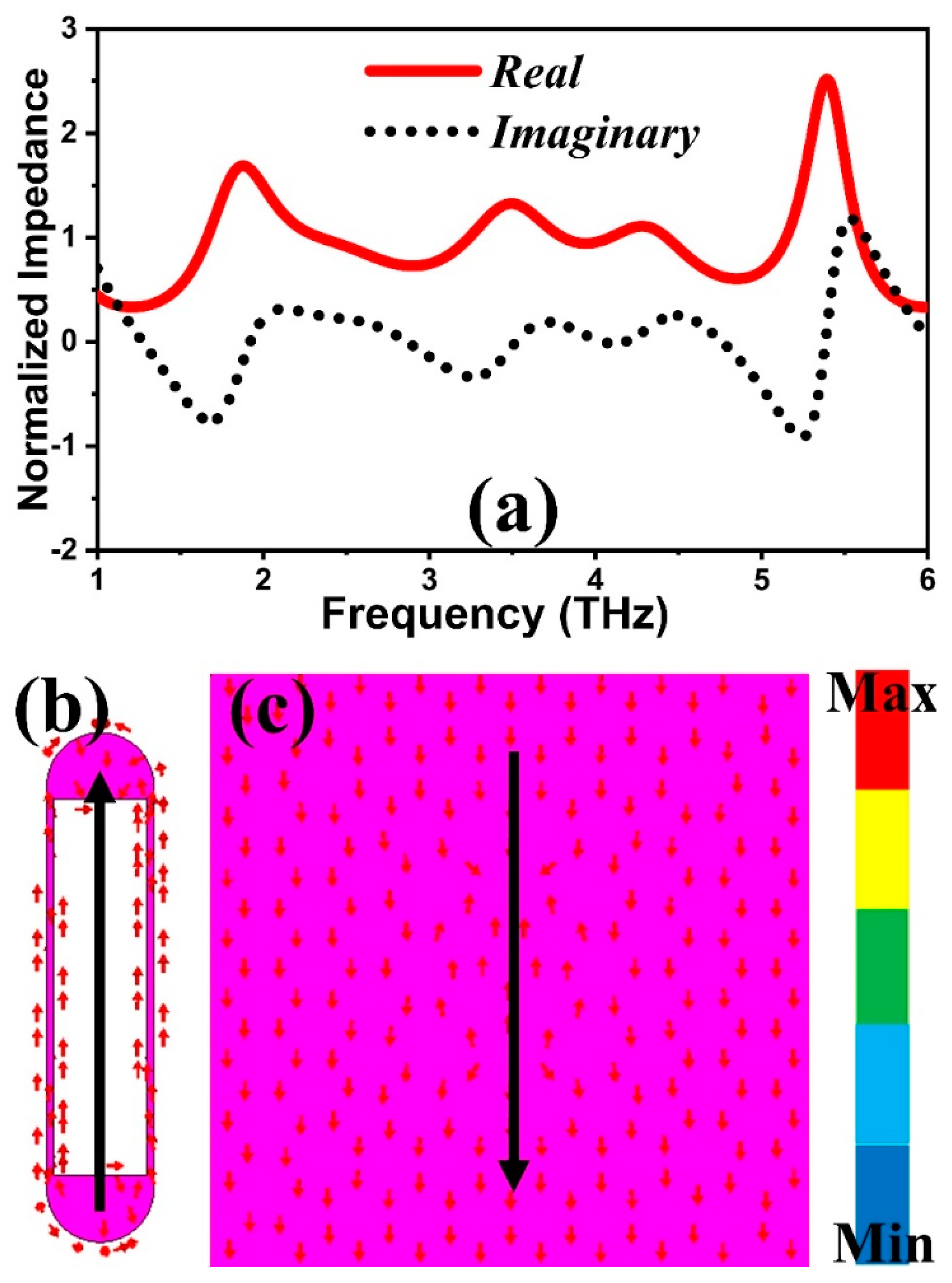
3.3. Equivalent Circuit Model
4. Effect of Model Parameters on Absorption Parameters
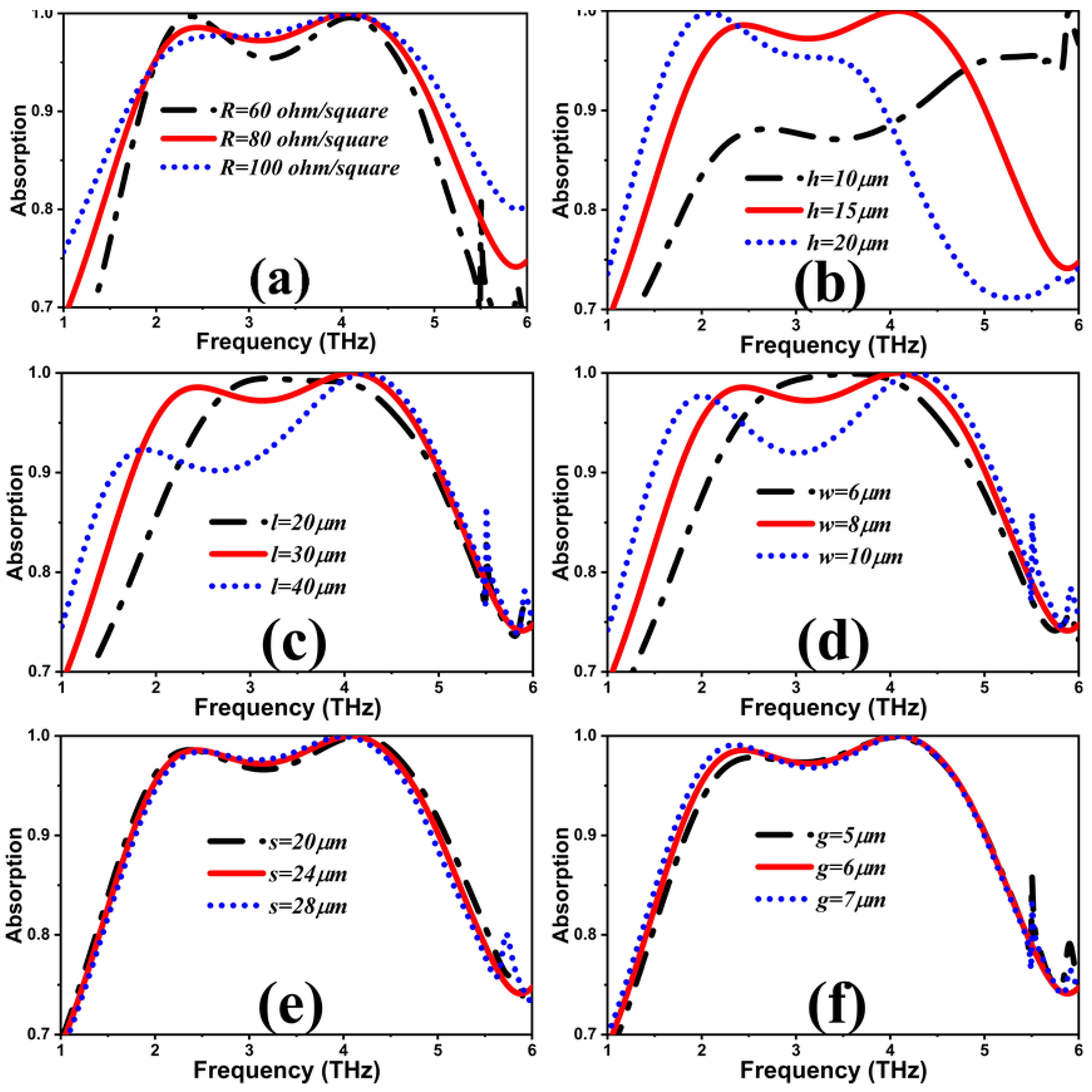
4.1. ITO Sheet Resistance
4.2. Substrate Height
4.3. Geometric Parameters of ITO Pattern
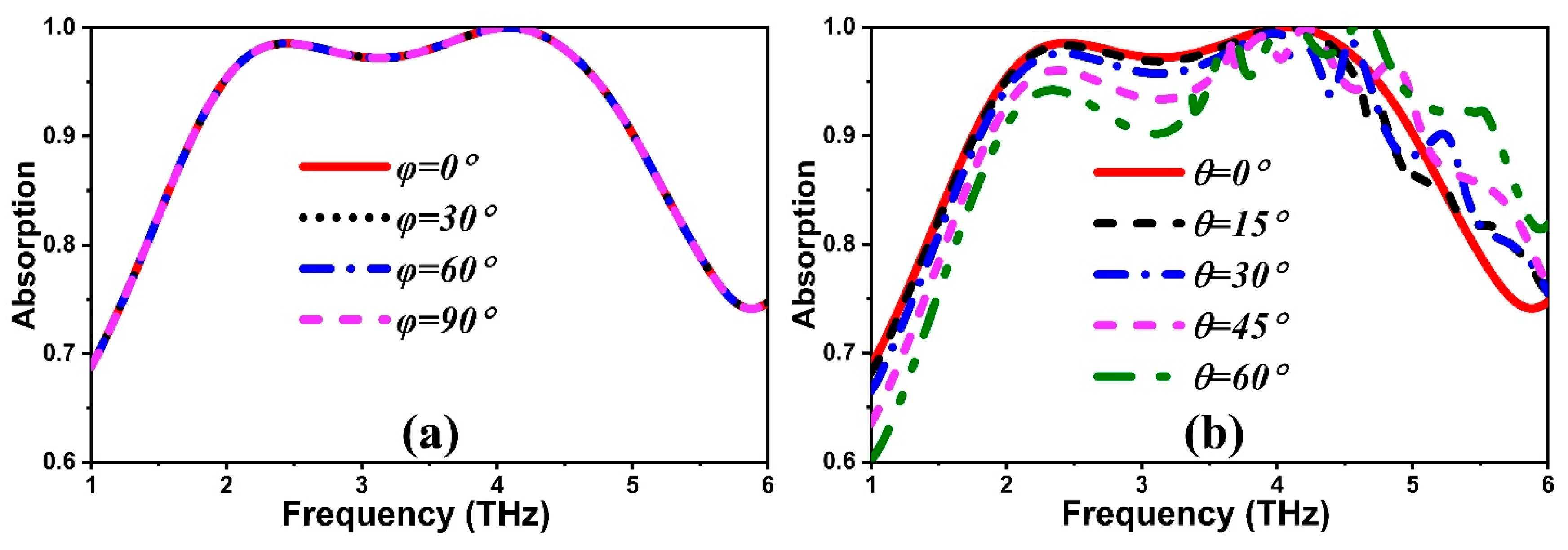
5. Angular Stability
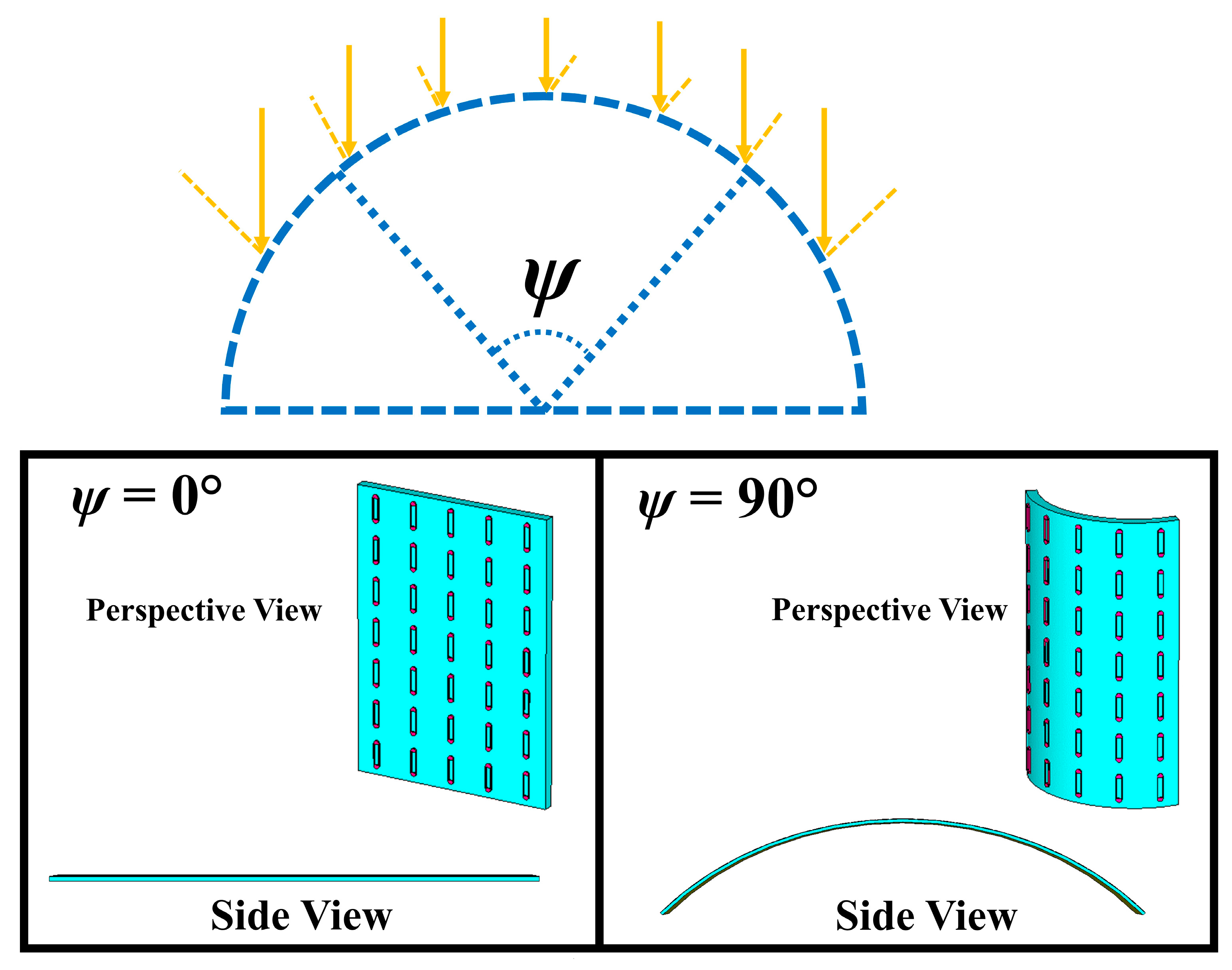
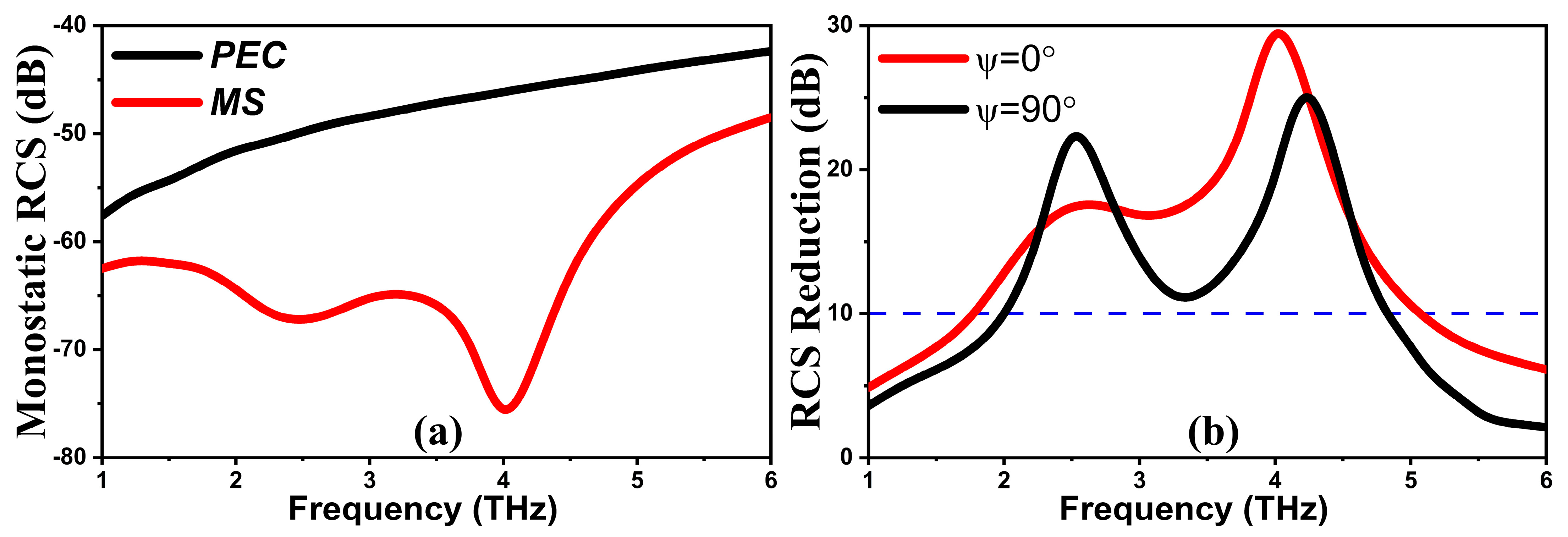
6. Radar Cross-Section (RCS) Analysis of Planar and Curved Structure
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, H.A.; Huang, C.; Xiao, Q.; Abbas, S.M. Polarization-dependent coding metasurface with switchable transmission and RCS reduction bands. Micromachines 2022, 14, 78. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Fan, Y.; Wang, J.; Li, Y.; Feng, M.; Chen, H.; Wang, W.; Zhang, J.; Qu, S. Ultra-wideband microwave absorber via an integrated metasurface and impedance-matching lattice design. J. Phys. D Appl. Phys. 2019, 52, 31LT01. [Google Scholar] [CrossRef]
- Majeed, A.; Jinling, Z.; Khan, H.A.; Ishfaq, M.; Hayat, B. Multiband dual polarization conversion metasurface based on three-quarter circular-shape in the terahertz regime. Results Phys. 2024, 57, 107398. [Google Scholar] [CrossRef]
- Crispin, J.; Maffett, A. Radar cross-section estimation for simple shapes. Proc. IEEE 1965, 53, 833–848. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Y.; Su, J.; Li, Z.; Liu, J.; Yang, Y. Coding diffusion metasurface for ultra-wideband RCS reduction. Electron. Lett. 2017, 53, 187–189. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, L.; Liu, L.; Dong, S.; Yu, W.; Han, L. RCS reduction on patterned graphene-based transparent flexible metasurface absorber. IEEE Trans. Antennas Propag. 2023, 71, 2005–2010. [Google Scholar] [CrossRef]
- Zhou, L.; Shen, Z. Absorptive coding metasurface with ultrawideband backscattering reduction. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1201–1205. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Li, Z.; Palacios, E.; Liu, Z.; Butun, S.; Aydin, K. Chiral-selective plasmonic metasurface absorbers operating at visible frequencies. IEEE Photonics Technol. Lett. 2017, 29, 295–298. [Google Scholar] [CrossRef]
- Xing, B.-B.; Liu, Z.-G.; Lu, W.-B.; Chen, H.; Zhang, Q.-D. Wideband microwave absorber with dynamically tunable absorption based on graphene and random metasurface. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2602–2606. [Google Scholar] [CrossRef]
- Pan, W.; Yu, X.; Zhang, J.; Zeng, W. A novel design of broadband terahertz metamaterial absorber based on nested circle rings. IEEE Photonics Technol. Lett. 2016, 28, 2335–2338. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, C.; Ren, Y. Broadband terahertz metamaterial absorber based on graphene resonators with perfect absorption. Results Phys. 2021, 26, 104466. [Google Scholar] [CrossRef]
- Lee, C.; Kim, K.; Park, P.; Jang, Y.; Jo, J.; Choi, T.; Lee, H. Ultra-Wideband Electromagnetic Composite Absorber Based on Pixelated Metasurface with Optimization Algorithm. Materials 2023, 16, 5916. [Google Scholar] [CrossRef] [PubMed]
- Lian, X.; Ma, M.; Tian, J.; Yang, R.; Wu, X. Vanadium dioxide based bifunctional metasurface for broadband absorption and cross-polarization conversion in THz range. AEU-Int. J. Electron. Commun. 2023, 170, 154784. [Google Scholar] [CrossRef]
- Norouzi, M.; Jarchi, S.; Ghaffari-Miab, M.; Esfandiari, M.; Lalbakhsh, A.; Koziel, S.; Reisenfeld, S.; Moloudian, G. 3D metamaterial ultra-wideband absorber for curved surface. Sci. Rep. 2023, 13, 1043. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Long, J.; Chen, X.; Sievenpiper, D. Electrically tunable metasurface absorber based on dissipating behavior of embedded varactors. Appl. Phys. Lett. 2016, 109, 071107. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Lim, S. Angle-and polarization-insensitive broadband metamaterial absorber using resistive fan-shaped resonators. Appl. Phys. Lett. 2018, 112, 021605. [Google Scholar] [CrossRef]
- Olszewska-Placha, M.; Salski, B.; Janczak, D.; Bajurko, P.R.; Gwarek, W.; Jakubowska, M. A broadband absorber with a resistive pattern made of ink with graphene nano-platelets. IEEE Trans. Antennas Propag. 2014, 63, 565–572. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, J.; Pang, Y.; Wang, J.; Ma, H.; Qu, S. Transparent broadband metamaterial absorber enhanced by water-substrate incorporation. Opt. Express 2018, 26, 15665–15674. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, K.; Jiang, T.; Zhao, J.; Feng, Y. Multi-octave microwave absorption via conformal metamaterial absorber with optical transparency. J. Phys. D Appl. Phys. 2019, 52, 335101. [Google Scholar] [CrossRef]
- Khan, H.A.; Zhang, J.W.; Liang, J.C.; Xia, J.; Zhang, J. A conformal coding metasurface for dual polarization conversion and radar cross section (RCS) reduction. J. Opt. 2023, 25, 125102. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Y.; Wu, Y.; Lai, S.; Gu, W. A single-resonant-structure and optically transparent broadband THz metamaterial absorber. J. Infrared Millim. Terahertz Waves 2019, 40, 648–656. [Google Scholar] [CrossRef]
- Liu, J.; Wu, S.; Ren, Z.; Xu, J.; Sheng, Z. Tunable broadband terahertz properties in an architecture optimized ITO/VO2 hybrid metamaterial. Opt. Commun. 2023, 537, 129402. [Google Scholar] [CrossRef]
- Yin, W.; Shen, Z.; Li, S.; Gao, F.; Hao, H.; Zhang, L.; Chen, X. Flexible broadband terahertz absorbers for RCS reduction on conformal surfaces. Opt. Commun. 2022, 520, 128502. [Google Scholar] [CrossRef]
- Yan, X.; Liang, L.; Yang, J.; Liu, W.; Ding, X.; Xu, D.; Zhang, Y.; Cui, T.; Yao, J. Broadband, wide-angle, low-scattering terahertz wave by a flexible 2-bit coding metasurface. Opt. Express 2015, 23, 29128–29137. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Xiao, R.; Zhang, R.; Shen, Z.; Hu, W.; Wang, L.; Lu, Y. Tunable terahertz absorber based on transparent and flexible metamaterial. Chin. Opt. Lett. 2020, 18, 092403. [Google Scholar] [CrossRef]
- Barzegar-Parizi, S.; Rejaei, B.; Khavasi, A. Analytical circuit model for periodic arrays of graphene disks. IEEE J. Quantum Electron. 2015, 51, 1–7. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statemen28ts, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafeez, S.; Yu, J.; Umrani, F.A.; Majeed, A.; Yun, W. A Broadband Meta-Absorber for Curved Terahertz Stealth Applications. Electronics 2024, 13, 2966. https://doi.org/10.3390/electronics13152966
Hafeez S, Yu J, Umrani FA, Majeed A, Yun W. A Broadband Meta-Absorber for Curved Terahertz Stealth Applications. Electronics. 2024; 13(15):2966. https://doi.org/10.3390/electronics13152966
Chicago/Turabian StyleHafeez, Saima, Jianguo Yu, Fahim Aziz Umrani, Abdul Majeed, and Wang Yun. 2024. "A Broadband Meta-Absorber for Curved Terahertz Stealth Applications" Electronics 13, no. 15: 2966. https://doi.org/10.3390/electronics13152966
APA StyleHafeez, S., Yu, J., Umrani, F. A., Majeed, A., & Yun, W. (2024). A Broadband Meta-Absorber for Curved Terahertz Stealth Applications. Electronics, 13(15), 2966. https://doi.org/10.3390/electronics13152966








