An Autonomous Cooperative Navigation Approach for Multiple Unmanned Ground Vehicles in a Variable Communication Environment
Abstract
:1. Introduction
- A comprehensive multi-agent pattern is combined into the multi-UGV collaborative navigation system, and the optimal coordination of multi-UGVs within the communication coverage area is formulated as a real-time multi-agent Markov decision process (MDP) model. All UGVs are set as independent agents with self-control capabilities.
- A multi-agent collaborative navigation method with enhanced communication coverage is proposed. By introducing a mobile base station, the communication coverage environment is dynamically changed. Simulation results show that this method effectively improves the communication quality during navigation.
- A GA-based hyperparameter adaptive approach is presented for optimizing UGV communication coverage and navigation. It assigns weights to hyperparameters according to the degree of algorithm updating and makes a choice based on the size of the weight at the next selection, which is different from the traditional fixed-hyperparameter strategy and can escape local optima.
2. MDP for Navigation and Communication Coverage for Multi-UGVs in Environments
2.1. Problem Description
2.2. Modeling of the Environment
2.3. Modeling of the Communication Coverage
2.4. The State and Action of the UGVs
2.5. Reward Function
3. RL Multi-Agent Communication Coverage Navigation with GA
3.1. MDP Model
3.2. Fundamentals of the DDPG Approach
3.3. Multi-Agent Deep Deterministic Policy Gradient
3.4. Genetic Algorithm
3.5. GA-MADDPG for Addressing Communication Coverage and Navigation in Its Own Abstract Formulation
| Algorithm 1 GA-MADDPG algorithm |
|
4. Simulation Results
4.1. Settings of the Experiments
4.2. Indicators of Evaluation for UGV Navigation
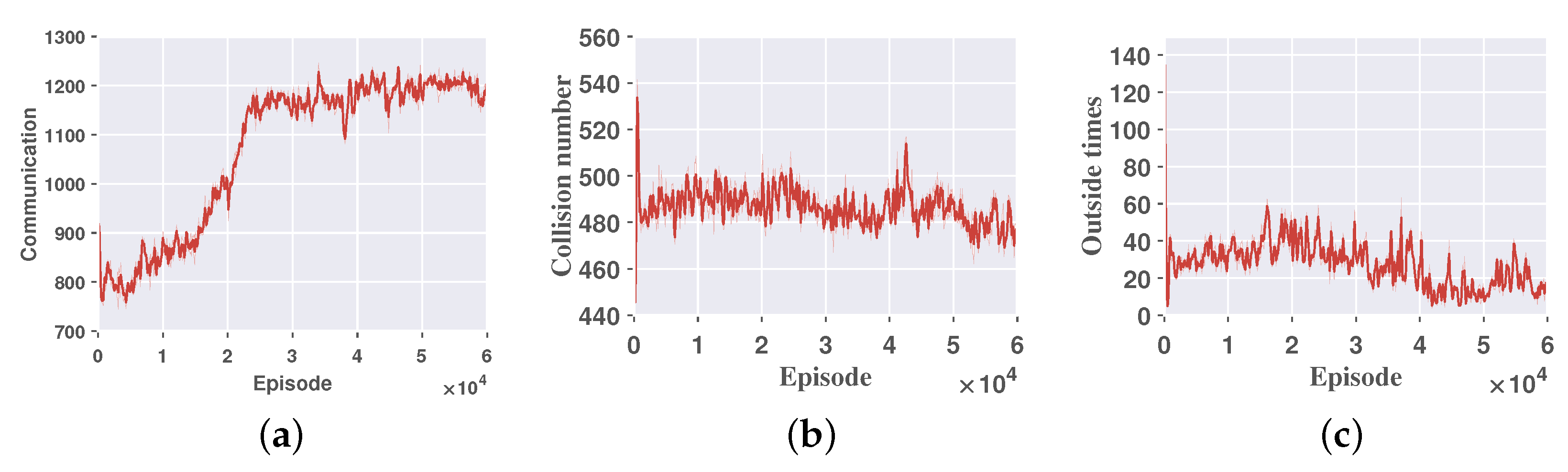
- Communication return.The communication return is the average communication quality per episode for the UGVs and is calculated based on Equation (1). The communication returns converge quickly from the initial –800 to –300 as shown by Figure 5a, which indicates that the communication quality has been improved and has stabilized in an interval.
- Collision times: The collision times are the sum of collisions between UGVs and obstacles and between drones and drones in an average round. The collision indicator converges from 540 to below 480, as shown by Figure 5b, indicating that the number of collisions has also been reduced somewhat, and since this study allows UGVs to have a certain number of collisions, the collision indicator is not the main optimization objective.
- Outside times: The outside times are the number of times the UGVs go out of bounds and run out of the environment we set. From Figure 5c, the rapid reduction in the number of times going out of bounds indicates that our research has significantly limited ineffective boundary violations, demonstrating that our study effectively operates within the designated area.
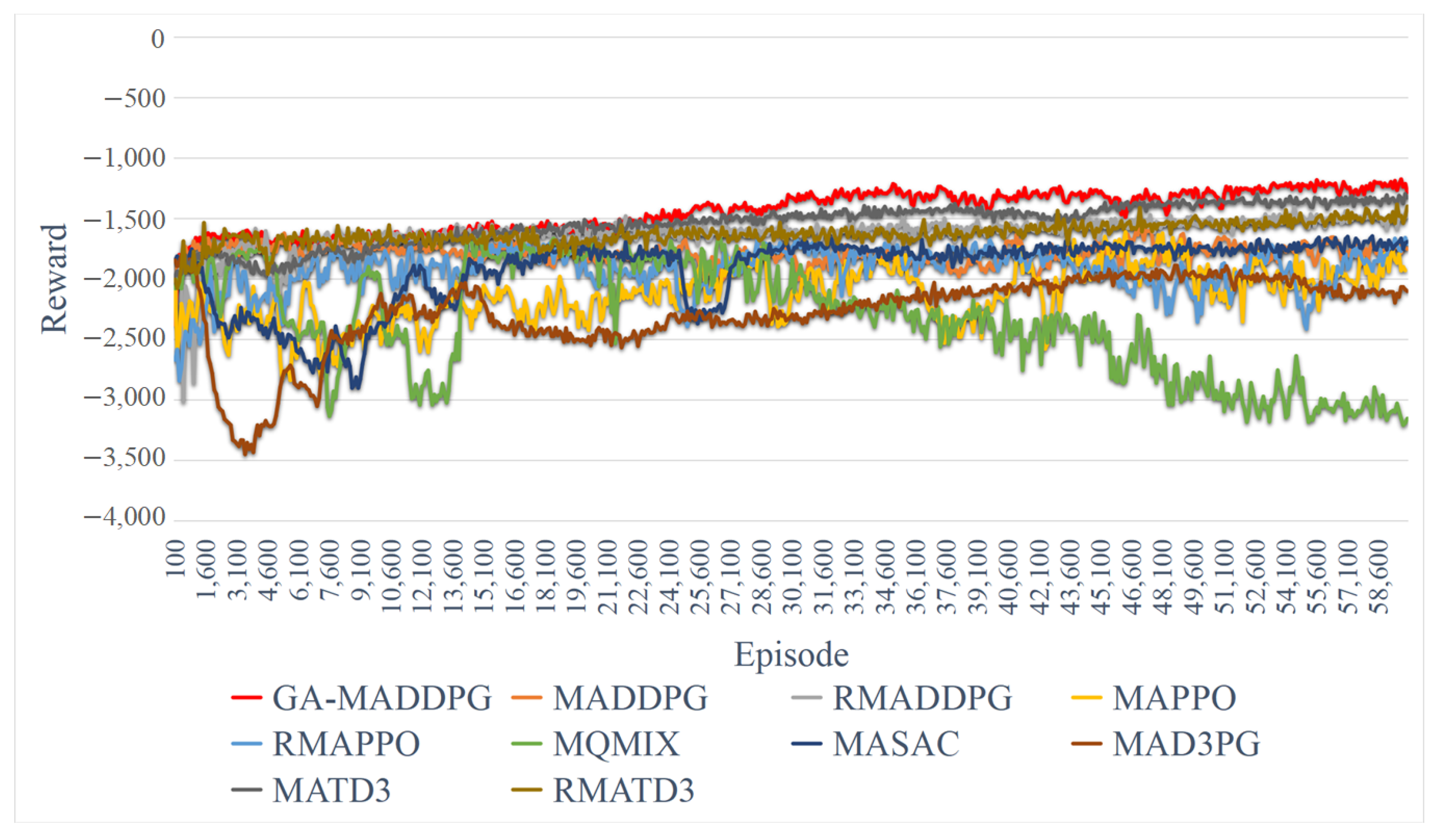
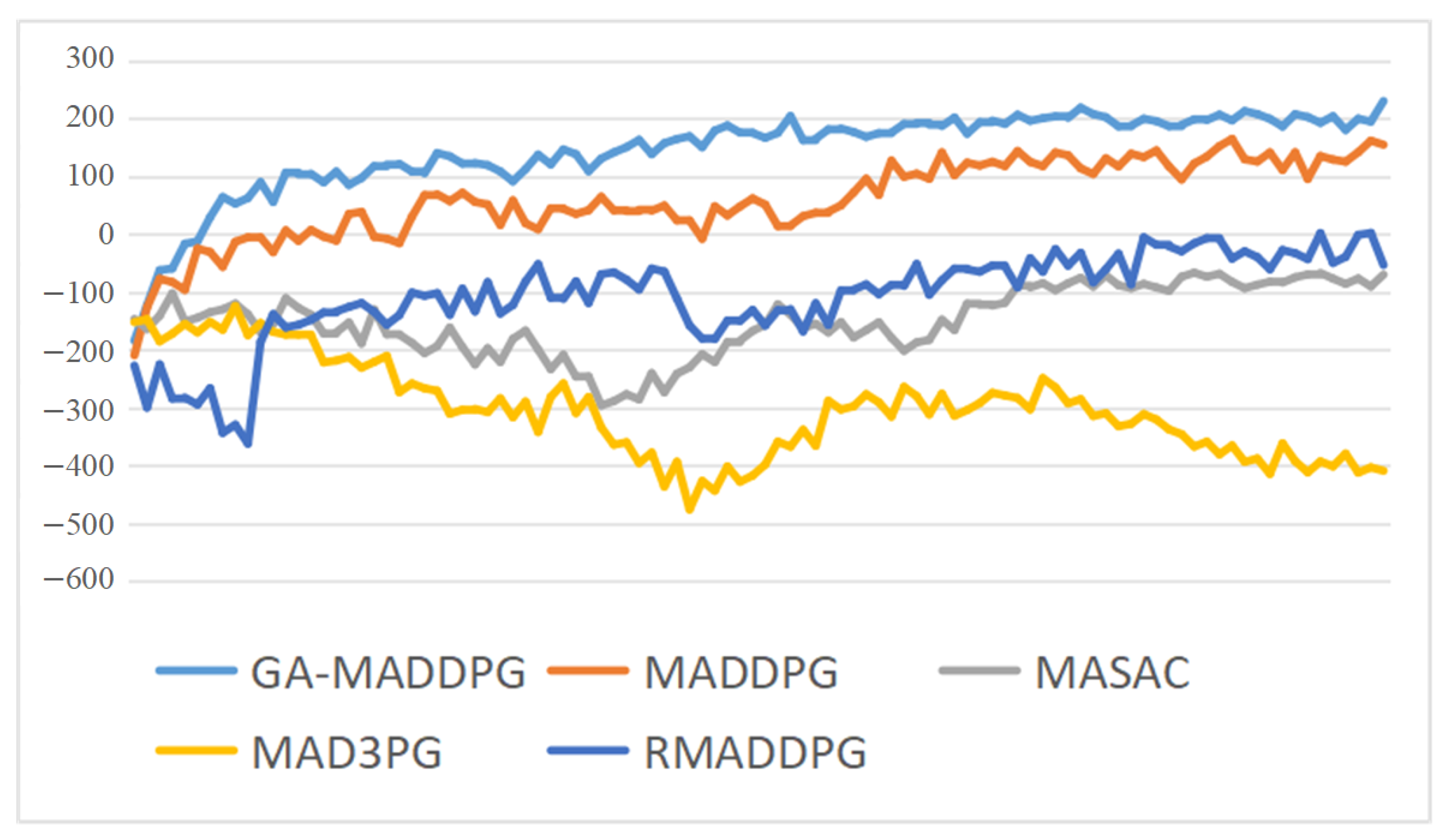
4.3. Comparative GA-MADDPG Experimentation
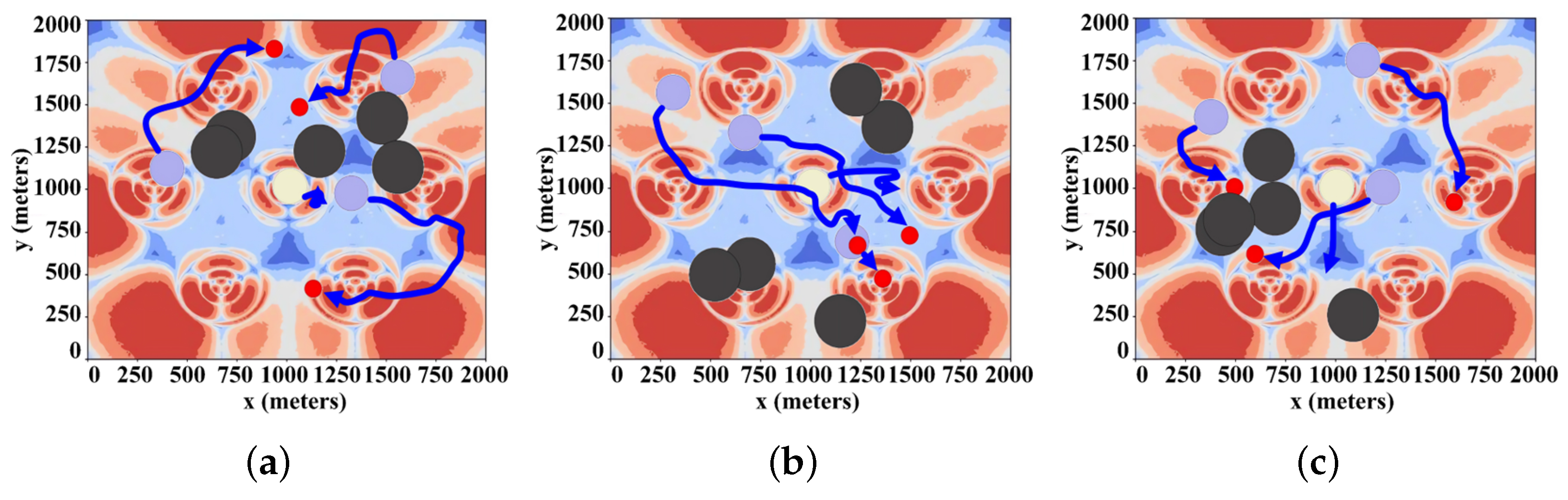
4.4. Generalization Experiment of GA-MADDPG
4.4.1. Simulation with Different Numbers of UGVs
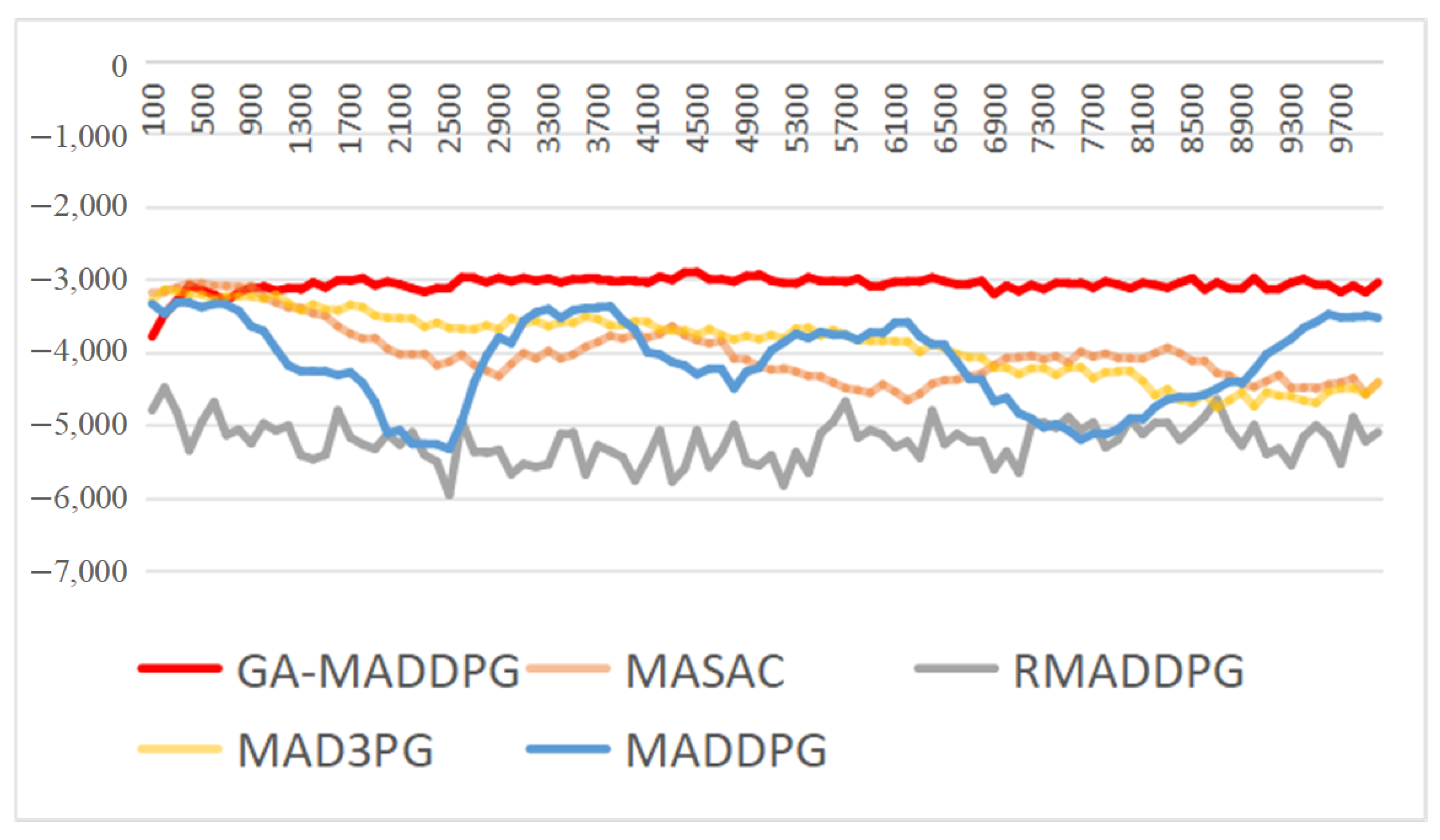
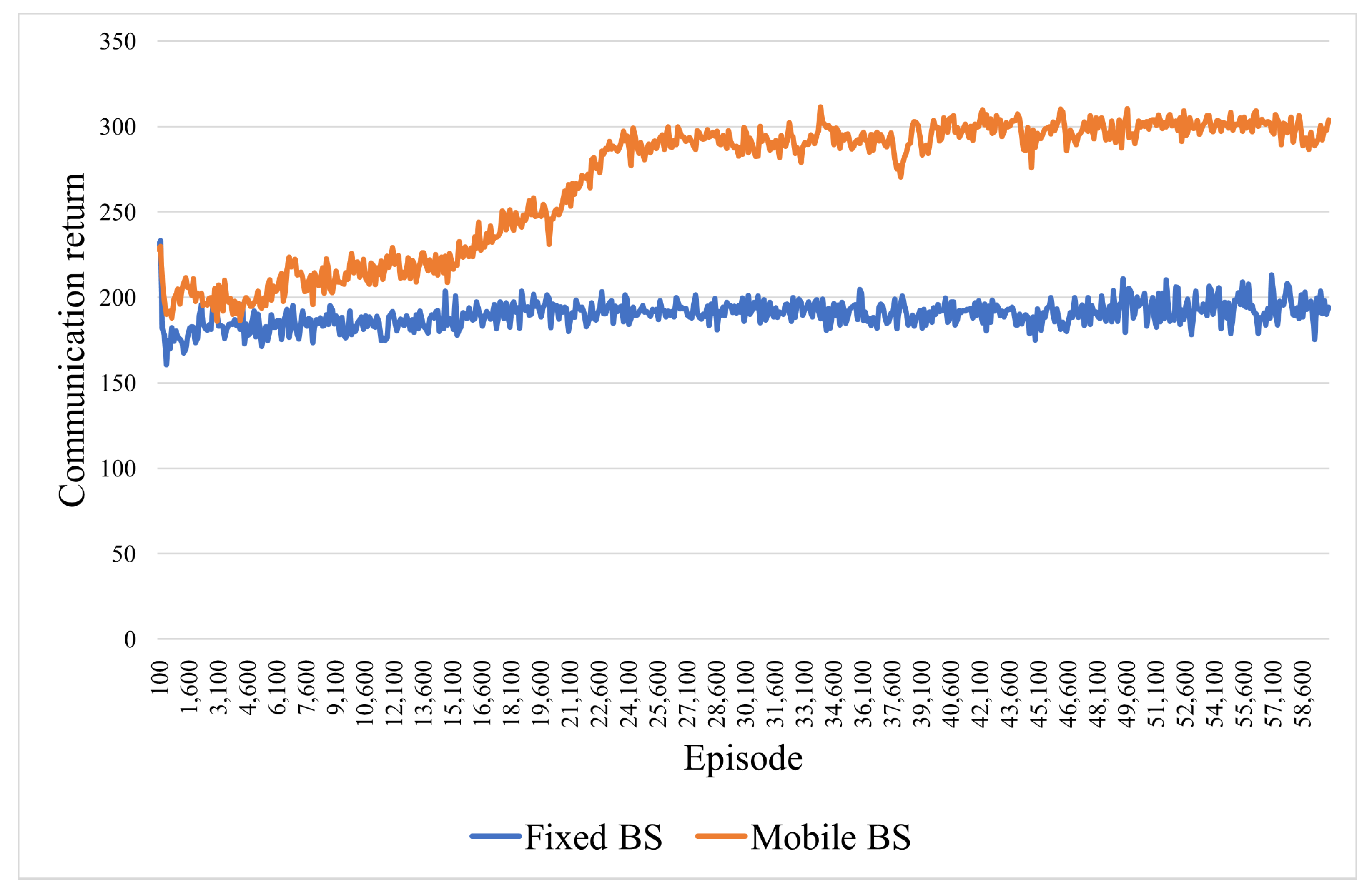
4.4.2. Experiments on the Effectiveness of the Mobile BS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Afzali, S.R.; Shoaran, M.; Karimian, G. A Modified Convergence DDPG Algorithm for Robotic Manipulation. Neural Process. Lett. 2023, 55, 11637–11652. [Google Scholar] [CrossRef]
- Chai, R.; Niu, H.; Carrasco, J.; Arvin, F.; Yin, H.; Lennox, B. Design and experimental validation of deep reinforcement learning-based fast trajectory planning and control for mobile robot in unknown environment. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5778–5792. [Google Scholar] [CrossRef]
- Dong, X.; Wang, Q.; Yu, J.; Lü, J.; Ren, Z. Neuroadaptive Output Formation Tracking for Heterogeneous Nonlinear Multiagent Systems with Multiple Nonidentical Leaders. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 3702–3712. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Liang, J.; Wen, M.; Yue, Y.; Wang, D. Integrated Localization and Planning for Cruise Control of UGV Platoons in Infrastructure-Free Environments. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10804–10817. [Google Scholar] [CrossRef]
- Tran, V.P.; Perera, A.; Garratt, M.A.; Kasmarik, K.; Anavatti, S.G. Coverage Path Planning with Budget Constraints for Multiple Unmanned Ground Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12506–12522. [Google Scholar] [CrossRef]
- Wu, Y.; Li, Y.; Li, W.; Li, H.; Lu, R. Robust Lidar-Based Localization Scheme for Unmanned Ground Vehicle via Multisensor Fusion. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5633–5643. [Google Scholar] [CrossRef]
- Zhang, W.; Zuo, Z.; Wang, Y. Networked multiagent systems: Antagonistic interaction, constraint, and its application. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3690–3699. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Weng, J.; Huang, F.; Zhou, J.; Mao, Y.; Liu, X. Heuristic Monte Carlo algorithm for unmanned ground vehicles realtime localization and mapping. IEEE Trans. Veh. Technol. 2020, 69, 10642–10655. [Google Scholar] [CrossRef]
- Unlu, H.U.; Patel, N.; Krishnamurthy, P.; Khorrami, F. Sliding-window temporal attention based deep learning system for robust sensor modality fusion for UGV navigation. IEEE Robot. Autom. Lett. 2019, 4, 4216–4223. [Google Scholar] [CrossRef]
- Lyu, X.; Hu, B.; Wang, Z.; Gao, D.; Li, K.; Chang, L. A SINS/GNSS/VDM integrated navigation fault-tolerant mechanism based on adaptive information sharing factor. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Sun, C.; Ye, M.; Hu, G. Distributed optimization for two types of heterogeneous multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1314–1324. [Google Scholar] [CrossRef]
- Shan, Y.; Fu, Y.; Chen, X.; Lin, H.; Lin, J.; Huang, K. LiDAR based Traversable Regions Identification Method for Off-road UGV Driving. IEEE Trans. Intell. Veh. 2023, 9, 3544–3557. [Google Scholar] [CrossRef]
- Garaffa, L.C.; Basso, M.; Konzen, A.A.; de Freitas, E.P. Reinforcement learning for mobile robotics exploration: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3796–3810. [Google Scholar] [CrossRef]
- Huang, C.Q.; Jiang, F.; Huang, Q.H.; Wang, X.Z.; Han, Z.M.; Huang, W.Y. Dual-graph attention convolution network for 3-D point cloud classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 4813–4825. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Garratt, M.; Bui, L.T.; Abbass, H. Supervised deep actor network for imitation learning in a ground-air UAV-UGVs coordination task. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Han, Z.; Yang, Y.; Wang, W.; Zhou, L.; Gadekallu, T.R.; Alazab, M.; Gope, P.; Su, C. RSSI Map-Based Trajectory Design for UGV Against Malicious Radio Source: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2022, 24, 4641–4650. [Google Scholar] [CrossRef]
- Feng, Z.; Huang, M.; Wu, Y.; Wu, D.; Cao, J.; Korovin, I.; Gorbachev, S.; Gorbacheva, N. Approximating Nash equilibrium for anti-UAV jamming Markov game using a novel event-triggered multi-agent reinforcement learning. Neural Netw. 2023, 161, 330–342. [Google Scholar] [CrossRef]
- Huang, X.; Deng, H.; Zhang, W.; Song, R.; Li, Y. Towards multi-modal perception-based navigation: A deep reinforcement learning method. IEEE Robot. Autom. Lett. 2021, 6, 4986–4993. [Google Scholar] [CrossRef]
- Wu, S.; Xu, W.; Wang, F.; Li, G.; Pan, M. Distributed federated deep reinforcement learning based trajectory optimization for air-ground cooperative emergency networks. IEEE Trans. Veh. Technol. 2022, 71, 9107–9112. [Google Scholar] [CrossRef]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Tran, T.H.; Nguyen, M.T.; Kwok, N.M.; Ha, Q.P.; Fang, G. Sliding mode-PID approach for robust low-level control of a UGV. In Proceedings of the 2006 IEEE International Conference on Automation Science and Engineering, Shanghai, China, 8–10 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 672–677. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
- Mirjalili, S.; Mirjalili, S. Genetic algorithm. Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Sehgal, A.; La, H.; Louis, S.; Nguyen, H. Deep reinforcement learning using genetic algorithm for parameter optimization. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 596–601. [Google Scholar]
- Chen, R.; Yang, B.; Li, S.; Wang, S. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Comput. Ind. Eng. 2020, 149, 106778. [Google Scholar] [CrossRef]
- Alipour, M.M.; Razavi, S.N.; Feizi Derakhshi, M.R.; Balafar, M.A. A hybrid algorithm using a genetic algorithm and multiagent reinforcement learning heuristic to solve the traveling salesman problem. Neural Comput. Appl. 2018, 30, 2935–2951. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, B.; Zhou, H.; Koushik, G.; Hebert, M.; Zhao, D. Mapper: Multi-agent path planning with evolutionary reinforcement learning in mixed dynamic environments. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 11748–11754. [Google Scholar]
- Huang, M.; Lin, X.; Feng, Z.; Wu, D.; Shi, Z. A multi-agent decision approach for optimal energy allocation in microgrid system. Electr. Power Syst. Res. 2023, 221, 109399. [Google Scholar] [CrossRef]
- Qiu, C.; Hu, Y.; Chen, Y.; Zeng, B. Deep deterministic policy gradient (DDPG)-based energy harvesting wireless communications. IEEE Internet Things J. 2019, 6, 8577–8588. [Google Scholar] [CrossRef]
- Littman, M.L. Markov games as framework for multi-agent reinforcement learning. In Proceedings of the Proc International Conference on Machine Learning, New Brunswick, NJ, USA, 10–13 July 1994; pp. 157–163. [Google Scholar]
- Feng, Z.; Huang, M.; Wu, D.; Wu, E.Q.; Yuen, C. Multi-Agent Reinforcement Learning with Policy Clipping and Average Evaluation for UAV-Assisted Communication Markov Game. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14281–14293. [Google Scholar] [CrossRef]
- Liu, H.; Zong, Z.; Li, Y.; Jin, D. NeuroCrossover: An intelligent genetic locus selection scheme for genetic algorithm using reinforcement learning. Appl. Soft Comput. 2023, 146, 110680. [Google Scholar] [CrossRef]
- Köksal Ahmed, E.; Li, Z.; Veeravalli, B.; Ren, S. Reinforcement learning-enabled genetic algorithm for school bus scheduling. J. Intell. Transp. Syst. 2022, 26, 269–283. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, M.; Xu, Q.; Wang, H.; Wang, J. Reinforcement Learning-Based Genetic Algorithm in Optimizing Multidimensional Data Discretization Scheme. Math. Probl. Eng. 2020, 2020, 1698323. [Google Scholar] [CrossRef]
- Yang, J.; Sun, Z.; Hu, W.; Steinmeister, L. Joint control of manufacturing and onsite microgrid system via novel neural-network integrated reinforcement learning algorithms. Appl. Energy 2022, 315, 118982. [Google Scholar] [CrossRef]
- Shi, H.; Liu, G.; Zhang, K.; Zhou, Z.; Wang, J. MARL Sim2real Transfer: Merging Physical Reality with Digital Virtuality in Metaverse. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 2107–2117. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of ppo in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]
- Rashid, T.; Farquhar, G.; Peng, B.; Whiteson, S. Weighted qmix: Expanding monotonic value function factorisation for deep multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 10199–10210. [Google Scholar]
- Wu, T.; Wang, J.; Lu, X.; Du, Y. AC/DC hybrid distribution network reconfiguration with microgrid formation using multi-agent soft actor-critic. Appl. Energy 2022, 307, 118189. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C.; Li, F.; Wang, X.; Xu, X.; Shen, L. PASCAL: PopulAtion-Specific Curriculum-based MADRL for collision-free flocking with large-scale fixed-wing UAV swarms. Aerosp. Sci. Technol. 2023, 133, 108091. [Google Scholar] [CrossRef]
- Ackermann, J.J.; Gabler, V.; Osa, T.; Sugiyama, M. Reducing Overestimation Bias in Multi-Agent Domains Using Double Centralized Critics. arXiv 2019, arXiv:1910.01465. [Google Scholar]
- Xing, X.; Zhou, Z.; Li, Y.; Xiao, B.; Xun, Y. Multi-UAV Adaptive Cooperative Formation Trajectory Planning Based on an Improved MATD3 Algorithm of Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024. [Google Scholar] [CrossRef]





| Definition | Value | Definition | Value |
|---|---|---|---|
| Max episodes | 60,000 | Minibatch size | 512 |
| Replay buffer capacity | 1,000,000 | Discount factor | 0.99 |
| Steps per update | 100 | Learning rate | 0.0001 |
| Max steps per episode | 25 | Update population rate | 100 |
| Time step length | 1 | Hidden dimension | 64 |
| Discount Factor | Learning Rate | Replay Buffer Capacity | Minibatch Size |
|---|---|---|---|
| 0.9 | 0.01 | 10,000 | 512 |
| 0.95 | 0.001 | 100,000 | 1024 |
| 0.99 | 0.0005 | 1,000,000 | 2048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Huang, M. An Autonomous Cooperative Navigation Approach for Multiple Unmanned Ground Vehicles in a Variable Communication Environment. Electronics 2024, 13, 3028. https://doi.org/10.3390/electronics13153028
Lin X, Huang M. An Autonomous Cooperative Navigation Approach for Multiple Unmanned Ground Vehicles in a Variable Communication Environment. Electronics. 2024; 13(15):3028. https://doi.org/10.3390/electronics13153028
Chicago/Turabian StyleLin, Xudong, and Mengxing Huang. 2024. "An Autonomous Cooperative Navigation Approach for Multiple Unmanned Ground Vehicles in a Variable Communication Environment" Electronics 13, no. 15: 3028. https://doi.org/10.3390/electronics13153028
APA StyleLin, X., & Huang, M. (2024). An Autonomous Cooperative Navigation Approach for Multiple Unmanned Ground Vehicles in a Variable Communication Environment. Electronics, 13(15), 3028. https://doi.org/10.3390/electronics13153028





