Adaptive Active Disturbance Rejection Control with Recursive Parameter Identification
Abstract
:1. Introduction
2. Active Disturbance Rejection Control—Overview
2.1. The Basics of the ADRC Idea
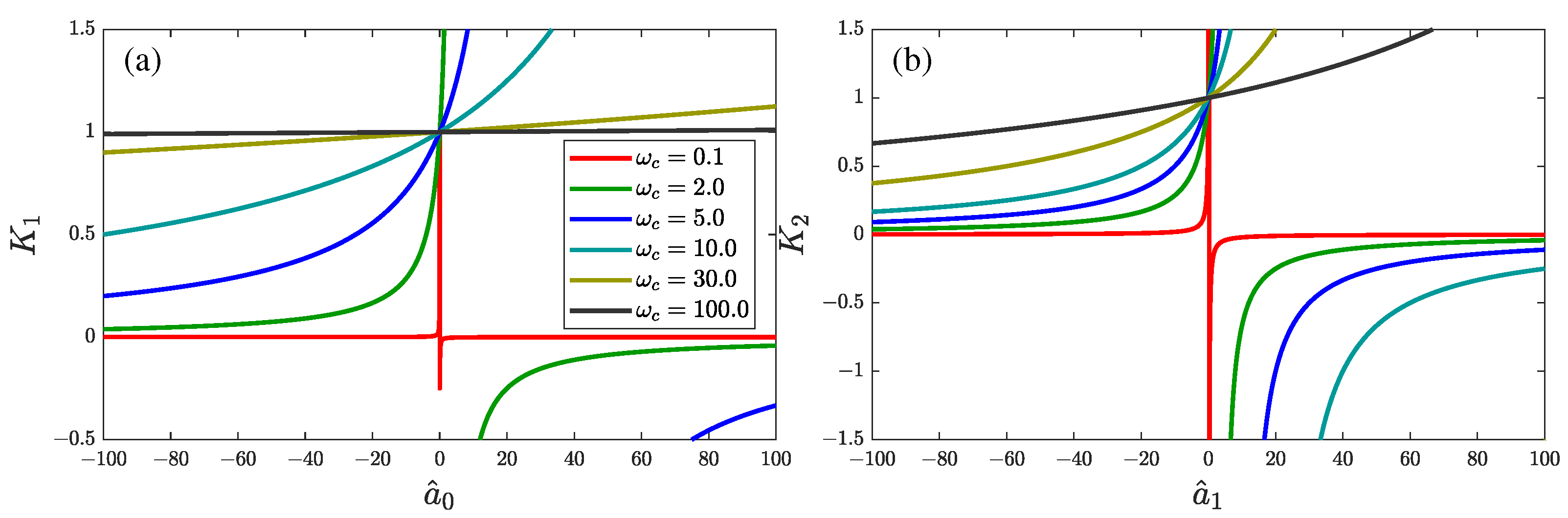
2.2. ADRC Gains Selection
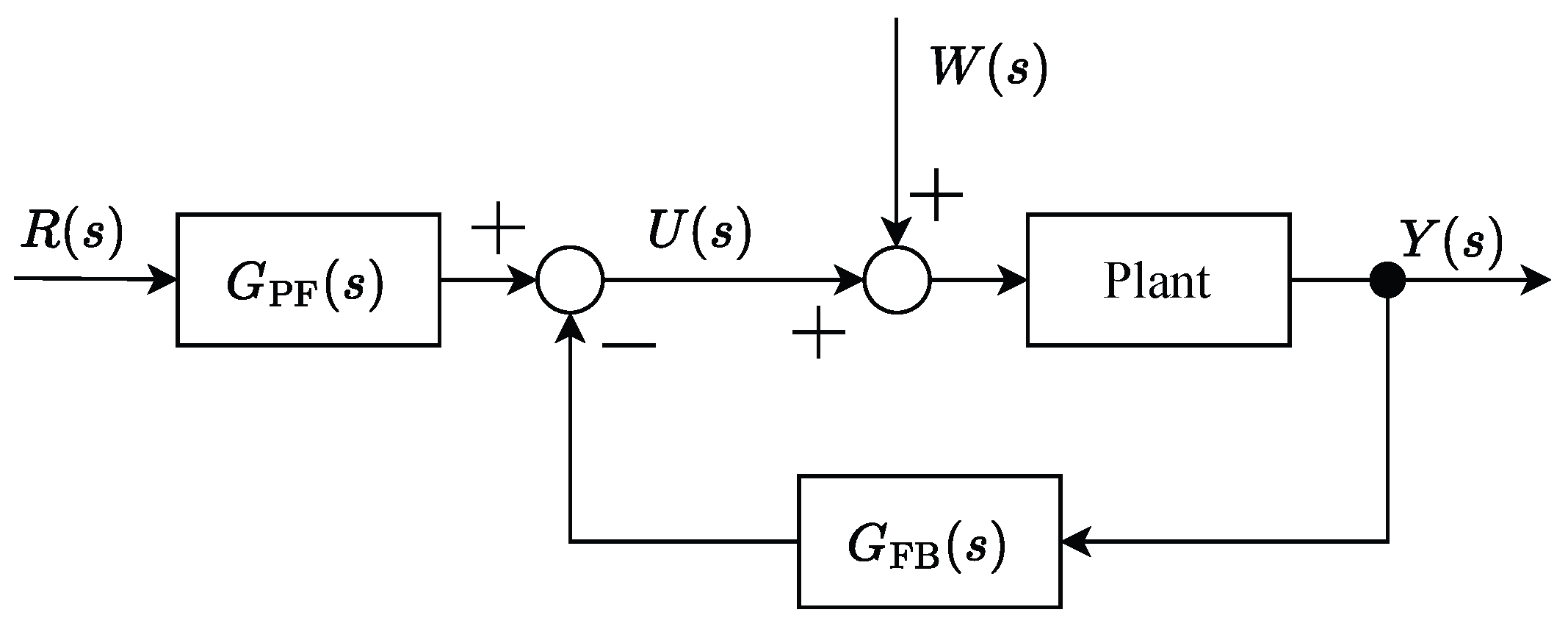
2.3. Control Design for Second-Order System
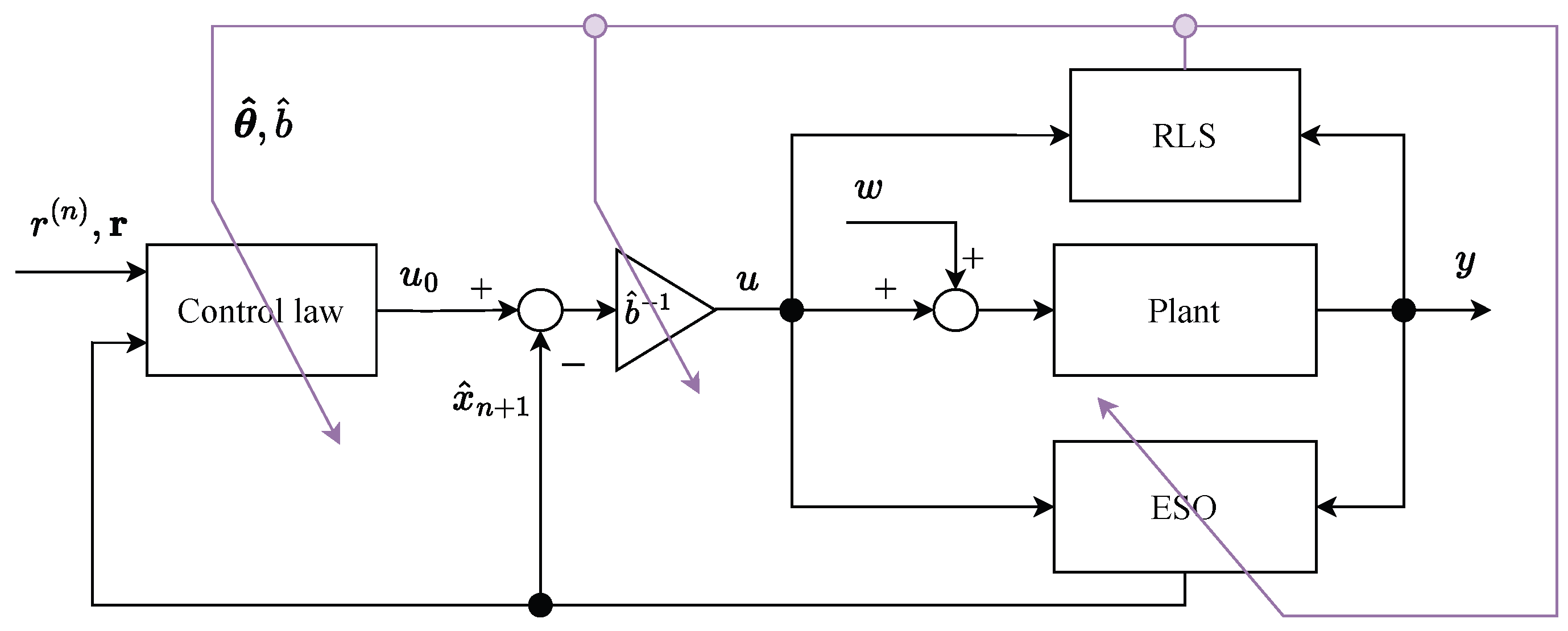
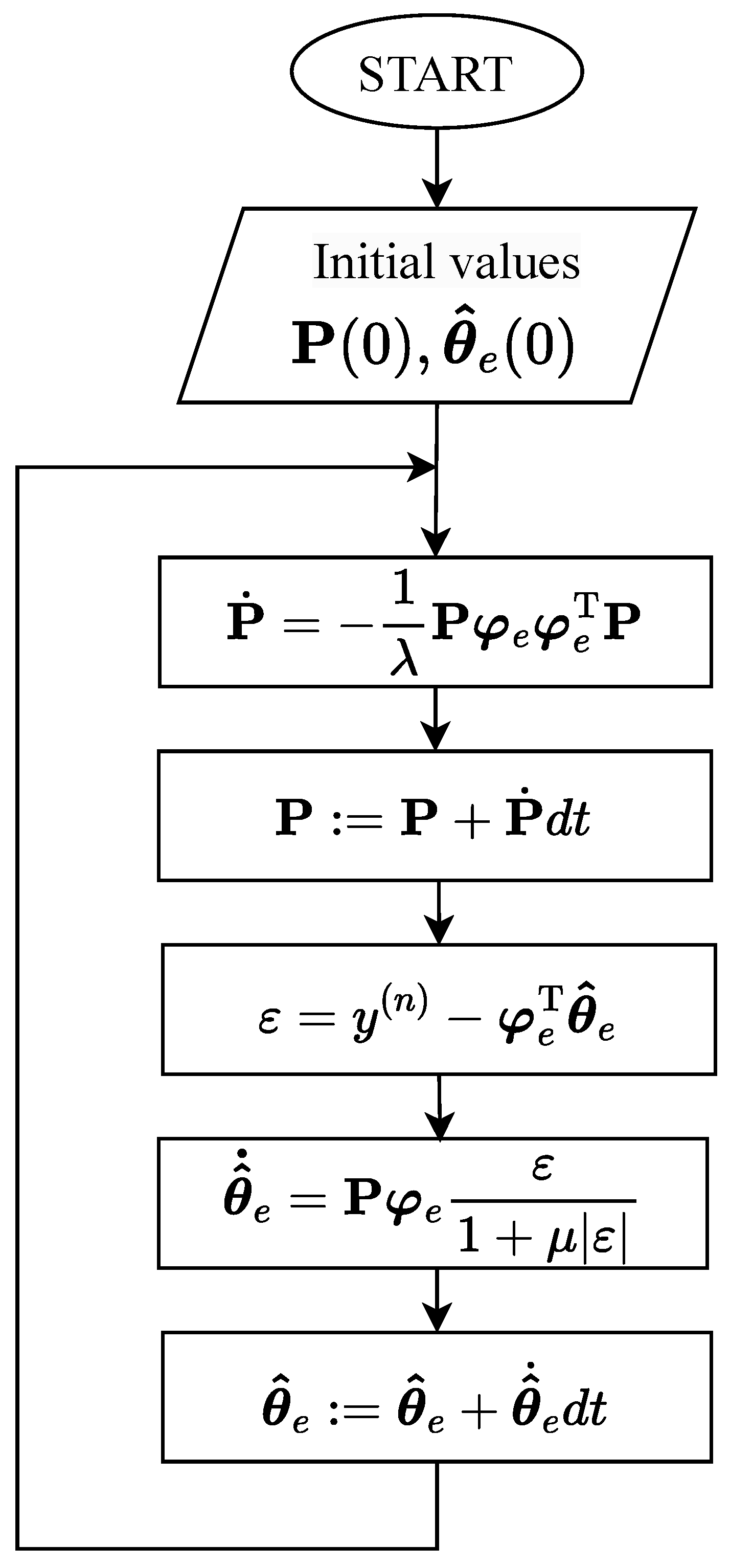
3. Adaptive ADRC Approach
Stability Analysis of Adaptive ADRC
4. Results of the Experiments and Simulations
4.1. Influence of System Parameters on the Control Quality
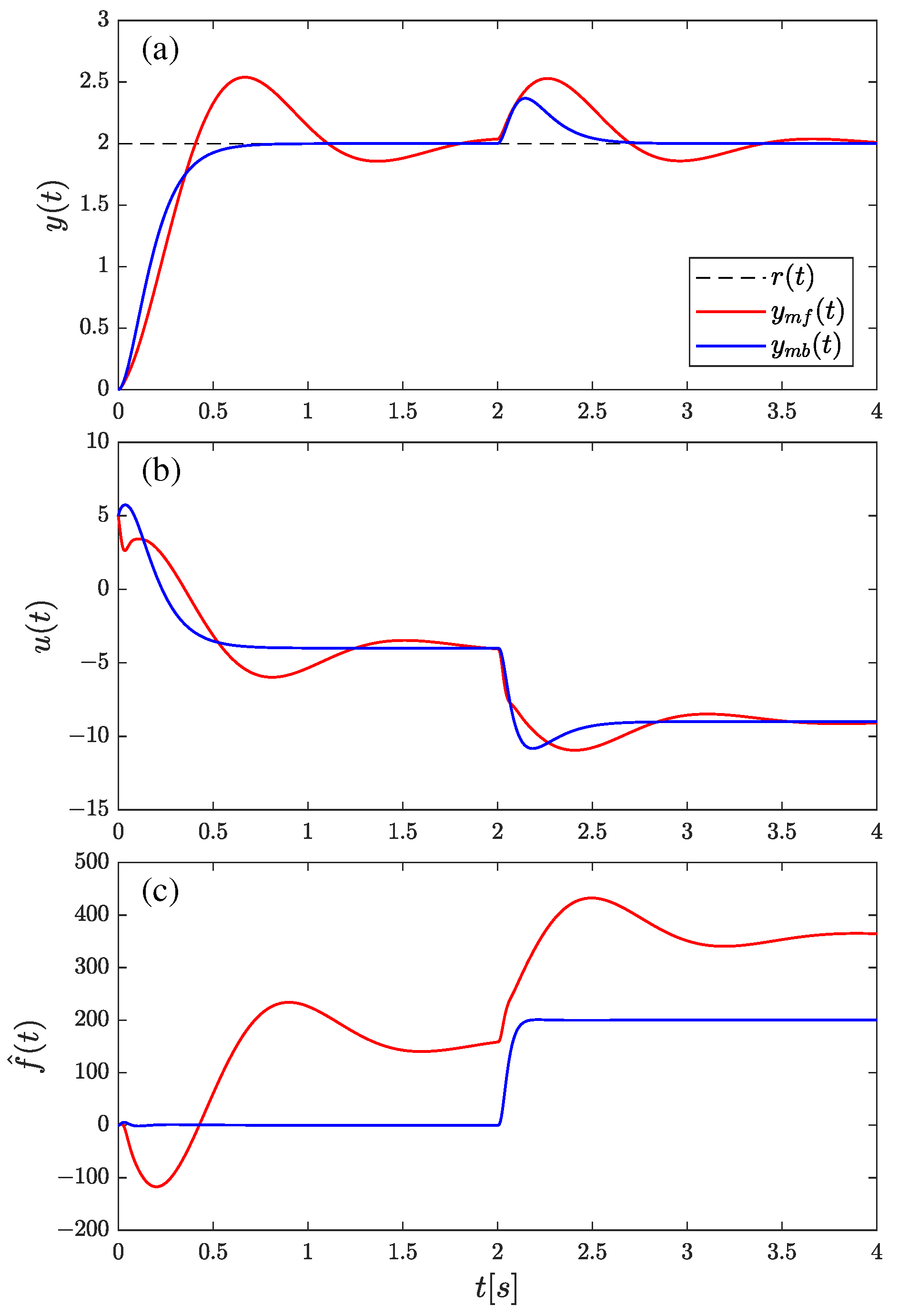
4.2. Simulation Plant–Control System Analysis for mfADRC and mbADRC
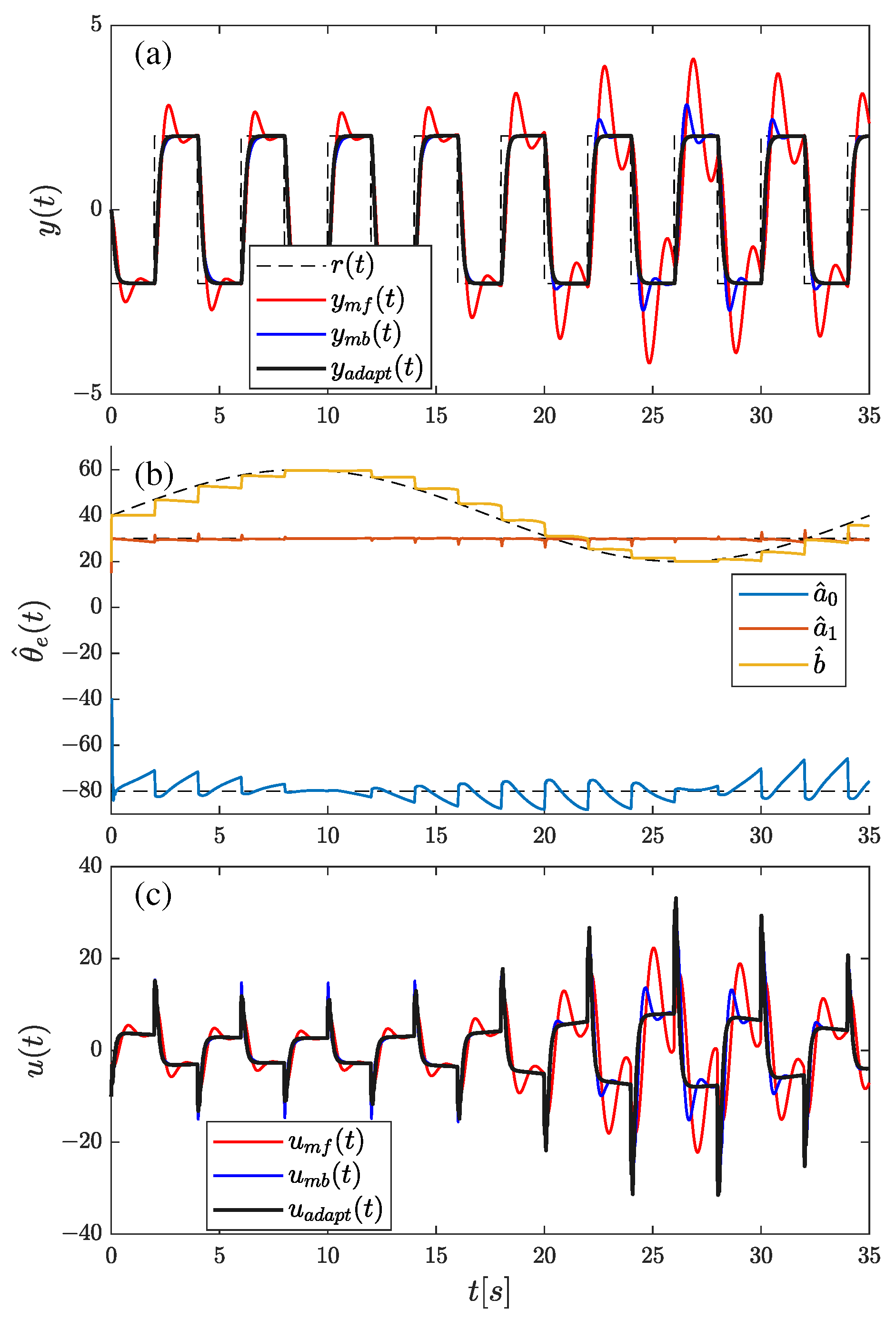
4.3. Simulation Plant–Control Plant with Time-Varying Parameter
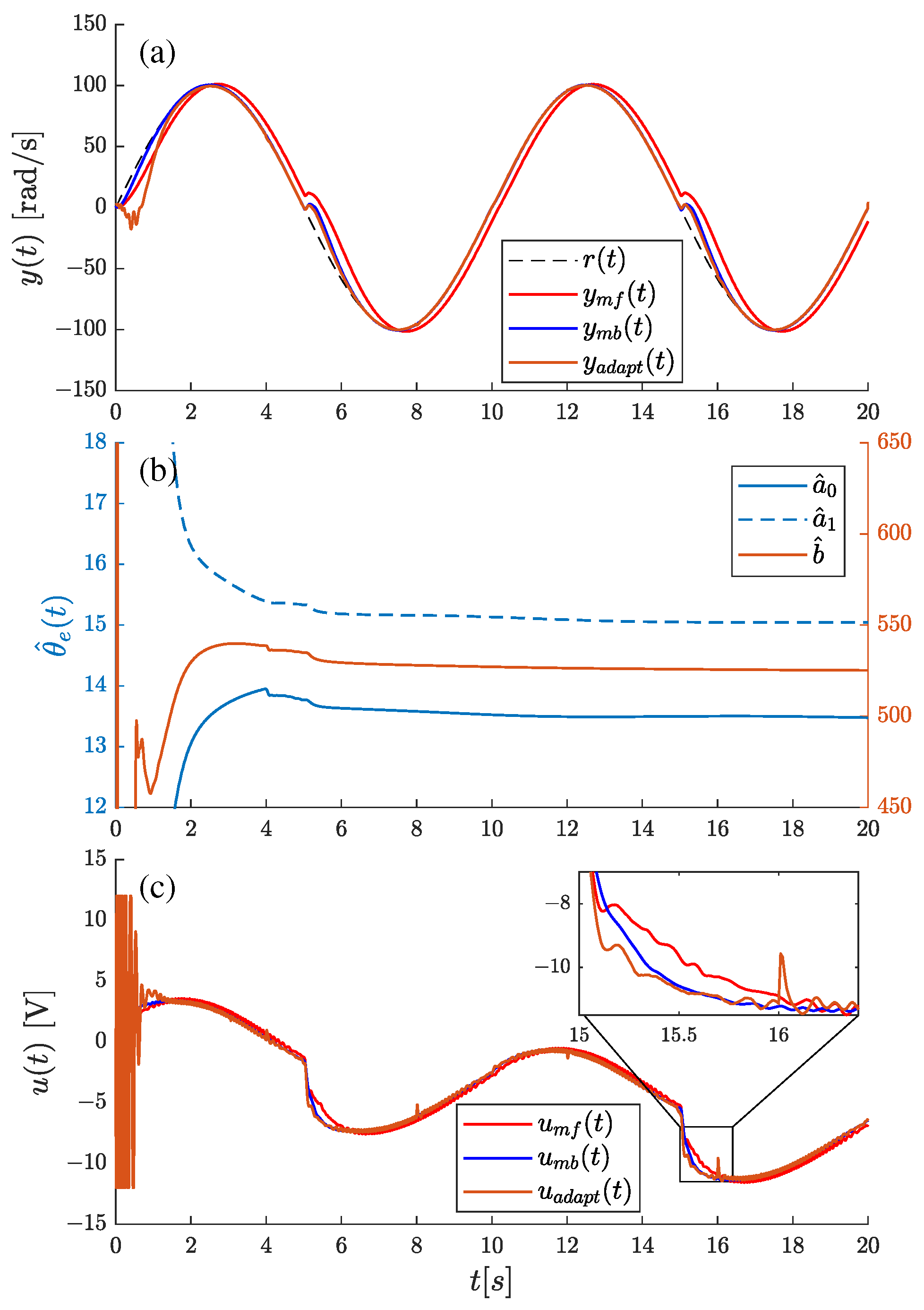
4.4. Real Plant–DC Motor
- Constant-value control, for which the reference velocity yields
- Trajectory tracking control, for which the reference velocity yields
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Symbols
| n | order of system dynamics |
| extended state vector at the time t | |
| estimate of extended state vector | |
| derivative of x variable | |
| n-th derivative of x signal | |
| vector of zeros | |
| estimate of non-extended state vector (contains first n coefficients of vector) | |
| identity matrix with dimensions | |
| y | system output (measurement) signal |
| u | system input (control) signal |
| observer bandwidth | |
| vector of observer gains | |
| closed-loop (controller) bandwidth | |
| vector of controller gains | |
| r | reference signal (set-point) |
| vector reference signal and its derivatives from 1 to -th | |
| n-th derivative of reference signal | |
| w | external disturbance signal |
| internal dynamics of the system | |
| total disturbance of the system | |
| estimate total disturbance of the system (from ESO) | |
| b | input gain coefficient |
| estimate of input gain coefficient | |
| coefficients of the linear part of the system dynamics | |
| the linear system part estimated coefficients | |
| system parameters vector | |
| vector of estimates of system parameters | |
| extended parameters vector | |
| vector of estimates of extended system parameters | |
| regression vector | |
| Heaveside step function | |
| time horizon of the experiment |
Abbreviations
| ADRC | Active Disturbance Rejection Control |
| DC | Direct Current |
| ESO | Extended State Observer |
| IAE | Integral of Absolute Error |
| adaptADRC | Adaptive ADRC |
| mbADRC | Model-Based ADRC |
| mfADRC | Model-Free ADRC |
| RLS | Recursive Least Squares |
| SVF | State Variable Filter |
References
- Aoudni, Y.; Kalra, A.; Azhagumurugan, R.; Ahmed, M.A.; Wanjari, A.K.; Singh, B.; Bhardwaj, A. Metaheuristics based tuning of robust PID controllers for controlling voltage and current on photonics and optics. Opt. Quantum Electron. 2022, 54, 809. [Google Scholar] [CrossRef]
- Feng, X.; Li, X.; Li, S.; Pan, F. Secure state estimation for unmanned aircraft cyber-physical systems under multiple attacks. Asian J. Control 2022, 24, 818–833. [Google Scholar] [CrossRef]
- Gao, Z. Active disturbance rejection control: A paradigm shift in feedback control system design. In Proceedings of the 2006 American Control Conference, Minneapolis, MI, USA, 14–16 June 2006; pp. 2399–2405. [Google Scholar] [CrossRef]
- Guo, B.; Bacha, S.; Alamir, M. A review on ADRC based PMSM control designs. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 1747–1753. [Google Scholar] [CrossRef]
- Yang, X.; Huang, Q.; Jing, S.; Zhang, M.; Zuo, Z.; Wang, S. Servo system control of satcom on the move based on improved ADRC controller. Energy Rep. 2022, 8, 1062–1070. [Google Scholar] [CrossRef]
- Fang, Q.; Zhou, Y.; Ma, S.; Zhang, C.; Wang, Y.; Huangfu, H. Electromechanical Actuator Servo Control Technology Based on Active Disturbance Rejection Control. Electronics 2023, 12, 1934. [Google Scholar] [CrossRef]
- Bai, K.; Luo, Y.; Dan, Z.; Zhang, S.; Wang, M.; Qian, Q.; Zhong, J. Extended State Observer based Attitude Control of a Bird-like Flapping-wing Flying Robot. J. Bionic Eng. 2020, 17, 708–717. [Google Scholar] [CrossRef]
- Tan, L.; Liang, S.; Su, H.; Qin, Z.; Li, L.; Huo, J. Research on Amphibious Multi-Rotor UAV Out-of-Water Control Based on ADRC. Appl. Sci. 2023, 13, 4900. [Google Scholar] [CrossRef]
- Chang, S.; Wang, Y.; Zuo, Z.; Zhang, Z.; Yang, H. On fast finite-time extended state observer and its application to wheeled mobile robots. Nonlinear Dyn. 2022, 110, 1473–1485. [Google Scholar] [CrossRef]
- Hai, X.; Wang, Z.; Feng, Q.; Ren, Y.; Xu, B.; Cui, J.; Duan, H. Mobile robot ADRC with an automatic parameter tuning mechanism via modified pigeon-inspired optimization. IEEE/ASME Trans. Mechatron. 2019, 24, 2616–2626. [Google Scholar] [CrossRef]
- Gao, J.; Liang, X.; Chen, Y.; Zhang, L.; Jia, S. Hierarchical image-based visual serving of underwater vehicle manipulator systems based on model predictive control and active disturbance rejection control. Ocean Eng. 2021, 229, 108814. [Google Scholar] [CrossRef]
- Chen, C.F.; Du, Z.J.; He, L.; Wang, J.Q.; Wu, D.M.; Dong, W. Active disturbance rejection with fast terminal sliding mode control for a lower limb exoskeleton in swing phase. IEEE Access 2019, 7, 72343–72357. [Google Scholar] [CrossRef]
- Dao, Q.T.; Dinh, V.V.; Trinh, M.C.; Tran, V.C.; Nguyen, V.L.; Duong, M.D.; Bui, N.T. Nonlinear Extended Observer-Based ADRC for a Lower-Limb PAM-Based Exoskeleton. Actuators 2022, 11, 369. [Google Scholar] [CrossRef]
- Michalski, J.; Retinger, M.; Kozierski, P.; Giernacki, W. Position Control of Crazyflie 2.1 Quadrotor UAV Based on Active Disturbance Rejection Control. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; pp. 1106–1113. [Google Scholar] [CrossRef]
- Lakomy, K.; Giernacki, W.; Michalski, J.; Madonski, R. Active Disturbance Rejection Control (ADRC) Toolbox for MATLAB/Simulink. arXiv 2021, arXiv:2112.01614. [Google Scholar]
- Madonski, R.; Shao, S.; Zhang, H.; Gao, Z.; Yang, J.; Li, S. General error-based active disturbance rejection control for swift industrial implementations. Control Eng. Pract. 2019, 84, 218–229. [Google Scholar] [CrossRef]
- Madonski, R.; Herbst, G.; Stankovic, M. ADRC in output and error form: Connection, equivalence, performance. Control Theory Technol. 2023, 21, 56–71. [Google Scholar] [CrossRef]
- Herbst, G. Transfer function analysis and implementation of active disturbance rejection control. Control Theory Technol. 2021, 19, 19–34. [Google Scholar] [CrossRef]
- Herbst, G.; Madonski, R. Tuning and implementation variants of discrete-time ADRC. Control Theory Technol. 2023, 21, 72–88. [Google Scholar] [CrossRef]
- Miklosovic, R.; Radke, A.; Gao, Z. Discrete implementation and generalization of the extended state observer. In Proceedings of the 2006 American Control Conference, Minneapolis, MI, USA, 14–16 June 2006; pp. 2209–2214. [Google Scholar] [CrossRef]
- Carvajal, B.V.M.; Sáez, J.S.; Rodríguez, S.G.N.; Iranzo, M.M. Modified Active Disturbance Rejection Predictive Control: A fixed-order state–space formulation for SISO systems. ISA Trans. 2023, 142, 148–163. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Z.; Zhou, G.; Liu, S.; Zhou, D.; Chen, S.; Zhang, X. Adaptive fuzzy active-disturbance rejection control-based reconfiguration controller design for aircraft anti-skid braking system. Actuators 2021, 10, 201. [Google Scholar] [CrossRef]
- Lv, C.; Wang, B.; Chen, J.; Zhang, R.; Dong, H.; Wan, S. Research on a Torque Ripple Suppression Method of Fuzzy Active Disturbance Rejection Control for a Permanent Magnet Synchronous Motor. Electronics 2024, 13, 1280. [Google Scholar] [CrossRef]
- Kicki, P.; Łakomy, K.; Lee, K.M.B. Tuning of extended state observer with neural network-based control performance assessment. Eur. J. Control 2022, 64, 100609. [Google Scholar] [CrossRef]
- Bai, C.; Zhang, Z. A least mean square based active disturbance rejection control for an inertially stabilized platform. Optik 2018, 174, 609–622. [Google Scholar] [CrossRef]
- Zhang, Z.; Cheng, J.; Guo, Y. PD-based optimal ADRC with improved linear extended state observer. Entropy 2021, 23, 888. [Google Scholar] [CrossRef]
- Zhou, R.; Tan, W. A generalized active disturbance rejection control approach for linear systems. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 248–255. [Google Scholar] [CrossRef]
- Fu, C.; Tan, W. Tuning of linear ADRC with known plant information. ISA Trans. 2016, 65, 384–393. [Google Scholar] [CrossRef]
- Hao, S.; Liu, T.; Geng, X.; Wang, Y. Anti-windup ADRC design for temperature control systems with output delay against asymmetric input constraint. ISA Trans. 2023, 2023, 519–530. [Google Scholar] [CrossRef]
- Liang, J.; Lu, Y.; Yin, G.; Fang, Z.; Zhuang, W.; Ren, Y.; Xu, L.; Li, Y. A distributed integrated control architecture of AFS and DYC based on MAS for distributed drive electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 5565–5577. [Google Scholar] [CrossRef]
- Yu, H.; Wang, J.; Xin, Z. Model predictive control for PMSM based on discrete space vector modulation with RLS parameter identification. Energies 2022, 15, 4041. [Google Scholar] [CrossRef]
- Patelski, R.; Pazderski, D. Novel Adaptive Extended State Observer for Dynamic Parameter Identification with Asymptotic Convergence. Energies 2022, 15, 3602. [Google Scholar] [CrossRef]
- Patelski, R.; Pazderski, D. Parameter Identifying Disturbance Rejection Control With Asymptotic Error Convergence. IEEE Robot. Autom. Lett. 2024, 9, 1035–1042. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, R.; Xing, H. An improved ADRC with RLS for torque control of permanent magnet starter. IFAC-PapersOnLine 2021, 54, 471–476. [Google Scholar] [CrossRef]
- Qi, X.; Sheng, C.; Guo, Y.; Su, T.; Wang, H. Parameter Identification of a Permanent Magnet Synchronous Motor Based on the Model Reference Adaptive System with Improved Active Disturbance Rejection Control Adaptive Law. Appl. Sci. 2023, 13, 12076. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the ACC, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar] [CrossRef]
- Yin, B.; Oruganti, R.; Panda, S.K.; Bhat, A.K. A simple single-input–single-output (SISO) model for a three-phase PWM rectifier. IEEE Trans. Power Electron. 2009, 24, 620–631. [Google Scholar] [CrossRef]
- Patelski, R.; Pazderski, D. Improving the Active Disturbance Rejection Controller Tracking Quality by the Input-Gain Underestimation for a Second-Order Plant. Electronics 2021, 10, 907. [Google Scholar] [CrossRef]
- Madonski, R.; Ramirez-Neria, M.; Stanković, M.; Shao, S.; Gao, Z.; Yang, J.; Li, S. On vibration suppression and trajectory tracking in largely uncertain torsional system: An error-based ADRC approach. Mech. Syst. Signal Process. 2019, 134, 106300. [Google Scholar] [CrossRef]
- Herbst, G. A simulative study on active disturbance rejection control (ADRC) as a control tool for practitioners. Electronics 2013, 2, 246–279. [Google Scholar] [CrossRef]
- Okyere, E.; Bousbaine, A.; Poyi, G.T.; Joseph, A.K.; Andrade, J.M. LQR controller design for quad-rotor helicopters. J. Eng. 2019, 2019, 4003–4007. [Google Scholar] [CrossRef]
- Curiel-Olivares, G.; Linares-Flores, J.; Guerrero-Castellanos, J.; Hernández-Méndez, A. Self-balancing based on active disturbance rejection controller for the two-in-wheeled electric vehicle, experimental results. Mechatronics 2021, 76, 102552. [Google Scholar] [CrossRef]
- Escobar, J.; Poznyak, A. Robust parametric identification for ARMAX models with non-Gaussian and coloured noise: A survey. Mathematics 2022, 10, 1291. [Google Scholar] [CrossRef]
- Ma, P.; Wang, L. Filtering-based recursive least squares estimation approaches for multivariate equation-error systems by using the multiinnovation theory. Int. J. Adapt. Control Signal Process. 2021, 35, 1898–1915. [Google Scholar] [CrossRef]
- Islam, S.A.U.; Bernstein, D.S. Recursive least squares for real-time implementation [lecture notes]. IEEE Control Syst. Mag. 2019, 39, 82–85. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, H.; Dai, M. The data-filtering based bias compensation recursive least squares identification for multi-input single-output systems with colored noises. J. Frankl. Inst. 2023, 360, 4753–4783. [Google Scholar] [CrossRef]
- Dong, S.; Yu, L.; Zhang, W.A.; Chen, B. Robust extended recursive least squares identification algorithm for Hammerstein systems with dynamic disturbances. Digit. Signal Process. 2020, 101, 102716. [Google Scholar] [CrossRef]
- González, R.A.; Rojas, C.R.; Pan, S.; Welsh, J.S. Consistent identification of continuous-time systems under multisine input signal excitation. Automatica 2021, 133, 109859. [Google Scholar] [CrossRef]
- Nowak, P.; Stebel, K.; Klopot, T.; Czeczot, J.; Fratczak, M.; Laszczyk, P. Flexible function block for industrial applications of active disturbance rejection controller. Arch. Control Sci. 2018, 28, 379–400. [Google Scholar] [CrossRef]
- Wei, Q.; Wu, Z.; Zhou, Y.; Ke, D.; Zhang, D. Active Disturbance-Rejection Controller (ADRC)-Based Torque Control for a Pneumatic Rotary Actuator with Positional Interference. Actuators 2024, 13, 66. [Google Scholar] [CrossRef]



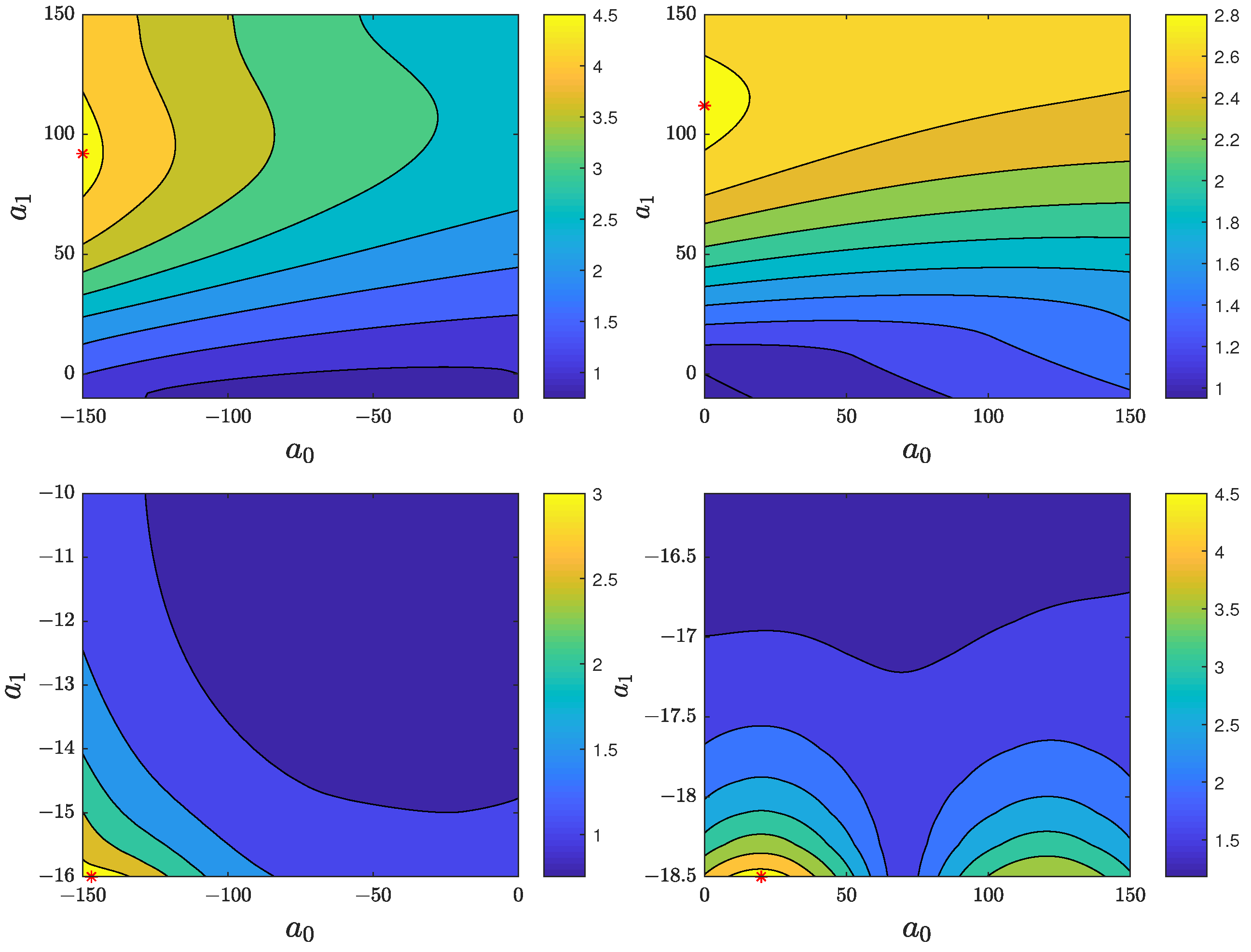



| Symbol | Unit | Value | Name |
|---|---|---|---|
| R | Ω | armature resistance | |
| L | H | armature inductance | |
| J | kg·m2 | shaft inertia | |
| c | Nm/rad | damping coefficient | |
| Vs/rad | torque constant |
| Approach | Parameter | ||||
|---|---|---|---|---|---|
| mfADRC | const | 0 | const | const | const |
| mbADRC | const | const | const | const | const |
| adaptADRC (our) | const | var * | var * | var | var |
| Approach | IAE | IAE | ||||
|---|---|---|---|---|---|---|
| The Whole Experiment | After Adaptation Process | |||||
| Rectangular reference signal | ||||||
| mfADRC | 291.2230 | 116.0525 | 874.1242 | 185.0328 | 67.8664 | 821.9041 |
| mbADRC | 207.7081 | 35.3479 | 893.9396 | 132.7821 | 17.9658 | 839.0451 |
| adaptADRC (our) | 282.869 | 111.1597 | 932.4270 | 130.0112 | 16.8768 | 837.1188 |
| Sinusoidal reference signal | ||||||
| mfADRC | 210.9012 | 210.9012 | 729.0449 | 102.5087 | 102.5087 | 521.9984 |
| mbADRC | 43.4767 | 43.4767 | 724.9985 | 19.1165 | 19.1165 | 519.6592 |
| adaptADRC (our) | 60.2311 | 60.2311 | 788.1805 | 13.4748 | 13.4748 | 520.1384 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michalski, J.; Mrotek, M.; Retinger, M.; Kozierski, P. Adaptive Active Disturbance Rejection Control with Recursive Parameter Identification. Electronics 2024, 13, 3114. https://doi.org/10.3390/electronics13163114
Michalski J, Mrotek M, Retinger M, Kozierski P. Adaptive Active Disturbance Rejection Control with Recursive Parameter Identification. Electronics. 2024; 13(16):3114. https://doi.org/10.3390/electronics13163114
Chicago/Turabian StyleMichalski, Jacek, Mikołaj Mrotek, Marek Retinger, and Piotr Kozierski. 2024. "Adaptive Active Disturbance Rejection Control with Recursive Parameter Identification" Electronics 13, no. 16: 3114. https://doi.org/10.3390/electronics13163114






