Abstract
To address the issues of blurred edges and contours, insufficient extraction of low-frequency information, and unclear texture details in ancient murals, which lead to decreased ornamental value and limited research significance of the murals, this paper proposes a novel ancient mural super-resolution reconstruction method, based on an attention mechanism and a multi-level residual network, termed AM-ESRGAN. This network builds a module for Multi-Scale Dense Feature Fusion (MDFF) to adaptively fuse features at different levels for more complete structural information regarding the image. The deep feature extraction module is improved with a new Sim-RRDB module, which expands capacity without increasing complexity. Additionally, a Simple Parameter-Free Attention Module for Convolutional Neural Networks (SimAM) is introduced to address the issue of insufficient feature extraction in the nonlinear mapping process of image super-resolution reconstruction. A new feature refinement module (DEABlock) is added to extract image feature information without changing the resolution, thereby avoiding excessive loss of image information and ensuring richer generated details. The experimental results indicate that the proposed method improves PSNR/dB by 3.4738 dB, SSIM by 0.2060, MSE by 123.8436, and NIQE by 0.1651 at a scale factor. At a scale factor, PSNR/dB improves by 4.0280 dB, SSIM increases by 3.38%, MSE decreases by 62.2746, and NIQE reduces by 0.1242. Compared to mainstream models, the objective evaluation metrics of the reconstructed images achieve the best results, and the reconstructed ancient mural images exhibit more detailed textures and clearer edges.
1. Introduction
Ancient murals are artistic creations painted on walls in ancient times, representing valuable cultural and aesthetic assets of high academic significance. However, due to human factors and natural environmental damage, surviving ancient murals often exhibit low resolution and diminished visual appeal [1]. With advancements in scientific technology, the application of digital image processing techniques for the restoration and enhancement of mural images has become increasingly prevalent. One significant approach involves super-resolution reconstruction of mural images to enhance and repair them, thereby improving the viewing experience.
Image super-resolution reconstruction (SR) technology is a key technique in computer vision for enhancing image resolution. It aims to recover high-resolution (HR) images from degraded low-resolution (LR) counterparts and has long been a fundamental and active research area in computer vision [2]. Super-resolution reconstruction technology not only enhances the image quality of old documents and artworks, aiding in the digital preservation and analysis of these valuable materials, but also has extensive applications in many other fields. In medical imaging, super-resolution reconstruction can improve the resolution of CT, MRI, and X-ray images, allowing doctors to view lesions more clearly thus increasing diagnostic accuracy. In remote sensing, it can enhance the resolution of satellite images, making terrain, buildings, and other features more detailed, which supports more accurate environmental monitoring and disaster assessment. In satellite image processing, super-resolution reconstruction can improve the detail of low-resolution images captured by satellites, providing clearer features and supporting more precise geographic information system applications. In the entertainment industry, such as in movies and games, super-resolution technology can enhance the quality of images and videos, making visual effects more detailed and realistic thus improving the user experience. Overall, super-resolution reconstruction technology has broad potential in improving image and video quality and enhancing visual details.
With the widespread use of high-resolution images in daily life, an increasing number of researchers are studying this area. Currently, there are the following three main methods for high-resolution image research: reconstruction-based, interpolation-based, and learning-based methods [3,4,5]. Due to significant performance degradation at large scaling factors in the first two methods, recent super-resolution (SR) methods predominantly adopt learning-based approaches, aiming to learn prior knowledge from low-resolution (LR) and high-resolution (HR) images. In deep learning-based methods, networks can automatically extract image features and learn the mapping between HR and LR images from large datasets, ultimately generating HR images with rich detail textures and clear visual perception [6]. Among these, Generative Adversarial Networks (GANs) have been widely used in super-resolution tasks in recent years because they can learn more about image information [7].
The combination of deep learning and SR has achieved good reconstruction results on natural images; however, in the reconstruction of ancient mural images, there are still issues such as the loss of a large amount of high-frequency information during feature extraction, resulting in unclear edges and blurred details in the reconstructed images [8]. Addressing these issues, this paper proposes an ancient mural super-resolution reconstruction method, AM-ESRGAN, based on attention mechanisms and multi-level residual networks. To tackle the problem of blurry edges in reconstructed ancient murals, this paper introduces the Multi-Scale Dense Feature Fusion (MDFF) module between the shallow and deep feature extraction modules. This module utilizes two sets of convolutional kernels to extract local and global information from low-resolution images, enriching the diversity of critical features in multiple receptive fields. This enhancement allows the network to extract richer features without increasing parameters, thereby improving reconstruction performance. To address the inadequate extraction of low-frequency information by the model, this paper improves the deep feature extraction module by adding additional residuals to expand network capacity without increasing complexity. Furthermore, it introduces a parameter-free attention mechanism to resolve issues with poor representation of low-frequency information caused by stacked RRDB blocks. To tackle the problem of blurry texture details in reconstructed mural images, this paper introduces the DEABlock, which combines attention mechanisms across channel, spatial, and pixel levels to prevent excessive loss of image information, thereby enriching the reconstruction with deeper texture information. The contributions of this paper can be summarized as follows:
- We propose an ancient mural super-resolution reconstruction method, AM-ESRGAN, based on attention mechanisms and multi-level residual networks to address the low resolution of ancient murals, effectively enhancing the network’s structural and detail information. Both subjective and objective comparisons demonstrate superior performance over other representative SR methods.
- We design the MDFF module. This module introduces a hierarchical fusion mechanism that combines feature information from different scales and layers. It can adaptively detect multi-scale detail information in ancient murals, achieving efficient multi-scale feature extraction.
- We improve on the deep feature extraction module with the SimAM-RRDB module. This module utilizes SimAM to rapidly extract feature information from shallow to deep layers, ensuring constant model parameterization while enhancing the efficiency of super-resolution reconstruction for ancient murals.
2. Related Works
In this section, we briefly reviewed relevant literature in the field of image super-resolution based on GAN networks, summarized mainstream feature fusion modules, common building blocks in deep learning, and finally introduced popular attention mechanisms and their categories.
2.1. GAN-Based Super-Resolution Reconstruction Methods
The GAN model consists of two components as follows: the generator and the discriminator. The outstanding performance of GANs in the field of image processing has attracted a large number of researchers, infusing new vitality and hope into the super-resolution reconstruction of mural images. Depending on the network architecture, GAN-based super-resolution reconstruction techniques can be categorized into two types—those based on residual networks and those based on transformers.
Methods based on residual network architectures address the gradient vanishing problem in deep networks through skip connections, making network training more stable. Dense residual blocks are introduced to further enhance feature extraction capabilities through nested residual blocks. The first application of this architecture was the SRGAN network proposed by Ledig et al. [9] Wang et al. [10] improved SRGAN’s components to develop the enhanced ESRGAN, resulting in more realistic and natural image textures. Rakotonirina et al. [11] proposed further improvements with the enhanced super-resolution generative adversarial network ESRGAN+, which features novel basic blocks and incorporates a feasible perceptual loss function and generator network based on RRDB. Wang et al. [12] introduced Real-ESRGAN, which uses purely synthetic data to train for real-world blind super-resolution, incorporating higher-order degradation modeling processes to better simulate complex real-world degradations.
Methods based on the transformer architectures handle image super-resolution tasks by using self-attention mechanisms and transformer structures to improve the modeling of long-range feature dependencies. The self-attention mechanism enables the transformer architectures to capture global features in images. The combination of multi-head self-attention mechanisms and hierarchical structures allows the model to process information in parallel across different feature subspaces, enhancing feature representation capabilities. The first application of this architecture was SwinIR, proposed by Liang et al. [13], which effectively handles information at different scales through hierarchical feature extraction methods, making image restoration tasks more accurate. Li et al. [14] proposed the Cross-Refinement Adaptive Feature Modulation Transformer, which integrates the advantages of convolutional and transformer structures. Zhang et al. [15] introduced a set of auxiliary adaptive token dictionaries to the Transformer, establishing the ATD-SR method.
The emergence of new technologies continues to drive the development of super-resolution reconstruction techniques, with applications in areas such as multimodal imaging, sonar digital twins, and video super-resolution. Cross-modal super-resolution allows for the generation of high-resolution images in one modality from low-resolution images in another modality. By combining images from different modalities, such as fusing low-resolution visible light images with low-resolution depth images, high-resolution fused images can be produced. Applied to sonar digital twins, this can significantly enhance the performance of sonar systems, increasing image clarity and detection accuracy. It can be used to improve the detection and identification of underwater targets, enhance the quality of ocean environment monitoring images, and provide clearer images in underwater rescue operations, aiding in the localization and identification of trapped individuals or objects. Video super-resolution technology can improve the accuracy of road and obstacle recognition in autonomous driving systems and enhance the real-time video quality of drones during flight. In the fields of film restoration and archival preservation, super-resolution technology can be utilized to restore and enhance the quality of old video footage.
2.2. Feature Fusion Module
Single feature learning methods cannot guarantee robustness across all complex scenes. Ancient mural images contain various features and details, and a single feature learning method may only capture a subset of these. Therefore, feature fusion methods have been proposed by scholars [16,17]. Feature fusion modules integrate feature information from different levels or sources within network models to enhance performance and generalization capability. Due to their effectiveness, this approach is highly popular in advanced computer vision tasks. In transfer learning, when there is a domain discrepancy between the source and target tasks, feature fusion modules can help align features from different domains, enabling the knowledge learned from the source task to be more effectively transferred to the target task, thus reducing the differences between the domains. In multi-modal learning tasks, feature fusion modules combine features from different data sources (such as images, text, audio, etc.) to utilize the complementary information from each modality, enhancing model performance. In object detection and segmentation, by fusing features from different scales and levels, the performance for detecting and segmenting objects of different sizes and complexities is improved.
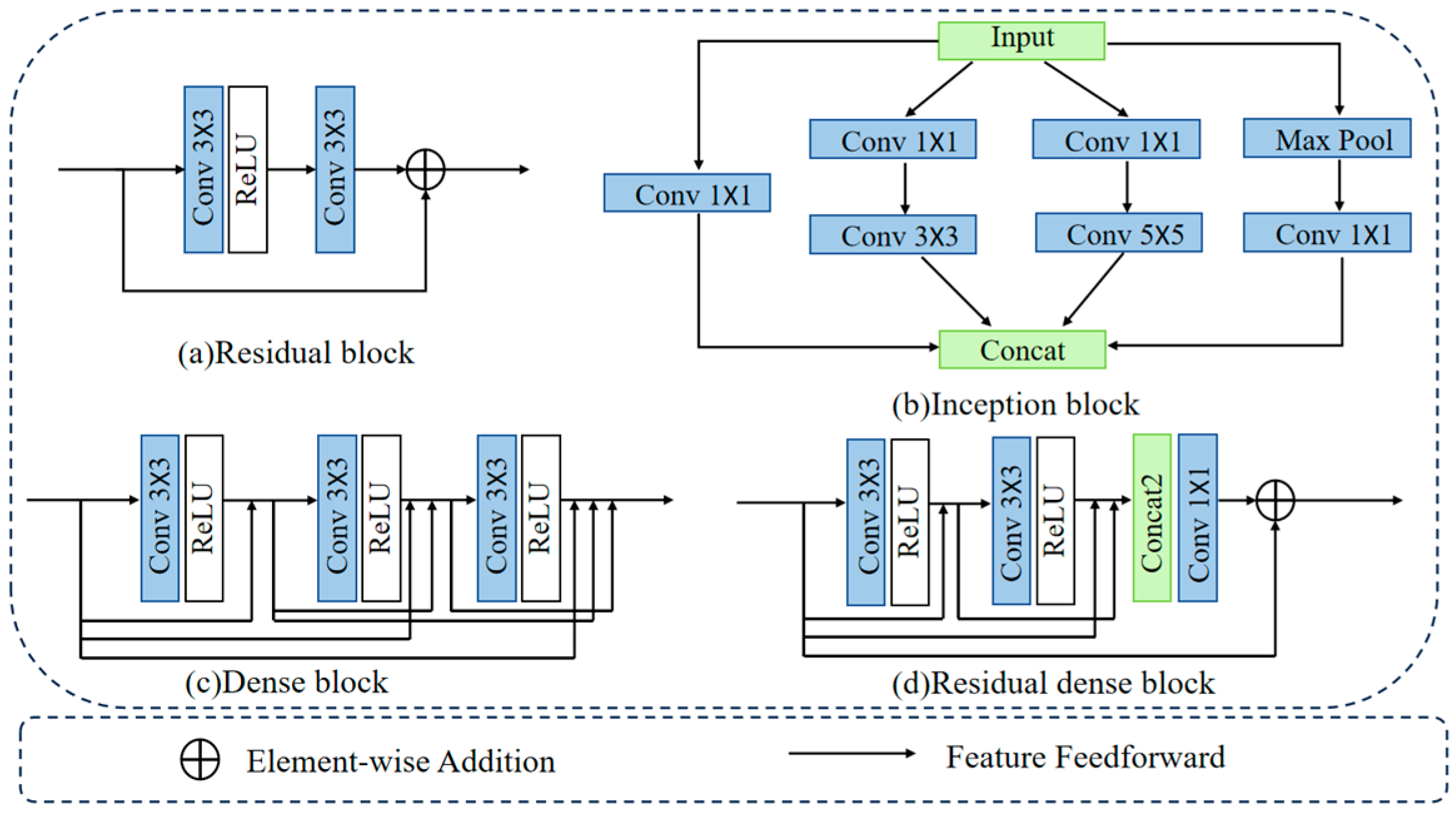
Mainstream feature fusion modules rely on common building blocks in deep learning, such as residual blocks, Inception blocks, dense blocks, and residual dense blocks, as shown in Figure 1. Residual blocks [18], a primary building block in ResNet architecture, introduce skip connections thus allowing networks to learn residual mappings, addressing the issues of gradient vanishing and exploding. Inception blocks, a key component of GoogLeNet, utilize parallel convolution paths with different filter sizes to capture multi-scale features. Dense blocks, a core component of DenseNet, connect all the preceding layer feature maps, promoting feature reuse and gradient flow while reducing parameter count to mitigate gradient vanishing. Residual dense blocks [19] combine the advantages of residual and dense connections, effectively extracting local and global features through hierarchical layers of densely connected structures, facilitating the integration of multi-scale feature information. Given these considerations, this paper incorporates the concept of residual dense blocks into MDFF.
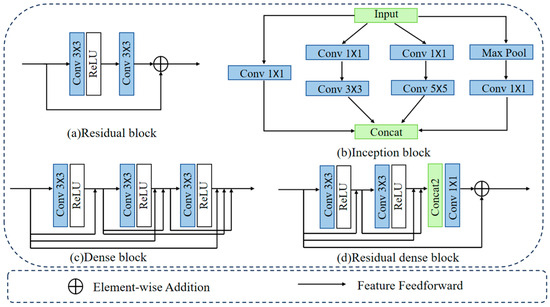
Figure 1.
Common Basic Building Blocks in Deep Learning. (a) represents Residual block, (b) represents Inception block, (c) represents Dense block, (d) represents Residual Dense block.
2.3. Attention Mechanism
Attention mechanism is a commonly used technique in computer science and machine learning that enhances the accuracy and effectiveness of models when processing sequential data [20]. It plays a crucial role in deep learning by allowing models to focus on key regions of images, thereby improving model performance. The core idea is to assign weights to each element in the input data to indicate its importance. These weights can be learned automatically during training, enabling the model to effectively attend to critical information in the input data. The inception of attention mechanisms dates back to Bahdanau et al.’s [21] proposal of Bahdanau Attention in 2015, which aligned the hidden states of the decoder with all the positions’ outputs of the encoder through linear combinations to generate context vectors, thereby enhancing sequence-to-sequence translation models. With the rapid development in computer vision, numerous new attention mechanisms have emerged. Existing attention methods can be categorized into the following six types: channel attention, spatial attention, temporal attention, channel-wise and spatial attention, spatial and temporal attention [22].
3. Methods
In this section, we first introduce the overall network architecture of the proposed method AM-ESRGAN, and then provide detailed descriptions of the key modules within the network, MDFF, the deep feature extraction module, and the DEABlock.
3.1. Network Details
The generator structure of the proposed AM-ESRGAN network in this paper is shown in Figure 2, capable of reconstructing at ×1, ×2, and ×4 magnification factors. The generator employs an end-to-end nonlinear mapping module as its core, consisting of the following six main components: shallow feature extraction, MDFF, deep feature extraction, DEABlock, upsampling module, and reconstruction module. The network first applies the inverse operation of pixel shuffling to reduce spatial dimensions and expand channel dimensions. Subsequently, the low-resolution ancient mural image is input into two 3 × 3 convolutional layers, which extract shallow features of the low-resolution image in a lower-dimensional space and reduce network parameters. The extracted features are then fed into the specially designed MDFF module, which refines the multi-scale feature extraction of mural images by combining multiple convolutional kernels of different sizes in parallel. This allows for maximal and effective extraction of multi-scale details from mural images. Subsequently, the features are passed to the deep feature extraction module, comprising 23 Sim-RRDB basic units. The sequential stacking of Sim-RRDB modules enhances the network’s capability to extract deep features. Under SimAM, meaningful feature enhancement and suppression of redundant feature information are achieved to capture more structural information from the images. Residual connections are used to efficiently fuse feature information between consecutive modules. The output is then passed to the DEABlock, which extracts features from spatial, channel, and pixel dimensions to comprehensively restore the image’s details. Finally, through the upsampling and reconstruction module, consisting of two convolutional layers and one upsampling layer, features extracted from the previous two stages are fused and sampled to reconstruct the image to its original size. This process results in an RGB three-channel color image . The entire network can be represented as follows:
Here, represents the mapping function of the network, where denotes the network parameters.

Figure 2.
Diagram of the generator network architecture of AM-ESRGAN.
Figure 2.
Diagram of the generator network architecture of AM-ESRGAN.

The discriminator employs a U-Net network with spectral normalization (SN), which focuses not only on the overall image but also on local features. SN helps alleviate training instability caused by complex datasets and intricate networks.
3.2. Multi-Scale Dense Feature Fusion Module
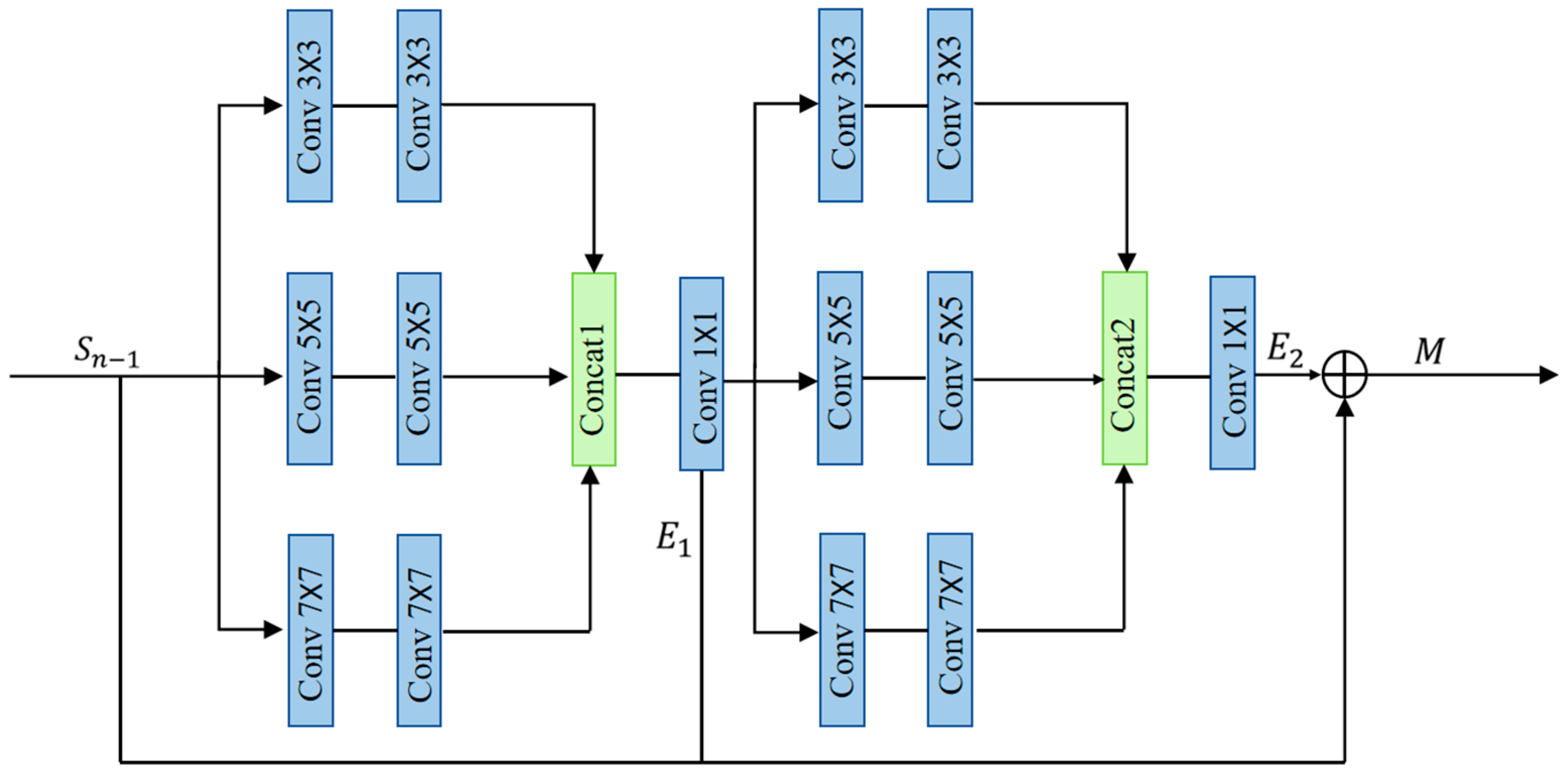
When reconstructing ancient murals using mainstream Super-Resolution (SR) algorithms, the network often struggles with accurately handling edge details, resulting in blurry edge contours, particularly where the original image edges are blurry or unclear. During the feature extraction process, the feature information is typically of different scales. However, most networks currently use a single convolution kernel for feature extraction, which often leads to the loss of structural information. To mitigate this issue, inspired by commonly used building blocks in deep learning, we propose using convolution kernels of different sizes through parallel paths for feature extraction and subsequent feature fusion. This approach aims to obtain more complete structural information of the image. In this paper, we construct a Multi-Scale Detail Fusion Framework (MDFF) between shallow and deep feature extraction modules, as illustrated in Figure 3, to enhance edge details.
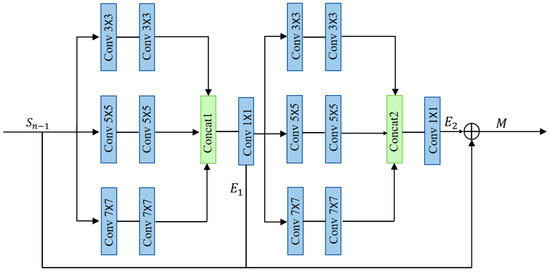
Figure 3.
Multi-Scale Dense Feature Fusion Module Structure Diagram.
This module introduces a hierarchical fusion mechanism. In the first stage, the multi-scale features are extracted and fused, while the second stage processes the fused features through multi-scale branches. Compared to traditional single-scale feature extraction and fusion, this approach more precisely integrates multi-scale information. By combining feature information from different scales and levels, it provides more comprehensive and richer data, enabling more accurate preservation and recovery of image details and edge features. As a result, the reconstructed image is more realistic and clearer, thereby enhancing reconstruction performance.
The module consists of two structurally identical multi-scale convolutional phases. In each phase, three convolution kernels of different scales (7 × 7, 5 × 5, 3 × 3) are arranged in parallel for feature extraction. Following each parallel path, an LReLU function is applied after the second convolution kernel. Overall, skip connections are utilized to merge the initial features with those extracted in the first and second phases, obtaining multi-scale feature information. The implementation of the first phase is shown in Equations (2)–(9).
Similarly, we can derive the implementation of the second phase as shown in Equations (10)–(18).
where A, B, and D denote the convolution operations of three branches with kernel sizes 7 × 7, 5 × 5, and 3 × 3, respectively. C represents the features concatenated with A, B, and D. W and b denote the weights and biases of neurons, respectively. E1 and E2 denote operations with 1 × 1 convolution. The superscripts and subscripts of symbols indicate the sizes of convolution kernels and their positions in the layers. M represents the output of multi-scale feature extraction.
denotes the LReLU function, as shown in Equation (19). The equations for and denote the cascade operation.
3.3. Deep Feature Extraction Module
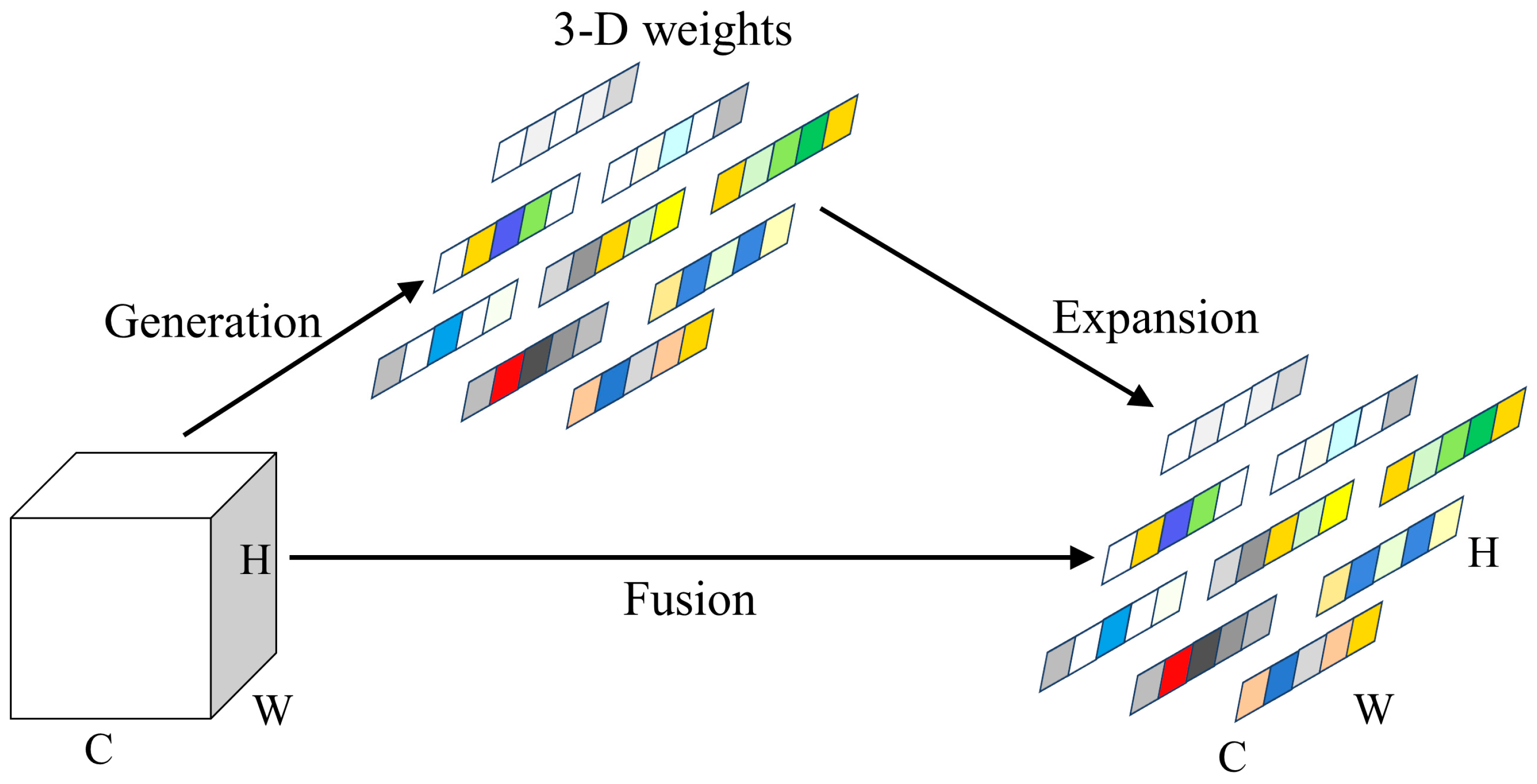
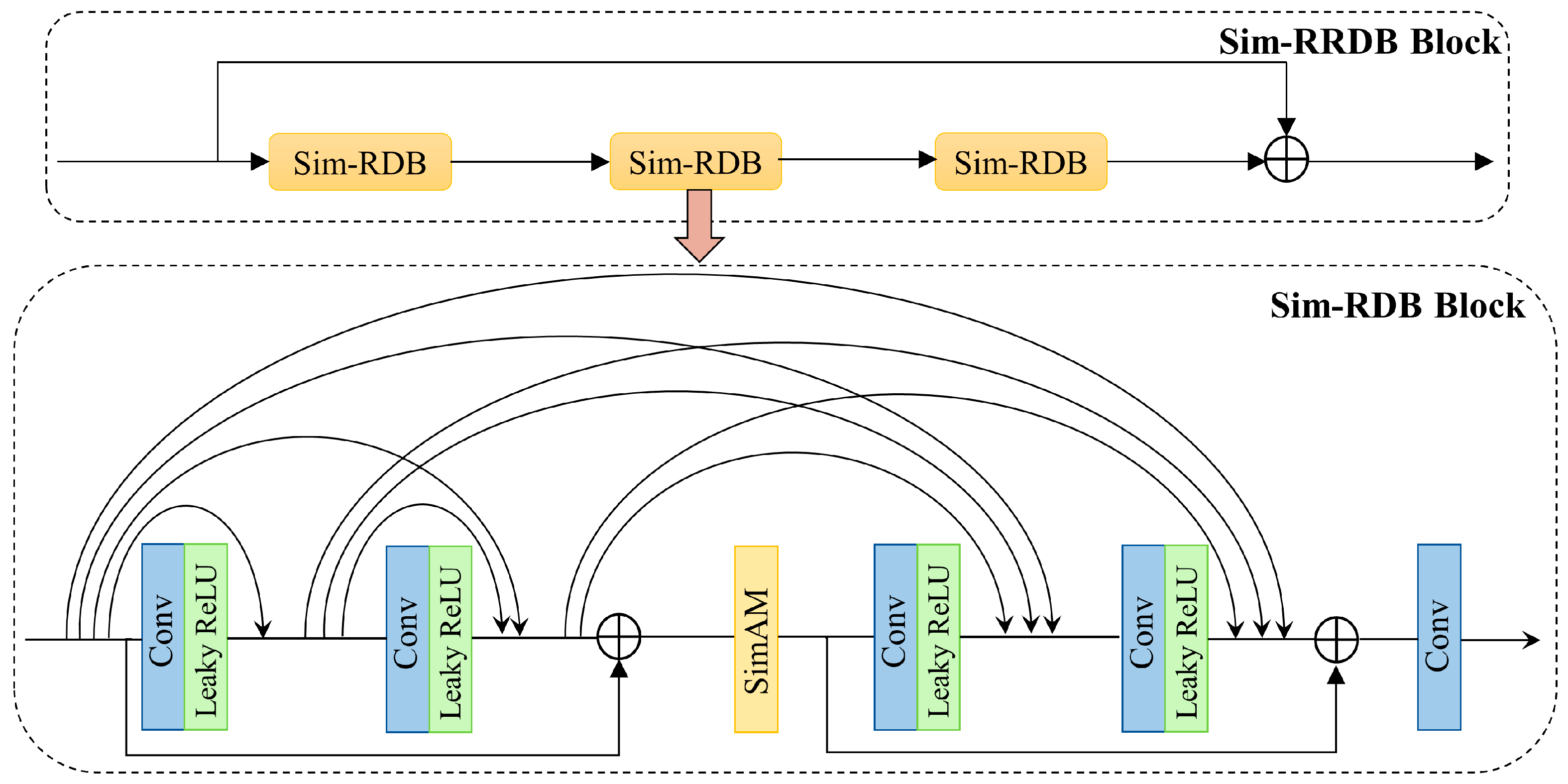
The basic module for deep feature extraction in the Real-ESRGAN model is the RDDB (Residual in Residual Dense Block), consisting of three RDBs (Residual Dense Blocks) each [12]. There is information exchange between each RRDB module, enhancing information and gradient flow through local and global feature fusion by connecting shallow and deep feature residuals. As the fundamental unit for deep feature extraction in the cascaded modules, RRDB employs deep residual dense connections to effectively utilize information from each convolutional layer to reconstruct image features. However, stacking RDDB blocks increases model complexity, leading to optimization challenges and suboptimal performance in extracting low-frequency information. To address these issues, this paper introduces SimAM into the RRDB module to enlarge the receptive field, improving the extraction of low-frequency information. The network structure is depicted in Figure 4.
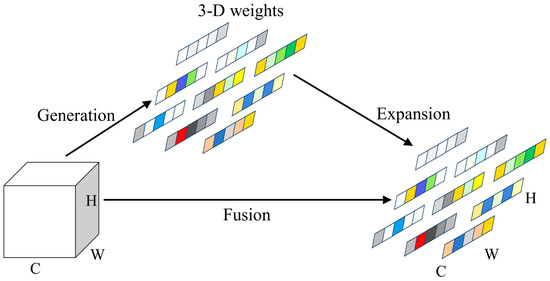
Figure 4.
Schematic Diagram of Parameter-Free Attention Mechanism.
SimAM is a lightweight, parameter-free convolutional neural network attention mechanism that derives 3D attention weights for feature maps at each layer, allowing convolutional neural networks to better focus on important parts of images without increasing the original network parameters [23]. In images, adjacent pixels typically exhibit strong similarity, while similarity decreases between pixels that are farther apart. SimAM leverages this property by computing attention weights based on the similarity between each pixel and its neighboring pixels in the feature map. The computation formula is as follows:
Here, is the attention weight for the -th pixel; is the normalization constant; is the set of neighboring pixels for the -th pixel; represents the similarity between the i-th pixel and the j-th pixel. SimAM employs a simple yet effective similarity measurement method, namely the Euclidean distance.
Following these improvements, an additional residual learning path was incorporated into the RRDB block to expand capacity without increasing complexity and alleviate gradient vanishing issues [24]. With these enhancements, the detailed structure of Sim-RRDB, integrating SimAM and the added residual path, is illustrated in Figure 5.
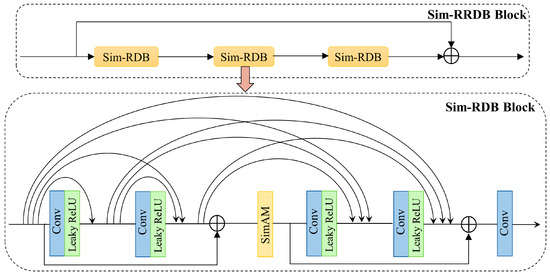
Figure 5.
Detailed structure of the core block Sim-RRDB in the deep feature extraction module.
3.4. Feature Refinement Module
When images are downscaled, some high-frequency details can be lost. Existing mainstream super-resolution (SR) algorithms still struggle to accurately restore some details and textures in the reconstructed images. To enhance the reconstruction results, it is crucial to establish a more precise mapping between high-resolution and low-resolution images. Therefore, this paper introduces the DEABlock, which further extracts features from the reconstructed images without altering their resolution. This step aims to prevent excessive loss of image information and comprehensively restore details [25]. By optimizing existing features, removing irrelevant information, emphasizing useful details, and enhancing feature representation, the network’s reconstruction performance is improved.
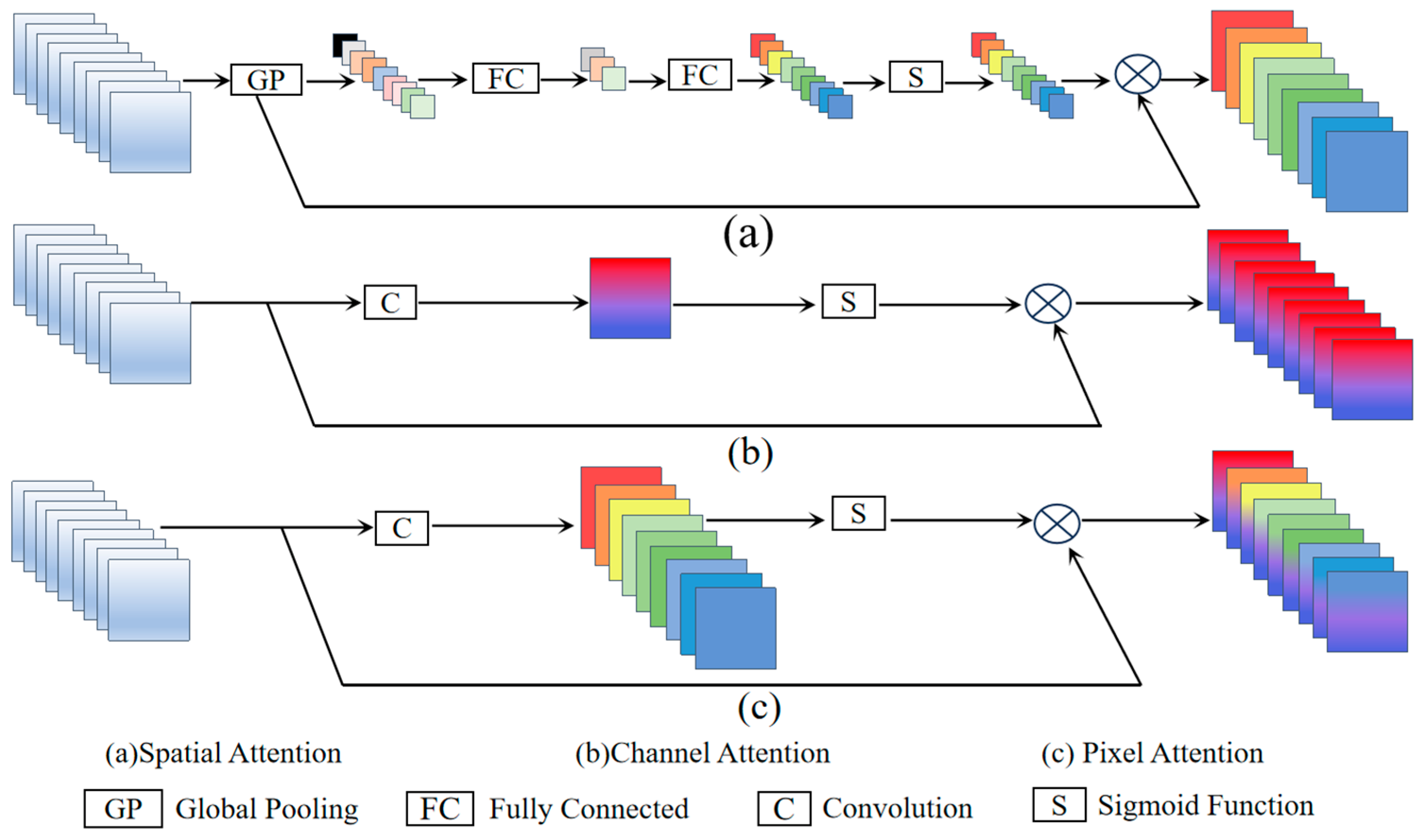
This paper draws inspiration from attention mechanisms and adopts a stacked attention block approach to learn features from ancient mural paintings for detail enhancement [26]. The DEABlock consists of the following three components: Spatial Attention (SA), Channel Attention (CA), and Pixel Attention (PA). SA computes two 2D spatial attention maps by performing average pooling and max pooling over the channels of the feature map. These attention maps are merged and processed through convolution and activation functions to generate the final spatial attention map, emphasizing important image regions [27]. CA generates a 1D channel attention vector by globally averaging the feature map, which is then processed through fully connected layers and activation functions to produce the final channel attention map, highlighting the importance of different channels [28]. PA concatenates the previously generated attention maps with the feature map and, through group convolution and activation functions, produces the final pixel attention map, further emphasizing the importance of different pixels within channels [29]. By stacking attention mechanisms, the network can better extract crucial features and suppress less important ones, focusing on information beneficial for super-resolution reconstruction. This approach enhances feature representation, improves model robustness, and is depicted in the schematic structure in Figure 6.
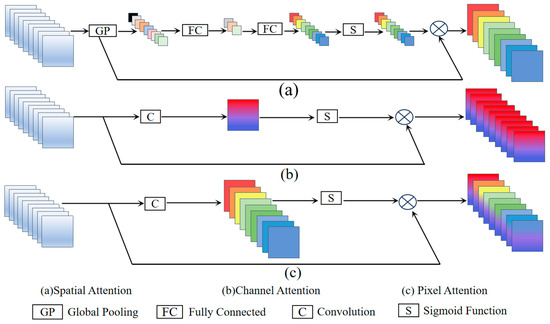
Figure 6.
Schematic Diagram of the Basic Composition Structure of the Feature Refinement Module.
4. Experiments
In this section, we will introduce the details of dataset construction for image restoration, environment configuration, model parameters, and evaluation metrics. We will also discuss ablation experiments to verify the effectiveness of each module improvement, determine the optimal number of Sim-RRDB blocks, and select the scaling factor β. Furthermore, we will compare with mainstream algorithms, conducting both quantitative and qualitative evaluations to demonstrate the superiority of the proposed model in this paper.
4.1. Basic Setup
Currently, there is no publicly available dataset for super-resolution reconstruction of ancient mural paintings. Therefore, this study collected 667 ancient mural paintings with resolutions higher than 1024 from online media, replicas by renowned artists, and published mural books. These images were randomly split into a training set of 567 images and a test set of 100 images. Employing multi-threading techniques, the original images were cropped and split into 28,017 sub-images sized at 480 × 480 pixels each, significantly enhancing the efficiency and speed of large-scale image data processing. A multi-scale resizing strategy was applied to downsample the high-resolution images to generate standard reference images at ×2 and ×4 scales. An illustration of the dataset composition is provided in Figure 7.

Figure 7.
Figure 7 Dataset Examples. It shows two sets of images (a,b), including the original images and images with magnification factors of 2 and 4.
The experiments use Structural Similarity Index (SSIM), Peak Signal-To-Noise Ratio (PSNR), Mean Squared Error (MSE), and Naturalness Image Quality Evaluator (NIQE) as evaluation metrics to assess the algorithm’s performance [30]. PSNR is used to measure the relative error between two images. SSIM is an index for measuring the similarity between two images. MSE is used to measure the mean squared error between two images. The formulas for each evaluation metric are shown sequentially in Equations (22)–(24).
PSNR measures the relative error between two images, with higher values indicating smaller relative errors and thus less image quality loss. SSIM ranges between −1 and 1, where 1 indicates identical images, 0 indicates no similarity, and −1 indicates complete dissimilarity. A smaller MSE indicates less difference between two images, indicating a greater similarity. Conversely, a larger MSE indicates a greater difference between the images.
NIQE (Naturalness Image Quality Evaluator) aims to measure the naturalness and realism of images. It is based on “quality-aware” features and fits them into an MVG model [31]. The quality of distorted images is represented by the distance between the NSS feature model and the MVG that extracts features from the distorted images, as shown in Equation (25):
where denote the mean vectors and covariance matrices of the natural MVG model and the distorted image MVG model, respectively.
4.2. Training Details
This experiment is implemented on the NVIDIA GeForce RTX 4090 graphics card using the PyTorch framework, with a worker thread count of eight and a batch size of four. The training process of the experiment is divided into two stages. First, a PSNR-oriented model is trained using L1 loss, with an initial learning rate set to . The learning rate is halved every iterations, and the total training is performed for 1,000,000 iterations. The pre-trained PSNR-oriented model is used to initialize the generator. Combined with L1 loss, perceptual loss, and GAN loss, with weights of {1, 1, 0.1}, the final model AM-ESRGAN is trained. The learning rate for the second stage is set to , and it is halved at [50 k, 100 k, 200 k, 300 k] iterations, with a total of 400,000 iterations. Both stages use the Adam optimizer, alternately updating the generator and discriminator networks until the model converges [15]. The loss function for the generation part of the model is given by Equation (26) as follows:
In the equation, is 0.1, is 1. represents the perceptual loss function, represents the adversarial loss function, represents the L1 loss. The optimization of the discriminator model is divided into two steps, as shown in Equations (27) and (28):
- (1)
- Optimizing the model to discern real capabilities. Construct a vector filled entirely with 1. Calculate and of the BECLoss:
- (2)
- Optimizing the model to discern fake capabilities. Construct a vector filled entirely with 0.
Calculate and of the BECLoss:
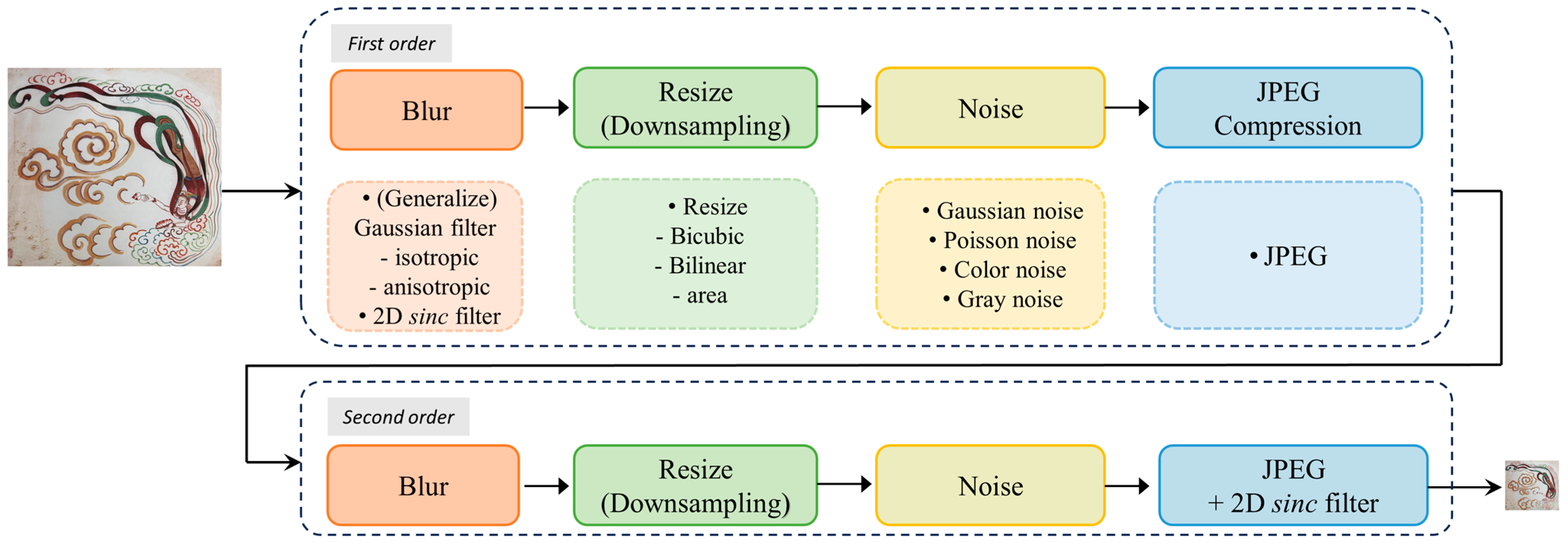
The model utilizes a second-order degradation process to model more realistic degradation, where each degradation process employs classic degradation models—blur, scaling, noise, and JPEG compression [12]. The entire degradation model iterates twice through these four degradation processes, as depicted in Figure 8.
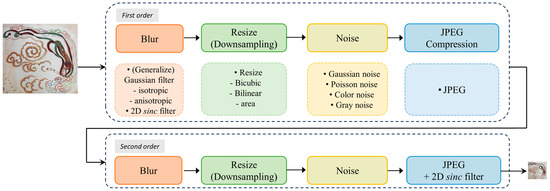
Figure 8.
Example of second-order degradation.
4.3. Ablation Study
To better understand the proposed method, this paper conducts ablation studies from the perspectives of the impact of each component, Sim-RRDB base number, and scaling factor β.
- (1)
- Study on the impact of each component: This experiment compared the baseline model with various improvements and additional structures through ablation studies. Comparisons were made under scaling factors of four and two, incrementally adding each module. The values of PSNR and SSIM improved, while MSE and NIQE values decreased. In Table 1 for a scaling factor of four, our model showed the following improvements over the baseline model: PSNR increased by 3.4738, SSIM increased by 0.206, MSE decreased by 123.8437, and NIQE decreased by 0.1651. In Table 2, for a scaling factor of two, our model exhibited the following improvements over the baseline model: PSNR increased by 4.0280, SSIM increased by 3.38%, MSE decreased by 62.2746, and NIQE decreased by 0.1242. The proposed model in this paper demonstrated significant numerical improvements across metrics.
 Table 1. Comparison results of different modules on the test dataset with a scaling factor of 4.
Table 1. Comparison results of different modules on the test dataset with a scaling factor of 4. Table 2. Comparison results of different modules on the test dataset with a scaling factor of 2.
Table 2. Comparison results of different modules on the test dataset with a scaling factor of 2.
- (2)
- Study on Sim-RRDB blocks: Experimental investigation into the impact of different numbers of Sim-RRDB modules on the network. Under a scaling factor of four, as the number of Sim-RRDB blocks increased from 20 to 23, the performance of the proposed AM-ESRGAN network improved. However, when the number of Sim-RRDB blocks exceeded 23, there was a tendency for the metrics to decline. The increase in network depth led to feature redundancy during the reconstruction process, resulting in overfitting of the AM-ESRGAN network and hence performance degradation. Despite minimal change in network parameter count with increasing Sim-RRDB blocks, this paper determined 23 as the optimal number for Sim-RRDB modules in the deep feature extraction process, achieving better reconstruction of ancient mural paintings. Specific metrics are detailed in Table 3.
 Table 3. Measurement of the importance of Sim-RRDB block count.
Table 3. Measurement of the importance of Sim-RRDB block count.
- (3)
- Study on scaling factor β: Experimental investigation into the impact of different scaling factor sizes on the network. According to Table 4, under a scaling factor of four, different scaling factor β have a significant impact on the final network metrics. There is a noticeable increase in performance from 0.1 to 0.2, followed by a significant decrease in metrics within the range of 0.2 to 1. The worst and best results differ by 15.4642 dB in PSNR and 0.6191 in SSIM. The scaling parameter β helps to mitigate gradient vanishing or exploding issues, thereby stabilizing the training process and allowing the model to update parameters more effectively. Therefore, this paper selects a scaling factor β value of 0.2, which effectively controls the scale of feature values and achieves optimal performance of the network.
 Table 4. Measurement of the importance of scaling factor β.
Table 4. Measurement of the importance of scaling factor β.
4.4. Comparison with Prior Work
This paper conducts quantitative and qualitative comparisons with the following series of advanced and representative super-resolution methods: FLKSR [32], ATD-SR [15], SPAN [33], CRAFT [14], SRFormer [34], HAT [35], VapSR [36], CAT [37], SwinFIR [38], and ESRGAN [10].
Quantitative comparison. Table 5 and Table 6 show the values of different objective evaluation metrics when the magnification factors are four and two, respectively. The numbers highlighted in bold represent the optimal values obtained from the reconstruction experiments of the 12 algorithms under the same conditions. Observing the data within the tables, it can be seen that the proposed algorithm demonstrates good performance in reconstructing mural images at different scaling factors. Compared to the worst baseline model, at a magnification factor of four, the proposed method’s PSNR/dB value improves by an average of 3.4738, the SSIM value increases by an average of 0.2060, the MSE decreases by an average of 123.8436, and the NIQE value reduces by an average of 0.1651. At a magnification factor of two, the proposed method’s PSNR/dB value improves by an average of 4.0280, the SSIM value increases by an average of 0.0338, the MSE decreases by an average of 62.2746, and the NIQE value reduces by an average of 0.1242. In summary, it can be concluded that our model outperforms other models in terms of performance.

Table 5.
Quantitative comparison of objective evaluation metrics for different algorithms at a scaling factor of 4 on the test dataset.

Table 6.
Quantitative comparison of objective evaluation metrics for different algorithms at a scaling factor of 2 on the test dataset.
Qualitative comparison. To visually validate the reconstruction performance of the AM-ESRGAN network, images reconstructed by different algorithms were compared visually. Two images with typical features were selected from the test set for super-resolution reconstruction experiments and comparison. Each image was further divided into ×2 and ×4 magnifications. The reconstruction performance of the proposed algorithm was validated based on the results of these two sets of simulation experiments, as shown in Figure 9 and Figure 10.

Figure 9.
Shows the visualization results of mural image reconstruction from the test dataset with ID 0, the red boxes highlight the areas where there are significant differences in image reconstruction results produced by the aforementioned algorithm. The first two rows display the reconstructed images with a magnification factor of 4, while the last two rows show the reconstructed images with a magnification factor of 2. The images reconstructed using our method have clearer edges and do not exhibit structural distortions in the hand and ornament sections. Compared to the baseline methods, our approach reveals more texture details. Both PSNR/dB and SSIM values are the optimal values.

Figure 10.
Shows the visualization results of mural image reconstruction from the test dataset with ID 29, the red boxes highlight the areas where there are significant differences in image reconstruction results produced by the aforementioned algorithm. The first two rows display the reconstructed images with a magnification factor of 4, while the last two rows show the reconstructed images with a magnification factor of 2. The images reconstructed using our method exhibit high texture detail restoration and good color preservation, without any artifacts. Both PSNR/dB and SSIM values are the optimal values.
Other SR methods can infer some texture details during the reconstruction process, but due to significant differences in the details and degradation patterns of ancient murals, these methods often suffer from insufficient feature utilization, resulting in blurry reconstructed images. Additionally, excessive smoothing weakens the texture and details of the image, while excessive sharpening makes the image appear unnatural. Over-reliance on high-frequency information can also lead to artifacts [39,40,41], resulting in poor reconstruction quality. In contrast, the method proposed in this paper achieves clearer reconstruction of details and structures. Compared to baseline models, our AM-ESRGAN network shows an improved performance in various objective evaluation metrics. With a scaling factor of four, PSNR/dB for the first set of images increased by 4.2800 and SSIM increased by 0.0764; for the second set, PSNR/dB increased by 2.6400 and SSIM increased by 0.0787. With a scaling factor of two, PSNR/dB for the first set increased by 6.4000 and SSIM increased by 0.0608; for the second set, PSNR/dB increased by 5.8700 and SSIM increased by 0.0965. The results of the remaining 10 models showed blurry or low-quality characteristics, while our AM-ESRGAN network accurately generated detail and structural information, presenting a more natural visual effect. Qualitative comparisons indicate that our AM-ESRGAN outperforms other methods in recovering high-resolution images.
5. Conclusions
This paper proposes an ancient mural super-resolution reconstruction method, AM-ESRGAN, based on attention mechanisms and a multi-level residual network. The method consists of the following six components: shallow feature extraction, MDFF, deep feature extraction, DEABlock, upsampling module, and reconstruction module. MDFF integrates multi-scale features extracted by different convolutional kernels to capture rich structural information in mural images. Sim-AM is then introduced, and an additional residual learning level is added to enhance the basic RRDB blocks in the deep feature extraction module, addressing the issue of poor performance in low-frequency image information. DEABlock, constructed with stacked channel, spatial, and pixel attention mechanisms, enhances high-frequency details in reconstructed mural images. Experimental results demonstrate that the proposed method outperforms other methods across various evaluation metrics, yielding clearer and more detailed reconstructed image structures. This proves the method’s ability to achieve a balanced improvement between image quality and objective evaluation metrics. Due to the large number of model parameters caused by stacking Sim-RRDB blocks, future research will focus on model optimization. This can be achieved by employing lightweight convolutions such as depth-wise separable convolutions, group convolutions, and phantom convolutions, as well as reducing model parameters through network pruning or knowledge distillation. Additionally, collecting more images of wall paintings in different styles will help improve the model’s generalization ability.
Author Contributions
Conceptualization, C.X.; methodology, C.X.; software, C.X.; validation, C.X. and Y.C.; formal analysis, C.S.; investigation, C.S. and R.L.; data curation, C.X. and L.Y.; writing—review and editing, C.X.; visualization, C.X.; supervision, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request due to restrictions (e.g., privacy, legal or ethical reasons). The data provided in this study can be made available upon request from the corresponding author, as the self-constructed ancient mural dataset may involve sensitive ethnic, religious, or cultural content.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cao, J.; Yan, M.; Jia, Y.; Tian, X.; Zhang, Z. Application of a Modified Inception-v3 Model in the Dynasty-Based Classification of Ancient Murals. EURASIP J. Adv. Signal Process. 2021, 2021, 49. [Google Scholar] [CrossRef]
- Lepcha, D.C.; Goyal, B.; Dogra, A.; Goyal, V. Image super-resolution: A comprehensive review, recent trends, challenges and applications. Inf. Fusion 2023, 91, 230–260. [Google Scholar] [CrossRef]
- Liu, H.; Li, Z.; Shang, F.; Liu, Y.; Wan, L.; Feng, W.; Timofte, R. Arbitrary-Scale Super-Resolution via Deep Learning: A Comprehensive Survey. Inf. Fusion 2024, 102, 102015. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, S.; Hu, Y.; Xie, C. Single-Image Super-Resolution Challenges: A Brief Review. Electronics 2023, 12, 2975. [Google Scholar] [CrossRef]
- Moser, B.B.; Raue, F.; Frolov, S.; Palacio, S.; Hees, J.; Dengel, A. Hitchhiker’s Guide to Super-Resolution: Introduction and Recent Advances. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9862–9882. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Pei, Z.; Li, W.; Gao, G.; Wang, L.; Wang, Y.; Zeng, T. A Systematic Survey of Deep Learning-Based Single-Image Super-Resolution. ACM Comput. Surv. 2024, 56, 249. [Google Scholar] [CrossRef]
- Wang, X.; Sun, L.; Chehri, A.; Song, Y. A Review of GAN-Based Super-Resolution Reconstruction for Optical Remote Sensing Images. Remote Sens. 2023, 15, 5062. [Google Scholar] [CrossRef]
- Cao, J.; Hu, X.; Cui, H.; Liang, Y.; Chen, Z. A Generative Adversarial Network Model Fused with a Self-Attention Mechanism for the Super-Resolution Reconstruction of Ancient Murals. IET Image Process. 2023, 17, 2336–2349. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Computer Vision—ECCV 2018 Workshops; Leal-Taixé, L., Roth, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 11133, pp. 63–79. ISBN 978-3-030-11020-8. [Google Scholar]
- Rakotonirina, N.C.; Rasoanaivo, A. ESRGAN+: Further Improving Enhanced Super-Resolution Generative Adversarial Network. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3637–3641. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Li, A.; Zhang, L.; Liu, Y.; Zhu, C. Feature Modulation Transformer: Cross-Refinement of Global Representation via High-Frequency Prior for Image Super-Resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Paris, France, 2–6 October 2023; pp. 12514–12524. [Google Scholar]
- Zhang, L.; Li, Y.; Zhou, X.; Zhao, X.; Gu, S. Transcending the Limit of Local Window: Advanced Super-Resolution Transformer with Adaptive Token Dictionary. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 2856–2865. [Google Scholar]
- Song, H.; Xu, W.; Liu, D.; Liu, B.; Liu, Q.; Metaxas, D.N. Multi-Stage Feature Fusion Network for Video Super-Resolution. IEEE Trans. Image Process. 2021, 30, 2923–2934. [Google Scholar] [CrossRef] [PubMed]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More Diverse Means Better: Multimodal Deep Learning Meets Remote-Sensing Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4340–4354. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Lu, S.; Liu, M.; Yin, L.; Yin, Z.; Liu, X.; Zheng, W. The Multi-Modal Fusion in Visual Question Answering: A Review of Attention Mechanisms. PeerJ Comput. Sci. 2023, 9, e1400. [Google Scholar] [CrossRef] [PubMed]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2016, arXiv:1409.0473. [Google Scholar] [CrossRef]
- Hassanin, M.; Anwar, S.; Radwan, I.; Khan, F.S.; Mian, A. Visual Attention Methods in Deep Learning: An in-Depth Survey. Inf. Fusion 2024, 108, 102417. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, R.-Y.; Li, L.; Xie, X. SimAM: A Simple, Parameter-Free Attention Module for Convolutional Neural Networks. In Proceedings of the 38th International Conference on Machine Learning, ICML 2021, Virtual Event, 18–24 July 2021; pp. 11863–11874. [Google Scholar]
- Vo, K.D.; Bui, L.T. StarSRGAN: Improving Real-World Blind Super-Resolution. arXiv 2023, arXiv:2307.161692023. [Google Scholar]
- Chen, Z.; He, Z.; Lu, Z.-M. DEA-Net: Single Image Dehazing Based on Detail-Enhanced Convolution and Content-Guided Attention. IEEE Trans. Image Process. 2024, 33, 1002–1015. Available online: https://ieeexplore.ieee.org/abstract/document/10411857 (accessed on 5 July 2024). [CrossRef] [PubMed]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 294–310. [Google Scholar]
- Israel, M.M.; Jolicoeur, P.; Cohen, A. Spatial Attention across Perception and Action. Psychol. Res. 2018, 82, 255–271. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Zhao, H.; Kong, X.; He, J.; Qiao, Y.; Dong, C. Efficient Image Super-Resolution Using Pixel Attention. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Yue, L.; Shen, H.; Li, J.; Yuan, Q.; Zhang, H.; Zhang, L. Image super-resolution: The techniques, applications, and future. Signal Process. 2016, 128, 389–408. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Lee, D.; Yun, S.; Ro, Y. Partial Large Kernel CNNs for Efficient Super-Resolution. arXiv 2024, arXiv:2404.11848. [Google Scholar]
- Wan, C.; Yu, H.; Li, Z.; Chen, Y.; Zou, Y.; Liu, Y.; Yin, X.; Zuo, K. Swift Parameter-free Attention Network for Efficient Super-Resolution. arXiv 2023, arXiv:2311.112770. [Google Scholar]
- Zhou, Y.; Li, Z.; Guo, C.-L.; Bai, S.; Cheng, M.-M.; Hou, Q. SRFormer: Permuted Self-Attention for Single Image Super-Resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 12780–12791. [Google Scholar]
- Chen, X.; Wang, X.; Zhou, J.; Qiao, Y.; Dong, C. Activating More Pixels in Image Super-Resolution Transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 22367–22377. [Google Scholar]
- Zhou, L.; Cai, H.; Gu, J.; Li, Z.; Liu, Y.; Chen, X.; Qiao, Y.; Dong, C. Efficient Image Super-Resolution Using Vast-Receptive-Field Attention. In Proceedings of the Computer Vision—ECCV 2022 Workshops, Tel Aviv, Israel, 23–27 October 2022; Karlinsky, L., Michaeli, T., Nishino, K., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 256–272. [Google Scholar]
- Chen, Z.; Zhang, Y.; Gu, J.; Zhang, Y.; Kong, L.; Yuan, X. Cross Aggregation Transformer for Image Restoration. arXiv 2022, arXiv:2211.13654. [Google Scholar]
- Zhang, D.; Huang, F.; Liu, S.; Wang, X.; Jin, Z. SwinFIR: Revisiting the SwinIR with Fast Fourier Convolution and Improved Training for Image Super-Resolutio. arXiv 2022, arXiv:2208.11247. [Google Scholar]
- Chu, S.-C.; Dou, Z.-C.; Pan, J.-S.; Weng, S.; Li, J. HMANet: Hybrid Multi-Axis Aggregation Network for Image Super-Resolution. arXiv 2024, arXiv:2405.05001. [Google Scholar]
- Gao, H.; Dang, D. Learning Accurate and Enriched Features for Stereo Image Super-Resolution. arXiv 2024, arXiv:2406.16001. [Google Scholar]
- Chen, Q.; Shao, Q. Single image super-resolution based on trainable feature matching attention network. Pattern Recognit. 2024, 149, 110289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).