Research on DC Electric Shock Protection Method Based on Sliding Curvature Accumulation Quantity
Abstract
:1. Introduction
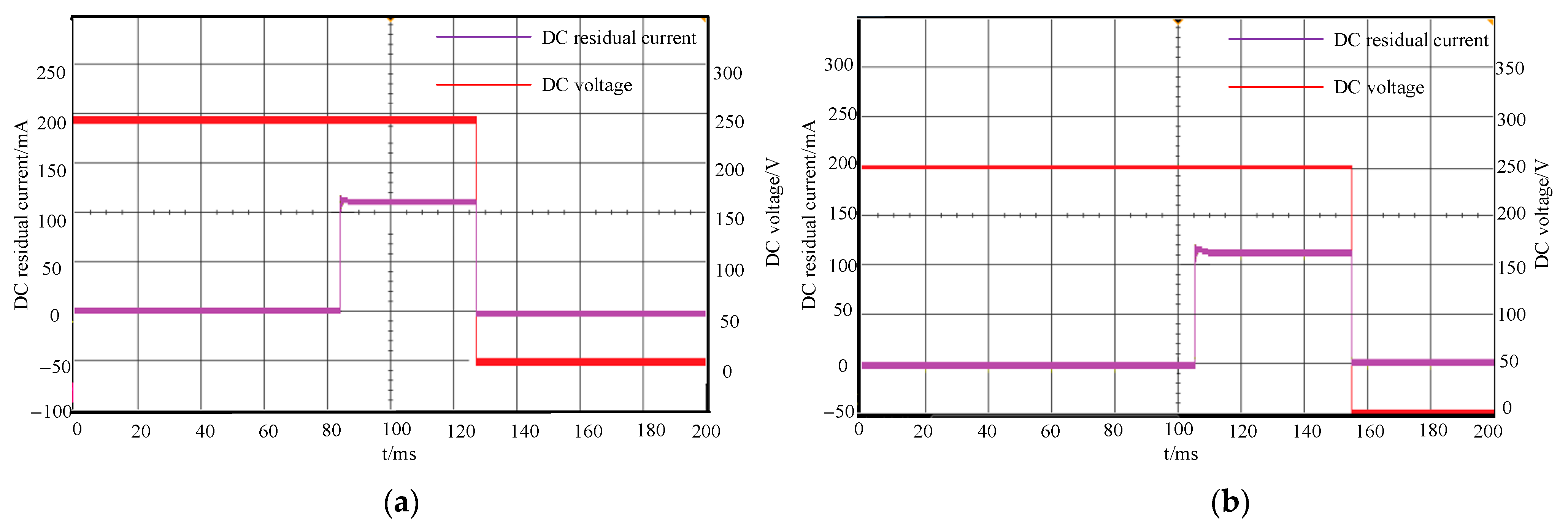
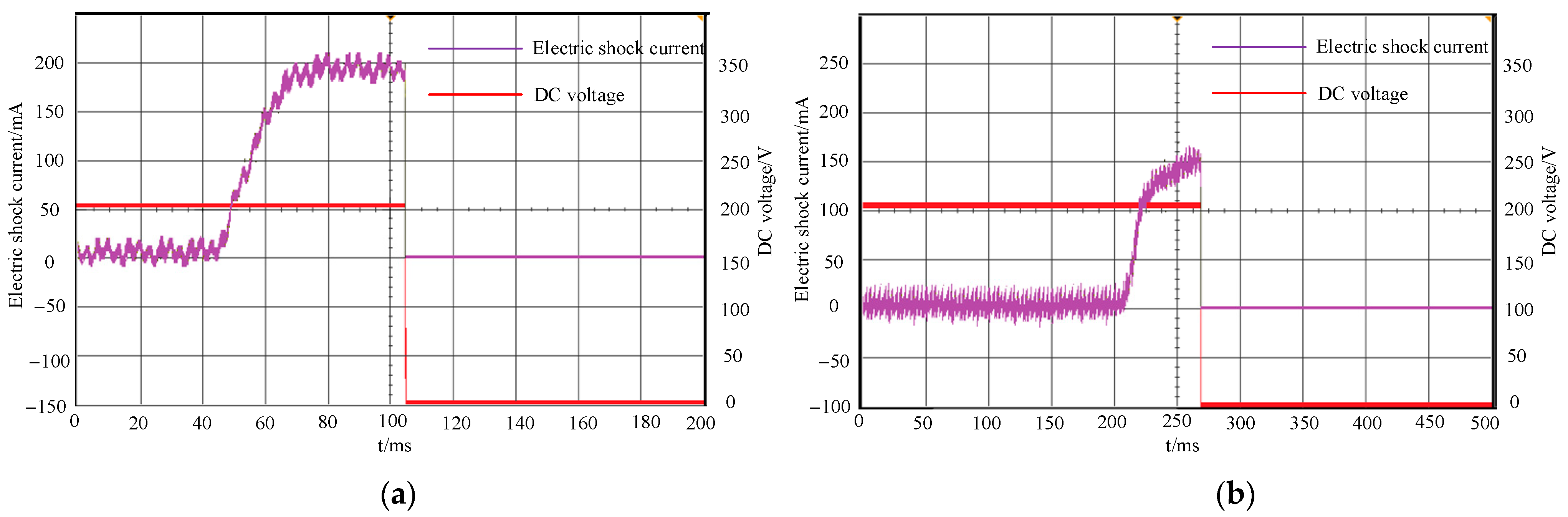
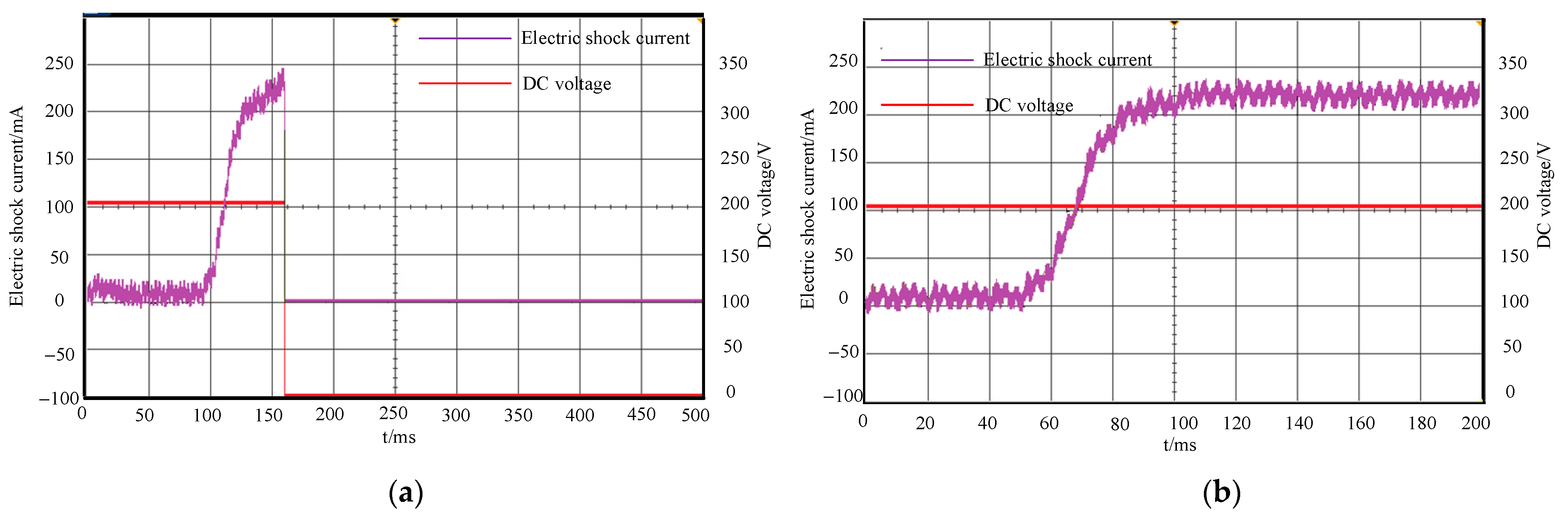
2. LVDC Electric Shock Simulation Test
3. Analysis of the Feature Quantities of DC Electric Shock Currents
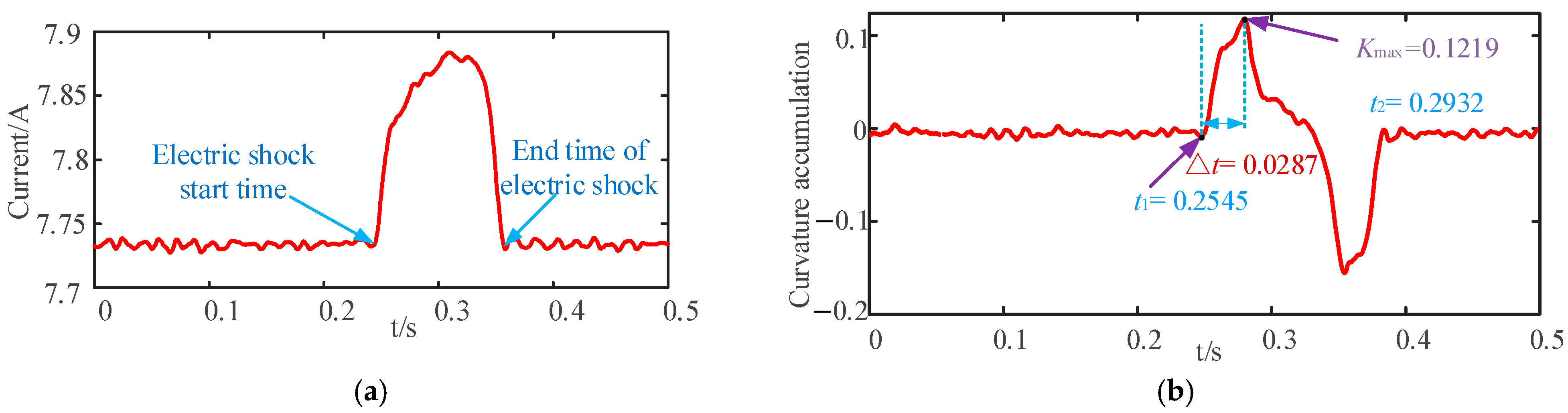
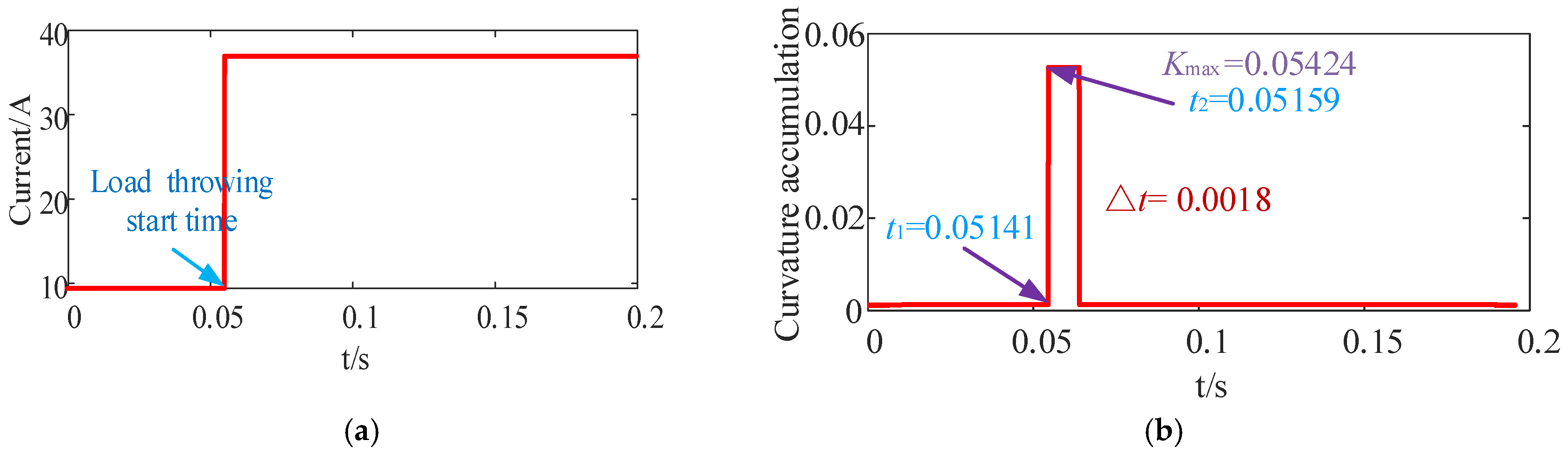
3.1. Characterization of Sliding Curvature Accumulation and Peak Rise Time
- (1)
- Data preprocessing. There are clutter interference signals in the sampled DC current signal Ig, the wavelet soft-threshold filtering algorithm [25] is the wavelet detail coefficients on each scale to establish the corresponding threshold, according to the coefficients exceed the threshold with or without it to take different processing methods, applicable to the filtering of DC current signals, the filtering algorithm is:where H is the wavelet decomposition detail coefficients, Gs is the threshold value, the scale factor α is: , sgn() is the sign function.
- (2)
- Determine the sliding window size. The window size should be determined according to the sampling frequency of the DC current data and the frequency of current change, and select the appropriate window length L. In this paper, the sliding window size is 100.
- (3)
- Calculate the curvature of the current within the sliding window. In the DC current signal Ih(t) to build L points Ih(t), Ih(t + Δt), …, I[t + (L − 1)Δt] in the sliding window current data, according to the Formula (5) to calculate the curvature of the current, where y′ and y″ can be expressed by the following equation:
- (4)
- The window is moved, and the window is moved forward by a distance of one step, and then the calculation of the previous step is repeated to calculate the amount of curvature accumulation within this window.
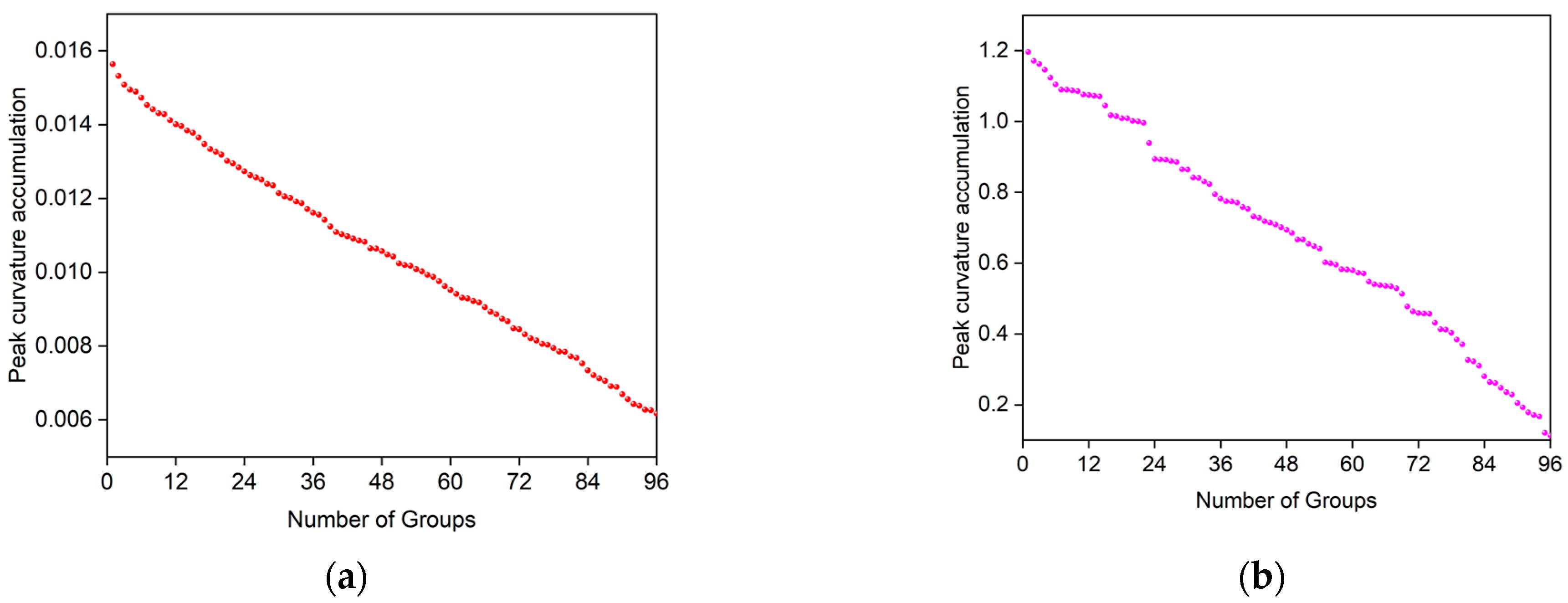
3.2. Analysis of the Effects of Various Factors on the Features of DC Electric Shock
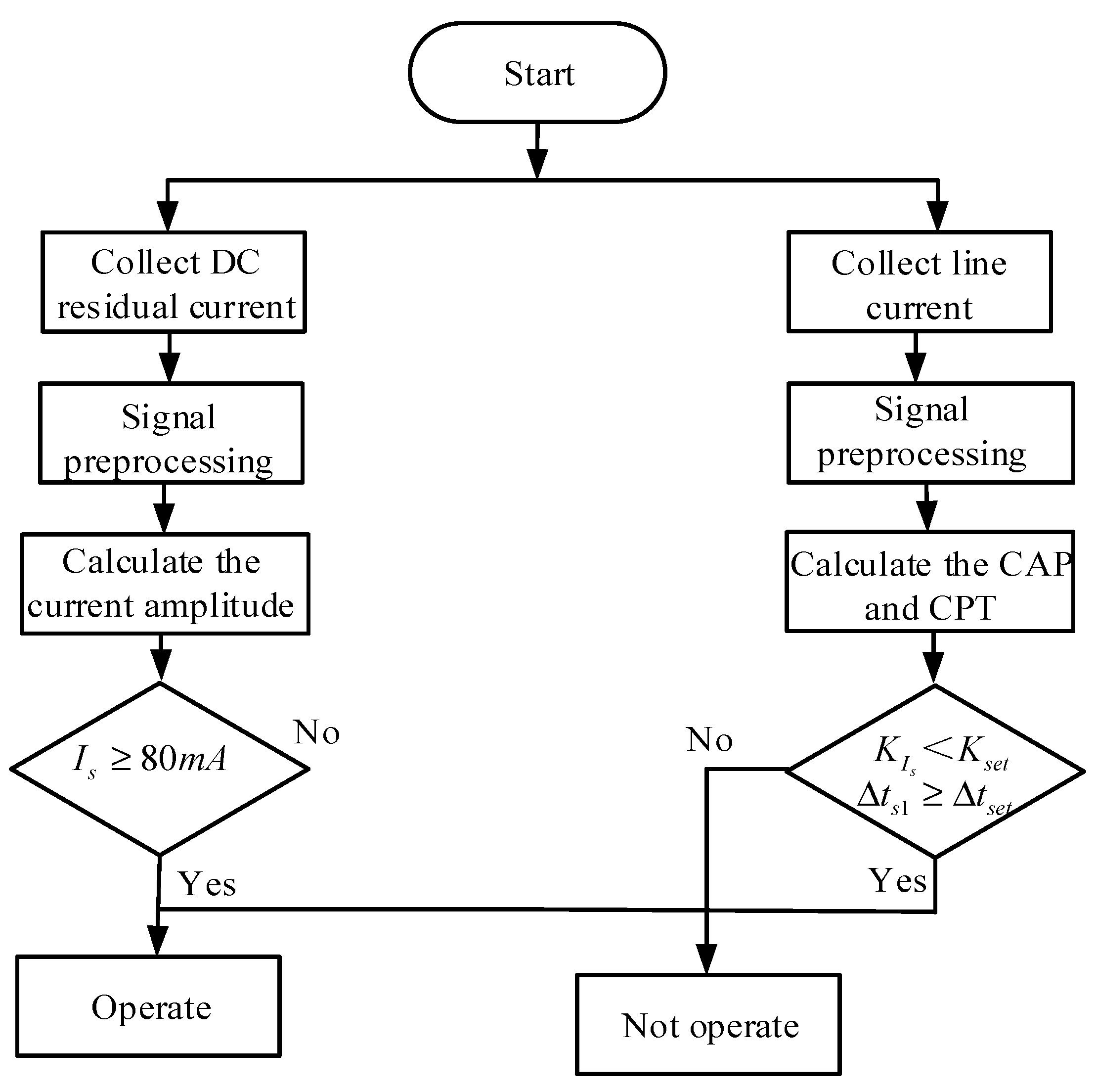
4. Recognition Model Based on DC Electric Shock Current Features
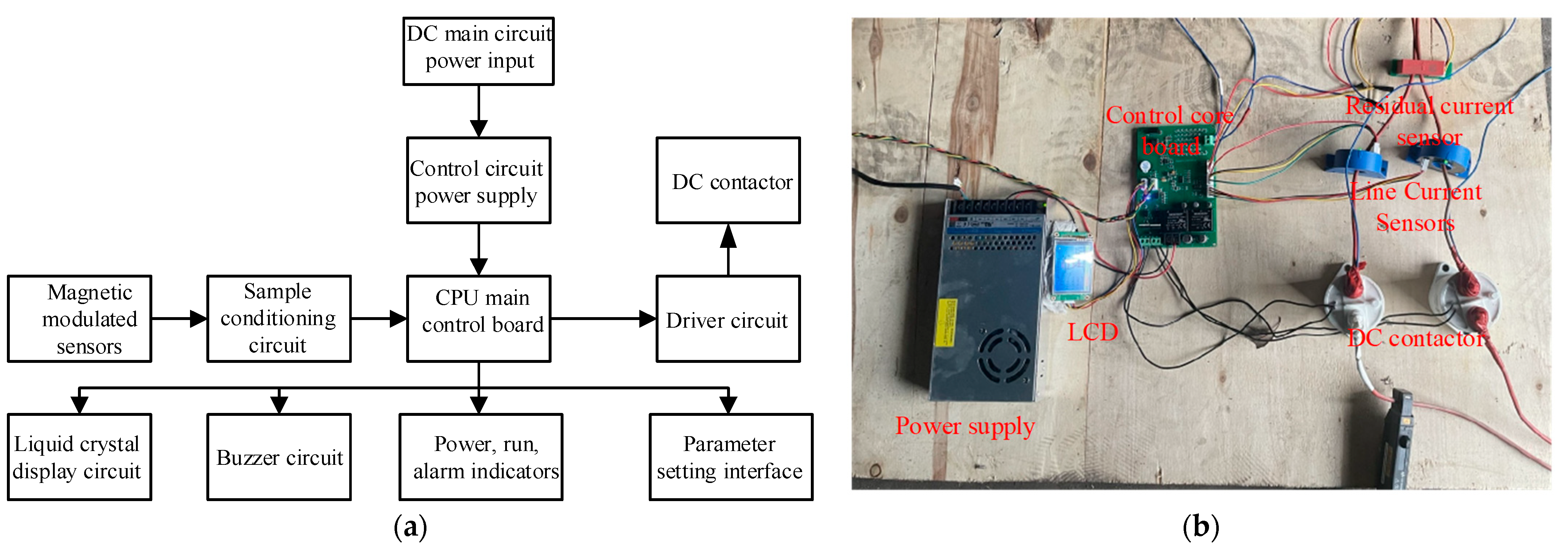
5. Experimental Verification of DC-RCD Prototype
6. Conclusions
- (1)
- The electric shock current of the animal body is a slowly rising nonlinear current signal. The current from battery load burst current and basic residual current are rapid rising step signals.
- (2)
- As the current increases, the curvature accumulation of the animal body’s electric shock current increases, while the sliding curvature accumulation of the non-animal body’s current decreases.
- (3)
- The method proposed in this paper is based on the features of DC electric shock. It effectively solves the problem of the inability to protect when there are two-point side faults in the IT system. The DC-RCD action time is ts < 70 ms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, W.; Dai, C.; Chen, W. Application of PV generation in AC/DC traction power supply system and the key problem analysis under the background of rail transit energy internet. Proc. CSEE 2019, 39, 5692–5702. [Google Scholar]
- Huang, S.; Xiong, L.; Zhou, Y.; Gao, F.; Jia, Q.; Li, X.; Li, X.; Wang, Z.; Khan, M.W. Distributed predefined-time control for power system with time delay and input saturation. IEEE Trans. Power Syst. 2024. [Google Scholar] [CrossRef]
- Tong, M.; Ming, C.; Xu, Z. Key issues and solutions of integrated on-board chargers for electric vehicles. Trans. China Electrotech. Soc. 2021, 36, 5125–5142. [Google Scholar]
- Sarangi, S.; Sahu, B.K.; Rout, P.K. A comprehensive review of distribution generation integrated DC microgrid protection: Issues, strategies, and future direction. Int. J. Energy Res. 2021, 45, 5006–5031. [Google Scholar] [CrossRef]
- Li, L.; Ying, J.; Liang, S. A review of civil low voltage DC distribution system protection. Trans. China Electrotech. Soc. 2015, 30, 139–149. [Google Scholar]
- Wang, Y.; Li, K.; Ren, B.; Zou, X.; Ge, L.; Ye, H. Study of fluxgate current detecting method for AC-DC earth leakage current based on apFFT. Trans. China Electrotech. Soc. 2015, 30, 254–260. [Google Scholar]
- Xie, Z.; Li, X.; Wang, J.; Chen, S. Study of measurement and detection algorithm of LVDC residual current. In Proceedings of the 2020 IEEE 66th Holm Conference on Electrical Contacts and Intensive Course (HLM), San Antonio, TX, USA, 30 September–7 October 2020; pp. 1–5. [Google Scholar]
- Wang, S.; Li, H.; Liu, Q.; Huang, Q.; Liu, Y. Design of a DC residual current sensor based on the improved DC component method. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Li, L.; Yong, J.; Zeng, L.; Wang, X. Investigation on the system grounding types for low voltage direct current systems. In Proceedings of the 2013 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 21–23 August 2013; pp. 1–5. [Google Scholar]
- Wang, T.; Monti, A.; Goldbeck, R.; De Doncker, R.W. Voltage selection and personal safety in low voltage direct current networks at customer end. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–6. [Google Scholar]
- Yong, J.; Xu, X.; Zeng, L. A review of low voltage DC power distribution system. Proc. CSEE 2013, 33, 42–52. [Google Scholar]
- Li, T.; Guo, F. Electric shock protection technology and its development of low-voltage distribution. Distrib. Utiliz. 2019, 36, 2–8. [Google Scholar]
- Lai, C.; Zhong, Q.; Zhao, Y.; Qiu, Y.; Liu, G. Risk assessment method for electric shock of electrical equipment in low-voltage DC power supply system. Autom. Electr. Power Syst. 2021, 45, 141–147. [Google Scholar]
- Yu, D.; Yang, C.; Jiang, L.; Li, T.; Yan, G.; Gao, F.; Liu, H. Review on safety protection of electric vehicle charging. Proc. Chin. Soc. Elect. Eng. 2022, 42, 2145–2164. [Google Scholar]
- Wang, S.; Li, H.; Liu, Q.; Su, W.; Wang, C. Research on the requirements for the break time of DC-RCD under different voltage levels and grounding modes in LVDC system. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 3675–3680. [Google Scholar]
- Lim, S.T.; Lee, K.Y.; Chae, D.J.; Oh, C.-H.; Lim, S.-H. Resistors and capacitors in series mid-point grounding for protection application in unipolar low voltage DC system. IEEE Access 2024, 12, 1461–1469. [Google Scholar] [CrossRef]
- Cheng, D.; Zhang, B.; Xiong, S.; Xie, Z.; Xue, Z. Residual current detection prototype and simulation method in low voltage DC system. IEEE Access 2022, 10, 51100–51109. [Google Scholar] [CrossRef]
- Liao, J.; Guo, C.; Zeng, L.; Kang, W.; Zhou, N.; Wang, Q. Analysis of residual current in low-voltage bipolar DC system and improved residual current protection scheme. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Xue, Z.; Chen, S.; Wang, J.; Li, X.; Ge, S. The influence of line impedance on leakage current detection in low voltage DC systems. In Proceedings of the 2022 IEEE 67th Holm Conference on Electrical Contacts (HLM), Tampa, FL, USA, 23–26 October 2022; pp. 1–5. [Google Scholar]
- Lim, S.T.; Lee, K.Y.; Chae, D.J.; Lim, S.H. Design of mid-point ground with resistors and capacitors in mono-polar LVDC system. Energies 2022, 15, 8653. [Google Scholar] [CrossRef]
- Ding, K.; Cheng, K.W.E.; Wang, D.H.; Ye, Y.M.; Wang, X.L.; Liu, J.F.; Cheung, N.C. Low voltage DC distribution system. Energy 2014, 40, 5. [Google Scholar]
- Oliveira, T.R. Design of a low-cost residual current sensor for LVDC power distribution application. In Proceedings of the 2018 13th IEEE International Conference on Industry Applications (INDUSCON), Sao Paulo, Brazi, 12–14 November 2018; pp. 1313–1319. [Google Scholar]
- Zhu, H.; Wu, C.; Zhou, Y.; Xie, Y.; Zhou, T. Electric shock feature extraction method based on adaptive variational mode decomposition and singular value decomposition. IET Sci. Meas. Technol. 2023, 17, 361–372. [Google Scholar] [CrossRef]
- Xie, F.; Hao, Z.; Ye, D.; Yang, S.; Li, C.; Dai, G.; Zhang, B.; Wang, T. A non-unit line protection method for MMC-HVDC grids based on the currents of backward traveling waves. Int. J. Electr. Power Energy Syst. 2023, 153, 109373. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, L. A novel denoising algorithm based on wavelet and non-local moment mean filtering. Electronics 2023, 12, 1461. [Google Scholar] [CrossRef]
- IEC Standard 60755-1; General Safety Requirements for Residual Current Operated Protective Devices—Part 1: Residual Current Operated Protective Devices for DC Systems. IEC: Geneva, Switzerland, 2022.
- IEC Technical Specification 63053; General Requirements for Residual Current Operated Protective Devices for DC Systems. IEC: Geneva, Switzerland, 2017.





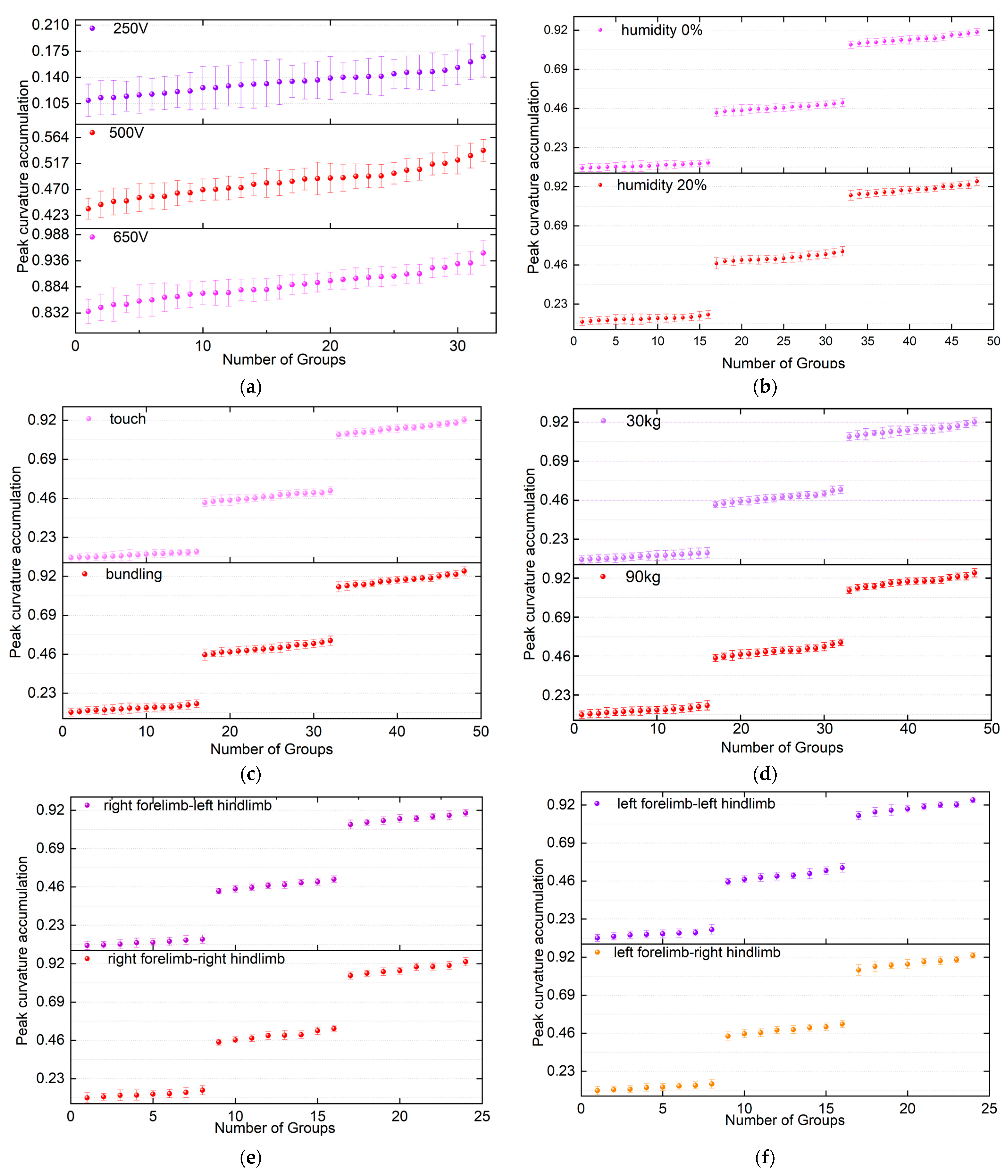
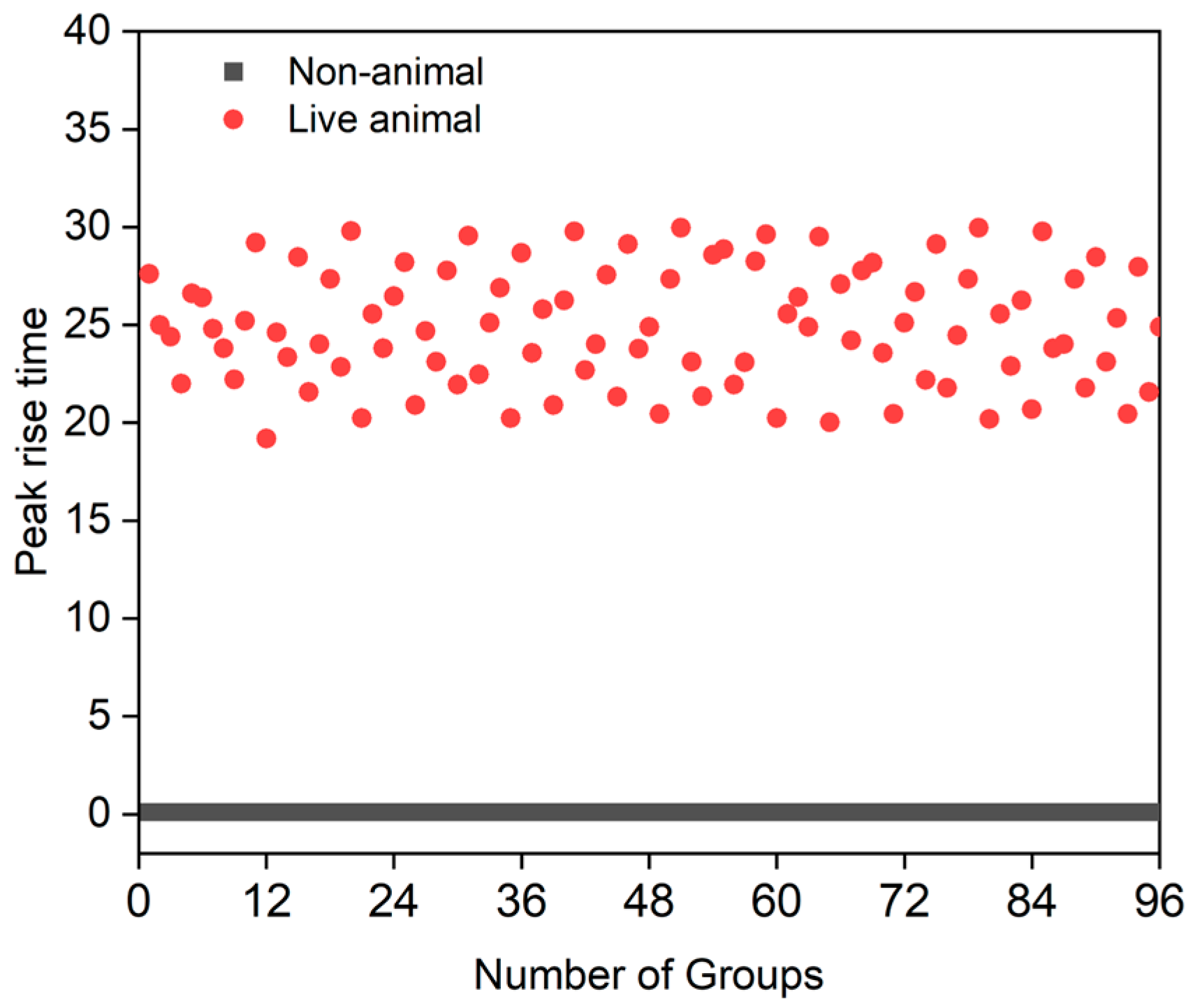
| Test Groups | Electric Shock Paths | Skin Surface Humidity Levels | Electric Shock Methods |
|---|---|---|---|
| 1 | left forelimb-left hindlimb | humidity 0% | touch |
| 2 | left forelimb-left hindlimb | humidity 0% | bundling |
| 3 | left forelimb-left hindlimb | humidity 20% | touch |
| 4 | left forelimb-left hindlimb | humidity 20% | bundling |
| 5 | left forelimb-right hindlimb | humidity 0% | touch |
| 6 | left forelimb-right hindlimb | humidity 0% | bundling |
| 7 | left forelimb-right hindlimb | humidity 20% | touch |
| 8 | left forelimb-right hindlimb | humidity 20% | bundling |
| 9 | right forelimb-left hindlimb | humidity 0% | touch |
| 10 | right forelimb-left hindlimb | humidity 0% | bundling |
| 11 | right forelimb-left hindlimb | humidity 20% | touch |
| 12 | right forelimb-left hindlimb | humidity 20% | bundling |
| 13 | right forelimb-right hindlimb | humidity 0% | touch |
| 14 | right forelimb-right hindlimb | humidity 0% | bundling |
| 15 | right forelimb-right hindlimb | humidity 20% | touch |
| 16 | right forelimb-right hindlimb | humidity 20% | bundling |
| Non-Animal Grounding Faults | Two-Point Electric Shock Fault on the Same Side | Two-Point Electric Shock Fault on the Opposite Sides | ||||||
|---|---|---|---|---|---|---|---|---|
| Electric shock current value | Action time | IEC Standards | Electric shock current value | Action time | IEC Standards | Electric shock current value | Action time | IEC Standards |
| 110 mA | 0.053 s | <0.3 s | 158 mA | 0.06 s | <0.15 s | 186 mA | 0.061 s | <0.15 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Wu, C.; Xie, Y.; Zhou, Y.; Liao, X.; Li, J. Research on DC Electric Shock Protection Method Based on Sliding Curvature Accumulation Quantity. Electronics 2024, 13, 3336. https://doi.org/10.3390/electronics13163336
Zhu H, Wu C, Xie Y, Zhou Y, Liao X, Li J. Research on DC Electric Shock Protection Method Based on Sliding Curvature Accumulation Quantity. Electronics. 2024; 13(16):3336. https://doi.org/10.3390/electronics13163336
Chicago/Turabian StyleZhu, Hongzhang, Chuanping Wu, Yao Xie, Yang Zhou, Xiujin Liao, and Jian Li. 2024. "Research on DC Electric Shock Protection Method Based on Sliding Curvature Accumulation Quantity" Electronics 13, no. 16: 3336. https://doi.org/10.3390/electronics13163336
APA StyleZhu, H., Wu, C., Xie, Y., Zhou, Y., Liao, X., & Li, J. (2024). Research on DC Electric Shock Protection Method Based on Sliding Curvature Accumulation Quantity. Electronics, 13(16), 3336. https://doi.org/10.3390/electronics13163336







