Z-OFDM: A New High-Performance Solution for Underwater Acoustic Communication
Abstract
:1. Introduction
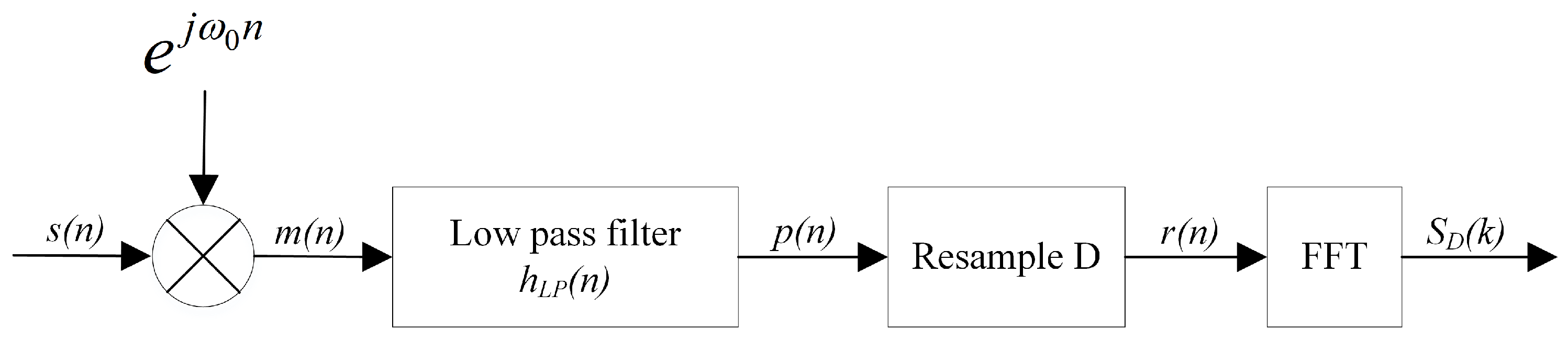
2. ZoomFFT Algorithm
2.1. Principle
2.2. Energy Efficiency
3. Communication System Model
3.1. Theory
3.1.1. Transmitter Model
3.1.2. Receiver Model
3.2. Performance Analysis
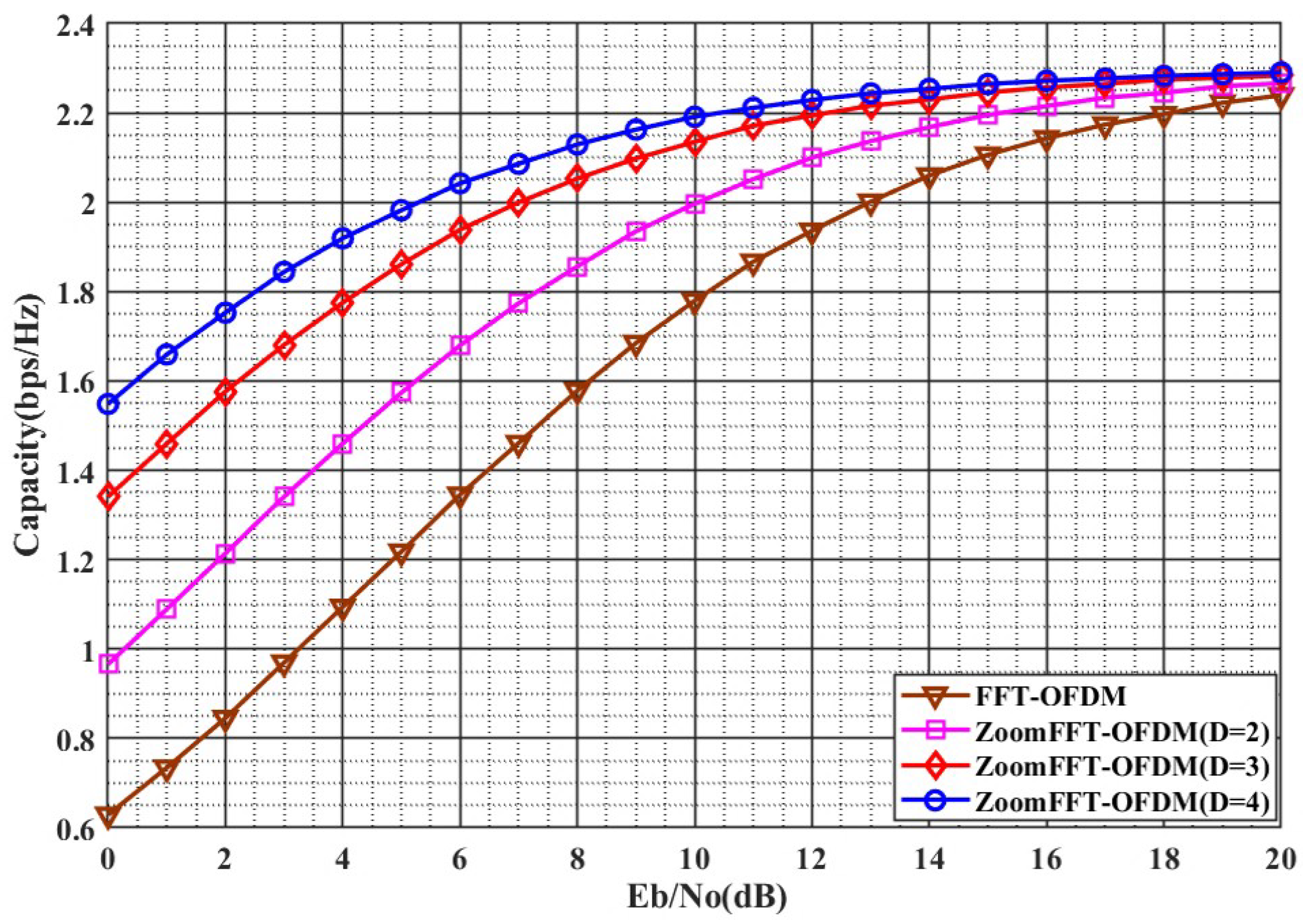
3.2.1. Channel Capacity
3.2.2. Signal Interference plus Noise Ratio
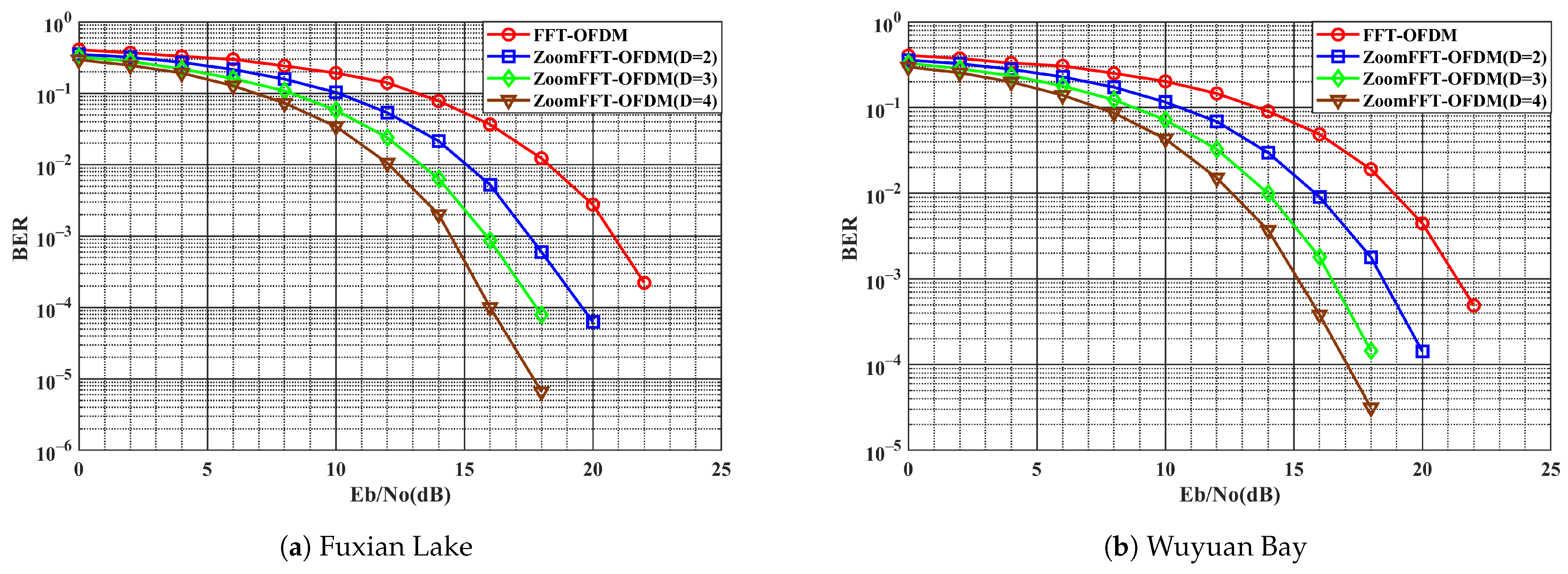
3.2.3. Bit Error Rate
4. Computer Simulation Experiments
4.1. Underwater Acoustic Channels
4.1.1. Fuxian Lake
4.1.2. Wuyuan Bay
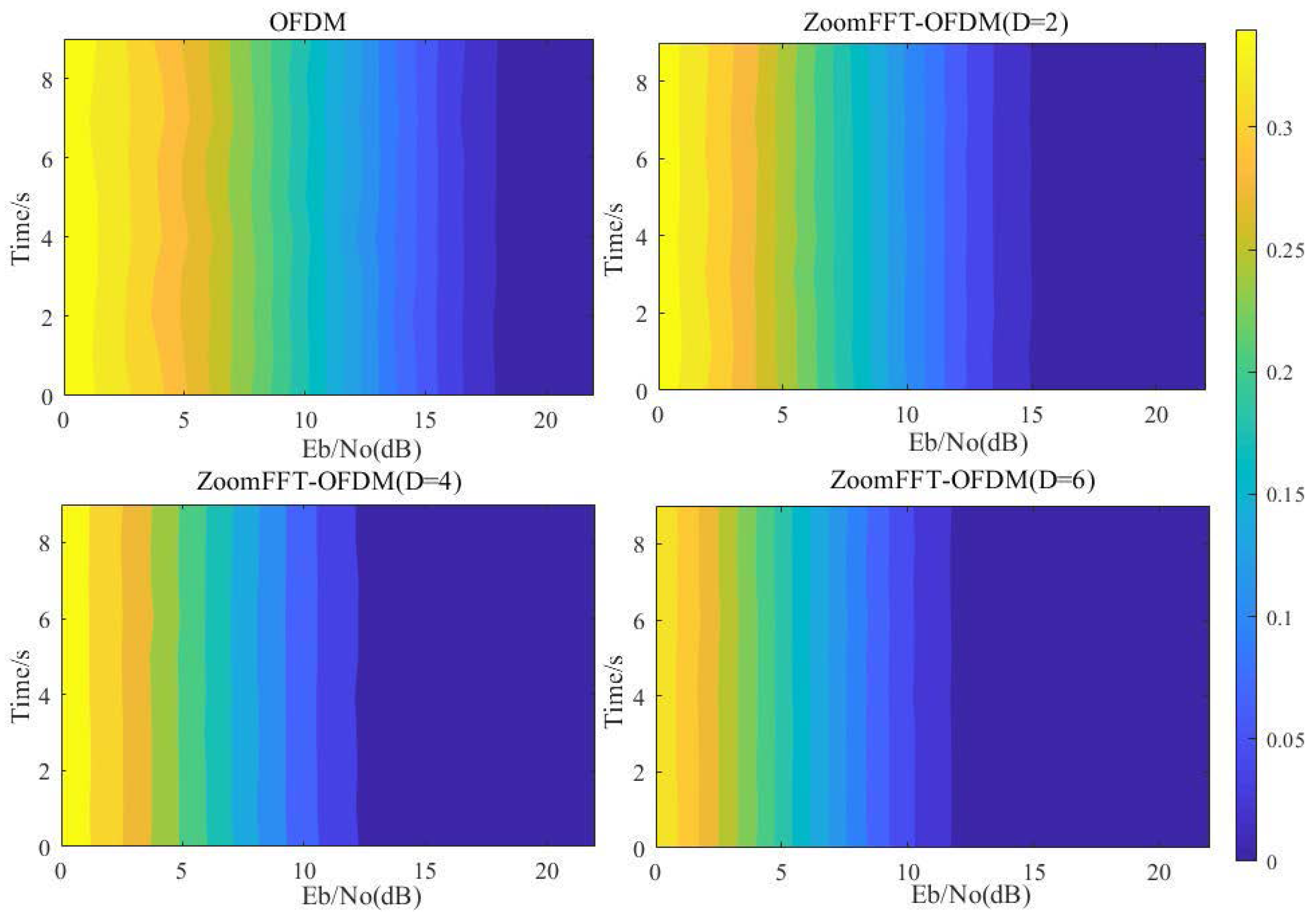
4.2. Experimental Results
4.2.1. Fuxian Lake
4.2.2. Wuyuan Bay
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumara, S.; Vatsb, C. Underwater communication: A detailed review. In Proceedings of the CEUR Workshop Proceedings, Naples, Italy, 4–5 October 2021. [Google Scholar]
- Liu, L.; Cai, L.; Ma, L.; Qiao, G. Channel State Information Prediction for Adaptive Underwater Acoustic Downlink OFDMA System: Deep Neural Networks Based Approach. IEEE Trans. Veh. Technol. 2021, 70, 9063–9076. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Wang, H.; Wang, J.; Yang, F.; Meriaudeau, F. Deep learning aided OFDM receiver for underwater acoustic communications. Appl. Acoust. 2022, 187, 108515. [Google Scholar] [CrossRef]
- Feng, X.; Wang, J.; Kuai, X.; Zhou, M.; Sun, H.; Li, J. Message Passing-Based Impulsive Noise Mitigation and Channel Estimation for Underwater Acoustic OFDM Communications. IEEE Trans. Veh. Technol. 2022, 71, 611–625. [Google Scholar] [CrossRef]
- Su, Y.; Dong, L.; Zhou, Z.; Liu, X.; Wei, X. A General Embedded Underwater Acoustic Communication System Based on Advance STM32. IEEE Embed. Syst. Lett. 2021, 13, 90–93. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Li, C.; Chen, X.; Meriaudeau, F. On the performance of deep neural network aided channel estimation for underwater acoustic OFDM communications. Ocean Eng. 2022, 259, 111518. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, W.; Hu, Q.; Zeng, Z.; Li, Z. Time-Varying Channel and Intrablock Carrier Frequency Offset Estimation for OFDM Underwater Acoustic Communication. IEEE Sens. J. 2024, 24, 18405–18417. [Google Scholar] [CrossRef]
- Qasem, Z.A.H.; Wang, J.; Kuai, X.; Sun, H.; Esmaiel, H. Enabling Unique Word OFDM for Underwater Acoustic Communication. IEEE Wirel. Commun. Lett. 2021, 10, 1886–1889. [Google Scholar] [CrossRef]
- Yin, J.w.; Zhu, G.j.; Han, X.; Ge, W.; Li, L.; Tian, Y.n. Iterative channel estimation-based soft successive interference cancellation for multiuser underwater acoustic communications. J. Acoust. Soc. Am. 2021, 150, 133–144. [Google Scholar] [CrossRef]
- Tasadduq, I.A.; Murad, M.; Otero, P. CPM-OFDM Performance over Underwater Acoustic Channels. J. Mar. Sci. Eng. 2021, 9, 1104. [Google Scholar] [CrossRef]
- Zhou, J.; Lei, L.; Liu, N. Research on Rough and Detailed Combination Spectrum Analysis of Electromagnetic Signals Based on Complex Modulation ZoomFFT. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; pp. 786–789. [Google Scholar] [CrossRef]
- Shen, W.; Sun, H.; Cheng, E.; Su, W.; Zhang, Y. Narrowband interference suppression in underwater acoustic OFDM system. In Proceedings of the 2010 2nd International Asia Conference on Informatics in Control, Automation and Robotics (CAR 2010), Wuhan, China, 6–7 March 2010; Volume 1, pp. 496–499. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, S.; Giannakis, G.B.; Berger, C.R.; Huang, J. Frequency-Domain Oversampling for Zero-Padded OFDM in Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2012, 37, 14–24. [Google Scholar] [CrossRef]
- Li, B.; Zhou, S.; Stojanovic, M.; Freitag, L.; Willett, P. Multicarrier Communication Over Underwater Acoustic Channels with Nonuniform Doppler Shifts. IEEE J. Ocean. Eng. 2008, 33, 198–209. [Google Scholar] [CrossRef]
- Ramadan, K.; Dessouky, M.I.; El-Samie, F.E.A. Equalization and Co-Carrier Frequency Offsets Compensations for UWA-OFDM Communication Systems. Wirel. Pers. Commun. 2022, 124, 2229–2245. [Google Scholar] [CrossRef]
- Su, Y.; Zuo, Y.; Jin, Z.; Fu, X. OSPG-MAC: An OFDMA-Based Subcarrier Pregrouping MAC Protocol for Underwater Acoustic Wireless Sensor Networks. J. Sens. 2019, 2019, 4965231. [Google Scholar] [CrossRef]
- Ashri, R.M.; Shaban, H.A.; El-Nasr, M.A. BER of FRFT-based OFDM system for underwater wireless communication. In Proceedings of the 2016 33rd National Radio Science Conference (NRSC), Aswan, Egypt, 22–25 February 2016; pp. 266–273. [Google Scholar] [CrossRef]
- Singh, A.K.; Saxena, R. Doppler Estimation from Echo Signal Using FRFT. Wirel. Pers. Commun. 2013, 72, 405–413. [Google Scholar] [CrossRef]
- Dida, M.A.; Hao, H.; Ran, T.; Teng, W.; Urynbassarova, D. Constant envelope FrFT OFDM: Spectral and energy efficiency analysis. J. Syst. Eng. Electron. 2019, 30, 467–473. [Google Scholar] [CrossRef]
- Ding, Y.; Sun, L.; Zhang, H.; Zheng, B. A multi-component LFM signal parameters estimation method using STFT and Zoom-FRFT. In Proceedings of the 2016 8th IEEE International Conference on Communication Software and Networks (ICCSN), Beijing, China, 4–6 June 2016; pp. 112–117. [Google Scholar] [CrossRef]
- Yanhua, J.; Gun, L.; Kaiyu, Q. Study of a Novel Zoom Spectrum Analysis Approach for Wireless Communication Analyzer. In Proceedings of the 2009 WRI International Conference on Communications and Mobile Computing, Kunming, China, 6–8 January 2009; Volume 1, pp. 367–371. [Google Scholar] [CrossRef]
- Carter, T.; Pergande, A.; DeLisio, M. Zoom FFT for millimeterwave additive noise measurement. In Proceedings of the Infrared and Millimeter Waves, Conference Digest of the 2004 Joint 29th International Conference on 2004 and 12th International Conference on Terahertz Electronics, Karlsruhe, Germany, 27 September–1 October 2004; pp. 335–336. [Google Scholar] [CrossRef]
- Aval, Y.M.; Stojanovic, M. Partial FFT demodulation for coherent detection of OFDM signals over underwater acoustic channels. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, Norway, 10–14 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Shuohan, M.; Qishuang, M.; Xinbo, L. Applications of chirp z transform and multiple modulation zoom spectrum to pulse phase thermography inspection. NDT E Int. 2013, 54, 1–8. [Google Scholar] [CrossRef]
- Wu, C.; Gao, Y.; Li, C.; Cao, Y.; Iravani, R. Analytic Mode Decomposition and Windowed Three-Point Interpolated Chirp-Z Transform for Voltage Flicker Components Detection. Electr. Power Syst. Res. 2020, 186, 106382. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Wang, H.; Luo, Q. Improved Algorithm for Parameter Estimation of LFM Signal Based on Chirp-Z Transform. In Proceedings of the 2020 International Conference on Computers, Information Processing and Advanced Education, New York, NY, USA, 16–18 October 2020; CIPAE 2020. pp. 125–129. [Google Scholar] [CrossRef]
- Watanabe, T. An optimized SAW chirp -Z Transform for OFDM systems. In Proceedings of the 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time Forum, Besancon, France, 20–24 April 2009; pp. 416–419. [Google Scholar] [CrossRef]
- Watanabe, T. Study of SAW Chirp- Z transform for an enhancement of OFDM/OFDMA systems. In Proceedings of the 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time Forum, Besancon, France, 20–24 April 2009; pp. 801–806. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X.; Tian, G. The Analysis of Seismic Signal Spectrum Based on ZFFT. In Proceedings of the 2013 5th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2013; Volume 2, pp. 290–293. [Google Scholar] [CrossRef]
- Hossen, A.; Heute, U. A novel simple adaptive spectral analysis zoom for narrow-band signals. In Proceedings of the 2002 11th European Signal Processing Conference, Toulouse, France, 3–6 September 2002; pp. 1–4. [Google Scholar]
- Dahi, K.; Elhani, S.; Guedira, S.; Sadiki, L.; Ouachtouk, I. High-resolution spectral analysis method to identify rotor faults in WRIM using Neutral Voltage. In Proceedings of the 2015 International Conference on Electrical and Information Technologies (ICEIT), Marrakech, Morocco, 25–27 March 2015; pp. 82–87. [Google Scholar] [CrossRef]
- Lee, J.S.; Yoon, T.M.; Lee, K.B. Bearing Fault Detection of IPMSMs using Zoom FFT. J. Electr. Eng. Technol. 2016, 11, 1235–1241. [Google Scholar] [CrossRef]
- Al-Qudsi, B.; Joram, N.; Strobel, A.; Ellinger, F. Zoom FFT for Precise Spectrum Calculation in FMCW Radar using FPGA. In Proceedings of the 2013 9th Conference on PH. D. Research in Microelectronics and Electronics (PRIME 2013), 345 E 47TH ST, Villach, Austria, 24–27 June 2013; pp. 337–340. [Google Scholar]
- Almradi, A.; Hamdi, K.A. Spectral Efficiency of OFDM Systems With Random Residual CFO. IEEE Trans. Commun. 2015, 63, 2580–2590. [Google Scholar] [CrossRef]
- Chao, W.; Yi, Z.; Jun-cheng, W.; Hui, L.; Qing-feng, M. A Simple and Effective Algorithm for Sinusoidal Frequency Estimation. In Proceedings of the 2012 International Conference on Computer Distributed Control and Intelligent Environmental Monitoring, Zhangjiajie, China, 5–6 March 2012; pp. 70–73. [Google Scholar] [CrossRef]
- Guo, Q.; Li, A.; Wu, J.; Su, H. ZoomFFT-Based Demodulation Algorithm for Underwater Acoustic OFDM Signals. J. Syst. Simul. 2022, 34, 314–322. [Google Scholar]
- Huang, X. Analysis and Optimization of OFDM Underwater Acoustic Communications; Stevens Institute of Technology: Hoboken, NJ, USA, 2011. [Google Scholar]
- Huang, X.; Lawrence, V.B. OFDM with Pilot Aided Channel Estimation for Time-Varying Shallow Water Acoustic Channels. In Proceedings of the 2010 International Conference on Communications and Mobile Computing, Shenzhen, China, 12–14 April 2010; Volume 2, pp. 442–446. [Google Scholar] [CrossRef]
- Huang, Y.; Wan, L.; Zhou, S.; Wang, Z.; Huang, J. Comparison of sparse recovery algorithms for channel estimation in underwater acoustic OFDM with data-driven sparsity learning. Phys. Commun. 2014, 13, 156–167. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, X.; Cao, S.; Zhao, J.; Li, X. Joint Compressed Sensing and Enhanced Whale Optimization Algorithm for Pilot Allocation in Underwater Acoustic OFDM Systems. IEEE Access 2019, 7, 95779–95796. [Google Scholar] [CrossRef]
- Ma, L.; Li, T.; Liu, S.; Qiao, G.; Jia, H. Efficient interpolation based OMP for sparse channel estimation in underwater acoustic OFDM. Appl. Acoust. 2021, 172, 107606. [Google Scholar] [CrossRef]
- Ramos, J. Maximal restriction estimates and the maximal function of the Fourier transform. Proc. Am. Math. Soc. 2020, 148, 1131–1138. [Google Scholar] [CrossRef]
- Zhao, K. Underwater Acoustic Signal Processing and Its Applications. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2014. [Google Scholar]
- Ramadan, K.; Fiky, A.S.; Dessouky, M.I.; Abd El-Samie, F.E. Equalization and carrier frequency offset compensation for UWA-OFDM communication systems based on the discrete sine transform. Digit. Signal Process. 2019, 90, 142–149. [Google Scholar] [CrossRef]
- Huang, J. Progressive Receiver Design for Underwater Acoustic OFDM Communications. Ph.D. Thesis, University of Connecticut, Storrs, CT, USA, 2012. [Google Scholar]
- Hoseyni, S.M.J. OFDM Carrier Frequency Offset Correction in Spectral Domain Using a Single Pilot Tone. Master’s Thesis, Dalhousie University, Halifax, NS, Canada, 2010. [Google Scholar]
- Li, B.; Zhou, S.; Stojanovic, M.; Freitag, L. Pilot-tone based ZP-OFDM demodulation for an underwater acoustic channel. In Proceedings of the OCEANS 2006, Boston, MA, USA, 18–22 September 2006; p. 929+. [Google Scholar]
- Cai, G.; Wang, L.; Huang, T. Channel capacity of M-ary Differential Chaos Shift Keying modulation over AWGN channel. In Proceedings of the 2013 13th International Symposium on Communications and Information Technologies (ISCIT), Samui Island, Thailand, 4–6 September 2013; pp. 91–95. [Google Scholar] [CrossRef]
- Effros, M.; Goldsmith, A.; Liang, Y. Generalizing Capacity: New Definitions and Capacity Theorems for Composite Channels. IEEE Trans. Inf. Theory 2010, 56, 3069–3087. [Google Scholar] [CrossRef]
- Motahari, A.S.; Khandani, A.K. Capacity Bounds for the Gaussian Interference Channel. IEEE Trans. Inf. Theory 2009, 55, 620–643. [Google Scholar] [CrossRef]
- Chang, M.K. SINR Analysis and Power Control for Downlink W-CDMA and Multiuser OFDM Systems. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2003. [Google Scholar]
- Yang, F.; Pei, G.; Hu, L.; Ding, L.; Li, Y. Joint optimization of SINR and maximum sidelobe level for hybrid beamforming systems with sub-connected structure. Digit. Signal Process. 2021, 109, 102917. [Google Scholar] [CrossRef]
- Zhang, J. Narrowband Interference Suppression in OFDM-based Communication Systems. Ph.D. Thesis, University of New Brunswick, Fredericton, NB, Canada, 2010. [Google Scholar]
- Kumhom, P. Design, Optimization, and Implementation of a Universal FFT Processor. Ph.D. Thesis, Drexel University, Pennsylvania, PA, USA, 2001. [Google Scholar]
- Jiang, W.; Yang, X.; Tong, F.; Yang, Y.; Zhou, T. A Low-Complexity Underwater Acoustic Coherent Communication System for Small AUV. Remote Sens. 2022, 14, 3405. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, H.; Pan, C.; Liu, S. Measurement-based analysis of characteristics of fast moving underwater acoustic communication channel. In Proceedings of the 2022 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 12–13 December 2022; pp. 47–52. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, Y.; Wang, R.; Tong, F. Research and Implementation on a Real-Time OSDM MODEM for Underwater Acoustic Communications. IEEE Sens. J. 2023, 23, 18434–18448. [Google Scholar] [CrossRef]
- Xiao, F.; He, Y.; Xu, X.; Huang, L.; Tao, Y.; Chen, Y. Transmission Characteristics of High-Frequency Underwater Acoustic Channels with High-Frequency Marine Noise in Shallow Sea. In Proceedings of the 2021 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Xiamen, China, 28–30 July 2021; pp. 244–249. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Y.; Yang, X.; Tong, F.; Wu, J. Design and Implementation of a Multi-Function Hydrophone for Underwater Acoustic Application. J. Mar. Sci. Eng. 2023, 11, 2203. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Thi, H.L.N.; Nguyen, Q.K.; Nguyen, T.H. Low Complexity Non-Uniform FFT for Doppler Compensation in OFDM-Based Underwater Acoustic Communication Systems. IEEE Access 2022, 10, 82788–82798. [Google Scholar] [CrossRef]
- Yang, C.; Wang, L.; Peng, C.; Zhang, S.; Cui, Y.; Ma, C. A Robust Time-Frequency Synchronization Method for Underwater Acoustic OFDM Communication Systems. IEEE Access 2024, 12, 21908–21920. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| DFT Point | 1024 |
| Number of Sub-carrier | 512 |
| Number of Data Sub-carrier | 324 |
| Number of Pilot Sub-carrier | 103 |
| Sampling Rate (kHz) | 144 |
| Bandwidth (kHz) | 3.6 |
| Band (kHz) | 29.1∼32.7 |
| Guard Interval | 0.125 × Symbol Length |
| Sub-carrier Spacing (Hz) | 3.516 |
| Refinement Factor D | [2 3 4] |
| Feature/Metric | Z-OFDM | FFT-OFDM |
|---|---|---|
| Spectral Resolution | High (refined with Zoom-FFT) | Moderate (limited by FFT size) |
| Channel Capacity | High | Low |
| BER | Low, especially under interference | High |
| SINR | High | Low |
| Computational Complexity | Moderate (efficient spectral refinement) | High (requires larger FFT size for similar resolution) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Chen, J.; Li, A.; Hu, H.; Xu, C. Z-OFDM: A New High-Performance Solution for Underwater Acoustic Communication. Electronics 2024, 13, 3543. https://doi.org/10.3390/electronics13173543
Su H, Chen J, Li A, Hu H, Xu C. Z-OFDM: A New High-Performance Solution for Underwater Acoustic Communication. Electronics. 2024; 13(17):3543. https://doi.org/10.3390/electronics13173543
Chicago/Turabian StyleSu, Haitao, Jiaxuan Chen, Angdi Li, Hongzhi Hu, and Cuifeng Xu. 2024. "Z-OFDM: A New High-Performance Solution for Underwater Acoustic Communication" Electronics 13, no. 17: 3543. https://doi.org/10.3390/electronics13173543
APA StyleSu, H., Chen, J., Li, A., Hu, H., & Xu, C. (2024). Z-OFDM: A New High-Performance Solution for Underwater Acoustic Communication. Electronics, 13(17), 3543. https://doi.org/10.3390/electronics13173543







