Modeling, Design, and Application of Analog Pre-Distortion for the Linearity and Efficiency Enhancement of a K-Band Power Amplifier
Abstract
1. Introduction
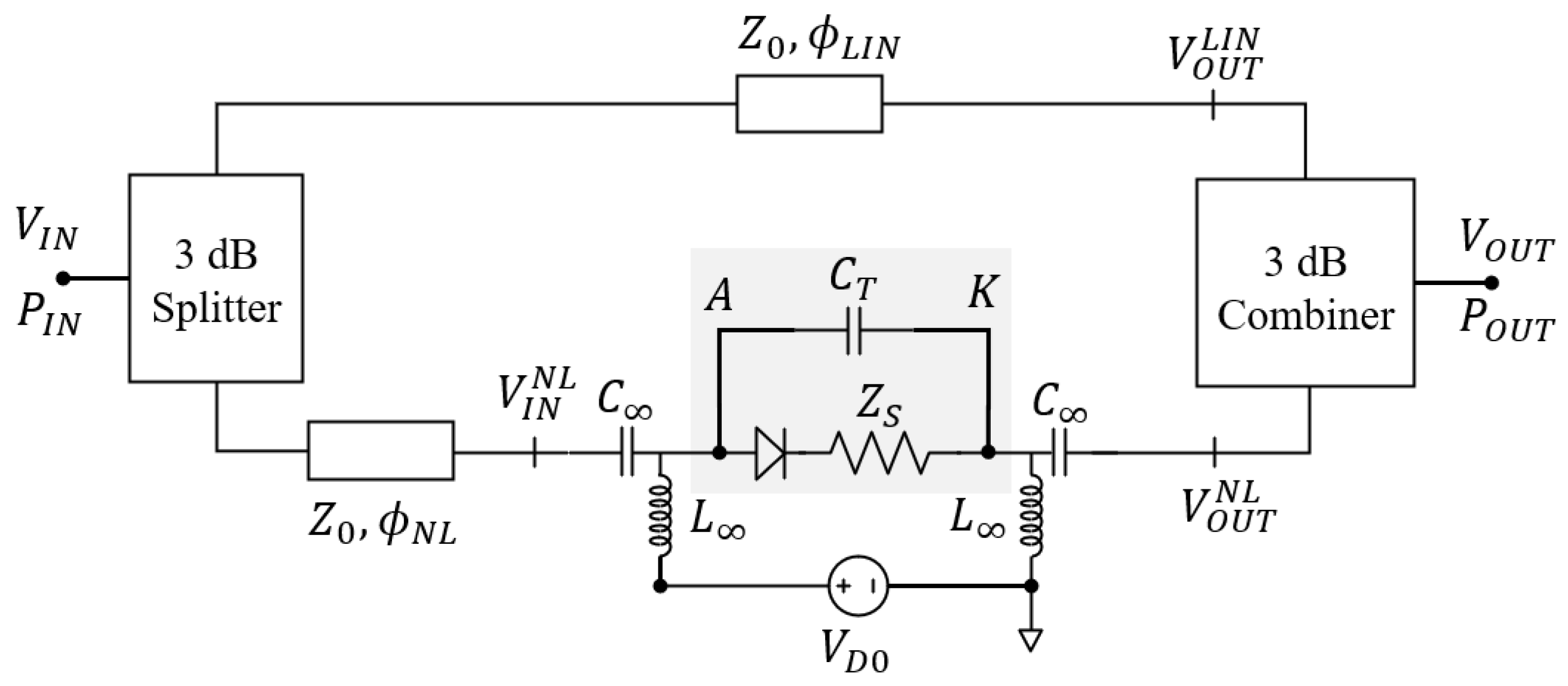
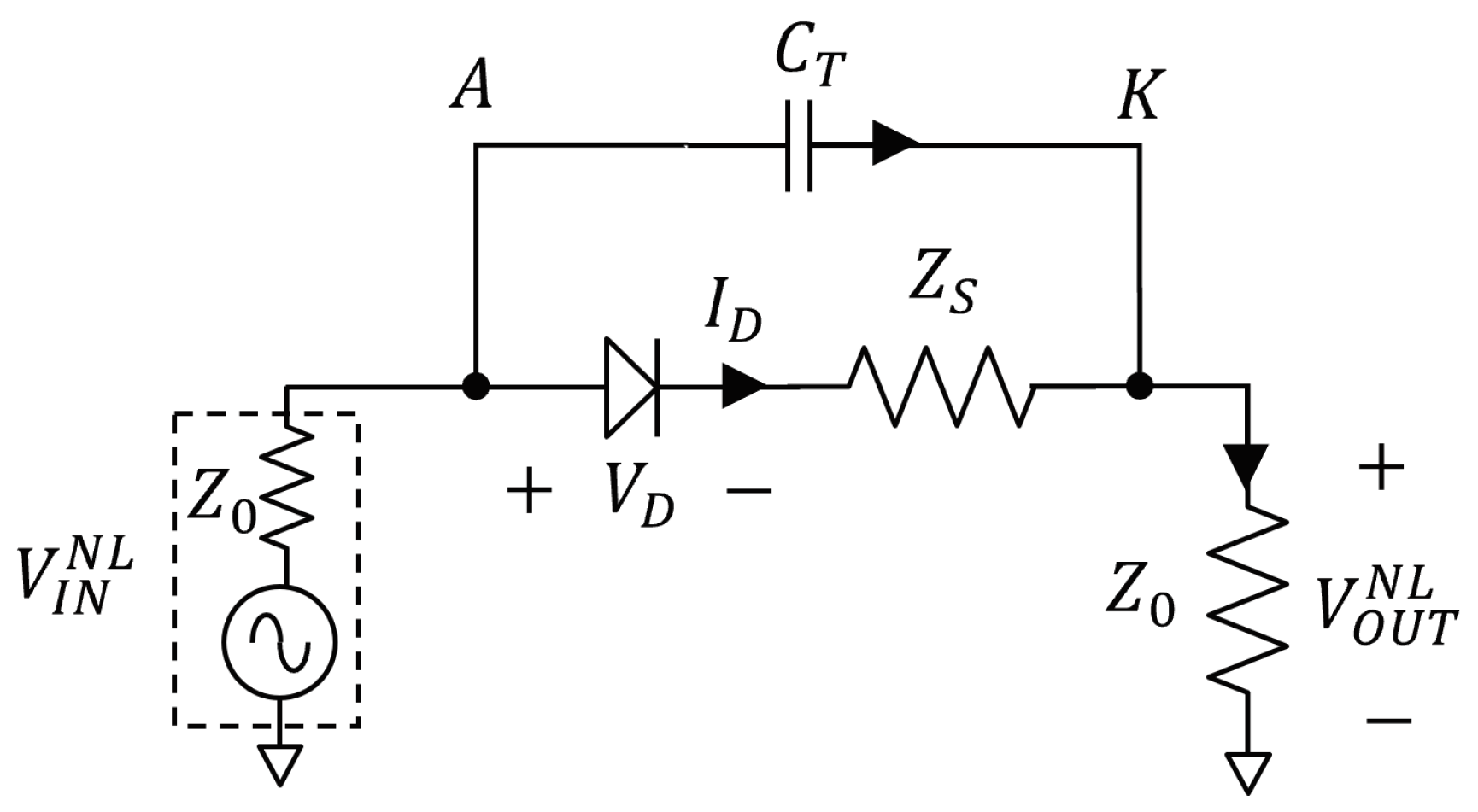
2. Wideband Large-Signal APD Model
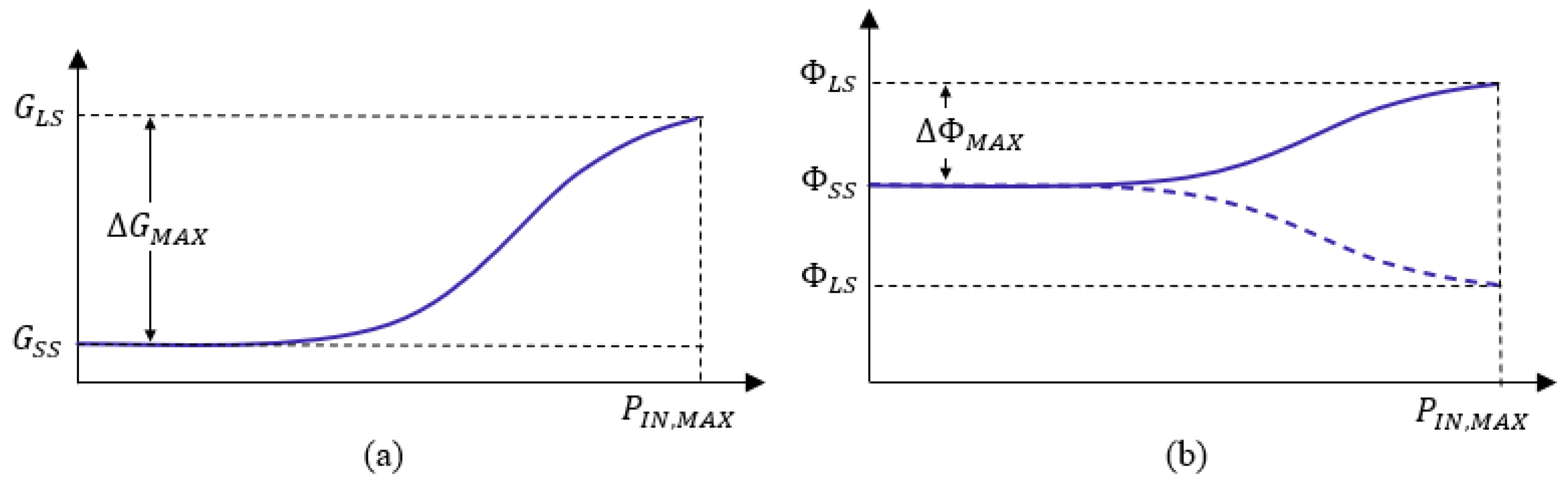
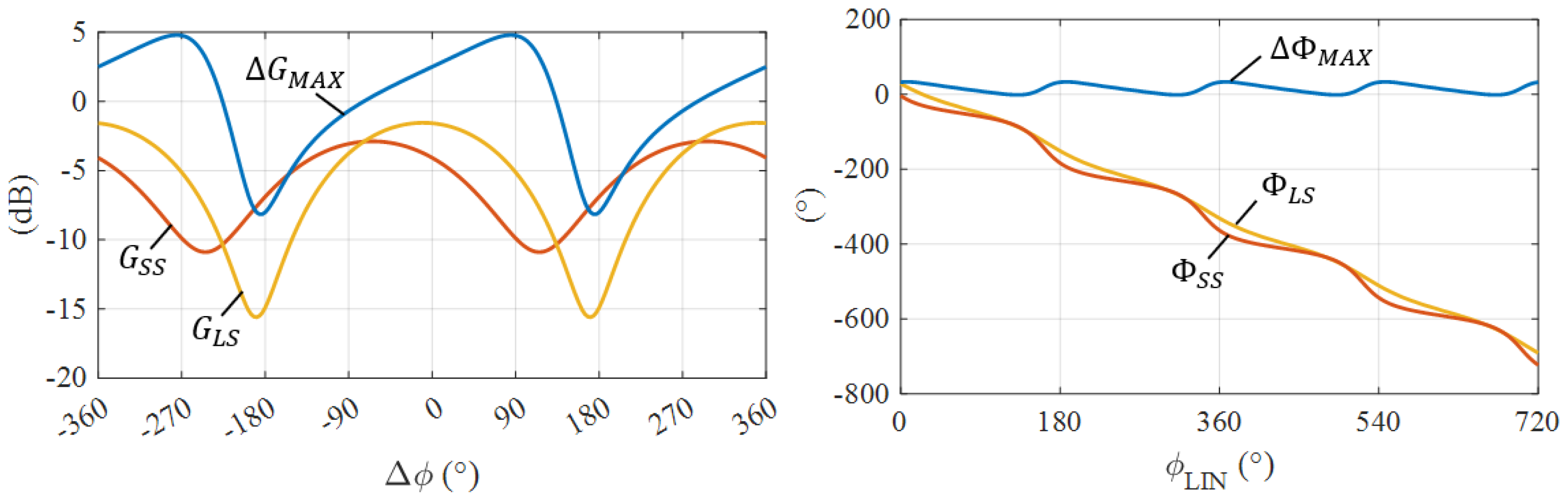
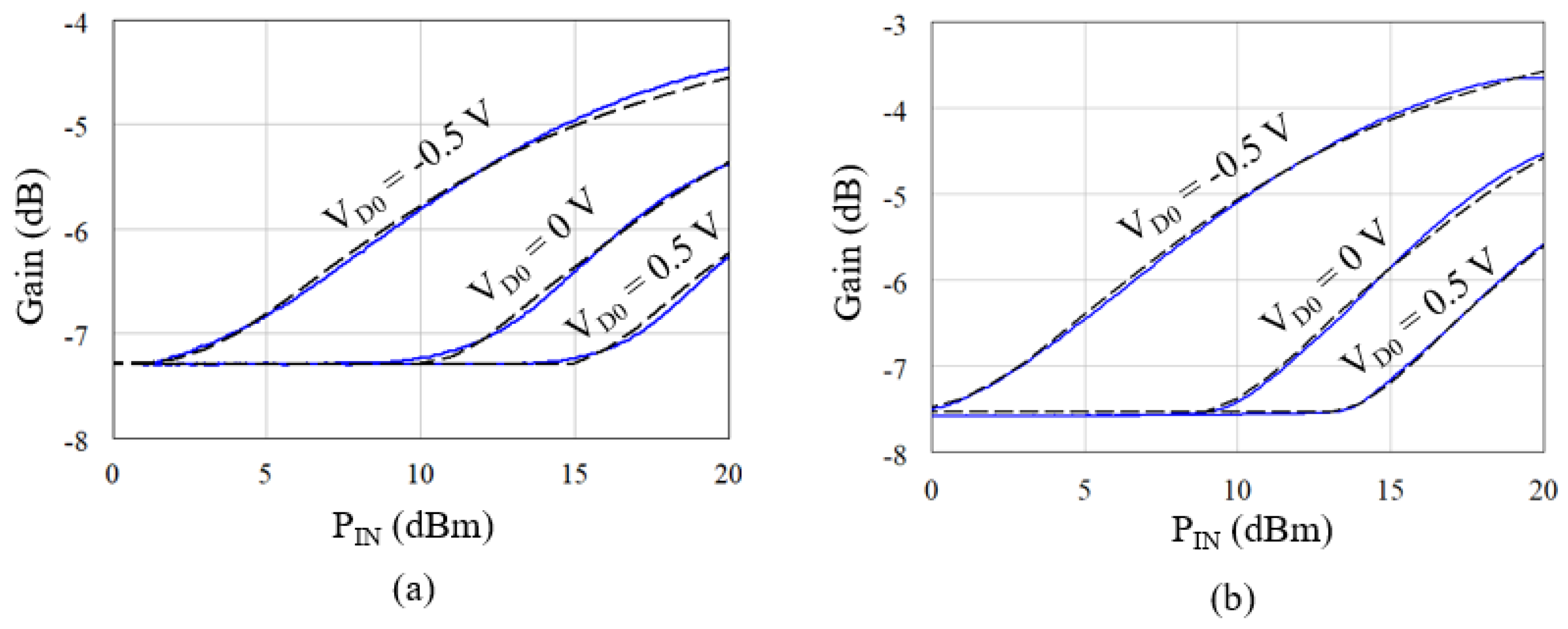
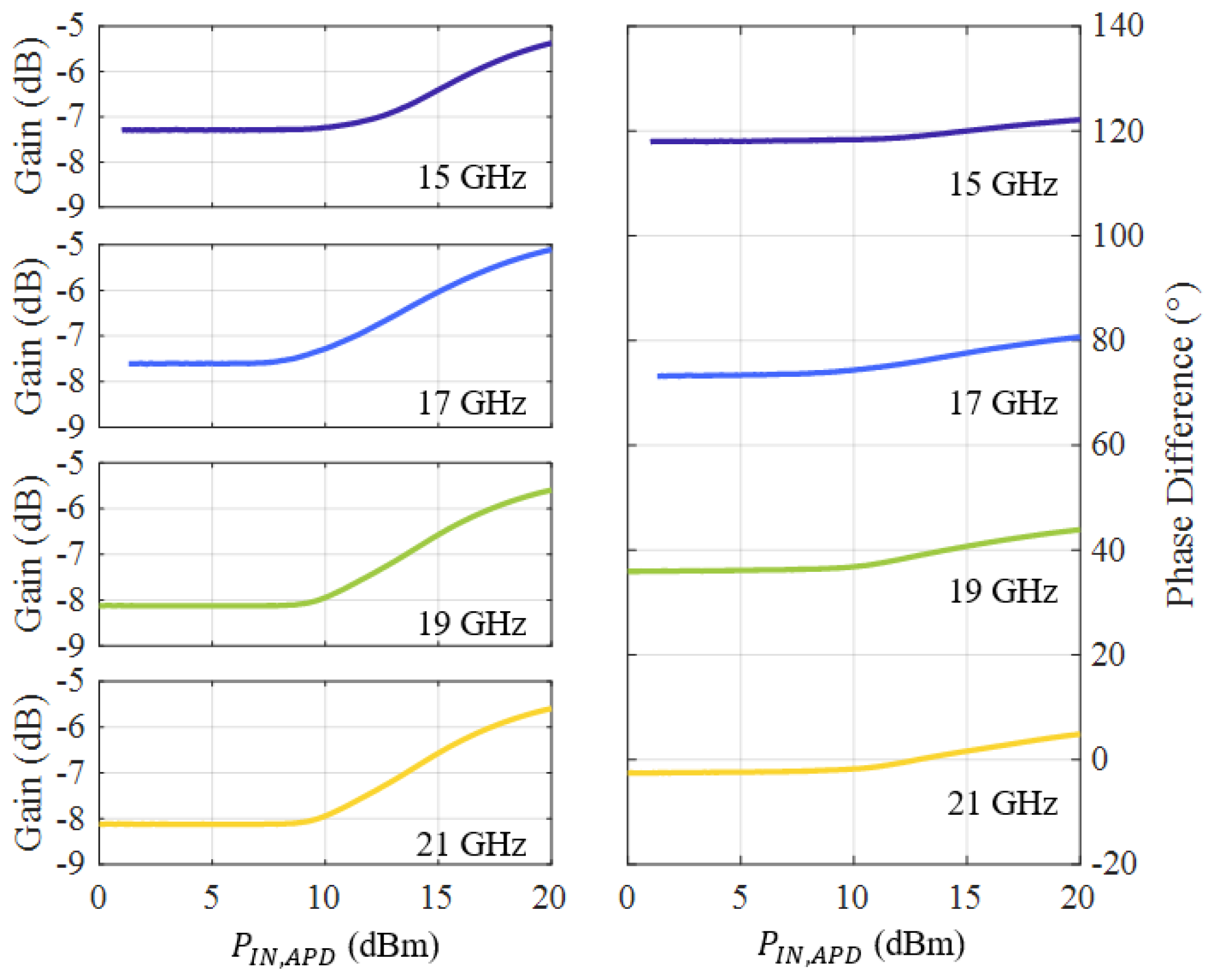
2.1. APD Amplitude Range
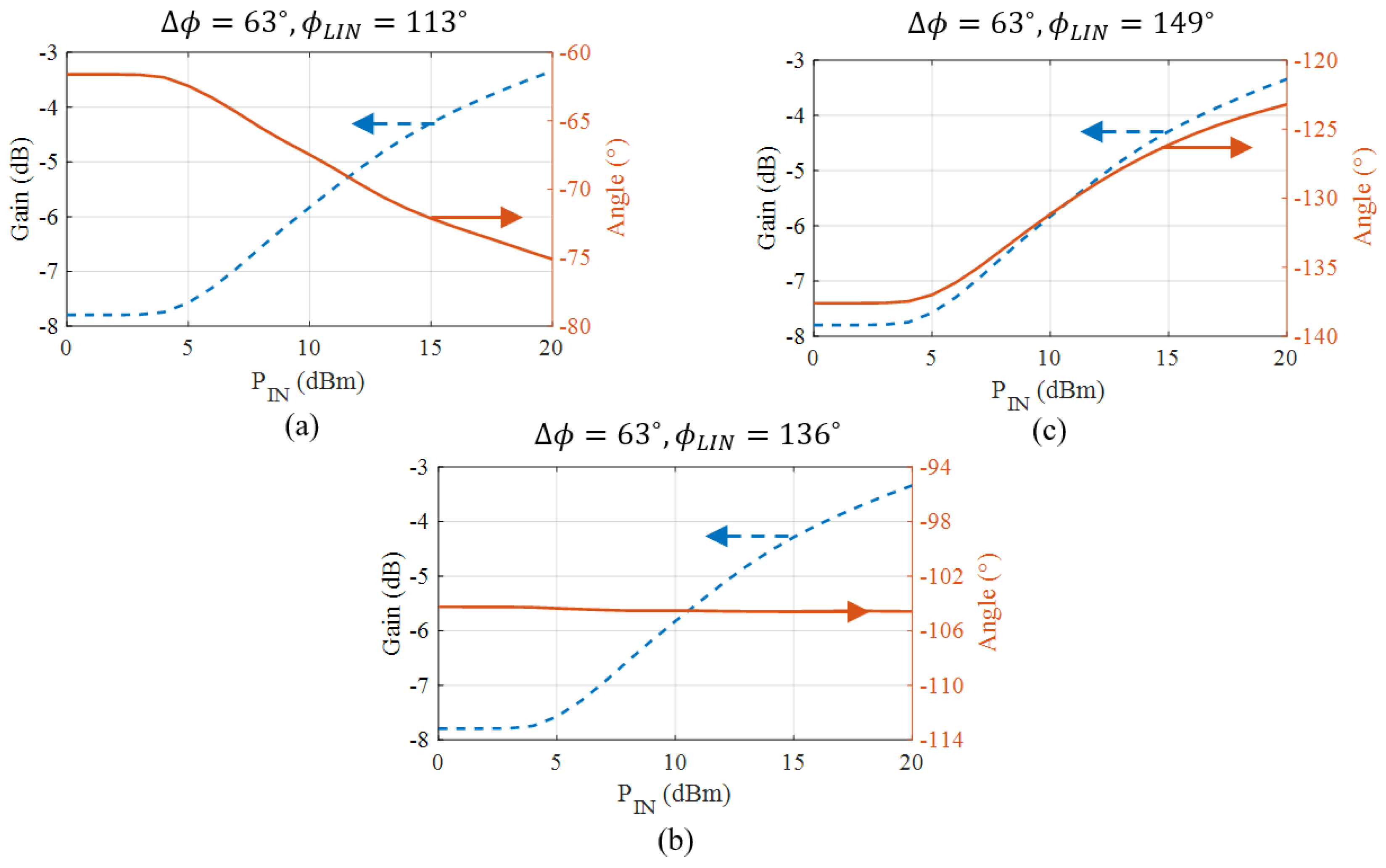
2.2. APD Phase Range
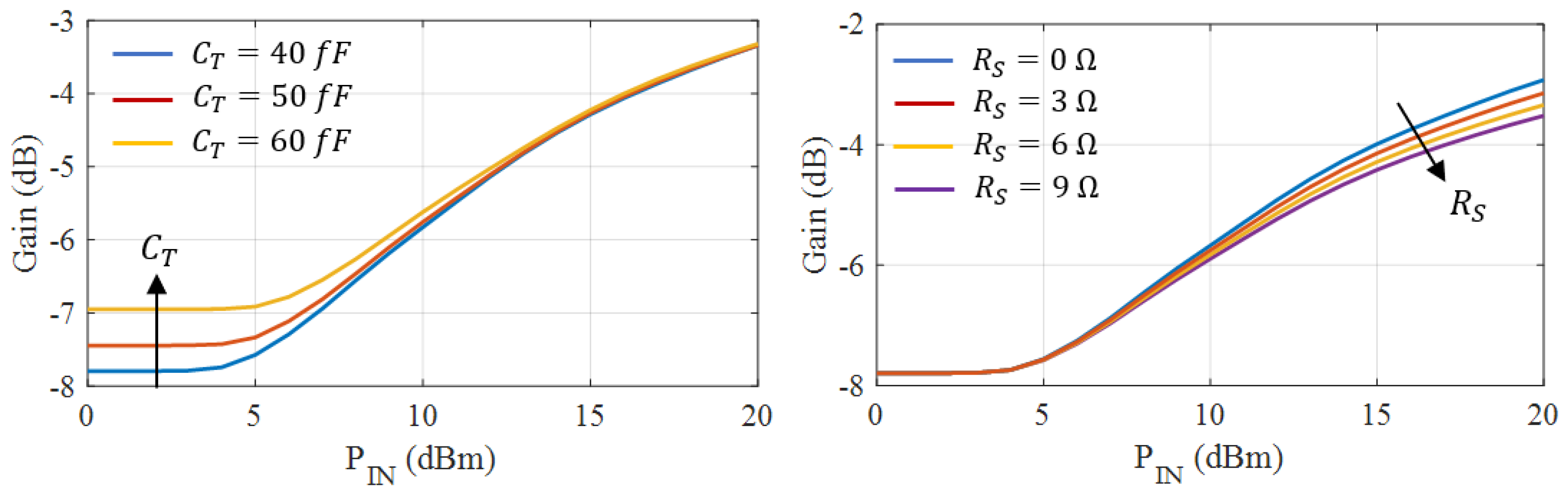
2.3. Impact of Diode Capacitance on APD Characteristics
2.4. Impact of Diode Series Resistance on APD Characteristics
2.5. Impact of Diode Ideality Factor on APD Characteristics
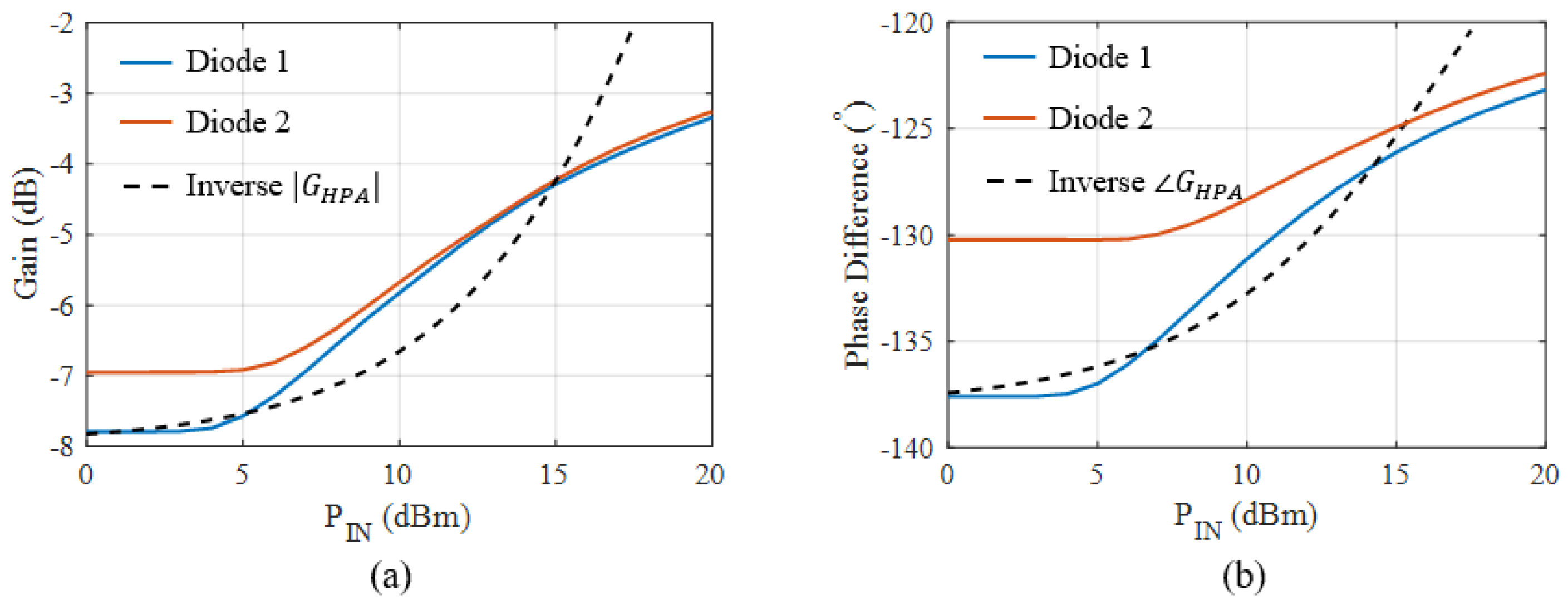
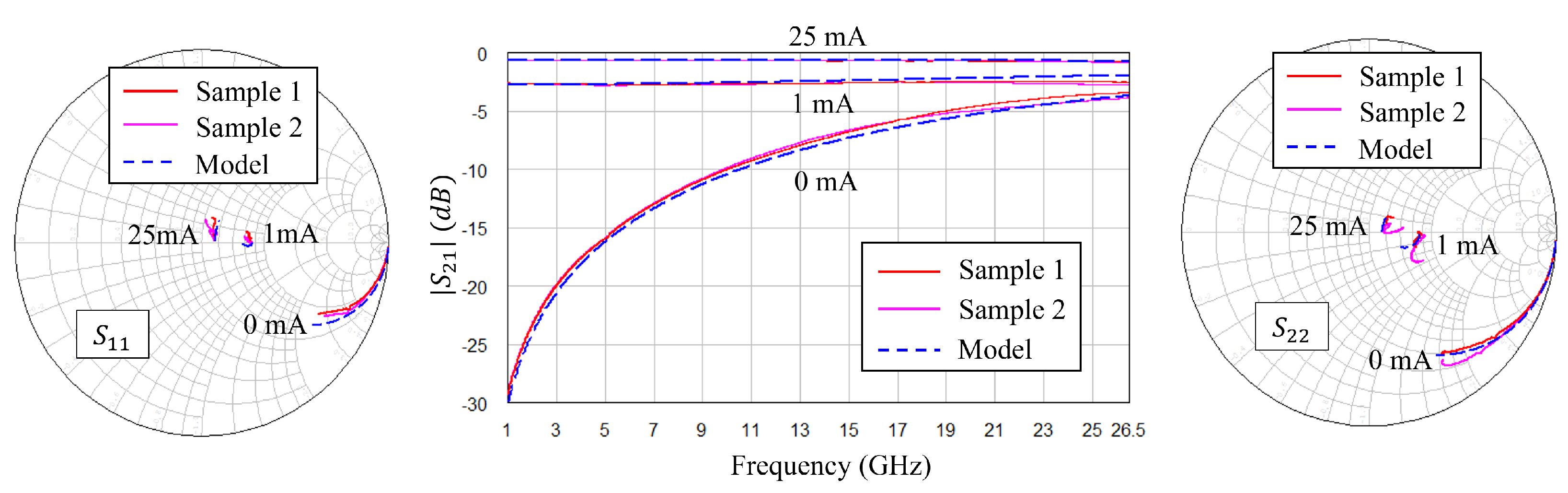
2.6. Model Validation
2.7. Diode Selection
3. Diode Modeling for APD Design
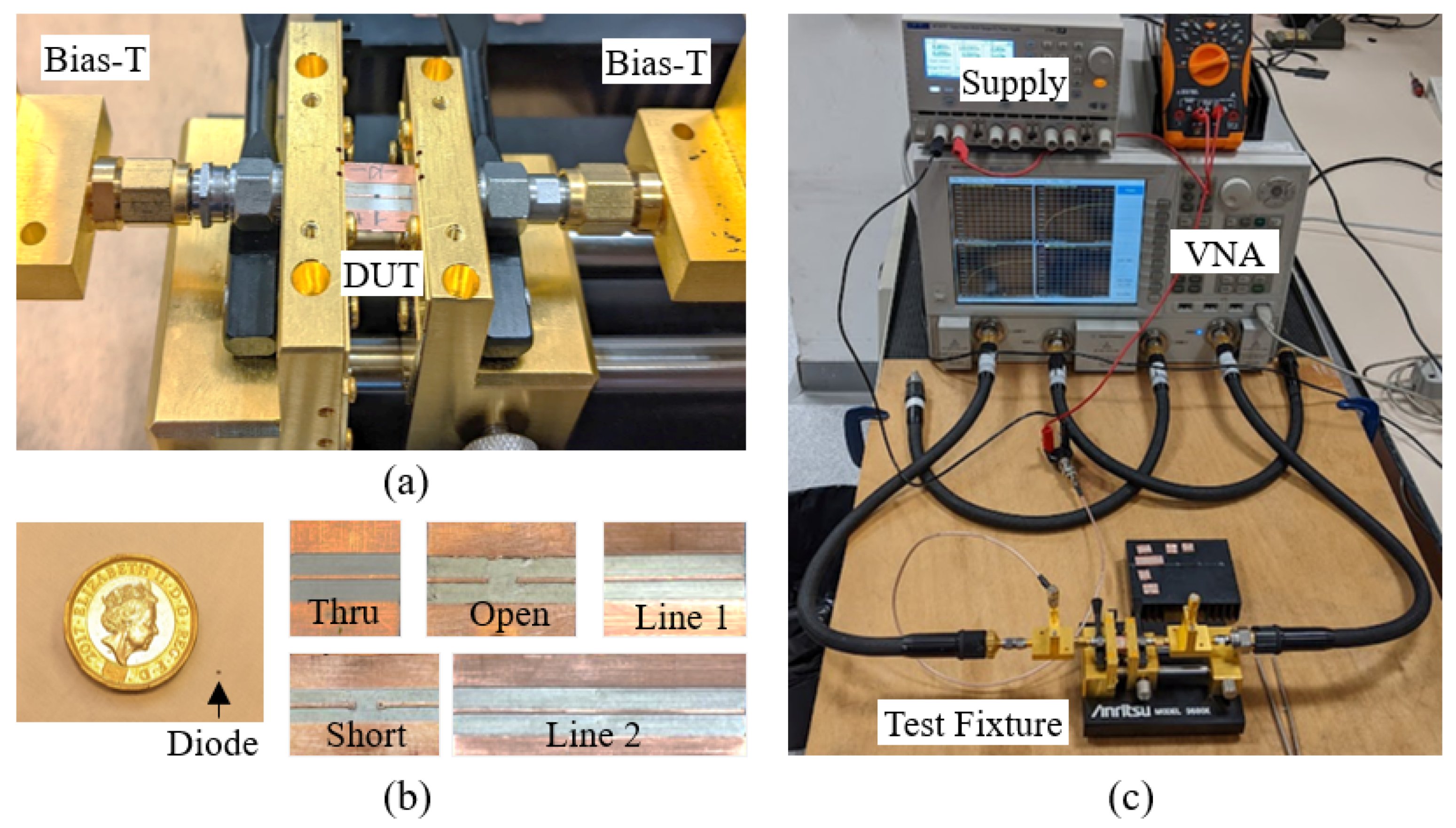
3.1. Diode Characterization
3.2. Diode Modeling
4. Linearizer Design and Characterization
4.1. Simulated APD with Measured HPA-in-the-Loop
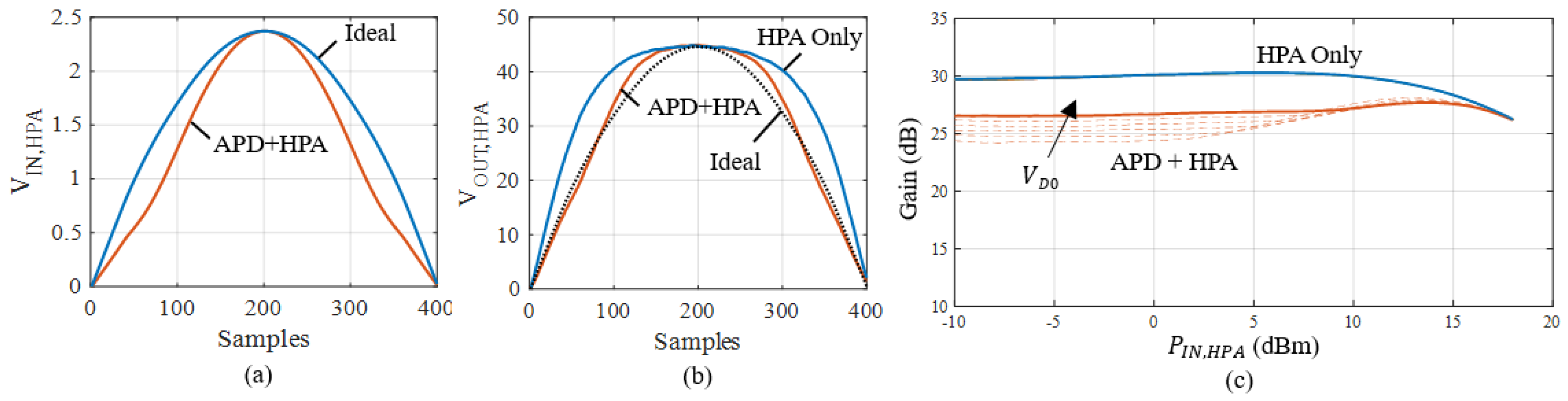
- A simulation with an amplitude-modulated sine wave at the APD input is performed to generate the pre-distorted signal, Figure 17a. This simulation is a time-domain harmonic balance (APLAC Transient in MWO);
- The pre-distorted signal is transferred to the measurement setup and is then applied to the HPA input. An optimal diode bias of V is found by iterating between (1) and (2). For V, the APD+HPA output amplitude approximates the ideal sine wave amplitude, Figure 17b.
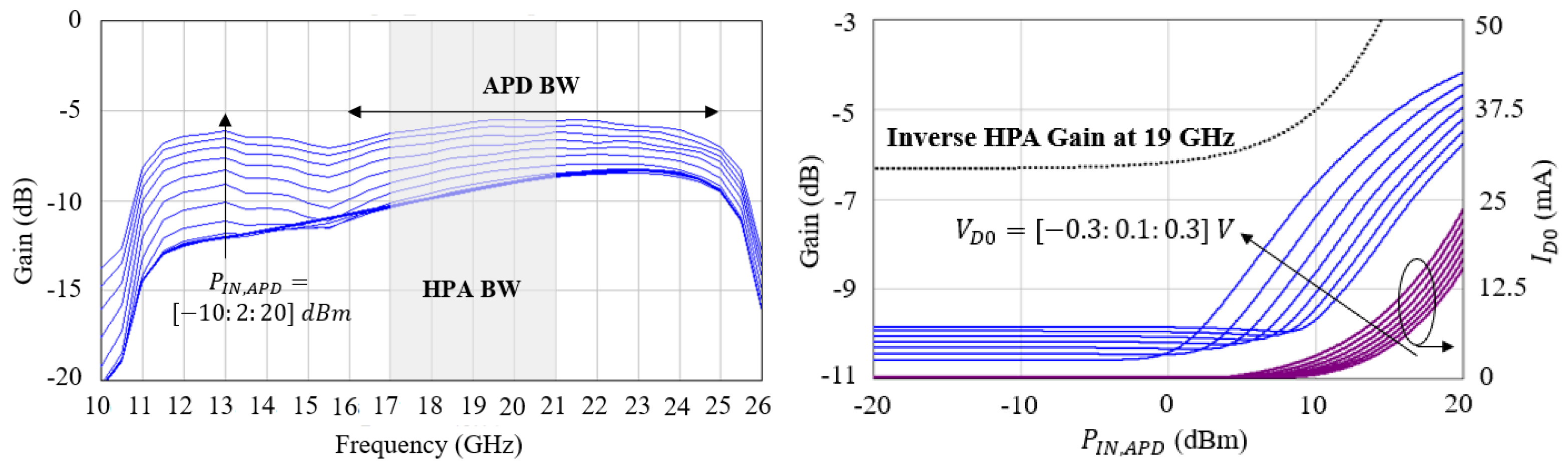
- The HPA gain with and without simulated APD is computed and reported in Figure 17c. As can be seen, the small-signal gain with APD at 19 GHz is reduced by approximately 4 dB, while at a large-signal, APD reduces the HPA gain compression (hence less distortion) for the same maximum output power.
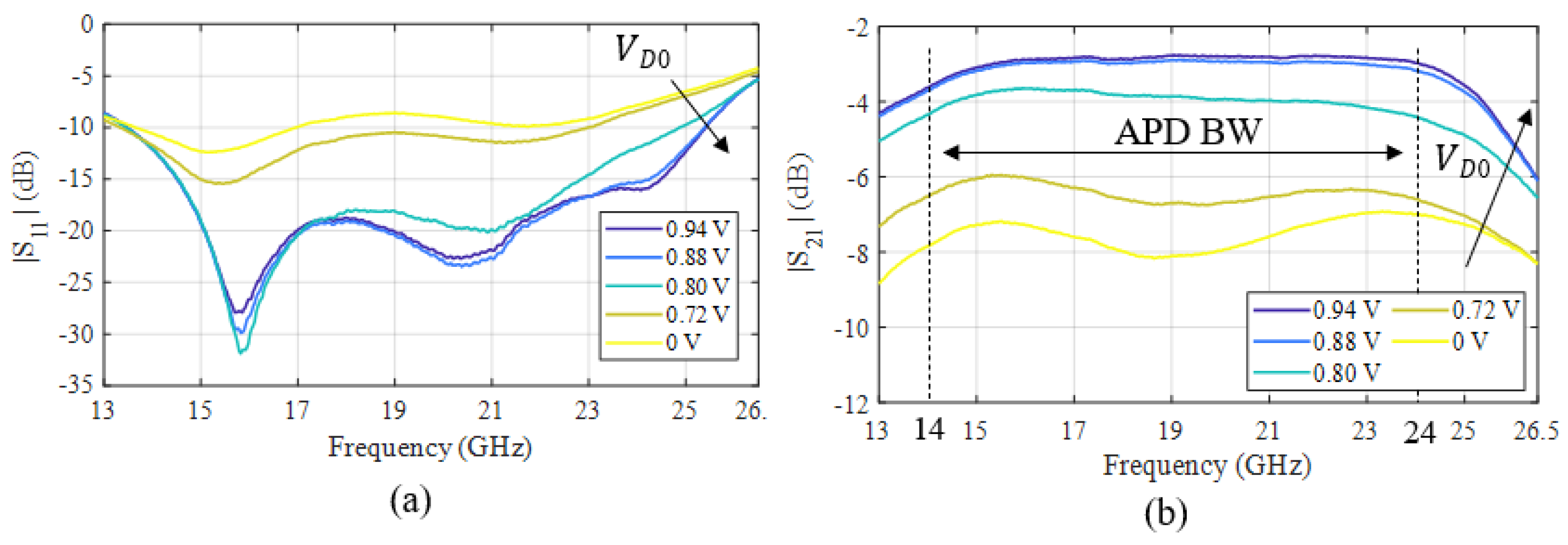
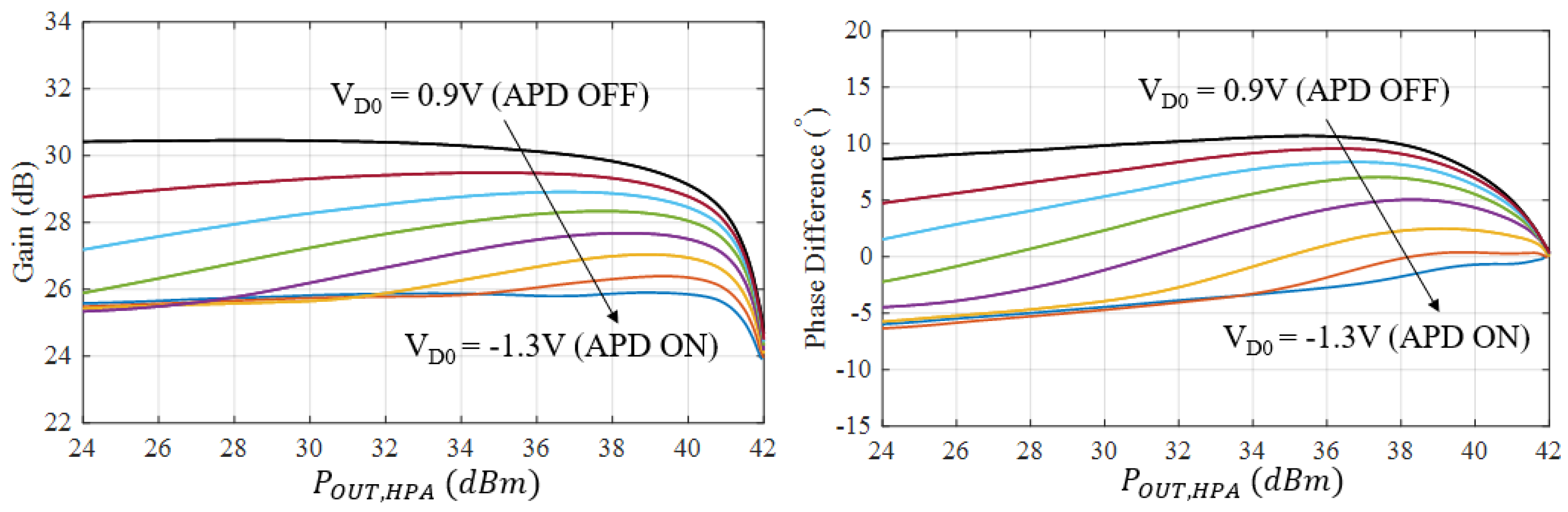
4.2. Small- and Large-Signal APD Characterization
5. APD-HPA Performance Evaluation
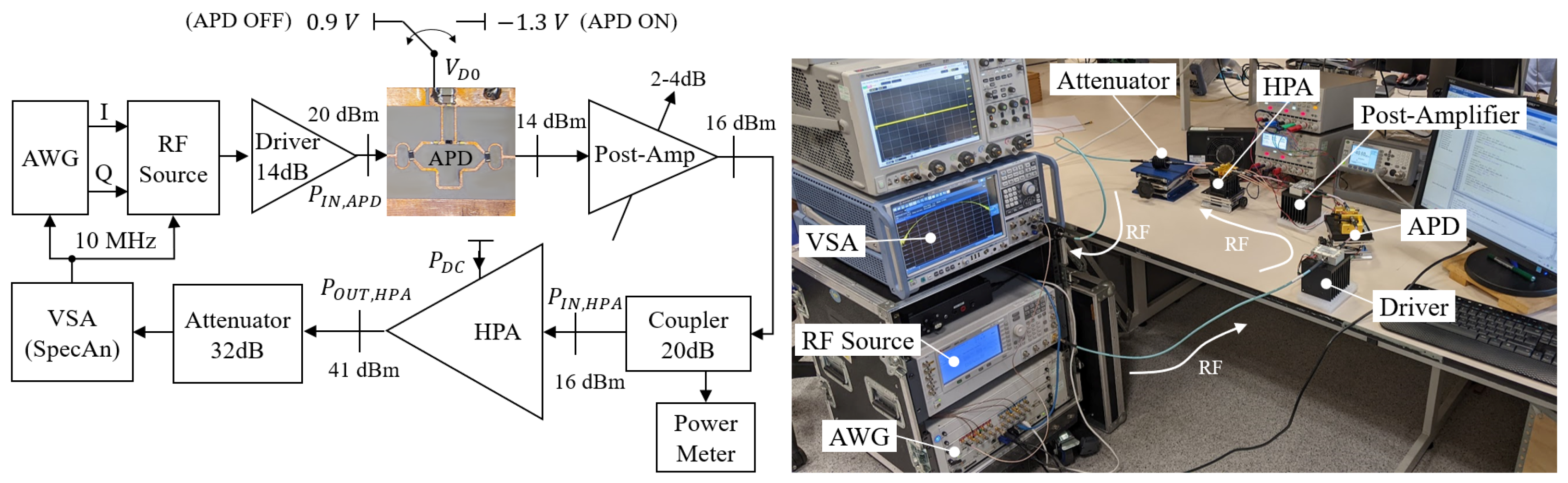
5.1. Wideband Measurement Setup
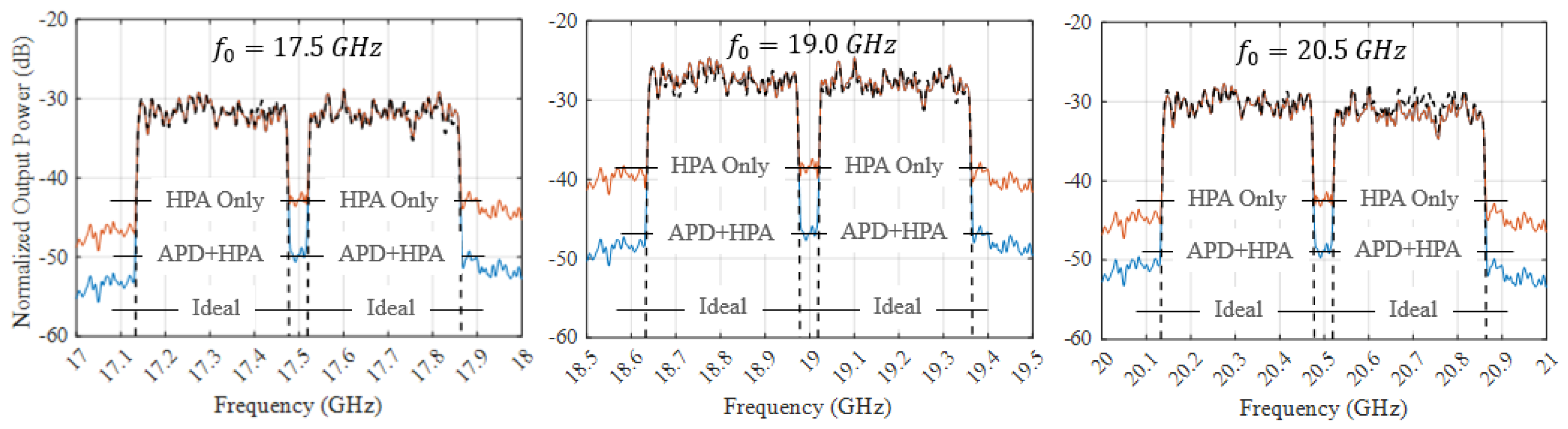
5.2. Performance with APD
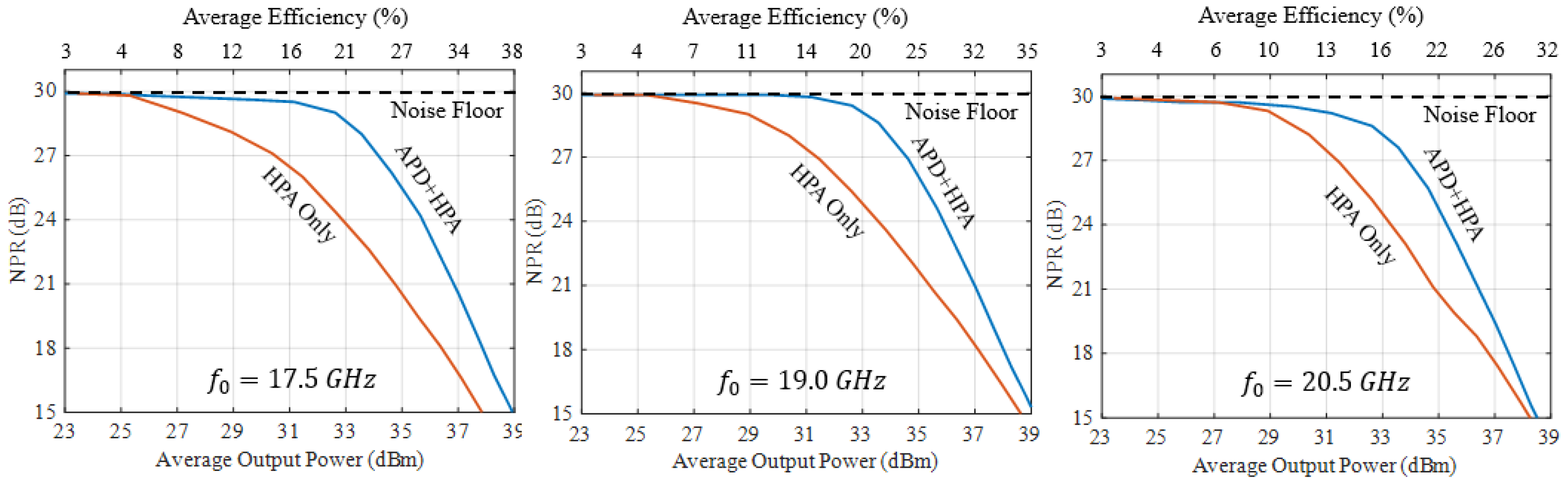
5.3. Estimated APD+HPA Efficiency Including Post-Amplifier
5.4. Comparison with State-of-the-Art
| Ref. | Archi. | Nonlinearity Generator | (GHz) | BW (GHz) | Fractional BW (%) | Small-Signal Gain (dB) | Gain Expansion (dB) | Phase Expansion (°) |
|---|---|---|---|---|---|---|---|---|
| [6] | Single Branch APD | Two Shunt Schottky Diodes | 2 | 0.1 | 5% | 12 | 5 | 25 |
| [9] | Single Shunt Diodes | 14 | 0.75 | 5% | - | 4 | 30 | |
| [10] | Two Shunt Schottky Diodes | 60 | 2 | 3% | 16 * | 8 | 28 | |
| [25] | Shunt Diodes | 6 | 0.4 | 7% | 17 | 6 | 20 | |
| [26] | Schottky + Varactor Diodes | 5 | - | - | 20 * | 4 | 30 | |
| [11] | Dual Branch APD | PIN Diodes | 30 | 2 | 7% | 20 * | 5 | 23 |
| [13] | Schottky Diode (MMIC) | 29 | 4 | 14% | 14 * | 8 * | 40 * | |
| [14] | Shunt Schottky Diode | 20 | 2 | 10% | 27 * | 4 * | 9 * | |
| [28] | GaN Amplifier | 0.8 | 0.2 | 25% | - | 2 * | 10 * | |
| [29] | GaAs Amp. + Diode (MMIC) | 26 | 2 | 8% | 10 | 4 | 40 | |
| [12] | Schottky Diode | 19 | 3 | 16% | - | 13 | 50 | |
| This | GaAs Schottky Diode | 18 | 6 | 33% | 8 | 3 | 8 |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Katz, A.; Gray, R.; Dorval, R. Truly wideband linearization. IEEE Microw. Mag. 2009, 10, 20–27. [Google Scholar] [CrossRef]
- Katz, A.; Wood, J.; Chokola, D. The evolution of pa linearization: From classic feedforward and feedback through analog and digital predistortion. IEEE Microw. Mag. 2016, 17, 32–40. [Google Scholar] [CrossRef]
- UMS. CHA8252-99F—10W K-Band High Power Amplifier. 2021. Available online: https://www.ums-rf.com (accessed on 7 May 2023).
- Kenington, P.B. High-Linearity RF Amplifier Design; Artech House: London, UK, 2000. [Google Scholar]
- Yamauchi, K.; Mori, K.; Nakayama, M.; Mitsui, Y.; Takagi, T. A microwave miniaturized linearizer using a parallel diode with a bias feed resistance. IEEE Trans. Microw. Theory Tech. 1997, 45, 2431–2435. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, C.; Liu, G.; Li, Q.; Wu, Y.; Xiao, G. A novel analog linearizer for solid-state power amplifier in satellite communication system. In Proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Chengdu, China, 7–11 May 2018; pp. 1–3. [Google Scholar]
- Yamauchi, K.; Mori, K.; Nakayama, M.; Itoh, Y.; Mitsui, Y.; Ishida, O. A novel series diode linearizer for mobile radio power amplifiers. In Proceedings of the 1996 IEEE MTT-S International Microwave Symposium Digest, San Francisco, CA, USA, 17–21 June 1996; Volume 2, pp. 831–834. [Google Scholar]
- Nakayama, M.; Mori, K.; Yamauchi, K.; Itoh, Y.; Takagi, T. A novel amplitude and phase linearizing technique for microwave power amplifiers. In Proceedings of the 1995 IEEE MTT-S International Microwave Symposium, Orlando, FL, USA, 16–20 May 1995; Volume 3, pp. 1451–1454. [Google Scholar]
- Mallet, C.; Duvanaud, C.; Carré, L.; Bachir, S. Analog predistortion for high power amplifier over the ku-band (13,75–14,5 ghz). In Proceedings of the 2017 47th European Microwave Conference (EuMC), Nuremberg, Germany, 10–12 October 2017; pp. 848–851. [Google Scholar]
- Jing, Y.; Xia, L.; Lv, S.; Liu, Y. A V-Band Diode-Based Analog Predistortion Linearizer for Traveling Wave Tube Amplifiers. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 7–10 May 2021. [Google Scholar]
- Gumber, K.; Rawat, M. Analogue predistortion lineariser control schemes for ultra-broadband signal transmission in 5g transmitters. IET Microwaves Antennas Propag. 2020, 14, 718–727. Available online: https://ietresearch.onlinelibrary.wiley.com/doi/abs/10.1049/iet-map.2019.0253 (accessed on 7 May 2023). [CrossRef]
- Liu, T.; Su, X.; Wang, G.; Zhao, B.; Fu, R.; Zhu, D. A Broadband Analog Predistortion Linearizer Based on GaAs MMIC for Ka-Band TWTAs. Electronics 2023, 12, 1503. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, D.; Lv, D.; Zhou, D.; Zhang, Y. Analog predistortion linearizer with independently tunable gain and phase conversions for ka-band twta. IEEE Trans. Electr. Devices 2019, 66, 1533–1539. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, W.; Feng, Z. A broadband analog predistortion linearizer based on tunable diodes for ka band power amplifier. In Proceedings of the 2020 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shanghai, China, 20–23 September 2020. [Google Scholar]
- Zhang, L.; Shi, H.; Yu, F. A k-band hybrid analog predistortion linearizer for dual inflection amplifier. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 28–31 October 2020. [Google Scholar]
- Cappello, T.; Ozan, S.; Tucker, A.; Krier, P.; Williams, T.; Morris, K. Enhancing the output power and efficiency for a set noise-power ratio of a k-band power amplifier by means of analog pre-distortion. In Proceedings of the 2024 IEEE Topical Conference on RF/Microwave Power Amplifiers for Radio and Wireless Applications (PAWR), San Antonio, TX, USA, 21–24 January 2024; pp. 1–4. [Google Scholar]
- Cappello, T.; Ozan, S.; McDonald, L.; Tucker, A.; Krier, P.; Williams, T.; Morris, K. A low loss, 6 ghz large-signal bandwidth analog pre-distortion linearizer for k-band high power amplifiers. In Proceedings of the 2023 53rd European Microwave Conference (EuMC), Berlin, Germany, 19–21 September 2023; pp. 368–371. [Google Scholar]
- Piacibello, A.; Rubio, J.J.M.; Quaglia, R.; Camarchia, V. Am/pm characterization of wideband power amplifiers. In Proceedings of the 2022 IEEE Topical Conference on RF/Microwave Power Amplifiers for Radio and Wireless Applications (PAWR), Las Vegas, NV, USA, 16–19 January 2022; pp. 82–85. [Google Scholar]
- MACOM. MA4E1310—Gaas Flip Chip Schottky Barrier Diode. 2022. Available online: https://cdn.macom.com/datasheets/MA4E1310.pdf (accessed on 7 May 2023).
- Luo, H.; Hu, W.; Guo, Y. Parameter extraction and modeling of schottky diodes: An extension of the resonance based inductance extraction method. In Proceedings of the 2021 IEEE MTT-S International Wireless Symposium (IWS), Nanjing, China, 23–26 May 2021; pp. 1–3. [Google Scholar]
- NASA. EEE Parts Derating. Available online: https://extapps.ksc.nasa.gov/Reliability/Documents/Preferred_Practices/1201.pdf (accessed on 7 May 2023).
- Cappello, T.; Popovic, Z.; Morris, K.; Cappello, A. Gaussian pulse characterization of rf power amplifiers. IEEE Microw. Wirel. Compon. Lett. 2021, 31, 417–420. [Google Scholar] [CrossRef]
- Cappello, T.; Duh, A.; Barton, T.W.; Popovic, Z. A dual-band dual-output power amplifier for carrier aggregation. IEEE Trans. Microw. Theory Tech. 2019, 67, 3134–3146. [Google Scholar] [CrossRef]
- UMS. CHA4253aQQG—17–24GHz Medium Power Amplifier. 2020. Available online: https://www.ums-rf.com/product/cha4253aqqg/ (accessed on 7 May 2023).
- MACOM. MAAM-011132—16.4–23.6 GHz Driver Amplifier. Available online: https://cdn.macom.com/datasheets/MAAM-011132.pdf (accessed on 7 May 2023).
- Qorvo. CMD291—16–24 GHz Driver Amplifier. 2022. Available online: https://www.qorvo.com/products/p/CMD291 (accessed on 7 May 2023).
- Deng, H.; Lv, D.; Zhang, Y.; Zhang, D.; Zhou, D. Compact analog predistorter with shape tuning capability using power-dependent impedance matching network. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1705–1709. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, D.; Ma, J.; Yan, M.; Bian, C. Reflective adjustable analog predistorter for dual inflection point amplifiers. In Proceedings of the 2023 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Qingdao, China, 14–17 May 2023; pp. 1–3. [Google Scholar]
- Hu, Y.; Boumaiza, S. Doherty power amplifier distortion correction using an rf linearization amplifier. IEEE Trans. Microw. Theory Tech. 2018, 66, 2246–2257. [Google Scholar] [CrossRef]
- Villemazet, J.-F.; Yahi, H.; Lefebvre, B.; Baudeigne, F.; Maynard, J.; Soubercaze-Pun, G.; Lapierre, L. New ka-band analog predistortion linearizer allowing a 2.9 ghz instantaneous wideband satellite operation. In Proceedings of the 2017 12th European Microwave Integrated Circuits Conference (EuMIC), Nuremberg, Germany, 8–10 October 2017; pp. 302–305. [Google Scholar]


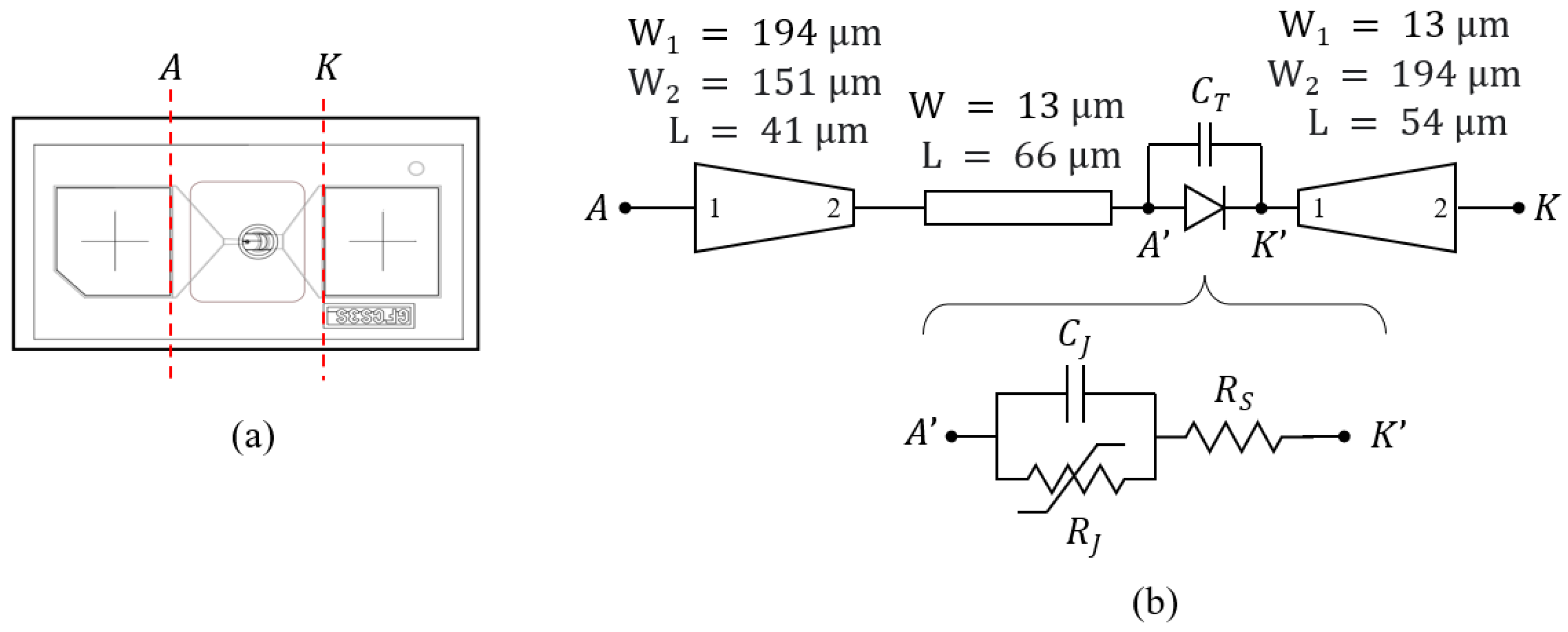


| Diode ID | BV | n | ||||
|---|---|---|---|---|---|---|
| Diode 1 | 7 V | 0.2 pA | 1.2 | 6 | 40 fF | 663 GHz |
| Diode 2 | 7 V | 3.0 pA | 1.4 | 4 | 50 fF | 765 GHz |
| Case | NPR | Frequency | |||||
|---|---|---|---|---|---|---|---|
| HPA Only | 28 dB | 19 GHz | 31.0 dBm | 9.0 W | - | 14% | 14% |
| APD + HPA | 28 dB | 19 GHz | 34.2 dBm | 11.4 W | 0.7 W | 23% | 22% |
| HPA Only | 24 dB | 19 GHz | 33.5 dBm | 10.7 W | - | 21% | 21% |
| APD + HPA | 24 dB | 19 GHz | 36.0 dBm | 13.7 W | 0.7 W | 29% | 27% |
| HPA Only | 20 dB | 19 GHz | 35.8 dBm | 14.1 W | - | 27% | 27% |
| APD + HPA | 20 dB | 19 GHz | 37.1 dBm | 15.9 W | 0.7 W | 32% | 31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappello, T.; Ozan, S.; Tucker, A.; Krier, P.; Williams, T.; Morris, K. Modeling, Design, and Application of Analog Pre-Distortion for the Linearity and Efficiency Enhancement of a K-Band Power Amplifier. Electronics 2024, 13, 3818. https://doi.org/10.3390/electronics13193818
Cappello T, Ozan S, Tucker A, Krier P, Williams T, Morris K. Modeling, Design, and Application of Analog Pre-Distortion for the Linearity and Efficiency Enhancement of a K-Band Power Amplifier. Electronics. 2024; 13(19):3818. https://doi.org/10.3390/electronics13193818
Chicago/Turabian StyleCappello, Tommaso, Sarmad Ozan, Andy Tucker, Peter Krier, Tudor Williams, and Kevin Morris. 2024. "Modeling, Design, and Application of Analog Pre-Distortion for the Linearity and Efficiency Enhancement of a K-Band Power Amplifier" Electronics 13, no. 19: 3818. https://doi.org/10.3390/electronics13193818
APA StyleCappello, T., Ozan, S., Tucker, A., Krier, P., Williams, T., & Morris, K. (2024). Modeling, Design, and Application of Analog Pre-Distortion for the Linearity and Efficiency Enhancement of a K-Band Power Amplifier. Electronics, 13(19), 3818. https://doi.org/10.3390/electronics13193818






