A Prediction Model for Pressure and Temperature in Geothermal Drilling Based on Physics-Informed Neural Networks
Abstract
:1. Introduction
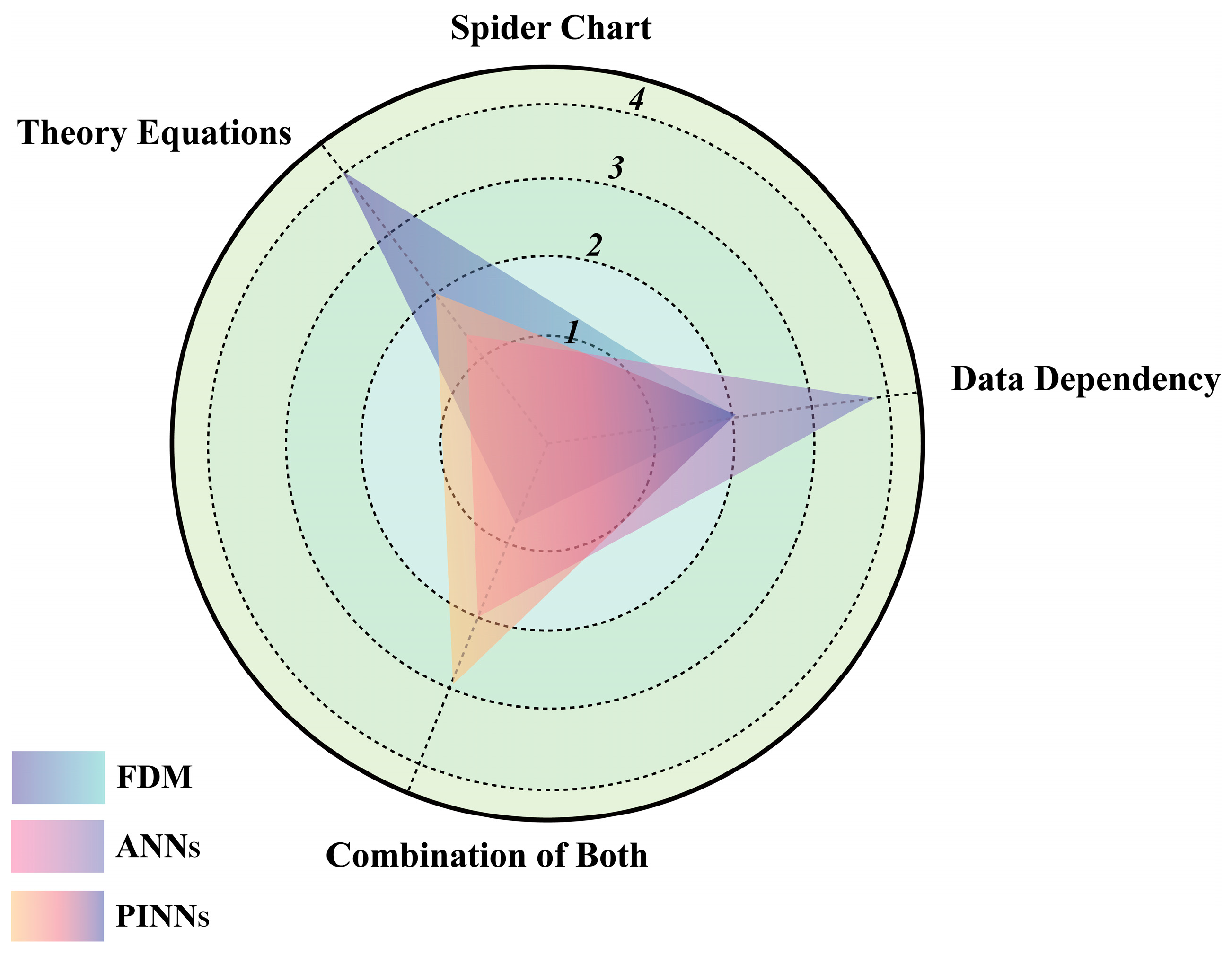
- It is the first to apply Physics-Informed Neural Networks (PINNs) to geothermal drilling modeling;
- The model enhances applicability in situations with limited data by reducing dependence on large-scale datasets;
- The predictive capabilities of ANNs and PINNs were tested through a real-world case, validating the model’s generalization ability.
2. Methodology
2.1. Gas–Liquid Two-Phase Flow
2.2. Physics-Informed Neural Networks
3. Wellbore Prediction Model Based on PINNs
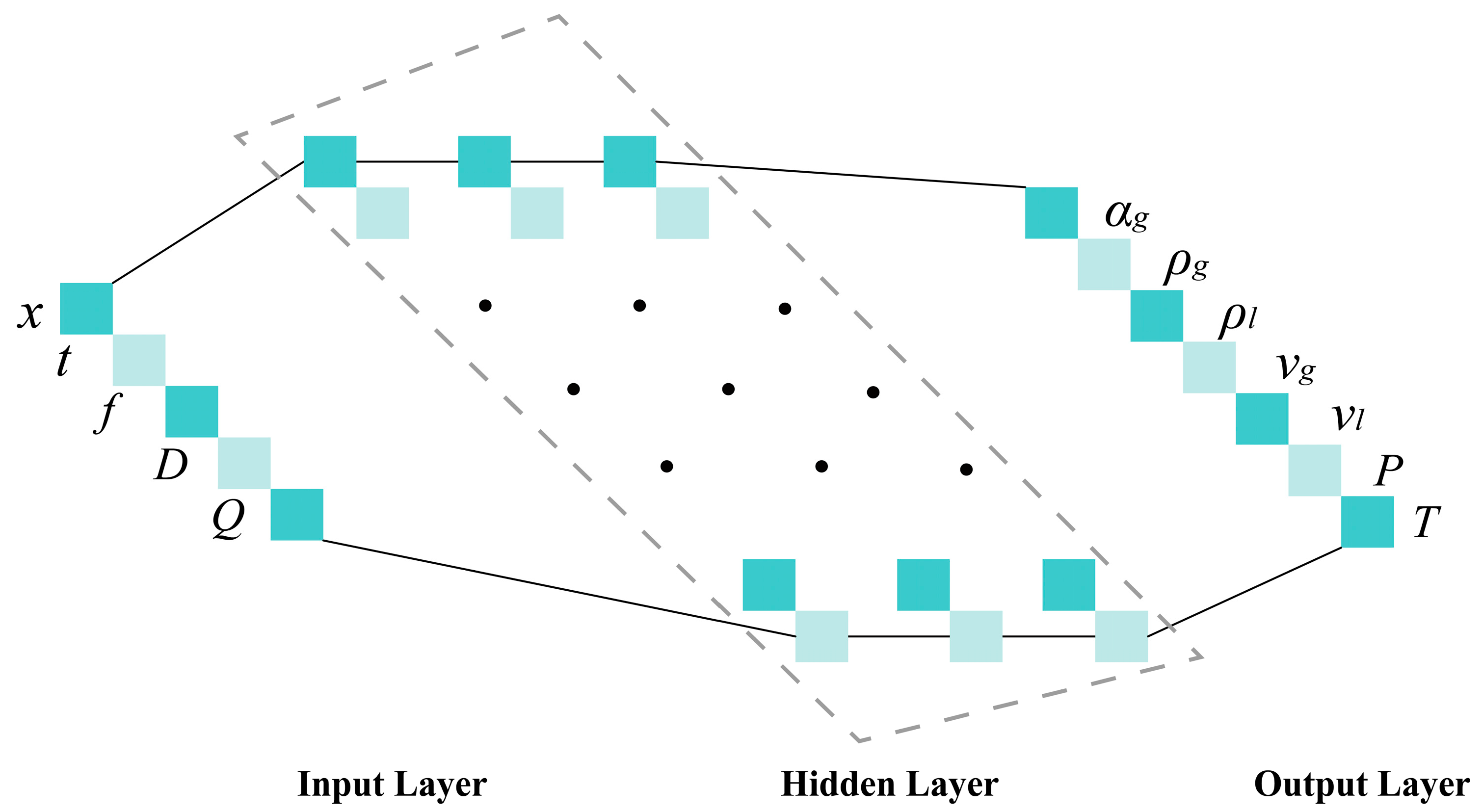
3.1. PINN Design
3.1.1. Network Input and Output Parameters
3.1.2. Network Structure
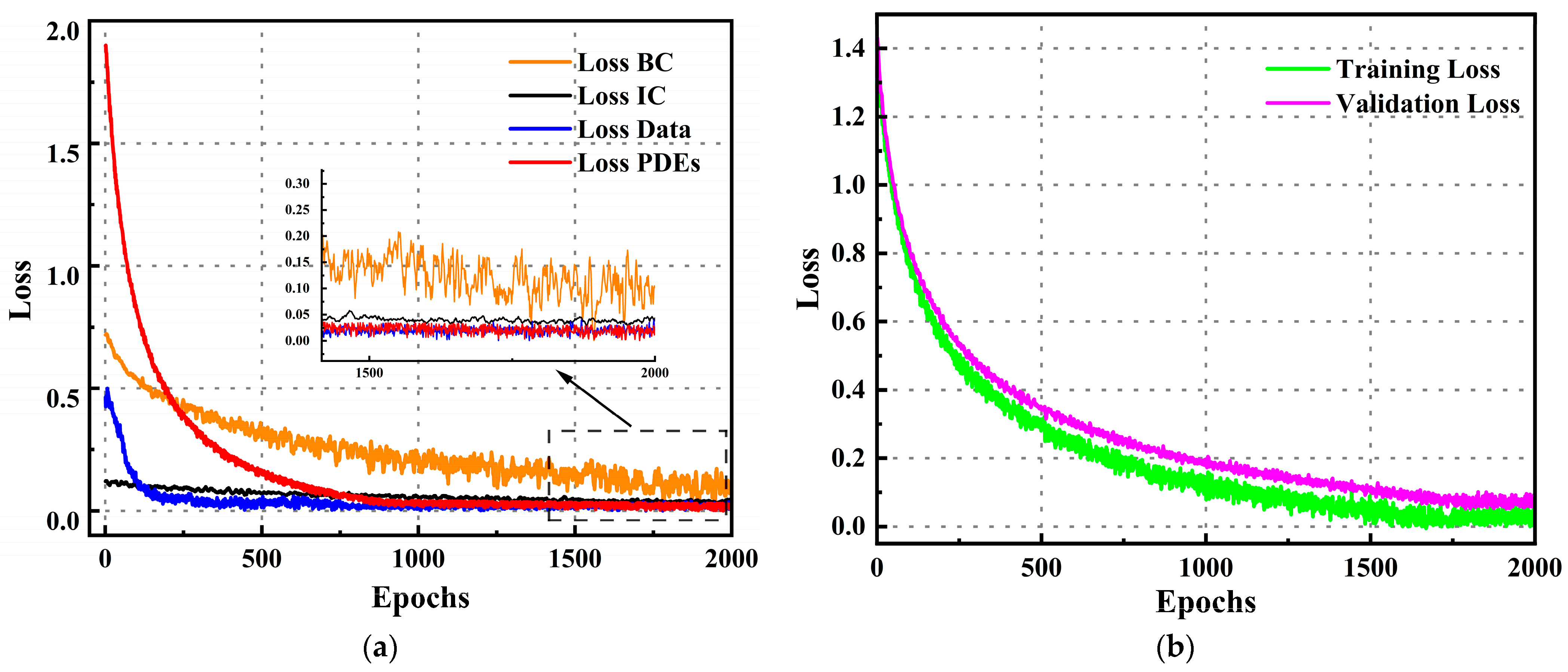
3.2. Network Training
3.2.1. Training Data Setup
3.2.2. Model Loss Function
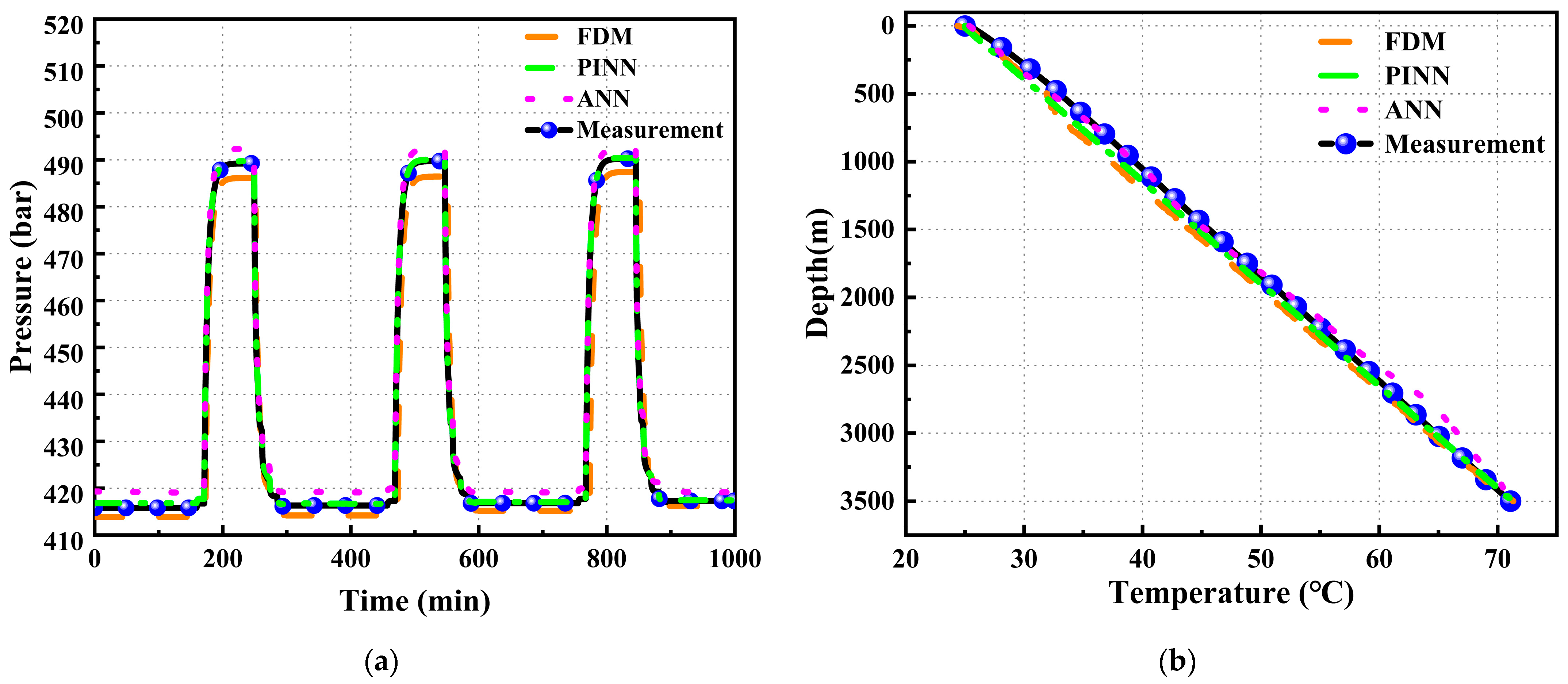
3.3. Prediction Model Validation Analysis
4. Results and Discussion
4.1. Network Test
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | wellbore diameter, mm |
| e | specific internal energy, J/kg |
| f | wellbore friction coefficient |
| kf | formation thermal conductivity |
| P | wellbore pressure, Pa |
| Q | energy change value, W/m2 |
| ri | wellbore radius, mm |
| v | velocity, m/s |
| vm | mixture velocity, m/s |
| ρ | phase density, kg/m3 |
| α | volume fraction |
| ρm | mixture density, kg/m3 |
| neural network | |
| w | weight |
| b | bias |
| λ | physical parameter |
| δi | weight coefficients for the loss |
| i(θ) | loss |
| η | learning rate |
| m | mini-batch size |
References
- Xu, C.; Li, J.; Yang, R.-Z.; Chen, J.-R.; Tan, H. An Improved Fracture Seismic Method for identifying the drilling targets of medium-deep geothermal resources: A case study on heishan geothermal area. Geothermics 2024, 120, 103019. [Google Scholar] [CrossRef]
- Zuo, Y.-H.; Sun, Y.-G.; Zhang, L.-Q.; Zhang, C.; Wang, Y.-C.; Jiang, G.-Z.; Wang, X.-G.; Zhang, T.; Cui, L.-Q. Geothermal resource evaluation in the Sichuan Basin and suggestions for the development and utilization of abandoned oil and gas wells. Renew. Energy 2024, 225, 120362. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, W.-Q.; Zhang, J.-W.; Lei, J.-K.; Xu, X.-H.; Bian, L.-H. A Novel Geothermal Wellbore Model Based on the Drift-Flux Approach. Energies 2024, 17, 3569. [Google Scholar] [CrossRef]
- Chen, X.; Wang, S.-W.; He, M.; Xu, M.-B. A comprehensive prediction model of drilling wellbore temperature variation mechanism under deepwater high temperature and high pressure. Ocean. Eng. 2024, 296, 117063. [Google Scholar] [CrossRef]
- Akbar, S.; Fathianpour, N.; Al-Khoury, R. A finite element model for high enthalpy two-phase flow in geothermal wellbores. Renew. Energy 2016, 94, 223–236. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Xiong, Y.-M.; Peng, G.; Wang, G.-R.; Lu, J.-S.; Zhong, L.; Wang, J.P.; Yan, Z.-Y.; Wei, R.-H. Study on borehole temperature distribution when the well-kick and the well-leakage occurs simultaneously during geothermal well drilling. Geothermics 2022, 104, 102441. [Google Scholar] [CrossRef]
- Xu, Z.-M.; Song, X.-Z.; Li, G.-S.; Wu, K.; Pang, Z.-Y.; Zhu, Z.-P. Development of a transient non-isothermal two-phase flow model for gas kick simulation in HTHP deep well drilling. Appl. Therm. Eng. 2018, 141, 1055–1069. [Google Scholar] [CrossRef]
- Alvarez Del Castillo, A.; Santoyo, E.; García-Valladares, O. A new void fraction correlation inferred from artificial neural networks for modeling two-phase flows in geothermal wells. Comput. Geosci. 2012, 41, 25–39. [Google Scholar] [CrossRef]
- Spesivtsev, P.; Sinkov, K.; Sofronov, I.; Zimina, A.; Umnov, A.; Yarullin, R.; Vetrov, D. Predictive model for bottomhole pressure based on machine learning. J. Pet. Sci. Eng. 2018, 166, 825–841. [Google Scholar] [CrossRef]
- Aydin, H.; Akin, S.; Senturk, E. A proxy model for determining reservoir pressure and temperature for geothermal wells. Geothermics 2020, 88, 101916. [Google Scholar] [CrossRef]
- Bassam, A.; Castillo, A.A.D.; García-Valladares, O.; Santoyo, E. Determination of pressure drops in flowing geothermal wells by using artificial neural networks and wellbore simulation tools. Appl. Therm. Eng. 2015, 75, 1217–1228. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.-R.; Zhao, Q.; Liu, W.; Song, X.-Z.; Ji, Y.-Y.; Wang, J.-S. A new method for intelligent prediction of drilling overflow and leakage based on multi-parameter fusion. Energies 2022, 15, 5988. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Alzayer, B.M.; Panagopoulos, G.; Kiomourtzi, P.; Kirmizakis, P.; Elkatatny, S.; Soupios, P. A New Empirical Correlation for Pore Pressure Prediction Based on Artificial Neural Networks Applied to a Real Case Study. Processes 2024, 12, 664. [Google Scholar] [CrossRef]
- Muojeke, S.; Venkatesan, R.; Khan, F. Supervised data-driven approach to early kick detection during drilling operation. J. Pet. Sci. Eng. 2020, 192, 107324. [Google Scholar] [CrossRef]
- Zhu, Z.-P.; Liu, Z.-H.; Song, X.-Z.; Zhu, S.; Zhou, M.-M.; Li, G.-S.; Duan, S.-M.; Ma, B.-D.; Ye, S.-L.; Zhang, R. A physics-constrained data-driven workflow for predicting bottom hole pressure using a hybrid model of artificial neural network and particle swarm optimization. Geoenergy Sci. Eng. 2023, 224, 211625. [Google Scholar] [CrossRef]
- Wang, C.-G.; Evans, K.; Hartley, D.; Morrison, S.; Veidt, M.; Wang, G. A systematic review of artificial neural network techniques for analysis of foot plantar pressure. Biocybern. Biomed. Eng. 2024, 44, 197–208. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Chakraverty, S. Machine intelligence in dynamical systems:\A state-of-art review. WIREs Data Min. Knowl. Discov. 2022, 12, e1461. [Google Scholar] [CrossRef]
- Najjarpour, M.; Jalalifar, H.; Norouzi-Apourvari, S. Half a century experience in rate of penetration management: Application of machine learning methods and optimization algorithms—A review. J. Pet. Sci. Eng. 2022, 208, 109575. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Cai, S.-Z.; Mao, Z.-P.; Wang, Z.-C.; Yin, M.-L.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Zhang, C.; Shafieezadeh, A. Nested physics-informed neural network for analysis of transient flows in natural gas pipelines. Eng. Appl. Artif. Intell. 2023, 122, 106073. [Google Scholar] [CrossRef]
- Cai, S.-Z.; Wang, Z.-C.; Wang, S.-F.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks for heat transfer problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Nazari, L.F.; Camponogara, E.; Imsland, L.S.; Seman, L.O. Neural networks informed by physics for modeling mass flow rate in a production wellbore. Eng. Appl. Artif. Intell. 2024, 128, 107528. [Google Scholar] [CrossRef]
- Tonkin, R.A.; O’Sullivan, M.J.; O’Sullivan, J.P. A review of mathematical models for geothermal wellbore simulation. Geothermics 2021, 97, 102255. [Google Scholar] [CrossRef]
- Tonkin, R.A.; O’Sullivan, J.; Gravatt, M.; O’Sullivan, M. A transient geothermal wellbore simulator. Geothermics 2023, 110, 102653. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Wellbore heat-transfer modeling and applications. J. Pet. Technol. 2012, 86, 127–136. [Google Scholar] [CrossRef]
- Wang, S.-F.; Teng, Y.-J.; Perdikaris, P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Wang, S.-F.; Yu, X.; Perdikaris, P. When and why PINNs fail to train: A neural tangent kernel perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]
- Garg, S.K.; Pritchett, J.W.; Alexander, J.H. Development of New Geothermal Wellbore Holdup Correlations Using Flowing Well; Idaho National Lab. (INL): Idaho Falls, ID, USA, 2004. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Depth (m) | 3500 |
| Wellbore diameter (mm) | 222 |
| Drillpipe ID (mm) | 119 |
| Drillpipe OD (mm) | 159 |
| Gas injection rate (m3/s) | 0.263 |
| Surface temperature (°C) | 25 |
| Bottomhole temperature (°C) | 71.1 |
| Casing ID (mm) | 306 |
| Casing OD (mm) | 350 |
| Mud density (kg/m3) | 1066.45 |
| Parameter | Value |
|---|---|
| Depth (m) | 248.4 |
| Vertical depth (m) | 248.4 |
| Angle with vertical (degrees) | 0 |
| 0–159.7 m Internal diameter (mm) | 102 |
| 159.7–248.4 m Internal diameter (mm) | 99 |
| Depth (m) | 248.4 |
| Surface temperature (°C) | 22 |
| Bottomhole temperature (°C) | 163.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Li, W.; Bian, L.; Lei, J. A Prediction Model for Pressure and Temperature in Geothermal Drilling Based on Physics-Informed Neural Networks. Electronics 2024, 13, 3869. https://doi.org/10.3390/electronics13193869
Yuan Y, Li W, Bian L, Lei J. A Prediction Model for Pressure and Temperature in Geothermal Drilling Based on Physics-Informed Neural Networks. Electronics. 2024; 13(19):3869. https://doi.org/10.3390/electronics13193869
Chicago/Turabian StyleYuan, Yin, Weiqing Li, Lihan Bian, and Junkai Lei. 2024. "A Prediction Model for Pressure and Temperature in Geothermal Drilling Based on Physics-Informed Neural Networks" Electronics 13, no. 19: 3869. https://doi.org/10.3390/electronics13193869
APA StyleYuan, Y., Li, W., Bian, L., & Lei, J. (2024). A Prediction Model for Pressure and Temperature in Geothermal Drilling Based on Physics-Informed Neural Networks. Electronics, 13(19), 3869. https://doi.org/10.3390/electronics13193869





