Increasing Microwave Penetration Depth in the Human Body by a Complex Impedance Match of Skin Interface with a Two-Layered Medium
Abstract
:1. Introduction
2. Method
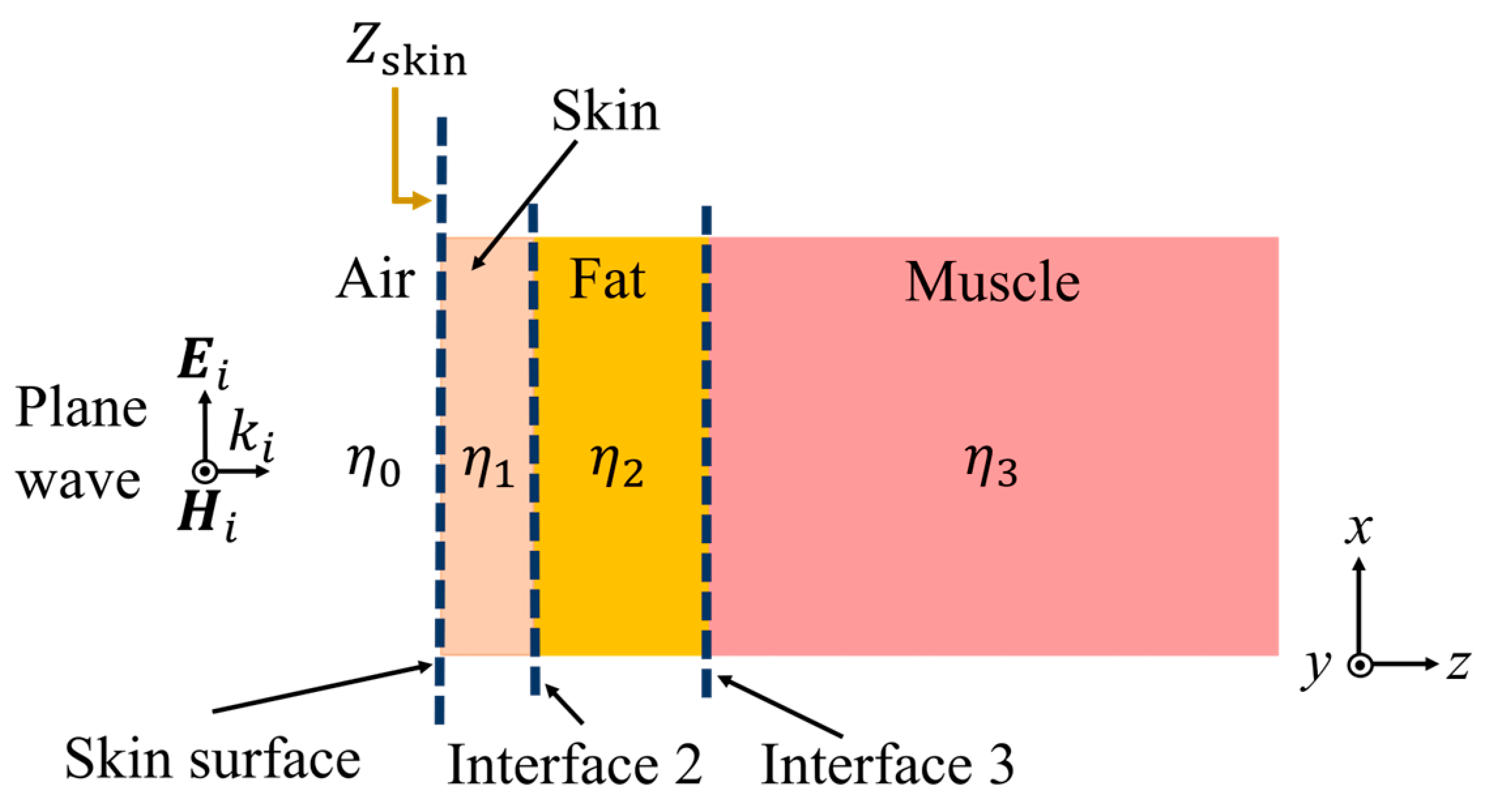
2.1. Impedance Deduction of the Skin Surface
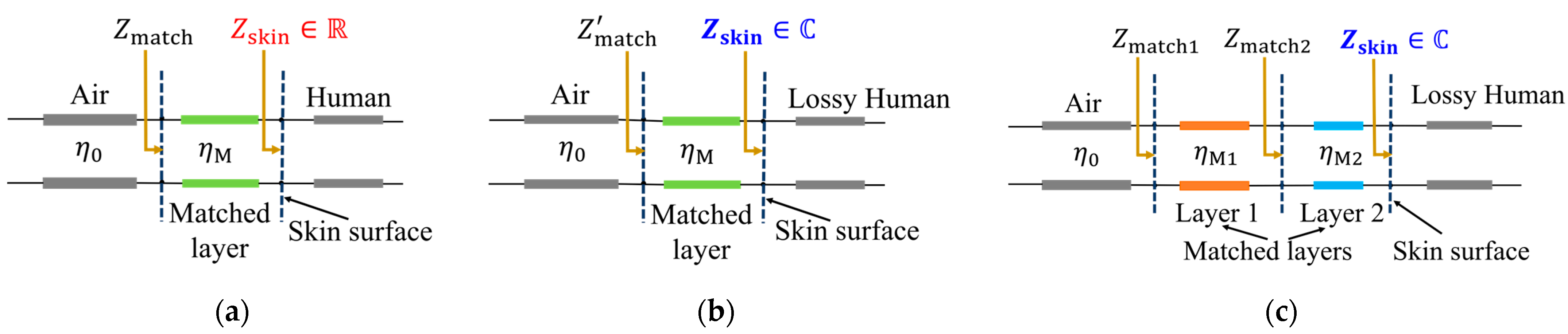
2.2. A Single-Layered Medium Match for a Real Impedance Model of the Skin Surface
2.3. A Single-Layered Medium Match for a Complex Impedance Model of the Skin Surface
2.4. A Two-Layered Medium Match for a Complex Impedance Model of the Skin Surface
3. Simulations and Results
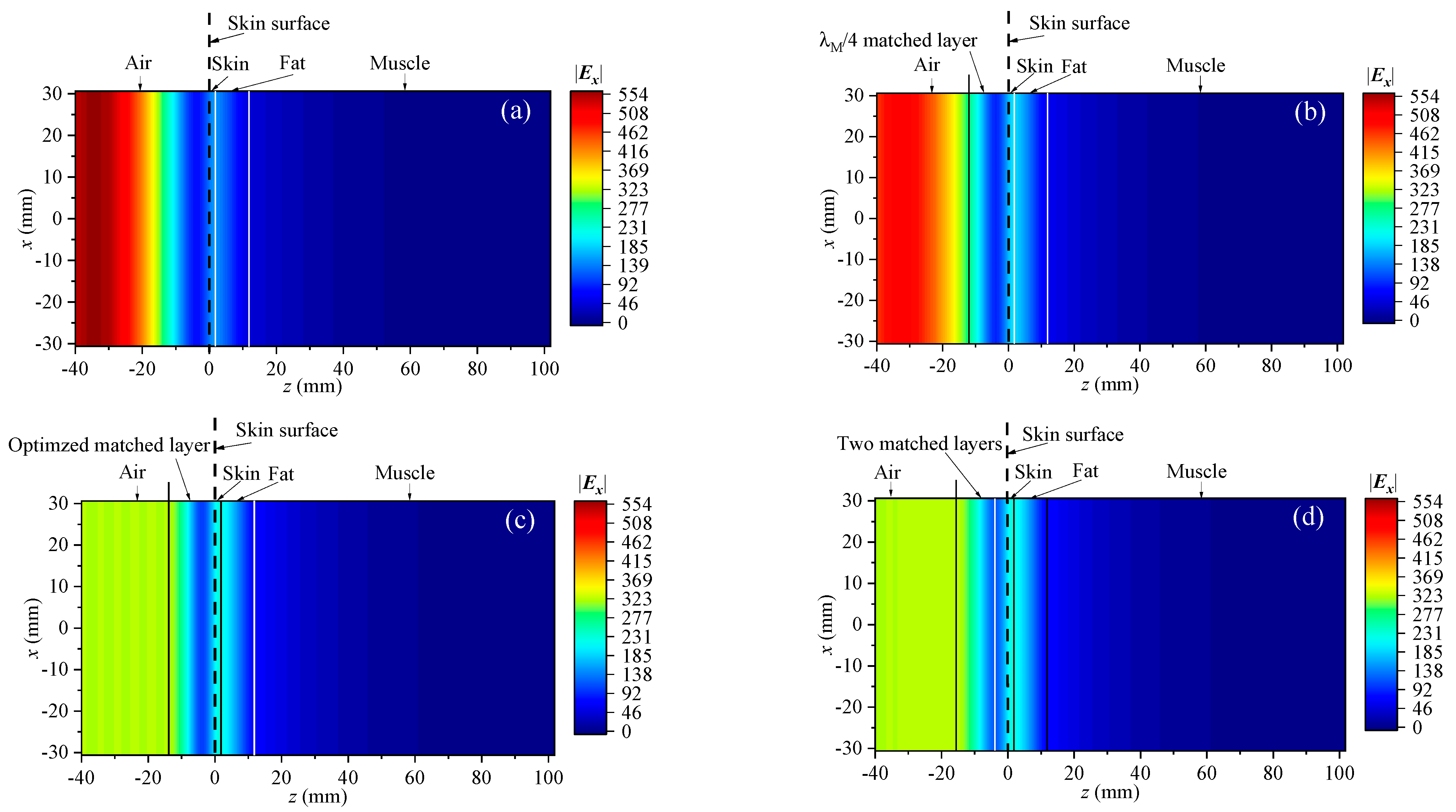
3.1. Simulation Models
3.2. Full-Wave Results
4. Discussion
4.1. Comparison of Different Impedance Match Methods on Microwave Penetration Effects
4.2. Comparison of Microwave Penetration Effects of the Proposed Method at Different Frequencies Commonly Used in Medicine Applications
4.3. Comparison of Microwave Penetration Effects of the Proposed Method in Different Human Tissue Models
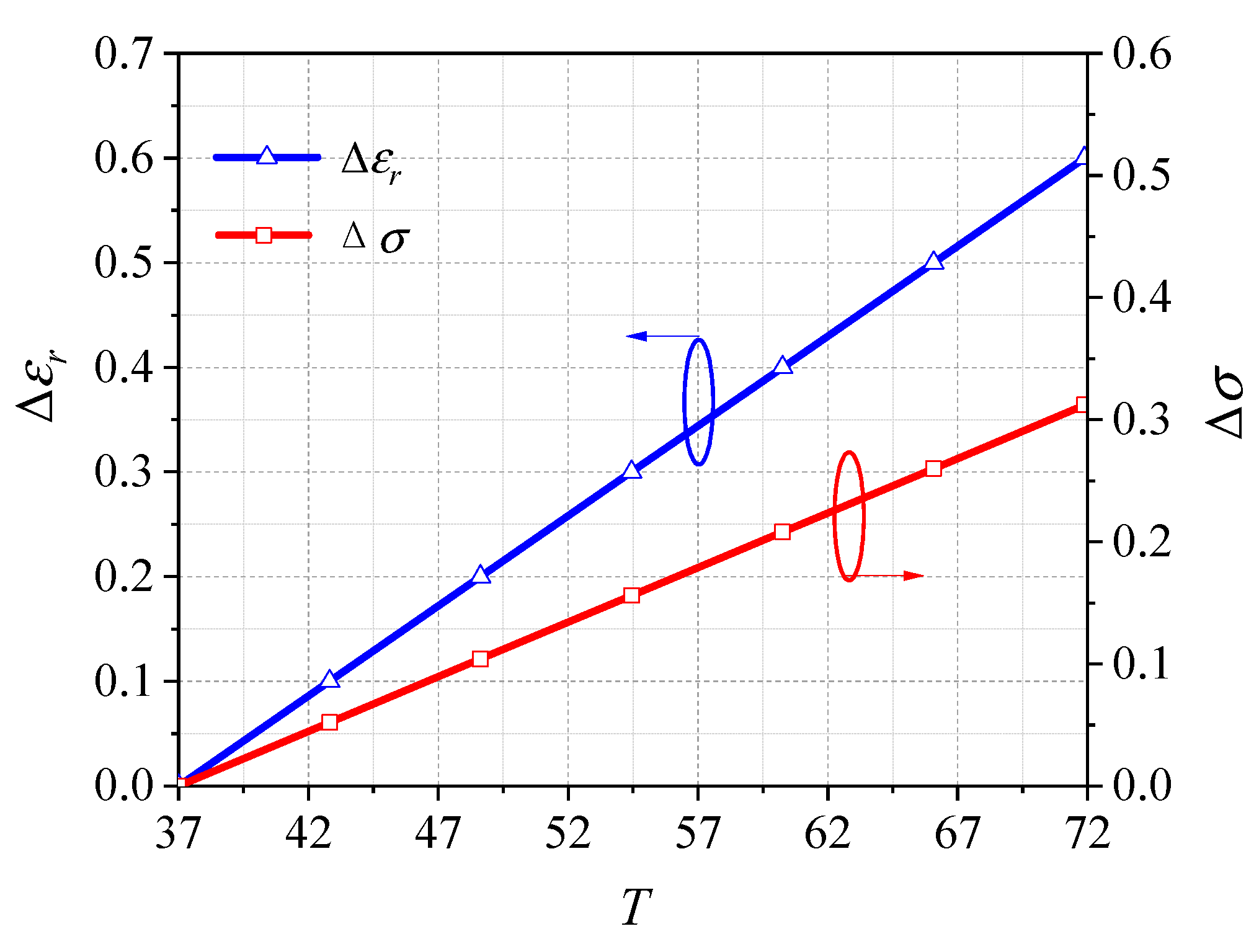
4.4. Influence of the Tissue Electrical Parameter Errors on the Microwave Penetration Effect of the Proposed Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alqadami, A.S.M.; Nguyen-Trong, N.; Stancombe, A.E.; Bialkowski, K.; Abbosh, A. Compact flexible wideband antenna for on-body electromagnetic medical diagnostic systems. IEEE Trans. Antennas Propag. 2020, 68, 8180–8185. [Google Scholar] [CrossRef]
- Misilmani, H.M.E.; Naous, T.A.; Khatib, S.K.A.; Kabalan, K.Y. A survey on antenna designs for breast cancer detection using microwave imaging. IEEE Access 2020, 8, 102570–102594. [Google Scholar] [CrossRef]
- Mobashsher, A.T.; Abbosh, A.M. Compact 3-D slot-loaded folded dipole antenna with unidirectional radiation and low impulse distortion for head imaging applications. IEEE Trans. Antennas Propag. 2016, 64, 3245–3250. [Google Scholar] [CrossRef]
- Mousavi, S.M.H.; Rezaeieh, S.A.; Darvazehban, A.; Mohammed, B.; Janani, A.S.; Abbosh, A.M. Tapered graded index lens antenna with enhanced penetration for near-field torso maging. IEEE Trans. Antennas Propag. 2023, 71, 78–88. [Google Scholar] [CrossRef]
- Zanoli, M.; Trefná, H.D. Iterative time-reversal for multi-frequency hyperthermia. Phys. Med. Biol. 2021, 66, 045027. [Google Scholar] [CrossRef]
- Baskaran, D.; Arunachalam, K. Design and experimental verification of 434 MHz phased array applicator for hyperthermia treatment of locally advanced breast cancer. IEEE Trans. Antennas Propag. 2021, 69, 1706–1715. [Google Scholar] [CrossRef]
- Geyikoğlu, M.D.; Çavuşoğlu, B. Microwave hyperthermia with X band flexible hyperthermia applicator for bone and joint cancer treatment. J. Electromagn. Waves Appl. 2022, 36, 1285–1297. [Google Scholar] [CrossRef]
- Baskaran, D.; Arunachalam, K. Implementation of thinned array synthesis in hyperthermia treatment planning of 434 MHz phased array breast applicator using genetic algorithm. IEEE J. Electromagn. RF Microw. Med. Biol. 2023, 7, 32–38. [Google Scholar] [CrossRef]
- Shah, I.A.; Zada, M.; Basir, A.; Yoo, H. Flexible metasurface-coupled efficient wireless Power transfer system for implantable devices. IEEE Trans. Microw. Theory Technol. 2024, 72, 2534–2547. [Google Scholar] [CrossRef]
- Shaw, T.; Samanta, G.; Mitra, D. Efficient wireless power transfer system for implantable medical devices using circular polarized antennas. IEEE Trans. Antennas Propag. 2021, 69, 4109–4122. [Google Scholar] [CrossRef]
- Iqbal, A.; Al-Hasan, M.; Mabrouk, I.B.; Basir, A.; Nedil, M.; Yoo, H. Biotelemetry and wireless powering of biomedical implants using a rectifier integrated self-diplexing implantable antenna. IEEE Trans. Microw. Theory Technol. 2021, 69, 3438–3451. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Liu, X.; Guo, H.; Yang, X. Near-field wireless power transfer to deep-tissue implants for biomedical applications. IEEE Trans. Antennas Propag. 2020, 68, 1098–1106. [Google Scholar] [CrossRef]
- Iliopoulos, I.; Meo, S.D.; Zhadobov, M.; Pouliguen, P.; Potier, P.; Perregrini, L.; Sauleau, R.; Ettorre, M. Enhancement of penetration of millimeter waves by field focusing applied to breast cancer detection. IEEE Trans. Biomed. Eng. 2021, 68, 959–966. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Gao, Y.M.; Du, M. Propagation characteristics of electromagnetic wave on multiple tissue interfaces in wireless deep implant communication. IET Microw. Antennas Propag. 2018, 12, 2034–2040. [Google Scholar] [CrossRef]
- Rodrigues, D.B.; Ellsworth, J.; Turner, P. Feasibility of heating brain tumors using a 915 MHz annular phased-array. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 423–427. [Google Scholar] [CrossRef]
- Chavez-Santiago, R.; Khaleghi, A.; Balasingham, I. Matching layer for path loss reduction in ultra-wideband implant communications. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014. [Google Scholar]
- Yang, F.; Luo, J.; Xu, S.; Li, M. Design of artificial matching layers with arbitrary permittivity using a metasurface. IEEE Antennas Wireless Propag. Lett. 2018, 17, 1445–1448. [Google Scholar] [CrossRef]
- Cao, X.; Sato, H.; Xu, K.D.; Jiang, W.; Gong, S.; Chen, Q. A systematic method for efficient wireless powering to implantable biomedical devices. IEEE Trans. Antennas Propag. 2023, 71, 2745–2757. [Google Scholar] [CrossRef]
- Dobšíček Trefná, H.; Crezee, J.; Schmidt, M.; Marder, D.; Lamprecht, U.; Ehmann, M.; Nadobny, J.; Hartmann, J.; Lomax, N.; Abdel-Rahman, S.; et al. C Quality assurance guidelines for superficial hyperthermia clinical trials: II. Technical requirements for heating devices. Strahlenther. Onkol. 2017, 193, 351–366. [Google Scholar] [CrossRef]
- Andreuccetti, D.; Fossi, R.; Petrucci, C. An Internet Resource for the Calculation of Thedielectric Properties of Body Tissues in the Frequency Range 10 Hz–100GHz. IFAC-CNR, Florence (Italy). 1997. Available online: http://niremf.ifac.cnr.it/tissprop/ (accessed on 1 March 2024).
- Rana, J.N.; Muntaz, S.; Han, I.; Choi, E.H. Formation of reactive species via high power microwave induced DNA damage and promoted intrinsic pathway-mediated apoptosis in lung cancer cells: An in vitro investigation. Fundam. Res. 2024. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Zhang, D.; Li, C.; Zhu, Y.; Zou, Y.; Chen, B.; Wu, T.; Wang, X. A preclinical system prototype for focused microwave breast hyperthermia guided by compressive thermoacoustic tomography. IEEE Trans. Biomed. Eng. 2021, 68, 2289–2300. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Sumser, K.; VilasBoas-Ribeiro, I.; Curto, S.; Drizdal, T.; van Rhoon, G.C.; Franckena, M.; Paulides, M.M. Standardization of patient modeling in hyperthermia simulation studies: Introducing the erasmus virtual patient repository. Int. J. Hyperth. 2020, 37, 608–616. [Google Scholar] [CrossRef] [PubMed]
- Deshazer, G.; Hagmann, M.; Merck, D.; Sebek, J.; Moore, K.B.; Prakash, P. Computational modeling of 915 MHz microwave ablation: Comparative assessment of temperature-dependent tissue dielectric models. Med. Phys. 2017, 44, 4859–4868. [Google Scholar] [CrossRef] [PubMed]






| Tissue | (GHz) | (S/m) | |
|---|---|---|---|
| Skin | 2.45 | 42.853 | 1.5915 |
| Fat | 2.45 | 5.2801 | 0.1045 |
| Muscle | 2.45 | 52.729 | 1.7388 |
| Model | (V/m) | (W/m2) | ||||
|---|---|---|---|---|---|---|
| Air–Skin | Skin–Fat | Fat–Muscle | Air–Skin | Skin–Fat | Fat–Muscle | |
| No-matched layer | 133.84 | 149.14 | 48.19 | 111.08 | 63.43 | 43.60 |
| Method 1 | 170.02 | 89.45 | 61.21 | 181.11 | 102.36 | 70.35 |
| Method 2 | 200.97 | 223.94 | 72.35 | 254.16 | 143.03 | 98.28 |
| Method 3 | 200.99 | 223.97 | 72.36 | 251.05 | 143.05 | 98.32 |
| Model | (mm) | ||
|---|---|---|---|
| * | |||
| No-matched layer | 11.43 | 27.36 | 42.7 |
| Method 1 | 17.31 | 32.65 | 48 |
| Method 2 | 21 | 36.31 | 51.52 |
| Method 3 | 21.01 | 36.35 | 51.65 |
| (GHz) | (mm) | |||||
|---|---|---|---|---|---|---|
| ) | Method 3 ) | ) | Method 3 ) | |||
| 0.740 | 0.016 | 97.84% | 34 | 54.40 | 60% | |
| 0.915 | 0.55 | 0.010 | 98.18% | 35.90 | 43.37 | 20.81% |
| 2.45 | 0.746 | 97.99% | 11.43 | 21.01 | ||
| 3.5 | 0.86 | 0.116 | 86.51% | 1.36 | 15.84 | 1064.71% |
| Human Tissue Model | (mm) | |||||
|---|---|---|---|---|---|---|
| *) | Method 3 *) | *) | Method 3 *) | |||
| Model 1 | 0.746 | 97.99% | 11.43 | 21.01 | ||
| Model 2 | 0.6076 | 0.0107 | 98.24% | 15.99 | 21.06 | 31.71% |
| Model 3 | 0.7409 | 0.00957 | 98.71% | 7.98 | 19.57 | 145.24% |
| Model 4 | 0.74178 | 0.0305 | 95.89% | 10.33 | 18.36 | 77.73% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.-L.; Zhao, D.; Hu, Z.-J.; Wang, Y.; Liang, F.; Wang, B.-Z. Increasing Microwave Penetration Depth in the Human Body by a Complex Impedance Match of Skin Interface with a Two-Layered Medium. Electronics 2024, 13, 3915. https://doi.org/10.3390/electronics13193915
Ma M-L, Zhao D, Hu Z-J, Wang Y, Liang F, Wang B-Z. Increasing Microwave Penetration Depth in the Human Body by a Complex Impedance Match of Skin Interface with a Two-Layered Medium. Electronics. 2024; 13(19):3915. https://doi.org/10.3390/electronics13193915
Chicago/Turabian StyleMa, Meng-Lu, Deshuang Zhao, Zai-Jun Hu, Yiling Wang, Feng Liang, and Bing-Zhong Wang. 2024. "Increasing Microwave Penetration Depth in the Human Body by a Complex Impedance Match of Skin Interface with a Two-Layered Medium" Electronics 13, no. 19: 3915. https://doi.org/10.3390/electronics13193915
APA StyleMa, M.-L., Zhao, D., Hu, Z.-J., Wang, Y., Liang, F., & Wang, B.-Z. (2024). Increasing Microwave Penetration Depth in the Human Body by a Complex Impedance Match of Skin Interface with a Two-Layered Medium. Electronics, 13(19), 3915. https://doi.org/10.3390/electronics13193915






