Research on the Construction of an Efficient and Lightweight Online Detection Method for Tiny Surface Defects through Model Compression and Knowledge Distillation
Abstract
:1. Introduction
2. Pre-Treatment and Methods
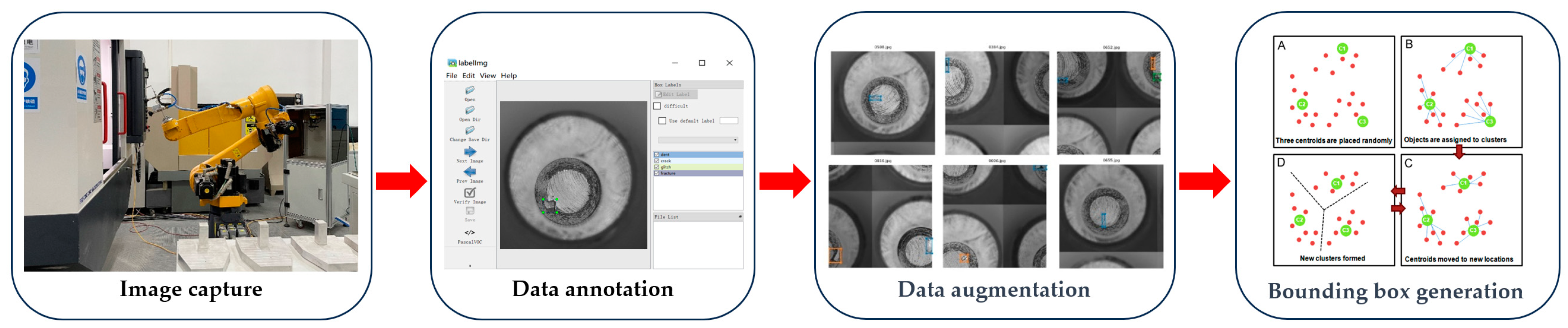
2.1. Sample Pre-Treatment
2.1.1. Data Augmentation Methods
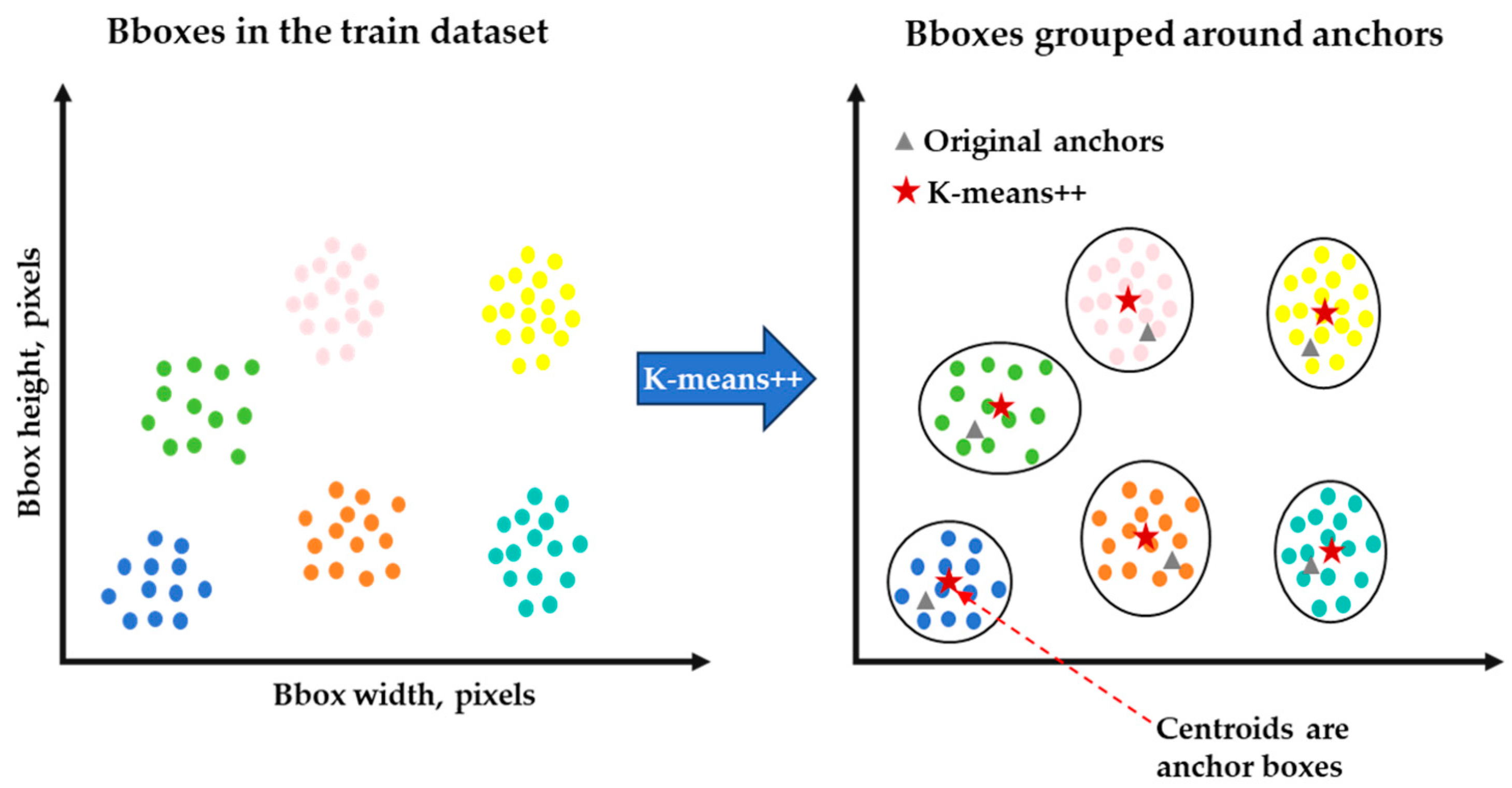
2.1.2. Bounding Box Generation Methods
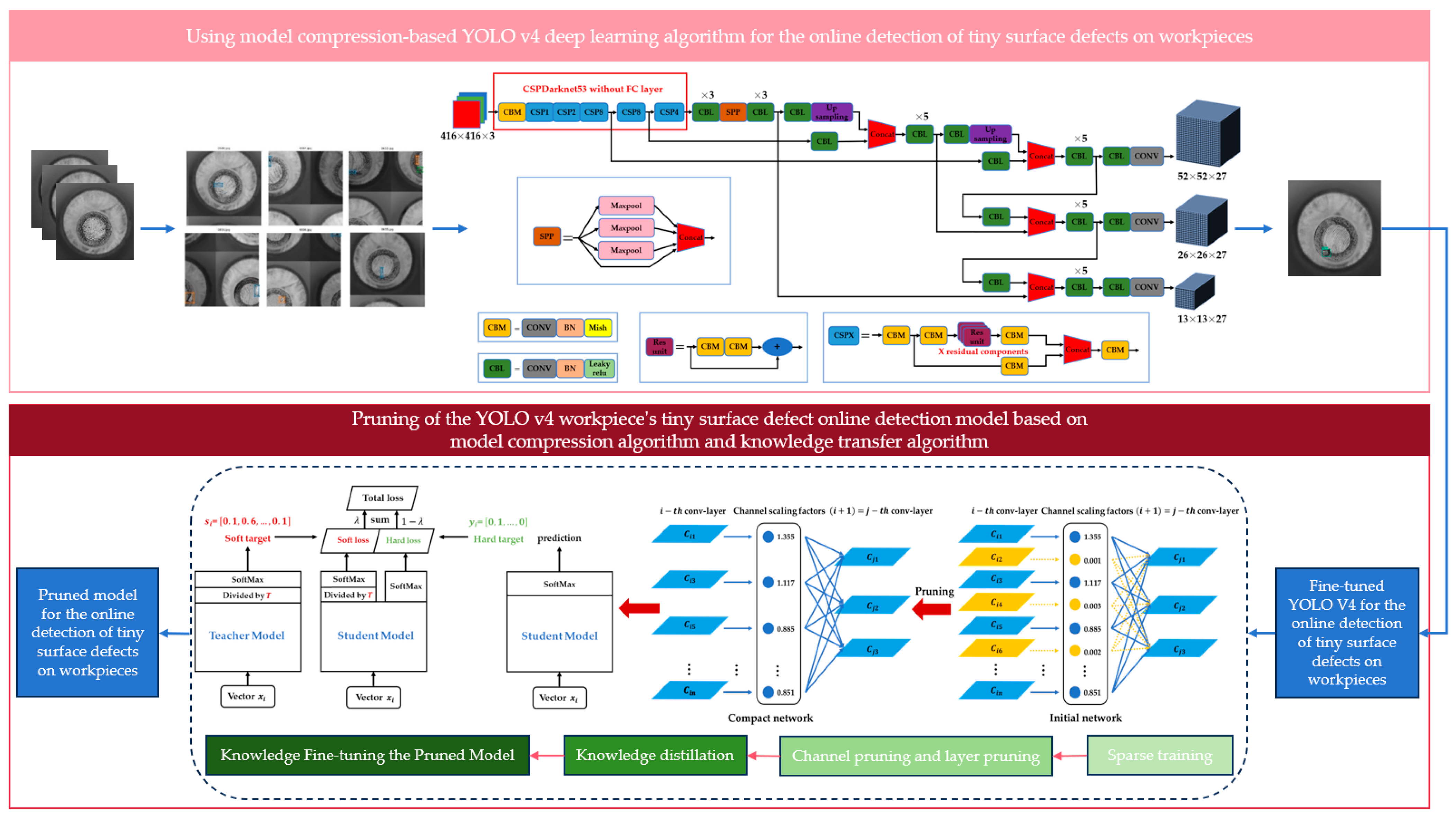
2.2. Using Model Compression-Based YOLOv4 Deep Learning Algorithm for the Online Detection of Tiny Surface Defects on Workpieces
2.2.1. Overall Technical Route
- Initially, manually labeled surface defect data for workpieces were used to train an improved YOLOv4 object detection network. This training process incorporated transfer learning, enabling the rapid detection and labeling of tiny surface defects on workpieces.
- After training the YOLOv4 model for workpiece surface defect detection, model compression and knowledge transfer techniques were applied. This involved model pruning and knowledge distillation algorithms, simplifying the model’s structure and parameters while maintaining model accuracy.
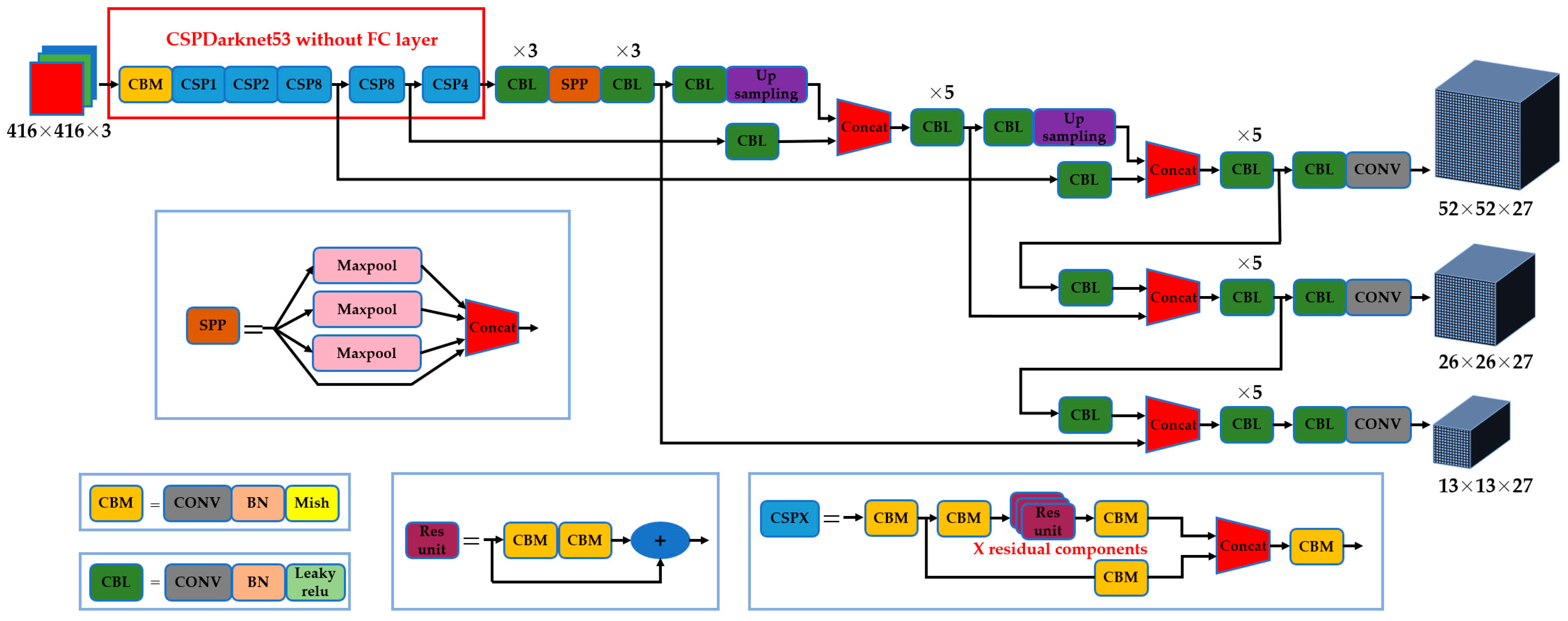
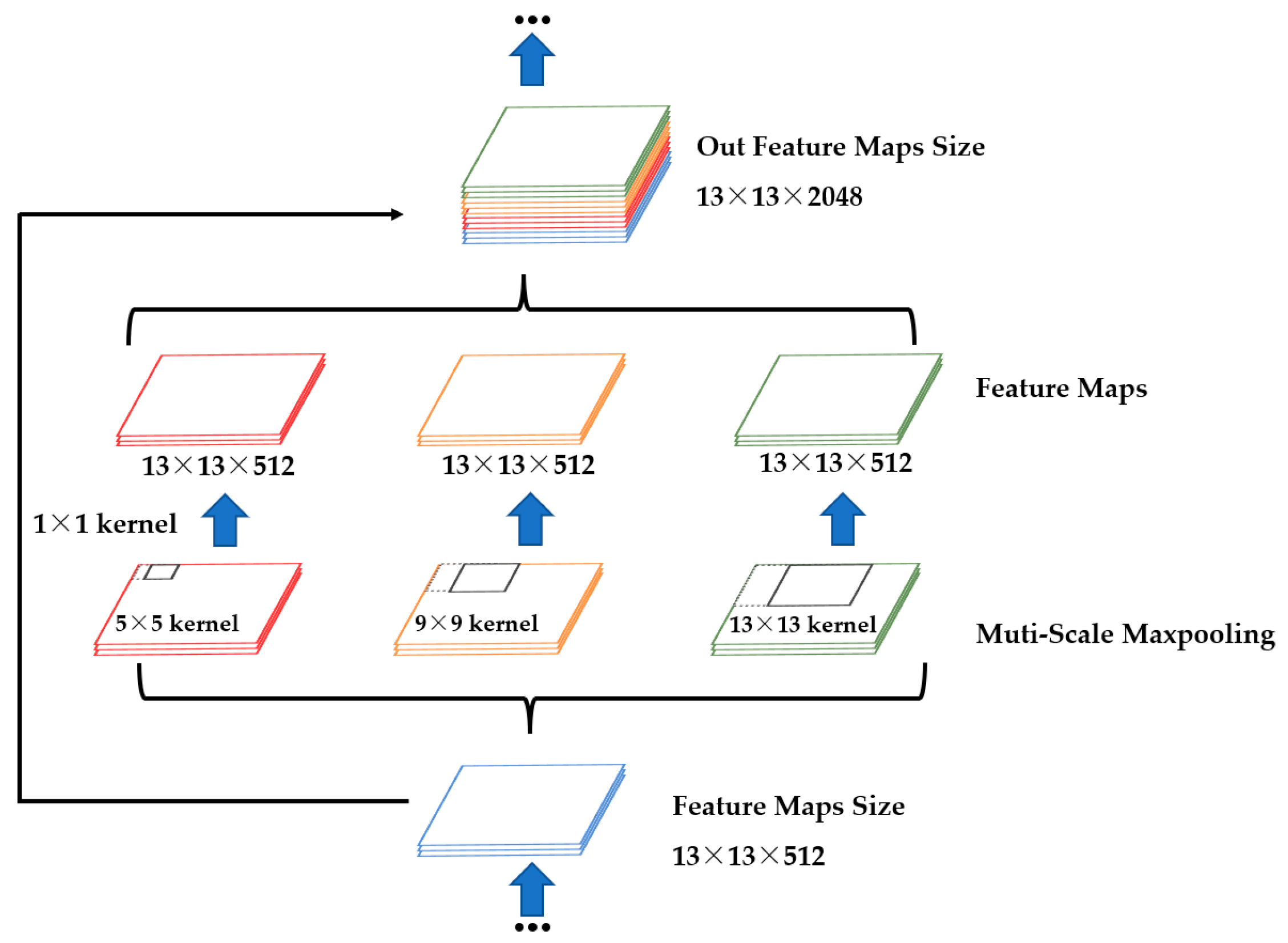
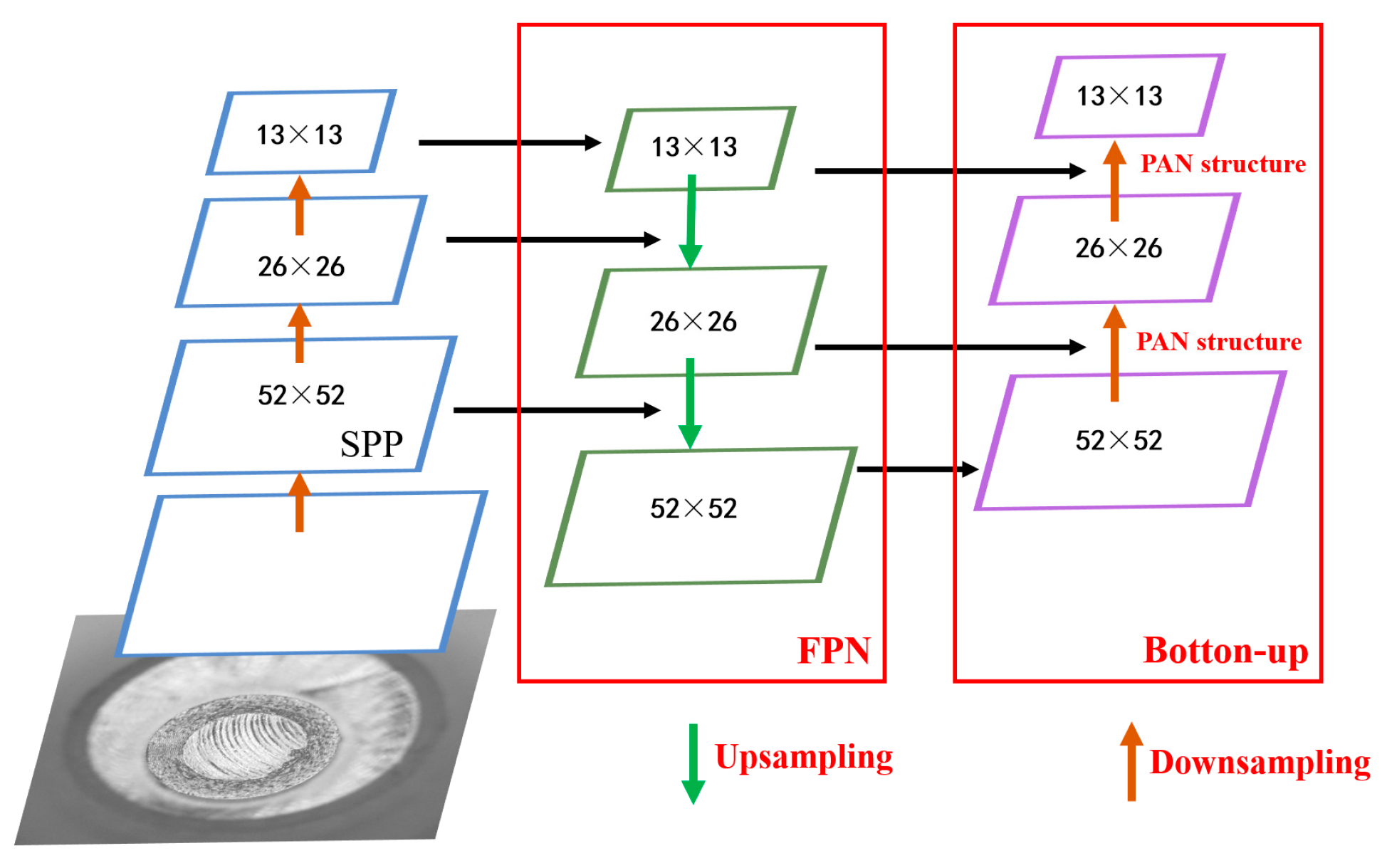
2.2.2. Construction of a Workpiece’s Tiny-Surface-Defect Online Detection Model Based on YOLOv4
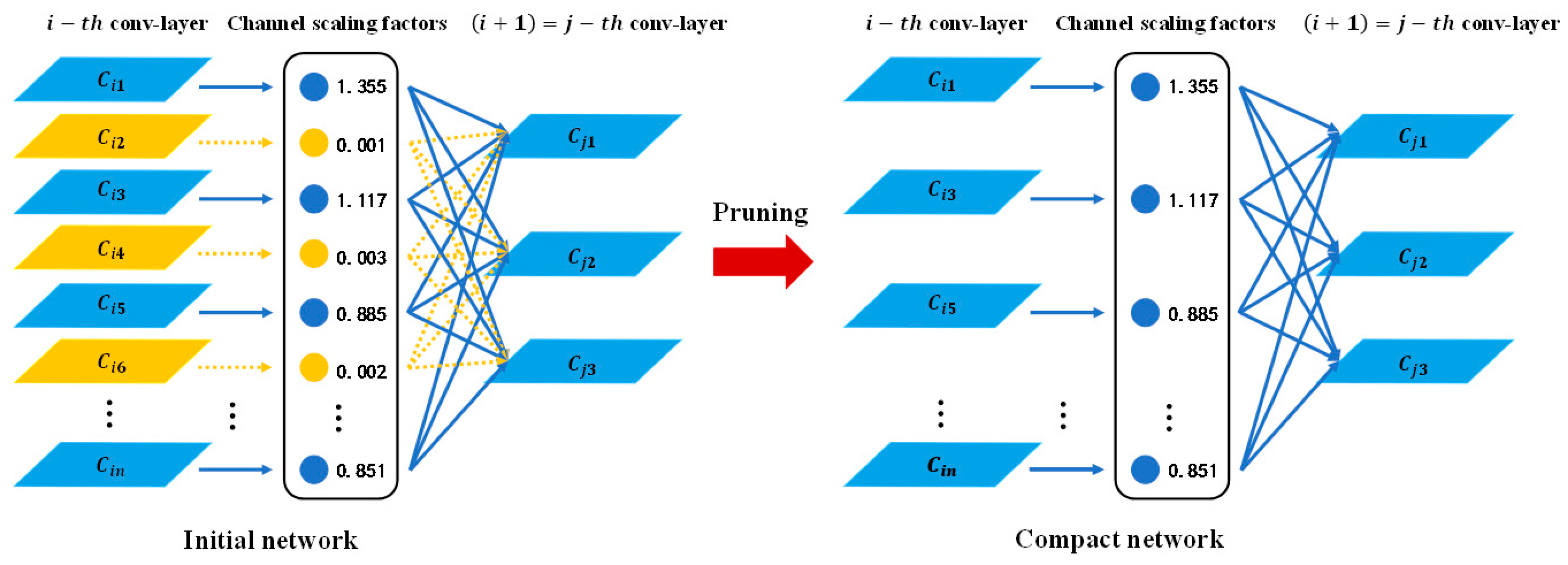
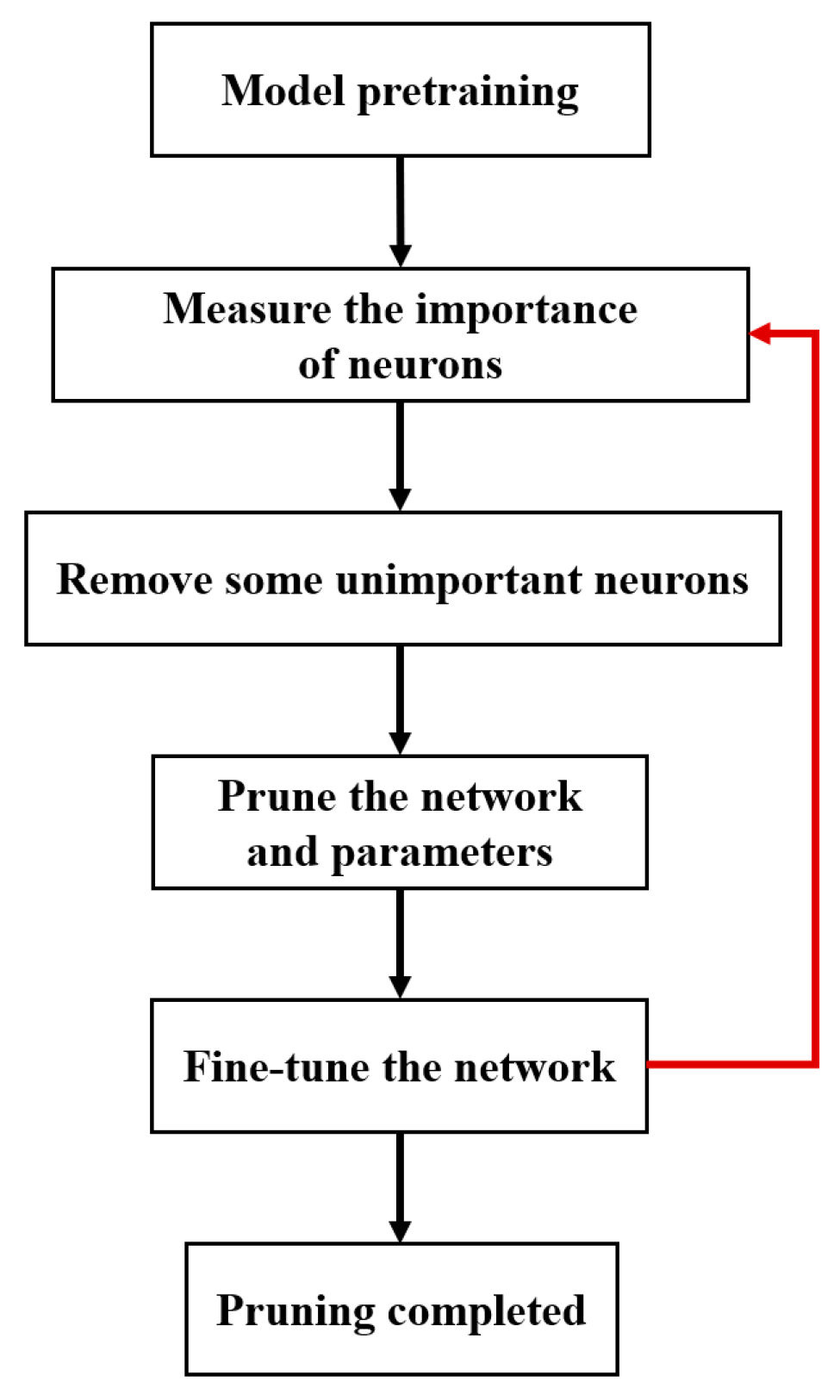
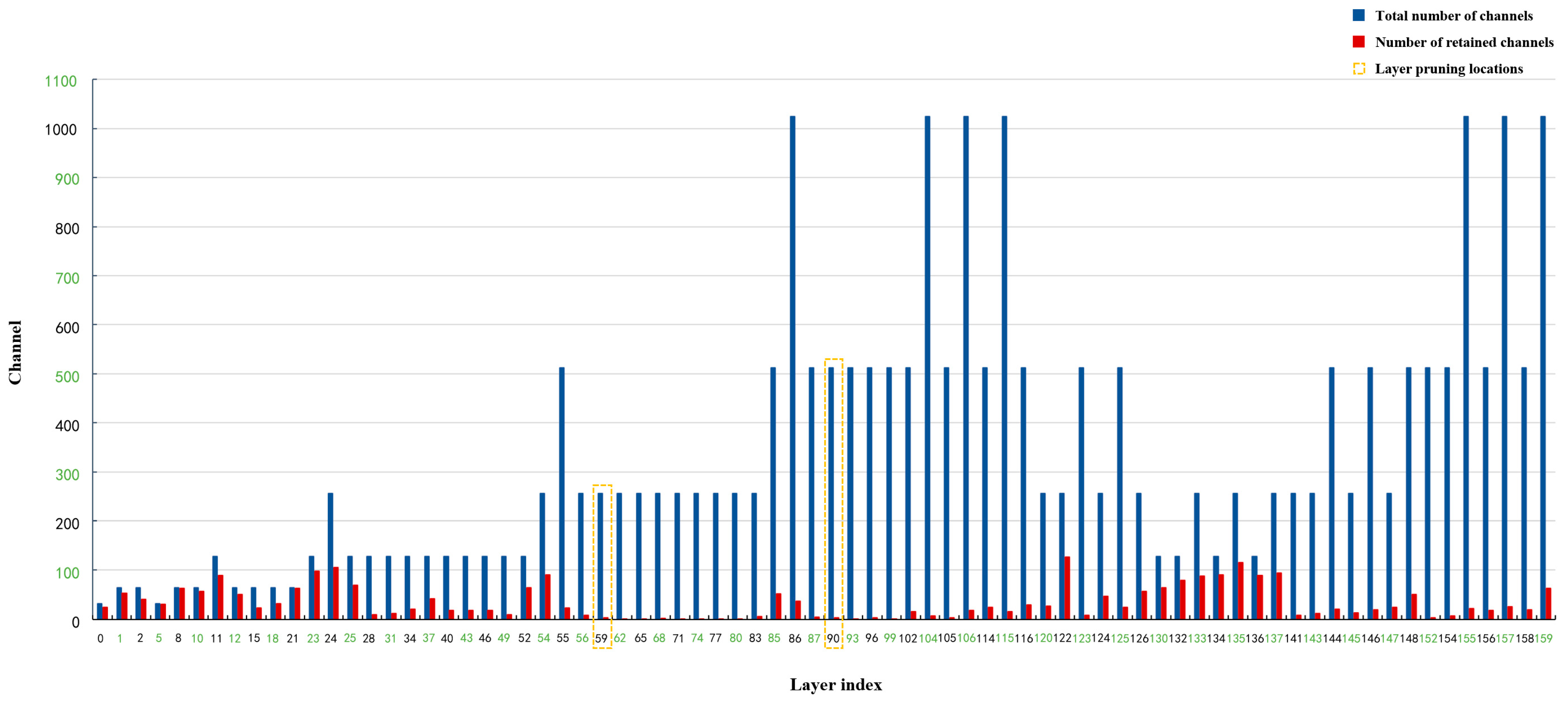
2.2.3. Pruning of the YOLOv4 Workpiece’s Tiny-Surface-Defect Online Detection Model Based on Model Compression Algorithm
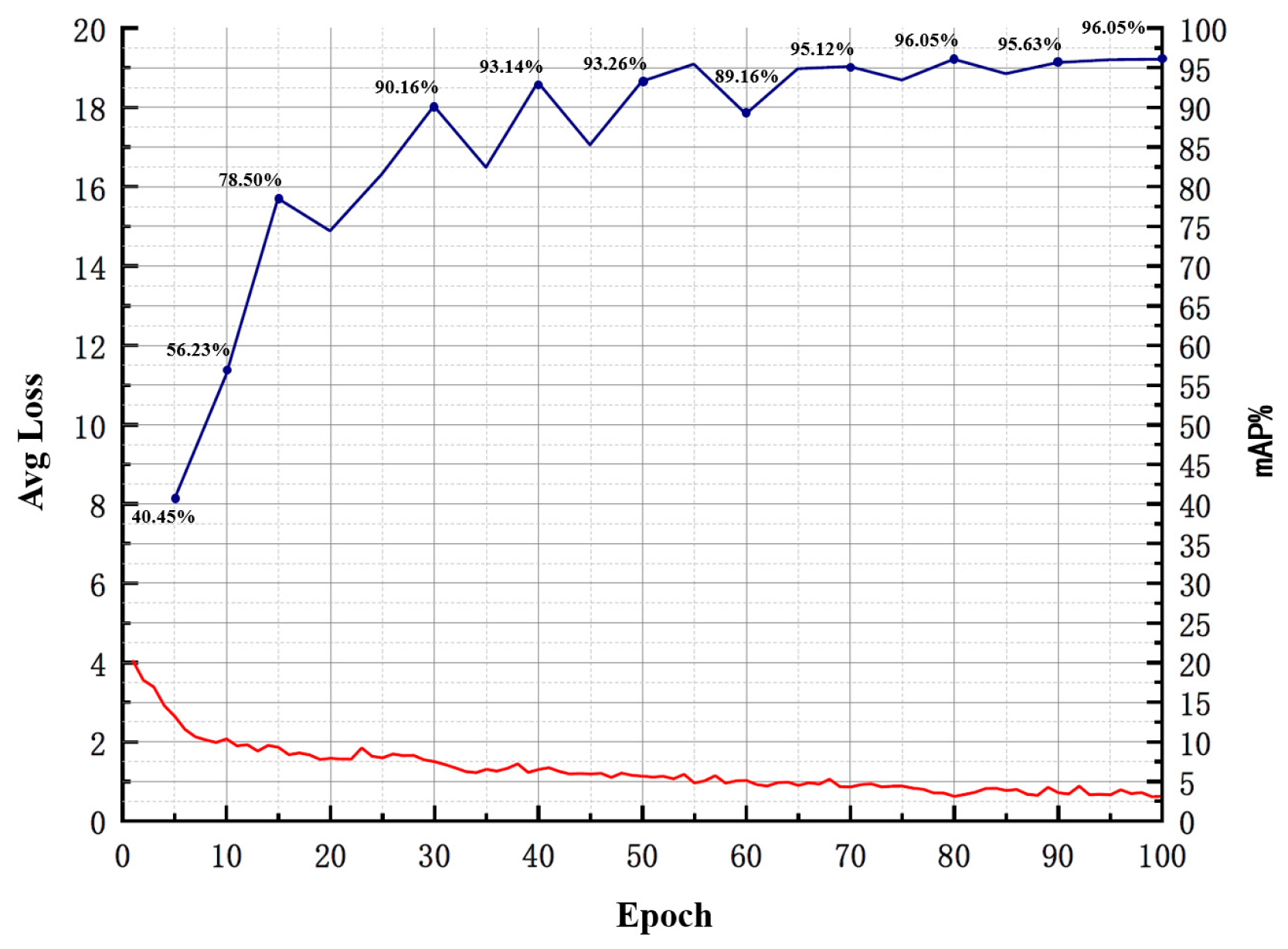
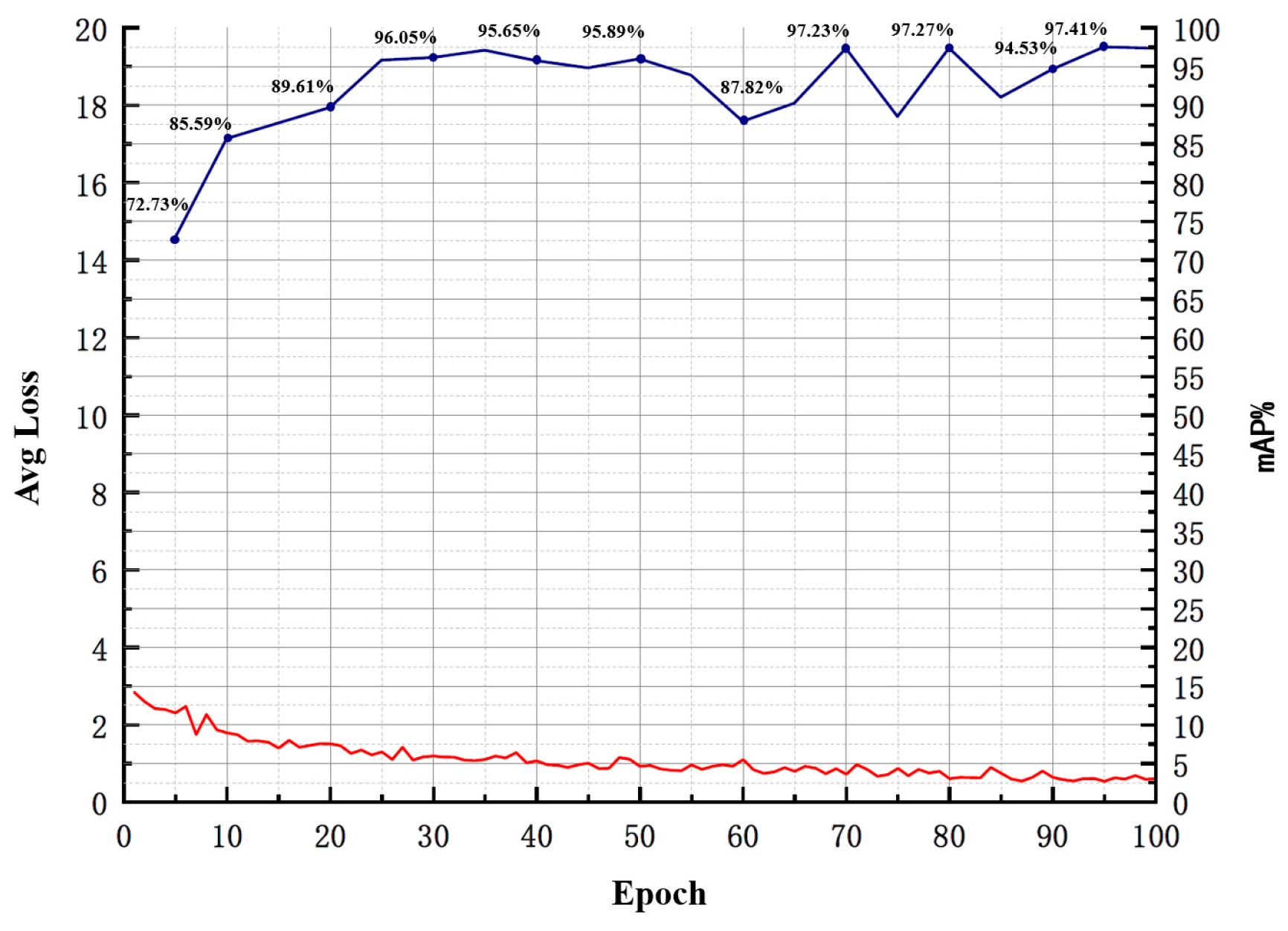
2.2.4. Compression and Post-Processing of the YOLOv4 Workpiece’s Tiny-Surface-Defect Online Detection Model Based on Knowledge Transfer Algorithm
2.3. Evaluation of the Model Performance
- mAP

- 2.
- FPS
3. Results and Analysis
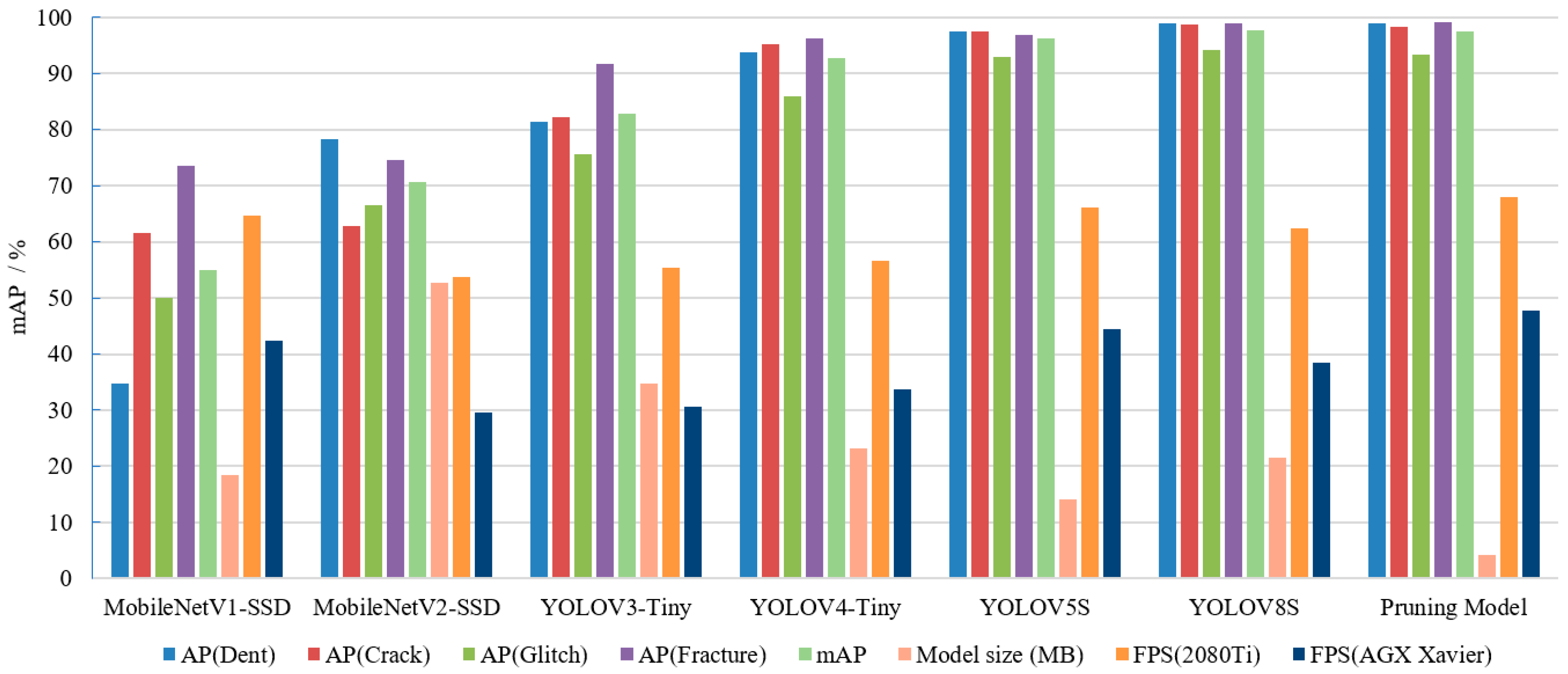
3.1. Comparison of Different Object Detection Algorithms
3.2. Comparison of the Proposed Method with Previous Studies
- 1.
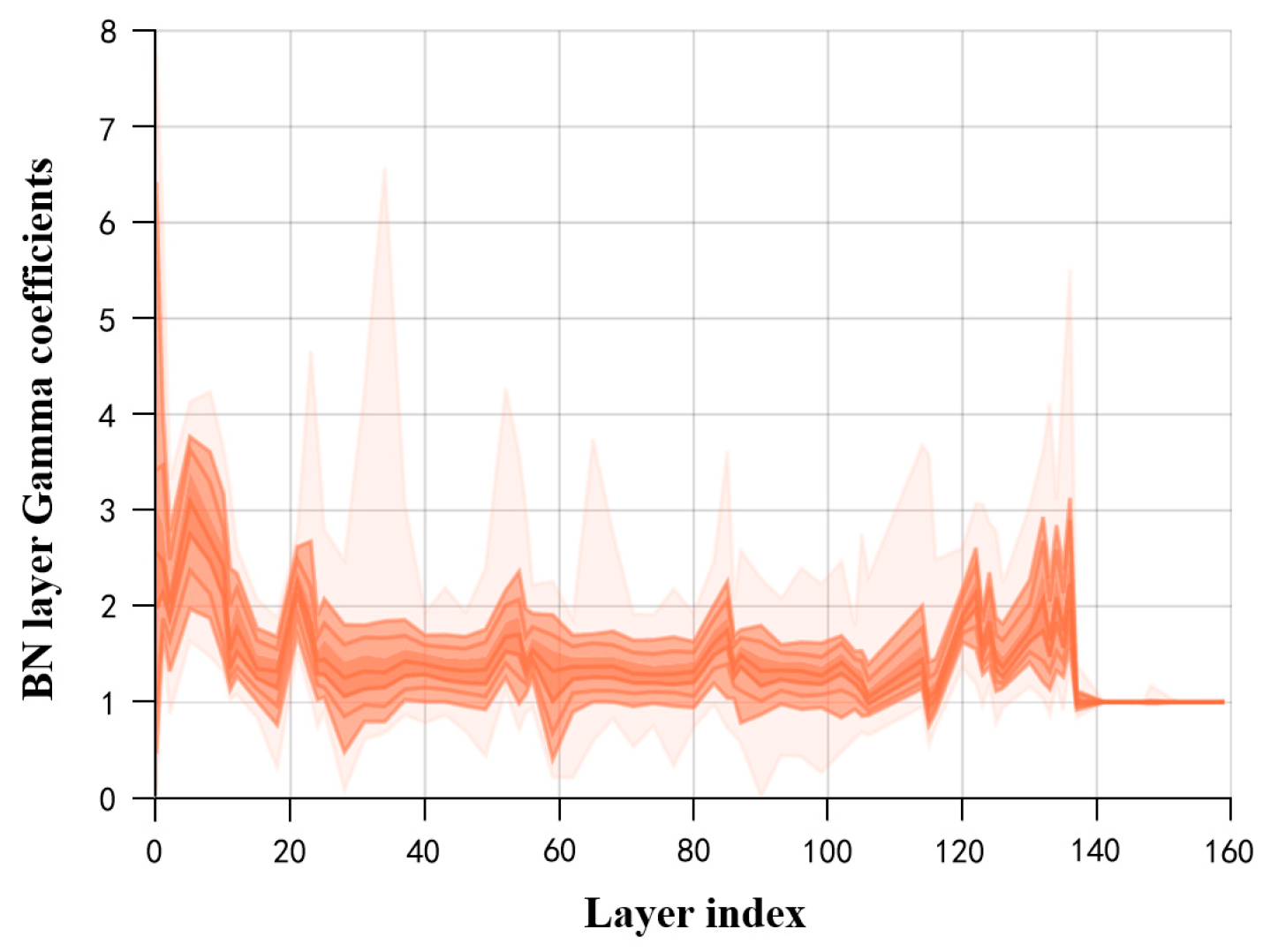
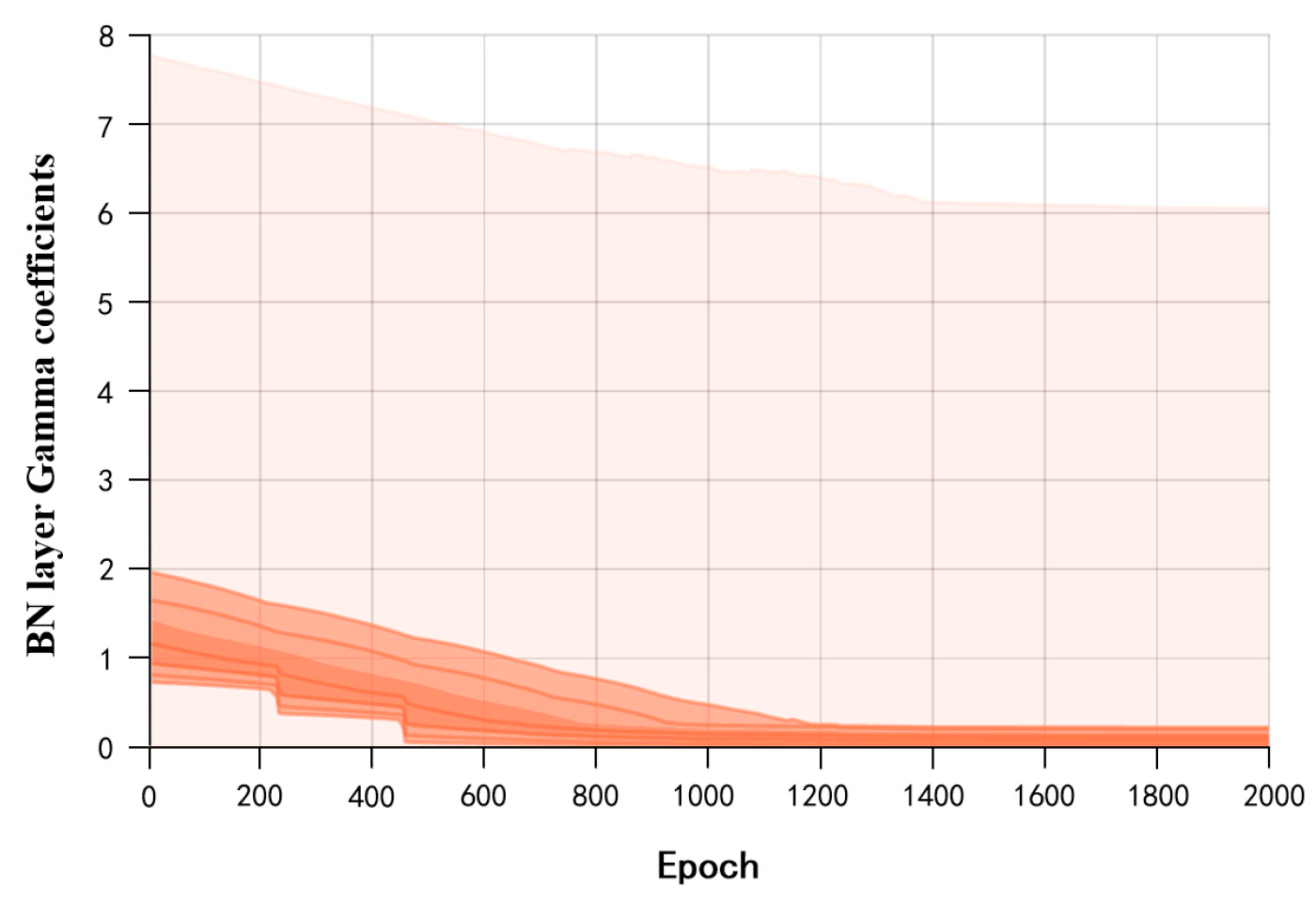
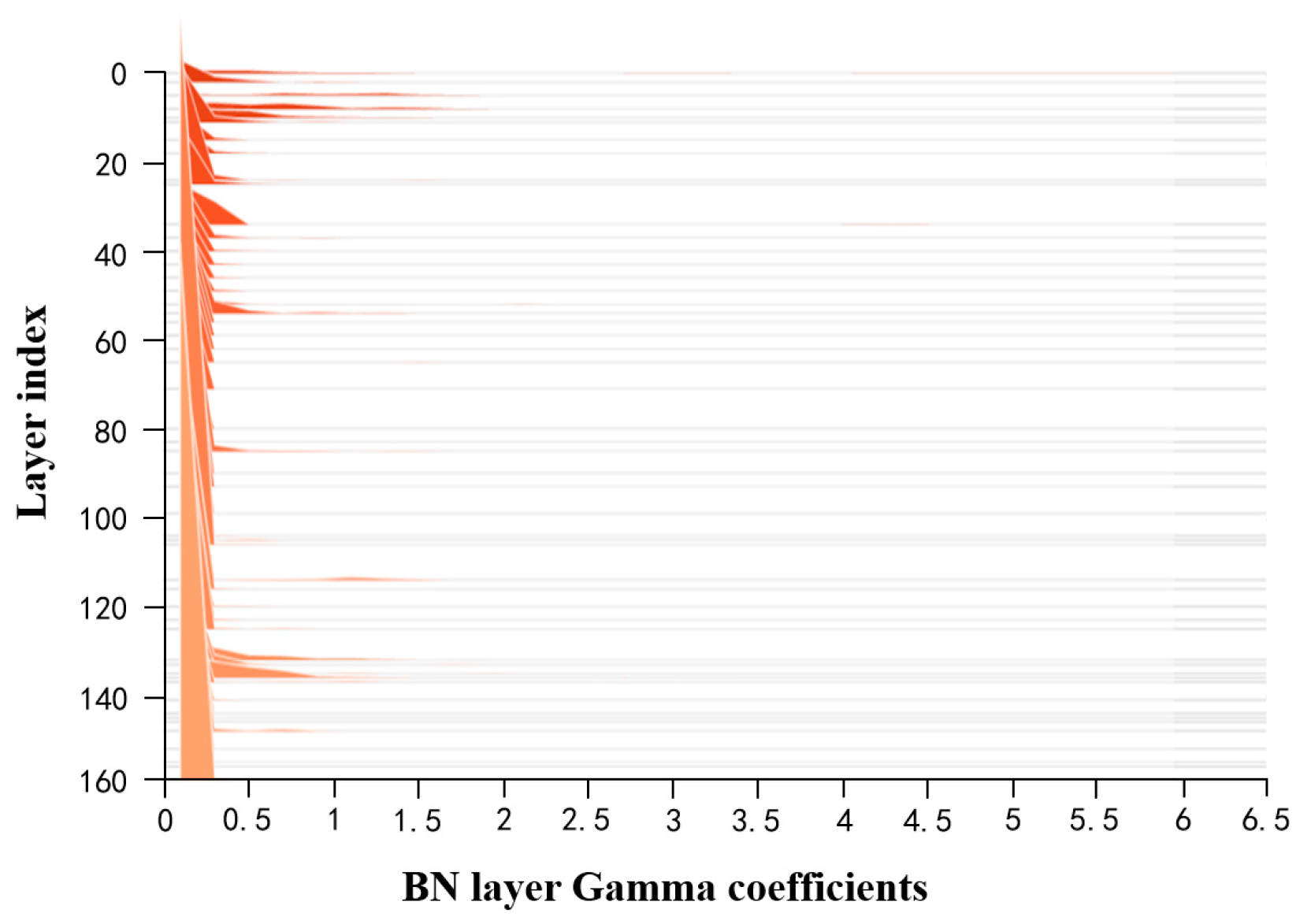
- Sparse Training: Apply L1 regularization constraints to the coefficients of the BN layers in the surface-quality online inspection model to adjust the sparsity of the model in the structural direction.
- 2.
- Pruning: After sparse training, perform channel pruning and layer pruning on the sparse model according to a certain pruning ratio to generate a compact model, reducing its storage space requirements.
- 3.
- Fine-tuning the Pruned Model: The primary purpose is to overcome the issue of excessive loss of accuracy after model pruning. Knowledge distillation is used to effectively recover the lost accuracy. The specific parameters for model compression are outlined in Table 4.
4. Conclusions
- 1.
- The study focused extensively on the combination of the YOLO network, model compression, and knowledge distillation algorithms. With the continuous development of object detection networks, future research will incorporate different attention mechanisms to improve network models, achieving better detection performance and lighter models.
- 2.
- The limited quantity of defect samples that the study could collect may be enhanced in the future by considering effective data augmentation using generative adversarial networks (GANs) on original samples. This approach generates new samples with different characteristics from the original data but possessing similar features, thereby enhancing the algorithm’s robustness.
- 3.
- The algorithm employed in the study belongs to supervised learning. Acquiring a large volume of annotated data in industrial sectors is challenging and requires substantial human resources. Therefore, focusing on how to apply unsupervised learning techniques to practical defect detection tasks will be a key area of future research direction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSP | Cross Stage Partial |
| SPP | Spatial Pyramid Pooling |
| BN | Batch Normalization |
| HOG | Histogram of Oriented Gradient |
| LBP | Local Binary Pattern |
| SVM | Support Vector Machine |
| RBF | Radial Basis Function |
| CNN | Convolutional Neural Networks |
| R-CNN | Region-based Convolutional Neural Network |
| YOLO | You Only Look Once |
| SSD | Single Shot Multibox Detector |
| GA | Genetic Algorithm |
| mAP | Mean Average Precision |
| DR | Defect Recognition |
| DSC | Depthwise Separable Convolution |
| HPFRCCs | High-performance Fiber-reinforced Cementitious Composites |
| CCD | Charge Coupled Device |
| IoU | Intersection over Union |
| FPN | Feature Pyramid Network |
| PAN | Path Aggregation Network |
| CBM | Convolution Batch Normalization Mish |
| FPS | Frames per Second |
| R | Recall |
| TP | True Positive |
| FN | False Negative |
| PR | Precision-Recall |
| AP | Average Precision |
| GANs | Generative Adversarial Networks |
References
- Tulbure, A.A.; Tulbure, A.A.; Dulf, E.H. A review on modern defect detection models using DCNNs–Deep convolutional neural networks. J. Adv. Res. 2022, 35, 33–48. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ding, Y.; Zhao, F.; Zhang, E.; Wu, Z.; Shao, L. Surface defect detection methods for industrial products: A review. Appl. Sci. 2021, 11, 7657. [Google Scholar] [CrossRef]
- Ren, Z.; Fang, F.; Yan, N.; Wu, J. State of the art in defect detection based on machine vision. Int. J. Precis. Eng. Manuf.-Green Technol. 2022, 9, 661–691. [Google Scholar] [CrossRef]
- Liu, L.; Wang, C.; Zhao, S.; Li, H. Research on solar cells defect detection technology based on machine vision. J. Electron. Meas. Instrum. 2018, 32, 47–52. [Google Scholar]
- Song, W.; Zuo, D.; Deng, B.; Zhang, H. Corrosion defect detection of earthquake hammer for high voltage transmission line. Chin. J. Sci. Instrum. 2016, 37, 113–117. [Google Scholar]
- Ge, Q.; Fang, M.; Xu, J. Defect Detection of Industrial Products based on Improved Hough Transform. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 832–836. [Google Scholar] [CrossRef]
- Ding, S.; Liu, Z.; Li, C. AdaBoost learning for fabric defect detection based on HOG and SVM. In Proceedings of the IEEE 2011 International Conference on Multimedia Technology, Hangzhou, China, 26–28 July 2011. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao HY, M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Jocher, G.; Stoken, A.; Borovec, J.; Stan, C.; Changyu, L.; Rai, P.; Ferriday, R.; Sullivan, T.; Xinyu, W.; Ribeiro, Y.; et al. Ultralytics/yolov5: v3. 0; Zenodo: Zurich, Switzerland, 2020. [Google Scholar]
- Li, C.; Li, L.; Jiang, H.; Weng, K.; Geng, Y.; Li, L.; Ke, Z.; Li, Q.; Cheng, M.; Nie, W.; et al. YOLOv6: A single-stage object detection framework for industrial applications. arXiv 2022, arXiv:2209.02976. [Google Scholar]
- Wang, C.Y.; Bochkovskiy, A.; Liao HY, M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Contributors, M. YOLOv8 by MMYOLO. 2023. Available online: https://github.com/open-mmlab/mmyolo/tree/main/configs/yolov8 (accessed on 13 May 2023).
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Part I 14, Amsterdam, The Netherlands, 11–14 October 2016; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar]
- Chen, M.; Yu, L.; Zhi, C.; Sun, R.; Zhu, S.; Gao, Z.; Ke, Z.; Zhu, M.; Zhang, Y. Improved faster R-CNN for fabric defect detection based on Gabor filter with Genetic Algorithm optimization. Comput. Ind. 2022, 134, 103551. [Google Scholar] [CrossRef]
- Duan, L.; Yang, K.; Ruan, L. Research on automatic recognition of casting defects based on deep learning. IEEE Access 2020, 9, 12209–12216. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Gong, C. Automatic detection method of tunnel lining multi-defects via an enhanced You Only Look Once network. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 762–780. [Google Scholar] [CrossRef]
- Li, Y.; Huang, H.; Xie, Q.; Yao, L.; Chen, Q. Research on a surface defect detection algorithm based on MobileNet-SSD. Appl. Sci. 2018, 8, 1678. [Google Scholar] [CrossRef]
- Guo, P.; Meng, W.; Bao, Y. Automatic identification and quantification of dense microcracks in high-performance fiber-reinforced cementitious composites through deep learning-based computer vision. Cem. Concr. Res. 2021, 148, 106532. [Google Scholar] [CrossRef]
- Wu, D.; Lv, S.; Jiang, M.; Song, H. Using channel pruning-based YOLOv4 deep learning algorithm for the real-time and accurate detection of apple flowers in natural environments. Comput. Electron. Agric. 2020, 178, 105742. [Google Scholar] [CrossRef]
- Geng, L.; Niu, B. A Survey of Deep Neural Network Model Compression. J. Front. Comput. Sci. Technol. 2020, 14, 1441–1455. [Google Scholar]
- Tan, X.; Wang, Z. Ping pong ball recognition using an improved algorithm based on YOLOv4. Technol. Innov. Appl. 2020, 27, 74–76. [Google Scholar]
- Zhou, J.; Jing, J.; Zhang, H.; Wanh, Z.; Huang, H. Real-time fabric defect detection algorithm based on S-YOLOV3 model. Laser Optoelectron. Prog. 2020, 57, 55–63. [Google Scholar]
- Zhang, Y.; Wu, J.; Ma, Z.; Cao, X.; Guo, W. Compression and implementation of neural network model base on YOLOv3. Micro/Nano Electron. Intell. Manuf. 2020, 178, 105742. [Google Scholar]
- Bai, S. Research on Traffic Signs Detection and Recognition Algorithm Base on Deep Learning. Ph.D. Thesis, Changchun University of Technology, Changchun, China, 2020; p. 159. [Google Scholar]
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning efficient convolutional networks through network slimming. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 736–2744. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Chen, G.; Choi, W.; Yu, X.; Han, T.; Chandraker, M. Learning efficient object detection models with knowledge distillation. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning—PMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE 32nd Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P. Microsoft coco: Common objects in context. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Part V 13, Zurich, Switzerland, 6–12 September 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 740–755. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Howard, A.; Zhmoginov, A.; Chen, L.C.; Sandler, M.; Zhu, M. Inverted residuals and linear bottlenecks: Mobile networks for classification, detection and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Guo, P.; Meng, X.; Meng, W.; Bao, Y. Monitoring and automatic characterization of cracks in strain-hardening cementitious composite (SHCC) through intelligent interpretation of photos. Compos. Part B Eng. 2022, 242, 110096. [Google Scholar] [CrossRef]
- Li, Y.; Fan, Q.; Huang, H.; Han, Z.; Gu, Q. A Modified YOLOv8 Detection Network for UAV Aerial Image Recognition. Drones 2023, 7, 304. [Google Scholar] [CrossRef]








| Equipment Name | Hardware Model | Parameter |
|---|---|---|
| Industrial robot | ESTUN ER6-K6B-P-D | AC380 V/3.4 KVA, maximum load 6 kg, Arm span 1600 mm, repeatable positioning accuracy ± 0.08 mm |
| Industrial CCD camera | COGNEX 821-0037-1R | 24VDC ± 10%/500 mA, 1/1.8 UI inch CCD, 1600 × 1200 resolution (pixels) |
| Industrial lens | COMPUTAR M5018-MP2 | 50 mm focal length, F1.8 aperture, 2/3″ target surface size |
| LED arc light source | AFT, RL12068W | Ring, PWM dimming |
| Light-shielding cabinet | Homemade | Shade: 42 cm × 55 cm, cabinet: 50 cm × 50 cm × 122 cm |
| Parameter | YOLOV4 | YOLOV4-Tiny |
|---|---|---|
| Number of batch training samples | 64 | 64 |
| Number of sample subsets | 8 | 8 |
| Image width | 416 | 416 |
| Image height | 416 | 416 |
| Number of channels | 3 | 3 |
| Momentum | 0.949 | 0.949 |
| Weight decay regularization coefficient | 0.0005 | 0.0005 |
| Random rotation angle | 0 | 0 |
| Randomly adjusted saturation | 1.5 | 1.5 |
| Randomly adjusted exposure | 1.5 | 1.5 |
| Randomly adjusted hues | 0.1 | 0.1 |
| Learning rate | 0.0001 | 0.0001 |
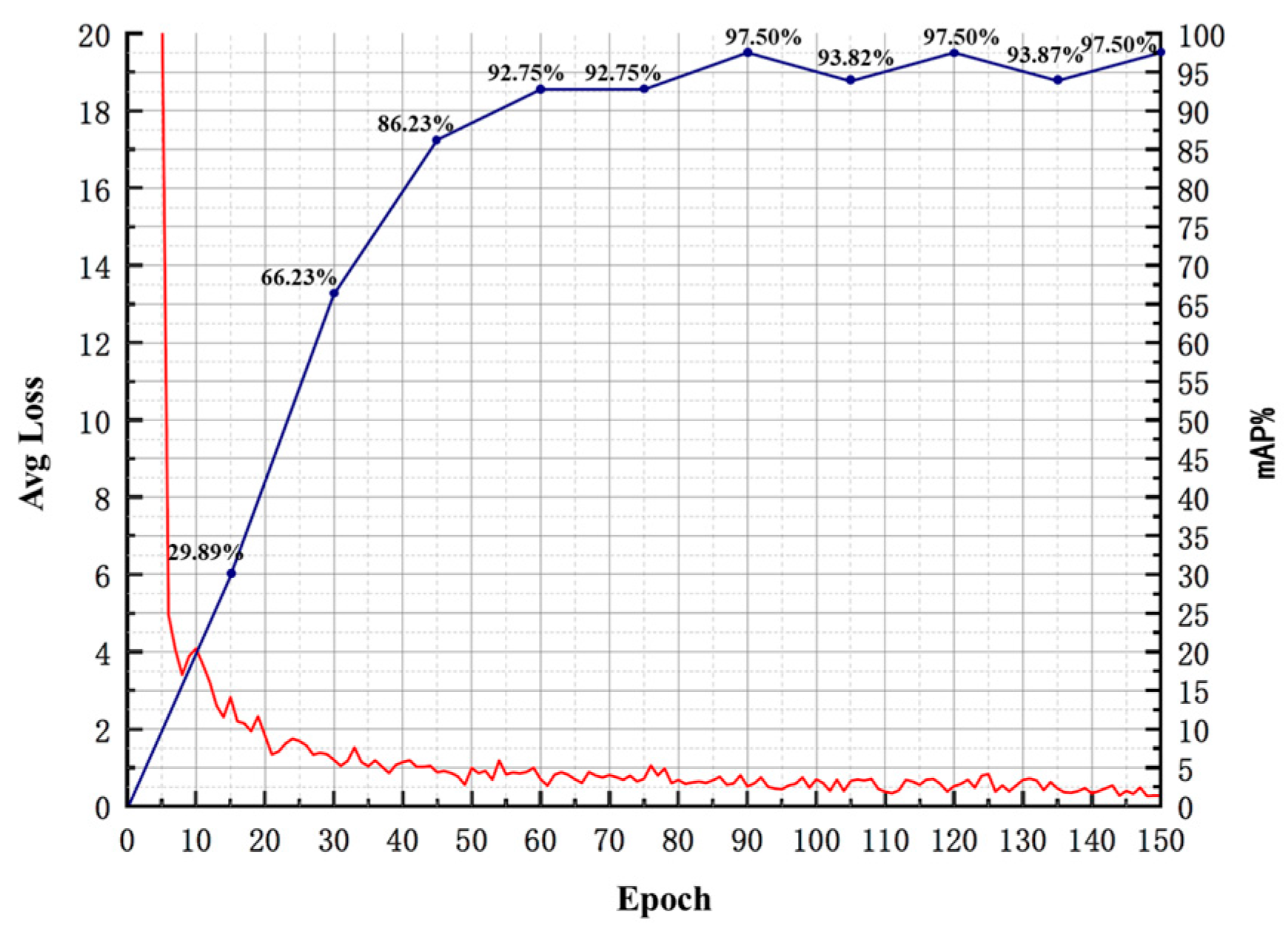
| Number of traversals | 150 | 150 |
| Network Model | SSD-Inception V2 | SSD-Inception V3 | YOLOV3 | YOLOV4-Tiny | Quality Detection Model |
|---|---|---|---|---|---|
| Number of Epochs | 100 | 100 | 100 | 150 | 150 |
| IoU | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 |
| mAP (%) | 70.59 | 76.65 | 92.54 | 92.74 | 97.50 |
| Model size (MB) | 52.6 | 994 | 236 | 23.1 | 244 |
| FPS (f/s) | 35.5 | 30.3 | 30.2 | 56.6 | 32.8 |
| Stage | Parameters | Numerical Value |
|---|---|---|
| Sparse training | Batch sample quantity | 8 |
| Learning rate | 0.003 | |
| Sparsity rate | 0.001 | |
| Number of traversals | 2000 | |
| Pruning | Channel pruning ratio | 0.90 |
| Number of layers pruning | 2 | |
| Fine-tuned pruned model | Number of traversals | 100 |
| Batch sample quantity | 8 |
| Parameters | Original Model | Channel Pruning | Layer Pruning |
|---|---|---|---|
| Total parameters | 63,953,841 | 1,107,904 | 1,080,754 |
| Average accuracy mean (%) | 97.50 | 95.14 | 95.14 |
| Model size (M) | 244 | 4.30 | 4.19 |
| Inference time (s) | 0.0305 | 0.0153 | 0.0147 |
| Parameters | MobileNetV1-SSD | MobileNetV2-SSD | YOLOV3-Tiny | YOLOV4-Tiny | YOLOV5S | YOLOV8S | Pruning Model |
|---|---|---|---|---|---|---|---|
| AP(Dent) | 34.77 | 78.33 | 81.37 | 93.65 | 97.37 | 98.85 | 98.82 |
| AP(Crack) | 61.63 | 62.79 | 82.23 | 95.24 | 97.45 | 98.63 | 98.35 |
| AP(Glitch) | 50 | 66.59 | 75.67 | 85.94 | 92.86 | 94.15 | 93.26 |
| AP(Fracture) | 73.5 | 74.64 | 91.65 | 96.13 | 96.84 | 98.97 | 99.21 |
| mAP | 54.98 | 70.59 | 82.73 | 92.74 | 96.13 | 97.65 | 97.41 |
| Model size (MB) | 18.5 | 52.6 | 34.7 | 23.1 | 14.1 | 21.5 | 4.19 |
| FPS (2080Ti) | 64.6 | 53.7 | 55.4 | 56.6 | 66.1 | 62.3 | 68.0 |
| FPS (AGX Xavier) | 42.3 | 29.6 | 30.6 | 33.8 | 44.5 | 38.4 | 47.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Xiong, Q.; Huang, H.; Tang, S.; Liu, Z. Research on the Construction of an Efficient and Lightweight Online Detection Method for Tiny Surface Defects through Model Compression and Knowledge Distillation. Electronics 2024, 13, 253. https://doi.org/10.3390/electronics13020253
Chen Q, Xiong Q, Huang H, Tang S, Liu Z. Research on the Construction of an Efficient and Lightweight Online Detection Method for Tiny Surface Defects through Model Compression and Knowledge Distillation. Electronics. 2024; 13(2):253. https://doi.org/10.3390/electronics13020253
Chicago/Turabian StyleChen, Qipeng, Qiaoqiao Xiong, Haisong Huang, Saihong Tang, and Zhenghong Liu. 2024. "Research on the Construction of an Efficient and Lightweight Online Detection Method for Tiny Surface Defects through Model Compression and Knowledge Distillation" Electronics 13, no. 2: 253. https://doi.org/10.3390/electronics13020253
APA StyleChen, Q., Xiong, Q., Huang, H., Tang, S., & Liu, Z. (2024). Research on the Construction of an Efficient and Lightweight Online Detection Method for Tiny Surface Defects through Model Compression and Knowledge Distillation. Electronics, 13(2), 253. https://doi.org/10.3390/electronics13020253








