Modeling, System Identification, and Control of a Railway Running Gear with Independently Rotating Wheels on a Scaled Test Rig
Abstract
1. Introduction
2. System and Sensor Setup
3. Motivation
4. Modeling and System Identification
4.1. Lateral Dynamics
4.1.1. Modeling
4.1.2. Parameter Identification
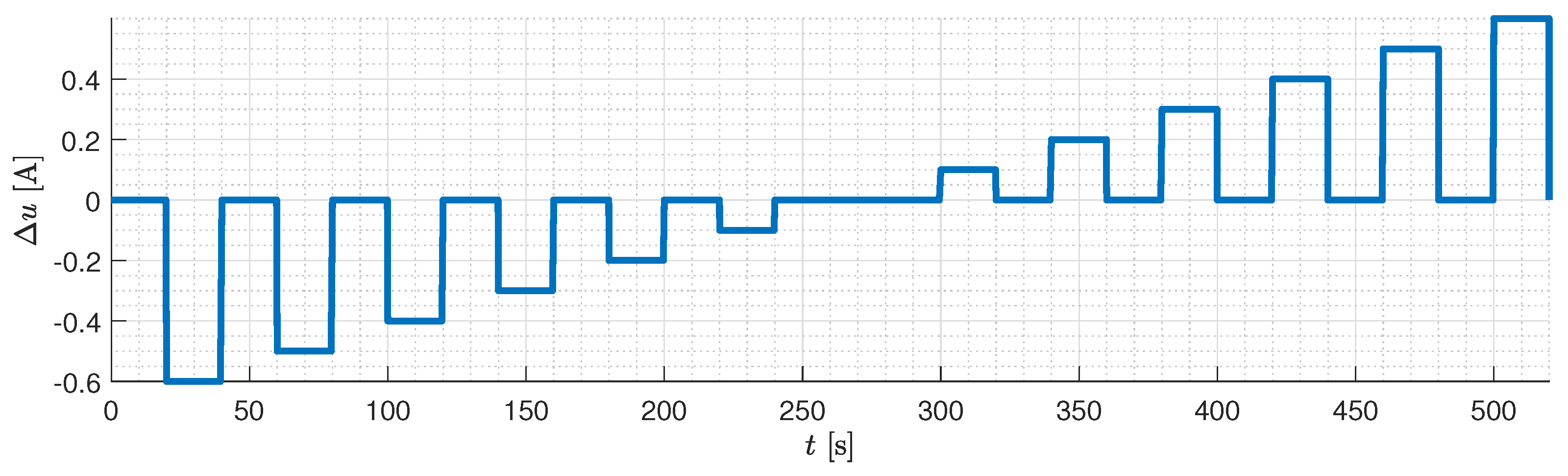
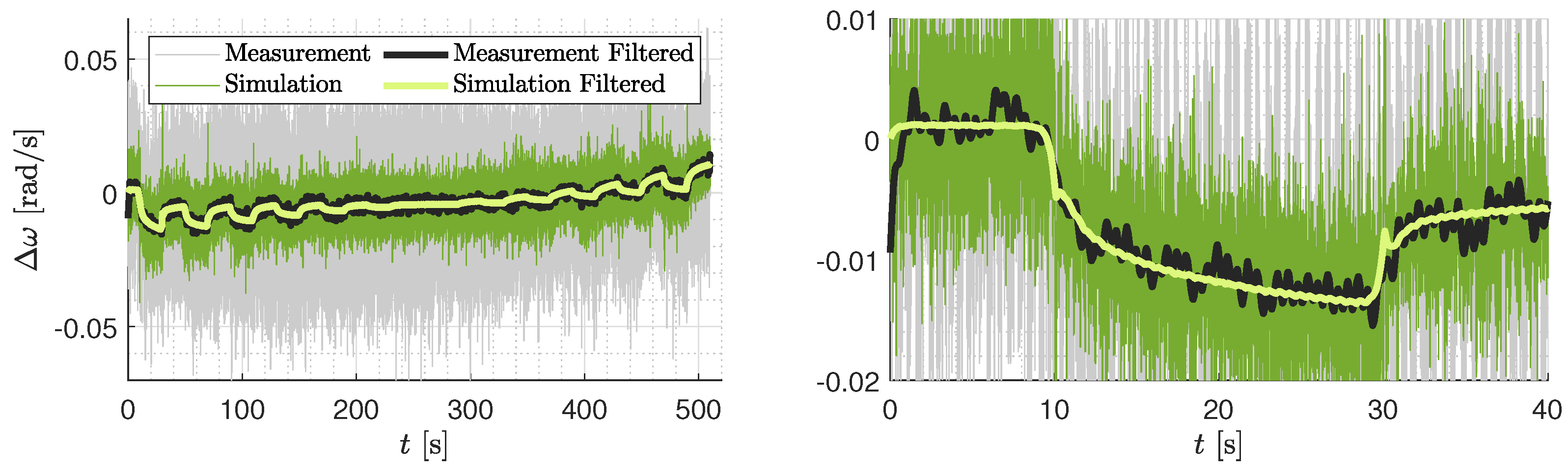
4.2. Angular Velocity Dynamics
Identification
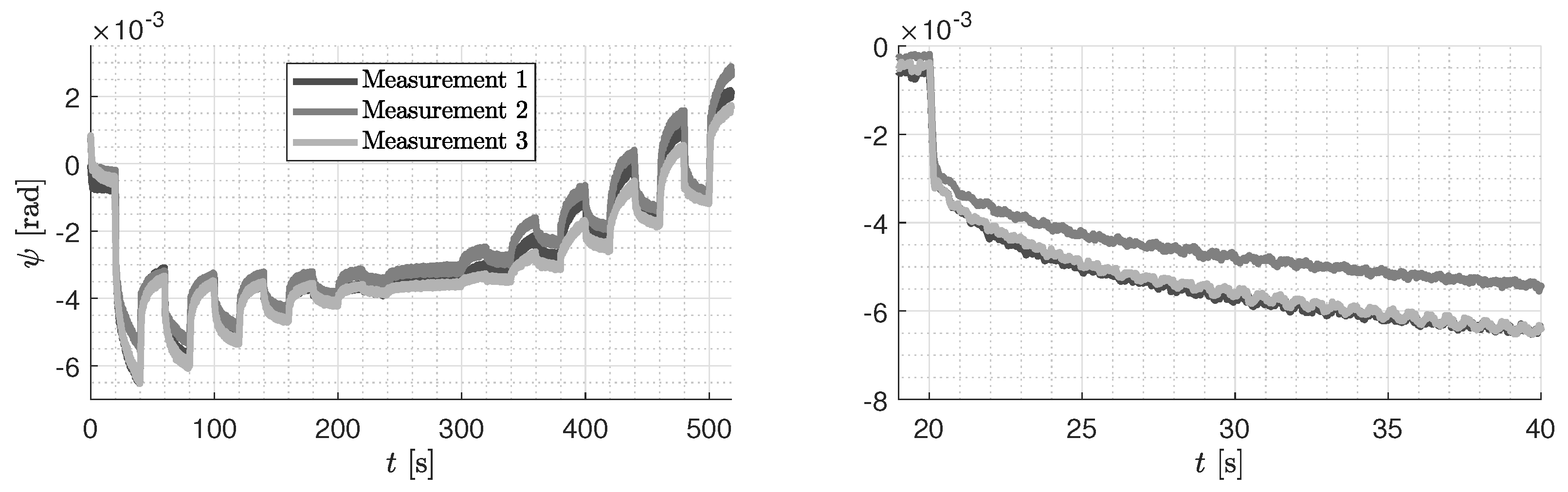
4.3. Yaw Dynamics
4.3.1. Modeling
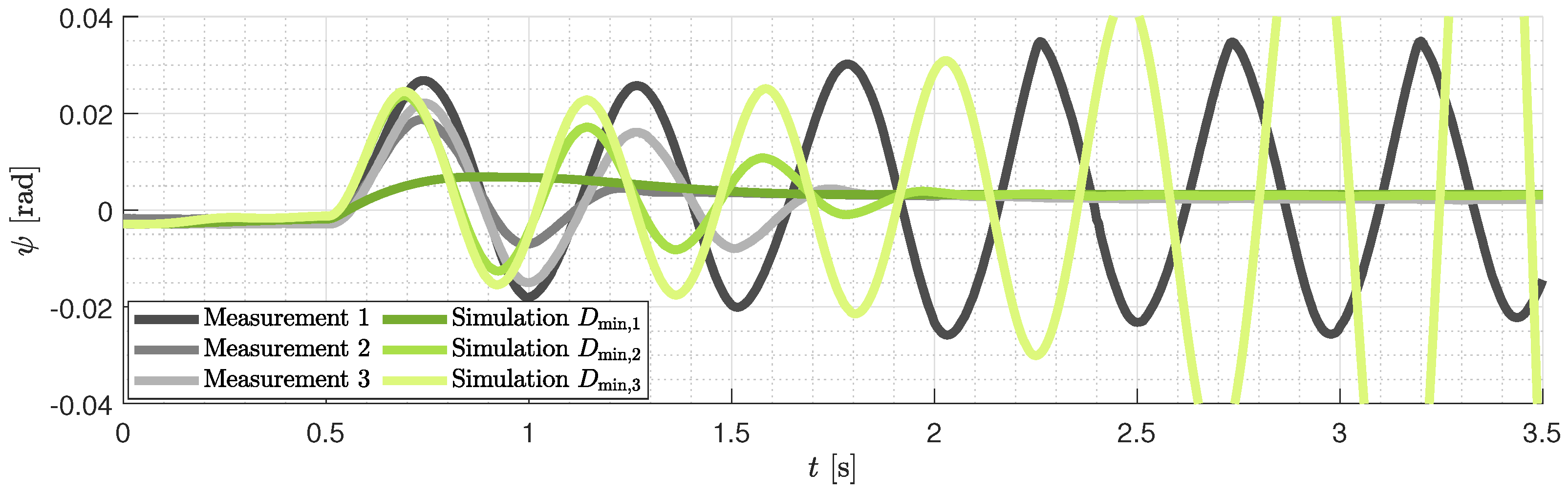
4.3.2. Natural Frequency Identification
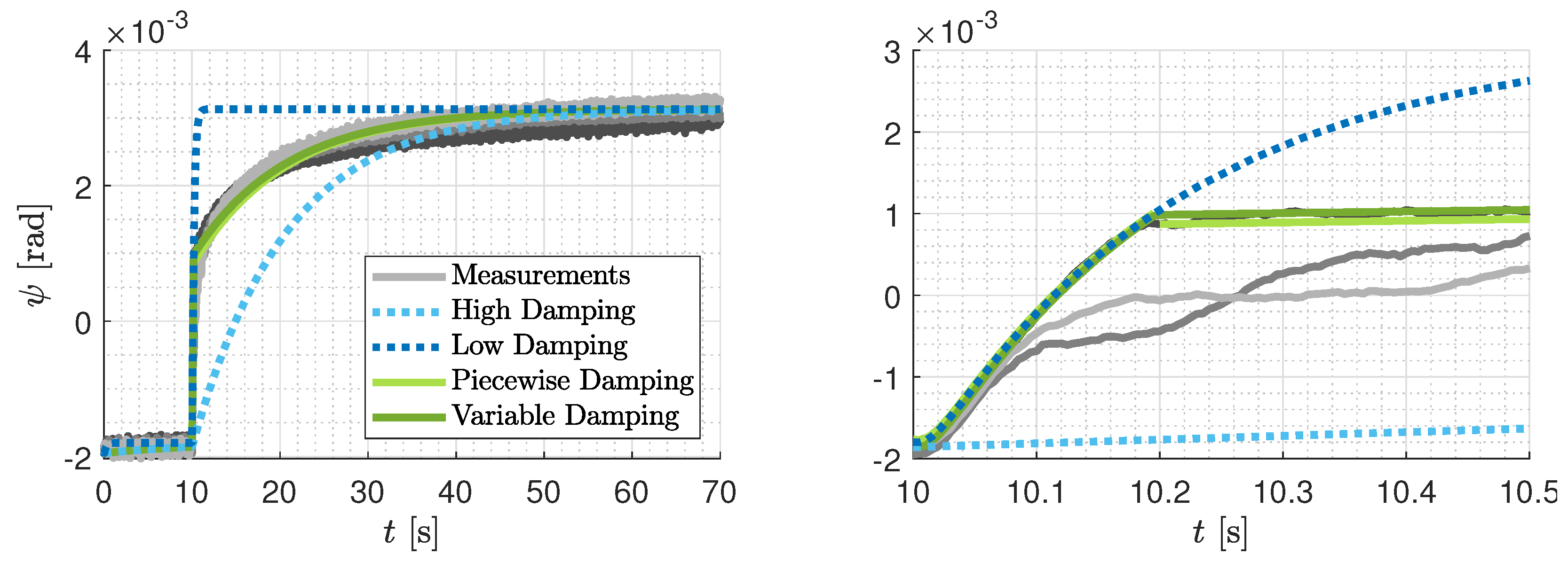
4.3.3. Damping Modeling and Identification
4.3.4. Hysteresis Modeling and Identification
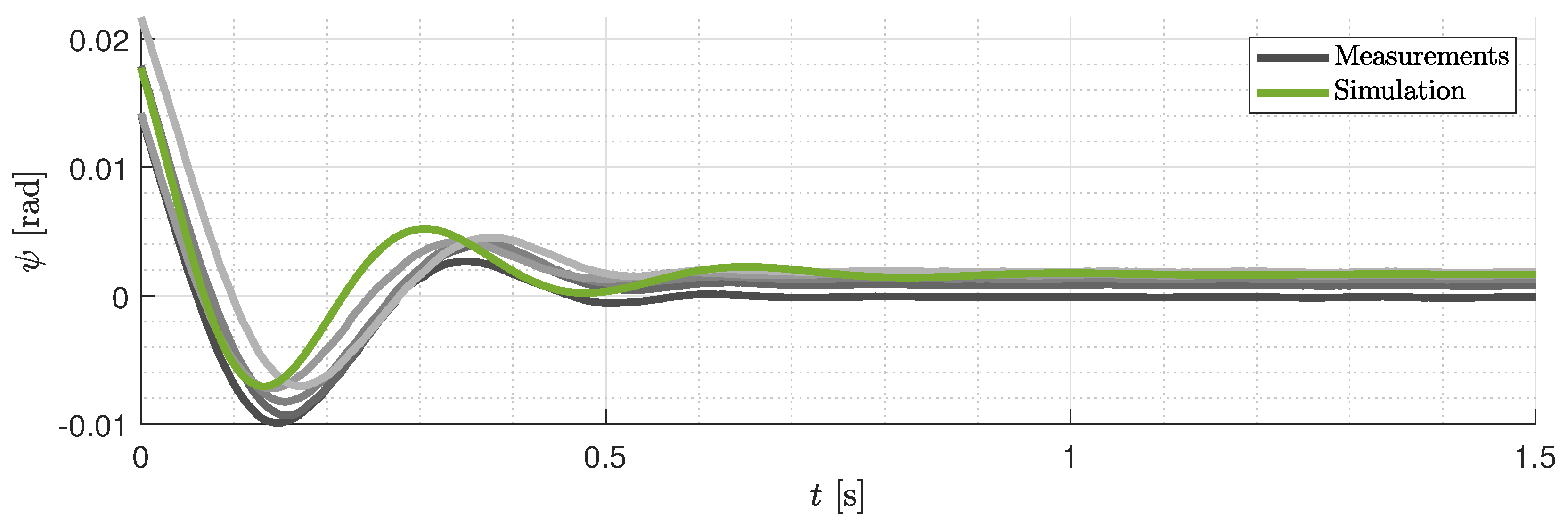
4.3.5. Verification
5. Closed-Loop System and Control Design
5.1. P Control Design
5.2. Cascaded PI-PD Control
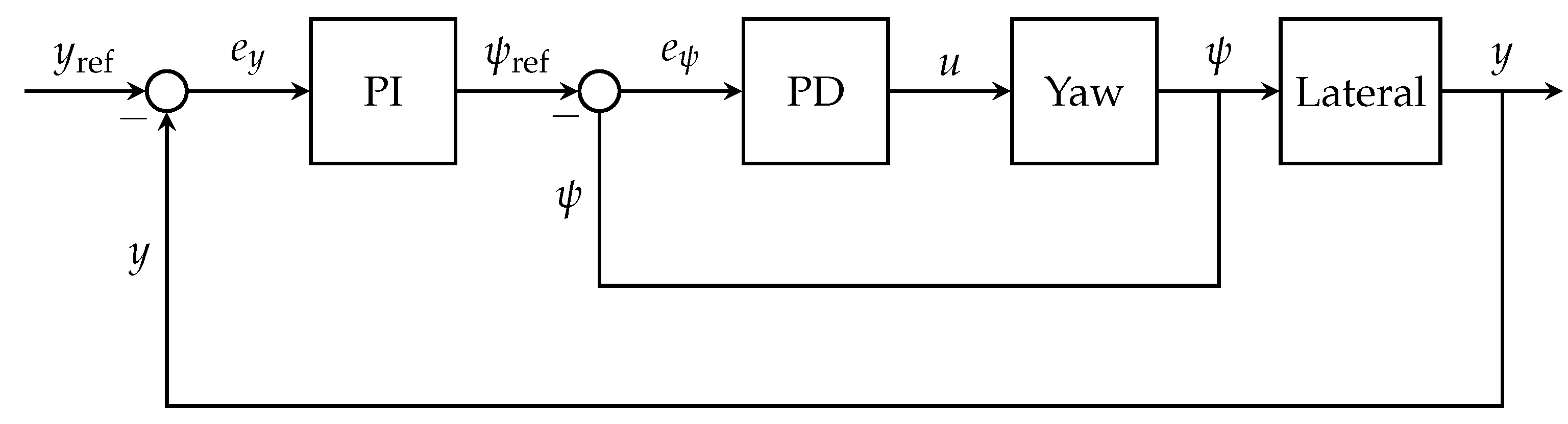
5.2.1. Control Structure
5.2.2. Closed-Loop Dynamics
5.2.3. Gain Tuning
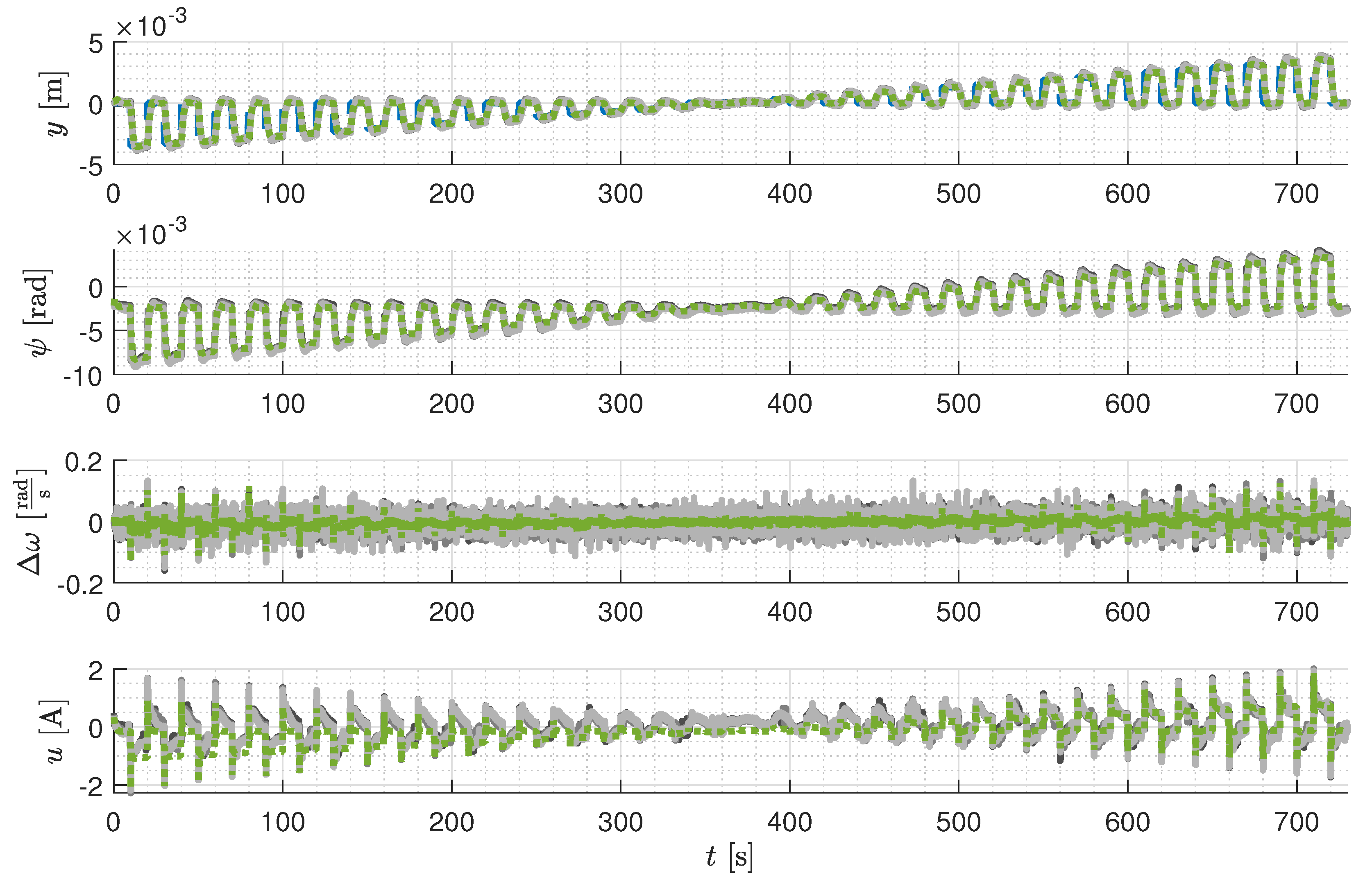
5.2.4. Performance
5.2.5. Robustness
5.2.6. Discussion
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Suda, Y.; Michitsuji, Y. Improved curving performance using unconventional wheelset guidance design and wheel-rail interface–Present and future solutions. Veh. Syst. Dyn. 2023, 61, 1881–1915. [Google Scholar] [CrossRef]
- Kurzeck, B.; Valente, L. A novel mechatronic running gear: Concept, simulation and scaled roller rig testing. In Proceedings of the World Congress on Railway Research, Mai 2011, Lille, France, 22–26 May 2011. [Google Scholar]
- Jaschinski, A. On the Application of Similarity Laws to a Scaled Railway Bogie Model. 1991. Available online: https://elibrary.ru/item.asp?id=6848485 (accessed on 3 October 2024).
- Kurzeck, B.; Heckmann, A.; Wesseler, C.; Rapp, M. Mechatronic track guidance on disturbed track: The trade-off between actuator performance and wheel wear. Veh. Syst. Dyn. 2014, 52, 109–124. [Google Scholar] [CrossRef]
- Keck, A.; Schwarz, C.; Meurer, T.; Heckmann, A.; Grether, G. Estimating the wheel lateral position of a mechatronic railway running gear with nonlinear wheel–rail geometry. Mechatronics 2020, 73, 102457. [Google Scholar] [CrossRef]
- Myamlin, S.; Kalivoda, J.; Neduzha, L. Testing of railway vehicles using roller rigs. Procedia Eng. 2017, 187, 688–695. [Google Scholar] [CrossRef]
- Kalivoda, J.; Bauer, P. Scaled roller rig to assess the influence of active wheelset steering on wheel-rail contact forces. In Proceedings of the IAVSD International Symposium on Dynamics of Vehicles on Roads and Tracks, Gothenburg, Sweden, 12–16 August 2019; pp. 82–89. [Google Scholar]
- Oh, Y.J.; Lee, J.K.; Liu, H.C.; Cho, S.; Lee, J.; Lee, H.J. Hardware-in-the-loop simulation for active control of tramcars with independently rotating wheels. IEEE Access 2019, 7, 71252–71261. [Google Scholar] [CrossRef]
- Jia, X.; Yin, Y.; Wang, W. Dynamic Modeling, Dynamic Characteristics, and Slight Self-Guidance Ability at High Speeds of Independently Rotating Wheelset for Railway Vehicles. Appl. Sci. 2024, 14, 1548. [Google Scholar] [CrossRef]
- Suda, Y.; Wang, W.; Nishina, M.; Lin, S.; Michitsuji, Y. Self-steering ability of the proposed new concept of independently rotating wheels using inverse tread conicity. Veh. Syst. Dyn. 2012, 50, 291–302. [Google Scholar] [CrossRef]
- Ji, Y.; Ren, L.; Zhou, J. Boundary conditions of active steering control of independent rotating wheelset based on hub motor and wheel rotating speed difference feedback. Veh. Syst. Dyn. 2018, 56, 1883–1898. [Google Scholar] [CrossRef]
- Perez, J.; Busturia, J.M.; Mei, T.; Vinolas, J. Combined active steering and traction for mechatronic bogie vehicles with independently rotating wheels. Annu. Rev. Control 2004, 28, 207–217. [Google Scholar] [CrossRef]
- Liu, X.; Goodall, R.; Iwnicki, S. Active control of independently-rotating wheels with gyroscopes and tachometers–simple solutions for perfect curving and high stability performance. Veh. Syst. Dyn. 2021, 59, 1719–1734. [Google Scholar] [CrossRef]
- Ahn, H.; Lee, H.; Go, S.; Cho, Y.; Lee, J. Control of the lateral displacement restoring force of IRWs for sharp curved driving. J. Electr. Eng. Technol. 2016, 11, 1042–1048. [Google Scholar] [CrossRef]
- Mei, T.; Goodall, R.M. Robust control for independently rotating wheelsets on a railway vehicle using practical sensors. IEEE Trans. Control. Syst. Technol. 2001, 9, 599–607. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Lu, Z.; Sun, X.; Zou, J.; Wan, H.; Yang, M.; Zhang, H. Robust LPV-H∞ control for active steering of tram with independently rotating wheels. Adv. Mech. Eng. 2022, 14, 16878132221130574. [Google Scholar] [CrossRef]
- Zaeim, A. Semi-Active Control for Independently Rotating Wheelset in Railway Vehicles with MR Dampers; University of Salford: Salford, UK, 2021. [Google Scholar]
- Mei, T.; Li, H.; Zaeim, A.; Dai, H. Semi-active control of independently rotating wheels in railway vehicles. Veh. Syst. Dyn. 2024, 62, 2686–2702. [Google Scholar] [CrossRef]
- Lu, Z.G.; Sun, X.J.; Yang, J.Q. Integrated active control of independently rotating wheels on rail vehicles via observers. J. Rail Rapid Transit 2017, 231, 295–305. [Google Scholar] [CrossRef]
- Grether, G.; Heckmann, A.; Looye, G. Lateral guidance control using information of preceding wheel pairs. In Proceedings of the International Association of Vehicle System Dynamics, Bergen, Norway, 19–24 July 2020; pp. 863–871. [Google Scholar]
- Wei, J.; Lu, Z.; Yin, Z.; Jing, Z. Multiagent Reinforcement Learning for Active Guidance Control of Railway Vehicles with Independently Rotating Wheels. Appl. Sci. 2024, 14, 1677. [Google Scholar] [CrossRef]
- Lu, Z.; Wei, J.; Wang, Z. Active Steering Controller for Driven Independently Rotating Wheelset Vehicles Based on Deep Reinforcement Learning. Processes 2023, 11, 2677. [Google Scholar] [CrossRef]
- Ewering, J.H.; Schwarz, C.; Ehlers, S.F.; Jacob, H.G.; Seel, T.; Heckmann, A. Integrated Model Predictive Control of High-Speed Railway Running Gears with Driven Independently Rotating Wheels. IEEE Trans. Veh. Technol. 2024, 73, 7852–7865. [Google Scholar] [CrossRef]
- Posielek, T.; Heckmann, A. Observer Design Based on Steady State and Reduced Model Information with Application to Running Gears with Independently Rotating Driven Wheels. In Proceedings of the Mediterranean Conference on Control and Automation, Crete, Greece, 11–14 June 2024; pp. 602–609. [Google Scholar]
- Damsongsaeng, P.; Persson, R.; Stichel, S.; Casanueva, C. Estimation of wheelset equivalent conicity using the dual extended Kalman filter. Multibody Syst. Dyn. 2024, 60, 563–579. [Google Scholar] [CrossRef]
- Schwarz, C.; Heckmann, A.; Keck, A. Different models of a scaled experimental running gear for the DLR RailwayDynamics Library. In Proceedings of the 11th International Modelica Conference, Versailles, France, 21–23 September 2015. [Google Scholar]
- Joos, H.D. A multiobjective optimisation-based software environment for control systems design. In Proceedings of the IEEE International Symposium on Computer Aided Control System Design, San Jose, CA, USA, 18–20 September 2002; pp. 7–14. [Google Scholar]
- Kalker, J.J. Three-Dimensional Elastic Bodies in Rolling Contact; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Polach, O. Creep forces in simulations of traction vehicles running on adhesion limit. Wear 2005, 258, 992–1000. [Google Scholar] [CrossRef]
- Knothe, K.; Stichel, S. Rail Vehicle Dynamics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ikhouane, F.; Rodellar, J. Systems with Hysteresis: Analysis, Identification and Control Using the Bouc-Wen Model; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Al-Bender, F.; Symens, W.; Swevers, J.; Van Brussel, H. Theoretical analysis of the dynamic behavior of hysteresis elements in mechanical systems. Int. J. -Non-Linear Mech. 2004, 39, 1721–1735. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Mathematical Models of Hysteresis and Their Applications; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Ikhouane, F. A survey of the hysteretic Duhem model. Arch. Comput. Methods Eng. 2018, 25, 965–1002. [Google Scholar] [CrossRef]
- Krasnosel’skii, M.A.; Pokrovskii, A.V. Systems with Hysteresis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc-Wen model, a survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, H.; Bockstedte, A.; Foliente, G.C.; Paevere, P. Parameter analysis of the differential model of hysteresis. J. Appl. Mech. 2004, 71, 342–349. [Google Scholar] [CrossRef]








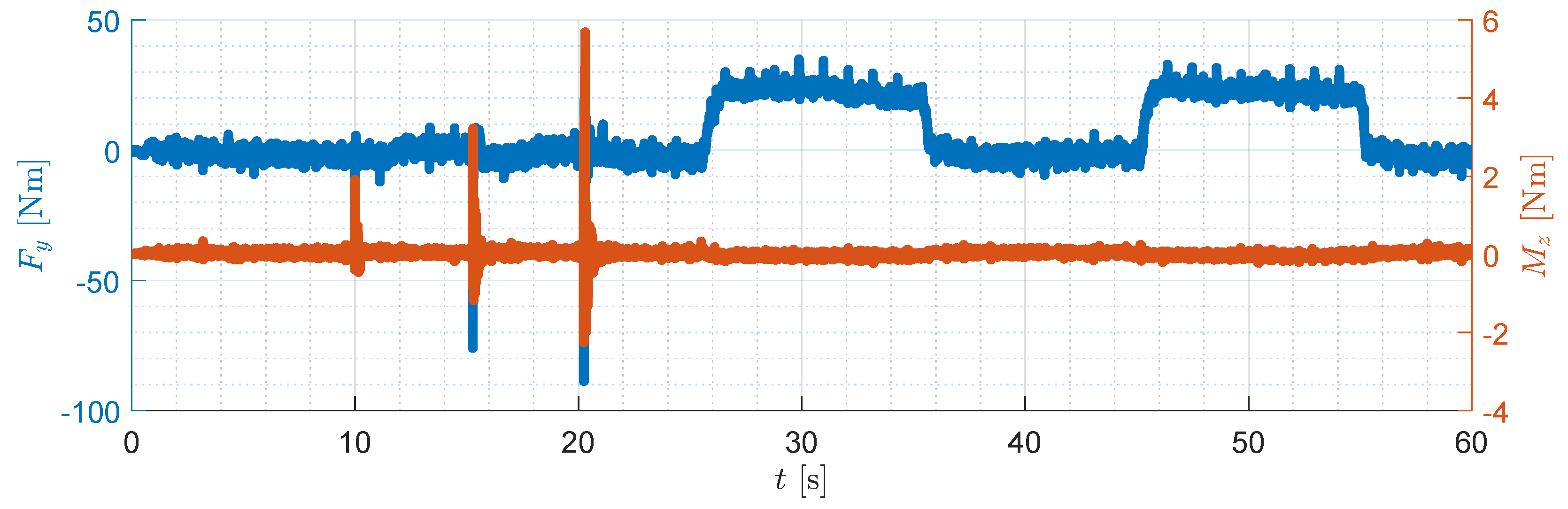
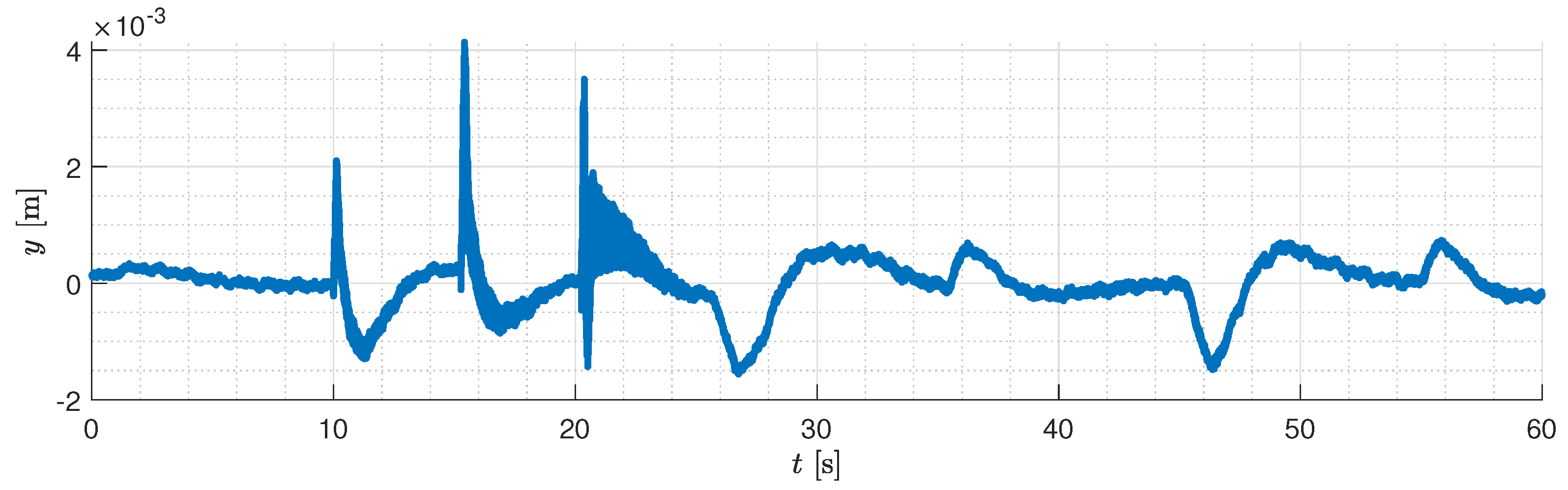
| Notation | Description | Nominal | Identified |
|---|---|---|---|
| v | longitudinal velocity | −1 | |
| wheel radius | |||
| b | track width | ||
| distance between laser sensors measuring lateral displacement | |||
| nominal distance from laser sensors to metal plates | |||
| distance between laser sensors measuring yaw angle | |||
| motor constant | −1 | ||
| distance wheel carrier and middle frame | |||
| equivalent conicity | |||
| offset lateral displacement | 0 | ||
| wheel inertia w.r.t rolling | |||
| extended Kalker friction coefficient | −1 | −1 | |
| offset angular velocity | 0 −1 | −1 | |
| axle bridge inertia w.r.t yawing | 2 | 2 | |
| equivalent stiffness | −1 | −1 | |
| equivalent damping | −1 | −1 | |
| offset yaw angle | 0 |
| Variables | Description | Value |
|---|---|---|
| y | lateral displacement | |
| yaw angle | ||
| angular velocity | −1 | |
| current input |
| Identification Scenario | D | K | ||||||
|---|---|---|---|---|---|---|---|---|
| Natural Frequency (Section 4.3.2) | 18.8 | 0.28 | - | - | - | - | - | |
| Damping Identification (Section 4.3.3) | 18.8 | [2.2, 100] | - | - | - | |||
| Hysteresis Identification (Section 4.3.4) | 18.8 | 100 | - | 0.48 | 7362 | −7164 |
| Inner Loop Parameter | Value | Outer Loop Parameter | Value |
|---|---|---|---|
| 40 | 3 | ||
| 5 | 9 | ||
| 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Posielek, T. Modeling, System Identification, and Control of a Railway Running Gear with Independently Rotating Wheels on a Scaled Test Rig. Electronics 2024, 13, 3983. https://doi.org/10.3390/electronics13203983
Posielek T. Modeling, System Identification, and Control of a Railway Running Gear with Independently Rotating Wheels on a Scaled Test Rig. Electronics. 2024; 13(20):3983. https://doi.org/10.3390/electronics13203983
Chicago/Turabian StylePosielek, Tobias. 2024. "Modeling, System Identification, and Control of a Railway Running Gear with Independently Rotating Wheels on a Scaled Test Rig" Electronics 13, no. 20: 3983. https://doi.org/10.3390/electronics13203983
APA StylePosielek, T. (2024). Modeling, System Identification, and Control of a Railway Running Gear with Independently Rotating Wheels on a Scaled Test Rig. Electronics, 13(20), 3983. https://doi.org/10.3390/electronics13203983






