Synthesis of High-Selectivity Two-Dimensional Filter Banks Using Sigmoidal Function
Abstract
1. Introduction
2. Theoretical Background
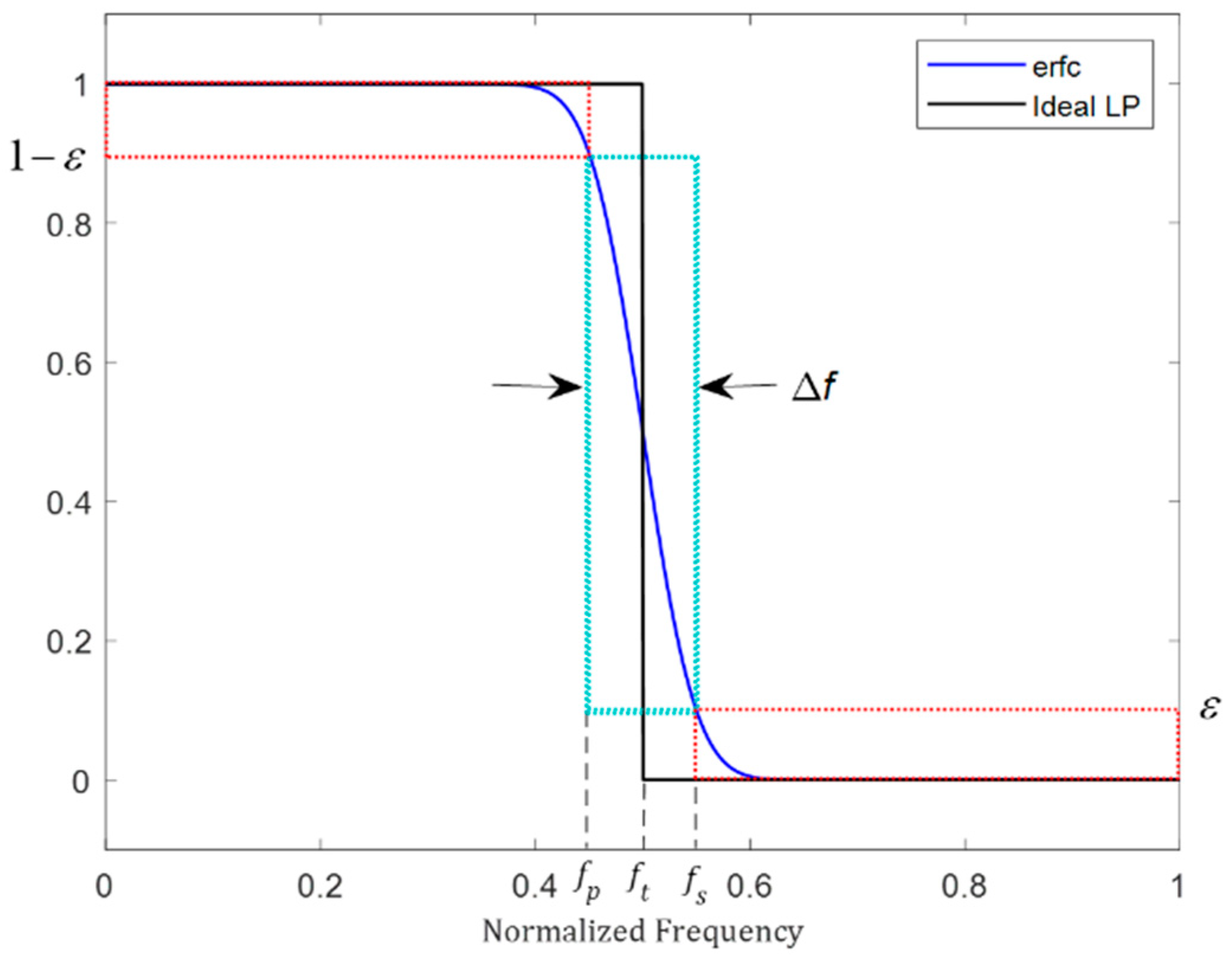
2.1. One-Dimensional Low-Pass Filter with Sigmoidal Function
2.2. One-Dimensional Band-Pass Filter Prototype
3. Two-Dimensional Filter Banks Synthesis
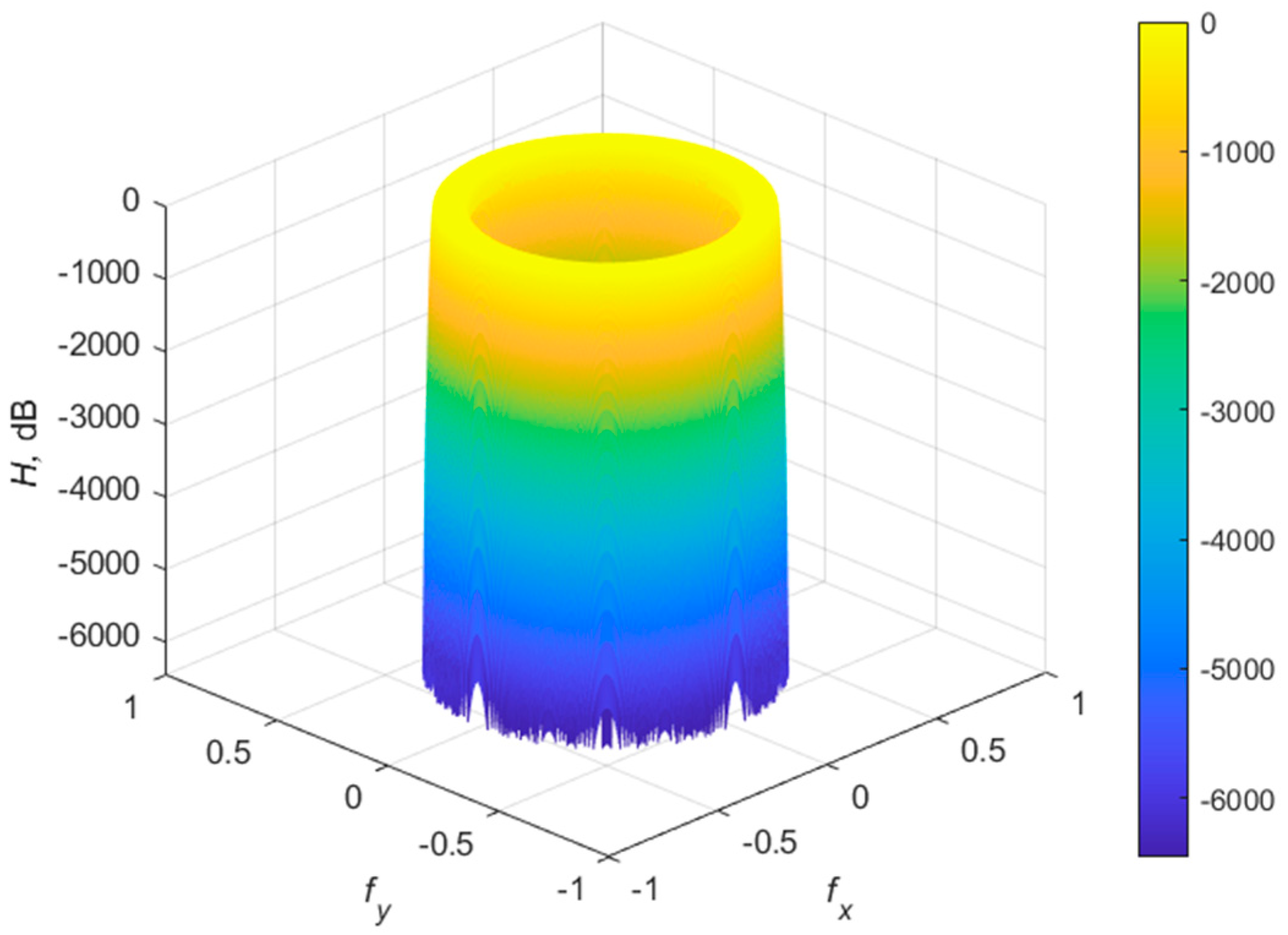
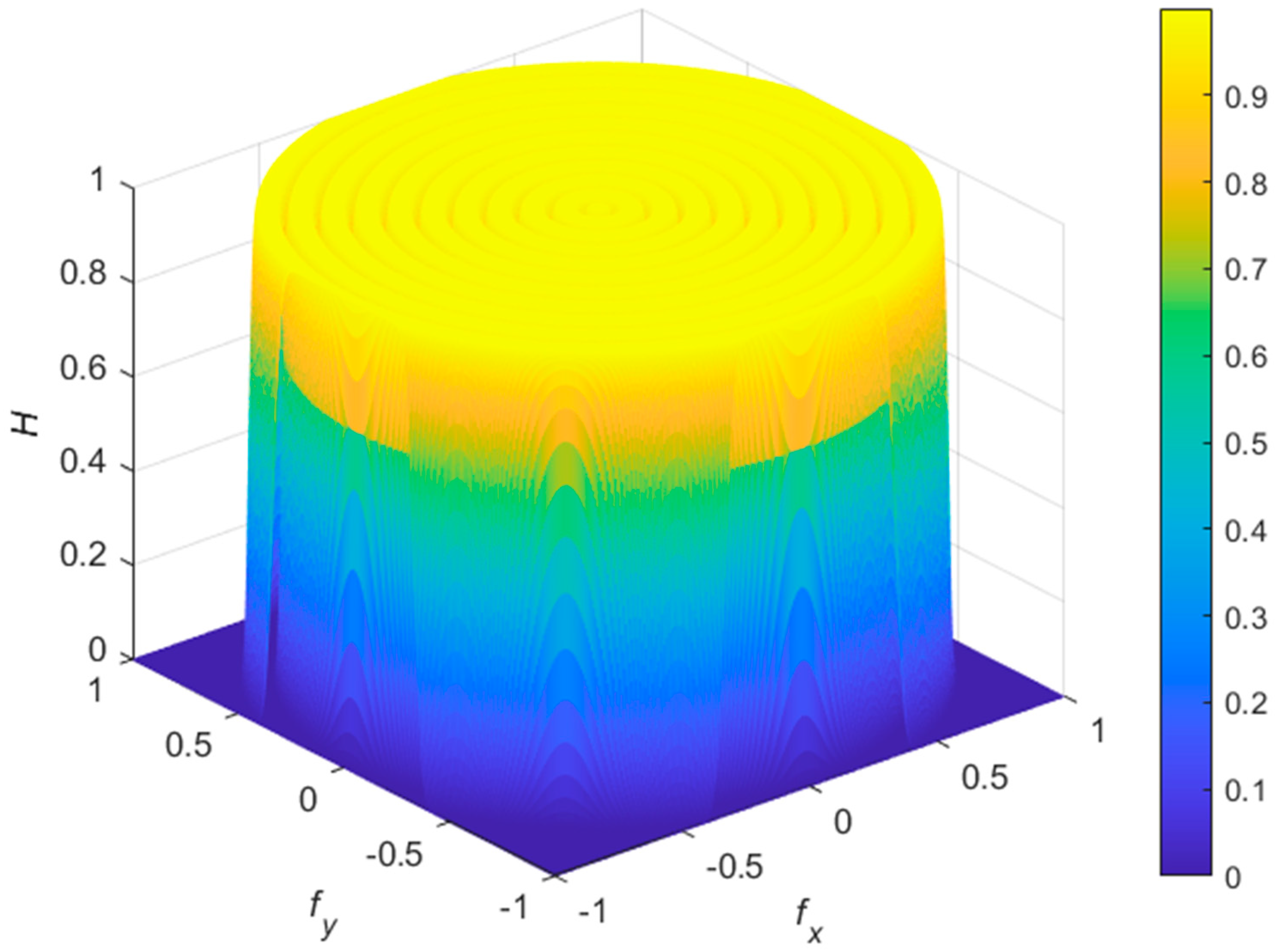
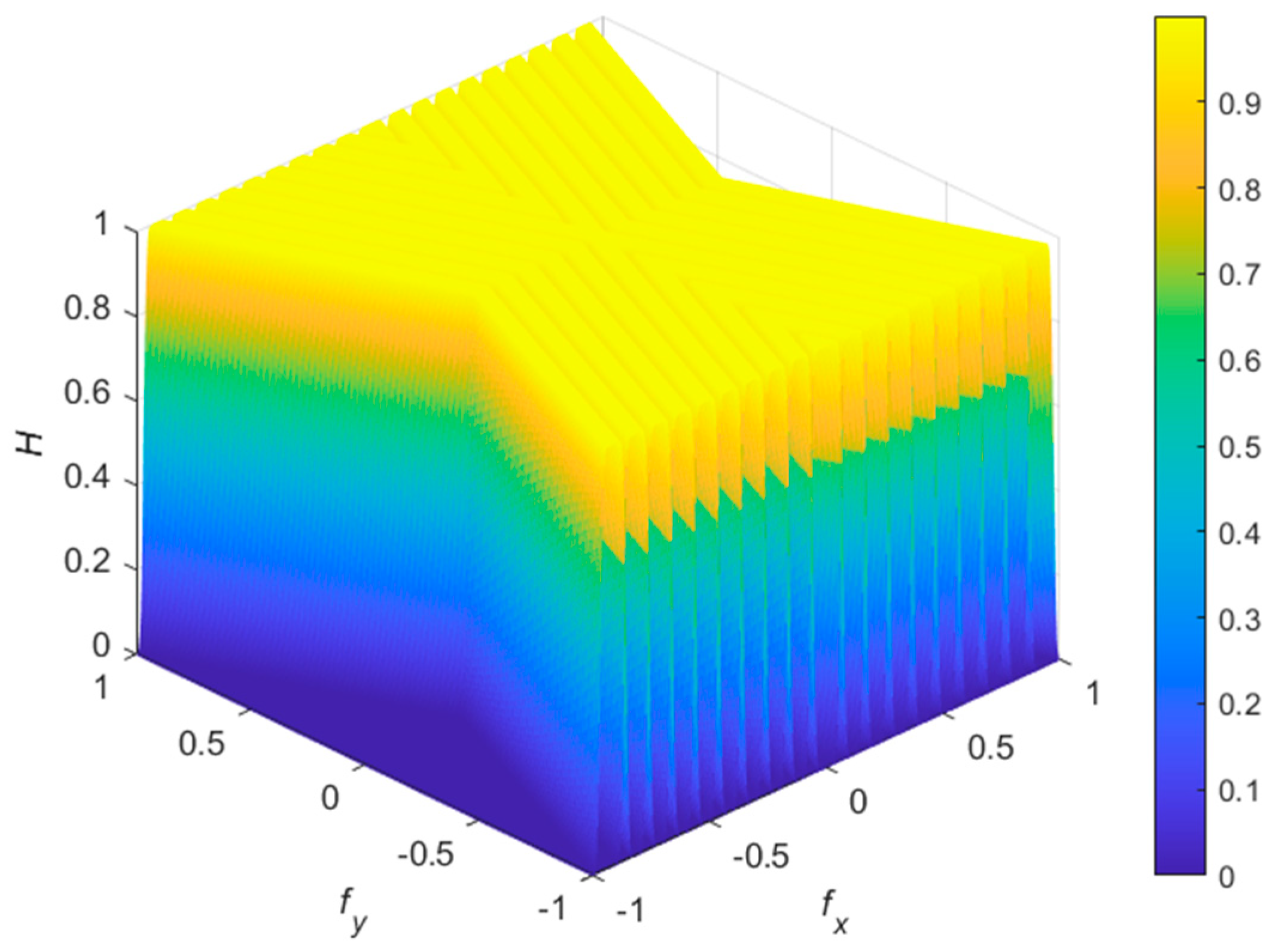
3.1. Two-Dimensional Uniform Filter Banks
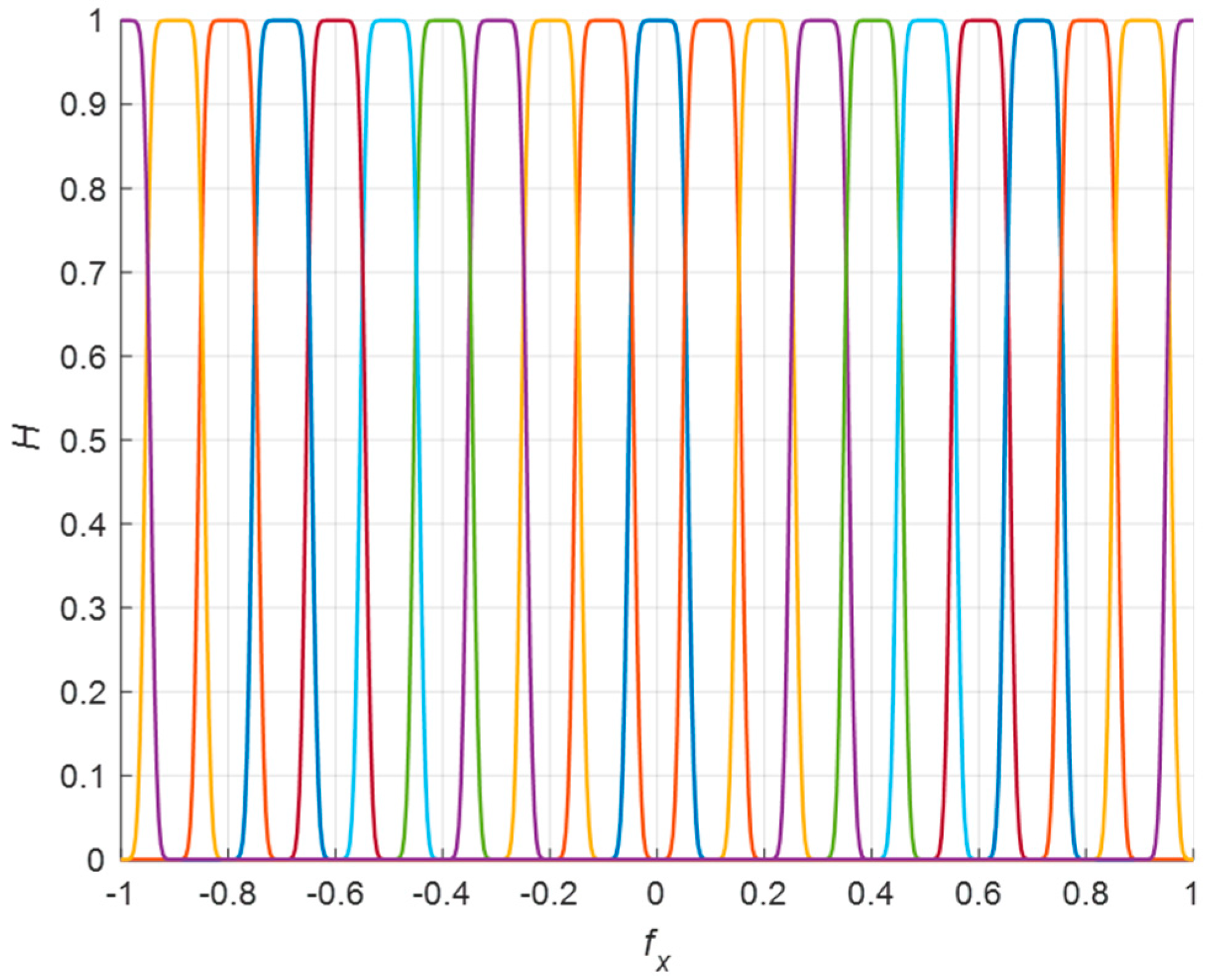
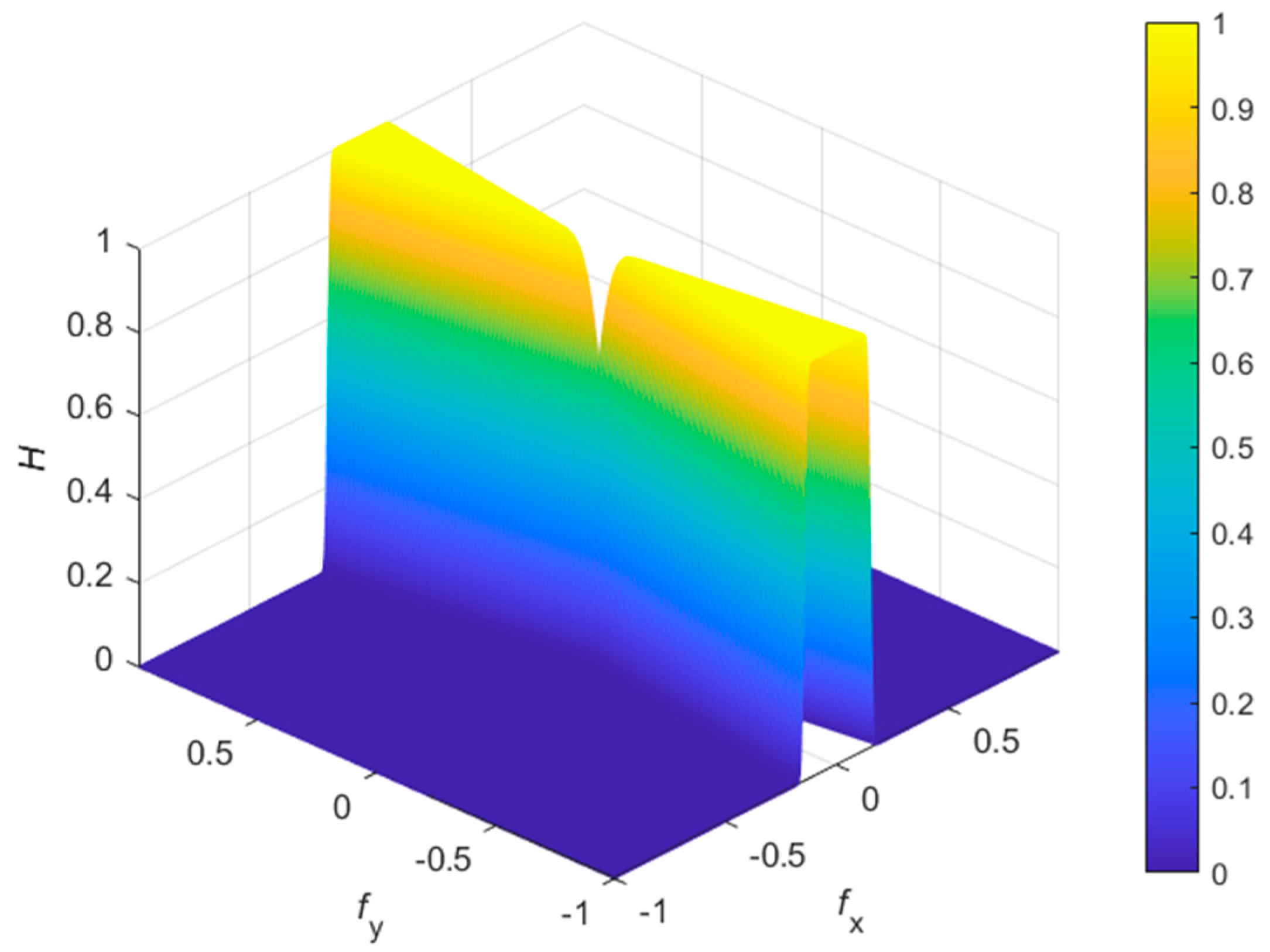
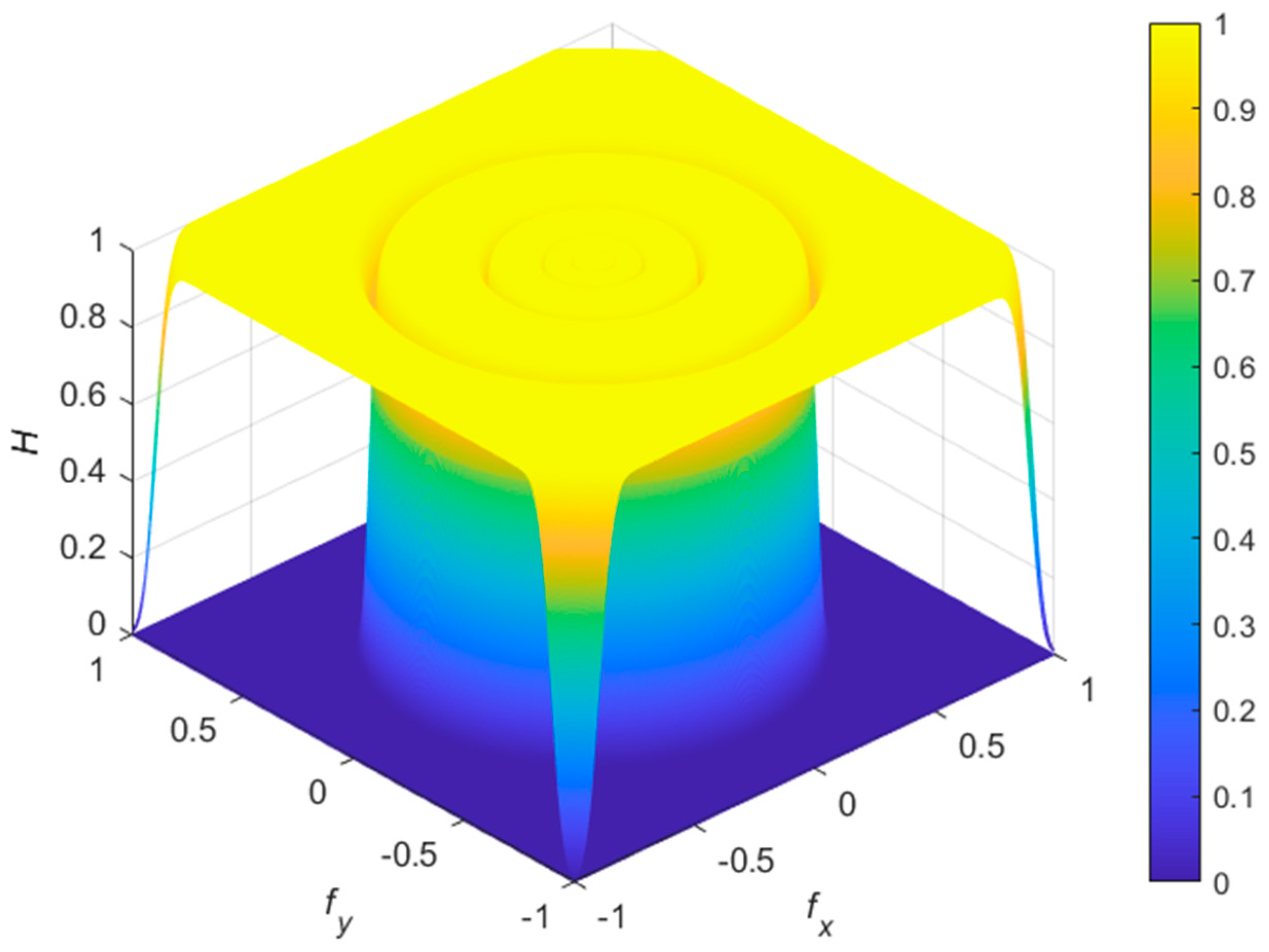
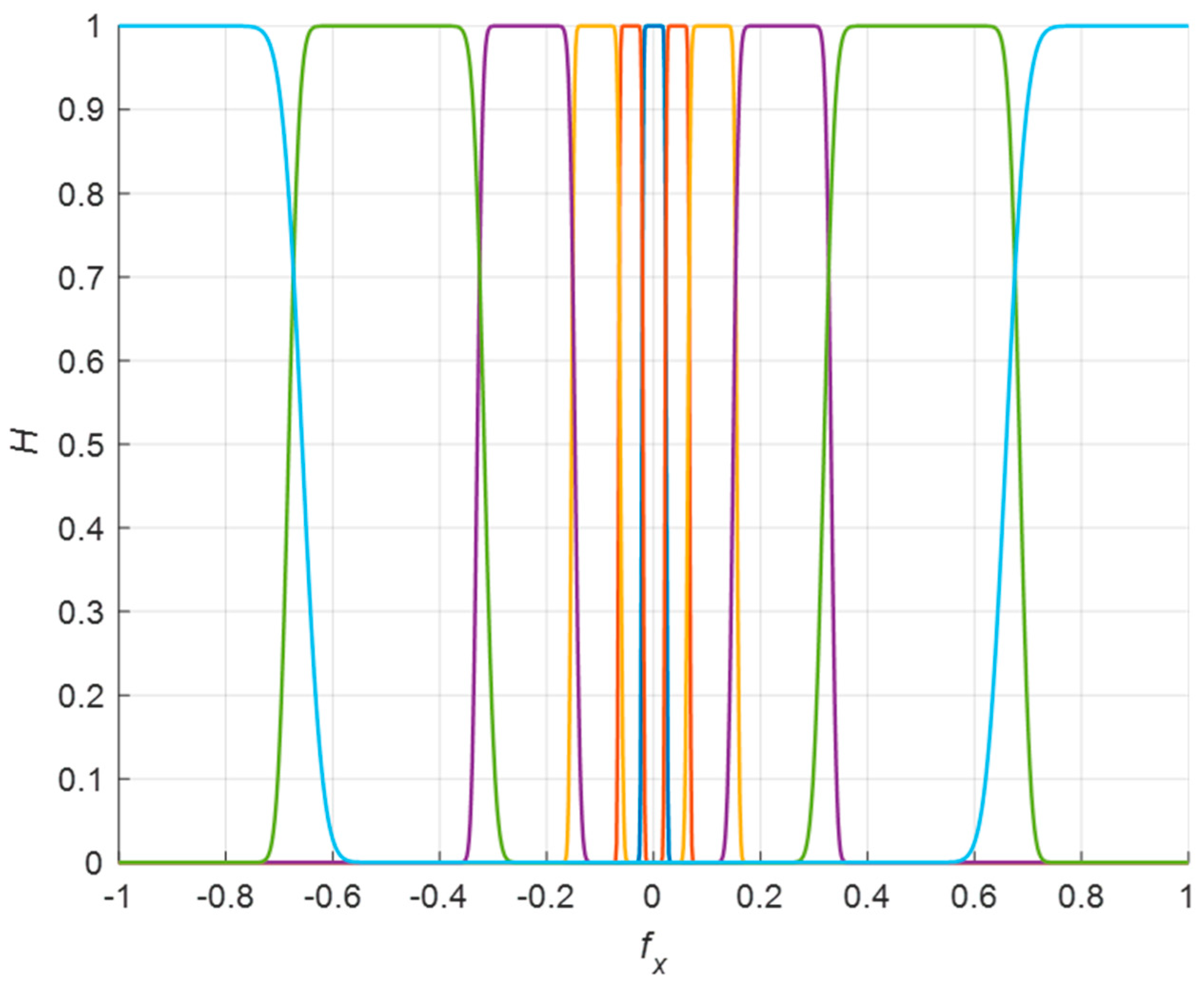
3.2. Two-Dimensional Nonuniform Filter Banks
3.3. Examples of Image Analysis with Described 2D Circular Filter Banks
4. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lim, J.S.; Antoniou, A. Two-Dimensional Signal and Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1990. [Google Scholar]
- Lu, W.; Antoniou, A. Two-Dimensional Digital Filters; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Lin, Y.P.; Vaidyanathan, P.P. Theory and design of two-dimensional filter banks: A review. Multidim. Syst. Signal Process. 1996, 7, 263–330. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, R. A comprehensive review and analysis on digital filter design. Int. J. Adv. Res. Eng. Technol. (IJARET) 2021, 12, 1131–1149. [Google Scholar]
- Kockanat, D.S.; Karaboga, N. The Design Approaches of Two-Dimensional Digital Filters Based on Metaheuristic Optimization Algorithms: A Review of the Literature; Springer Science+Business Media Dordrecht: Dordrecht, The Nederland, 2015; pp. 265–287. [Google Scholar]
- Shyu, J.-J.; Pei, S.-C.; Huang, Y.-D. Design of variable two-dimensional FIR digital filters by McClellan transformation. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 574–582. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, J.; Su, Y.; Liu, H. Design of two-dimensional zero-phase fir digital filter by McClellan transformation and interval global optimization. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 167–171. [Google Scholar] [CrossRef]
- Rusu, C.; Dumitrescu, B. Iterative reweighted l1 design of sparse FIR filters. Signal Process. 2012, 92, 905–911. [Google Scholar] [CrossRef]
- Dumitrescu, B. Trigonometric polynomials positive on frequency domains and applications to 2-D FIR filter design. IEEE Trans. Signal Process. 2006, 54, 4282–4292. [Google Scholar] [CrossRef]
- Hong, X.Y.; Lai, X.P.; Zhao, R.J. Matrixbased algorithms for constrained least-squares and minimax designs of 2-D FIR filters. IEEE Trans. Signal Process. 2013, 64, 3620–3631. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Jhaveri, R.H.; Gadekallu, T.R.; Zhu, M.; Ahanger, T.A.; Khowaja, S.A. Sparse Bayesian learning based channel estimation in FBMC/OQAM industrial IoT networks. Comput. Commun. 2021, 176, 40–45. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Modeling of Some Classes of Extended Oscillators: Simulations, Algorithms, Generating Chaos, and Open Problems. Algorithms 2024, 17, 121. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Yan, Z.; Gulliver, T.A. Low-Complexity MIMO-FBMC Sparse Channel Parameter Estimation for Industrial Big Data Communications. IEEE Trans. Ind. Inform. 2021, 17, 3422–3430. [Google Scholar] [CrossRef]
- Bindima, T.; Elias, E. Design and implementation of low complexity 2-D variable digital FIR filters using single-parameter-tunable 2-D Farrow structure. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 618–627. [Google Scholar] [CrossRef]
- Matei, R. Efficient design procedure for circular filter banks. In Proceedings of the IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), East Lansing, MI, USA, 9–11 August 2021; pp. 259–262. [Google Scholar] [CrossRef]
- Weiping, Z.; Nakamura, S. An efficient approach for the synthesis of 2-D recursive fan filters using 1-D prototypes. IEEE Trans. Signal Process. 1996, 44, 979–983. [Google Scholar] [CrossRef]
- Bindima, T.; Manuel, M.; Elias, E. An efficient transformation for two dimensional circularly symmetric wideband FIR filters. In Proceedings of the IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 2838–2841. [Google Scholar] [CrossRef]
- Hung, T.Q.; Tuan, H.D.; Nguyen, T.Q. Design of half-band diamond and fan filters by SDP. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007; Volume III, pp. 901–904. [Google Scholar]
- Matei, R. A class of directional zero-phase 2D filters designed using analytical approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 1629–1640. [Google Scholar] [CrossRef]
- Bamberger, R.H.; Smith, M.J.T. A filter bank for the directional decomposition of images: Theory and design. IEEE Trans. Signal Process. 1992, 40, 882–893. [Google Scholar] [CrossRef]
- Tirakis, A.; Delopoulos, A.; Kollias, S. Two-dimensional filter bank design for optimal reconstruction using limited subband information. IEEE Trans. Image Process. 1995, 4, 1160–1165. [Google Scholar] [CrossRef]
- Shi, G.; Liang, L.; Xie, X. Design of directional filter banks with arbitrary number of subbands. IEEE Trans. Signal Process. 2009, 57, 4936–4941. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ikehara, M.; Nguyen, T.Q. A new combination of 1D and 2D filter banks for effective multiresolution image representation. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 2820–2823. [Google Scholar] [CrossRef]
- Basu, S. Multidimensional causal, stable, perfect reconstruction filter banks. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 832–842. [Google Scholar] [CrossRef]
- Liang, L.; Shi, G.; Xie, X. Nonuniform directional filter banks with arbitrary frequency partitioning. IEEE Trans. Image Process. 2011, 20, 283–288. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Oraintara, S. A class of multiresolution directional filter banks. IEEE Trans. Signal Process. 2007, 55, 949–961. [Google Scholar] [CrossRef]
- Lu, Y.M.; Do, M.N. Multidimensional directional filter banks and surfacelets. IEEE Trans. Image Process. 2007, 16, 918–931. [Google Scholar] [CrossRef]
- Hendre, M.; Patil, S.; Abhyankar, A. Directional filter bank-based fingerprint image quality. Pattern Anal. Appl. 2022, 25, 379–393. [Google Scholar] [CrossRef]
- Li, M.; Zhao, Y.; Zhang, F.; Luo, B.; Yang, C.; Gui, W.; Chang, K. Multi-scale feature selection network for lightweight image super-resolution. Neural Netw. 2024, 169, 352–364. [Google Scholar] [CrossRef] [PubMed]
- Matei, R.; Chiper, D.F. Analytic design technique for 2D FIR circular filter banks and their efficient implementation using polyphase approach. Sensors 2023, 23, 9851. [Google Scholar] [CrossRef] [PubMed]
- Qobbi, H.; Zoulagh, T.; Barbosa, K.A.; Boukili, B.; Hmamed, A.; Chaibi, N. H∞ filtering of 2D linear FM II model delayed systems. In Proceedings of the ICEGC’2023, Proceedings of the E3S Web of Conferences, Blagoveschensk, Russia, 22–25 May 2023; Volume 469, pp. 1–10. [Google Scholar] [CrossRef]
- Apostolov, P.S.; Yurukov, B.P.; Stefanov, A.K. An easy and efficient method for synthesizing two-dimensional finite impulse response filters with improved selectivity [Tips & Tricks]. IEEE Signal Process. Mag. 2017, 34, 180–183. [Google Scholar] [CrossRef]
- Apostolov, P.; Stefanov, A.; Nedialkov, I. Efficient two dimensional filter synthesis. In Proceedings of the 2018 26th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Apostolov, P.; Stefanov, A.; Apostolov, S. A study of filters selectivity with maximally flat responses with respect to Harsdorff distance. In Proceedings of the 2018 IX National Conference with International Participation (ELECTRONICA), Sofia, Bulgaria, 17–18 May 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Apostolov, P.S.; Stefanov, A.K.; Bagasheva, M.S. Efficient FIR filter synthesis using sigmoidal function. In Proceedings of the 2019 X National Conference with International Participation (ELECTRONICA), Sofia, Bulgaria, 16–17 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Apostolov, P.; Meklyov, A.; Kostov, V. Band-pass and band-stop filters synthesis using sigmoidal function. In Proceedings of the 2021 12th National Conference with International Participation (ELECTRONICA), Sofia, Bulgaria, 27–28 May 2021; pp. 1–3. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apostolov, P. Synthesis of High-Selectivity Two-Dimensional Filter Banks Using Sigmoidal Function. Electronics 2024, 13, 4146. https://doi.org/10.3390/electronics13214146
Apostolov P. Synthesis of High-Selectivity Two-Dimensional Filter Banks Using Sigmoidal Function. Electronics. 2024; 13(21):4146. https://doi.org/10.3390/electronics13214146
Chicago/Turabian StyleApostolov, Peter. 2024. "Synthesis of High-Selectivity Two-Dimensional Filter Banks Using Sigmoidal Function" Electronics 13, no. 21: 4146. https://doi.org/10.3390/electronics13214146
APA StyleApostolov, P. (2024). Synthesis of High-Selectivity Two-Dimensional Filter Banks Using Sigmoidal Function. Electronics, 13(21), 4146. https://doi.org/10.3390/electronics13214146





