Adaptive Weighted Particle Swarm Optimization for Controlling Multiple Switched Reluctance Motors with Enhanced Deviatoric Coupling Control

Abstract

Switched reluctance motors (SRMs) are widely used in industrial applications due to their advantages. Multi-motor synchronous control systems are crucial in modern industry, as their control strategies significantly impact synchronization performance. Traditional deviation coupling control structures face limitations during the startup phase, leading to excessive tracking errors and exacerbated by uneven load distribution, resulting in desynchronized motor acceleration and increased speed synchronization errors. This study proposes a modified deviation coupling control method based on an adaptive weighted particle swarm optimization (PSO) algorithm to enhance multi-motor synchronization performance. Traditional deviation coupling control applies equal reference torque inputs to each motor’s current loop, failing to address uneven load distribution and causing inconsistent accelerations. To resolve this, a gain equation based on speed deviation is introduced, incorporating self-tracking error and gain coefficients for dynamic synchronization error compensation. The gain coefficients are optimized using the adaptive weighted PSO algorithm to improve system adaptability. A simulation model of a synchronization control system for three SRMs was developed in the Matlab/Simulink R2023b environment. This model compares the synchronization performance of traditional deviation coupling, Fuzzy-PID improved structure, and adaptive PSO improved structure during motor startup, sudden speed increases, and load disturbances. The validated deviation coupling control structure achieved the initial set speed in approximately 0.236 s, demonstrating faster convergence and a 6.35% reduction in settling time. In both the motor startup and sudden speed increase phases, the two optimized methods outperformed the traditional structure in dynamic performance and synchronization accuracy, with the adaptive PSO structure improving synchronization accuracy by 54% and 37.17% over the Fuzzy-PID structure, respectively. Therefore, the PSO-optimized control system demonstrates faster convergence, improved stability, and enhanced synchronization performance.

1. Introduction

In recent years, the switched reluctance motor (SRM) has garnered significant attention from researchers and industries due to its simple structure, reliable operation, flexible control, and low cost [1,2]. With the advancement of industrial automation, the synchronization and coordination of multiple motors have become critical as applications demand high power or high reliability. These applications include motion control systems [3], electric vehicles [4], textile printing and dyeing [5], and rolling mills. The synchronization performance of these motors directly influences the stability of industrial processes and the quality of the final product [6,7]. However, due to manufacturing discrepancies and other factors, achieving perfect consistency in the mechanical characteristics of each motor is challenging. This lack of uniformity results in significant synchronization errors during multi-motor operations, ultimately degrading system performance.

Addressing the issues of torque ripple and noise at low speeds caused by the doubly salient structure and magnetic saturation of SRM, [8] proposed an active boost power converter capable of controlling nonlinearity of the current and speed of SRM. To mitigate issues related to speed variations in the SRM, a PID controller was designed using a PSO, which significantly improved the speed control of the SRM, enhancing both the system’s accuracy and robustness. [9] provided a detailed analysis of the application of PSO in tuning the hysteresis current controller and direct instantaneous torque controller for a four-phase 8/6 SRM. The optimization of controller parameters and commutation angles aims to minimize torque ripple, improve efficiency, and enhance steady-state performance. [10] employed a direct torque control system and proposed an improved fuzzy control system based on self-tuning parameter regulation, effectively solving the response time and steady-state accuracy issues in SRM drive systems. [11], by introducing a fuzzy controller based on Mandani fuzzy control rules between the speed outer loop and current inner loop of the established SRM speed control system model, showed the speed fluctuation range of the unexcited start is reduced from 3.2% to 2.3%, the torque fluctuation range is reduced by 11.122%, and the current fluctuation range is greatly reduced. [12] analyzed the mechanism of torque ripple generation under traditional current chopping control and proposed a segmented PWM variable duty cycle control method based on current chopping. This method utilizes the inductance characteristic curve for segmented control, better accommodating the required rate of current change, leading to improved current tracking and more effective suppression of torque ripple.

Current research on multi-motor speed synchronization control primarily focuses on two key areas: the control structure of the system and the control algorithms employed [13]. The ultimate goal is to ensure that both synchronization and tracking performance meet the required specifications [14]. The widely adopted strategies for multi-motor synchronization integrate control structures with algorithms, with the master-slave and deviation coupling structures being the most commonly utilized synchronization control architectures in recent studies [15]. Ref. [16] introduced the master-slave control method, where the speed control outer loop and current control inner loop are implemented in the master and slave motors, respectively. In this approach, the actual speed and current of the master motor serve as reference inputs for the slave motor. However, due to significant signal delays, especially during startup and shutdown phases, this method is generally suitable for applications with lower synchronization performance requirements. Some researchers have sought to enhance its performance by incorporating sliding-mode control and fuzzy logic methods [17,18]. In 1980, Y. Koren [19] proposed a cross-coupling control structure, which introduced a closed-loop control system. This structure adds a speed error compensation module to the parallel motor control system, compensating for the speed difference between motors by feeding the error back into the subsequent controllers, thereby achieving operational coupling between motors. Additionally, ref. [20] applied the adjacent coupling control strategy to the position synchronization control of linear SRMs, successfully achieving synchronization between three motors. Ref. [21] introduced an improved cross-coupling control strategy based on sliding mode control (ISMC) for speed synchronization. The stability of this approach is demonstrated using Lyapunov-based analysis. However, the synchronization performance of the cross-coupling structure degrades as the number of motors increases. To optimize cross-coupling control for multi-motor scenarios, a deviation coupling structure has been proposed. This structure is well-suited for applications that require synchronization of three or more motors, offering reduced signal delays and demonstrating effective control in practical engineering applications [6]. The deviation coupling structure employs fixed gain compensation based on the motor’s rotational inertia, considering only the impact of inertia on synchronization performance. However, when subjected to significant load variations, the system experiences significant fluctuations, potentially leading to instability. To further enhance the synchronization performance and disturbance rejection capability of multi-motor systems, numerous researchers have focused on improving traditional coupled synchronization control strategies and optimizing the performance of individual motors within these systems. Ref. [22] proposed a proportional integral-based, deviation-coupled speed compensator for error compensation in the motor speed loop, with results demonstrating a significant reduction in synchronization errors. Ref. [23], by incorporating feedback compensation for individual motor speeds and positional errors, further improved the existing deviation-coupled control structure while employing an inverse fuzzy sliding mode control algorithm to enhance the performance of individual motors. The findings indicate improved synchronization stability and faster response times within the multi-motor system. Additionally, ref. [24] introduced a cooperative speed controller based on deviation coupling, which linearly combines the phase currents of individual motors, speed tracking errors and their integrals, and coordination errors and their integrals, as well as coordination errors and their integrals. Comparative analyses show that this controller offers superior synchronization performance and robustness. Ref. [25] enhanced the deviation coupling structure and designed a precise motor speed control using an ultra-twisting sliding mode controller. This approach suppresses chattering, reduces the convergence time of error variables, and ensures system stability with rapid convergence.

In multi-motor synchronous control systems, the selection of control parameters is crucial, as improper parameter values can significantly reduce control accuracy and even cause control failure. Traditional empirical and experimental approaches often suffer from low precision, time-consuming and labor-intensive debugging, and poor robustness. The PSO algorithm, inspired by the unpredictable movements of bird flocks, is designed to find optimal solutions in complex search spaces. Unlike genetic algorithms, PSO eliminates crossover and mutation operations, making it simpler, easier to implement, and highly convergent, which makes it particularly suitable for optimization problems in practical engineering. Ref. [26] applied PSO for PID controller parameter optimization in a permanent magnet servo motor, demonstrating the superiority of PSO. Similarly, ref. [27] employed the chicken swarm optimization algorithm to determine the optimal PID controller parameters, improving the system’s accuracy, response speed, and robustness. In literature [28], PSO was used to optimize a fuzzy PID control system, which enhanced the accuracy of the navigation path in an intelligent library robot system. Additionally, ref. [29] applied PSO with adaptive weights to optimize PID controller parameters, further improving the controller’s effectiveness.

In summary, for the synchronization control system of three or more motors, the deviation coupling structure is the optimal method for achieving synchronization. To address the issues within the deviation coupling structure, this paper proposes a deviation coupling controller with a synchronization error compensation method optimized using PSO with adaptive weights. This controller introduces a gain equation, where the gain is the product of the gain coefficient and the motor’s self-tracking error. The gain coefficient is optimized using the PSO algorithm with adaptive weights to ensure minimal global synchronization error.

The following is a summary of the contributions made by this paper:

(1)

Recent advances in SRM control systems and multi-motor synchronization strategies are reviewed.

(2)

The paper analyzes the basic equations of SRM, thus constituting the mathematical model of SRM, and neglect some of its nonlinear factors, solve the linear model of the motor, and design the corresponding control strategy for the model.

(3)

While aiming at the shortcomings of the traditional deviant coupling, certain improvements are made, and the process of realizing the idea of its improvement is discussed.

(4)

The principle of the PSO algorithm with adaptive weights is explained, and the cumulative sum expression of the absolute value of the synchronization error is used as the fitness function.

(5)

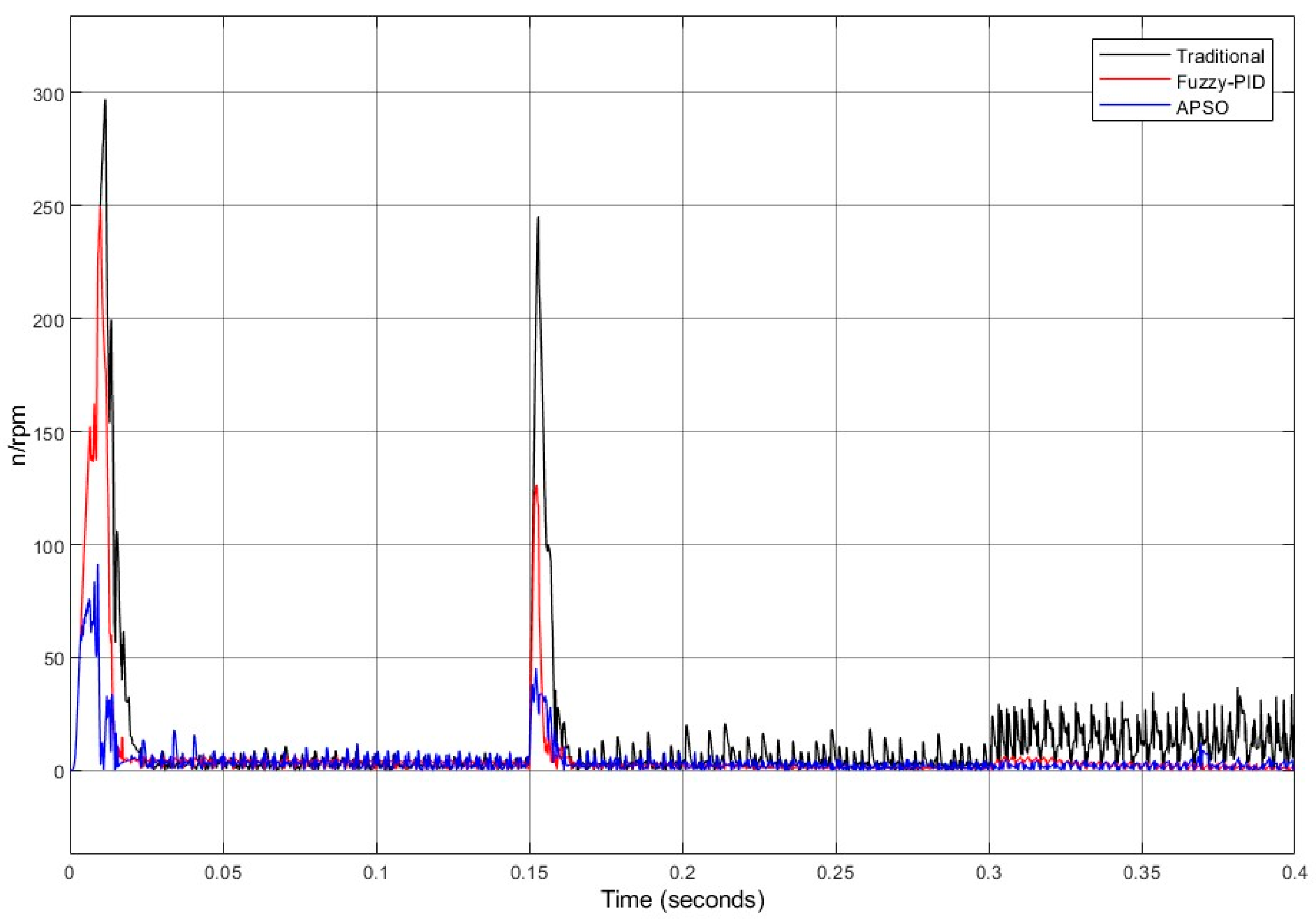
A multi-motor synchronous control simulation model is constructed to compare the synchronous performance of the traditional deviation-coupled structure, the fuzzy PID-based improved structure, and the improved structure in this paper, which proves the superiority of the synchronous control of multi-SRMs.

(6)

The research work in this paper is summarized, and the next steps in the research program are envisioned.

2. Switched Reluctance Motors

2.1. Working Principle

The stator and rotor poles of an SRM feature a convex pole structure. Concentrated windings are placed on the stator poles, with two radially opposite windings forming a phase. The rotor, composed of laminated silicon steel sheets, contains no windings. The operating principle of the SRM is based on the “principle of minimum reluctance” [30], wherein the magnetic flux follows the path of least reluctance. This principle drives the magnetic circuit elements to align with the position that minimizes magnetic reluctance. Consequently, the magnetic flux is always constrained to follow the path of lowest magnetic reluctance, forcing the magnetic circuit’s conductive elements to move into the position that minimizes the total magnetic reluctance. When the stator windings are energized, the magnetic circuit tends to follow the path of minimum reluctance. When the rotor’s convex poles are misaligned with the stator’s convex poles, the air gap is larger, leading to higher reluctance. Once the stator pole windings are energized, magnetic attraction is generated on the rotor poles, reducing the air gap and consequently decreasing the reluctance of the magnetic circuit. By energizing the phase windings of the stator in a specific sequence, electromagnetic torque, driven by the reduction in reluctance due to magnetic field distortion, is produced. This results in the continuous rotation of the motor rotor.

2.2. Mathematical Model

According to the principle of electromechanical energy conversion, the SRM can be modeled as a two-port device, with one pair of electrical ports and one pair of mechanical ports, coupled through a shared magnetic field. For simplification, the number of phases in the SRM is denoted as $m$, and each phase is assumed to be structurally and parametrically symmetric. In this analysis, iron losses and mutual inductance between phase windings are neglected. In the electrical port, the applied voltage, resistance, current, and induced electromotive force of the $k$-phase winding are denoted by $U_k$, $R_k$, $i_k$, and $e_k$$\left(k=1,2,\cdots ,m\right)$, respectively. The magnetic flux linkage of the $k$-phase winding in the coupled magnetic field is represented by ${\psi }_k\left(\theta ,i_k\right)$ and the rotor position angle by $\theta$. In the mechanical port, the electromagnetic torque, load torque, viscous friction coefficient, and moment of inertia are represented by $T_x$, $T_L$, $D$, and $J$, respectively.

2.2.1. Circuit Equation

According to the laws of electromagnetic induction:

$$e_k=-{\displaystyle \frac{d{\psi }_k\left(\theta ,i_k\right)}{dt}}$$

(1)

The voltage balance equation for phase $k$ of the SRM can be obtained as [31]:

$$u_k=R_k{i}_k-e_k=R_k{i}_k+{\displaystyle \frac{d{\psi }_k\left(\theta ,i_k\right)}{dt}}$$

(2)

The magnetic flux linkage of each phase winding is a function of the current and self-inductance of that phase, as well as the current and mutual inductance of the other phases and the rotor position angle. However, since the mutual inductance between phases in an SRM is negligible compared to the self-inductance, it is typically disregarded in SRM calculations for simplification. Thus, the magnetic flux linkage equation becomes [31]:

$${\psi }_k=L_k\left({\theta }_k,i_k\right)i_k$$

(3)

The inductance $L_k$ of each phase is a function of the phase current $i_k$ and the rotor position angle ${\theta }_k$. This relationship arises from the nonlinearity of the SRM’s magnetic circuit, which causes the inductance to depend on the current. The variation of inductance with rotor position is a key characteristic of the SRM and is fundamental to torque generation.

Substituting Equation (3) into Equation (2) results in the following expression [31]:

$$u_k=R_K{i}_k+{\displaystyle \frac{\partial {\psi }_k}{\partial i_k}}{\displaystyle \frac{d{i}_k}{dt}}+{\displaystyle \frac{\partial {\psi }_k}{\partial \theta }}{\displaystyle \frac{d\theta }{dt}}=R_K{i}_k+\left(L_k+i_k{\displaystyle \frac{\partial L_k}{\partial i_k}}\right){\displaystyle \frac{d{i}_k}{dt}}+i_k{\displaystyle \frac{\partial L_k}{\partial \theta }}{\displaystyle \frac{d\theta }{dt}}$$

(4)

The equation above indicates that the supply voltage is balanced by the voltage drops across three components of the circuit. The first term on the right-hand side represents the resistive voltage drop in the $k$-phase circuit. The second term corresponds to the electromotive force (EMF) induced by the variation in current, referred to as the transformer EMF. The third term represents the EMF induced by the change in rotor position, known as the motional EMF, which is directly related to the energy conversion process in the SRM.

2.2.2. Mechanical Equation

Based on the principles of mechanics, the rotor’s equation of motion under the influence of electromagnetic torque and load torque can be expressed as follows [11]:

$$T_x=J{\displaystyle \frac{d^2\theta }{dt}}+B{\displaystyle \frac{d\theta }{dt}}+T_L$$

(5)

where $J$ represents the moment of inertia and $B$ denotes the friction coefficient.

2.2.3. Electromechanical Linkage Equation

An analysis of the electromechanical energy conversion process for a single-phase winding of the SRM over one operating cycle is conducted. The instantaneous electromagnetic torque at any operating point is given by [31]:

$$T={\displaystyle \frac{\partial W^{\prime }}{\partial \theta }}{|}_{i=const}=-{\displaystyle \frac{\partial W}{\partial \theta }}{|}_{\psi =const}$$

(6)

The energy storage W of the winding at any point can be expressed as:

$$W={\displaystyle {\int }_0^{\psi }i\left(\psi ,\theta \right)}d\psi$$

(7)

The magnetic co-energy $W^{\prime }$ of the winding at any point can be expressed as:

$$W^{\prime }={\displaystyle {\int }_0^i\psi \left(i,\theta \right)}di$$

(8)

Since the SRM is a nonlinear electromechanical device, the integrals of its stored energy $W$ and co-energy $W^{\prime }$ are difficult to solve analytically, and the stored energy $W$ and co-energy $W^{\prime }$ are not equal. Due to the rotational inertia of both the motor and the load, the motor’s output and dynamic equilibrium are determined by the average torque. Assuming symmetrical windings for each phase, the average electromagnetic torque of the SRM is given by [11]:

$$T={\displaystyle \frac{m{N}_r}{2\pi }}{\displaystyle {\int }_0^{\raisebox{1ex}{$2\pi $}\!\left/ \!\raisebox{-1ex}{$N_r$}\right.}Tx\left(\theta ,i\left(\theta \right)\right)}d\theta$$

(9)

where m is the number of phases of the motor and $N_r$ is the number of rotor poles.

2.2.4. Linear Model

Equations (1)–(9) constitute the mathematical model of the SRM. Although this model provides a complete and accurate description of the electromagnetic and mechanical relationships of the SRM, it is challenging to apply in practice due to the difficulty of analytically solving $L\left(i,\theta \right)$ and $i\left(\theta \right)$. Therefore, in practical simulations and experiments, some minor factors are often neglected.

The paper employs a relatively simple linear modeling approach to account for variations in magnetic flux linkage, deliberately neglecting certain nonlinear factors such as electromagnetic saturation, eddy currents, and mutual inductance between phases. Linearized analytical expressions for magnetic flux linkage and torque are derived under the assumption that phase inductance depends solely on rotor position and is independent of phase current. The relationship between winding inductance and rotor position [32], assuming it varies linearly, is illustrated in Figure 1.

The relationship between the winding inductance of the SRM and the rotor position angle, as derived from the linear model, is as follows [32]:

$$L\left(\theta \right)=\left\{\begin{array}{cc}{L}_{\min }& {\theta }_1\le \theta \le {\theta }_2\\ K\left(\theta -{\theta }_2\right)+L_{\min }& {\theta }_2\le \theta \le {\theta }_3\\ L_{\max }& {\theta }_3\le \theta \le {\theta }_4\\ L_{\max }-K\left(\theta -{\theta }_4\right)& {\theta }_4\le \theta \le {\theta }_5\end{array}\right.$$

(10)

Here, $K=\left(L_{\max }-L_{\min }\right)/\left({\theta }_3-{\theta }_2\right)$, $L_{\max }$, and $L_{\min }$ are constants for a given fabricated SRM motor. These constants can be determined analytically based on the motor’s structural parameters or experimentally.

At the moment the main switch is activated, the initial state of the circuit is characterized by ${\psi }_0=0$ and ${\theta }_0={\theta }_{on}$. When the switch is deactivated at time $\theta ={\theta }_{off}$, the winding enters the continuity period $\psi ={\psi }_{\max }$. Based on the initial conditions and the fundamental equilibrium equations of the motor, a piecewise analytical expression for the winding magnetic flux linkage can be derived as follows:

$$\psi \left(\theta \right)=\left\{\begin{array}{cc}{\displaystyle \frac{U_s}{\omega }}\left(\theta -{\theta }_{on}\right)& {\theta }_{on}\le \theta \le {\theta }_{off}\\ {\displaystyle \frac{U_s}{\omega }}\left(2{\theta }_{off}-{\theta }_{on}-\theta \right)& {\theta }_{off}\le \theta \le 2{\theta }_{off}-{\theta }_{on}\end{array}\right.$$

(11)

where ${\theta }_{on}$ is the turn-on angle, ${\theta }_{off}$ is the turn-off angle, and $U_s$ represents the winding voltage.

Thus, the expression for the phase torque is [32]:

$$T={\displaystyle \frac{1}{2}}{i}^2{\displaystyle \frac{dL}{d\theta }}$$

(12)

Equations (11) and (12) provide simple analytical expressions for the magnetic flux linkage and torque within the linear model. The motor is controlled by optimizing parameters, such as the turn-on angle and turn-off angle, to ensure it meets the operational requirements.

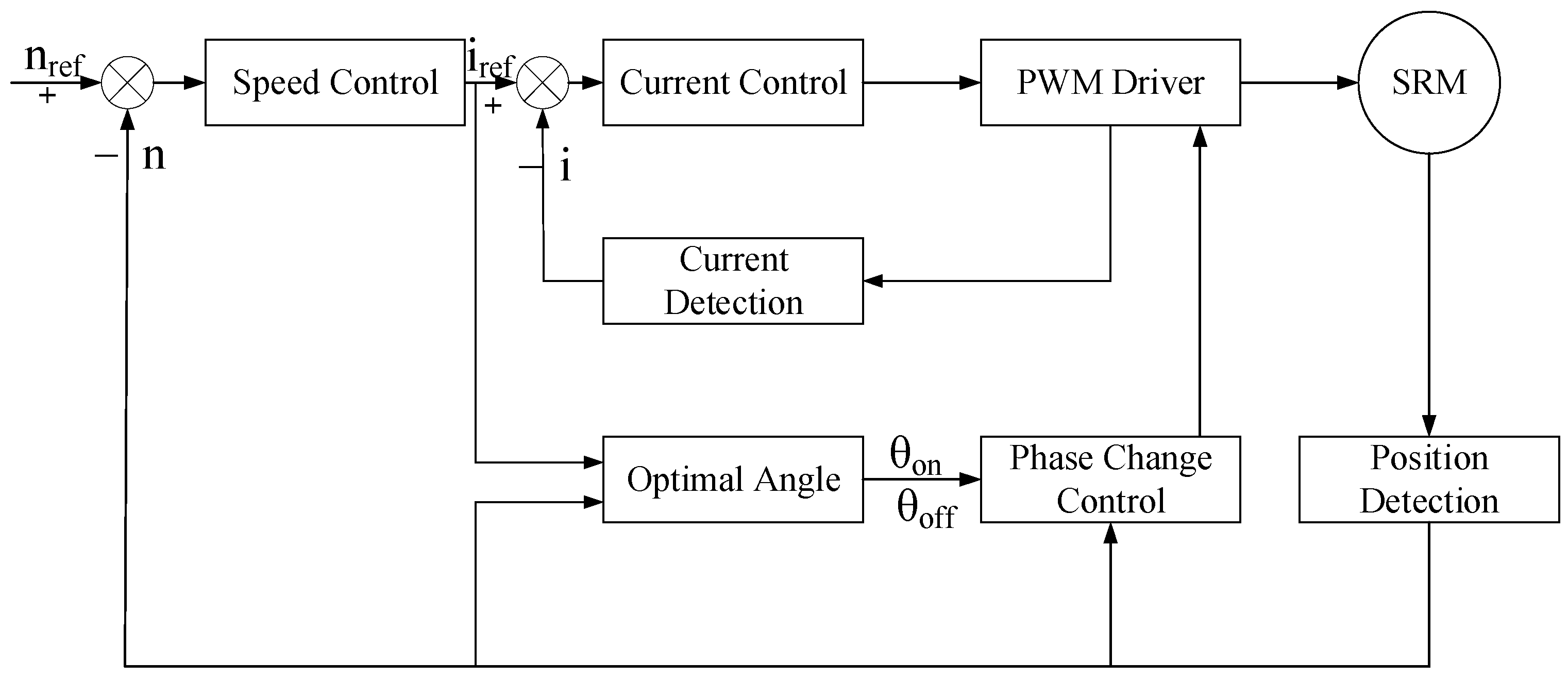
2.3. Control Strategies for SRM

Figure 2 illustrates the block diagram of the control strategy for the SRM speed control system.

The control strategy aims to achieve the desired motor speed by using proportional-integral (PI) control as the primary method. It incorporates two systematic closed-loop controls: speed and current. The variable-angle voltage PWM control method is employed to adjust the motor speed based on feedback. The speed regulator generates a current reference value i₁, which, along with the current feedback, forms the current closed-loop control. This control loop adjusts the PWM duty cycle to regulate the current, ensuring a rapid response. The controller manages the switching of the main power device at a constant chopping frequency and adjusts the average voltage across the phase winding by varying the on-off times, i.e., the duty cycle, to control the phase current.

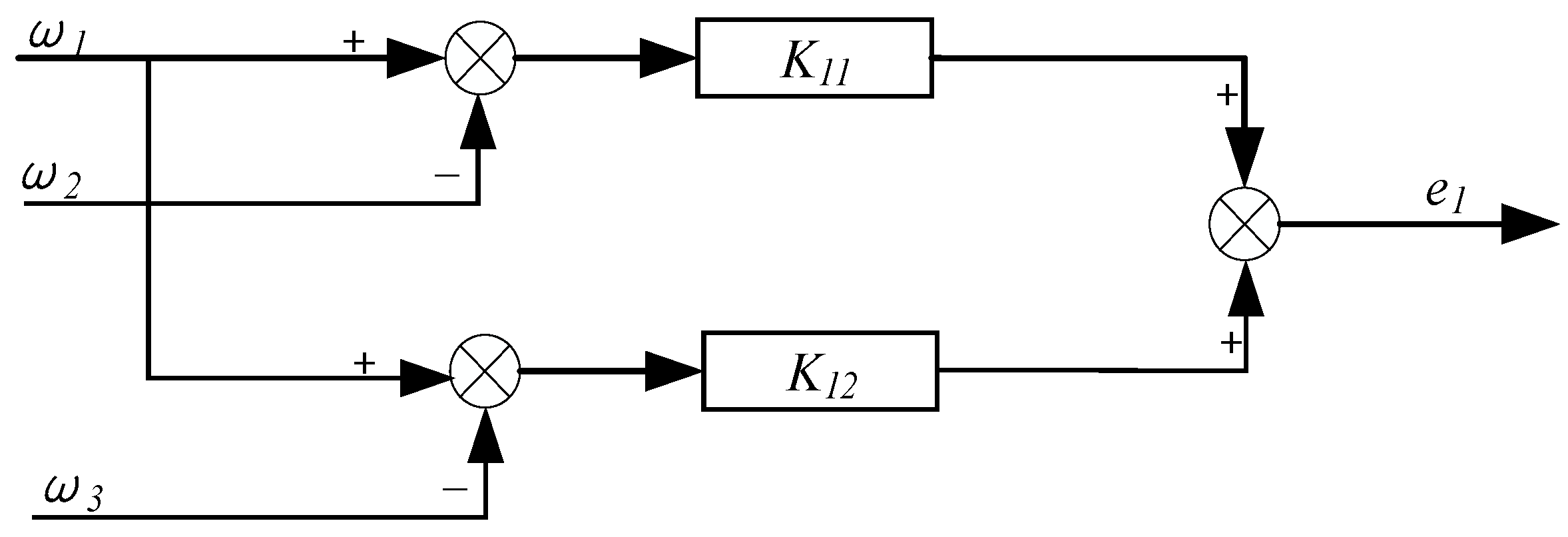
3. Improved Deviation Coupling Structure

3.1. Deviation Coupling Structures

The traditional deviation-coupling structure, illustrated in Figure 3, consists primarily of a speed loop controller, a speed compensator, and a multi-motor system [6]. This method modifies the cross-coupling approach by compensating the speed of each motor based on the operating status of the others. The compensation signal in the deviation coupling control is generated by multiplying the speed feedback of one motor by the deviation of the feedback from the other motors, applying the appropriate gain coefficients, and then summing these values.

Controllers 1, 2, and 3 are primarily designed as tracking error controllers, with their structure depicted in Figure 4.

In the deviation coupling structure, the speed compensator is crucial. For example, the structure of the speed feedback module for the first motor is illustrated in Figure 5.

In the figure, $K_{11}$ and $K_{12}$ represent the feedback gain coefficient for the motor speed difference. Its purpose is to compensate for the variation in rotational inertia between the motors, and its value can be expressed as:

$$K_{ij}=J_i/J_j$$

(13)

Based on the structure shown in Figure 5, the value of speed compensation for each motor, under the influence of the speed compensator, can be derived as follows:

$$e_1=K_{12}\left({\omega }_1-{\omega }_2\right)+K_{13}\left({\omega }_1-{\omega }_3\right)$$

(14)

$$e_2=K_{21}\left({\omega }_2-{\omega }_1\right)+K_{23}\left({\omega }_2-{\omega }_3\right)$$

(15)

$$e_3=K_{31}\left({\omega }_3-{\omega }_1\right)+K_{32}\left({\omega }_3-{\omega }_2\right)$$

(16)

In the equation, $e$ represents the speed compensation value of the corresponding motor, also known as the synchronization error, while $\omega$ represents the motor’s rotational speed. However, the compensation process suffers from excessive error oscillations and poor synchronization accuracy. To address this issue, an optimized synchronization error compensation method is proposed.

3.2. Improved Speed Compensator

The conventional synchronization error compensation value arises from differences in motor speeds, i.e., varying tracking errors. However, the root cause of synchronization error lies in the discrepancy between each motor’s actual rotational speed and its target speed, also known as self-tracking error. Therefore, the self-tracking error can be incorporated into the speed compensator of the traditional deviation coupling structure to measure the influence of motor speed on synchronization error and regulate the synchronization error compensation. The optimized structure is shown in Figure 6.

In the figure, ${\alpha }_i$ represents the gain equation, which is expressed as follows:

$${\alpha }_i=\left(1+k_i\left|x-y_i\right|\right)$$

(17)

where $\left|x-y_i\right|$ represents the absolute value of the tracking error ${\gamma }_i$ for the $i$-th motor, $k_i$ is the gain coefficient, $y_i$ is the real-time speed of the $i$-th motor, and $x$ is the desired speed. The improved synchronization error compensation value can thus be expressed as:

$$\begin{array}{cc}{\beta }_i=\left(1+k_i\left|x-y_i\right|\right)·{\displaystyle \sum _{j=1}^n\left(y_i-y_j\right)}& i=1,2,\cdots ,n\end{array}$$

(18)

To eliminate the potential negative effects of the sign of the self-tracking error on synchronization performance and to prevent under- or overcompensation, the gain equation is designed as the product of the absolute value of the self-tracking error and the gain coefficient $k$. This gain equation is then multiplied by the absolute value of the self-tracking error. The difference between the real-time speed of the $i$-th motor and the other motors is summed and further multiplied by the gain equation to obtain the synchronization error compensation value. This approach ensures effective coupling between the motors and allows for timely response to changes in motor speed. By dynamically adjusting the gain coefficient, the synchronization error compensation value is adaptively regulated in real time.

4. Adaptive Particle Swarm Optimization Algorithm

4.1. Standard Particle Swarm Optimization Algorithm

PSO is a modern intelligent optimization algorithm that belongs to the evolutionary class of algorithms. It is inspired by the collective behavior of flocks of birds foraging for food. In the PSO algorithm, each bird in the flock is abstracted as a particle with attributes of position and velocity. While individual particles (or birds) do not know the precise location of the food, they are aware of the positions of other particles and their respective distances to the food. This information-sharing mechanism allows the entire swarm to progressively converge toward the food source, even if individual particles may not always move closer to the target in each iteration.

The PSO algorithm begins by initializing a swarm of particles, each with a specified initial position and velocity. The fitness function evaluates each particle, and its fitness value is recorded as the current personal best. Particles then share information to determine the global best solution. The algorithm iterates by updating the particles’ velocities and positions, recalculating their fitness values. If a particle’s new fitness value exceeds its previous personal best, the new value becomes the updated personal best for that particle. After updating the personal bests of all particles, the global best solution is also updated. This process continues iteratively to refine the particles’ positions and velocities.

After determining the optimal solution identified by the particle itself, known as the personal best $P_{best}$, and the optimal solution found by the entire swarm, known as the global best $g_{best}$, the particle updates its velocity and position according to the following equation [33]:

$$V^{k+1}=\omega V^k+c_1\left(P_{best}-P\right)rand(0,1)+c_2\left(g_{best}-P\right)rand(0,1)$$

(19)

$$P^{k+1}=P+V^{k+1}$$

(20)

where $V$ is the particle velocity, $k$ denotes the iteration index, $P$ is the current position of the particle, $rand\left(0,1\right)$ represents a random number between 0 and 1, $c_1$ and $c_2$ are the learning factors, typically set to 2, and $\omega$ is the inertia weight, which ranges between 0.1 and 0.9. Figure 7 illustrates the flowchart of the PSO.

4.2. Particle Swarm Algorithm with Adaptive Weights

The inertia weight $\omega$ in the particle swarm algorithm influences the velocity of the particles, thereby affecting their search capabilities. A larger value of $\omega$ results in faster particle movement and a broader search range, enhancing global search capability. Conversely, a smaller value of $\omega$ leads to slower particle movement, a reduced search range, and improved local search capability. Therefore, the choice of $\omega$ is crucial for the overall effectiveness of the PSO algorithm.

To address the issue of the algorithm converging to a local optimum due to a fixed value of $\omega$, an adaptive approach is employed to adjust $\omega$ [34]. The expression used for this adaptive adjustment is as follows:

$$\omega =\left\{\begin{array}{cc}{\omega }_{\max }-\left({\omega }_{\max }-{\omega }_{\min }\right){\displaystyle \frac{f_{\max }-f}{f_{\max }-f_{avg}}}& f\ge f_{avg}\\ {\omega }_{\max }& f<f_{avg}\end{array}\right.$$

(21)

where ${\omega }_{\max }$ and ${\omega }_{\min }$ represent the maximum and minimum values of $\omega$, respectively; $f$ is the particle’s fitness value; $f_{avg}$ is the average fitness value; and $f_{\max }$ is the maximum fitness value.

When $\omega$ is small, the solution tends to be closer to the optimal value. Based on this concept, the minimum inertia weight is used as an adaptive weight. The value of $\omega$ is calculated according to different fitness values to determine the optimal weight for use. The corresponding expression is as follows:

$$\omega =\left\{\begin{array}{cc}{\omega }_{\min }+\left({\omega }_{\max }-{\omega }_{\min }\right){\displaystyle \frac{f_{\max }-f}{f_{\max }-f_{avg}}}& f\ge f_{avg}\\ {\omega }_{\min }& f<f_{avg}\end{array}\right.$$

(22)

When $f>f_{avg}$, there is still a significant difference between the particle and its optimal solution, so the inertia weight should be increased to expand the search range and move closer to the optimal solution. Conversely, when $f<f_{avg}$, the particle is closer to its optimal solution, and a local search becomes more critical to refine and explore the optimal solution.

4.3. Synchronization Error Compensation Optimized by Adaptive Weighted PSO

The absolute value of the self-tracking error ${\alpha }_i$ is obtained by calculating the difference $x$ between the desired speed $y_i$ and the real-time speed of each motor. The gain coefficient $k_i$ is then used to adjust ${\alpha }_i$. The adaptive PSO algorithm is employed to optimize $k_i$.The adaptation function is defined as follows:

$$f\left(u\right)={\displaystyle \sum _{i=1}^m\left|{\beta }_i\right|}$$

(23)

where $m$ is the number of sampling points, ${\beta }_i$ represents the synchronization error at the $i$-th sampling point, and the adaptation value $f\left(u\right)$ is obtained by calculating the cumulative sum of the absolute error values. The minimum adaptation value is used as the optimization objective to determine the corresponding optimal gain coefficient.

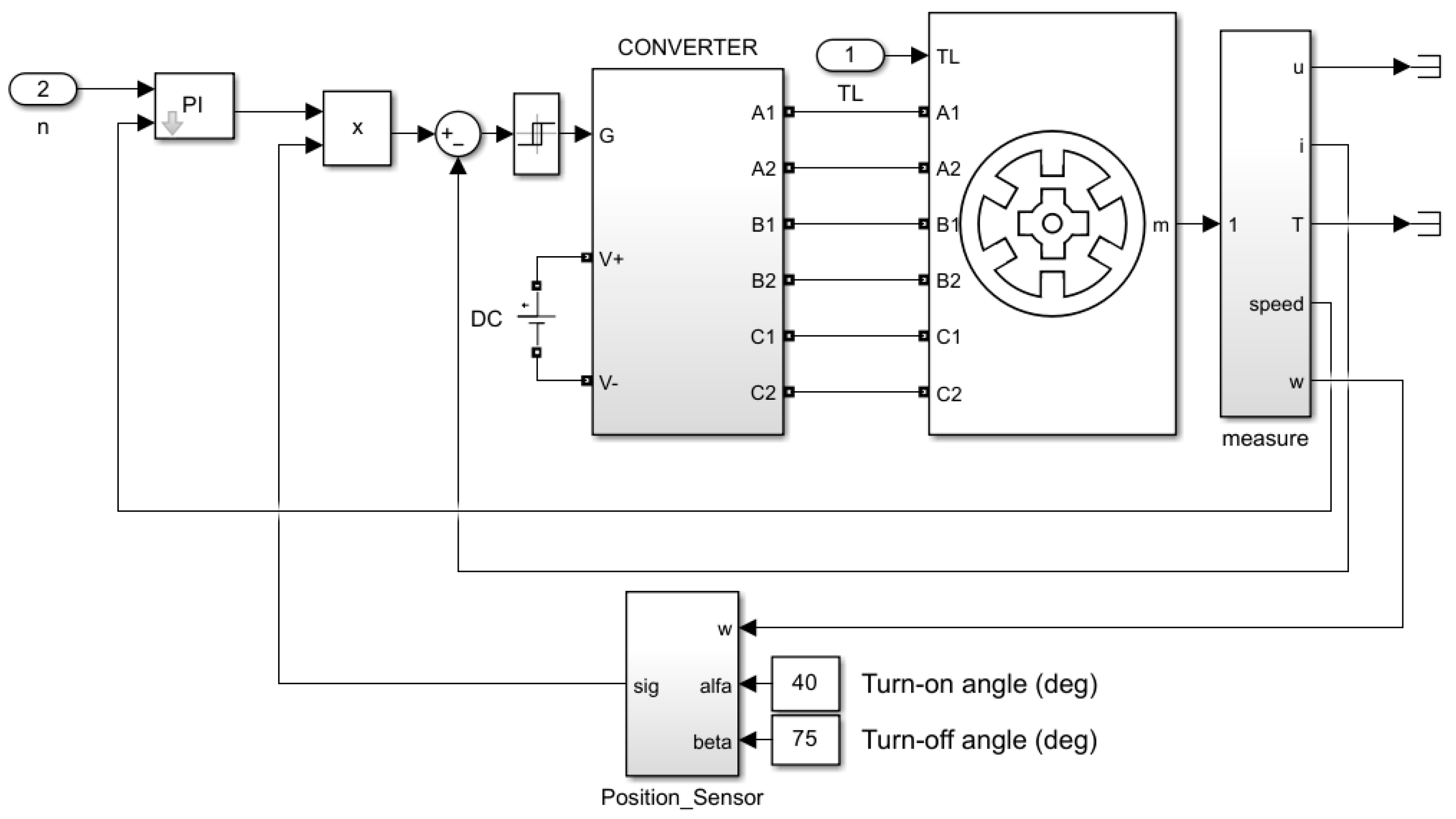
5. Simulation Results

5.1. Simulation Model

The control system of a single SRM is extended to a synchronous control system for three motors. Based on the traditional and improved deviation coupling control structures introduced in Section 3, a synchronous control model for three SRMs is constructed on the Simulink R2023b platform. Additionally, the self-adaptive weight PSO algorithm is applied to the improved control structure to further enhance system performance. To validate the effectiveness of the proposed strategy, a comparative analysis is conducted between the deviation coupling structure based on adaptive fuzzy PID [35] and the improved deviation coupling structure based on the self-adaptive weight PSO algorithm. The specific simulation model is shown in Figure 8. By comparing the synchronization accuracy and system response characteristics under different control strategies, the superiority of the improved control structure in terms of synchronization error suppression and dynamic performance improvement is demonstrated.

In Figure 8, the simulation model of the single-phase SRM control system is shown in Figure 9. The main modules of this system include the SRM motor module (switched reluctant motor model from the machines library in specialized power systems), current hysteresis control module, PI control module, position detection module, and power converter module. The system adopts a dual-loop control strategy, with the speed loop as the outer loop and the current loop as the inner loop. The current loop only includes negative feedback for current, without speed feedback, allowing the current (torque) to remain at the maximum permissible value during transients, thereby enabling the motor to quickly reach a stable operating state. Once the system reaches a steady-state speed, the speed feedback regulates the motor, maintaining the speed at a constant value. The system incorporates a PI controller and a position detection module.

In the three different deviation coupling structures established, the control systems of each SRM are kept identical, with consistent control parameters and a given speed reference. To evaluate the synchronization performance of each system, this study analyzes the synchronization error curves during motor startup, sudden speed changes, and varying load disturbances. The comparison is based on key performance metrics, including overshoot, global synchronization error, and settling time. This analysis aims to assess the dynamic response and steady-state performance of each deviation coupling structure under disturbances, providing a comprehensive evaluation of its applicability and robustness in multi-motor synchronization control.

The three SRMs had identical parameters except for their moment of inertia, as shown detailed in

Table 1. Motor Parameters.

Parameter	SRM1	SRM2	SRM3
Pole configuration	6/4	6/4	6/4
Stator resistance $\left(\Omega \right)$	0.01	0.01	0.01
Inertia $\left(\mathrm{kg}·{\mathrm{m}}^2\right)$	0.008	0.0085	0.009
Friction $\left(\mathrm{N}·\mathrm{m}/\mathrm{s}\right)$	0.02	0.02	0.02
Unaligned inductance $L_{\mathrm{q}} \left(\mathrm{mH}\right)$	0.67	0.67	0.67
Aligned Inductance $L_{\mathrm{d}} \left(\mathrm{mH}\right)$	23.6	23.6	23.6

.

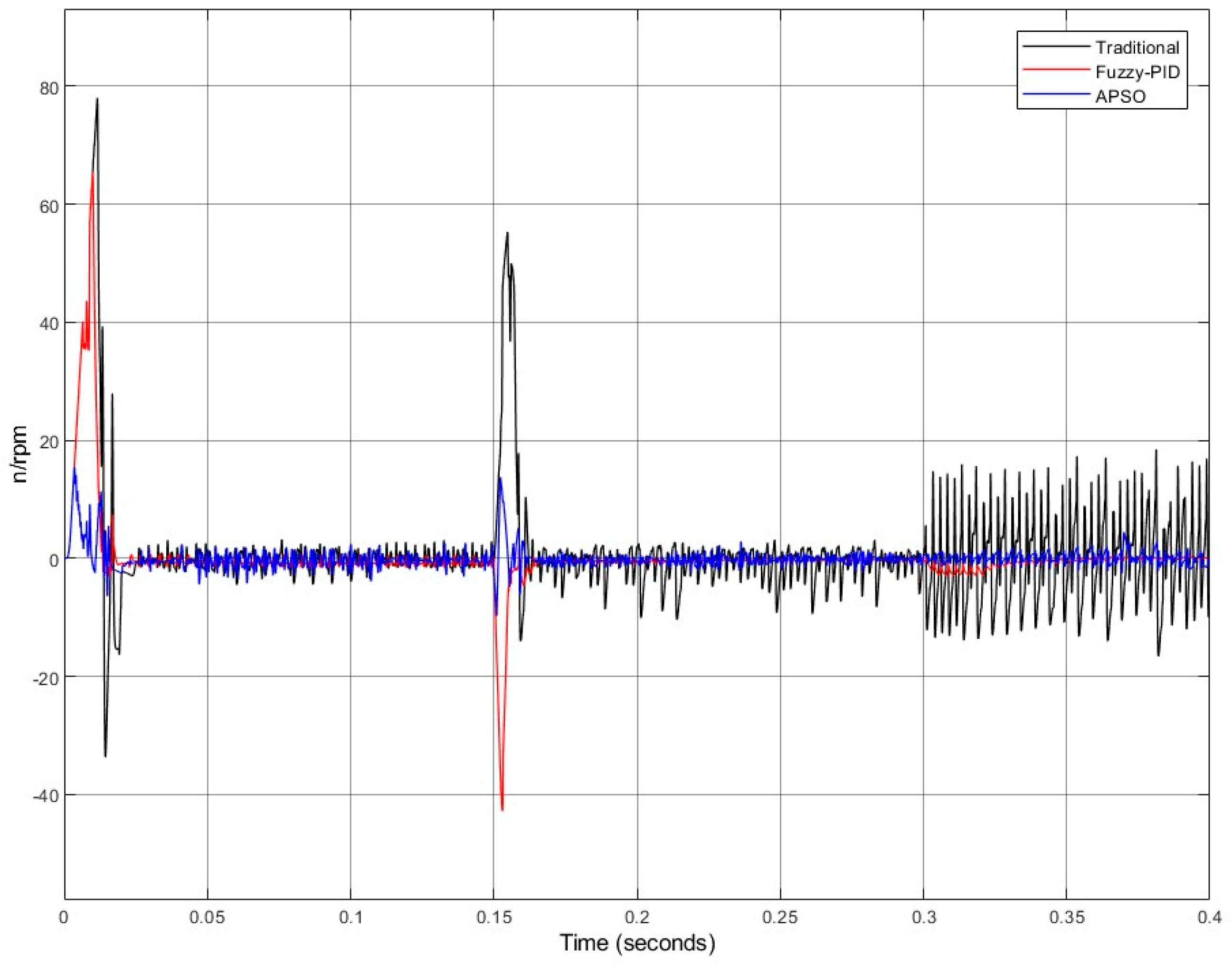
5.2. Analysis of Results

The initial reference speed of the motor is set to $n=1500 \mathrm{r}/\min$, and the motor is controlled to start. The simulation time is set to 0.4 s, during which the reference speed is abruptly increased from $n=1500 \mathrm{r}/\min$ to $n=2000 \mathrm{r}/\min$ over 0.15 s. At 0.3 s, an interference load with a step value of 15 $\mathrm{N}·\mathrm{m}$ is applied. The speed response curves of Motor 1 and Motor 2, Motor 1 and Motor 3, as well as the speed differences between Motor 2 and Motor 3, are depicted in Figure 10, Figure 11, and Figure 12, respectively. The absolute value of the global synchronization error is illustrated in Figure 13.

The initial rotational speed is set to $1500 \mathrm{r}/\min$. The stage is localized and enlarged, as shown in Figure 14. Compare (a), (b), and (c) in Figure 14 to plot Figure 10, Figure 11 and Figure 12 clearly demonstrate that, compared to the traditional structure and the fuzzy PID improved structure, the adaptive PSO-based structure significantly reduces the speed difference between the motors. In Figure 13, the maximum synchronization error during the startup phase is reduced by 15.9% and 69.9% for the fuzzy PID and adaptive PSO improvements, respectively, compared to the traditional structure. This clearly highlights the advantage of the adaptive PSO-based structure in enhancing synchronization accuracy. As shown in

Table 2. Evaluation of Starting Process Performance.

Motor	Sports Event	Overshoot $\mathit{\sigma }$ (%)	Stabilization Time (ms)
SRM1	Traditional	1.2	25.2
	Fuzzy PID	0.6	24.1
	APSO	1.07	23.6
	APSO Optimization	10.83	6.35%
SRM2	Traditional	2.1	25.3
	Fuzzy PID	0.53	23.9
	APSO	0.8	23.6
	APSO Optimization	61.9	6.35%
SRM3	Traditional	1.3	252
	Fuzzy PID	0.46	23.4
	APSO	0.93	23.4
	APSO Optimization	28.2	6.35%

, the overshoot and settling time for both the fuzzy PID and adaptive PSO structures are comparable, but both are significantly better than the traditional deviation coupling structure, indicating that both improved structures enhance the dynamic response performance of the system.

Figure 10, Figure 11 and Figure 12 clearly demonstrate that, compared to the traditional structure and the fuzzy PID improved structure, the adaptive PSO-based structure significantly reduces the speed difference between the motors. In Figure 13, the maximum synchronization error during the startup phase is reduced by 15.9% and 69.9% for the fuzzy PID and adaptive PSO improvements, respectively, compared to the traditional structure. This clearly highlights the advantage of the adaptive PSO-based structure in enhancing synchronization accuracy. As shown in Table 2, the overshoot and settling time for both the fuzzy PID and adaptive PSO structures are comparable, but both are significantly better than the traditional deviation coupling structure, indicating that both improved structures enhance the dynamic response performance of the system.

When the reference speed suddenly increases to $2000 \mathrm{r}/\min$ at 0.15 s, Figure 10, Figure 11 and Figure 12 illustrate that the speed difference between the rotors increases to varying degrees. However, compared to the traditional structure, both optimization schemes significantly reduce the speed difference between the motors. As shown in Figure 13, the fuzzy PID and adaptive PSO optimization methods reduce the maximum synchronization error during the speed transient phase by 48.95% and 86.12%, respectively, significantly improving synchronization accuracy during this phase.

At 0.3 s, a step disturbance load of 15 $\mathrm{N}·\mathrm{m}$ is applied to all three motors. Figure 10, Figure 11 and Figure 12 show that after introducing the disturbance, the speed regulation time for the three structures is largely consistent. Once the system reaches steady state, both optimized structures significantly reduce the speed difference between the SRMs, keeping the fluctuations within a smaller range and noticeably improving disturbance rejection capability. However, further analysis of the global synchronization error curve in Figure 13 reveals that the difference in disturbance rejection between the fuzzy PID and adaptive PSO improvements is minimal, with both being significantly superior to the traditional structure.

6. Conclusions and Outlook

6.1. Conclusions

A deviation coupling structure based on an optimized synchronization error compensation method is proposed to enhance multi-motor synchronization control accuracy, which is susceptible to external disturbances and other factors. The optimization method involves dynamically adjusting the synchronization error compensation value by introducing a gain equation and using real-time comparisons of the absolute value of the tracking error to adjust the gain coefficient within the equation. The PSO algorithm with adaptive weights is employed to optimize the gain coefficient values, thereby facilitating intelligent parameter selection.

To evaluate the feasibility of the optimization methods, a synchronization control simulation of three SRMs was conducted, comparing the traditional deviation coupling structure, the fuzzy PID improved structure, and the adaptive PSO improved structure in terms of synchronization performance during motor startup, sudden speed increase, and load disturbance. The results show that in both the motor startup and sudden speed increase stages, the two optimized methods outperformed the traditional structure in terms of dynamic performance and synchronization accuracy. Specifically, the synchronization accuracy of the adaptive PSO improved structure was 54% and 37.17% higher than that of the fuzzy PID improved structure in these two stages, respectively. Under load disturbances, the difference in disturbance rejection capability between the two optimized structures was minimal, but both were significantly superior to the traditional structure. These findings indicate that the optimization methods exhibit excellent robustness and effectiveness when the control system is subjected to disturbances.

6.2. Outlook

In practical industrial production, numerous motors with differences in internal structures must work in coordination to meet production demands. The speed coupling among these motors is critical. Compared to traditional coupling methods, multi-motor systems face limitations in response stability and rapidity. This paper, based on a deviation coupling structure, introduces a novel algorithm and achieves certain progress in the research on synchronization strategies for multi-SRMs. However, there remain challenges and areas for improvement in this research:

• The paper primarily addresses speed synchronization in multi-SRM systems. However, in practical applications, synchronization systems must also account for torque and power synchronization. These aspects are crucial for enhancing the overall performance and efficiency of multi-motor systems. Future research should focus on incorporating strategies for torque and power synchronization to further optimize system performance and meet the complex demands of industrial applications.
• This study is limited to simulation analysis, and the experimental component, including hardware and software design, has not yet been conducted. Future work will focus on completing these aspects to validate the simulation results and further enhance the practical applicability of the proposed system.
• The linear mathematical model of the SRM used in this paper involves several approximations, with some secondary factors being neglected. While these approximations do not significantly affect the simulation results, they are subject to certain limitations. In applications requiring higher control precision, these approximations may need further refinement to improve the model’s accuracy and reliability. Future work should focus on enhancing the model to better suit high-precision control scenarios.