Research on a Passenger Flow Prediction Model Based on BWO-TCLS-Self-Attention
Abstract
1. Introduction
- Propose a two-layer LSTM network structure and add a Dropout layer to fully extract complex time series features and enhance the generalization ability.
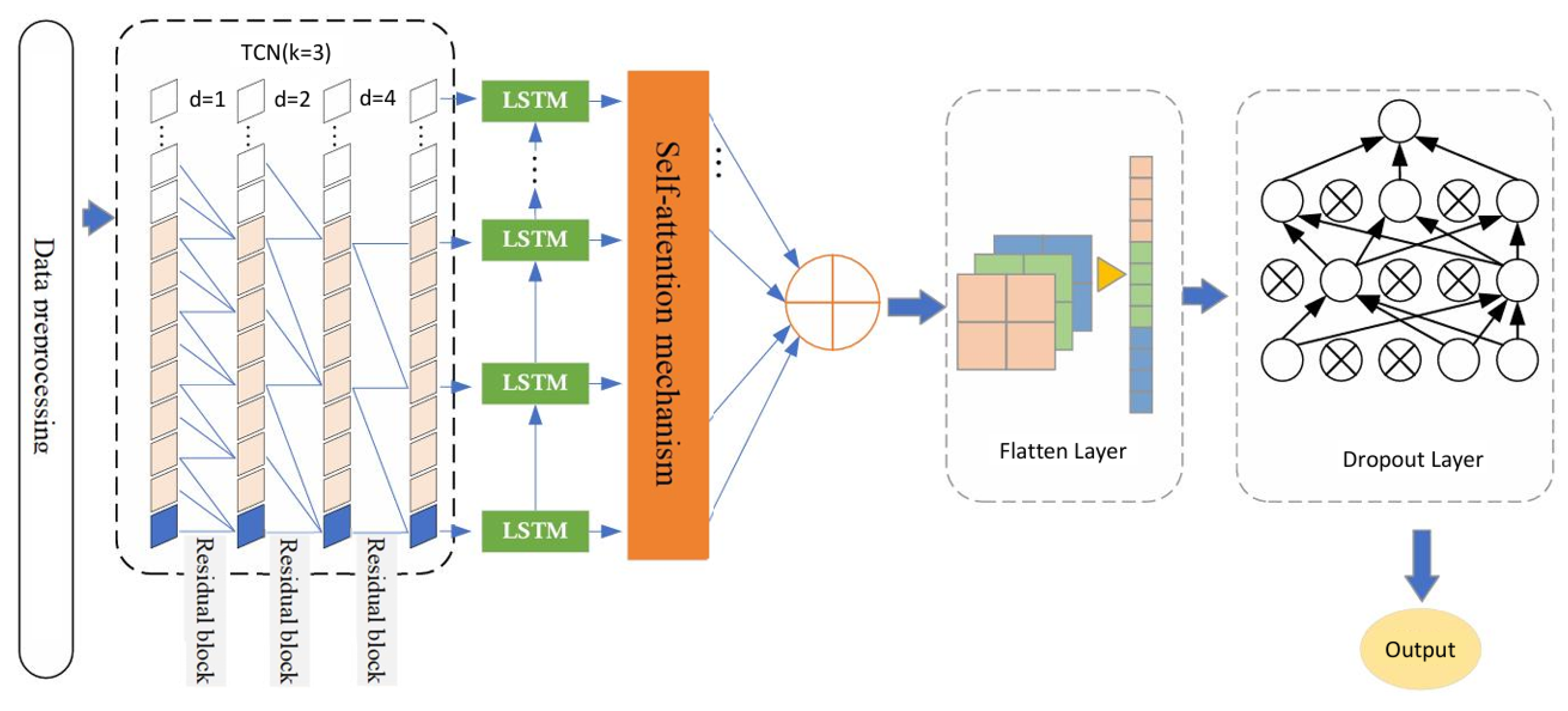
- Introduce a Self-Attention mechanism module (Self-Attention) and TCN network to construct a LSTM-TCN fusion model to reduce redundant feature data and increase the performance and speed of the model.
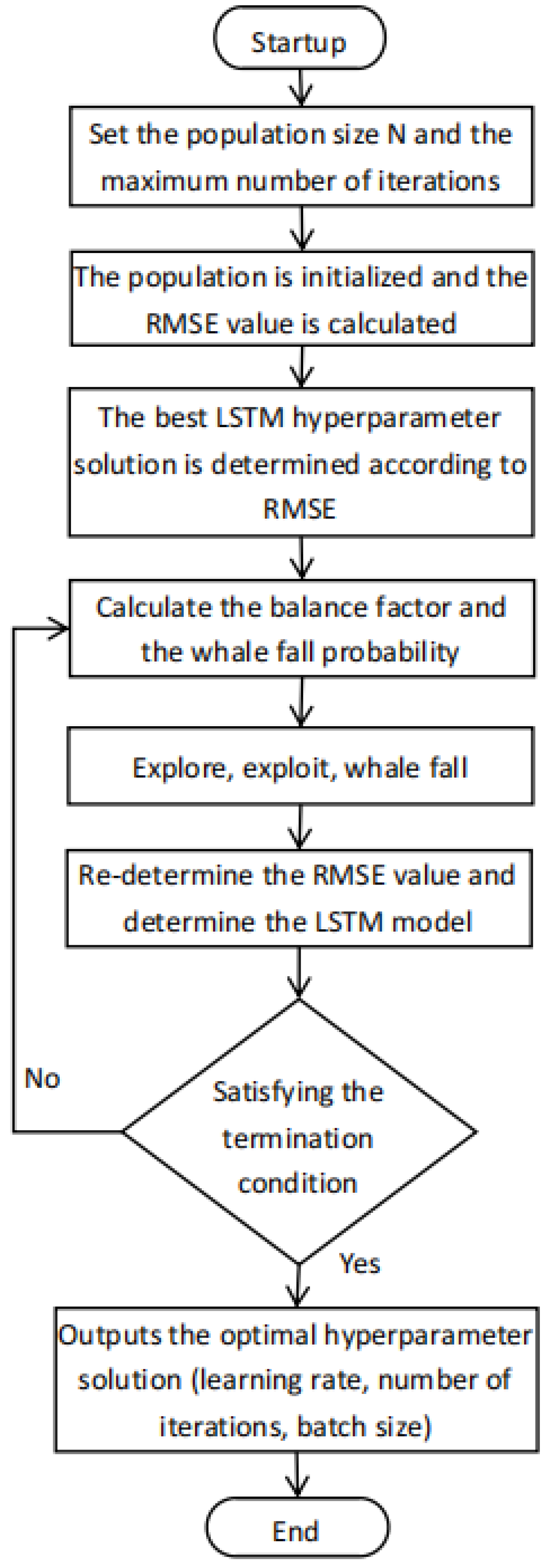
- Introduce the BWO algorithm for model hyper-parameter optimization and propose a BWO-TCLS-Self-Attention prediction network structure.
2. Related Works
3. Methods
3.1. Optimization Algorithm Selection
3.2. Improved LSTM Network
3.3. BWO-TCLS-Self-Attention Network
3.4. Evaluation Metrics
4. Results
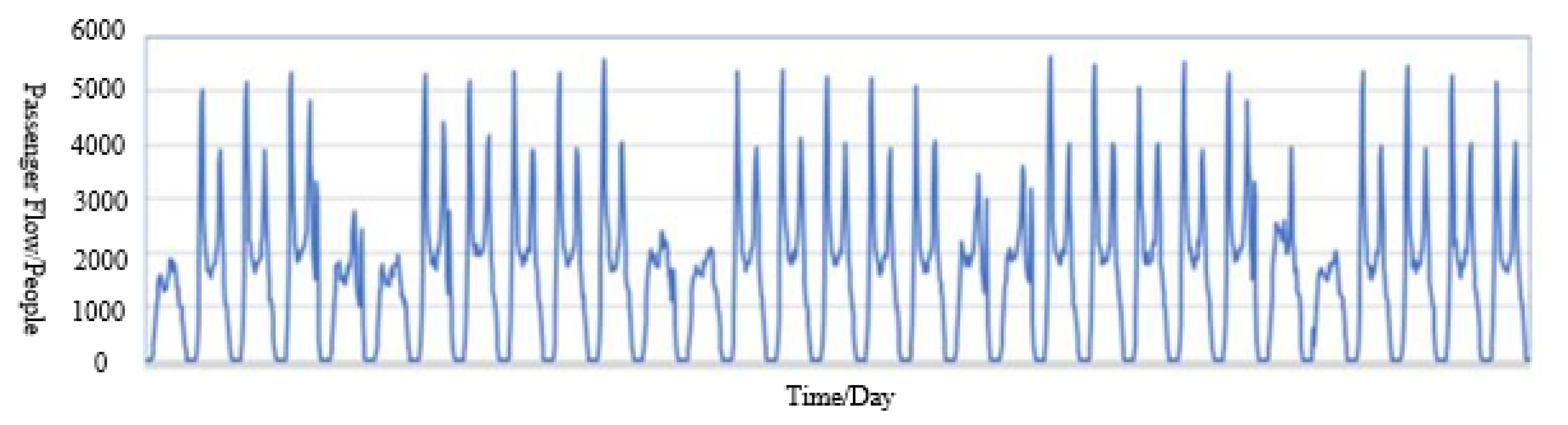
4.1. Data Set Establishment and Preprocessing
4.1.1. Data Set Establishment
4.1.2. Data Normalization
4.1.3. Dataset Partitioning
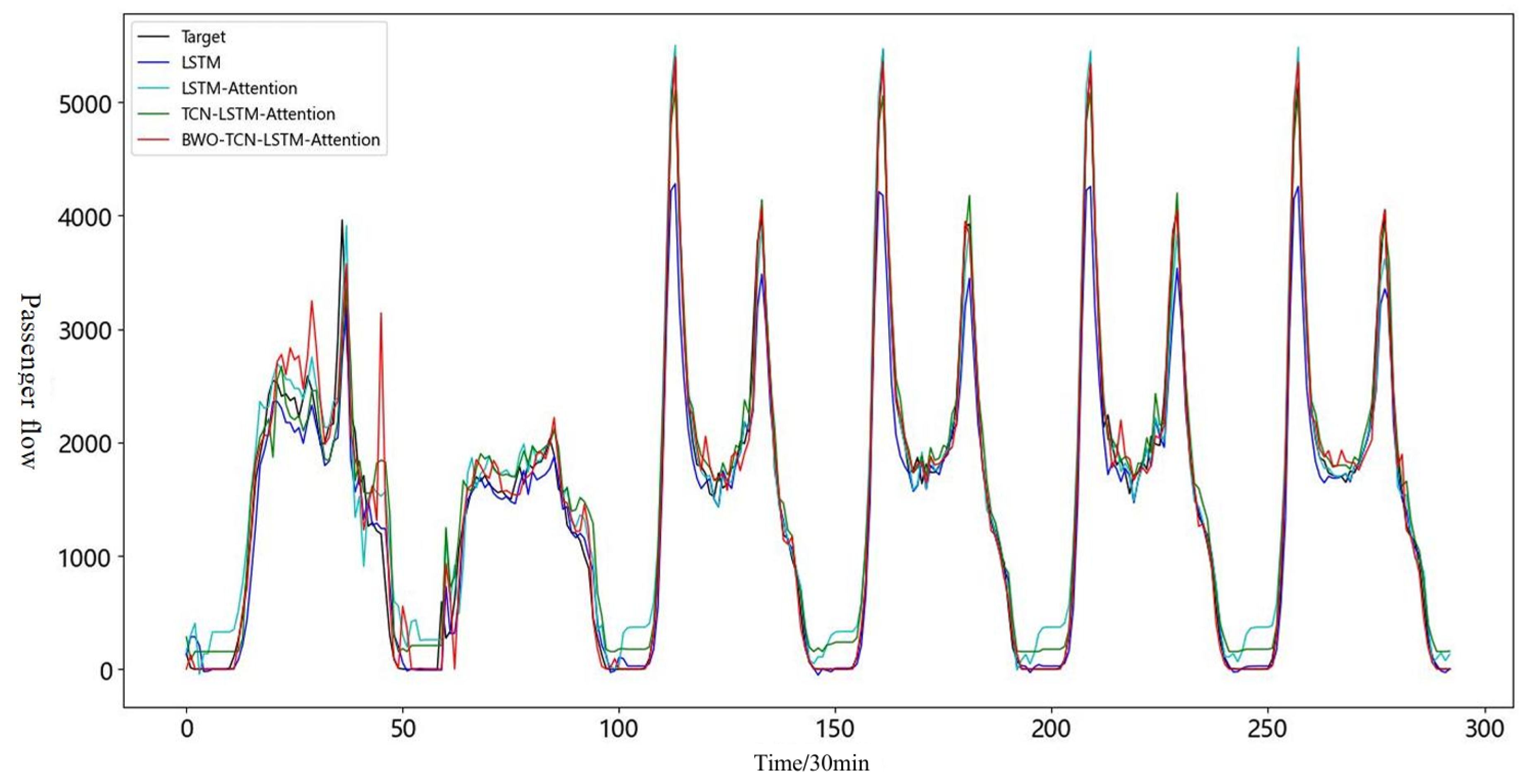
4.2. Ablation Experiment
4.3. Comparison of Different Model Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bobylev, N. Underground space in the Alexanderplatz area, Berlin: Research into the quantification of urban underground space use. Tunn. Undergr. Space Technol. 2010, 25, 495–507. [Google Scholar] [CrossRef]
- Cui, J.; Broere, W.; Lin, D. Underground space utilisation for urban renewal. Tunn. Undergr. Space Technol. 2021, 108, 103726. [Google Scholar] [CrossRef]
- Bobylev, N. Underground space as an urban indicator: Measuring use of subsurface. Tunn. Undergr. Space Technol. 2016, 55, 40–51. [Google Scholar] [CrossRef]
- Liu, L.; Chen, R.-C.; Zhu, S. Impacts of weather on short-term metro passenger flow forecasting using a deep LSTM neural network. Appl. Sci. 2020, 10, 2962. [Google Scholar] [CrossRef]
- Hewage, P.; Behera, A.; Trovati, M.; Pereira, E.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, K.; Huang, Y.; Zhu, Y.; Chen, B. Parallel spatio-temporal attention-based TCN for multivariate time series prediction. Neural Comput. Appl. 2023, 35, 13109–13118. [Google Scholar] [CrossRef]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal Convolutional Networks for action segmentation and detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 156–165. [Google Scholar]
- Yao, L.; Zhang, S.; Li, G. Neural network-based passenger flow prediction: Take a campus for example. In Proceedings of the 2020 13th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 12–13 December 2020; pp. 384–387. [Google Scholar]
- Liu, Y.; Lyu, C.; Liu, X.; Liu, Z. Automatic feature engineering for bus passenger flow prediction based on modular convolutional neural network. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2349–2358. [Google Scholar] [CrossRef]
- Feng, J.; Feng, X.; Chen, J.; Cao, X.; Zhang, X.; Jiao, L.; Yu, T. Generative adversarial networks based on collaborative learning and attention mechanism for hyperspectral image classification. Remote Sens. 2020, 12, 1149. [Google Scholar] [CrossRef]
- Wang, L.; Fang, S.; Meng, X.; Li, R. Building extraction with vision transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5625711. [Google Scholar] [CrossRef]
- Li, Y.; Mavromatis, S.; Zhang, F.; Du, Z.; Sequeira, J.; Wang, Z.; Zhao, X.; Liu, R. Single-image super-resolution for remote sensing images using a deep generative adversarial network with local and global attention mechanisms. IEEE Trans. Geosci. Remote Sens. 2021, 60, 3000224. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Yao, S.; Liu, M. DCGCN: Double-Channel Graph Convolutional Network for passenger flow prediction in urban rail transit. In Proceedings of the 2022 8th International Conference on Big Data Computing and Communications (BigCom), Xiamen, China, 6–7 August 2022; pp. 304–313. [Google Scholar]
- Du, B.; Peng, H.; Wang, S.; Bhuiyan, M.Z.A.; Wang, L.; Gong, Q.; Liu, L.; Li, J. Deep irregular convolutional residual LSTM for urban traffic passenger flows prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 972–985. [Google Scholar] [CrossRef]
- Nagaraj, N.; Gururaj, H.L.; Swathi, B.H.; Hu, Y.C. Passenger flow prediction in bus transportation system using deep learning. Multimed. Tools Appl. 2022, 81, 12519–12542. [Google Scholar] [CrossRef] [PubMed]
- Jiao, F.; Huang, L.; Song, R.; Huang, H. An improved STL-LSTM model for daily bus passenger flow prediction during the COVID-19 pandemic. Sensors 2021, 21, 5950. [Google Scholar] [CrossRef] [PubMed]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Jing, Y.; Hu, H.; Guo, S.; Wang, X.; Chen, F. Short-term prediction of urban rail transit passenger flow in external passenger transport hub based on LSTM-LGB-DRS. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4611–4621. [Google Scholar] [CrossRef]
- Rigatti, S.J. Random Forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient Gradient Boosting Decision Tree. In Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]




| Features | Data | Numerical Value |
|---|---|---|
| Weather | Cloudy/cloudy | 1 |
| Cloudy/sunny | 2 | |
| Cloudy/Light rain | 3 | |
| Thundery/cloudy | 4 | |
| Thundery/thundery | 5 | |
| Sunny/cloudy | 6 | |
| Sunny/sunny | 7 | |
| Light rain/cloudy | 8 | |
| Light rain/thunder | 9 | |
| Overcast/cloudy | 10 | |
| Hours of operation | Working day | 1 |
| Non-working day | 2 | |
| Major events | Major events | 1 |
| Non major event | 0 |
| Prediction Model | MAE | RMSE | |
|---|---|---|---|
| LSTM | 180.208 | 282.033 | 0.9489 |
| LSTM-Self-Attention | 201.098 | 261.517 | 0.9561 |
| TCN-LSTM-Self-Attention | 185.579 | 244.442 | 0.9616 |
| BWO-TCLS-Self-Attention | 118.464 | 218.118 | 0.9694 |
| Prediction Model | MAE | RMSE | |
|---|---|---|---|
| Linear Regression LR | 417.804 | 667.728 | 0.7138 |
| Random Forest RF | 317.129 | 513.216 | 0.8309 |
| Gradient lifting decision tree GBDT | 401.906 | 638.567 | 0.7383 |
| LSTM | 180.208 | 282.033 | 0.9489 |
| LSTM-Self-Attention | 201.098 | 261.517 | 0.9561 |
| TCN-LSTM-Self-Attention | 185.579 | 244.442 | 0.9616 |
| BWO-TCLS-Self-Attention | 118.464 | 218.118 | 0.9694 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Du, L.; Cao, T.; Zhang, T. Research on a Passenger Flow Prediction Model Based on BWO-TCLS-Self-Attention. Electronics 2024, 13, 4849. https://doi.org/10.3390/electronics13234849
Liu S, Du L, Cao T, Zhang T. Research on a Passenger Flow Prediction Model Based on BWO-TCLS-Self-Attention. Electronics. 2024; 13(23):4849. https://doi.org/10.3390/electronics13234849
Chicago/Turabian StyleLiu, Sheng, Lang Du, Ting Cao, and Tong Zhang. 2024. "Research on a Passenger Flow Prediction Model Based on BWO-TCLS-Self-Attention" Electronics 13, no. 23: 4849. https://doi.org/10.3390/electronics13234849
APA StyleLiu, S., Du, L., Cao, T., & Zhang, T. (2024). Research on a Passenger Flow Prediction Model Based on BWO-TCLS-Self-Attention. Electronics, 13(23), 4849. https://doi.org/10.3390/electronics13234849







