A Wideband dB-Linear Analog Baseband for a Millimeter-Wave Receiver with Error Compensation in 40 nm CMOS Technology
Abstract
:1. Introduction
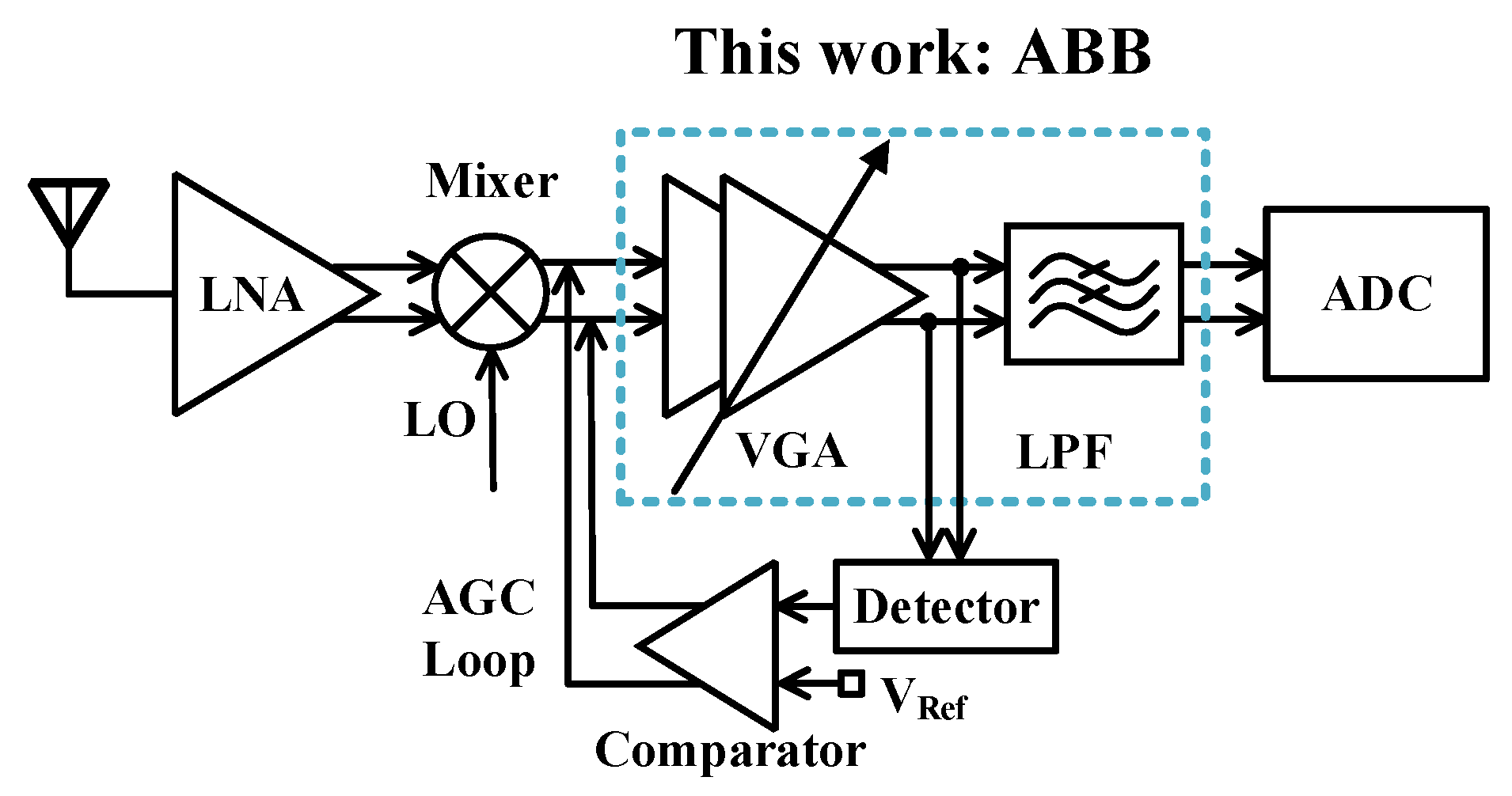
2. Analog Baseband Architecture
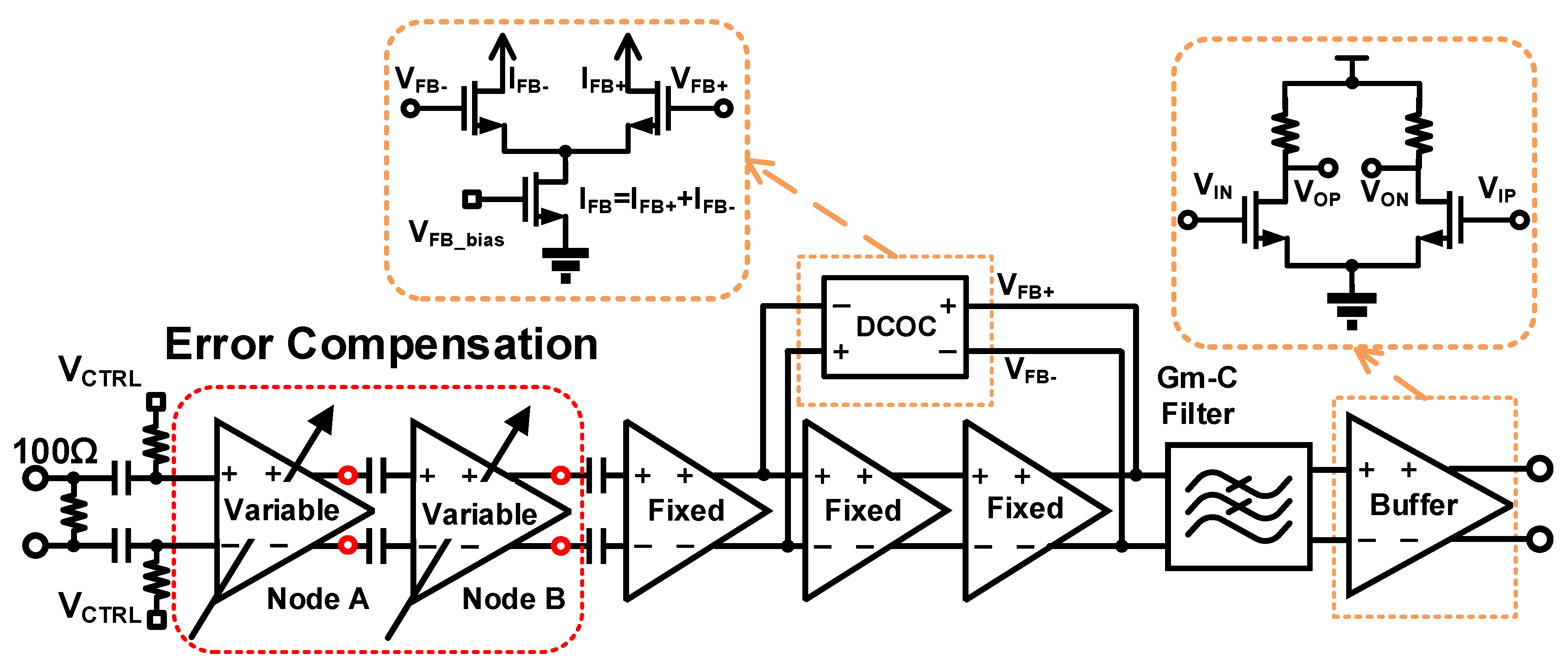
3. Detailed Circuit Designs of the Analog Baseband
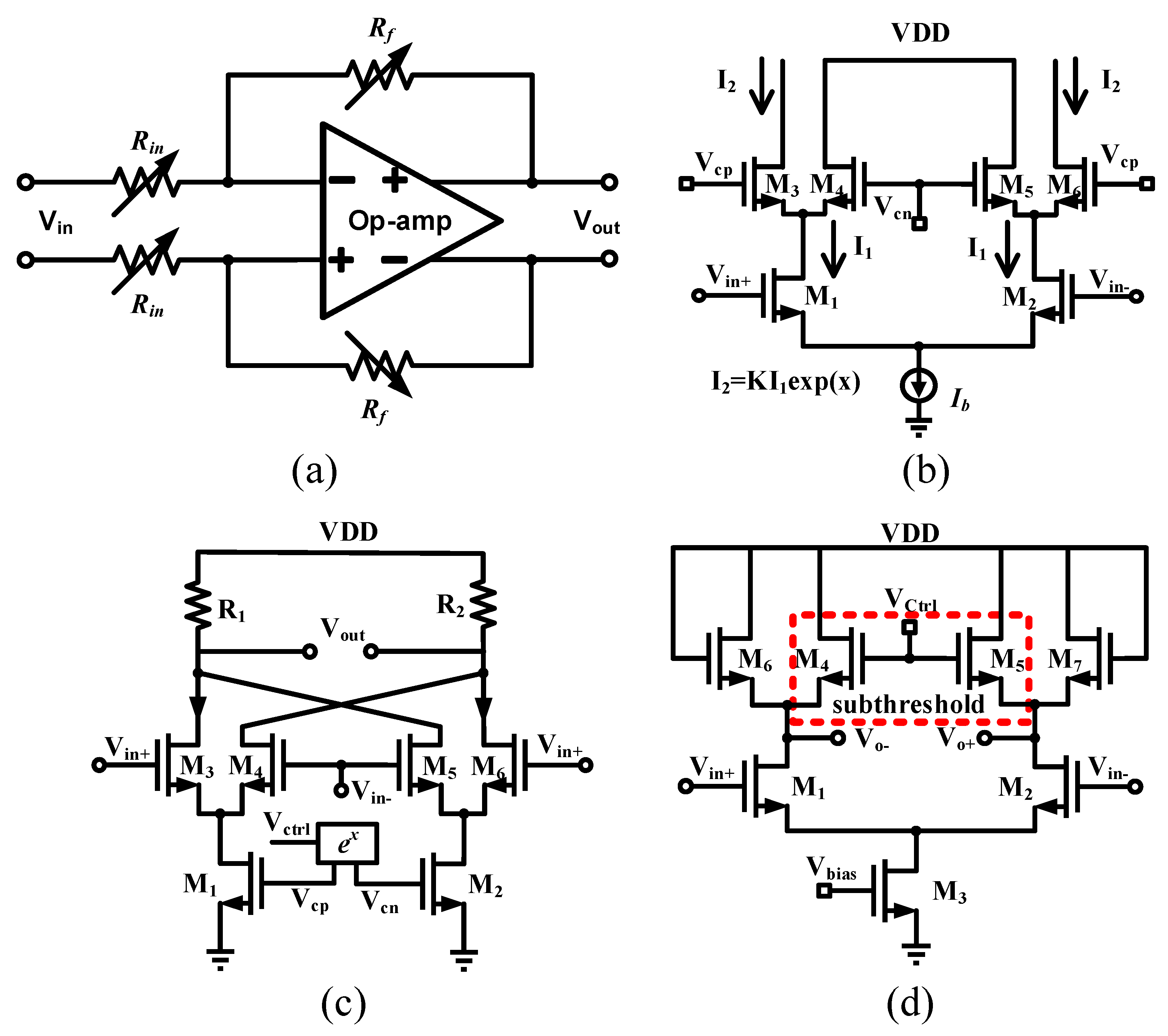
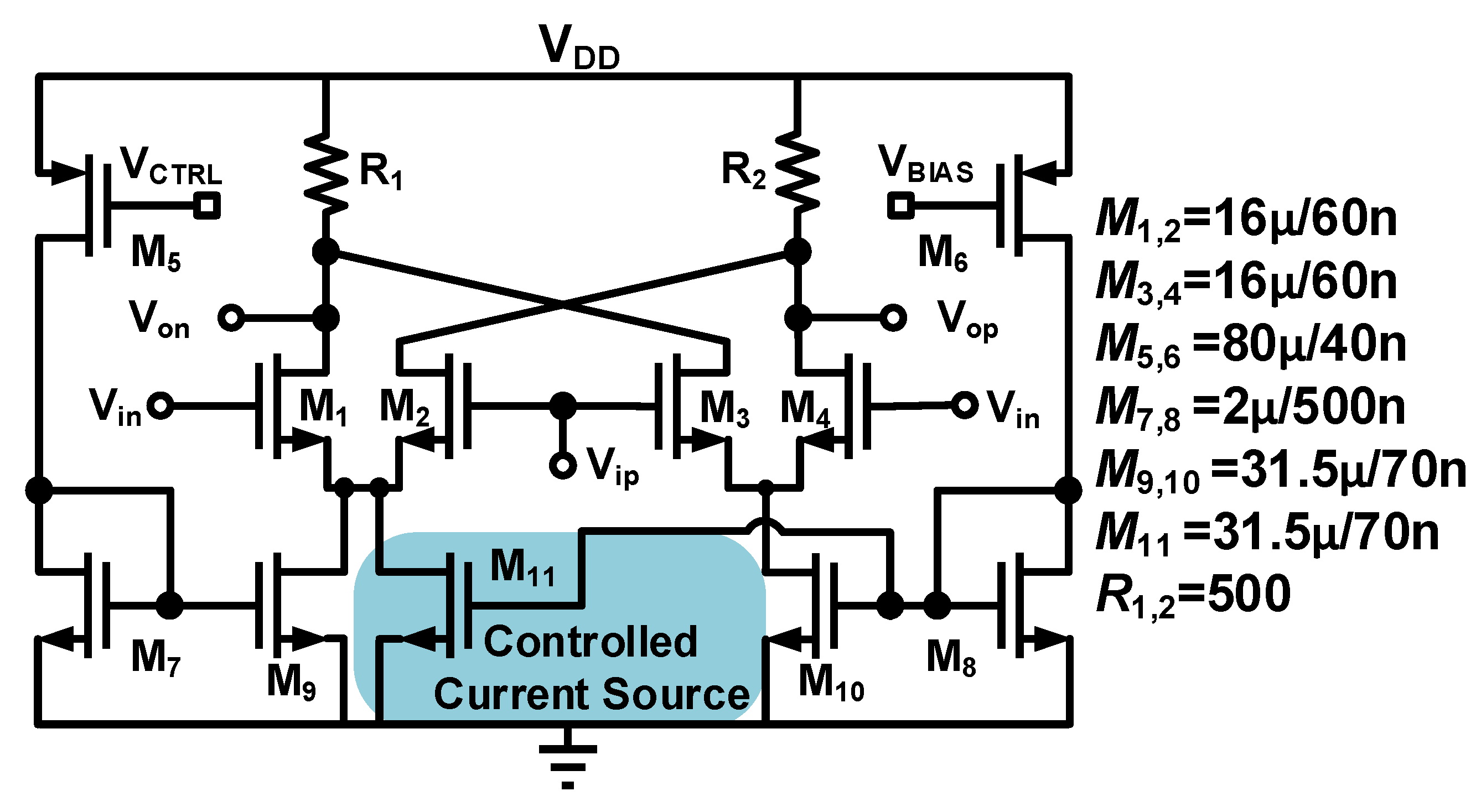
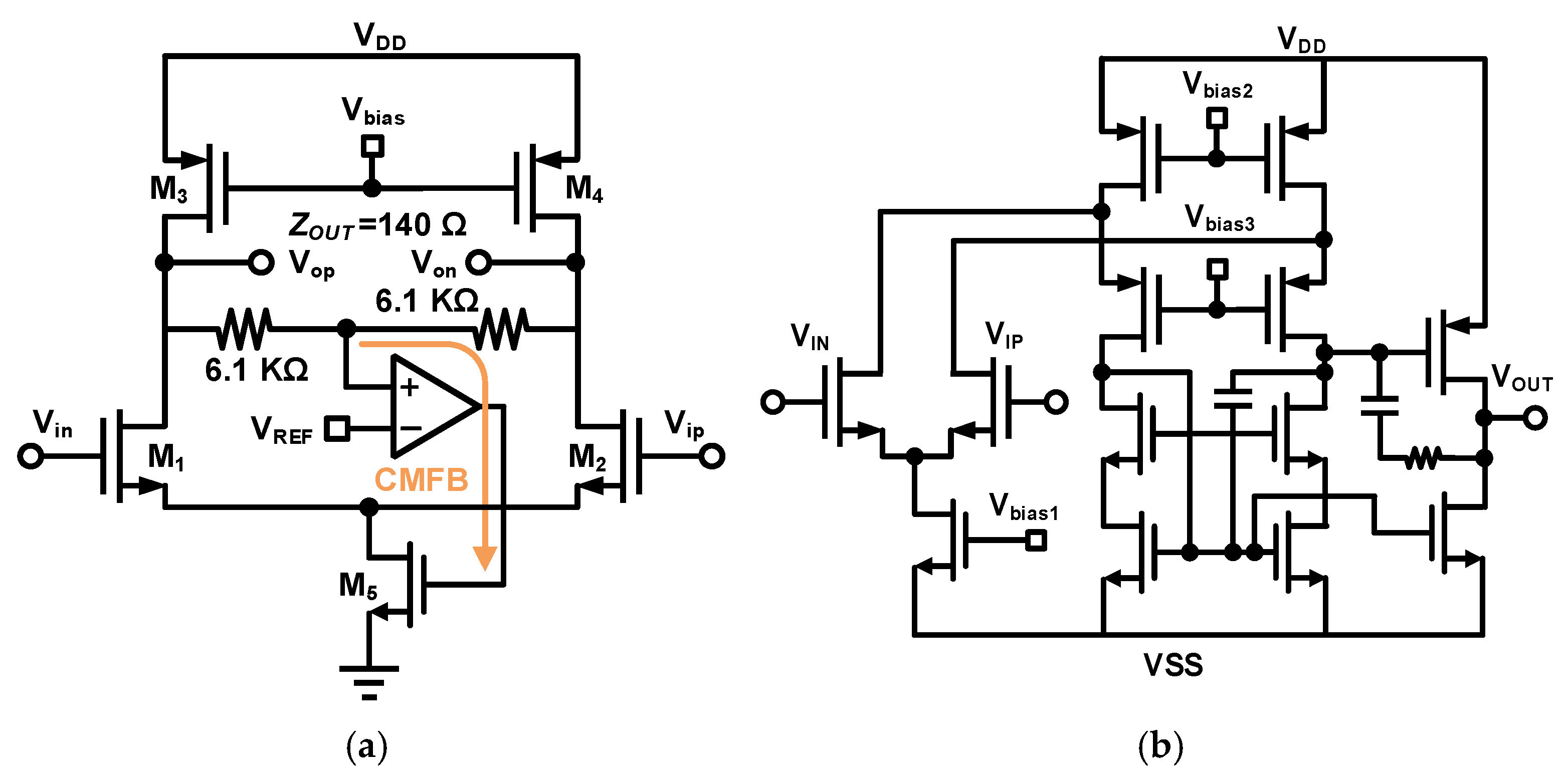
3.1. dB-Linear Variable Gain Unit Core
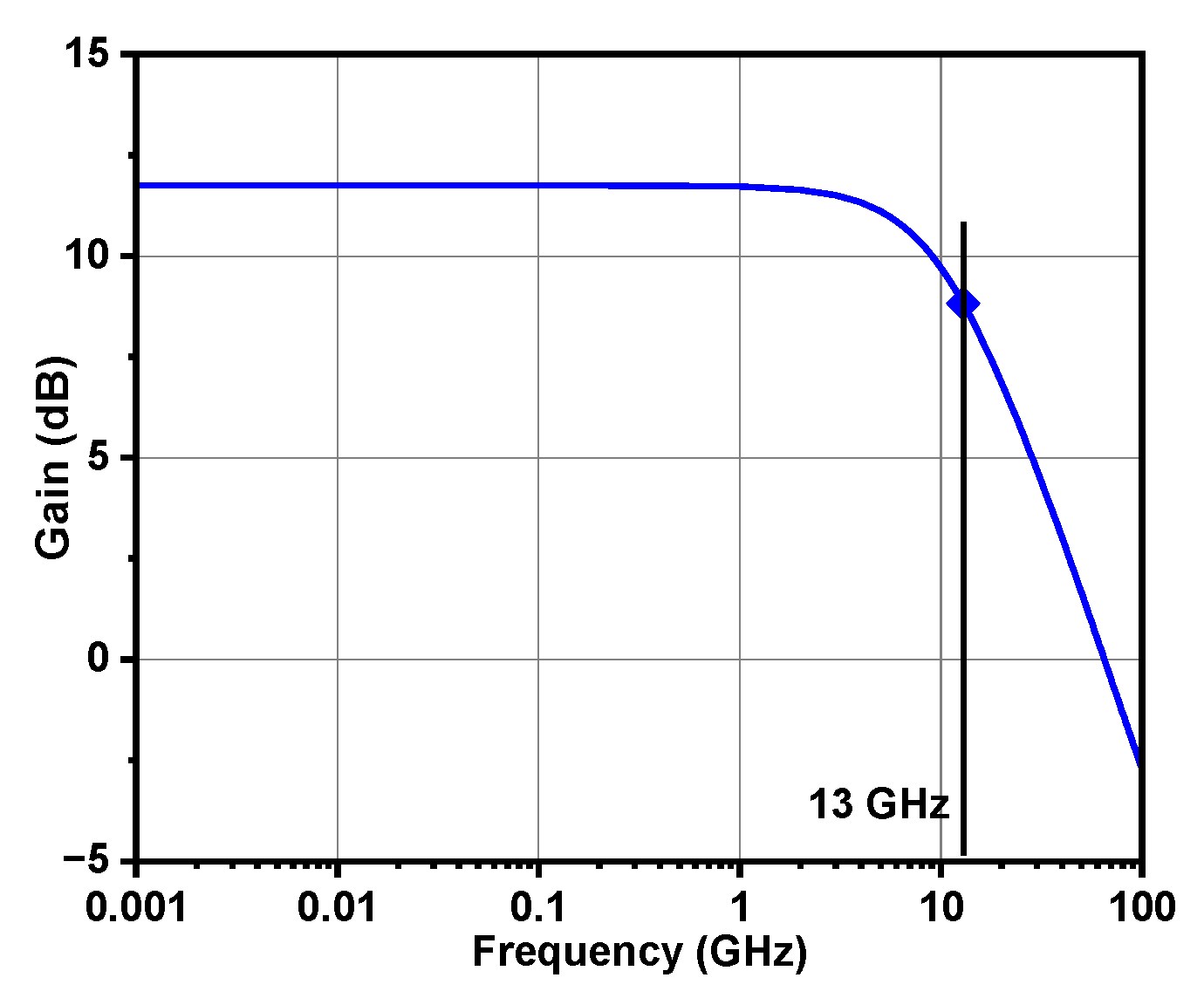
3.2. Fixed Gain Amplifier
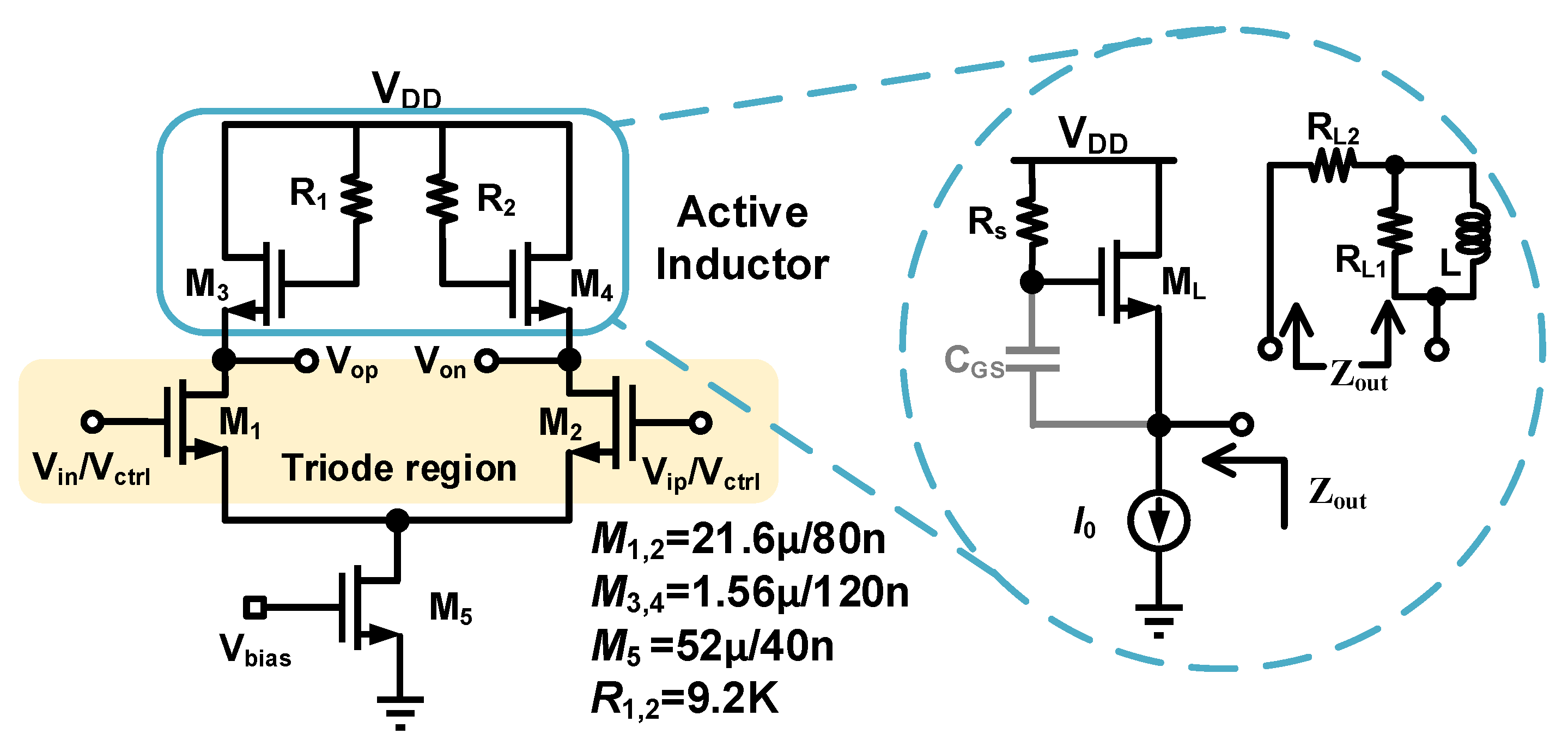
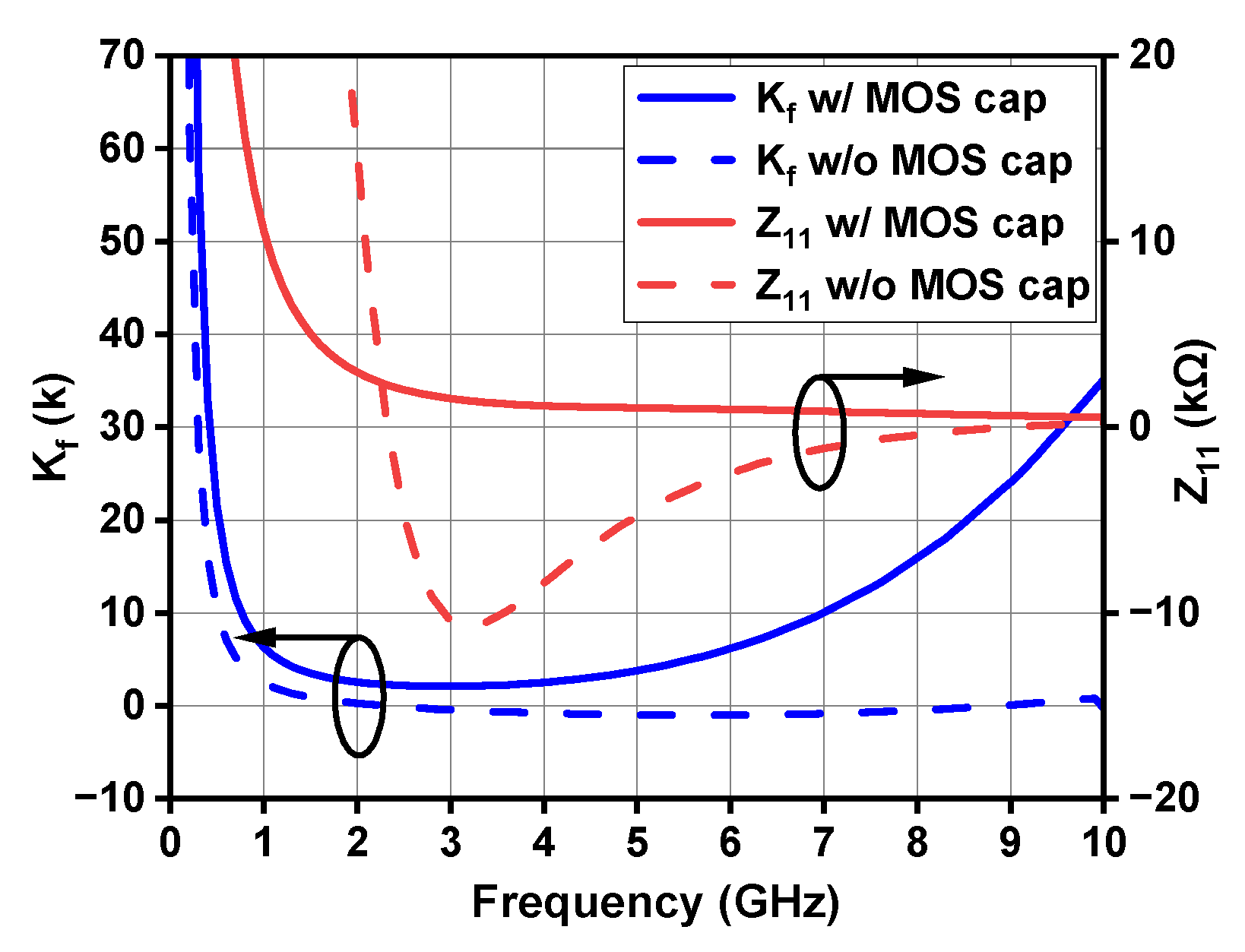
3.3. Low-Pass Filter
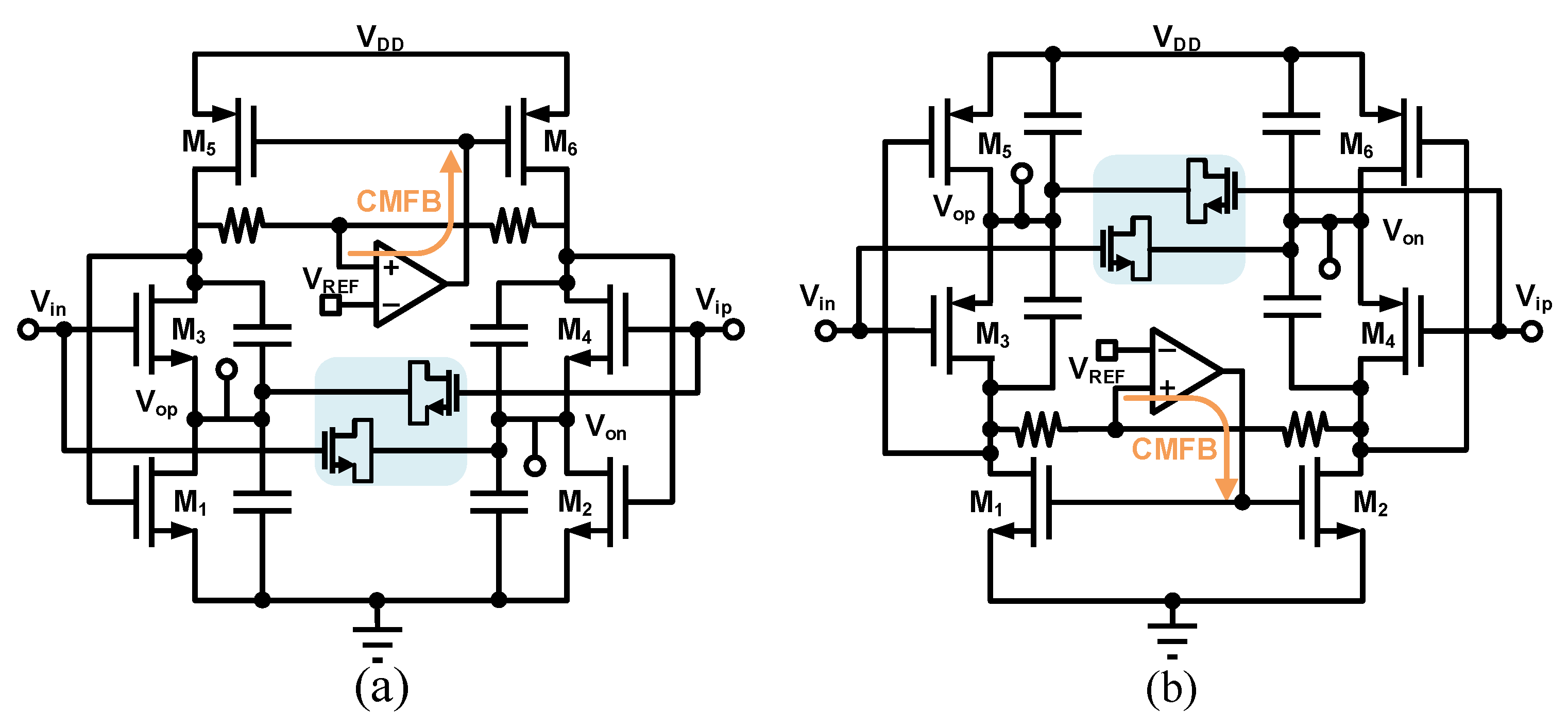
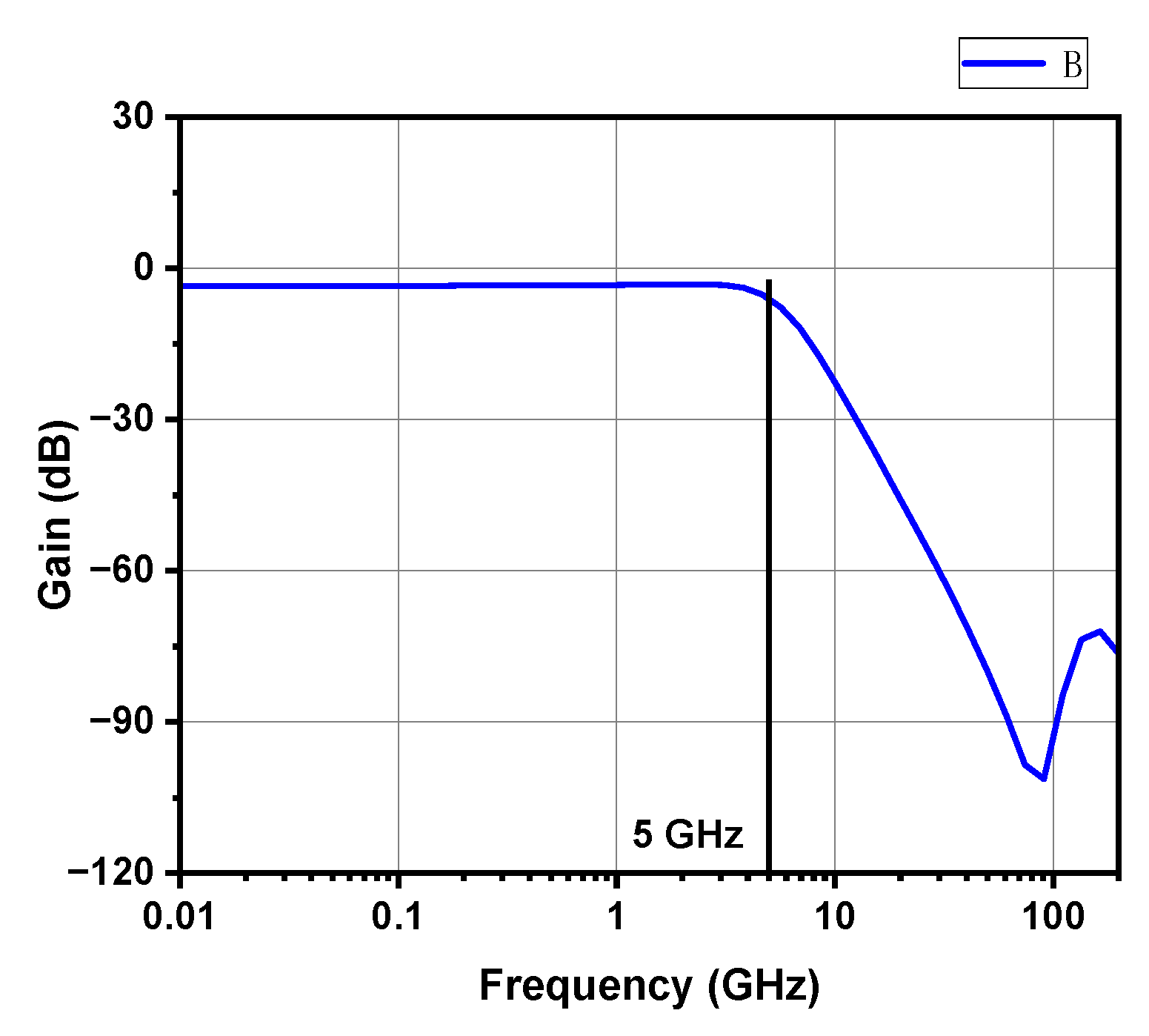
3.4. DCOC Network
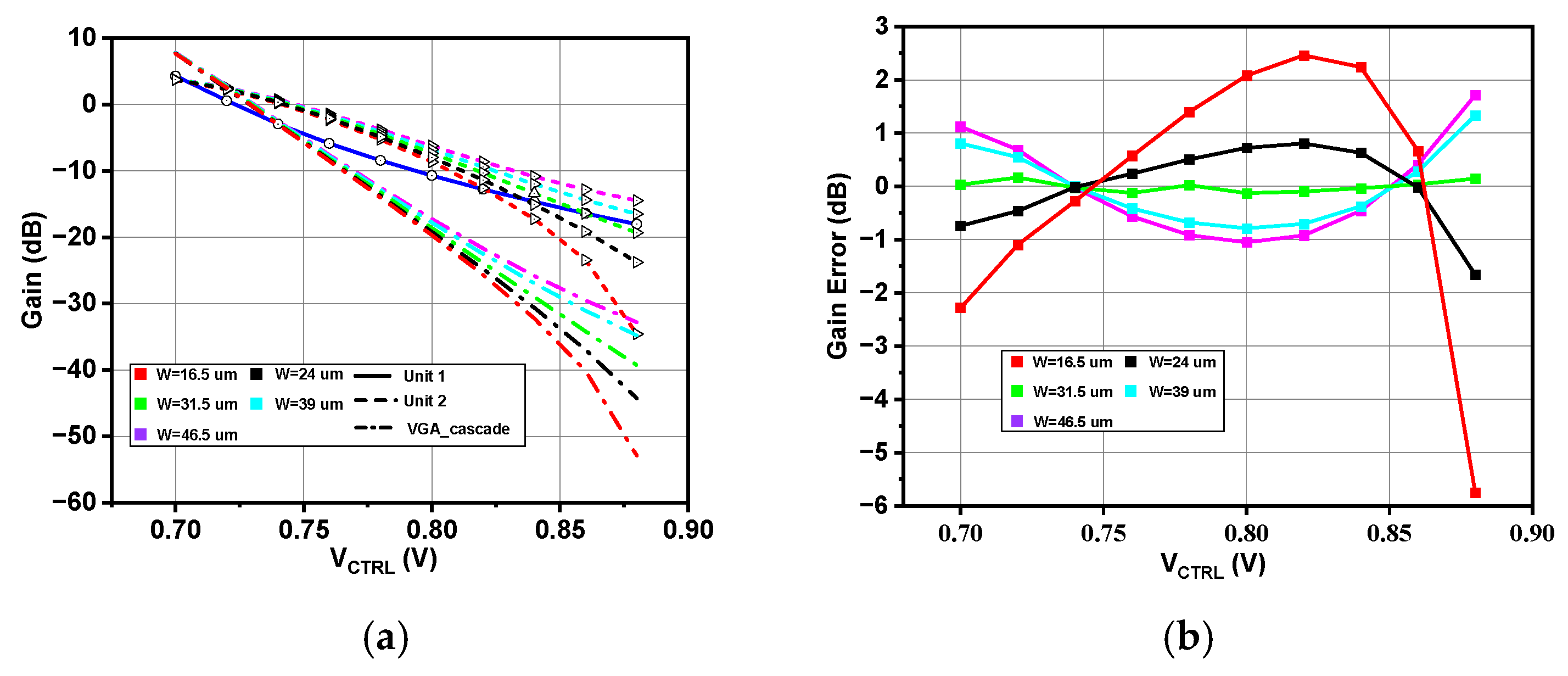
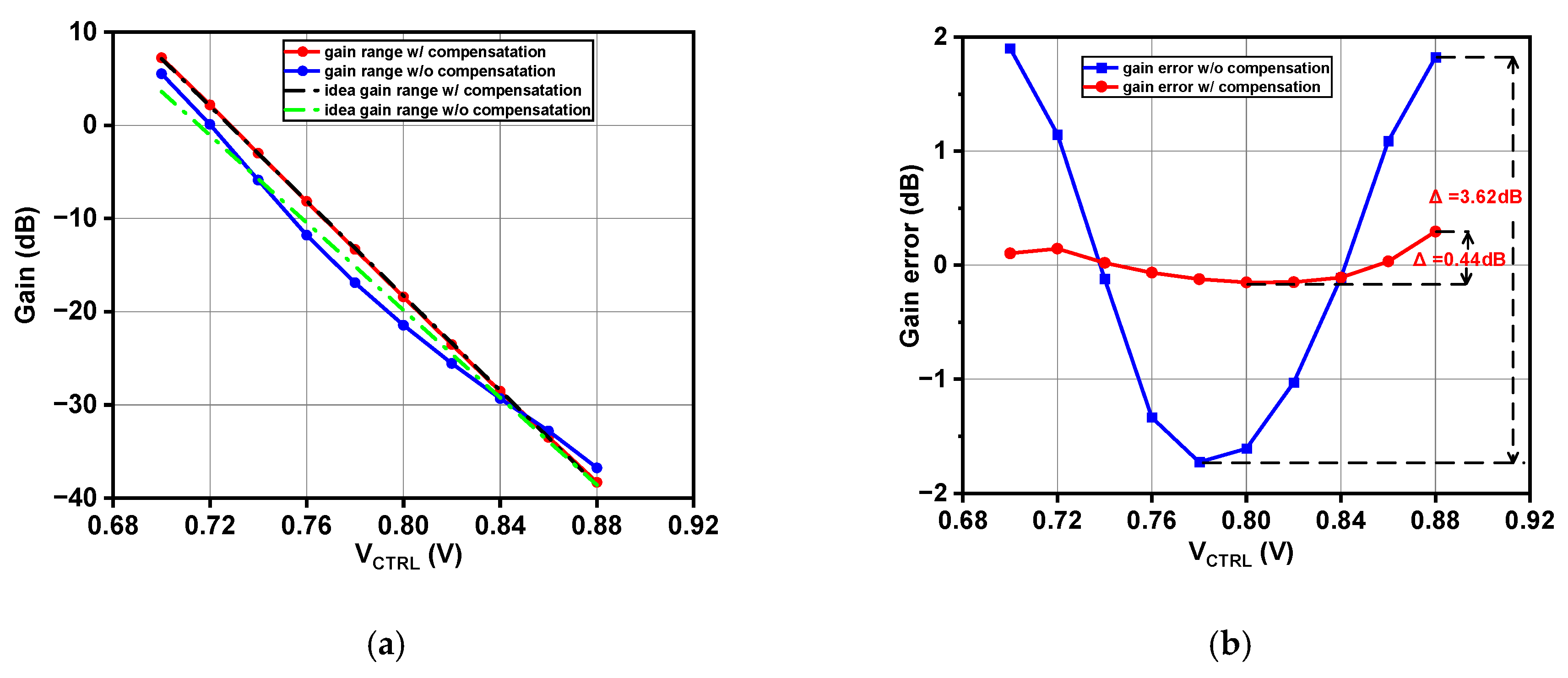
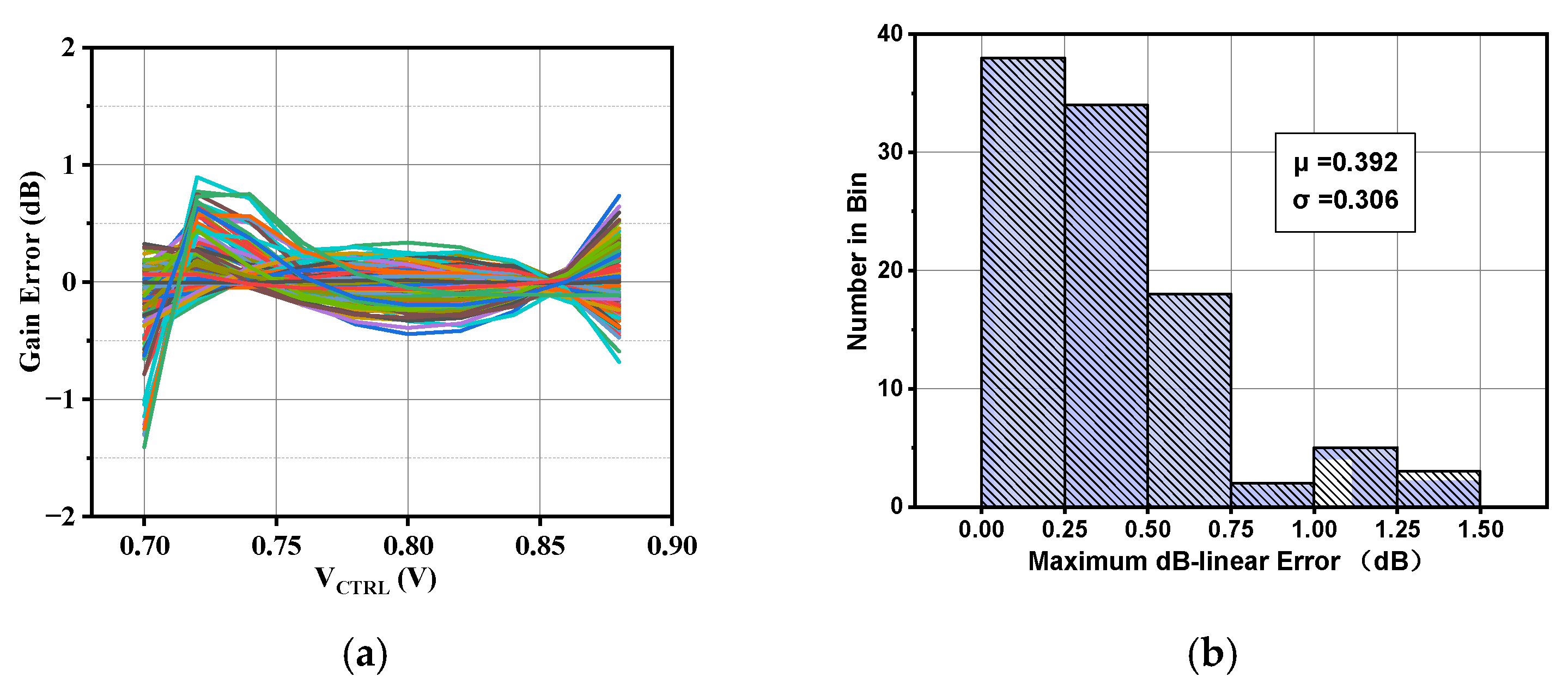
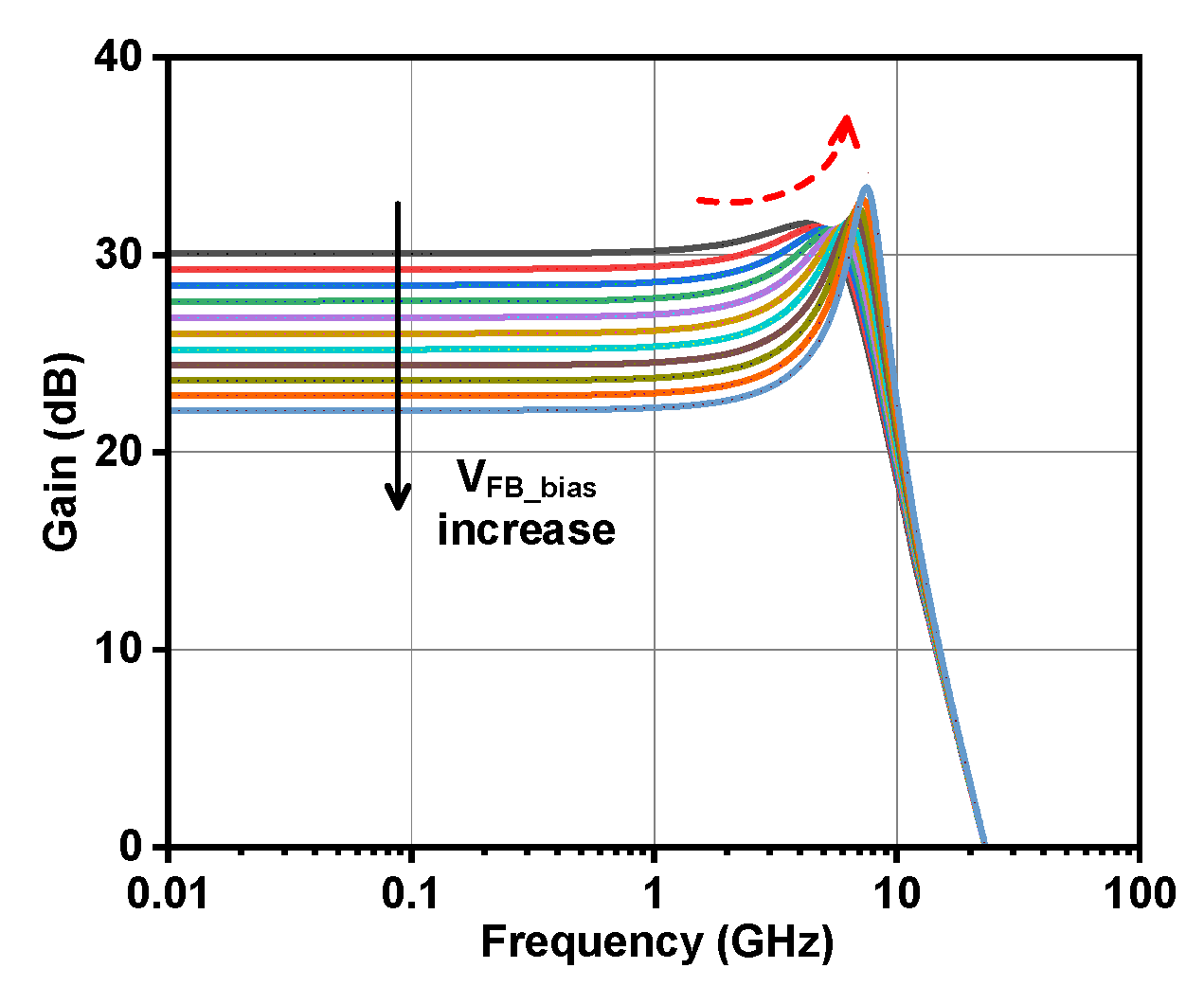
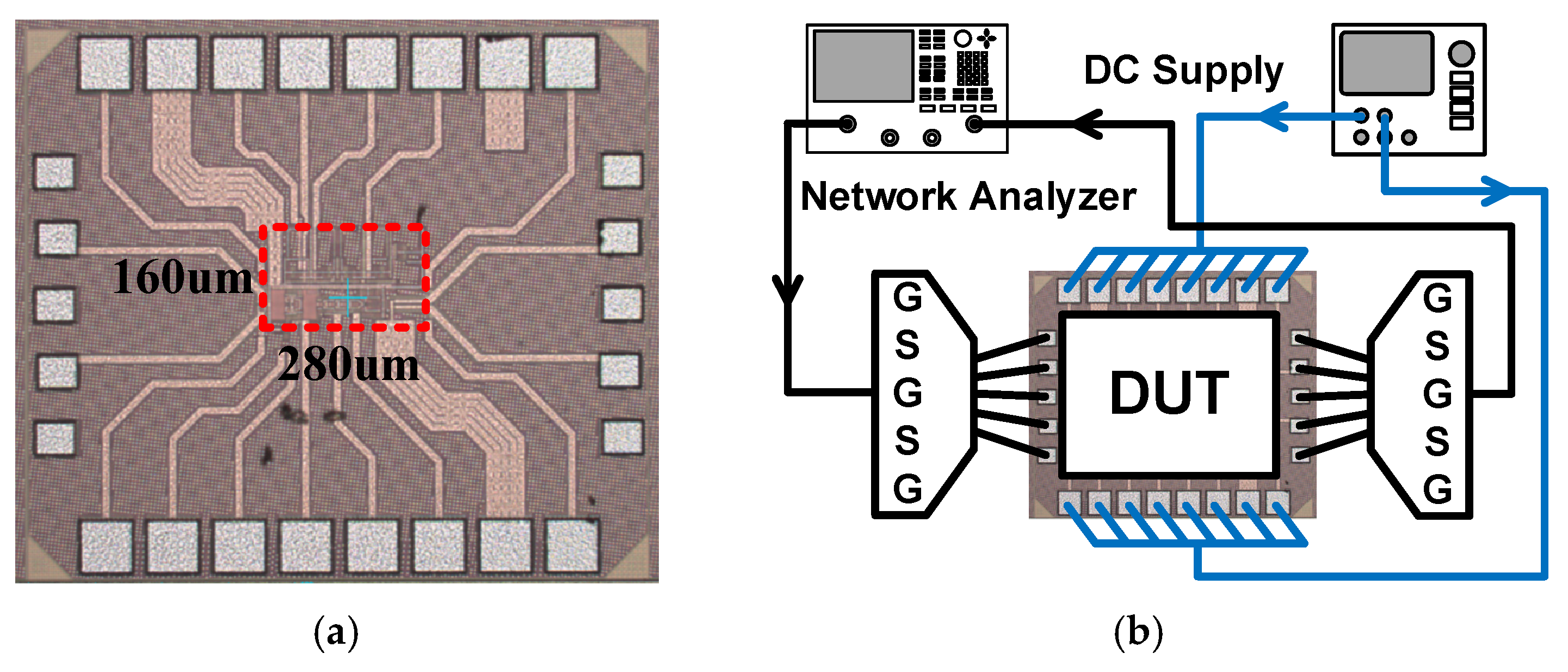
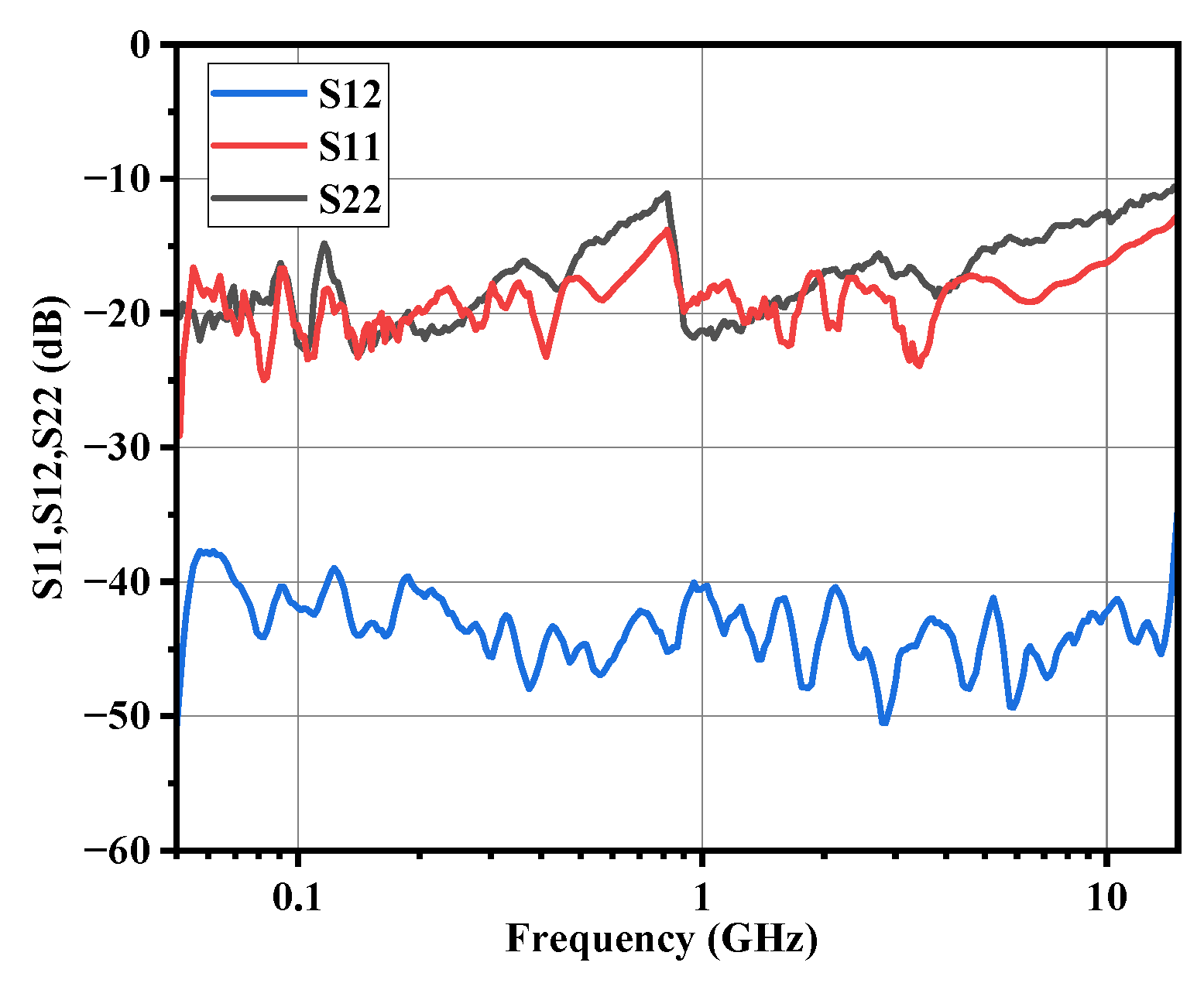
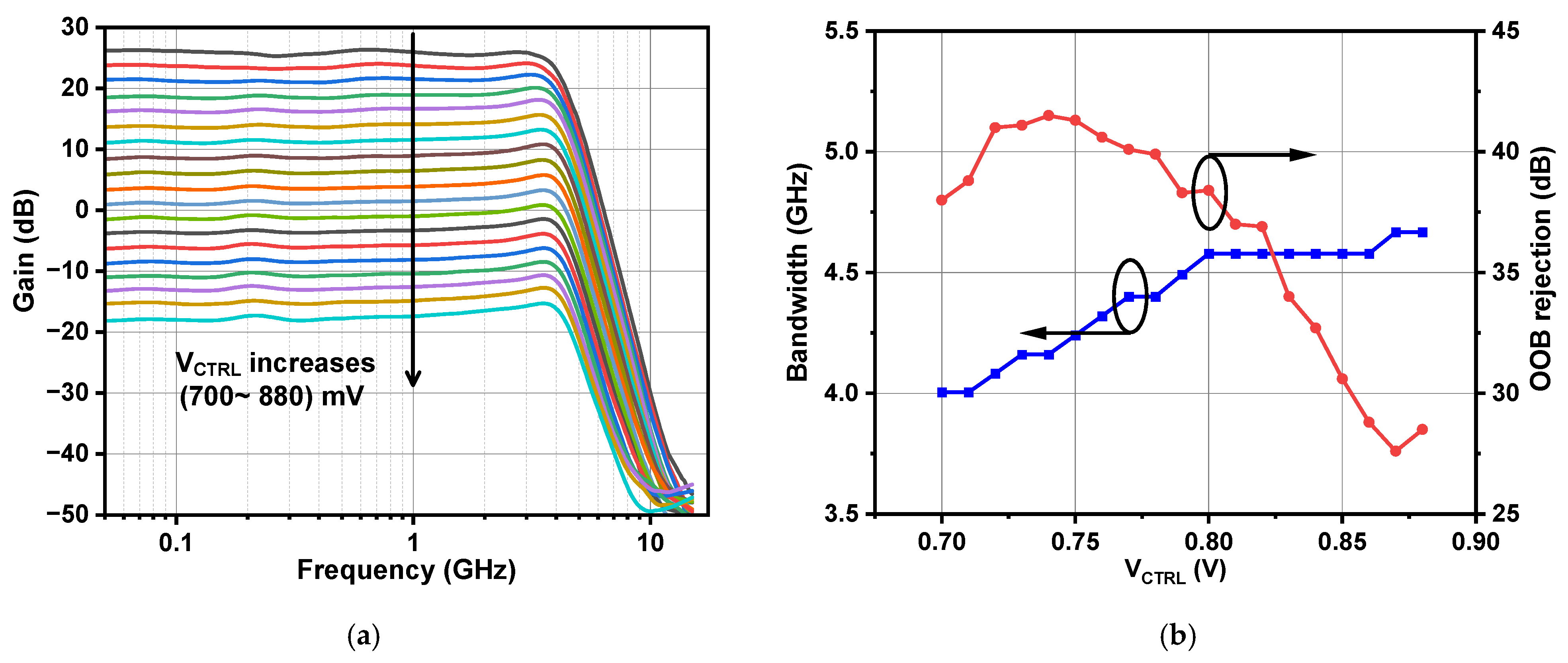
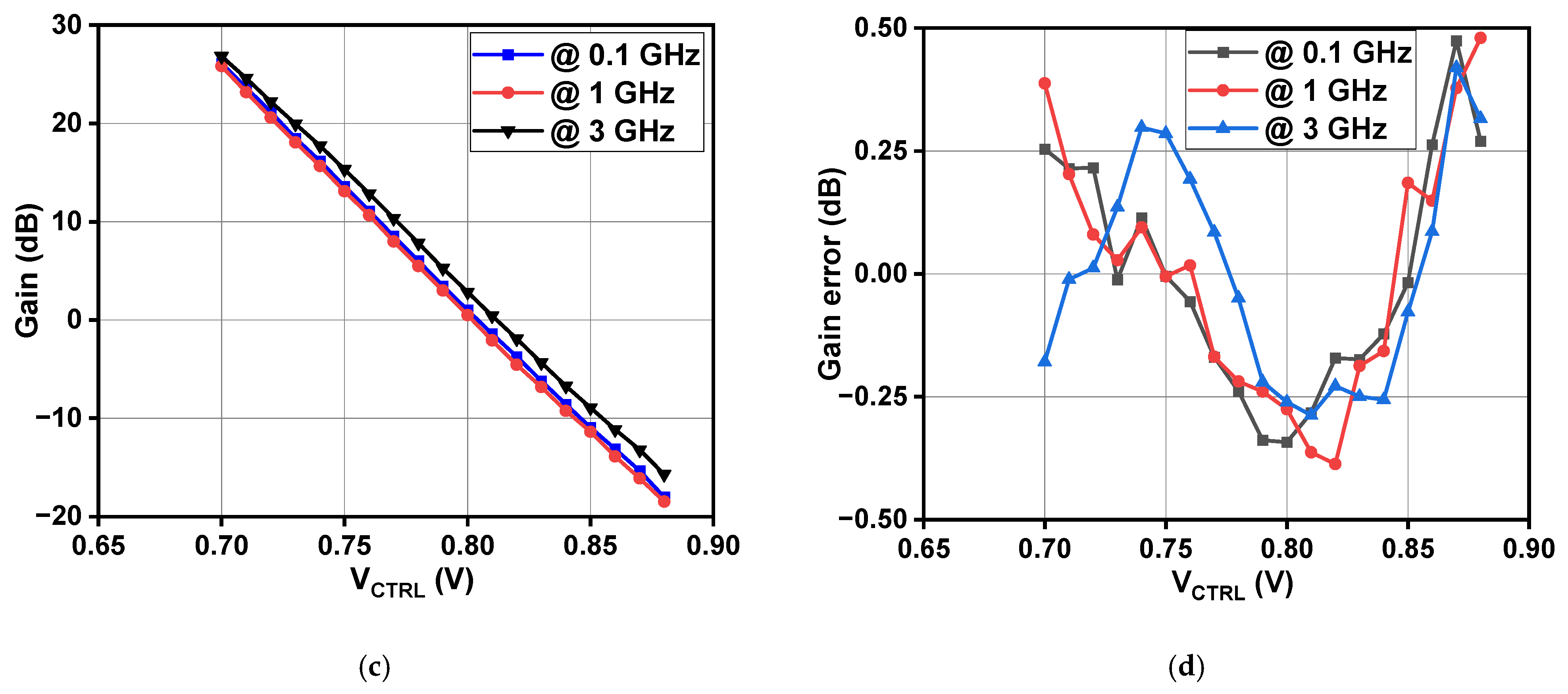
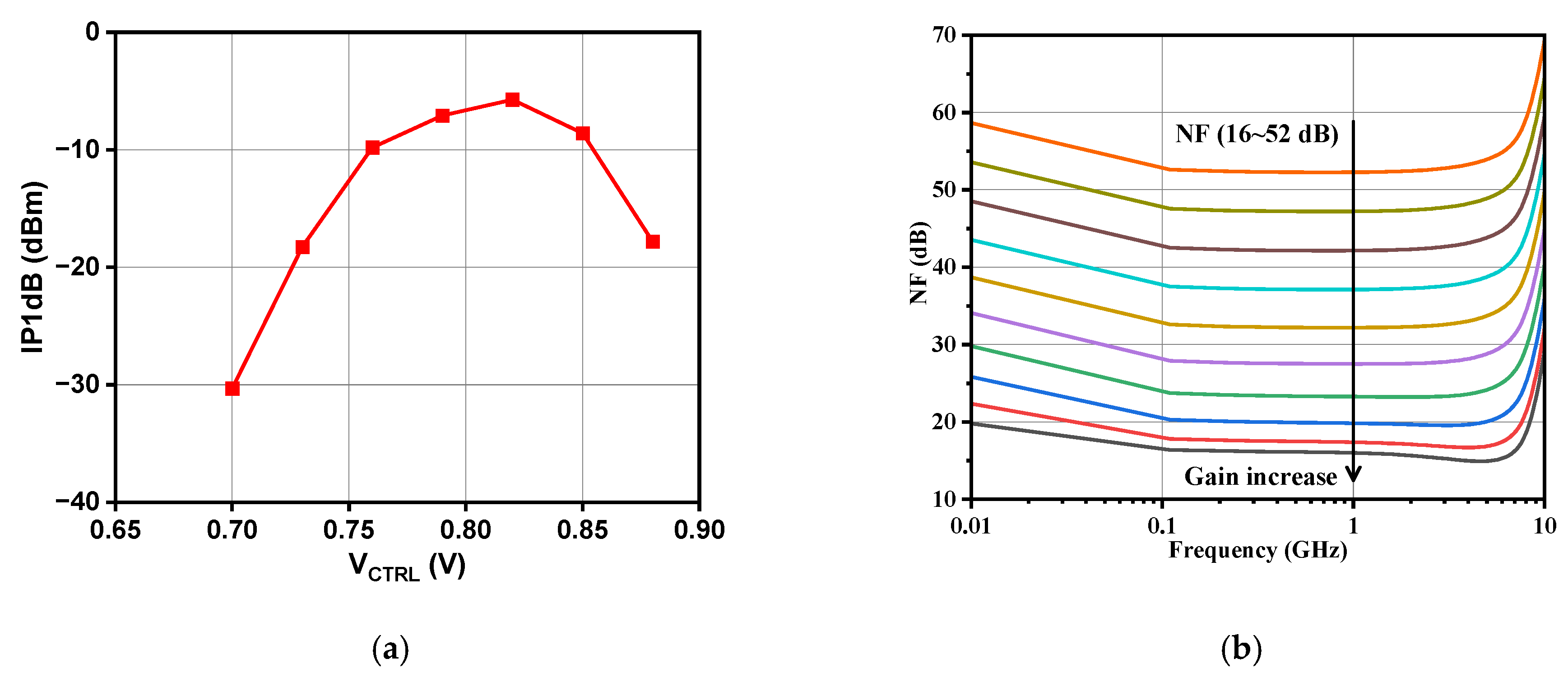
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Doan, C.H.; Emami, S.; Niknejad, A.M.; Brodersen, R.W. Design of CMOS for 60GHz applications. In Proceedings of the 2004 IEEE International Solid-State Circuits Conference (IEEE Cat. No.04CH37519), San Francisco, CA, USA, 15–19 February 2004; pp. 440–441. [Google Scholar] [CrossRef]
- Doan, C.H.; Emami, S.; Niknejad, A.M.; Brodersen, R.W. Millimeter-wave CMOS design. IEEE J. Solid-State Circuits 2005, 40, 144–155. [Google Scholar] [CrossRef]
- Ghittori, N.; Vigna, A.; Malcovati, P.; D’Amico, S.; Baschirotto, A. A 1.2-V 30.4-dBm OIP3 Reconfigurable Analog Baseband Channel for UMTS/WLAN Transmitters. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 2125–2131. [Google Scholar] [CrossRef]
- Siligaris, A.; Richard, O.; Martineau, B.; Mounet, C.; Chaix, F.; Ferragut, R.; Dehos, C.; Lanteri, J.; Dussopt, L.; Yamamoto, S.D.; et al. A 65-nm CMOS Fully Integrated Transceiver Module for 60-GHz Wireless HD Applications. IEEE J. Solid-State Circuits 2011, 46, 3005–3017. [Google Scholar] [CrossRef]
- Kulkarni, R.; Kim, J.; Jeon, H.-J.; Xiao, J.; Silva-Martinez, J. UHF Receiver Front-End: Implementation and Analog Baseband Design Considerations. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2012, 20, 197–210. [Google Scholar] [CrossRef]
- Liao, C.-F.; Liu, S.-I. A 10Gb/s CMOS AGC Amplifier with 35dB Dynamic Range for 10Gb Ethernet. In Proceedings of the 2006 IEEE International Solid State Circuits Conference-Digest of Technical Papers, San Francisco, CA, USA, 6–9 February 2006; pp. 2092–2101. [Google Scholar] [CrossRef]
- He, L.; Li, L.; Wu, X.; Wang, Z. A Low-Power Wideband dB-Linear Variable Gain Amplifier With DC-Offset Cancellation for 60-GHz Receiver. IEEE Access 2018, 6, 61826–61832. [Google Scholar] [CrossRef]
- Liu, C.; Yan, Y.-P.; Goh, W.-L.; Xiong, Y.-Z.; Zhang, L.-J.; Madihian, M. A 5-Gb/s Automatic Gain Control Amplifier With Temperature Compensation. IEEE J. Solid-State Circuits 2012, 47, 1323–1333. [Google Scholar] [CrossRef]
- Kong, L.; Chen, Y.; Boon, C.C.; Mak, P.-I.; Martins, R.P. A wideband inductorless dB-linear automatic gain control amplifier using a single branch negative exponential generator for wireline applications. IEEE Trans. Circuits Syst. I Reg. Pap. 2018, 65, 3196–3206. [Google Scholar] [CrossRef]
- Cai, L.; Song, X.; Lu, Z.; Yu, X.P.; Yeo, K.S.; Chen, J.M.; Thangarasu, B.K. A Linear-in-Decibel Automatic Gain Control Amplifier With Dual Mode Continuous Gain Tuning. IEEE Trans. Circuits Syst. I Reg. Pap. 2023, 70, 2752–2761. [Google Scholar] [CrossRef]
- Thangarasu, B.K.; Ma, K.; Yeo, K.S. A 0.029 mm2 8 Gbit/s current-mode AGC amplifier with reconfigurable closed-loop control in 65 nm CMOS. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 107–110. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, L.; Liao, H.; Huang, R.; Wang, Y. Highly Reconfigurable Analog Baseband for Multistandard Wireless Receivers in 65-nm CMOS. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 296–300. [Google Scholar] [CrossRef]
- D’Amico, S.; Spagnolo, A.; Donno, A.; Chironi, V.; Wambacq, P.; Baschirotto, A. A Low-Power Analog Baseband Section for 60-GHz Receivers in 90-nm CMOS. IEEE Trans. Microw. Theory Tech. 2014, 62, 1724–1735. [Google Scholar] [CrossRef]
- Wang, Y.; Hull, C.; Murata, G.; Ravid, S. A linear-in-dB analog baseband circuit for low power 60GHz receiver in standard 65nm CMOS. In Proceedings of the 2013 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Seattle, WA, USA, 2–4 June 2013; pp. 225–228. [Google Scholar] [CrossRef]
- Miyahara, M.; Sakaguchi, H.; Shimasaki, N.; Matsuzawa, A. An 84 mW 0.36 mm2 analog baseband circuits for 60 GHz wireless transceiver in 40 nm CMOS. In Proceedings of the 2012 IEEE Radio Frequency Integrated Circuits Symposium, Montreal, QC, Canada, 17–19 June 2012; pp. 495–498. [Google Scholar] [CrossRef]
- Fan, C.; Chen, Z.; Liu, Z.; Li, X.; Li, X.; Qi, Q.; Gu, W.; Wang, X. Design of a Wideband dB-Linear Variable Gain Amplifier With Continuous Gain Adjusting in 90-nm CMOS Technology. IEEE Access 2021, 9, 152646–152656. [Google Scholar] [CrossRef]
- Dong, Y.; Kong, L.; Boon, C.C.; Yang, K.; Liu, Z.; Li, C.; Zhou, A. A Wideband dB-Linear Variable-Gain Amplifier With a Compensated Negative Pseudo-Exponential Generation Technique. IEEE Trans. Microw. Theory Tech. 2021, 69, 2809–2821. [Google Scholar] [CrossRef]
- Ray, S.; Hella, M.M. A 10 Gb/s inductorless AGC amplifier with 40 dB linear variable gain control in 0.13 μm CMOS. IEEE J. Solid State Circuits 2016, 51, 440–456. [Google Scholar] [CrossRef]
- Liu, H.; Boon, C.C.; He, X.; Zhu, X.; Yi, X.; Kong, L.; Heimlich, M.C. A wideband analog-controlled variable-gain amplifier with dB-linear characteristic for high-frequency applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 533–540. [Google Scholar] [CrossRef]
- Elwan, H.; Tekin, A.; Pedrotti, K. A Differential-Ramp Based 65 dB-Linear VGA Technique in 65 nm CMOS. IEEE J. Solid-State Circuits 2009, 44, 2503–2514. [Google Scholar] [CrossRef]
- Baghtash, H.F. A 37-μW, binary-weighted PGA based on a novel degeneration transistor-ladder. IEEE Trans. Circuits Syst. II Exp. Briefs 2018, 65, 36–40. [Google Scholar] [CrossRef]
- Wang, L.-S.; Ku, P.-C.; Ko, P.-T.; Chung, C.-J.; Lu, L.-H. A 40.4-dB range, 0.73-dB step, and 0.07-dB error programmable gain amplifier using gain error shifting technique. IEEE Trans. Circuits Syst. II Exp. Briefs 2019, 66, 1109–1113. [Google Scholar] [CrossRef]
- Kumar, T.B.; Ma, K.; Yeo, K.S. A 7.9-mW 5.6-GHz Digitally Controlled Variable Gain Amplifier With Linearization. IEEE Trans. Microw. Theory Tech. 2012, 60, 3482–3490. [Google Scholar] [CrossRef]
- Kang, S.-Y.; Ryu, S.-T.; Park, C.-S. A Precise Decibel-Linear Programmable Gain Amplifier Using a Constant Current-Density Function. IEEE Trans. Microw. Theory Tech. 2012, 60, 2843–2850. [Google Scholar] [CrossRef]
- Yamaji, T.; Kanou, N.; Itakura, T. A temperature-stable CMOS variable-gain amplifier with 80-dB linearly controlled gain range. IEEE J. Solid-State Circuits 2002, 37, 553–558. [Google Scholar] [CrossRef]
- Lee, H.D.; Lee, K.A.; Hong, S. A Wideband CMOS Variable Gain Amplifier With an Exponential Gain Control. IEEE Trans. Microw. Theory Tech. 2007, 55, 1363–1373. [Google Scholar] [CrossRef]
- Song, X.; Lu, Z.; Cai, L.; Yu, X.-P.; Yeo, K.-S.; Chen, J.-M. A Wideband dB-Linear VGA With Temperature Compensation and Active Load. IEEE Trans. Circuits Syst. I Reg. Pap. 2019, 66, 3279–3287. [Google Scholar] [CrossRef]
- Choi, I.; Seo, H.; Kim, B. Accurate dB-Linear Variable Gain Amplifier With Gain Error Compensation. IEEE J. Solid-State Circuits 2013, 48, 456–464. [Google Scholar] [CrossRef]
- Abdelfattah, K.M.; Soliman, A.M. Variable gain amplifiers based on a new approximation method to realize the exponential function. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 1348–1354. [Google Scholar] [CrossRef]
- Zheng, Y.; Yan, J.; Xu, Y.P. A CMOS VGA With DC Offset Cancellation for Direct-Conversion Receivers. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 103–113. [Google Scholar] [CrossRef]
- Wang, H.; Feng, G.; Wang, Y. A Wideband Analog Baseband with Accurate dB-Linear Characteristic in 40nm CMOS. In Proceedings of the 2023 IEEE MTT-S International Wireless Symposium (IWS), Qingdao, China, 14–17 May 2023; pp. 1–3. [Google Scholar] [CrossRef]
- Razavi, B. The Active Inductor [A Circuit for All Seasons]. IEEE Solid-State Circuits Mag. 2020, 12, 7–11. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, X.; Boon, C.C.; He, X. Cell-Based Variable-Gain Amplifiers With Accurate dB-Linear Characteristic in 0.18 µm CMOS Technology. IEEE J. Solid-State Circuits 2015, 50, 586–596. [Google Scholar] [CrossRef]
- Kong, L.; Liu, H.; Zhu, X.; Boon, C.C.; Li, C.; Liu, Z.; Yeo, K.S. Design of a Wideband Variable-Gain Amplifier With Self-Compensated Transistor for Accurate dB-Linear Characteristic in 65 nm CMOS Technology. IEEE Trans. Circuits Syst. I Reg. Pap. 2020, 67, 4187–4198. [Google Scholar] [CrossRef]
- Wang, Y.; Afshar, B.; Ye, L.; Gaudet, V.C.; Niknejad, A.M. Design of a Low Power, Inductorless Wideband Variable-Gain Amplifier for High-Speed Receiver Systems. IEEE Trans. Circuits Syst. I Reg. Pap. 2012, 59, 696–707. [Google Scholar] [CrossRef]
- De Matteis, M.; Galante, N.; Fary, F.; Vallicelli, E.; Baschirotto, A. 64 dB Dynamic-Range 810 μW 90 MHz Fully-Differential Flipped-Source-Follower Analog Filter in 28nm-CMOS. IEEE Trans. Circuits Syst. II Exp. Briefs 2021, 68, 3068–3072. [Google Scholar] [CrossRef]
- De Matteis, M.; Pezzotta, A.; D’Amico, S.; Baschirotto, A. A 33 MHz 70 dB-SNR super-source-follower-based low-pass analog filter. IEEE J. Solid-State Circuits 2015, 50, 1516–1524. [Google Scholar] [CrossRef]
- Wang, Y.; Afshar, B.; Cheng, T.-Y.; Gaudet, V.; Niknejad, A.M. A 2.5 mW inductorless wideband VGA with dual feedback DC-offset correction in 90nm CMOS technology. In Proceedings of the 2008 IEEE Radio Frequency Integrated Circuits Symposium, Atlanta, GA, USA, 15–17 June 2008; pp. 91–94. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, R.; Qi, H.; Wang, S.; Qiao, S.; Zhang, H.; Liu, L. Simultaneous Bandwidth-Extended and Precisely-Gain-Controlled dB-Linear PGA Based on Active Feedback and Binary-Weighted Switches. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4729–4733. [Google Scholar] [CrossRef]

| CMOS technology | 40 nm CMOS |
| Characteristic | dB-linear, wideband |
| Gain range (dB) | ≥40 dB |
| Bandwidth (GHz) | ≥2 GHz |
| dB-linear gain error (dB) | ≤±1 dB |
| Out of band rejection (dB) | >20 dB (at twice the bandwidth) |
| n | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Ac (dB) | 30 | 15 | 10 | 7.5 | 6 | 5 |
| BWc (GHz) | 4 | 6.2 | 7.8 | 9.2 | 10.4 | 11.4 |
| GBWc (dB·GHz) | 120 | 93 | 78 | 69 | 62.4 | 57 |
| This Work | [13] 2014 | [14] 2013 | [15] 2012 | |
|---|---|---|---|---|
| Technology | 40 nm | 90 nm | 65 nm | 40 nm |
| dB-linear characteristic | Yes | No | No | No |
| LPF order | 4th | 6th | 3th | 5th |
| Gain range (dB) | –18~26 | 0.1~19.6 | 3~31 | 0~40 |
| Bandwidth (GHz) | 4 | 0.915 | 0.98 | 1 |
| IP1dB (dBm) | –30~–5.7 | N/A | –31~–4 | N/A |
| Power (mW) | 11.3 | 9.5 | 32 | 18 |
| Area (mm2) | 0.045 | 0.156 | 0.2 | 0.36 |
| This Work | [9] 2018 | [10] 2023 | [22] 2021 | [23] 2016 | [27] 2019 | [34] 2020 | |
|---|---|---|---|---|---|---|---|
| CMOS Technology | 40 nm | 65 nm | 55 nm | 40 nm | 130 nm | 55 nm | 65 nm |
| Gain range (dB) | 44 (–18~26) | 40 (–18~22) | 42.2 (–30~12.2) | 51 (–34~17) | 40 (–15~25) | 45 (–31~14) | 40 (–19~21) |
| dB-linear gain error (dB) | ±0.5 | ±1 | ±0.79 | ±1 | ±1 | ±0.85 | ±1 |
| Bandwidth (GHz) | 4 | 7 | 0.14 | 7 | 5 | 0.74 | 4 |
| IP1dB (dBm) | –30~–5.7 | N/A | –15~0 | N/A | N/A | N/A | –13~–8 |
| Power (mW) | 11.3 (8.3 *) | 28 | 4.5 | 27 | 50 | 2.49 | 3.5 |
| NF (dB) | 16~52 ** | N/A | 21.3 | 30.5 | N/A | 30 | 17~47 |
| Area (mm2) | 0.045 (0.027 *) | 0.045 | 0.026 | 0.038 | 0.4 | 0.033 | 0.012 |
| FOM | 1570.6 | 222 | 63.9 | 347.4 | 10 | 476.7 | 3808.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Wang, H.; Wang, Y. A Wideband dB-Linear Analog Baseband for a Millimeter-Wave Receiver with Error Compensation in 40 nm CMOS Technology. Electronics 2024, 13, 5012. https://doi.org/10.3390/electronics13245012
Hu S, Wang H, Wang Y. A Wideband dB-Linear Analog Baseband for a Millimeter-Wave Receiver with Error Compensation in 40 nm CMOS Technology. Electronics. 2024; 13(24):5012. https://doi.org/10.3390/electronics13245012
Chicago/Turabian StyleHu, Shiwei, Hao Wang, and Yanjie Wang. 2024. "A Wideband dB-Linear Analog Baseband for a Millimeter-Wave Receiver with Error Compensation in 40 nm CMOS Technology" Electronics 13, no. 24: 5012. https://doi.org/10.3390/electronics13245012
APA StyleHu, S., Wang, H., & Wang, Y. (2024). A Wideband dB-Linear Analog Baseband for a Millimeter-Wave Receiver with Error Compensation in 40 nm CMOS Technology. Electronics, 13(24), 5012. https://doi.org/10.3390/electronics13245012






