Power-Law Negative Group Delay Filters
Abstract
1. Introduction
2. Integer-Order Negative Group Delay Filter Transfer Functions
3. Non-Integer Negative Group Delay Filter Transfer Functions
4. Implementations of the Power-Law Bilinear Negative Group Delay Filters
- (a)
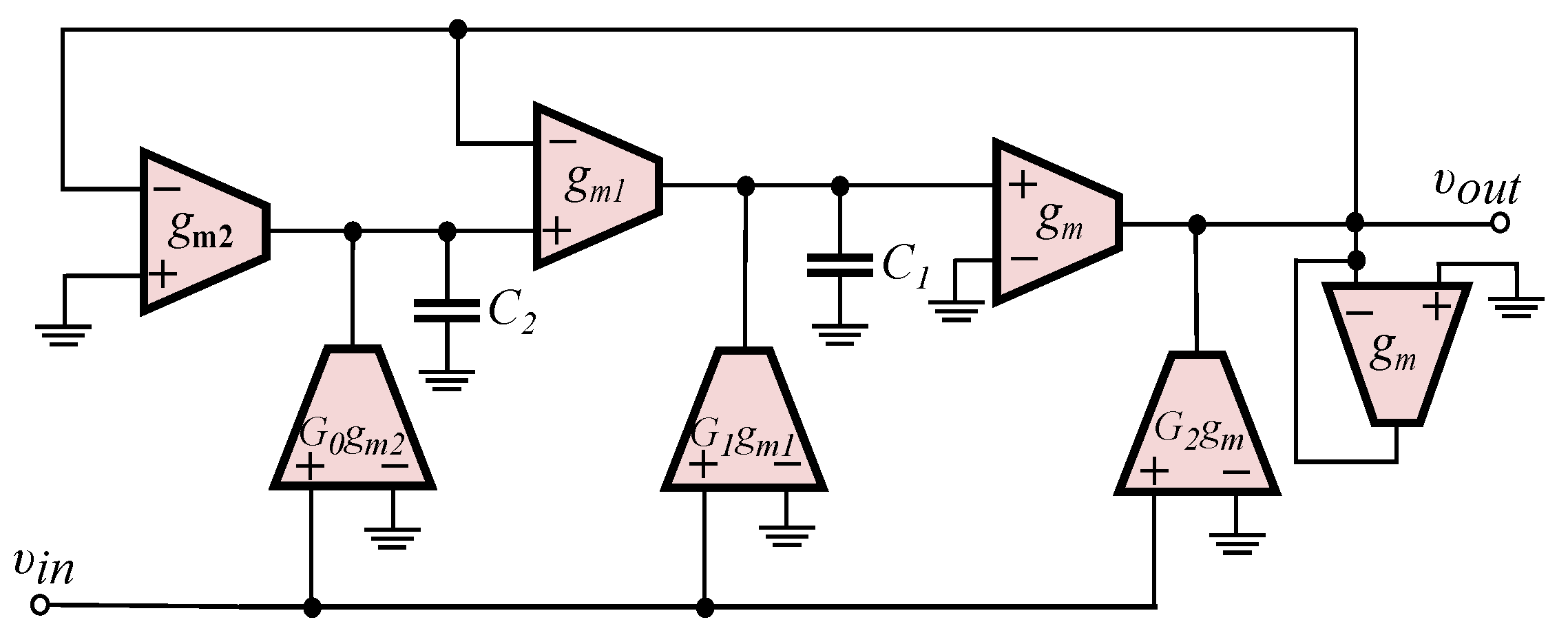
- Employing the functional block diagram of a multi-feedback topology, e.g., the Inverse-Follow-the-Leader Feedback (IFLF), and using suitable active elements that offer electronic adjustment of the required time constants and scaling factors [32].Choosing Operational Transconductance Amplifiers (OTAs) as active elements, the resulting structure is depicted in Figure 4, with the realized transfer function being
- (b)
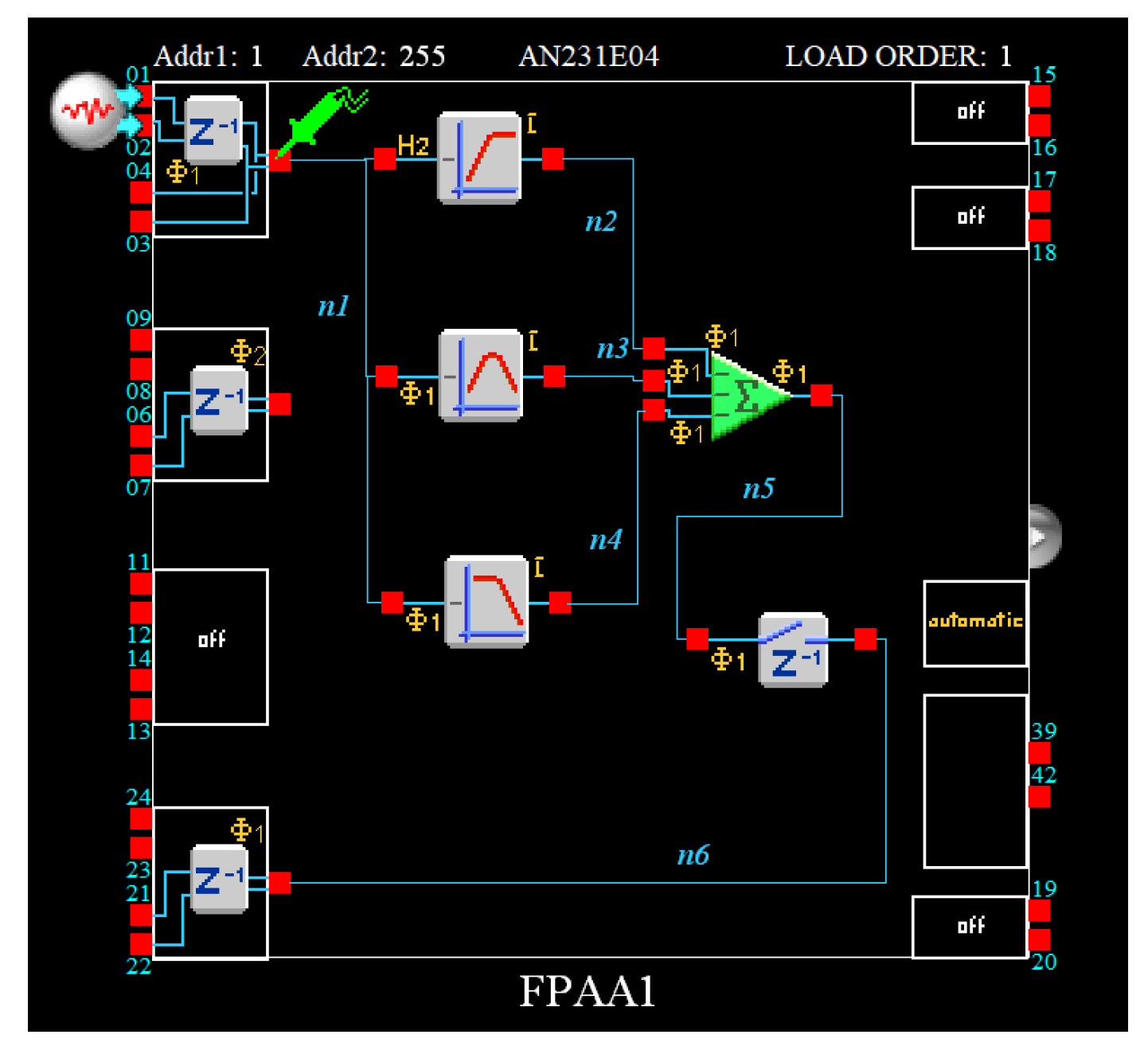
- Employing a Field Programmable Analog Array (FPAA) device, such as the Anadigm AN231E04 device [35,36], where programmability is achieved through the utilization of the switched-capacitor technique. For this purpose, the transfer function in (26) is alternatively expressed as a sum of high-pass, band-pass, and low-pass biquad filters
- (c)
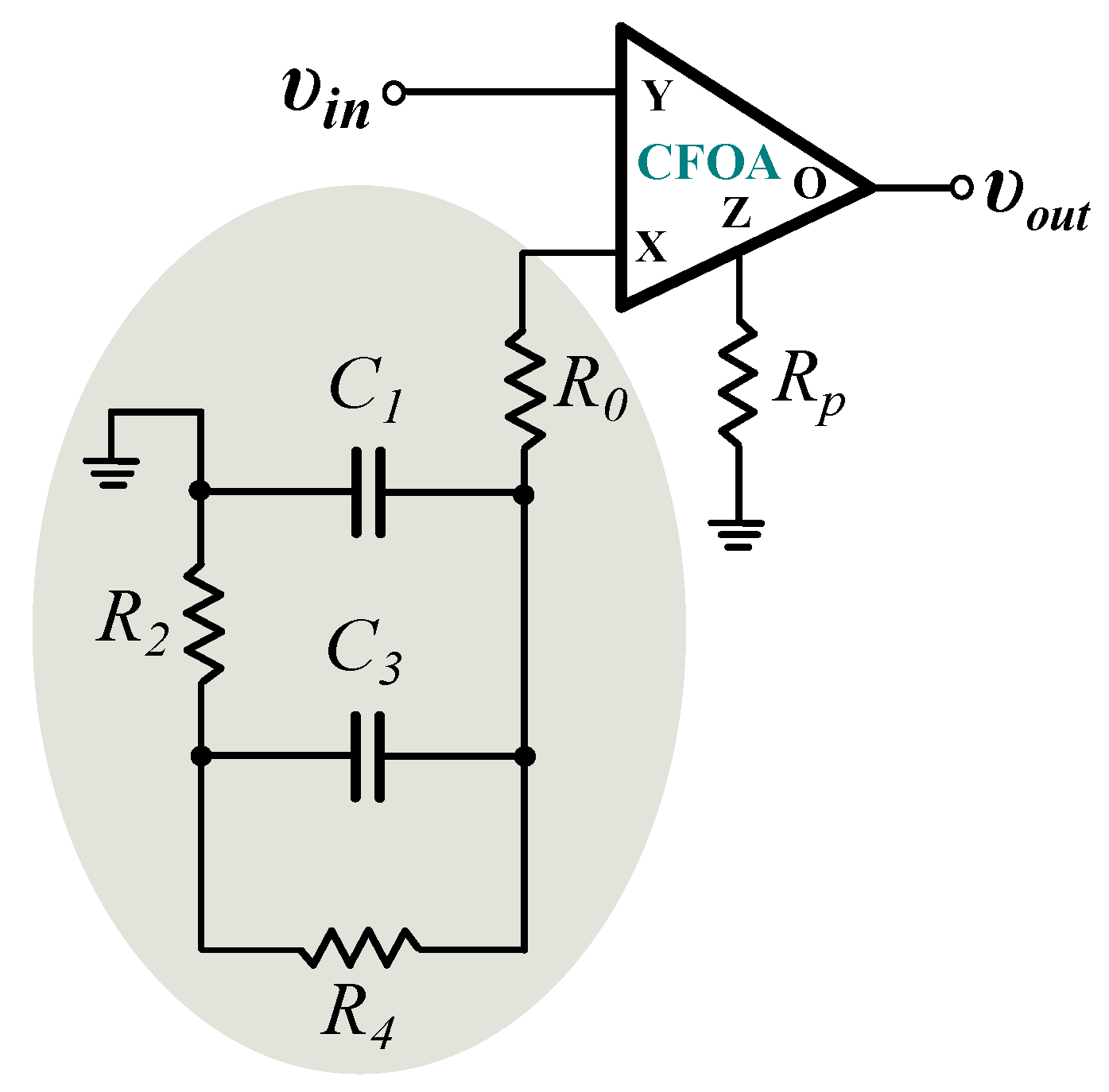
- Employing the concept in [37], the transfer function in (26) is expressed as a ratio of two impedances, i.e., . According to [31], the choice of the impedances depends on the transfer function that will be realized. Additionally, in order for the impedance to be realizable by a Cauer or Foster network, its frequency response must have the form of a low-pass filter. Inspecting the gain responses in Figure 3, it is obtained that the response of the filter has the form of an inverse high-pass filter in the range of interest. Therefore, the impedance will be implemented by a Cauer/Foster network, and will be equal to , while , with being an ohmic resistor with an arbitrary value. The resulting scheme is demonstrated in Figure 6, where the Cauer type-I network is utilized for implementing the impedance . The corresponding design equations are summarized in (30) as,where are the coefficients of the continued fraction expansion of the transfer function [38].
5. Simulation and Experimental Results
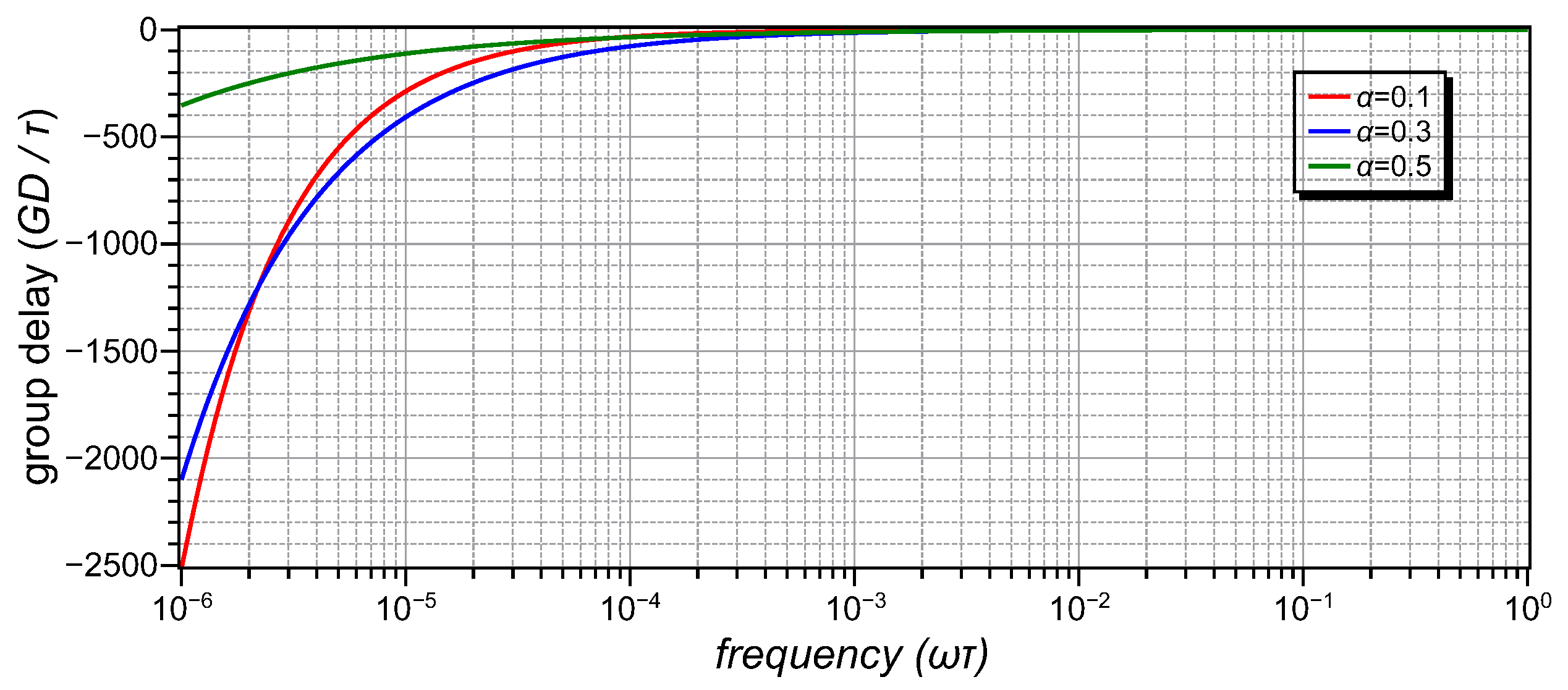
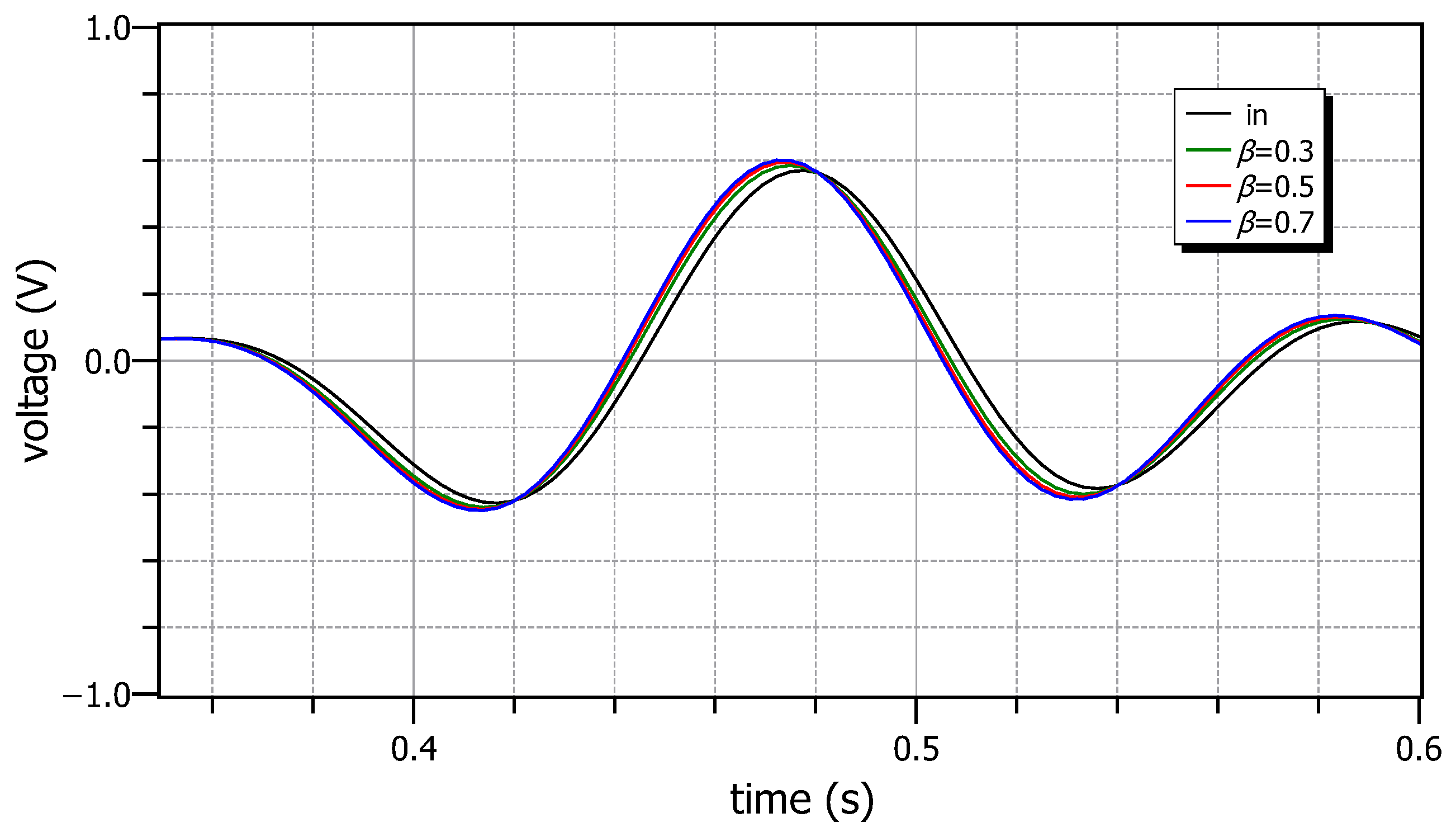
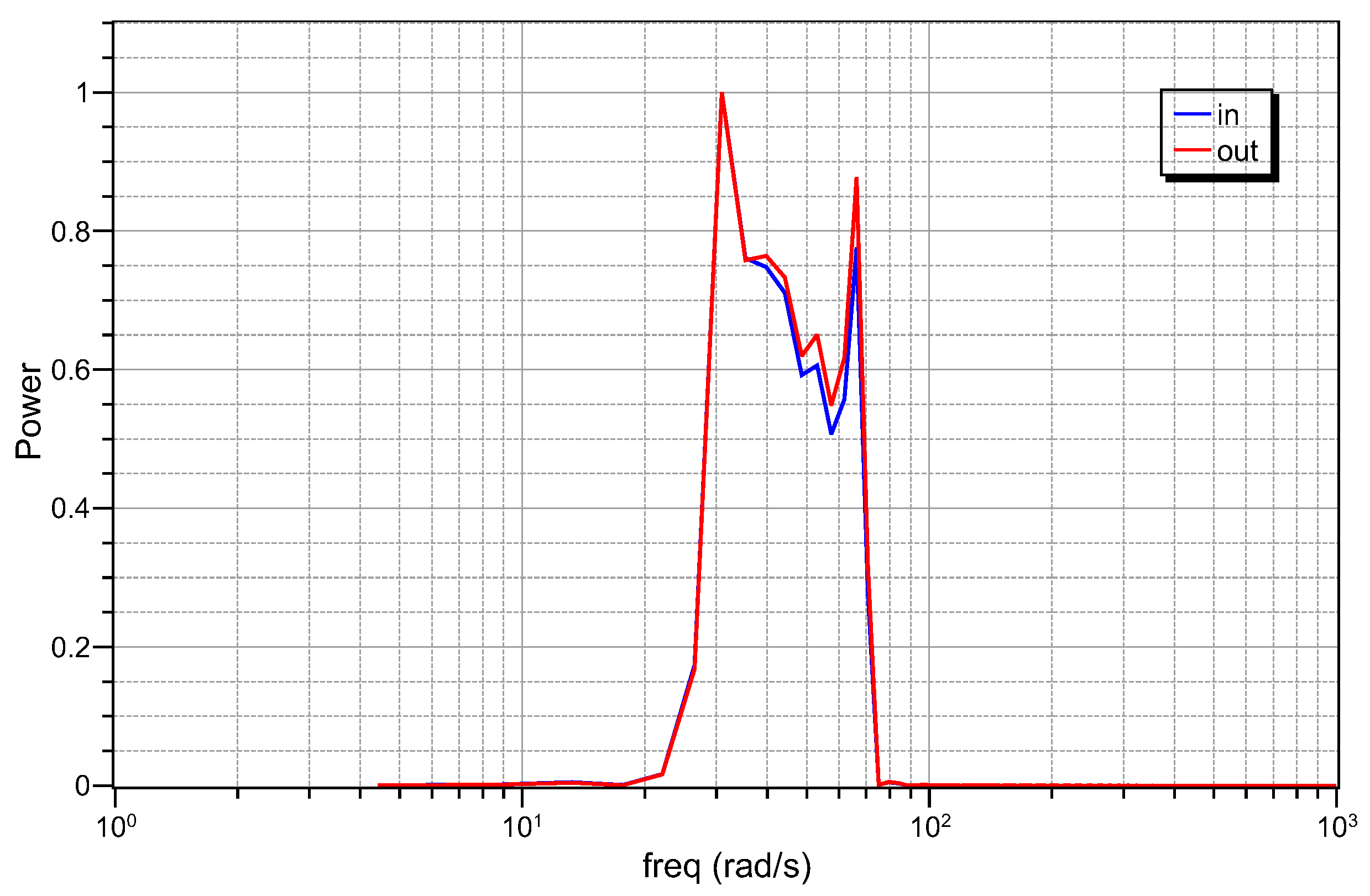
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMS | Austria Mikro Systeme |
| CAMs | Configured Analog Modules |
| CFOA | Current Feedback Operational Amplifier |
| CMOS | Complimentary Metal-Oxide Semiconductor |
| ECG | Electrocardiogram |
| FO | Fractional-Order |
| FPAA | Field Programmable Analog Array |
| IC | Integrated Circuit |
| IFLF | Inverse-Follow-the-Leader-Feedback |
| LHP | Left Half-Plane |
| MOS | Metal-Oxide Semiconductor |
| NGD | Negative Group Delay |
| OTA | Operational Transconductance Amplifier |
| RF | Radio Frequency |
| RC | Resistor Capacitor |
References
- Mitchell, M.W.; Chiao, R.Y. Negative group delay and ’fronts’ in a causal system: An experiment with very low frequency bandpass amplifiers. Phys. Lett. A 1997, 230, 133–138. [Google Scholar] [CrossRef]
- Mitchell, M.W.; Chiao, R.Y. Causality and negative group delays in a simple bandpass amplifier. Am. J. Phys. 1998, 66, 14–19. [Google Scholar] [CrossRef]
- Solli, D.; Chiao, R.; Hickmann, J. Superluminal effects and negative group delays in electronics, and their applications. Phys. Rev. E 2002, 66, 056601. [Google Scholar] [CrossRef]
- Kitano, M.; Nakanishi, T.; Sugiyama, K. Negative group delay and superluminal propagation: An electronic circuit approach. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 43–51. [Google Scholar] [CrossRef]
- Munday, J.; Henderson, R. Superluminal time advance of a complex audio signal. Appl. Phys. Lett. 2004, 85, 503–505. [Google Scholar] [CrossRef]
- Voss, H.U.; Stepp, N. A negative group delay model for feedback-delayed manual tracking performance. J. Comput. Neurosci. 2016, 41, 295–304. [Google Scholar] [CrossRef]
- Voss, H.U. A delayed-feedback filter with negative group delay. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 113113. [Google Scholar] [CrossRef] [PubMed]
- Pyragiene, T.; Pyragas, K. Design of a negative group delay filter via reservoir computing approach: Real-time prediction of chaotic signals. Phys. Lett. A 2019, 383, 3088–3094. [Google Scholar] [CrossRef]
- Wan, F.; Miao, X.; Ravelo, B.; Yuan, Q.; Cheng, J.; Ji, Q.; Ge, J. Design of multi-scale negative group delay circuit for sensors signal time-delay cancellation. IEEE Sens. J. 2019, 19, 8951–8962. [Google Scholar] [CrossRef]
- Pyragiene, T.; Pyragas, K. Anticipatory synchronization via low-dimensional filters. Phys. Lett. A 2017, 381, 1893–1898. [Google Scholar] [CrossRef]
- Wan, F.; Yuan, Z.; Ravelo, B.; Ge, J.; Rahajandraibe, W. Low-pass NGD voice signal sensoring with passive circuit. IEEE Sens. J. 2020, 20, 6762–6775. [Google Scholar] [CrossRef]
- Chou, P.Y.; Chien, J.F.; Chen, K.S.; Huang, Y.T.; Chen, C.C.; Chan, C. Anticipation and negative group delay in a retina. Phys. Rev. E 2021, 103, L020401. [Google Scholar] [CrossRef]
- Baloglu, O.; Cicekoglu, O.; Herencsar, N. OTA-C signal delay compensation circuit for transimpedance-mode audio signal processing systems. Integration 2023, 90, 205–213. [Google Scholar] [CrossRef]
- Baloglu, O.; Cicekoglu, O.; Herencsar, N. Single CFOA-based active Negative Group Delay circuits for signal anticipation. Eng. Sci. Technol. Int. J. 2023, 48, 101590. [Google Scholar] [CrossRef]
- Ravelo, B.; Pérennec, A.; Le Roy, M.; Boucher, Y.G. Active microwave circuit with negative group delay. IEEE Microw. Wirel. Components Lett. 2007, 17, 861–863. [Google Scholar] [CrossRef]
- Ravelo, B. Synthesis of RF circuits with negative time delay by using LNA. Adv. Electromagn. 2013, 2, 44–54. [Google Scholar] [CrossRef]
- Ravelo, B. Similitude between the NGD function and filter gain behaviours. Int. J. Circuit Theory Appl. 2014, 42, 1016–1032. [Google Scholar] [CrossRef]
- Xiao, J.K.; Wang, Q.F.; Ma, J.G. Negative group delay circuits and applications: Feedforward amplifiers, phased-array antennas, constant phase shifters, non-foster elements, interconnection equalization, and power dividers. IEEE Microw. Mag. 2021, 22, 16–32. [Google Scholar] [CrossRef]
- Wan, F.; Gu, T.; Li, B.; Li, B.; Rahajandraibe, W.; Guerin, M.; Lalléchère, S.; Ravelo, B. Design and Experimentation of Inductorless Low-Pass NGD Integrated Circuit in 180-nm CMOS Technology. IEEE Transcations Comput. Aided Des. Integr. Circuits Syst. 2022, 41, 4965–4974. [Google Scholar] [CrossRef]
- Ravelo, B.; Bilal, H.; Rakotonandrasana, S.; Guerin, M.; Haddad, F.; Ngoho, S.; Rahajandraibe, W. Transient Characterization of New Low-Pass Negative Group Delay RC-Network. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 126–130. [Google Scholar] [CrossRef]
- Nakanishi, T.; Sugiyama, K.; Kitano, M. Demonstration of negative group delays in a simple electronic circuit. Am. J. Phys. 2002, 70, 1117–1121. [Google Scholar] [CrossRef]
- Ravelo, B. Methodology of elementary negative group delay active topologies identification. IET Circuits Devices Syst. 2013, 7, 105–113. [Google Scholar] [CrossRef]
- Ravelo, B. First-order low-pass negative group delay passive topology. Electron. Lett. 2016, 52, 124–126. [Google Scholar] [CrossRef]
- Abuelmaatti, M.T.; Khalifa, Z.J. A new CFOA-based negative group delay cascadable circuit. Analog Integr. Circuits Signal Process. 2018, 95, 351–355. [Google Scholar] [CrossRef]
- Wan, F.; Wang, L.; Ji, Q.; Ravelo, B. Canonical transfer function of band-pass NGD circuit. IET Circuits Devices Syst. 2019, 13, 125–130. [Google Scholar] [CrossRef]
- Randriatsiferana, R.; Gan, Y.; Wan, F.; Rahajandraibe, W.; Vauché, R.; Murad, N.M.; Ravelo, B. Study and experimentation of a 6-dB attenuation low-pass NGD circuit. Analog. Integr. Circuits Signal Process. 2022, 110, 105–114. [Google Scholar] [CrossRef]
- Yuan, A.; Fang, S.; Wang, Z.; Liu, H. A novel multifunctional negative group delay circuit for realizing band-pass, high-pass and low-pass. Electronics 2021, 10, 1742. [Google Scholar] [CrossRef]
- Maundy, B.; Elwakil, A.; Psychalinos, C. Systematic design of negative group delay circuits. AEU Int. J. Electron. Commun. 2024, 174, 155060. [Google Scholar] [CrossRef]
- Banchuin, R. On the fractional domain analysis of negative group delay circuits. Int. J. Circuit Theory Appl. 2023; in press. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Power law filters: A new class of fractional-order filters without a fractional-order Laplacian operator. AEU-Int. J. Electron. Commun. 2021, 129, 153537. [Google Scholar] [CrossRef]
- Nako, J.; Psychalinos, C.; Elwakil, A.S. One active element implementation of fractional-order Butterworth and Chebyshev filters. AEU-Int. J. Electron. Commun. 2023, 168, 154724. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A. Design of CMOS Analog Integrated Fractional-Order Circuits: Applications in Medicine and Biology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Shen, H.; Wang, Z. A Circuit Principle and Simulation Test for Negative Group Delay. Int. J. Adv. Netw. Monit. Control. 2022, 7, 46–57. [Google Scholar] [CrossRef]
- Nako, J.; Psychalinos, C.; Elwakil, A.S.; Minaei, S. Non-Integer Order Generalized Filters Designs. IEEE Access 2023, 11, 116846–116859. [Google Scholar] [CrossRef]
- Anadigm. AN231E04 dpASP: The AN231E04 dpASP Dynamically Reconfigurable Analog Signal Processor. Available online: https://www.anadigm.com (accessed on 4 December 2023).
- Hassanein, A.M.; Madian, A.H.; Radwan, A.G.; Said, L.A. On the Design Flow of the Fractional-Order Analog Filters between FPAA Implementation and Circuit Realization. IEEE Access 2023, 11, 29199–29214. [Google Scholar] [CrossRef]
- Nako, J.; Psychalinos, C.; Elwakil, A.S. A 1 + α Order Generalized Butterworth Filter Structure and Its Field Programmable Analog Array Implementation. Electronics 2023, 12, 1225. [Google Scholar] [CrossRef]
- Tsirimokou, G. A systematic procedure for deriving RC networks of fractional-order elements emulators using MATLAB. AEU-Int. J. Electron. Commun. 2017, 78, 7–14. [Google Scholar] [CrossRef]
- Analog Devices. AD844 60 MHz 2000 V/us Monolithic Op Amp with Quad Low Noise, Data Sheet, rev. G. Available online: https://www.analog.com/en/products/ad844.html (accessed on 26 November 2023).
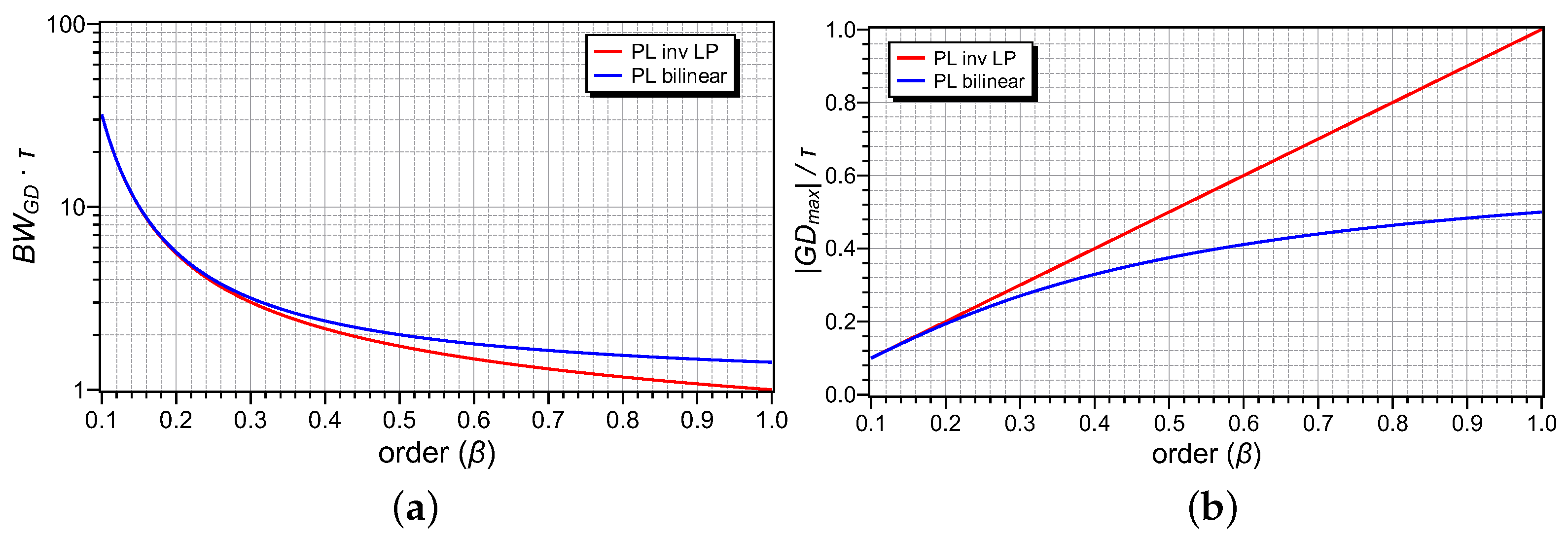
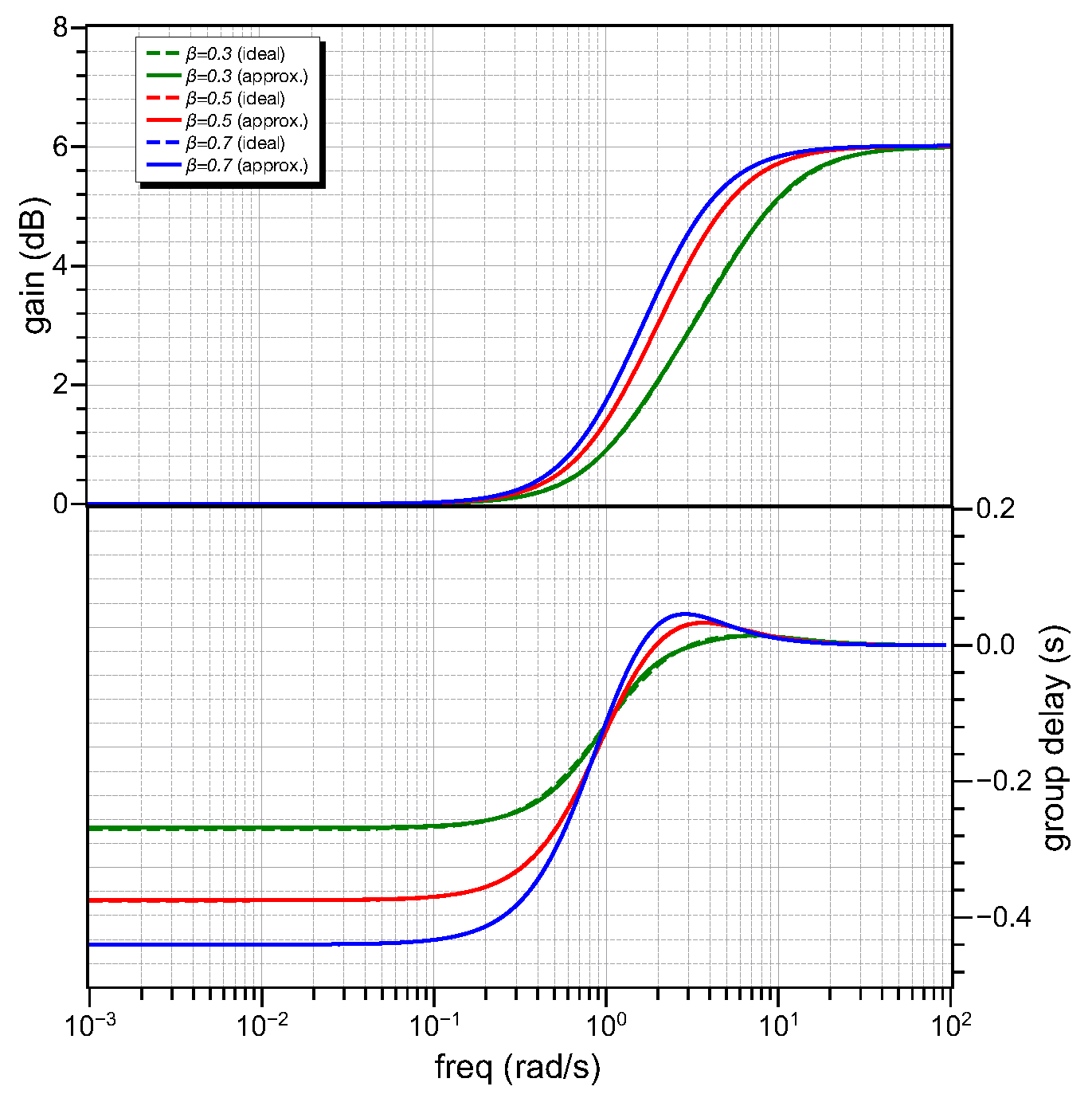


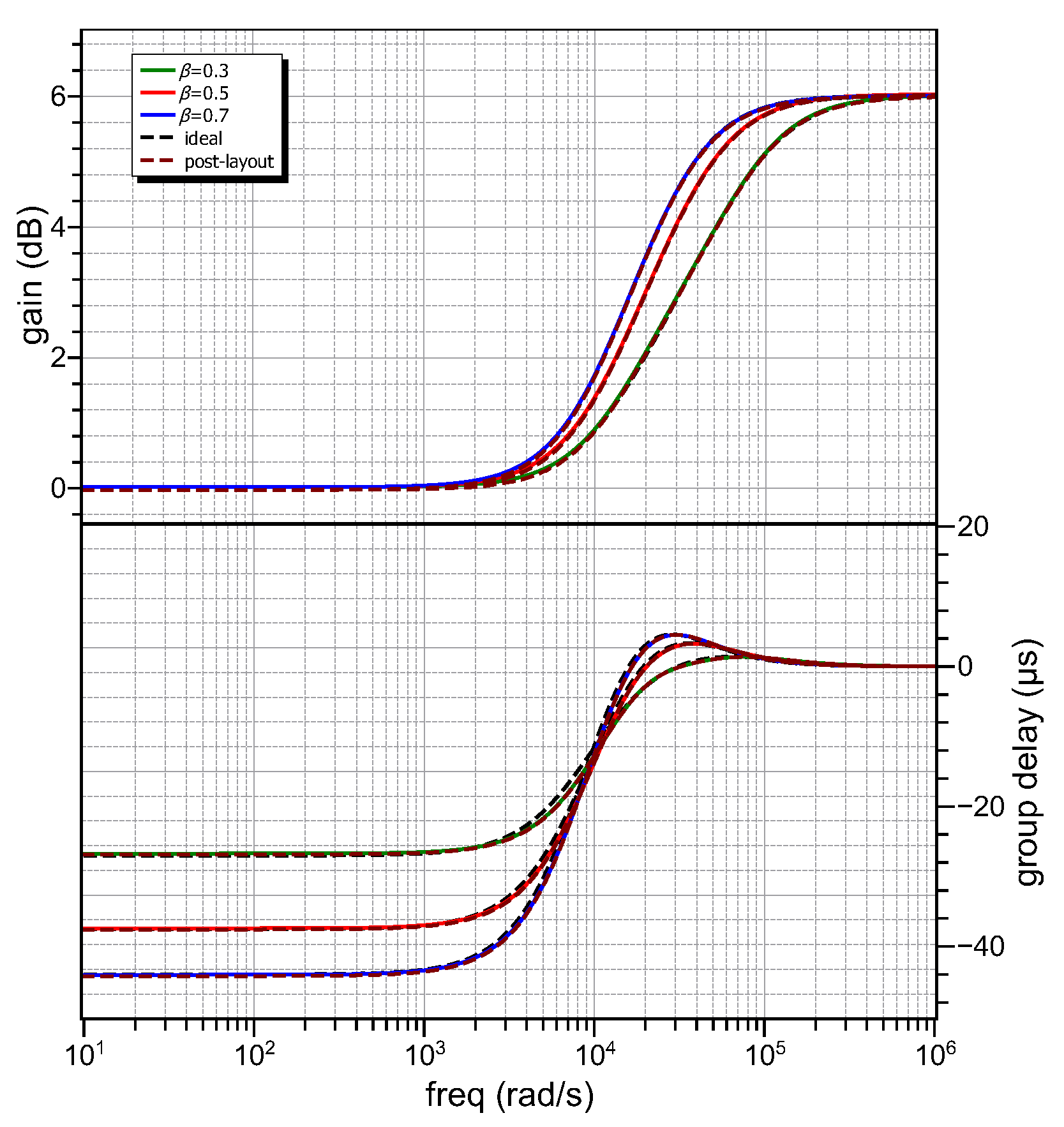


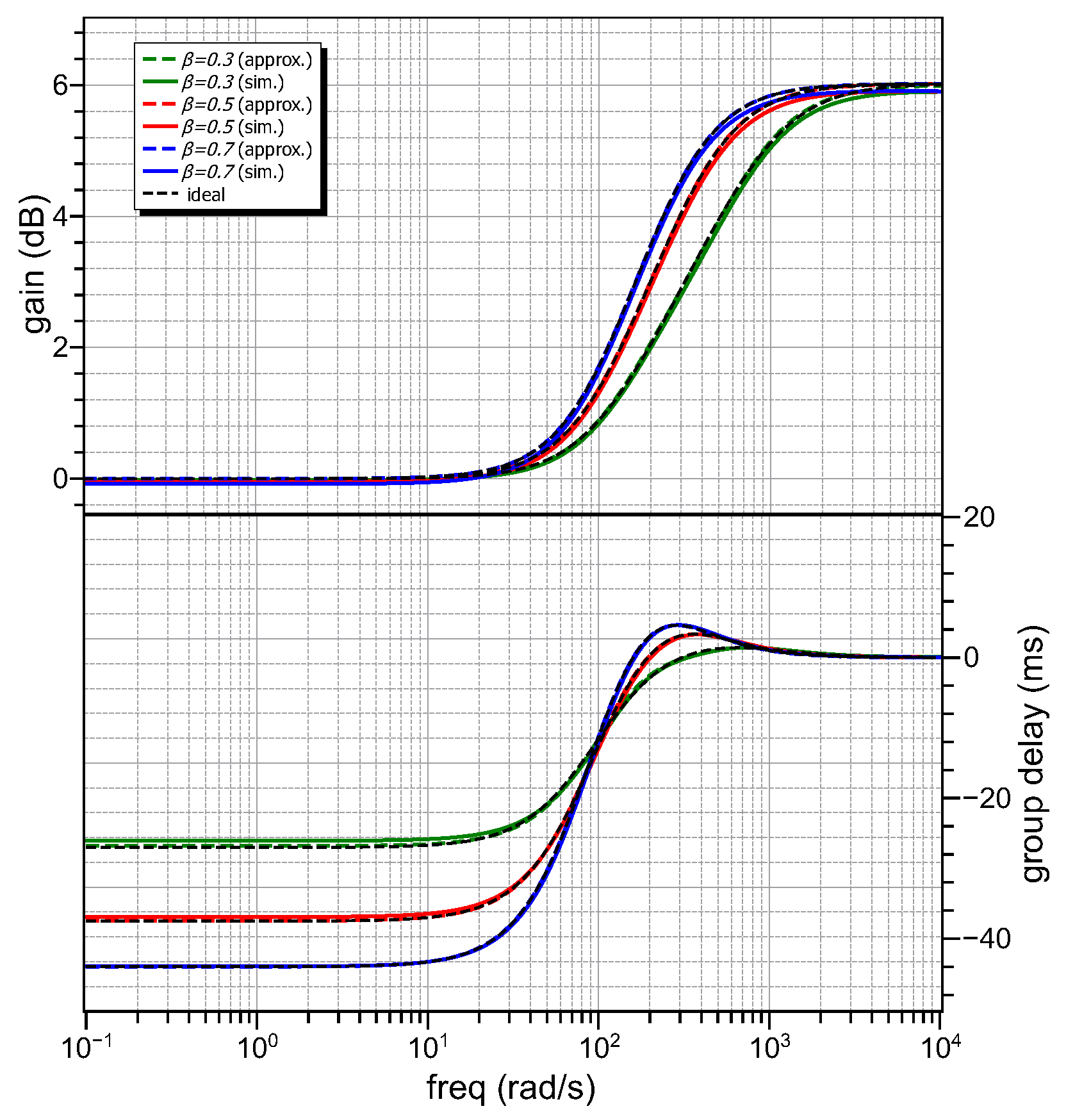


| Type of Filter | Bandwidth () | Max. GD () |
|---|---|---|
| inv. IO-LP | ||
| inv. PL-LP | ||
| IO-bilinear | ||
| PL-bilinear |
| Parameter | |||
|---|---|---|---|
| (S) | 87.07 | 50.45 | 40.20 |
| (S) | 73.29 | 54.38 | 46.74 |
| 1 | 1 | 1 | |
| 1.393 | 1.407 | 1.411 | |
| 1.996 | 1.999 | 2 | |
| (A) | 9.81 | 4.88 | 3.72 |
| (A) | 7.81 | 5.35 | 4.45 |
| Element | |||
|---|---|---|---|
| () | 4990 | 4990 | 4990 |
| () | 3570 | 4320 | 4750 |
| () | 1370 | 649 | 261 |
| (F) | 0.75 | 1.33 | 1.69 |
| (F) | 4.12 | 9.76 | 25.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nako, J.; Psychalinos, C.; Elwakil, A.S.; Maundy, B.J. Power-Law Negative Group Delay Filters. Electronics 2024, 13, 522. https://doi.org/10.3390/electronics13030522
Nako J, Psychalinos C, Elwakil AS, Maundy BJ. Power-Law Negative Group Delay Filters. Electronics. 2024; 13(3):522. https://doi.org/10.3390/electronics13030522
Chicago/Turabian StyleNako, Julia, Costas Psychalinos, Ahmed S. Elwakil, and Brent J. Maundy. 2024. "Power-Law Negative Group Delay Filters" Electronics 13, no. 3: 522. https://doi.org/10.3390/electronics13030522
APA StyleNako, J., Psychalinos, C., Elwakil, A. S., & Maundy, B. J. (2024). Power-Law Negative Group Delay Filters. Electronics, 13(3), 522. https://doi.org/10.3390/electronics13030522








