Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach
Abstract
:1. Introduction
1.1. Literature Review
1.2. Motivation and Contributions
- Asymptotic stability is ensured for the considered multiagent systems through novel design and analysis in a discrete-time setting. In particular, a constructed Lyapunov candidate is used by using both logarithmic and quadratic functions to rigorously prove the stability of the proposed control strategies. This contributes to the reliability and predictability of uncertain multiagent systems in executing complex tasks in the presence of coupled dynamics;
- A novel approach is adopted by integrating a user-assigned Laplacian matrix and nullspace in the design of the control algorithms. This incorporation significantly enhances the flexibility in agent positioning and the ability to induce cooperative behaviors among agents. It allows for a more tailored and efficient multiagent system configuration, catering to the specific needs and constraints of various applications;
- Discrete observer dynamics is introduced into the control architectures to manage unmeasurable coupled dynamics in multiagent systems effectively. An extensive validation of the proposed algorithm is provided by including detailed proofs of all the results, ensuring a rigorous verification of the theoretical foundations. The observer dynamics addition allows for more accurate and stable control and tracking, further enhancing the system’s adaptability and performance in dynamic environments;
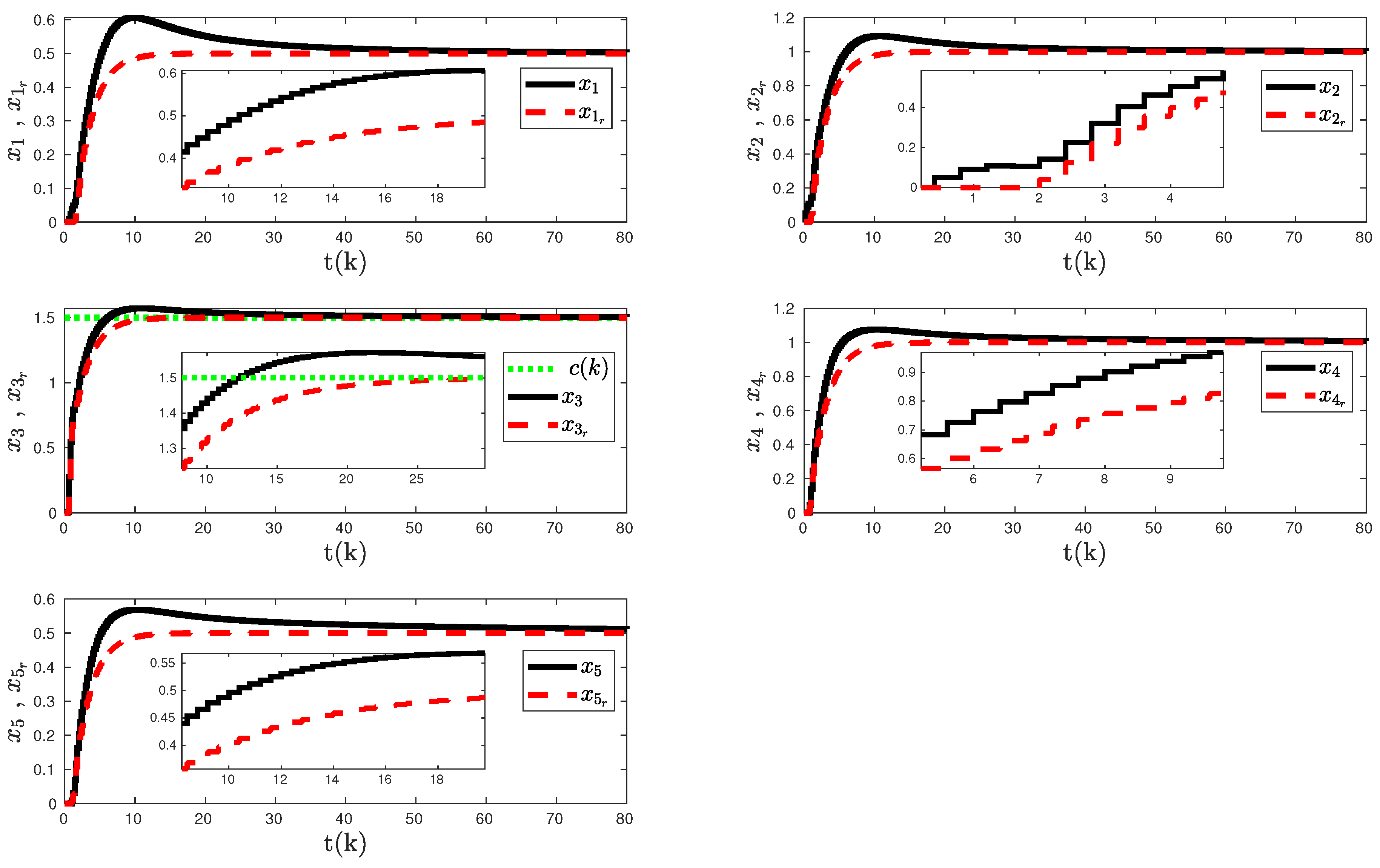
- A detailed simulation study is given to demonstrate the effectiveness and practical applicability of our control strategies. The selected case in the illustrative numerical example shows that the standard discrete-time adaptive control in the absence of the observer dynamics cannot guarantee the reference state vector tracking; hence, the closed-loop dynamical system is not reliable. This result can be expected since there is no compensation for the coupled dynamics in the control design.
1.3. Organization
1.4. Notation and Mathematical Preliminaries
2. Adaptation for Agent-Based Uncertainty
3. Adaptation for Both Agent-Based Uncertainty and Coupled Dynamics
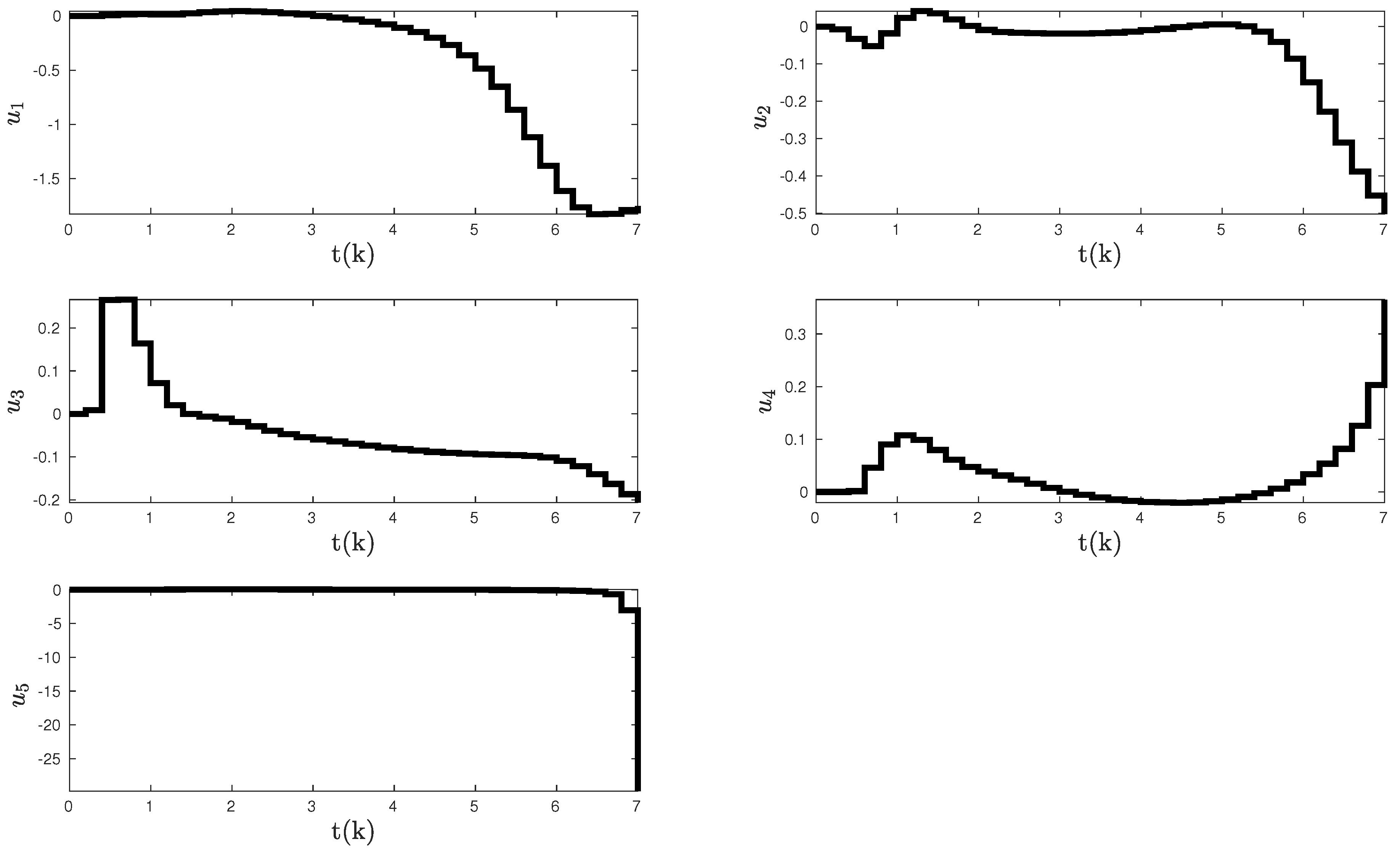
4. Illustrative Numerical Example Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Ren, W.; Atkins, E. Distributed multi-vehicle coordinated control via local information exchange. Int. J. Robust Nonlinear Control 2007, 17, 1002–1033. [Google Scholar] [CrossRef]
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Lewis, F.L.; Zhang, H.; Hengster-Movric, K.; Das, A. Cooperative Control of Multi-Agent Systems: Optimal and Adaptive Design Approaches; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rohrs, C.; Valavani, L.; Athans, M.; Stein, G. Robustness of continuous-time adaptive control algorithms in the presence of unmodeled dynamics. IEEE Trans. Autom. Control 1985, 30, 881–889. [Google Scholar] [CrossRef]
- Nguyen, N.; Urnes, J. Aeroelastic modeling of elastically shaped aircraft concept via wing shaping control for drag reduction. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Nobleheart, W.; Chakravarthy, A.; Nguyen, N. Active wing shaping control of an elastic aircraft. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3059–3064. [Google Scholar]
- Pequito, S.D.; Kar, S.; Aguiar, A.P. A Framework for Structural Input/Output and Control Configuration Selection in Large-Scale Systems. IEEE Trans. Automat. Contr. 2016, 61, 303–318. [Google Scholar]
- Hou, Z.G.; Cheng, L.; Tan, M. Decentralized robust adaptive control for the multiagent system consensus problem using neural networks. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 39, 636–647. [Google Scholar]
- Das, A.; Lewis, F.L. Distributed adaptive control for synchronization of unknown nonlinear networked systems. Automatica 2010, 46, 2014–2021. [Google Scholar] [CrossRef]
- Yucelen, T.; Egerstedt, M. Control of multiagent systems under persistent disturbances. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 5264–5269. [Google Scholar]
- Yucelen, T.; Johnson, E.N. Control of multivehicle systems in the presence of uncertain dynamics. Int. J. Control 2013, 86, 1540–1553. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C.; Huang, J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances. Automatica 2017, 77, 133–142. [Google Scholar] [CrossRef]
- Sarsilmaz, S.B.; Yucelen, T. A Distributed Adaptive Control Approach for Heterogeneous Uncertain Multiagent Systems. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Dogan, K.M.; Gruenwald, B.C.; Yucelen, T.; Muse, J.A.; Butcher, E.A. Distributed adaptive control and stability verification for linear multiagent systems with heterogeneous actuator dynamics and system uncertainties. Int. J. Control 2018, 92, 2620–2638. [Google Scholar] [CrossRef]
- Pan, Y.; Ji, W.; Lam, H.K.; Cao, L. An improved predefined-time adaptive neural control approach for nonlinear multiagent systems. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Chen, L.; Liang, H.; Pan, Y.; Li, T. Human-in-the-loop consensus tracking control for UAV systems via an improved prescribed performance approach. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8380–8391. [Google Scholar] [CrossRef]
- Dogan, K.M.; Yucelen, T.; Ristevki, S.; Muse, J.A. Distributed adaptive control of uncertain multiagent systems with coupled dynamics. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 3497–3502. [Google Scholar]
- Dogan, K.M.; Yucelen, T.; Muse, J.A. Stability verification for uncertain multiagent systems in the presence of heterogeneous coupled and actuator dynamics. In Proceedings of the AIAA Scitech 2021 Forum, Online, 11–15 January 2021; p. 0530. [Google Scholar]
- Aly, I.A.; Dogan, K.M. Uncertain multiagent system in the presence of coupled dynamics: An asymptotic approach. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0359. [Google Scholar]
- DeVries, L.D.; Kutzer, M.D. Kernel design for coordination of autonomous, time-varying multi-agent configurations. In Proceedings of the 2016 American Control Conference, Boston, MA, USA, 6–8 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1975–1980. [Google Scholar]
- DeVries, L.; Sims, A.; Kutzer, M.D. Kernel Design and Distributed, Self-Triggered Control for Coordination of Autonomous Multi-Agent Configurations. Robotica 2018, 36, 1077–1097. [Google Scholar] [CrossRef]
- Tran, D.; Yucelen, T. On new Laplacian matrix with a user-assigned nullspace in distributed control of multiagent systems. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Dogan, K.M.; Yucelen, T. Distributed Adaptive Control for Uncertain Multiagent Systems with User-Assigned Laplacian Matrix Nullspaces. In Proceedings of the 2021 IEEE Conference on Control Technology and Applications (CCTA), Online, 9–11 August 2021. [Google Scholar]
- Kurttisi, A.; Aly, I.A.; Dogan, K.M. Coordination of Uncertain Multiagent Systems with Non-Identical Actuation Capacities. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 3947–3952. [Google Scholar]
- Aly, I.A.; Kurttisi, A.; Dogan, K.M. An Observer-Based Distributed Adaptive Control Algorithm for Coordination of Multiagent Systems in the Presence of Coupled Dynamics. In Proceedings of the 2023 American Control Conference (ACC), San Diego, CA, USA, 31 May–2 June 2023; pp. 521–526. [Google Scholar]
- Santillo, M.A.; Bernstein, D.S. Adaptive control based on retrospective cost optimization. J. Guid. Control Dyn. 2010, 33, 289–304. [Google Scholar] [CrossRef]
- Goodwin, G.; Ramadge, P.; Caines, P. Discrete-time multivariable adaptive control. IEEE Trans. Autom. Control 1980, 25, 449–456. [Google Scholar] [CrossRef]
- Kanellakopoulos, R. A discrete-time adaptive nonlinear system. In Proceedings of the American Control Conference, Baltimore, MD, USA, 29 June–1 July 1994; pp. 867–869. [Google Scholar]
- Venugopal, R.; Rao, V.; Bernstein, D. Lyapunov-based backward-horizon discrete-time adaptive control. Adapt. Contr. Sig. Proc. 2003, 17, 67–84. [Google Scholar]
- Hayakawa, T.; Haddad, W.M.; Leonessa, A. A Lyapunov-based adaptive control framework for discrete-time non-linear systems with exogenous disturbances. Int. J. Control 2004, 77, 250–263. [Google Scholar] [CrossRef]
- Akhtar, S.; Venugopal, R.; Bernstein, D.S. Logarithmic Lyapunov functions for direct adaptive stabilization with normalized adaptive laws. Int. J. Control 2004, 77, 630–638. [Google Scholar] [CrossRef]
- Johansson, R. Global Lyapunov stability and exponential convergence of direct adaptive control. Int. J. Control 1989, 50, 859–869. [Google Scholar] [CrossRef]
- Johansson, R. Supermartingale analysis of minimum variance adaptive control. Control-Theory Adv. Technol. 1995, 10, 993–1013. [Google Scholar]
- Haddad, W.M.; Hayakawa, T.; Leonessa, A. Direct adaptive control for discrete-time nonlinear uncertain dynamical systems. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 1773–1778. [Google Scholar]
- Hoagg, J.B.; Santillo, M.A.; Bernstein, D.S. Discrete-time adaptive command following and disturbance rejection with unknown exogenous dynamics. IEEE Trans. Autom. Control 2008, 53, 912–928. [Google Scholar] [CrossRef]
- Li, H.; Wu, Y.; Chen, M. Adaptive fault-tolerant tracking control for discrete-time multiagent systems via reinforcement learning algorithm. IEEE Trans. Cybern 2020, 51, 1163–1174. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Fan, J.; Gao, W.; Chai, T.; Lewis, F.L. Cooperative adaptive optimal output regulation of nonlinear discrete-time multi-agent systems. Automatica 2020, 121, 109149. [Google Scholar] [CrossRef]
- Yildirim, E.; Yucelen, T. Discrete-Time Control of Multiagent Systems with a Misbehaving Node. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 48–53. [Google Scholar]
- Aly, I.A.; Dogan, K.M. Discrete-Time Adaptive Control Algorithm for Coordination of Multiagent Systems in the Presence of Coupled Dynamics. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 5366–5371. [Google Scholar]
- Godsil, C.D.; Royle, G. Algebraic Graph Theory; Springer: New York, NY, USA, 2001. [Google Scholar]
- Haddad, W.M.; Chellaboina, V. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Topsok, F. Some bounds for the logarithmic function. Inequal. Theory Appl. 2006, 4, 137. [Google Scholar]
- Bhatia, R. Positive Definite Matrices; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]






| set of non-negative integers | |
| set of real numbers | |
| set of positive real numbers | |
| set of real column vectors | |
| set of real matrices | |
| set of positive definite real matrices | |
| ≜ | equality by definition |
| transpose of a matrix | |
| inverse of a matrix | |
| trace operator | |
| natural logarithm | |
| Euclidean norm | |
| eigenvalues of the real matrix | |
| maximum eigenvalue of the real matrix | |
| minimum eigenvalue of the real matrix | |
| identity matrix | |
| zero matrix | |
| diag(·) | diagonalized vector |
| Initial Execution: k = 0 |
|---|
| 1: Using and , calculate |
| 2: Using , , , and , calculate |
| 3: Apply to obtain |
| from the physical system |
| Repetitive Execution: k ≥ 1 |
| 4: Using and , calculate |
| 5: Using and , calculate |
| 6: Using , , , and , |
| calculate |
| 7: Using and , |
| calculate |
| 8: Using and , calculate |
| 9: Using , , , and , calculate |
| 10: Apply to obtain from the system |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aly, I.A.; Dogan, K.M. Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach. Electronics 2024, 13, 524. https://doi.org/10.3390/electronics13030524
Aly IA, Dogan KM. Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach. Electronics. 2024; 13(3):524. https://doi.org/10.3390/electronics13030524
Chicago/Turabian StyleAly, Islam A., and Kadriye Merve Dogan. 2024. "Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach" Electronics 13, no. 3: 524. https://doi.org/10.3390/electronics13030524
APA StyleAly, I. A., & Dogan, K. M. (2024). Discrete-Time Adaptive Control for Uncertain Scalar Multiagent Systems with Coupled Dynamics: A Lyapunov-Based Approach. Electronics, 13(3), 524. https://doi.org/10.3390/electronics13030524








