A Novel Three-Dimensional Sigma–Delta Modulation for High-Switching-Frequency Three-Phase Four-Wire Active Power Filters
Abstract
:1. Introduction
1.1. Modulation Techniques
1.2. Wide-Bandgap Semiconductors
1.3. Proposal
- Working with a variable switching frequency and, consequently, reducing the switching losses;
- Compensating for homopolar currents in four-wire systems when applied in 3L4W converters.
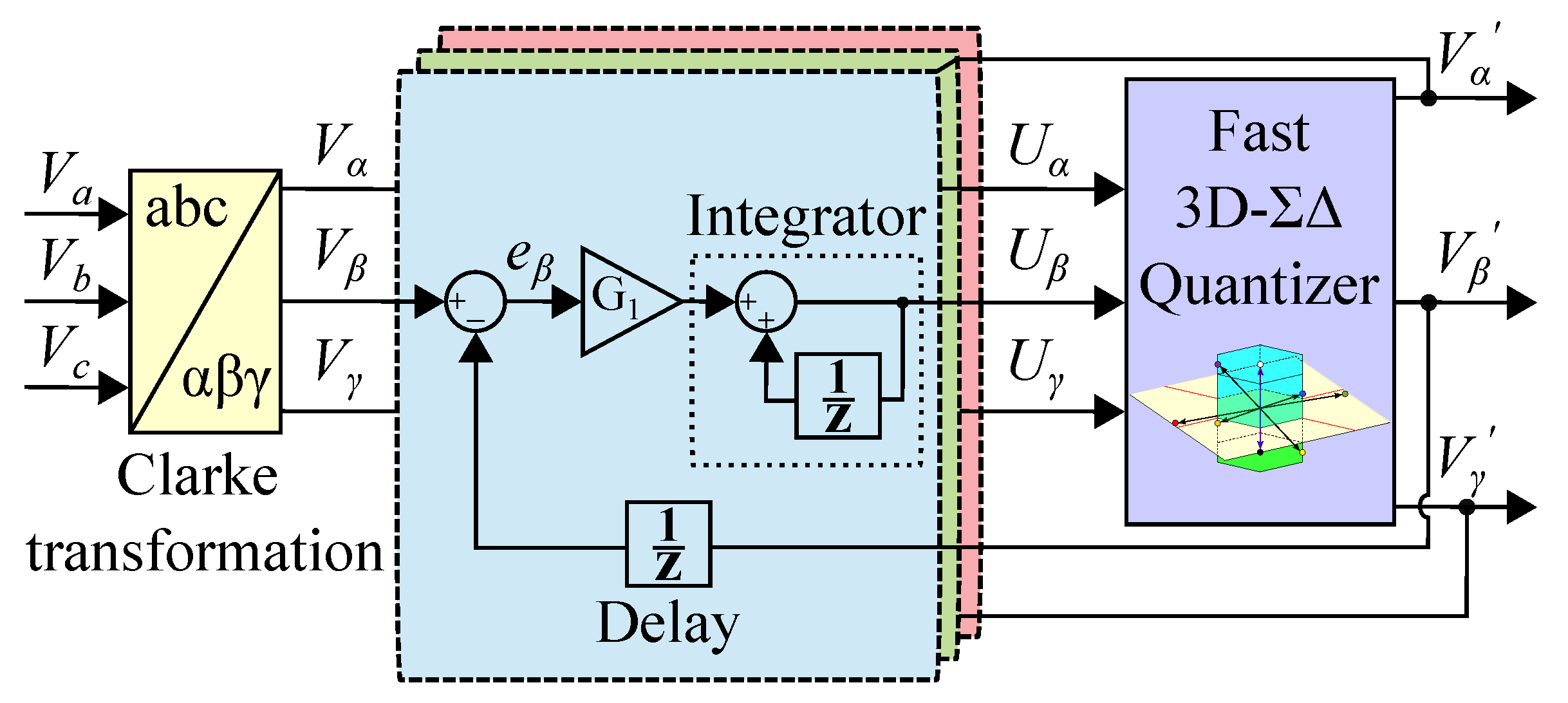
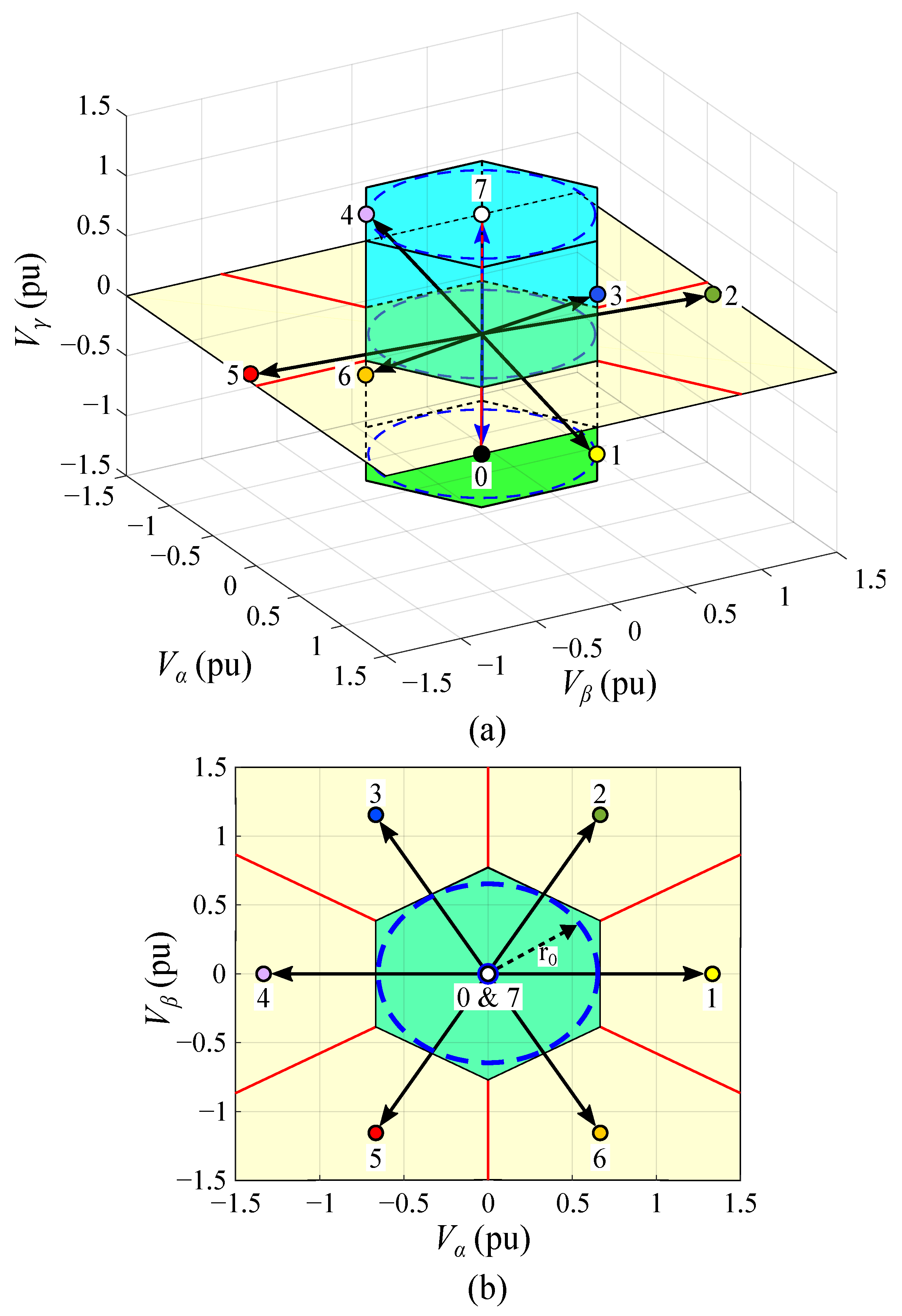
2. Proposed Three-Dimensional Sigma–Delta
3. Control Strategy
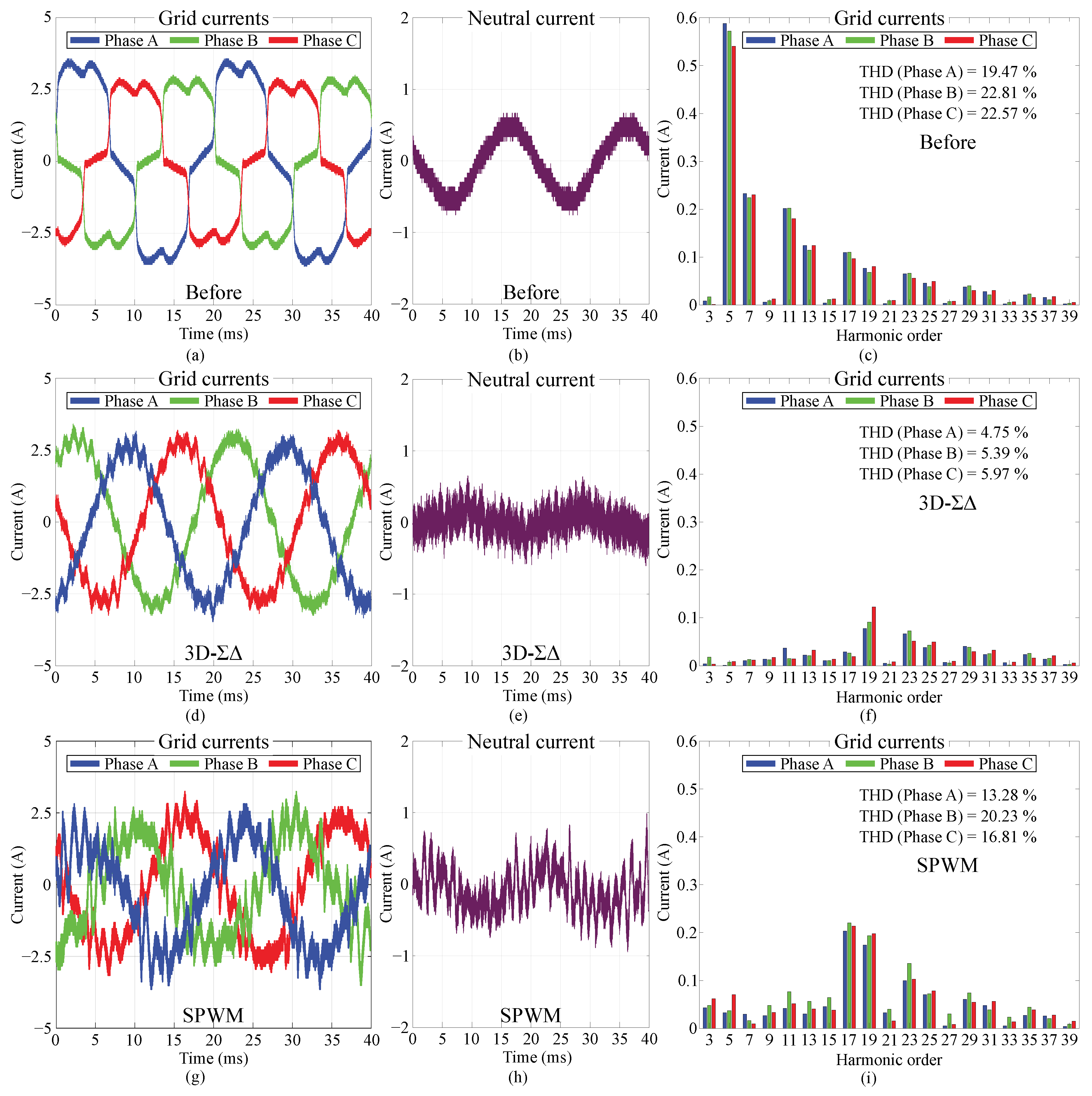
4. Simulation Results
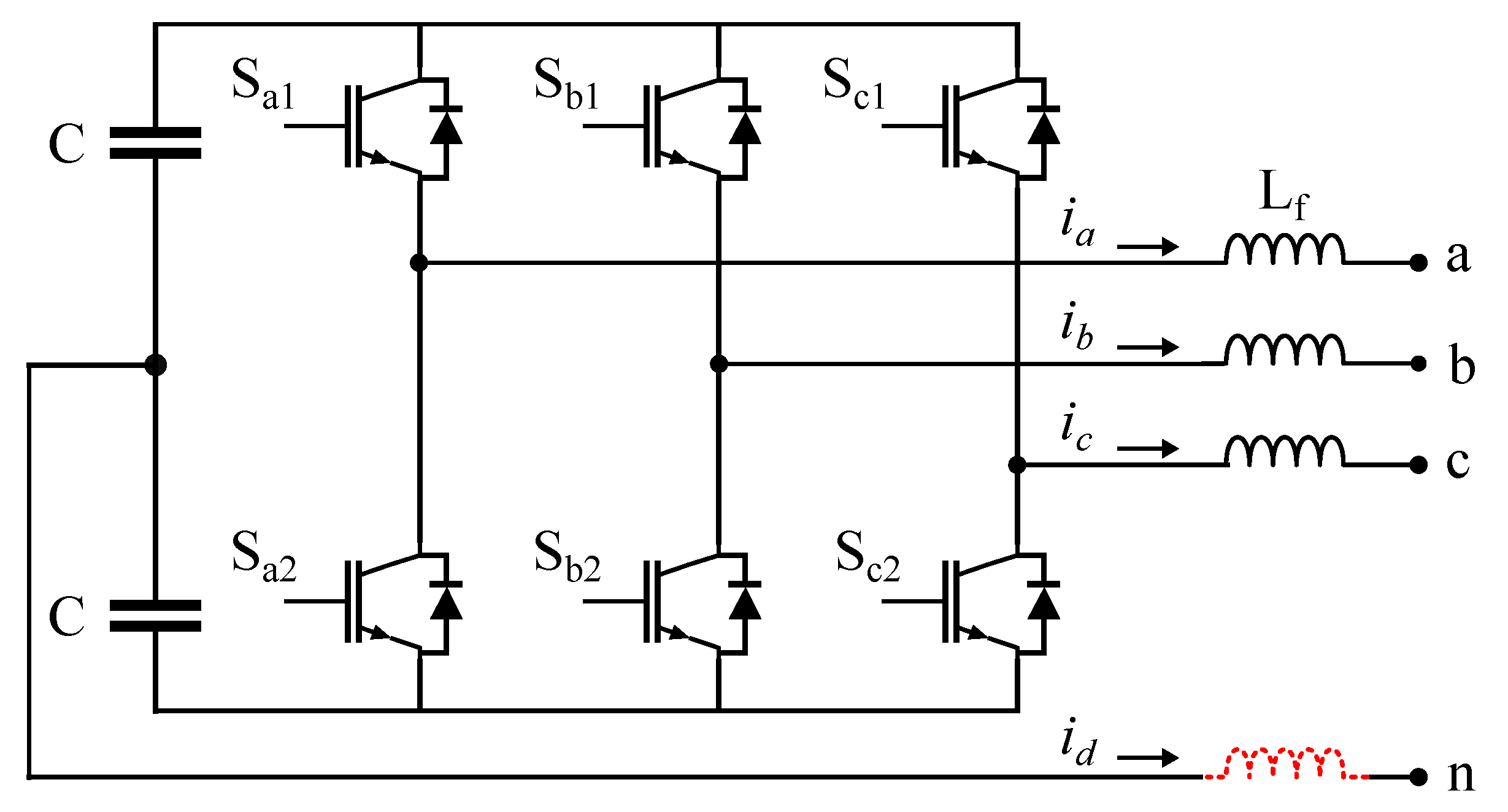
4.1. System Model
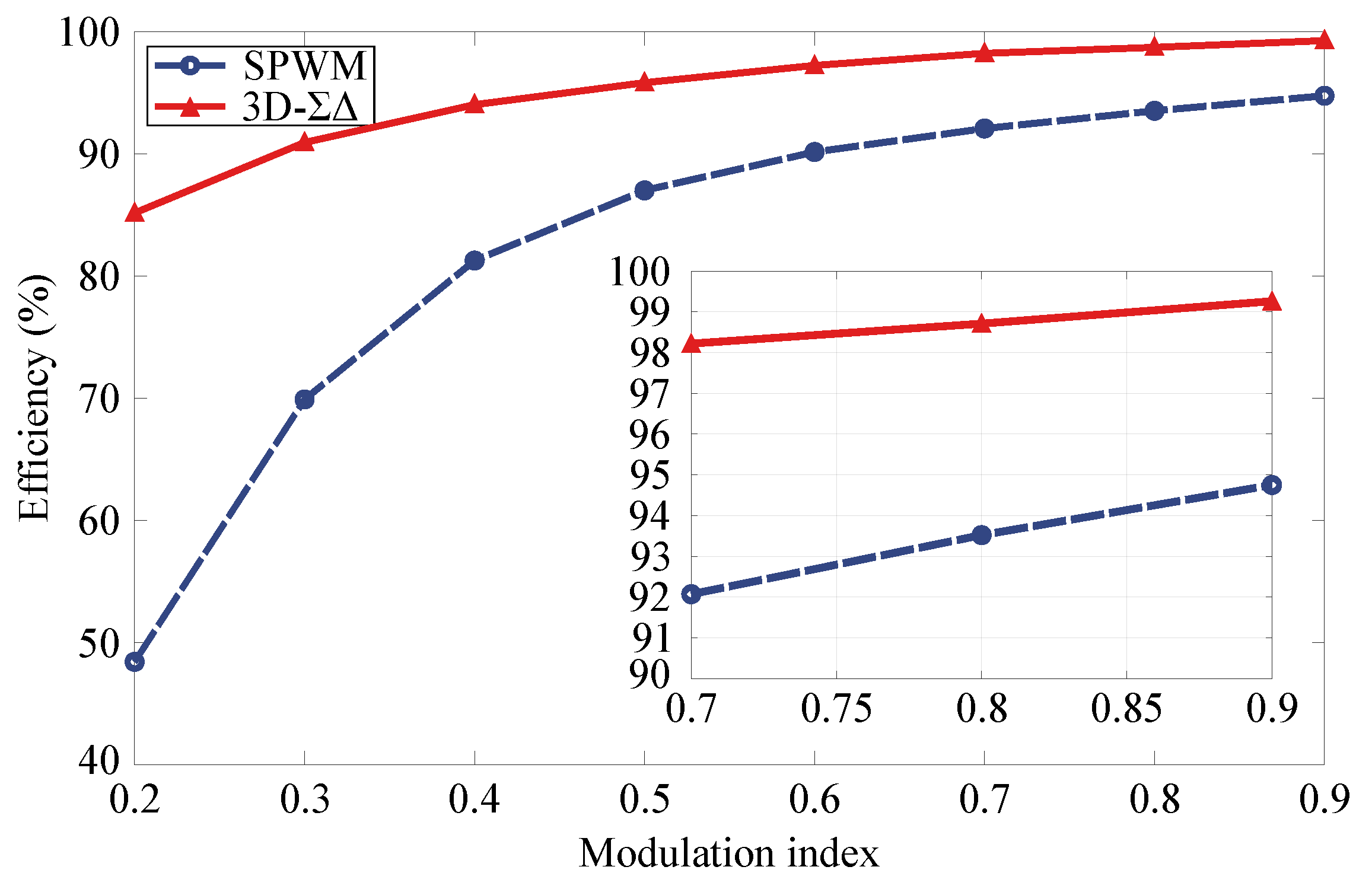
4.2. Analysis of Simulation Results
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kazmierkowski, M.P. Power quality: Problems and mitigation techniques [book news]. IEEE Ind. Electron. Mag. 2015, 9, 62. Available online: http://ieeexplore.ieee.org/document/7128811/ (accessed on 15 August 2023). [CrossRef]
- Li, H.; Li, B.; Luo, Z.; Li, H.; Zhao, Y.; Wang, T.; Sun, Y. Power Supply Reliability Enhancement for Low-Voltage Distribution Area with Power Quality Improvement Function. IEEE Access 2022, 10, 130619–130631. [Google Scholar] [CrossRef]
- Garcia, C.A.I.; Bindi, M.; Corti, F.; Luchetta, A.; Grasso, F.; Paolucci, L.; Piccirilli, M.C.; Aizenberg, I. Power Quality Analysis Based on Machine Learning Methods for Low-Voltage Electrical Distribution Lines. Energies 2023, 16, 3627. [Google Scholar] [CrossRef]
- Santiago, I.; López-Rodríguez, M.A.; de Castro, A.G.; Moreno-Munoz, A.; Luna-Rodríguez, J.J. Energy consumption of audiovisual devices in the residential sector: Economic impact of harmonic losses. Energy 2013, 60, 292–301. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Prats, M.Á.M.; Portillo, R.C.; Galvan, J.I.L.; Perales, M.A.; Carrasco, J.M.; Díez, E.G.; Jiménez, J.L.M. Three-dimensional space-vector modulation algorithm for four-leg multilevel converters using abc coordinates. IEEE Trans. Ind. 2006, 53, 458–466. [Google Scholar] [CrossRef]
- Fabricio, E.L.L.; Silva, S.C.; Jacobina, C.B.; Corrêa, M.B.D.R. Analysis of main topologies of shunt active power filters applied to four-wire systems. IEEE Trans. Power Electron. 2018, 33, 2100–2112. [Google Scholar] [CrossRef]
- Luo, F.; Loo, K.H.; Lai, Y.M. Simple carrier-based pulse-width modulation scheme for three-phase four-wire neutral-point-clamped inverters with neutral-point balancing. IET Power Electron. 2016, 9, 365–376. [Google Scholar] [CrossRef]
- Lumbreras, D.; Gálvez, E.; Collado, A.; Zaragoza, J. Trends in power quality, harmonic mitigation and standards for light and heavy industries: A review. Energies 2020, 13, 5792. Available online: https://www.mdpi.com/1996-1073/13/21/5792 (accessed on 22 October 2023). [CrossRef]
- Siemens. SINAMICS G130/G150 Line Harmonics Filter. Operating Instructions 07/2007 Edition. 2007. Available online: https://cache.industry.siemens.com/dl/files/997/26576997/att_73840/v1/SINAMICS_G130_G150_LHF_0707_eng.pdf (accessed on 22 October 2023).
- ABB. Power Quality Filters—PQFI—PQFM—PQFS. Electrification Products. 2017. Available online: https://search.abb.com/library/Download.aspx?DocumentID=9AKK106930A8906&LanguageCode=en&DocumentPartId=&Action=Launch (accessed on 5 June 2023).
- Circutor. AFQm Multifunction Active Filter. 2022. Available online: https://circutor.com/pdf/pdfdatasheet.php?lang=es&prod=R7MM2F (accessed on 17 September 2023).
- Popescu, M.; Bitoleanu, A.; Linca, M.; Suru, C.V. Improving power quality by a four-wire shunt active power filter: A case study. Energies 2021, 14, 1951. [Google Scholar] [CrossRef]
- Kim, J.-H.; Sul, S.-K. A carrier-based pwm method for three-phase four-leg voltage source converters. IEEE Trans. Power Electron. 2004, 19, 66–75. Available online: http://ieeexplore.ieee.org/document/1262054/ (accessed on 9 November 2023). [CrossRef]
- Perales, M.A.; Prats, M.M.; Portillo, R.; Mora, J.L.; León, J.I.; Franquelo, L.G. Three-dimensional space vector modulation in abc coordinates for four-leg voltage source converters. IEEE Power Electron. Lett. 2003, 1, 104–109. [Google Scholar] [CrossRef]
- Viatkin, A.; Mandrioli, R.; Hammami, M.; Ricco, M.; Grandi, G. Ac current ripple harmonic pollution in three-phase four-leg active front-end ac/dc converter for on-board EV chargers. Electronics 2021, 10, 116. [Google Scholar] [CrossRef]
- Pires, V.F.; Cordeiro, A.; Foito, D.; Pires, A.J.; Hao, C.; Martins, J.F.; Castro, R. Compensation of Unbalanced Low-Voltage Grids Using a Photovoltaic Generation System with a Dual Four-Leg, Two-Level Inverter. Electronics 2022, 11, 320. [Google Scholar] [CrossRef]
- Prats, M.; Franquelo, L.; Portillo, R.; León, J.; Galván, E.; Carrasco, J. A 3-d space vector modulation generalized algorithm for multilevel converters. IEEE Power Electron. Lett. 2003, 1, 110–114. [Google Scholar] [CrossRef]
- Dai, N.-Y.; Wong, M.-C.; Ng, F.; Han, Y.-D. A fpga-based generalized pulse width modulator for three-leg center-split and four-leg voltage source inverters. IEEE Trans. Power Electron. 2008, 23, 1472–1484. Available online: http://ieeexplore.ieee.org/document/4494750/ (accessed on 17 September 2023). [CrossRef]
- Mandrioli, R.; Viatkin, A.; Hammami, M.; Ricco, M.; Grandi, G. Variable switching frequency pwm for three-phase four-wire split-capacitor inverter performance enhancement. IEEE Trans. Power Electron. 2021, 36, 13674–13685. [Google Scholar] [CrossRef]
- Mandrioli, R.; Viatkin, A.; Hammami, M.; Ricco, M.; Grandi, G. A comprehensive ac current ripple analysis and performance enhancement via discontinuous pwm in three-phase four-leg grid-connected inverters. Energies 2020, 13, 4352. Available online: https://www.mdpi.com/1996-1073/13/17/4352 (accessed on 5 June 2023). [CrossRef]
- Li, B.; Li, Q.; Lee, F.C.; Liu, Z.; Yang, Y. A high-efficiency high-density wide-bandgap device-based bidirectional on-board charger. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1627–1636. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, Z.; Hu, B.; Tang, X.; Liu, C.; Wang, Z. Uniform carrier-based pwm method for three-phase three-level three-wire and four-wire converter system with neutral-point balancing. IET Power Electron. 2020, 13, 3081–3089. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, B.; Xie, F. A novel svpwm for three-level npc inverter based on m-mode controllability. IEEE Trans. Ind. 2018, 65, 6055–6065. Available online: http://ieeexplore.ieee.org/document/8240695/ (accessed on 12 July 2023). [CrossRef]
- Chen, H.-C.; Tsai, M.-J.; Wang, Y.-B.; Cheng, P.-T. A modulation technique for neutral point voltage control of the three-level neutral-point-clamped converter. IEEE Trans. Ind. Appl. 2018, 54, 2517–2524. Available online: https://ieeexplore.ieee.org/document/8274978/ (accessed on 20 November 2023). [CrossRef]
- Millan, J.; Godignon, P.; Perpina, X.; Perez-Tomas, A.; Rebollo, J. A survey of wide bandgap power semiconductor devices. IEEE Trans. Power Electron. 2014, 29, 2155–2163. Available online: http://ieeexplore.ieee.org/document/6532359/ (accessed on 20 November 2023). [CrossRef]
- Shenai, K. High-density power conversion and wide-bandgap semiconductor power electronics switching devices. Proc. IEEE 2019, 107, 2308–2326. [Google Scholar] [CrossRef]
- Gonzalez, J.O.; Wu, R.; Jahdi, S.; Alatise, O. Performance and reliability review of 650 v and 900 v silicon and sic devices: Mosfets, cascode jfets and igbts. IEEE Trans. Ind. Electron. 2020, 67, 7375–7385. [Google Scholar] [CrossRef]
- Lumbreras, D.; Zaragoza, J.; Mon, J.; Gálvez, E.; Collado, A. Efficiency analysis of wide band-gap semiconductors for two-level and three-level power converters. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 5126–5133. Available online: https://ieeexplore.ieee.org/document/8926766/ (accessed on 8 June 2023). [CrossRef]
- Xue, F.; Yu, R.; Huang, A.Q. A 98.3% efficient gan isolated bidirectional dc-dc converter for dc microgrid energy storage system applications. IEEE Trans. Ind. Electron. 2017, 64, 9094–9103. Available online: http://ieeexplore.ieee.org/document/7885035/ (accessed on 14 October 2023). [CrossRef]
- Li, H.; Zhang, Z.; Wang, S.; Tang, J.; Ren, X.; Chen, Q. A 300-khz 6.6-kw sic bidirectional llc onboard charger. IEEE Trans. Ind. Electron. 2020, 67, 1435–1445. [Google Scholar] [CrossRef]
- Matallana, A.; Ibarra, E.; López, I.; Andreu, J.; Garate, J.I.; Jordà, X.; Rebollo, J. Power module electronics in hev/ev applications: New trends in wide-bandgap semiconductor technologies and design aspects. Renew. Sustain. Energy Rev. 2019, 113, 109264. [Google Scholar] [CrossRef]
- Lumbreras, D. Development of an Active Power Filter Based on Wide-Bandgap Semiconductors. 2022. Available online: http://hdl.handle.net/10803/675092 (accessed on 8 June 2023).
- Lumbreras, D.; Zaragoza, J.; Berbel, N.; Mon, J.; Galvez, E.; Collado, A. Comprehensive analysis of hexagonal sigma-delta modulations for three-phase high-frequency vsc based on wide-bandgap semiconductors. IEEE Trans. Power Electron. 2021, 36, 7212–7222. Available online: https://ieeexplore.ieee.org/document/9266054/ (accessed on 28 November 2023). [CrossRef]
- Lumbreras, D.; Zaragoza, J.; Berbel, N.; Mon, J.; Galvez, E.; Collado, A. Fast-processing sigma–delta strategies for three-phase wide-bandgap power converters with common-mode voltage reduction. IEEE Trans. Power Electron. 2022, 37, 7989–8000. Available online: https://ieeexplore.ieee.org/document/9699032/ (accessed on 28 November 2023). [CrossRef]
- Acosta-Cambranis, F.; Zaragoza, J.; Martinez, L.R.; Berbel, N. New modulation strategy for five-phase high-frequency vsi based on sigma-delta modulators. IEEE Trans. Power Electron. 2021, 14, 3943–3953. Available online: https://ieeexplore.ieee.org/document/9582737/ (accessed on 28 November 2023). [CrossRef]
- Candy, J. A use of double integration in sigma delta modulation. IEEE Trans. Commun. 1985, 33, 249–258. Available online: http://ieeexplore.ieee.org/document/1096276/ (accessed on 14 October 2023). [CrossRef]
- Robles, E.; Ceballos, S.; Pou, J.; Martín, J.L.; Zaragoza, J.; Ibañez, P. Variable-frequency grid-sequence detector based on a quasi-ideal low-pass filter stage and a phase-locked loop. IEEE Trans. Power Electron. 2010, 25, 2552–2563. Available online: http://ieeexplore.ieee.org/document/5466221/ (accessed on 28 November 2023). [CrossRef]
- Asiminoael, L.; Blaabjerg, F.; Hansen, S. Detection is key - harmonic detection methods for active power filter applications. IEEE Ind. Appl. Mag. 2007, 13, 22–33. Available online: https://ieeexplore.ieee.org/document/4283506/ (accessed on 14 October 2023). [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple harmonics control for three-phase grid converter systems with the use of pi-res current controller in a rotating frame. IEEE Trans. Power Electron. 2006, 21, 836–841. Available online: http://ieeexplore.ieee.org/document/1629027/ (accessed on 28 November 2023). [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc.-Electr. Power Appl. 2006, 153, 750. Available online: http://digital-library.theiet.org/content/journals/10.1049/ip-epa_20030009 (accessed on 28 November 2023). [CrossRef]
- Campanhol, L.B.G.; da Silva, S.A.O.; Goedtel, A. Application of shunt active power filter for harmonic reduction and reactive power compensation in three phase four-wire systems. IET Power Electron. 2014, 7, 2825–2836. [Google Scholar] [CrossRef]
- PLECS User Manual, 4th ed.; Plexim GmbH: Zurich, Switzerland, 2019.
- EN 61000-3-2:2019; Electromagnetic Compatibility (EMC). Part 3-2: Limits. Limits for Harmonic Current Emissions (Equipment Input Current =16 A per Phase). (IEC 61000-3-2:2018). CENELEC: Brussels, Belgium, 2019.
- EN 61000-4-7:2004; Electromagnetic Compatibility (EMC). Part 4-7: Testing and Measurement Techniques. General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto. CENELEC: Brussels, Belgium, 2004.
- Holmes, D. A general analytical method for determining the theoretical harmonic components of carrier based pwm strategies. In Proceedings of the 1998 IEEE Industry Applications Conference. Thirty-Third IAS Annual Meeting (Cat. No.98CH36242), St. Louis, MO, USA, 12–15 October 1998; Volume 2, pp. 1207–1214. Available online: http://ieeexplore.ieee.org/document/730300/ (accessed on 28 November 2023). [CrossRef]





| Reference | Year | Modulation | Converter Topology | Modulation Type | Max. Switching Frequency |
|---|---|---|---|---|---|
| [17] | 2003 | 3D SVM | 3L4W | Vectorial | — |
| [18] | 2008 | 3D PWM | 3/4L4W | PWM | 5 kHz |
| [19] | 2021 | VSF-PWM | 3L4W | Spread-spectrum | 5.1 kHz |
| [20] | 2020 | Several PWM | 3L4W | PWM | 3.6 kHz |
| [21] | 2018 | Simplified PWM | 3L4W | PWM | 10 kHz |
| [22] | 2020 | CB-PWM | 3L3/4W | PWM | 20 kHz |
| [23] | 2018 | 18-mode SVPWM | 3L4W | PWM | 10 kHz |
| [24] | 2018 | Dipolar PWM | 3L3/4W | PWM | 10 kHz |
| This paper | 2023 | 3D- | 3L3/4W | Spread-spectrum | 200 kHz |
| Sector | Switching State | |||||
|---|---|---|---|---|---|---|
| 0 | Indifferent | 0 | 0 | 0 | −1−11 | |
| 0 | Indifferent | 0 | 0 | 1 | — | Indifferent |
| 0 | Indifferent | 0 | 1 | 0 | −111 | |
| 0 | Indifferent | 0 | 1 | 1 | 11−1 | |
| 0 | Indifferent | 1 | 0 | 0 | 1−11 | |
| 0 | Indifferent | 1 | 0 | 1 | 1−1−1 | |
| 0 | Indifferent | 1 | 1 | 0 | — | Indifferent |
| 0 | Indifferent | 1 | 1 | 1 | 11−1 | |
| 1 | 0 | Indifferent | Indifferent | Indifferent | −1−1−1 | |
| 1 | 1 | Indifferent | Indifferent | Indifferent | 111 |
| Standard 3D- | Fast 3D- | |
|---|---|---|
| Additions | 7 | 1 |
| Subtractions | 14 | 0 |
| Multiplications | 14 | 4 |
| Comparisons | 1 | 5 |
| ROM | No | Yes |
| Total | 36 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lumbreras, D.; Zaragoza, J.; Lamich, M.; Berbel, N.; Romero-Cadaval, E. A Novel Three-Dimensional Sigma–Delta Modulation for High-Switching-Frequency Three-Phase Four-Wire Active Power Filters. Electronics 2024, 13, 553. https://doi.org/10.3390/electronics13030553
Lumbreras D, Zaragoza J, Lamich M, Berbel N, Romero-Cadaval E. A Novel Three-Dimensional Sigma–Delta Modulation for High-Switching-Frequency Three-Phase Four-Wire Active Power Filters. Electronics. 2024; 13(3):553. https://doi.org/10.3390/electronics13030553
Chicago/Turabian StyleLumbreras, David, Jordi Zaragoza, Manel Lamich, Néstor Berbel, and Enrique Romero-Cadaval. 2024. "A Novel Three-Dimensional Sigma–Delta Modulation for High-Switching-Frequency Three-Phase Four-Wire Active Power Filters" Electronics 13, no. 3: 553. https://doi.org/10.3390/electronics13030553
APA StyleLumbreras, D., Zaragoza, J., Lamich, M., Berbel, N., & Romero-Cadaval, E. (2024). A Novel Three-Dimensional Sigma–Delta Modulation for High-Switching-Frequency Three-Phase Four-Wire Active Power Filters. Electronics, 13(3), 553. https://doi.org/10.3390/electronics13030553









