Specific Emitter Identification Based on Attractor Feature Space of System under Blind Equalization
Abstract
:1. Introduction
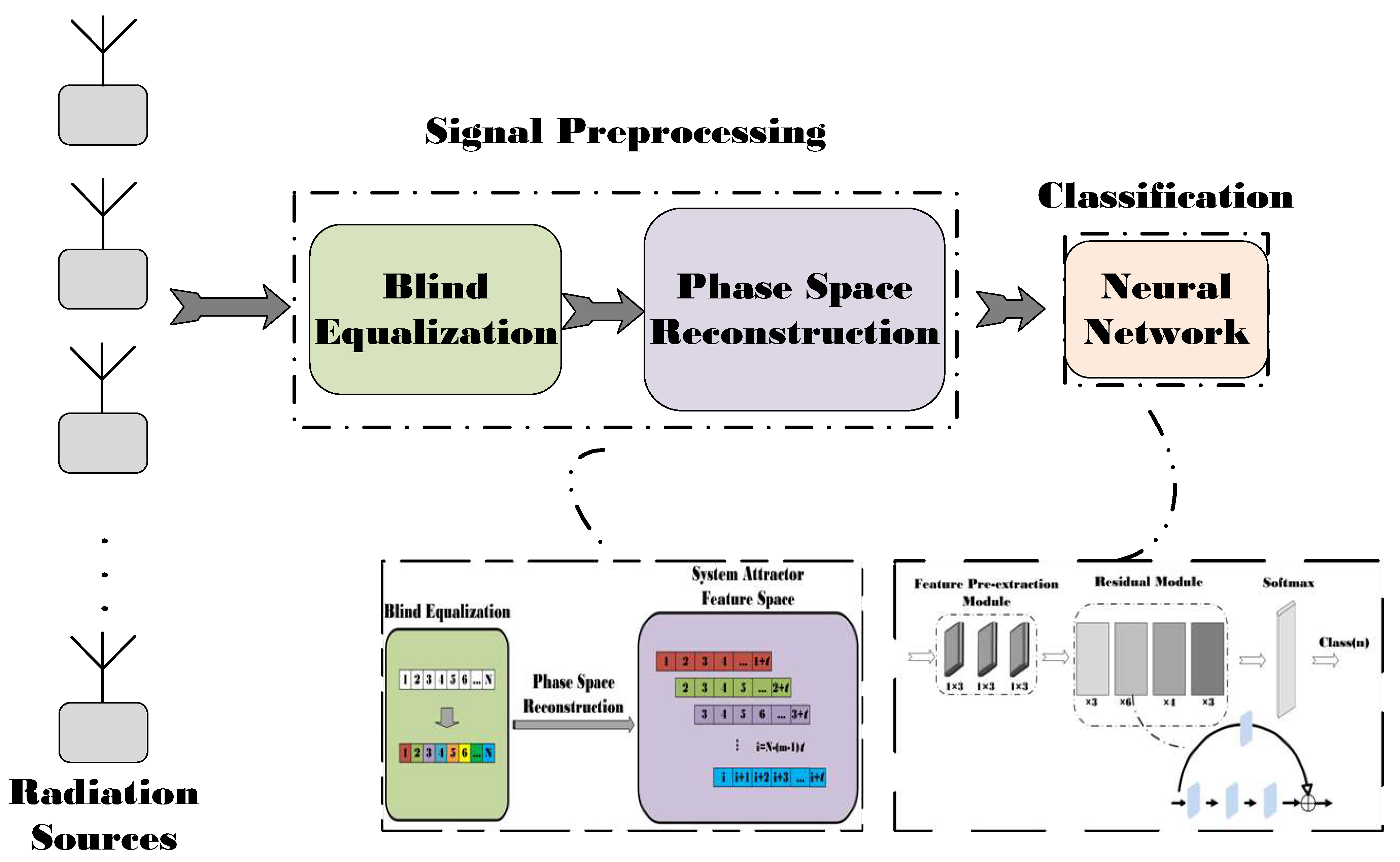
- In order to solve the problem of communication signals being seriously affected by multi-path channels and noise in a complex electromagnetic environment during transmission, this paper proposes to construct a system attractor feature space based on blind equalization, and effectively extracts fingerprint characteristics of different individuals of the target. An experimental verification shows that this method can effectively improve the individual recognition rate of radiation sources.
- This paper explores the adaptability of the neural network with respect to the embedding dimension and delay time of the attractor feature space of the target radiation source. Experiments show that when the embedding dimension and delay time of the feature space of each radio station are consistent, the adaptability of the network is the best, and the optimal embedding dimension and delay time are found out.
- Based on the model, the recognition model adapted to the complex electromagnetic environment is designed, and when recently compared with the more popular neural network, the superiority of our model is proved by experiments.
2. Methods
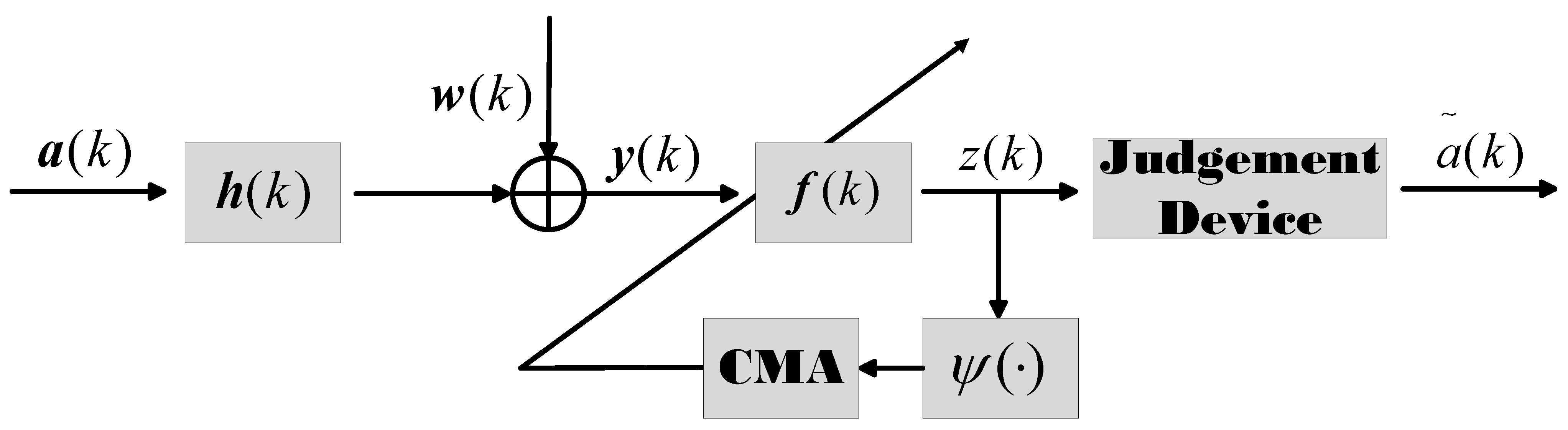
2.1. Blind Equalization
2.1.1. CMA
2.1.2. MMA
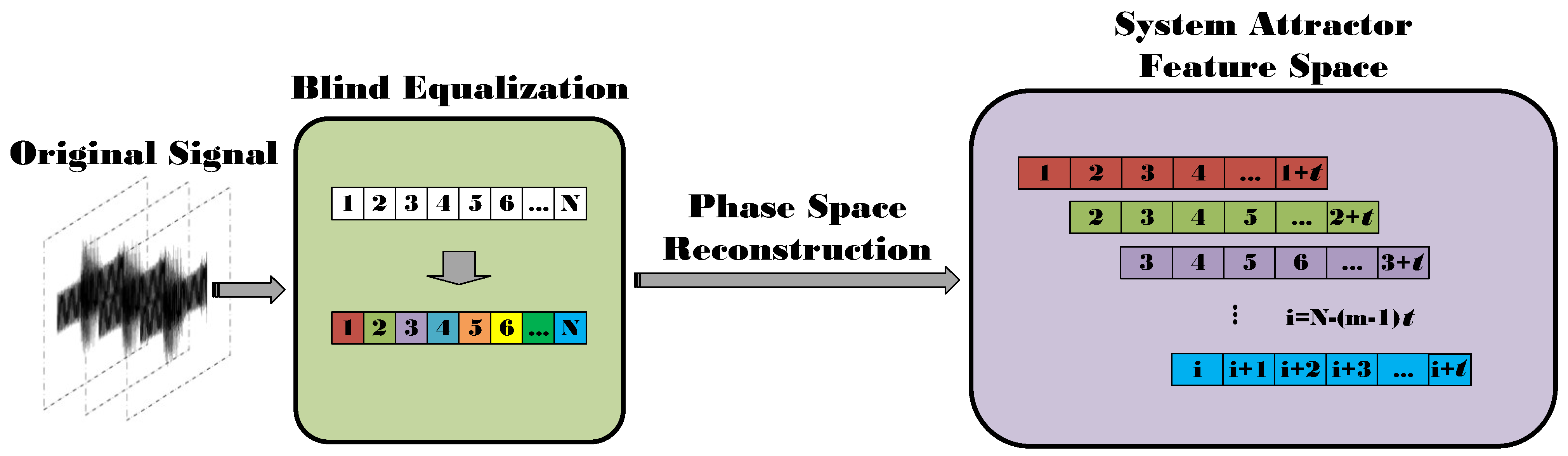
2.2. Phase Space Reconstruction
2.2.1. Delay Time
2.2.2. Embedding Dimension m
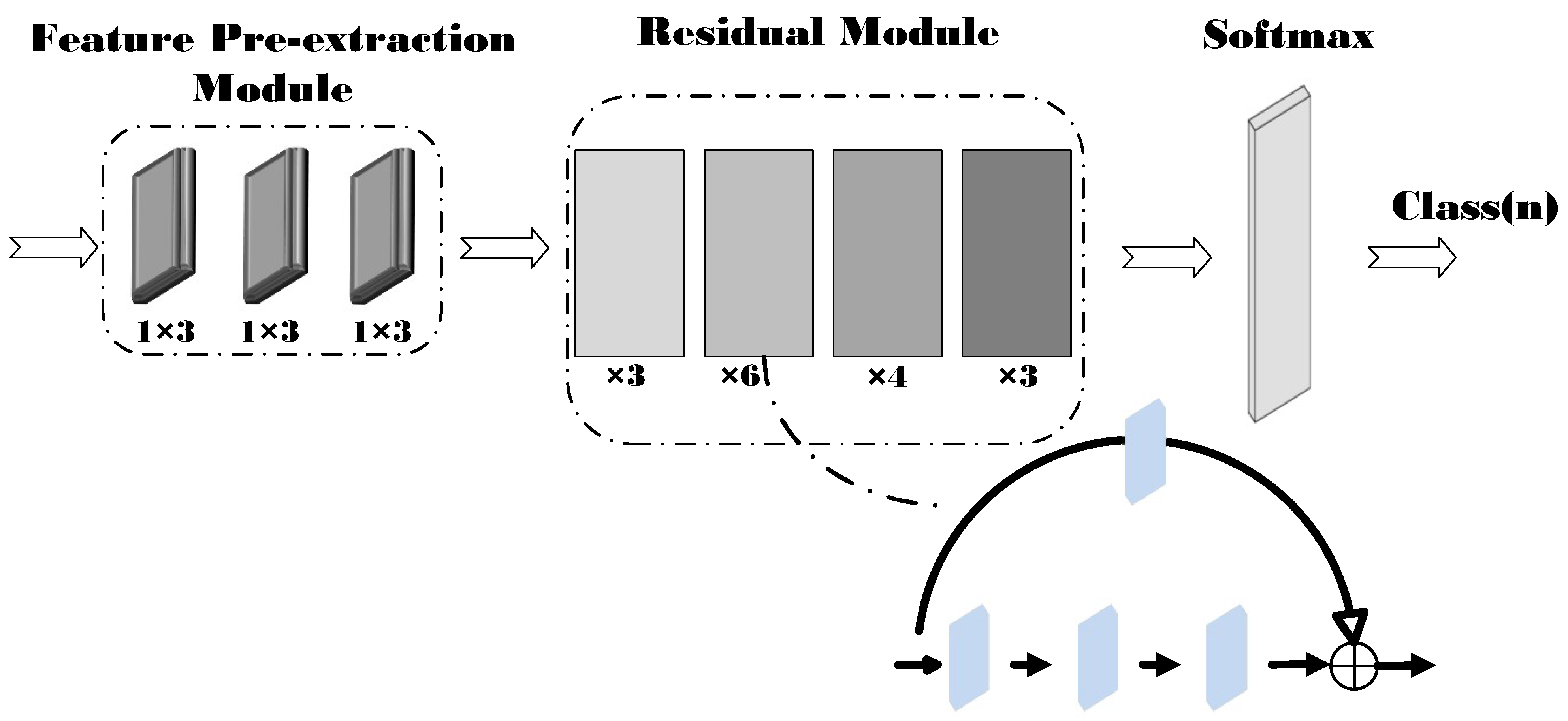
2.3. Neural Network
2.4. Attractor Feature Space Based on Blind Equalization Algorithm
| Algorithm 1 Attractor feature space based on blind equalization. |
| PREPROCESSING by (2) ∼ (9) by (14) ∼ (20) m by (21) ∼ (25) return TRAIN EPOCH, learning rate EPOCH model weight return TRAINED model TEST return |
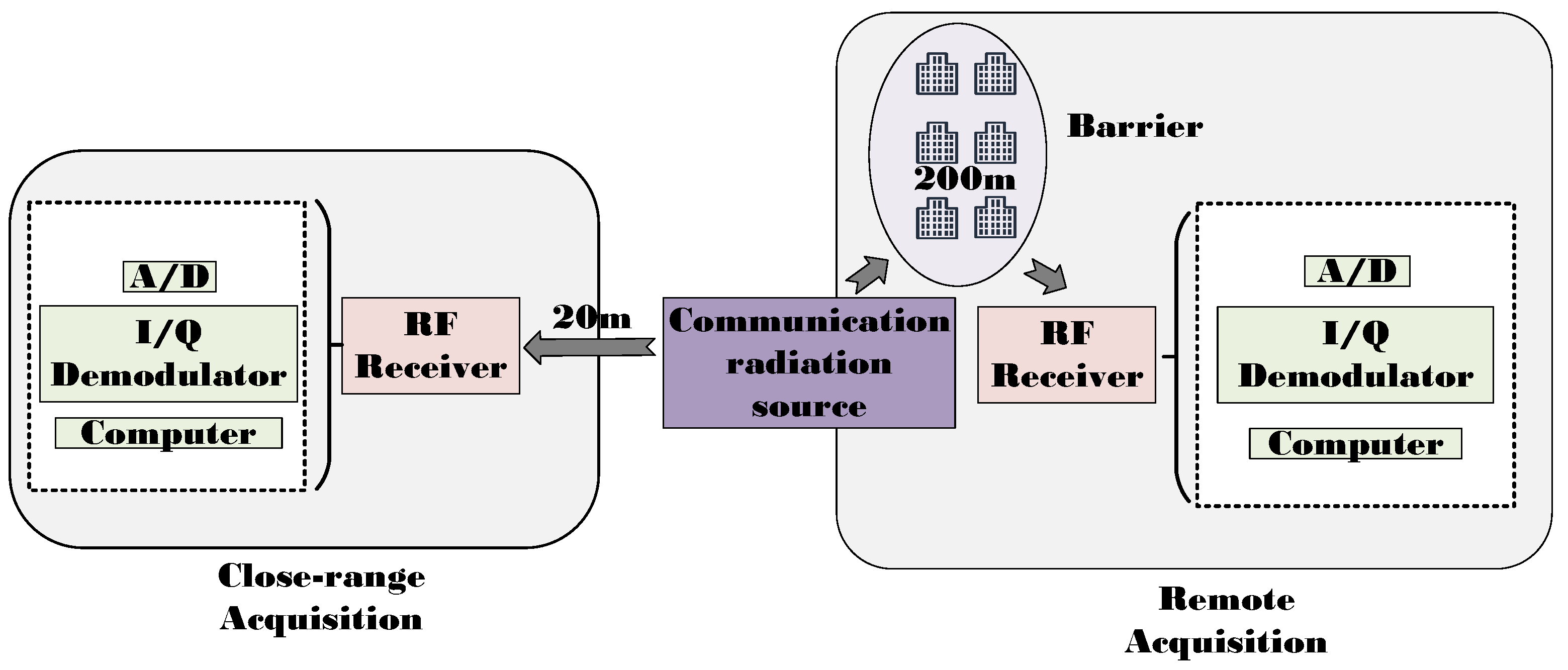
3. Datasets and Experiments
3.1. Datasets
3.2. Experiments
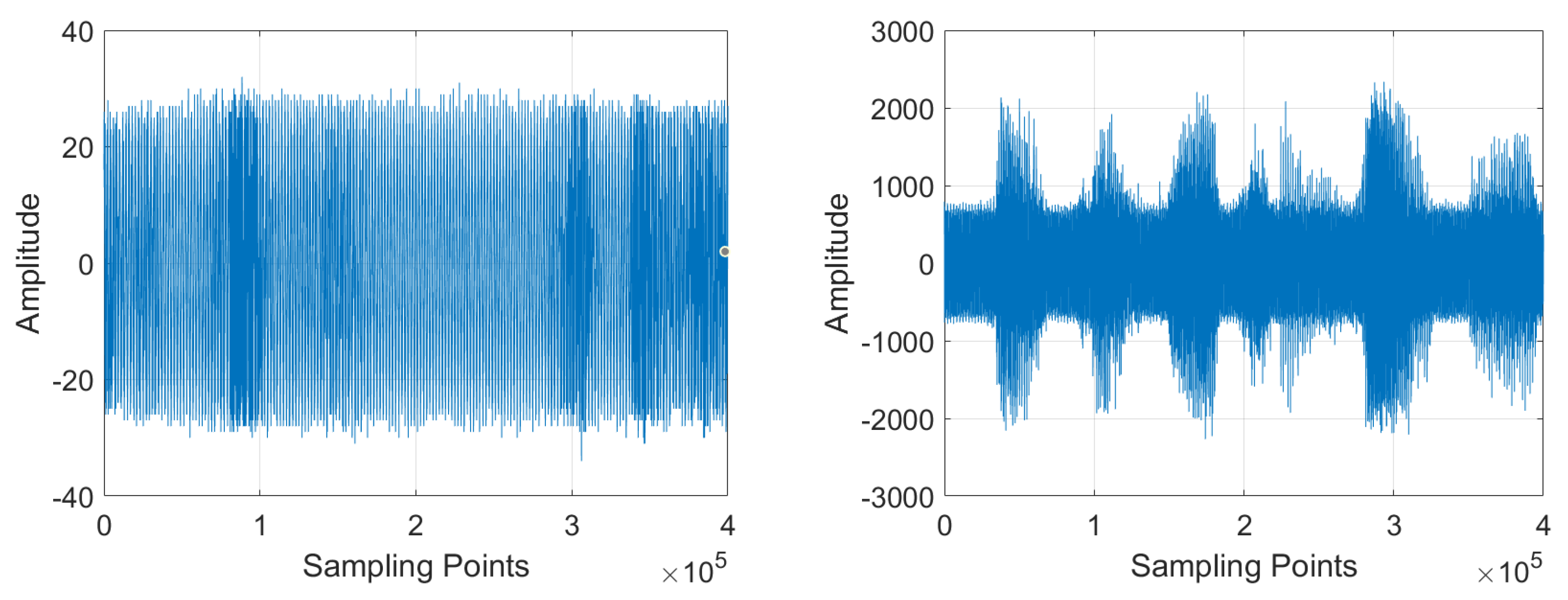
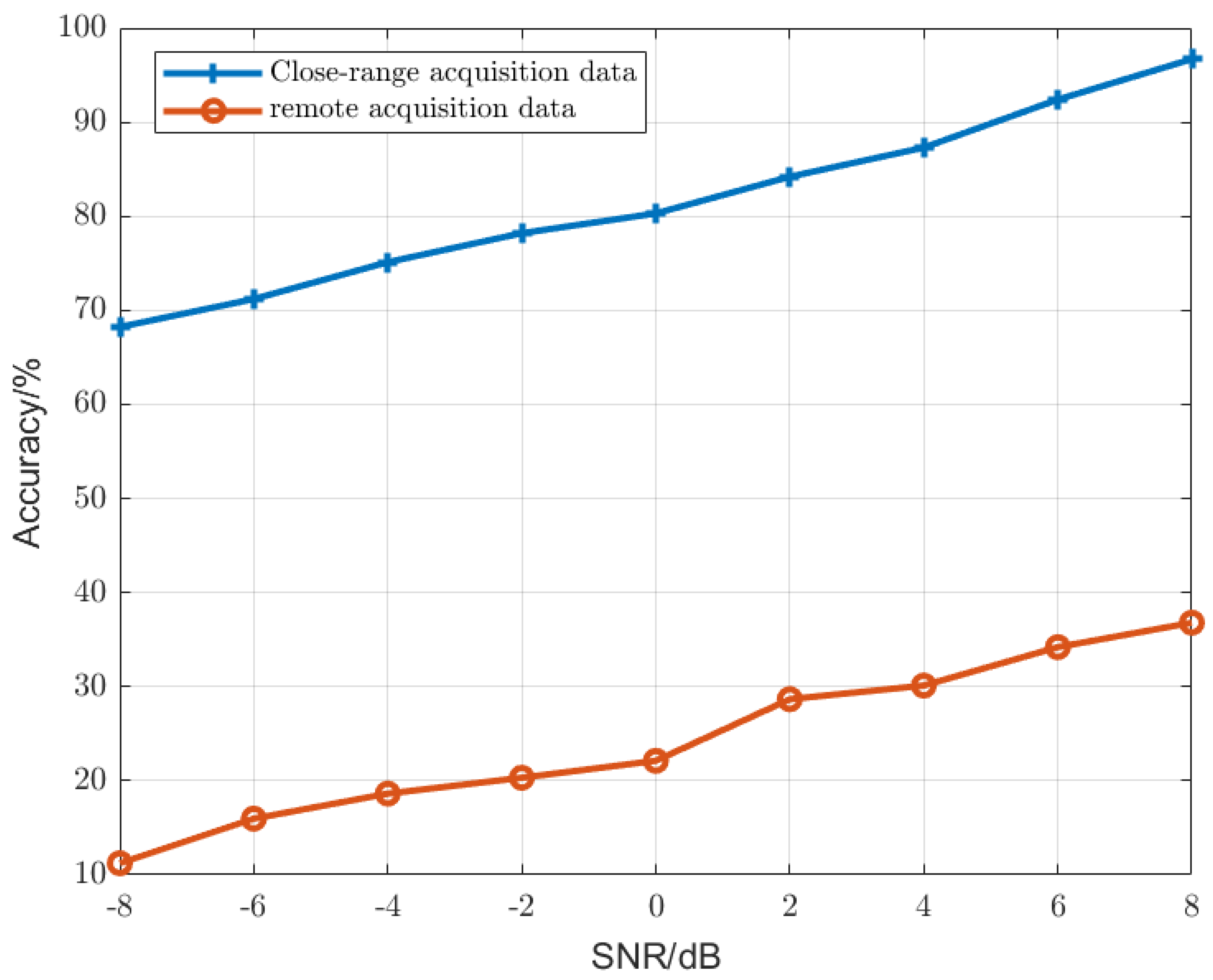
3.2.1. The Influence of Multi-Path Effect
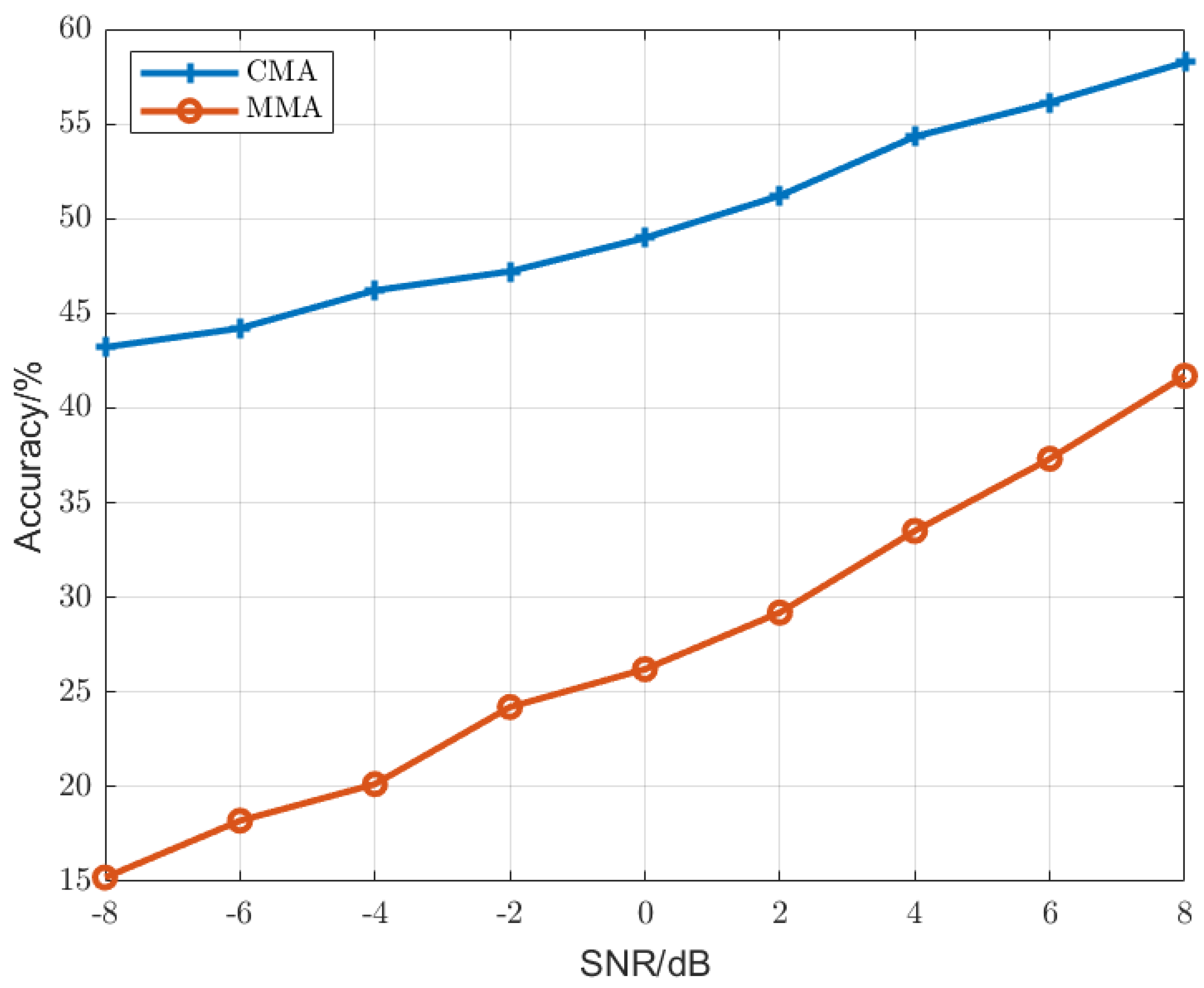
3.2.2. The Choice of Blind Equalization Method
3.2.3. Determination of Delay Time and Embedding Dimension
- According to the obtained delay time and embedding dimension of each radio station, the system attractor feature space of each radio station is constructed, respectively, and the recognition result is obtained using this as the input of the recognition model. The model adopts our improved model, and the other settings are the same as the first experiment.
- Controlling the delay time and embedding dimension of the attractor feature space of the system of each radio station is the same, and there are 10 different combinations according to the calculation. In the meantime, these 10 different combinations were input into the recognition model for training and testing. The model adopts our improved model, and the other settings are the same as in the first experiment.
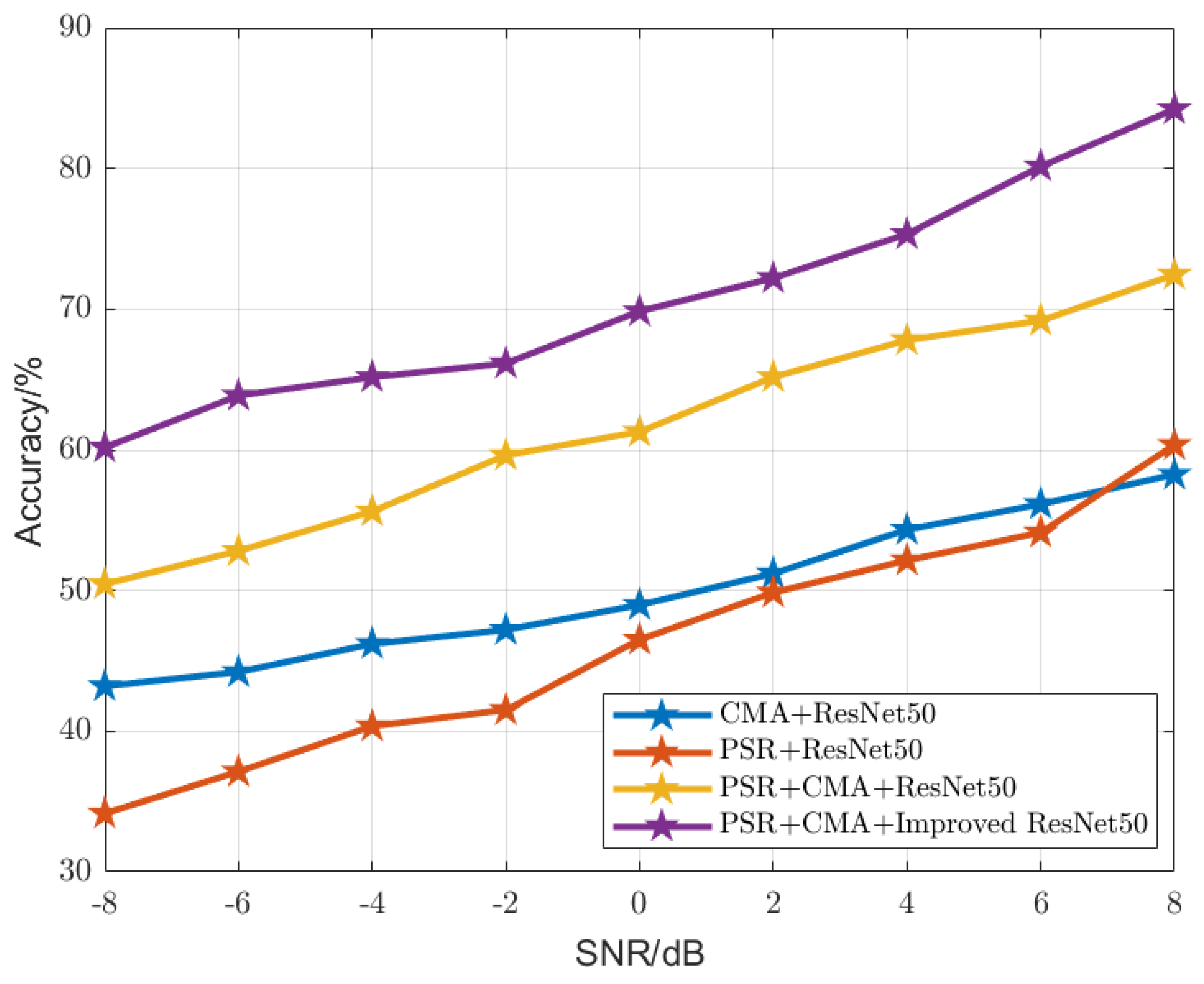
3.2.4. Ablation Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, L.-Y. Influence of receiver distortion on fingerprint characteristics of modulator in individual recognition of radiation source. Telecommun. Eng. 2021, 61, 979–985. [Google Scholar]
- Toonstra, J.; Kinsner, W. Transient analysis and genetic algorithms for classification. In Proceedings of the IEEE WESCANEX 95, Communications, Power, and Computing, Conference Proceedings, Winnipeg, MB, Canada, 15–16 May 1995; pp. 432–437. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zou, C.; Zhang, C. Aircarft signal feature extraction and recogniton based on deep learning. IEEE Trans. Veh. Technol. 2022, 71, 9625–9634. [Google Scholar] [CrossRef]
- Tang, C.; Chang, Z.-W.; Liang, H.-H.; Zhang, L.-H.; Pang, B. Feature extraction method of HPLC communication signal based on genetic algorithm. IET Commun. 2022, 17, 1553–1561. [Google Scholar] [CrossRef]
- Xin, Q.; Hu, S.-H.; Liu, S.-Q.; Zhao, L.; Zhang, Y.-D. An Attention-Based Wavelet Convolution Neural Network for Epilepsy EEG Classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 957–966. [Google Scholar] [CrossRef]
- Xing, C.-J.; Wang, L.-G. Radio individual recognition using deep neural networks and ensemble learning. Telecommun. Eng. 2021, 61, 1059–1065. [Google Scholar]
- He, K.-M.; Zhang, X.-Y.; Ren, S.-Q.; Sun, J. Identity mappings in deep residual networks. In Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016, European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Tang, J.; Deng, C.; Huang, G.-B.; Zhao, B. Compressed-Domain ship detection on spaceborne optical image using deep neural network and extreme learning machine. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1174–1185. [Google Scholar] [CrossRef]
- Doukim, C.; Dargham, J.; Chekima, A.; Omatu, S. Combining neural networks for skin detection. Signal Image Process. Int. J. 2018, 1, 1–11. [Google Scholar]
- He, B.; Wang, F. Specific Emitter Identification via Sparse Bayesian Learning Versus Model-Agnostic Meta-Learning. IEEE Trans. Inf. Forensics Secur. 2023, 18, 3677–3691. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, X.; Huang, Z. Concentrate on Hardware Imperfection via Aligning Reconstructed States. IEEE Commun. Lett. 2022, 26, 2934–2938. [Google Scholar] [CrossRef]
- Lin, S.-C.; Wang, P.; Akyildiz, I.F.; Luo, M. Towards optimal network planning for software-defined networks. IEEE Trans. Mobile Comput. 2018, 17, 2953–2967. [Google Scholar] [CrossRef]
- Ma, J.-T.; Qiu, T.-S.; Quan, T. Fast blind equalization using Bounded Non-Linear Function with Non-Gaussian noise. IEEE Commun. Lett. 2020, 24, 1812–1815. [Google Scholar] [CrossRef]
- Guo, Y.-C. Swarm Intelligence and Computational Intelligence Optimization Based Blind Equalization Algorithm; Tsinghua University Press: Beijing, China, 2018; pp. 4–5. [Google Scholar]
- Yang, D.-L.; Zhang, J.; Chen, Q.-Z. Multi-mode blind equalization carrier synchronization joint architecture and analysis. Signal Process. 2014, 30, 665–673. [Google Scholar]
- Yuan, J.; Lin, T. Equalization and carrier phase recovery of CMA and MMA in blind adaptive receivers. IEEE Trans. Signal Process. 2010, 58, 3206–3217. [Google Scholar] [CrossRef]
- Zhao, Y.-R.; Huang, Z.-T.; Wang, X. A Review of Individual Radiation Source Recognition Systems Based on Phase Space Reconstruction; School of Electronic Science, National University of Defense Technology: Changsha, China, 2022. [Google Scholar]
- Noakes, L. The Takens Embedding Theorem. Int. J. Bifurc. Chaos 1991, 1, 867–872. [Google Scholar] [CrossRef]
- Packard, N.-H.; Crutchfield, J.-P.; Farmer, J.-D. Geometry from a Time Series. Phys. Rev. Lett. 1980, 45, 712. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, C.-L. Determine the method of reconstruction phase space dimension. J. Natl. Univ. Def. Technol. 2005, 101–106. [Google Scholar]
- Kennel, M.-B.; Brown, R. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. 1992, 45, 3403. [Google Scholar] [CrossRef] [PubMed]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Qian, Y.; Qi, J.; Kuai, X.; Han, G.; Sun, H.; Hong, S. Specific emitter identification based on Multi-Level sparse representation in Automatic Identification System. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2872–2884. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.; Dobre, O.A.; Zhong, Z. Specific emitter identification via Hilbert-Huang transform in Single-Hop and relaying scenarios. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1192–1205. [Google Scholar] [CrossRef]
- Riyaz, S.; Sankhe, K.; Ioannidis, S.; Chowdhury, K. Deep learning convolutional neural networks for radio identification. IEEE Commun. Mag. 2018, 56, 146–152. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Comput. Vis. Pattern Recognit. 2015, 770–778. [Google Scholar]
- Liu, J.-L.; Jiang, Q.; Wang, J.; Huang, H. Specific emitter identification at different time based on multi-domain migration. In Proceedings of the 2022 APSIPA Annual Summit and Conference, Chiang Mai, Thailand, 7–10 November 2022. [Google Scholar]

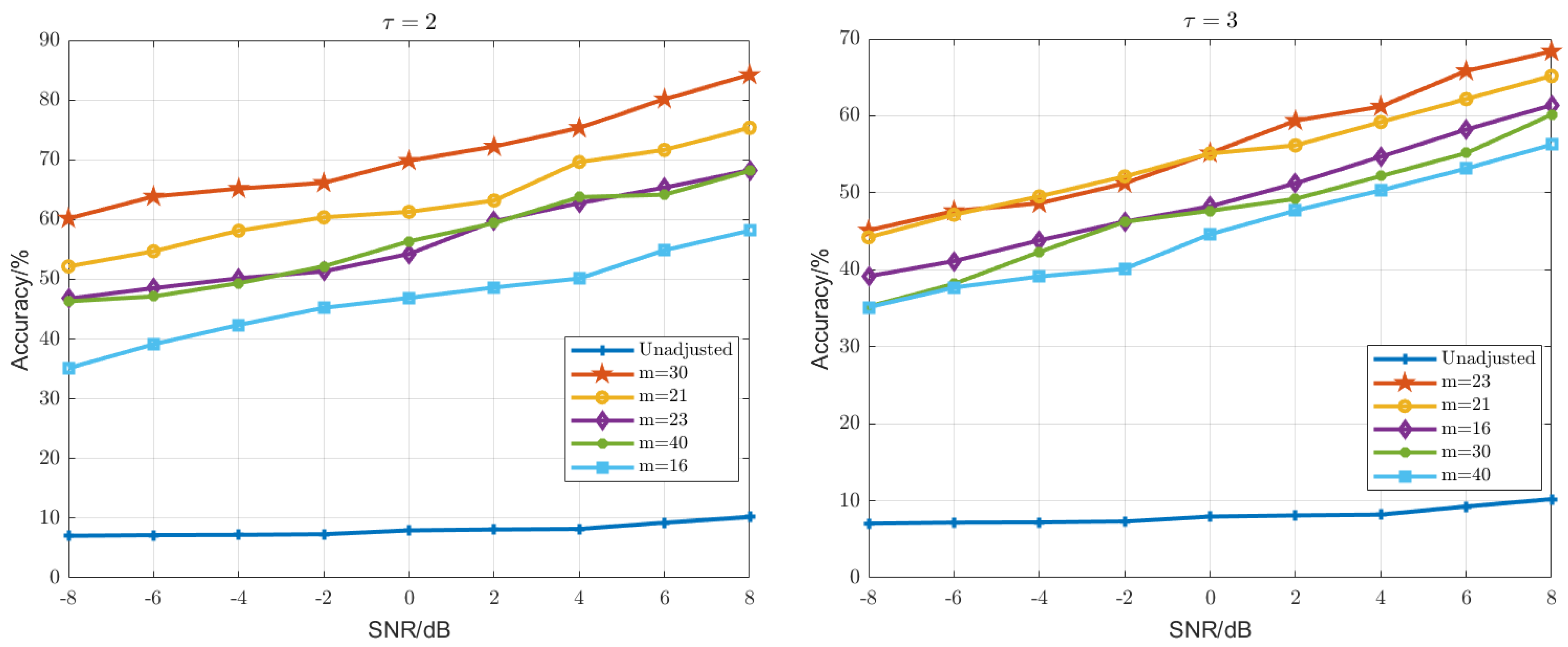
| Radio | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| m | 21 | 23 | 16 | 30 | 21 | 23 | 40 | 30 | 30 | 16 |
| 3 | 2 | 2 | 2 | 2 | 2 | 3 | 2 | 2 | 2 |
| SNR | −8 | −6 | −4 | −2 | 0 | 2 | 4 | 6 | 8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Algorithms | ||||||||||
| 43.12% | 45.68% | 46.39% | 48.31% | 51.88% | 53.19% | 54.36% | 55.28% | 57.58% | ||
| 46.91% | 48.67% | 51.28% | 52.91% | 54.04% | 55.24% | 57.31% | 59.82% | 61.93% | ||
| 60.88% | 62.27% | 64.11% | 65.97% | 67.82% | 69.08% | 72.34% | 74.86% | 76.11% | ||
| 60.28% | 63.89% | 65.28% | 66.48% | 70.31% | 73.67% | 76.68% | 81.39% | 84.21% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Lei, Y.; Jin, H.; Teng, F.; Lou, C. Specific Emitter Identification Based on Attractor Feature Space of System under Blind Equalization. Electronics 2024, 13, 611. https://doi.org/10.3390/electronics13030611
Shi W, Lei Y, Jin H, Teng F, Lou C. Specific Emitter Identification Based on Attractor Feature Space of System under Blind Equalization. Electronics. 2024; 13(3):611. https://doi.org/10.3390/electronics13030611
Chicago/Turabian StyleShi, Wenqiang, Yingke Lei, Hu Jin, Fei Teng, and Caiyi Lou. 2024. "Specific Emitter Identification Based on Attractor Feature Space of System under Blind Equalization" Electronics 13, no. 3: 611. https://doi.org/10.3390/electronics13030611
APA StyleShi, W., Lei, Y., Jin, H., Teng, F., & Lou, C. (2024). Specific Emitter Identification Based on Attractor Feature Space of System under Blind Equalization. Electronics, 13(3), 611. https://doi.org/10.3390/electronics13030611





