A Hybrid Group Multi-Criteria Approach Based on SAW, TOPSIS, VIKOR, and COPRAS Methods for Complex IoT Selection Problems

Abstract

The growth of Internet of Things (IoT) systems is driven by their potential to improve efficiency, enhance decision-making, and create new business opportunities across various domains. In this paper, the main selection problems in IoT-type systems, criteria used in multi-criteria evaluation, and multi-criteria methods used for solving IoT selection problems are identified. Then, a Hybrid Group Multi-Criteria Approach for solving selection problems in IoT-type systems is proposed. The approach contains the Best Worst Method (BWM) weighting method, multi-criteria Simple Additive Weighting (SAW), Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS), VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), and Complex Proportional Assessment Method (COPRAS), and a method that combines the solutions obtained using the four considered multi-criteria methods to obtain a single solution. The SAW, TOPSIS, VIKOR, and COPRAS methods were analyzed in relation to their advantages, disadvantages, inputs, outputs, measurement scale, type of normalization, aggregation method, parameters, complexity of implementation, and interactivity. An application of the Hybrid Group Multi-Criteria Approach for IoT platform selection and a comparison between the SAW, TOPSIS, VIKOR, and COPRAS solutions and the solution of the proposed approach is realized. A Spearman correlation analysis is presented.

1. Introduction

The growth of IoT systems is driven by their potential to improve efficiency, enhance decision-making, and create new business opportunities across various domains. As the ecosystem continues to evolve, it is expected that IoT will become increasingly integrated into our daily lives and industries, further shaping the way we interact with and understand the world. In 2022, the Global Internet of Things (IoT) market was valued at USD 347,313.43 million. This market is expected to increase to USD 1,029,962.66 million by 2029, while growing at a Compounded Annual Growth Rate (CAGR) of 16.8% [1]. As the IoT landscape continues to evolve and expand, organizations must carefully evaluate and select IoT solutions to meet their specific objectives, while addressing the unique challenges posed by the growth of IoT systems.

IoT applications have spread to almost every aspect of human activity, including consumer, commercial, industrial, and infrastructure applications [2]. IoT systems are expected to make a significant impact in various domains, including Smart Cities (to improve the efficiency of city services), Smart Homes (to automate and control various home appliances), healthcare (to monitor patients remotely and improve the efficiency of healthcare services), Transportation and Logistics (to improve the efficiency of transportation systems), Industrial IoT (to optimize industrial processes and improve supply chain management), Agriculture (for precision farming, smart irrigation, livestock monitoring).

The main selection problems in IoT-type systems are related to the selection of IoT devices, sensors, technologies, applications, service providers, protocols, communication networks, IoT services, or platforms in different fields such as Smart Cities, healthcare Smart Agriculture and Water Management, Retail and Logistics, Smart Living, Smart Environment [3], Industry 4.0 [4], and Supply Chain [5]. The domains where selection problems arise include IoT vendor selection and IoT design. Solving problems related to equipment procurement, software applications, or platforms and the realization of IoT-type systems require a selection process which plays a critical role in organization management. The selection procedure is difficult for several reasons. IoT encompasses a wide range of devices, sensors, communication protocols, applications, platforms, and technologies from different manufacturers in the market. Selection decisions must account for changing conditions and adaptability in dynamic and unpredictable environments. Another reason is the great diversity of functions, solutions, and performance levels offered by IoT platforms, technologies, and applications. IoT selection decisions involve multiple criteria such as cost, power consumption, data accuracy, security, and reliability. Customer preferences play a key role in determining the relative importance of these criteria. Balancing these criteria to meet specific objectives is a challenge. Cost is a significant factor for IoT projects. Selecting cost-effective components that align with budget constraints without sacrificing quality is a delicate balancing act.

This type of problem, in which an alternative is chosen from a set of alternatives, evaluated according to several criteria considered simultaneously, and which are often conflicting, falls into the category of multi-criteria problems. These problems can be solved using multi-criteria decision methods. In a multi-criteria problem, a set of alternatives is evaluated in relation to a set of criteria. The alternatives that can be considered in IoT selection problems can be IoT sensors, devices, technologies, communication channels, applications, or platforms. These are evaluated according to several criteria that are characteristic to each IoT selection problem. The goal of solving the multi-criteria problem is to find the best alternative or a ranking of the set of alternatives. Multi-criteria methods can help address selection problems by providing a structured approach for evaluating and comparing different alternatives based on multiple criteria. The selection depends on the application field of IoT and the criteria considered. Research related to multi-criteria selection in IoT problems has evolved significantly in recent years to address the growing complexity and importance of decision-making in IoT deployments.

Based on the literature, the main selection problems in IoT-type systems, criteria used in evaluation, and multi-criteria methods used for solving IoT selection problems were identified. Then, a Hybrid Group Multi-Criteria Approach for solving selection problems in IoT-type systems is proposed. The approach is based on the BWM weighting method, the multi-criteria SAW, TOPSIS, VIKOR, and COPRAS methods, and a method that combines the solutions obtained with the help of the above considered multi-criteria methods to obtain a single solution. The four considered methods were analyzed in relation to their advantages, disadvantages, inputs, outputs, measurement scale, type of normalization, aggregation method, parameters, complexity of implementation, and interactivity. An application of the Hybrid Group Multi-Criteria Approach for the IoT platform selection is presented. A comparison between the solutions of the four methods considered and the solution of the hybrid proposed method were achieved.

This paper’s contributions are as follows:

• The proposal of a Hybrid Group Multi-Criteria approach that includes BWM as a weighting method, the SAW, VIKOR, TOPSIS, and COPRAS multi-criteria methods as well as an original method for combining the SAW, VIKOR, TOPSIS, and COPRAS solutions to obtain a unique solution.
• The application of the proposed Hybrid Group Multi-Criteria approach in a case study for the selection of an IoT platform from a given set of IoT platforms.
• A comparative study of the SAW, VIKOR, TOPSIS, and COPRAS methods about the advantages, disadvantages, approach, type of normalization, inputs, outputs, measurement scale, aggregation method, best alternative, level of complexity, and interactivity.

The paper is organized as follows. In Section 2, an analysis of relevant research in the field of IoT selection problems through multi-criteria methods is performed. The motivations for the choice of the SAW, VIKOR, TOPSIS, and COPRAS methods for solving selection problems in IoT and a comparison of these methods are provided in Section 3. The proposed Hybrid Group Multi-Criteria Approach is described in Section 4. In Section 5, the application of the proposed approach for the selection of an IoT platform are presented. A comparison of the Hybrid Group Multi-Criteria Approach solution with each of the SAW, VIKOR, TOPSIS, and COPRAS solutions obtained is made. Section 6 concludes the paper.

2. Multi-Criteria Methods for IoT Selection Problems

Selection problems in IoT differ from general selection problems due to the unique characteristics and challenges associated with IoT systems. Evaluation and selection problems in IoT are distinct because they involve a unique set of considerations related to complexity, heterogeneity, scalability, security, data quality, and interoperability. IoT systems are often complex, involving multiple and different devices and sensors using different protocols and standards and this complexity and heterogeneity make it challenging to evaluate alternatives and select the best solution [5,6,7]. The IoT scalability (new devices and sensors are being added continuously) makes it challenging to select a solution that can accommodate future growth. Security is a critical concern in IoT, as it involves the protection of sensitive data and systems from unauthorized access, theft, or damage. IoT devices are often vulnerable to cyber attacks due to their increased exposure to the internet and their limited computing resources. IoT systems generate large amounts of data, which can be noisy, incomplete, or inconsistent. Ensuring the quality of data and security is crucial for making informed decisions and selecting the best solution. The selection process should be scalable to accommodate varying IoT system sizes. IoT systems are subject to regulations and standards related to data privacy, security, and environmental factors. Selection decisions must align with legal and compliance requirements.

The complexity, multidimensionality, and importance of selection decisions in IoT-type systems make multi-criteria methods a valuable tool for solving selection problems. They enable decision makers to navigate the intricacies of IoT environments, make informed choices, and optimize resource allocation to achieve their objectives effectively. IoT-type systems involve a multitude of alternatives (e.g., devices, sensors, protocols, technologies, applications, platforms) and criteria (e.g., cost, reliability, energy efficiency, security, compatibility). IoT selection problems often entail trade-offs between competing criteria. For example, selecting a more cost-effective device might compromise performance or security, and prioritizing energy efficiency may conflict with achieving a high performance.

Multi-criteria methods provide a structured approach to handle the complexity of evaluating these alternatives against multiple criteria simultaneously, effectively managing trade-offs, identifying compromise solutions, and considering both quantitative and qualitative aspects. IoT environments are dynamic and are subject to changes in technology, regulations, and user requirements. Multi-criteria methods can adapt to evolving criteria or incorporate new criteria as needed. IoT selection decisions may involve risks and uncertainties related to the data, technology, or external factors. Multi-criteria methods can incorporate probabilistic models and sensitivity analyses to assess and mitigate these uncertainties. IoT selection decisions often affect various stakeholders, including users, manufacturers, and regulatory bodies.

Some of the classic or newer multi-criteria methods used in selection problems in IoT are as follows: SAW—Simple Additive Weighting [8], ELECTRE—ÉLimination Et Choix Traduisant la REalité [9], AHP—Analytic Hierarchy Process [10], DEA—Data Envelopment Analysis [11], TOPSIS—Technique for Order Preference by Similarity to an Ideal Solution [12], PROMETHEE—Preference Ranking Organisation Method for Enrichment Evaluations [13], OWA—Ordered Weighted Averaging [14], TODIM—Interactive and Multi-criteria Decision Making in Portuguese [15], COPRAS—Complex Proportional Assessment Method [16], ANP—Analytic Network Process [17], VIKOR—VIseKriterijumska Optimizacija I Kompromisno Resenje [18], MOORA—Multi-Objective Optimization on the basis of Ratio Analysis [19], DBA—Distance-Based Approach [20], MABAC—Multi-Attribute Border approximation Area Comparison [21], MEREC—MEthod based on the Removal Effects of Criteria [22], CRADIS—Compromise Ranking of Alternatives from Distance to Ideal Solution [23]. The criteria can have different or equal weights. The weights or importance of the evaluation criteria can be determined using multi-criteria weighting methods. Examples of multi-criteria weighting methods are as follows: Entropy method [24], DEMATEL—Decision-Making Trial and Evaluation Laboratory [25], AHP [10], SMART—Simple Multi-Attribute Rating Technique [26], CRITIC—Criteria Importance Through Intercriteria Correlation [27], SWARA—Step-Wise Weight Assessment Ratio Analysis [28], WASPAS—Weighted Aggregated Sum Product Assessment [29], WINGS—Weighted Influence Non-linear Gauge System [30], BWM—Best–Worst Method [31], FWZIC—Fuzzy Weighted with Zero Inconsistency [32]. A summary of criteria weighting methods is presented in [33].

In the summary in

Table 1. A bibliographical study regarding the application of multi-criteria methods for selection problems in IoT systems.

Reference	Year	IoT Selection Problem	Multi-Criteria Method/Methods	Criteria
[34]	2017	Selection of IoT sensors	SAW + TOPSIS + VIKOR	Battery, price, frequency, energy consumption, response time.
[35]	2017	Selection of IoT service	ANP + TOPSIS	Response time, reliability.
[36]	2017	Selection of IoT devices	AHP	Energy, implementation time, hardware build/adaptation, cost, clock.
[37]	2017	Selection of IoT hardware platform	AHP	Energy, cost, clock, memory, memory used.
[38]	2018	Selection of IoT technology	AHP	Reliability, security, business, mobility, and heterogeneity.
[39]	2018	Prioritization of development factors for IoT technologies	Fuzzy ANP	Security and privacy factors, legal and regulatory factors, technological factors, cultural factors, business factors.
[40]	2018	Selection of cloud IoT services	Fuzzy AHP + Fuzzy TOPSIS	Availability, speed, capacity, cost, privacy.
[41]	2019	Selection of IoT sensors	R-Tree + TOPSIS	Lifetime, sensitivity, measurement accuracy, response time, start-up time, and power consumption.
[42]	2019	Selection of IoT platform	Multi-objective method with classification approach for weights	Reliability, trust, safety, and security.
[43]	2020	IoT service selection	Fuzzy TOPSIS + OWA	QoS metrics related to computing capacity, communications, and to objects.
[44]	2020	Selection of IoT applications	AHP + SAW	Smart objects (cost, power consumption, installation, interoperability), IoT application (ease of use, interface, privacy, reliability, and availability), vendor (customer support, reputation, number of customers).
[45]	2020	Selection of IoT service providers	AHP + TOPSIS	QoS metrics related to computing capacity, to communications, and to objects.
[46]	2020	Selection of IoT devices	DEMATEL, ANP și COPRAS	Cost, security, and reliability.
[47]	2020	Selection of IoT devices	AHP, ELECTRE	Power consumption, implementation time, hardware built/adapted, cost, and processing speed of the solution.
[4]	2020	Industrial IoT platform selection	AHP + PROMETHEE II	Technical (available region, managed integration, communication protocols, security, device management, display, variety of data analytics), economic (longevity in market, cost, free cost, training cost), social (community support, available resources, training).
[48]	2020	IoT platform selection	Probabilistic Linguistic BWM + Probabilistic Linguistic TODIM method.	Pricing, availability, integration flexibility, unique features, usability, security, market longevity, scalability.
[49]	2021	IoT cloud platform selection, with emphasis on specific user priorities	Weights estimation by fuzzy sets + DBA	Quality (functionality, reliability, usability, efficiency, maintainability, and portability), technical (storage capacity, CPU performance, memory usage, platform design, and network speed), and economic (service induction cost, maintenance cost, and promotion cost).
[50]	2021	Selection of IoT devices for Cyber–Physical Systems	AHP + PROMETHEE, ELECTRE	Power consumption, implementation time, built/adapted hardware, cost, and processing speed.
[51]	2022	Selection of IoT platform	Fuzzy TOPSIS	Return on investment, flexibility to change the IoT platform, performance, sustainability, maturity level, security, support services provided by the platform, previous relationships with the IoT platform provider company, IoT ecosystem strength, service scope and usability of IoT platform.
[52]	2022	Selection of IoT platform	Group TOPSIS	Privacy and security, operational handling, access to operations, process management, data set management, data communication and analysis.
[53]	2022	IoT solution selection in a fuzzy environment	MABAC with a specific distance measure via intuitionistic fuzzy values	Scalability, flexibility, data analytics, disaster recovery, stability, security, data ownership, protocol support, system performance, time to market, legacy architecture, attractive interface, pricing model, cloud ownership, interoperability, app. environment, hybrid cloud, platform migration, previous experience, edge intelligence, bandwidth.
[54]	2022	Benchmarking blockchain-based IoT healthcare Industry 4.0 systems	Spherical FWZIC + Grey Relational Analysis TOPSIS	User authentication, access control, privacy protection, integrity availability, and anonymity.
[55]	2023	IoT communication network selection	I-MEREC + TOPSIS	Bandwidth, delay, jitter, packet loss rate, bit error rate, and price.
[56]	2023	IoT service provider selection	CRITIC + fuzzy CRADIS	Usability, scalability, availability, innovation, privacy/security, and total cost.
[5]	2023	Evaluating and selecting a blockchain technology IoT platform in Supply Chain networks	Interval WINGS + VIKOR	Popularity and support (market recognition, community activity, previous experiments in deploying the platform to the sector, support plan for small partners (suppliers and retailers)), transition simplicity (cost-effective transition plan, agile and clear transition roadmap, high-quality documentation of platform information, interactivity with current platforms), supply chain operational features (improving the traceability of cargo, improving the traceability of inventory, customer-specific traceability feature, verifiable record of transactions among parties (supplier, distributors, retailers), supply chain analytics, integration with financing institutions, banks, and insurance, fraud traceability, property tokenizing), technical (modular architecture, performance efficiency, security, reliability, extensibility, privacy of customers).
[57]	2023	Selection of highly efficient IoT applications	Fuzzy TOPSIS	Ease of use, energy consumption, interoperability, privacy, availability, interface, customer service.

, the relevant results regarding the application of multi-criteria methods in selection problems in IoT systems are presented.

In [58,59], reviews of the literature on selection in IoT systems (selection methods and criteria) are carried out.

The results of the analysis carried out regarding the use of multi-criteria methods for solving selection problems in IoT systems highlight that the most used methods are AHP, TOPSIS, and SAW, and combinations of these methods with other methods. The AHP method is used particularly for the calculation of criteria weights. It is also used in combination with other multi-criteria methods. Both classic and newer methods are used, and many approaches are hybrid approaches or combinations of methods. The selection issues addressed are the selection of devices, sensors, applications, platforms, service providers, communication networks, IoT services for different fields: industry IoT, Supply Chain networks, healthcare, Cyber–Physical Systems. The criteria considered differ depending on the type of selection problem.

3. Choosing Multi-Criteria Methods for Solving Selection Problems in IoT

There is rich literature related to decision theory and Multi-Criteria Decision Making (MCDM), as well as their applications. A survey of MCDM approaches has been provided in [60,61,62]. There are many multi-criteria methods that differ in various aspects. Thus, some of these aspects are the typology of the decision problem, number of alternatives, or method of aggregation. Different classifications have been made. According to the type of decision problem, multi-criteria methods can be ranked (ordering the alternatives from the most preferred to the least preferred), ordinal sorting/classification (assigning the alternatives to predefined decision classes ordered according to preferences), clustering (dividing the alternatives into groups according to a measure of similarity or preference relations), and choosing (selecting the most preferred subset of alternatives) [63]. In [64], multi-criteria methods are classified according to the aggregation procedure, as follows: methods based on outranking relationships, utility functions, discrimination functions, and without functions. In [12], multi-criteria methods are classified into Multi-Objective Decision Making (MODM) and Multi-Attribute Decision Making (MADM). In MODM, the set of alternatives is infinite, whereas in MADM, the number of alternatives is finite. It is important to note that these classes were not mutually exclusive. For example, some methods may be used in both MADM and MODM categories.

In general, each multi-criteria method has its own advantages and disadvantages when used in the IoT selection problems. The choice of method depends mainly on the specific problem addressed, available data, and preferences of the decision makers.

Different MCDA methods may produce conflicting recommendations, making it challenging for decision makers to reconcile and choose a final solution. This can lead to uncertainty and confusion. Different MCDA methods may require different types of input data, criteria weighting schemes, and assumptions. Subjective choices made during the application of each method can lead to inconsistencies and potential biases in the final decision.

From a multitude of multi-criteria methods, in our multi-criteria approach, we selected four frequently used methods: SAW, VIKOR, TOPSIS, and COPRAS. These methods can be applied to the selection process in the IoT context. The choice of this set is dictated by the properties and popularity of these methods.

A brief presentation of the SAW, TOPSIS, COPRAS, and VIKOR advantages and disadvantages are presented in

Table 2. A brief presentation of the SAW, TOPSIS, COPRAS, and VIKOR advantages and disadvantages.

Multi-Criteria Method	Year	Advantages	Disadvantages
SAW	1968	Simple and easy to use. Does not require complex mathematical calculations. Can handle large data sets. Suitable for IoT selection problems with independent criteria. Intuitive method with simple algorithm.	Sensitive to the choice of weights. Does not handle negative values. Ignore the interdependence between criteria. It is necessary to convert the criteria of minimization into maximization.
TOPSIS	1981	Can handle both quantitative and qualitative data. Can handle negative values. Provides a simple way to rank the alternatives based on their similarity to the ideal solution. Relatively easy to understand and implement. Suitable for large-scale data.	Sensitive to variations in criteria weights and normalization methods. Does not take into account the relationships between the criteria. A strong deviation of an indicator from the ideal solution strongly influences the results. Problem of rank reversal.
COPRAS	1996	Allows for the interdependence of criteria. Incorporates flexibility in modeling the preferences of decision makers. Suitable for complex IoT selection problems with multiple criteria. Does not require criteria minimization.	Sensitive to the choice of criteria. Does not handle negative values. The complexity of the method can create challenges for inexperienced users. Less stable in case of data variation compared to other methods.
VIKOR	2002	Can handle both quantitative and qualitative data. Provides a compromise solution that balances conflicting criteria. Usable for problems with difficulties in expressing preferences.	Can be sensitive to changes in weights and thresholds. Complexity increases with the number of criteria and alternatives. Requires initial weights that are not equal.

[65,66,67,68,69].

These methods consider the same type of input data, and a solution process is generally common. Unlike these methods, the AHP and ANP methods consider the evaluation of the criteria in pairs to establish their weights, which implies effort and subjectivity for a large number of criteria. ELECTRE and PROMETHEE are outranking methods and require the choice of parameters and functions, which implies subjectivity. They are more complex and difficult to use methods for an increased number of criteria. Multi-criteria methods that consider the evaluation of the criteria in pairs (example: AHP and ANP) or those of the outranking type (example: ELECTRE and PROMETHEE) are not considered in the proposed approach because they use a different type of evaluation. The chosen multi-criteria methods start from the same set of input data and from the same type of evaluation of the alternatives relative to the criteria.

SAW, VIKOR, TOPSIS, and COPRAS are all decision-making methods used in Multi-Criteria Decision Analysis (MCDA) to rank and select the best alternatives from a set of alternatives. Combining these methods can provide a comprehensive approach to decision-making, considering different aspects.

SAW is a straightforward method for MCDM. It calculates a score for each alternative by multiplying the criterion value by its respective weight and summing these scores. The alternative with the highest score is chosen as the best.

VIKOR is a method that aims to find a compromise solution when there is a trade-off between conflicting criteria. It considers both the “maximum group utility” and “individual regret” to rank alternatives. VIKOR helps identify alternatives that strike a balance between different criteria.

TOPSIS is a method used to determine the best alternative by comparing each alternative’s similarity to the ideal solution. It calculates the distance between each alternative and the ideal solution and the worst solution based on the criteria considered. The alternative that is closest to the ideal solution and farthest from the worst solution is considered the best.

COPRAS is a method that considers the interdependencies between criteria and alternatives. It uses a complex proportional assessment approach to rank alternatives based on weighted criteria.

SAW was chosen for its simplicity and ease of implementation. The simplicity of SAW makes it a good complement to more complex methods in a hybrid approach. TOPSIS was chosen for its ability to consider both the best and worst solutions, providing a comprehensive ranking. TOPSIS complements SAW by addressing some of its limitations, such as sensitivity to weight assignments. VIKOR was chosen for its consideration of both the best and worst solutions, providing a compromise solution. VIKOR complements SAW and TOPSIS by introducing a compromise perspective, particularly relevant in decision problems with conflicting criteria. COPRAS was chosen for its ability to handle the interdependence and feedback effects between criteria. COPRAS complements the other methods by explicitly considering the relationships and interdependencies between criteria.

Together, these methods offer a comprehensive evaluation framework, considering the best, worst, compromise, and interdependent aspects of decision problems.

The combination of these methods allows for a more comprehensive assessment of alternatives, considering both the individual and collective aspects of criteria, trade-offs, and the stability of rankings.

These methods provide systematic approaches to evaluate and rank alternatives based on multiple criteria in IoT selection. The steps involved in each method may vary slightly, but the general process includes criteria identification, scoring or rating assignment, normalization, weighting, the calculation of aggregate values, and the ranking of alternatives.

Each method has its strengths and limitations in the context of IoT selection. SAW is simple and straightforward but may overlook criteria interactions. TOPSIS accounts for positive and negative aspects but is sensitive to extreme values. VIKOR provides a compromise solution for conflicting objectives but relies on subjective weight determination. COPRAS considers complex interdependencies but involves more complex calculations and subjective comparisons. TOPSIS is appropriate for prudent decision makers (e.g., risk averters) because they yearn for a compromise choice that has as much profit as possible and as least risk as possible at the same time. On the contrary, the value of compromise choices depends upon the group utility and individual regret in a VIKOR method. VIKOR method proposes a compromise solution with an advantage rate [18]. The SAW, TOPSIS, VIKOR, and COPRAS algorithms are considered to be among the most versatile algorithms that can be implemented using any kind of computer hardware system.

The choice of SAW, TOPSIS, VIKOR, and COPRAS and their synergies ultimately depends on the specific characteristics of the decision problem (selection process in the IoT context), simplicity and intuitiveness, the consideration of compromise solutions, robustness and flexibility, data availability and quality, the level of involvement and preferences of the decision-maker, sensitivity to criteria weights, and the handling of interactions.

A comparison of SAW, TOPSIS, VIKOR, and COPRAS is presented in

Table 3. A comparison of SAW, TOPSIS, VIKOR, and COPRAS.

	SAW	TOPSIS	VIKOR	COPRAS
Approach	In SAW, the ranking is based on the weighted sum of performance scores.	TOPSIS calculates the distances of each alternative from the ideal and negative ideal solutions and ranks based on relative closeness.	VIKOR determines the compromise solution by considering the maximum group utility and the minimum individual regret.	COPRAS evaluates alternatives by comparing their performance profiles with the best and worst profiles to determine dominance degrees.
Type of normalization	“max” normalization method	“vector” normalization method	“max-min” (linear) normalization method	“sum” normalization method
Inputs	A decision matrix obtained by the evaluation of all the alternatives in terms of each criterion. The criteria weight.	A decision matrix obtained by the evaluation of all the alternatives in terms of each criterion. The criteria weight.	A decision matrix obtained by the evaluation of all the alternatives in terms of each criterion. The criteria weight. A parameter that shows the balance between the global benefit and the maximum individual deviation.	A decision matrix obtained by the evaluation of all the alternatives in terms of each criterion. The criteria weight.
Outputs	Alternative ranking	Alternative ranking	Alternative ranking	Alternative ranking
Measurement Scale	Quantitative and qualitative	Quantitative and qualitative	Quantitative and qualitative	Quantitative and qualitative
Aggregation	Weighted sum of performance scores	Positive and negative ideal solutions, Euclidian distance	Importance and utility degree (Manhattan and Minkowski Distance)	Maximization indices, minimization indices, Relative Significance Value
Best alternative	Max value	Max value	Min value	Max value
Complexity	Very Low	Low	Low	Low
Interactivity	Low	Low	Moderate due to compromise solution adjustments	Moderate due to complex assessments
Applications in IoT problem selection	Selection of IoT sensors [34], selection of IoT applications [44]	Selection of IoT sensors [34,41], selection of IoT service [35,40,43], selection of IoT platform [51,52]	Selection of IoT sensors [34], selecting an IoT platform in Supply Chain networks [5]	Selection of IoT devices [47]
Comparisons between the methods	[65,68,69]	[65,66,67,69]	[65,66,67]	[65,66,67,68]

[65,66,67,68,69].

In [65], a comparison was made between the SAW, TOPSIS, ELECTRE, VIKOR, and COPRAS methods, considered separately, in the field of energy technology selection. It was found that changes in the weights had the greatest impact on the performance of the options. These methods were not combined but only analyzed independently. The article in [66] compares the TOPSIS, VIKOR, COPRAS, and PROMETHEE II methods. The analysis was carried out for various weighing methods and varied techniques of normalization of MCDA model input data. The comparative analyses showed the detailed influence of the values of particular parameters on the final form and similarity of the final rankings obtained by these methods. A comparison between the results obtained with the TOPSIS, VIKOR, and COPRAS methods for the COVID-19 Regional Safety Assessment is made in [67]. The rankings resulting from the application of the methods were compared with the rankings resulting from the application of a method presented in a report of the Deep Knowledge Group (DKG) consortium. Accordingly, it has been observed that the method that provides the closest results to the results of the report is the COPRAS method, and the method that gives the most distant results is the VIKOR method. A comparative analysis of solutions of the MCDA methods SAW and COPRAS is performed in [68] and a comprehensive comparison of solutions of SAW, TOPSIS, the Linear Programming Technique (LINMAP), VIKOR, Elimination and Choice Translating Priority III (ELECTRE-III), and the Net Flow Method (NFM) for industrial robot selection problems are performed [69].

In the above papers, solutions based on the combination of SAW, TOPSIS, VIKOR and COPRAS methods, taken together, were not considered. Only a comparison was made between the results obtained by each individual method.

A combination between the VIKOR and TOPSIS multi-criteria methods was made in [70] and a combination between SAW and TOPSIS was made in [71].

In this paper, a combination of these methods is proposed in a hybrid approach, resulting a unique solution based on the solutions obtained by each method separately. Combining TOPSIS, VIKOR, SAW (Simple Additive Weighting), and COPRAS in a multi-criteria hybrid approach offers several advantages that can lead to more robust and well-informed decisions. By using multiple methods, the risk of decision bias that may result from relying on a single approach can be reduced. Different methods provide different perspectives, helping to counterbalance biases. VIKOR is particularly useful for handling conflicting objectives. It identifies compromise solutions that strike a balance between competing criteria, helping to find alternatives that meet multiple, often conflicting, goals. TOPSIS calculates the distance between each alternative and the ideal and worst solutions. This helps identify alternatives that are closest to the ideal and farthest from the worst, providing a clear ranking. The combination of multiple methods provides a more robust and defensible decision-making process. This can enhance decision makers’ confidence in the selected alternative.

However, it is important to note that while combining these methods can offer advantages, it also adds complexity to the decision-making process. This complexity may be unwarranted for simpler decision problems and can make it challenging for decision makers to understand and manage the process effectively. Implementing and executing multiple MCDA methods can be resource-intensive in terms of time, effort, and data requirements. This may not be practical for all decision problems.

From the weighting methods, the BWM was selected for our approach. The BWM is one of the recent methods based on peer-to-peer comparison. In the BWM, two criteria are chosen from a set of n criteria: the most important (best) criterion and the least important (worst) criterion. Instead of assigning precise numerical weights to numerous criteria, decision makers only need to make pairwise comparisons between criteria. The pairwise comparisons are made for the most important criterion with each criterion and for the least important with each criterion. The consistency of pairwise comparisons is verified. If the pairwise comparisons are not consistent, the evaluation is repeated. The BWM is considered robust because it can handle inconsistencies in judgments. In order to calculate the criteria weights, a mathematical programming model is solved. Unlike the AHP, which involves an n × n matrix of pairwise comparisons, the BWM involves two vectors of the comparison of each criterion with the best and worst criteria. The BWM requires fewer pairwise comparisons than the AHP, and thus the complexity and the time required for experts to evaluate the criteria is greatly reduced. For the AHP, a number of n(n − 1)/2 pairwise comparisons are required; whereas, in the BWM, a number of 2n − 3 comparisons of the criteria with the best and the worst criterion are required. The BWM uses a simpler scale from 1 to 9. The AHP uses a larger scale from 1/9; 1/8, …, 1, 2, …, 9. This gives an advantage to the BWM over the AHP because the number of comparisons is smaller. In the case of inconsistency, a need to revise the AHP matrix comparisons is necessary. Revising pairwise comparisons for two vectors of the BWM is a much easier task than revising pairwise comparisons from a n × n matrix in the AHP. In the SMART method, only one comparison vector is necessary. From this point of view, SMART is very efficient in terms of the time required for comparisons. The main weakness is that the consistency of the pairwise comparisons cannot be easily verified.

4. The Hybrid Group Multi-Criteria Approach

The Hybrid Group Multi-Criteria Approach is a combination of the criteria weighting method BWM, the SAW, VIKOR, TOPSIS, and COPRAS multi-criteria methods and a combination method of the SAW, VIKOR, TOPSIS, and COPRAS solutions. The weights of the criteria obtained by the BWM are used in the multi-criteria methods SAW, VIKOR, TOPSIS, and COPRAS. Each of these methods leads to a ranking of the alternatives. A method that combines these solutions is proposed and a final rank of the alternatives is obtained. The combination of the SAW, VIKOR, TOPSIS, and COPRAS methods can provide a comprehensive approach to decision-making, considering different aspects of this method, a more comprehensive assessment of the alternatives, considering both the individual and collective aspects of the criteria, trade-offs, and the stability of the rankings.

The hybrid approach is presented in the following steps. In the first part (steps 1–6), the group BWM for calculating the criteria weights is presented. In the second part (steps 7–12), the SAW, VIKOR, TOPSIS, and COPRAS methods are presented, in parallel. Finally, in step 13, the combined method of the SAW, VIKOR, TOPSIS, and COPRAS solutions is presented. The result obtained is the ranking of the alternatives.

4.1. The Group BWM Method

Step 1. The group $D=\left\{D_1,D_2,\dots ,D_p\right\}$ of p DM (experts) is chosen. The DM group selects the set of n criteria $C=\left\{C_1,C_2,\dots ,C_n\right\}$. A criterion$C_{\mathrm{i}}$ can be a maximum (benefit) or minimum (cost) criterion. To each criterion from the set C of criteria can be assigned a weight (coefficient of importance). The n-dimensional vector with criteria weights is denoted by $\mathbf{w}=\left(w_j\right),j=1,2,\dots n$. The weights usually have numerical values in the range (0;1) and ${\sum }_{i=1}^n{w}_i=1$. The weight $w_i$shows the importance of the criterion $C_j$.

Step 2. Each DM, let us say $D_k$, $k=1,\dots ,p$, selects the best criterion $C_B^k$ and the worst criterion $C_W^k$ from the set C.

Step 3. For each DM, let us say $D_k$, $k=1,\dots ,p$, the preference of the best criterion $C_B^k$ over the other criteria, using a scale of scores from 1 to 9, is determined by pairwise comparisons. A vector ${\mathbf{a}}_B^k=\left(a_{Bj}^k\right); j=1,2,\dots ,n$ is obtained for each DM. Here, $a_{Bj}^k$ denotes the preference of criterion $C_B^k$ over criterion C_j for the k DM.

Step 4. For each $D_k$, the preference of all the criteria over the worst criterion $C_W^k$ using a scale of scores from 1 to 9 is determined by pairwise comparisons. A vector ${\mathbf{a}}_W^k=\left(a_{jW}^k\right); j=1,2,\dots ,n$ is obtained for each $D_k$. Here, $a_{jW}^k$ denotes the preference of criterion C_j over criterion $C_W^k$ for the $D_k$.

Step 5. To obtain the most consistent weights with the pairwise comparisons for every $k=1,\dots ,p,$ the following programming problem is considered:

$$\left\{\begin{array}{c}\begin{array}{c}\min \left[\underset{1\le j\le n}{\max }\left(\left|a_{Bj}^k{w}_j^k-w_B^k\right|,\left|a_{jW}^k{w}_W^k-w_j^k\right|\right)\right]\\ {\sum }_{j=1}^n{w}_j^k=1\end{array}\\ 0<w_W^k\le w_j^k\le w_B^k\mathrm{for}\mathrm{every}j=1,2,\dots ,n\end{array}\right.$$

(1)

The above problem is nonlinear since it contains absolute values. It can be transformed into an equivalent linear programming problem.

$$\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\min \left[{\xi }^k\right]\\ -{\xi }^k\le a_{Bj}^k{w}_j^k-w_B^k\le {\xi }^k,j=1,2,\dots ,n\end{array}\\ -{\xi }^k\le a_{jW}^k{w}_W^k-w_j^k\le {\xi }^k,j=1,2,\dots ,n\end{array}\\ {\sum }_{j=1}^n{w}_j^k=1\end{array}\\ 0<w_W^k\le w_j^k\le w_B^k\mathrm{for}\mathrm{every}j=1,2,\dots ,n\end{array}\\ {\xi }^k\ge 0\end{array}\right.$$

(2)

In the above model, the decision variables are $w_j^k$, j = 1, 2, …, n and ${\xi }^k$.

The vector ${\mathbf{w}}^{\mathit{k}}=\left(w_1^k,w_n^k,\dots ,w_n^k\right)$ is the solution of the above linear programming problem.

Step 6. The vector of the total criteria weights $\mathbf{w}=\left(w_1,w_2,\dots ,w_n\right)$ is calculated as an average of the vectors ${\mathbf{w}}^{\mathit{k}},k=1,2,\dots ,p.$

$$w_j=\frac{{\sum }_{k=1}^p{w}_j^k}{p}$$

(3)

4.2. The Combination of TOPSIS, VIKOR, SAW, and COPRAS Methods

Step 7. The DM group selects the set of m alternatives $V=\left\{V_1,V_2,\dots ,V_m\right\}$.

Step 8. Each DM evaluates each alternative according to each criterion and builds an evaluation matrix $E^k=\left(e_{ij}^k\right),i=1,2,\dots ,m;j=1,2,\dots ,n,k=1,2,\dots ,p$. The evaluation is carried out for quantitative criteria using measurement units and real positive values and for qualitative criteria using a measurement scale with numerical or linguistic values. The value $e_{ij}^k$ shows the k-th DM evaluation of alternative $V_i$ for criterion $C_j$.

Step 9. The total evaluation matrix $E=\left(e_{ij}\right),i=1,2,\dots ,m;j=1,2,\dots ,n$is calculated as an average of the p evaluation matrix $E^k$:

$$e_{ij}=\frac{{\sum }_{k=1}^p{e}_{ij}^k}{p}$$

(4)

Step 10. Normalization and weighting. The normalization of the evaluation matrix is performed to bring the entries of the evaluation matrix into the interval [0;1] and to transform the evaluations for the minimum criteria into the evaluations for the maximum criteria. All methods start from the evaluation matrix $E=\left(e_{ij}\right)$ and the vector of the total criteria weights $\mathbf{w}=\left(w_1,w_2,\dots ,w_n\right)$.

For the SAW method, the entries of the normalized matrix ${\overline{E}}^S=\left({\overline{e}}_{ij}^S\right),i=1,2,\dots ,m;j=1,2,\dots ,n$ are calculated. The $e_j^{max}=\underset{i}{\max }{e}_{ij}$ is calculated. The “max” normalization method is used as follows:

$${\overline{e}}_{ij}^S=\left\{\begin{array}{c}\frac{e_{ij}}{e_j^{max}}\mathrm{for}\mathrm{the}\mathrm{maximum}\mathrm{criteria}\\ 1-\frac{e_{ij}}{e_j^{max}}\mathrm{for}\mathrm{the}\mathrm{minimum}\mathrm{criteria}\end{array}\right.$$

(5)

The entries of the weighted normalized matrix ${\stackrel{̿}{E}}^S=\left({\stackrel{̿}{e}}_{ij}^S\right)$ are calculated as follows:

$${{\stackrel{̿}{e}}_{ij}^S=w}_j\ast {\overline{e}}_{ij}^S$$

(6)

For the VIKOR method, the normalized matrix ${\overline{E}}^V=\left({\overline{e}}_{ij}^V\right),i=1,2,\dots ,m;j=1,2,\dots ,n$ entries are calculated. The $e_j^{max}$ and $e_j^{min}$ are calculated as follows:

$$e_j^{min}=\left\{\begin{array}{c}\underset{i}{\max }{e}_{ij}\mathrm{i}\mathrm{f}{C}_j\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{n}\\ \underset{i}{\min }{e}_{ij}\mathrm{i}\mathrm{f}{C}_j\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{n}\end{array}\right.$$

(7)

$$e_j^{min}=\left\{\begin{array}{c}\underset{i}{\min }{e}_{ij}\mathrm{i}\mathrm{f}{C}_j\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{n}\\ \underset{i}{\max }{e}_{ij}\mathrm{i}\mathrm{f}{C}_j\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{n}\end{array}\right.$$

(8)

The “max-min” normalization method is used as follows:

$${\overline{e}}_{ij}^V=\frac{e_j^{max}-e_{ij}}{e_j^{max}-e_j^{min}}$$

(9)

The entries of the weighted normalized matrix ${\stackrel{̿}{E}}^V=\left({\stackrel{̿}{e}}_{ij}^V\right)$ are calculated as follows:

$${{\stackrel{̿}{e}}_{ij}^V=w}_j\ast {\overline{e}}_{ij}^V$$

(10)

For the TOPSIS method, the entries of the normalized matrix ${\overline{E}}^T=\left({\overline{e}}_{ij}^T\right),i=1,2,\dots ,m;j=1,2,\dots ,n$ are calculated according to the “vector” normalization method. Because within the TOPSIS method, the type of maximum or minimum criterion is considered, to preserve the type of criterion, only the normalization for the maximum criteria is used:

$${\overline{e}}_{ij}^T=\frac{e_{ij}}{\sqrt{{\sum }_{k=1}^m{\left(e_{kj}\right)}^2}}$$

(11)

The entries of the weighted normalized matrix ${\stackrel{̿}{E}}^T=\left({\stackrel{̿}{e}}_{ij}^T\right)$ are calculated as follows:

$${\stackrel{̿}{e}}_{ij}^T=w_i\ast {\overline{e}}_{ij}^T$$

(12)

For the COPRAS method, the entries of the normalized matrix ${\overline{E}}^C=\left({\overline{e}}_{ij}^C\right),i=1,2,\dots ,m;j=1,2,\dots ,n$ are calculated according to the “sum” normalization method. Because the method considers the type of maximum or minimum criterion, to preserve the type of criterion, only the normalization for the maximum criterion is used:

$${\overline{e}}_{ij}^C=\frac{e_{ij}}{{\sum }_{k=1}^m{e}_{kj}}$$

(13)

The entries of the weighted normalized matrix ${\stackrel{̿}{E}}^C=\left({\stackrel{̿}{e}}_{ij}^C\right)$ are calculated as follows:

$${\stackrel{̿}{e}}_{ij}^C=w_i\ast {\overline{e}}_{ij}^C$$

(14)

Step 11. Calculation of distances, importance, and utility degree:

For the VIKOR method, the entries of the vectors $Q=\left(q_i\right)$ and $S=\left(s_i\right)$ are calculated as follows:

$$q_i={\sum }_{j=1}^n{\stackrel{̿}{e}}_{ij}^V$$

(15)

$$s_i=\underset{1\le j\le n}{max}\left\{{\stackrel{̿}{e}}_{ij}^V\right\}$$

(16)

where $q_i$ represents the total group benefit and $r_i$ represents the individual deviation for the alternative $V_i$.

The TOPSIS method uses the Euclidean distance. The positive and negative ideal solutions $A^{+}=\left(a_j^{+}\right)$ and $A^{-}=\left(a_j^{-}\right)$ are calculated as follows:

$$a_j^{+}=\left\{\begin{array}{c}\underset{i}{\max }{\stackrel{̿}{e}}_{ij}^T\mathrm{if}{C}_j\mathrm{is}\mathrm{a}\mathrm{maximum}\mathrm{criterion}\\ \underset{i}{\min }{\stackrel{̿}{e}}_{ij}^T\mathrm{if}{C}_j\mathrm{is}\mathrm{a}\mathrm{minimum}\mathrm{criterion}\end{array}\right.$$

(17)

$$a_j^{-}=\left\{\begin{array}{c}\underset{i}{\min } {\stackrel{̿}{e}}_{ij}^T \mathrm{if} C_j \mathrm{is} \mathrm{a} \mathrm{maximum} \mathrm{criterion}\\ \underset{i}{\max } {\stackrel{̿}{e}}_{ij}^T\mathrm{if}{C}_j\mathrm{is}\mathrm{a}\mathrm{minimum}\mathrm{criterion}\end{array}\right.$$

(18)

For each $i=1,2,\dots ,m,$ the Euclidean distance vectors $D^{+}=\left(d_i^{+}\right)$ and $D^{-}=\left(d_i^{-}\right)$ are calculated with respect to the positive and negative ideal solutions as follows:

$$d_i^{+}=\sqrt{{\sum }_{j=1}^n{\left|{\stackrel{̿}{e}}_{ij}^T-a_j^{+}\right|}^2}$$

(19)

$$d_i^{-}=\sqrt{{\sum }_{j=1}^n{\left|{\stackrel{̿}{e}}_{ij}^T-a_j^{-}\right|}^2}$$

(20)

For the COPRAS method, the following sets are considered: $M^1=\left\{j\left|j\in \left\{1,2,\dots ,n\right\}:C_j\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{n}\right.\right\}\mathrm{a}\mathrm{n}\mathrm{d}{M}^2=\left\{j\left|j\in \left\{1,2,\dots ,n\right\}:C_j\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{n}\right.\right\}.$

The maximization indices (for the maximum criteria from the set $M^1$) $G^{+}=\left(g_i^{+}\right)$ and the minimization indices (for the minimum criteria from the set $M^2$) $G^{-}=\left(g_i^{-}\right)$ are calculated as follows:

$$g_i^{+}={\sum }_{j\in M^1}{\stackrel{̿}{e}}_{ij}$$

(21)

$$g_i^{-}={\sum }_{j\in M^2}{\stackrel{̿}{e}}_{\mathit{ij}}$$

(22)

For each $i=1,2,\dots ,m,$p_i, the Relative Significance Value (Relative Significance Value) is calculated.

$$p_i=g_i^{+}+\frac{{\sum }_{k=1}^m{g}_k^{-}}{g_i^{-}\ast {\sum }_{k=1}^m(\frac{1}{g_k^{-}})}$$

(23)

Step 12. Calculation of the ranking of alternatives:

For the SAW method, the entries of the vector $R^S=\left(r_i^S\right)$ are calculated as follows:

$$r_i^S={\sum }_{j=1}^n{\stackrel{̿}{e}}_{ij}^S$$

(24)

For the VIKOR method, the following is calculated:

$$q^{min}=\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}{q}_i;q^{max}=\underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}{q}_i$$

(25)

$$s^{min}=\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}{s}_i;{\mathrm{s}}^{max}=\underset{i}{\max s_i}$$

(26)

The value of the parameter is chosen as $\nu$∈[0;1]. The choice of the parameter $\upsilon$ shows the balance between the global benefit and the maximum individual deviation. The higher the values of the parameter $\nu$, the more the dominance of the group is highlighted, while small values of the parameter $\nu$ highlight the individual deviations. The case $\nu$ > 0.5 is called “Majority voting”. The case $\nu$ = 0.5 is called “by consensus” and the case $\nu$ < 0.5 is called “with veto”.

The entries of the vector $R^V=\left(r_i^V\right)$ are calculated as follows:

$$r_i^V=\nu \frac{q_i-q^{min}}{q^{max}-q^{min}}+\left(1-\nu \right)\frac{s_i-s^{min}}{s^{max}-s^{min}}\hspace{1em}$$

(27)

Ranking the alternatives. The entries of the vectors $R^V$, Q and S are ordered in ascending order. Let $\alpha ,\beta ,\gamma$ be the permutations of the set {1, 2, …, m}, such that

$$r_{\alpha \left(1\right)}^V\le r_{\alpha \left(2\right)}^V\le \cdots \le r_{\alpha \left(m\right)}^V$$

(28)

$$q_{\beta \left(1\right)}\le q_{\beta \left(2\right)}\le \cdots \le q_{\beta \left(m\right)}$$

(29)

$$s_{\gamma \left(1\right)}\le s_{\gamma \left(2\right)}\le \cdots \le s_{\gamma \left(m\right)}$$

(30)

The alternative $\alpha \left(1\right)$ is the best placed in the ranking (corresponds to the minimum value of the entries of the $R^V$ vector) if two conditions are met (in the VIKOR method):

Condition 1. “Acceptable Advantage”:

$$r_{\alpha \left(2\right)}^V-r_{\alpha \left(1\right)}^V\ge \frac{1}{m-1}$$

(31)

where the alternative $\alpha \left(2\right)$ is the alternative placed second in the ordered list of entries of the vector $R^V$.

Condition 2. “Acceptable stability in decision-making”: The alternative $\alpha \left(1\right)$ must also be the best placed in the list of entries of the vector Q or S, i.e., $\alpha \left(1\right)=\beta \left(1\right)$ or $\alpha \left(1\right)=\gamma \left(1\right)$.

If one of the two conditions above is not met, then a compromise solution is proposed:

• The alternatives $\alpha \left(1\right)$ and $\alpha \left(2\right)$ are the best if only Condition 2 is not fulfilled, or;
• The alternatives $\alpha \left(1\right),\alpha \left(2\right),\dots ,\alpha \left(k\right)$ are the best, if Condition 1 is not satisfied, and $r_{\alpha \left(i\right)}^V-r_{\alpha \left(1\right)}^V\le \frac{1}{m-1}$ for each i = 1, 2, …, k and $r_{\alpha \left(k+1\right)}^V-r_{\alpha \left(1\right)}^V>\frac{1}{m-1}$.

For the TOPSIS method, the relative distances to the ideal solutions are calculated. The best solution corresponds to the greatest entry of the vector $R^T=\left(r_i^T\right);i=1,2,\dots ,m$ The i-th entry of $R^T$ is defined as follows:

$$r_i^T=\frac{d_i^{-}}{{d_i^{+}+d}_i^{-}}$$

(32)

For the COPRAS method, the entries of the vector $R^C=\left(r_i^C\right)$ are calculated as follows:

$$r_i^C=\frac{p_i}{\underset{k}{\max }{p}_k}$$

(33)

The best alternative according to the SAW method (respectively, according to the TOPSIS and COPRAS methods) is the alternative corresponding to the entry of the vector $R^S$ (respectively, of the vectors $R^T$ and $R^C$) that has the maximum value. The best alternative according to the VIKOR method is the alternative corresponding to the entry of the vector $R^V$ that has the minimum value. To obtain the ranking of the alternatives, the entries of the vectors $R^S$, $R^T$, and $R^C$ are ordered in descending order. For the VIKOR method, the entries of the vector $R^V$ are ordered in ascending order.

Step 13. In order to obtain the ranking of the alternatives in our proposed method, we need to make the following computations:

$$r_{max}^S=\underset{i}{\max }{r}_i^S;r_{min}^S=\underset{i}{\min }{r}_i^S$$

(34)

$$r_{max}^V=\underset{i}{\max }{r}_i^V;r_{min}^V=\underset{i}{\min }{r}_i^V$$

(35)

$$r_{max}^T=\underset{i}{\max }{r}_i^T;r_{min}^T=\underset{i}{\min }{r}_i^T$$

(36)

$$r_{max}^C=\underset{i}{\max }{r}_i^C;r_{min}^C=\underset{i}{\min }{r}_i^C$$

(37)

$$z_i^S=(r_i^S-r_{min}^S)/\left({r_{max}^S-r}_{min}^S\right)$$

(38)

$$z_i^V=(r_{max}^V-r_i^V)/({r_{max}^V-r}_{min}^V)$$

(39)

$$z_i^T=(r_i^T-r_{min}^T)/\left({r_{max}^T-r}_{min}^T\right)$$

(40)

$$z_i^C=(r_i^C-r_{min}^C)/\left({r_{max}^C-r}_{min}^C\right)$$

(41)

The entries of the vector of the combined method $R^B=\left(r_i^B\right)$ are

$$r_i^B=z_i^S+z_i^V+z_i^T+z_i^C$$

(42)

The best alternative is k, where

$$r_k^B=\underset{i}{\max }{r}_i^B$$

(43)

For finding the alternative ranking, the entries of the vector $R^B$ are sorted in descending order.

5. Application of the Hybrid Group Multi-Criteria Approach for IoT Platform Selection

Selecting the right IoT platform and vendor is a critical decision for any organization looking to deploy IoT solutions. However, it can be a complex and challenging process due to several factors and considerations. For this purpose, the proposed approach will be used.

A group of DMs is selected based on solid knowledge and experience in the field of IoT platforms. It is a group composed of multidisciplinary experts that include representatives from IT, security, operations, and business units to ensure that all aspects of the decision are thoroughly considered. We consider a group D = {D₁, D₂, D₃} of three decision makers.

The DMs select a set of criteria (based on experience and literature reviews [4,37,42,48,49,51,52,59]). These criteria are of two categories: IoT platform requirements and criteria for IoT platform vendors. The selected criteria for requirements for the IoT platform are scalability, security, device management, data processing and analytics, integration and interoperability, ease of use, reliability and uptime, and complexity. The selected criteria for the IoT platform vendors are vendor support, industry focus, cost, and customization limitations. Information on these criteria is presented in

Table 4. A set of criteria for IoT platform selection.

Criteria	Description	Symbol	Type
Scalability	Scalability refers to the ability of an IoT platform to handle increasing amounts of data, devices, and users without compromising performance or reliability. The evaluation of the platform’s scalability features includes the ability to support large numbers of devices, data volume, and the option for auto-scaling resources as needed.	C1	max
Security	The IoT platform should have robust security features to protect data, devices, and communication from unauthorized access, theft, or damage. It should provide end-to-end encryption, data authentication, data encryption, access controls, identity management, threat detection, compliance with industry standards, and access control.	C2	max
Device management	Device management involves the management of a large number of devices and sensors. It requires the consideration of device configuration, monitoring and diagnostics, firmware updates, and remote monitoring.	C3	max
Data processing and analytics	Data processing and analytics refers to the fact that the IoT platform enables the efficient and effective use of IoT data and extracts valuable insights from it. It requires the careful consideration of various factors, such as data quality, data storage, and data visualization. It should provide real-time data analytics, predictive analytics, and reporting tools to extract actionable insights.	C4	max
Integration and interoperability	Integration and interoperability refer to the fact that the IoT platform enables the seamless exchange of data and information between different devices and systems. They ensure the compatibility and scalability of IoT systems.	C5	max
Ease of use	The ease of use refers to the fact that the IoT platform can be easily configured, deployed, and managed. A user-friendly interface and developer tools are important for efficient IoT application development and management. The IoT platform can be easily adopted and used by different stakeholders. Ease of use criteria require the consideration of user interface design, documentation, developer support, and training.	C6	max
Reliability and uptime	Reliability and uptime refer to the fact that the IoT platform functions correctly and continuously. A reliable platform with high uptime is essential to avoid service interruptions. It requires the consideration of device management, data processing, and analytics.	C7	max
Vendor support	Vendor support ensures that one has assistance when facing issues or challenges during deployment and operation, that the IoT platform can be properly configured, deployed, and maintained. It requires the consideration of vendor expertise, quality of vendor support, responsiveness, and availability.	C8	max
Industry focus	Industry focus refers to the fact that the IoT platform can be properly tailored to specific industry needs and requirements. Some IoT platforms cater to specific industries (e.g., healthcare, manufacturing). Industry-specific features and certifications may be essential. It requires the consideration of industry expertise, domain knowledge, aligns with the industry’s unique requirements, standards, and compliance regulations.	C9	max
Cost	Cost is a criterion for IoT platform selection, as it ensures that the IoT platform can be properly budgeted and financed. IoT projects often have budget constraints. This requires the consideration of pricing models, licensing fees, and total cost of ownership including subscription fees, data storage costs, and any variable charges.	C10	min
Complexity	Complexity is a common challenge in IoT, as IoT systems are often complex, involving multiple devices, sensors, and data sources. IoT complexity requires the consideration of various factors, such as system design, data processing, and analytics. Complexity is a criterion for IoT platform selection, as it ensures that IoT systems can be easily managed and maintained.	C11	min
Customization limitations	Customization limitations refer to the fact that the IoT platform can be properly tailored to specific needs and requirements. It requires the consideration of platform flexibility, extensibility, and modularity.	C12	min

.

The BWM is applied for the criteria weight’s calculation. Each DM chooses the best and the worst criteria. For each DM, the preference of the best criterion over the other criteria, using a scale of scores from 1 to 9, is determined by pairwise comparisons. The preference vectors ${\mathbf{a}}_{\mathit{B}}=\left(a_{B1},a_{B2},\dots ,a_{B5}\right)$ and ${\mathbf{a}}_{\mathit{W}}=\left(a_{1W},a_{2W},\dots ,a_{5W}\right)$ are obtained for each DM. The vector of criteria weights for each DM is calculated as a solution of the linear programming by Equation (2). Then, the vector of the total criteria weights $\mathbf{w}=\left(w_1,w_2,\dots ,w_5\right)$ is calculated based on Equation (3), (

Table 5. The vector of criteria weights for each DM and the total criteria weights.

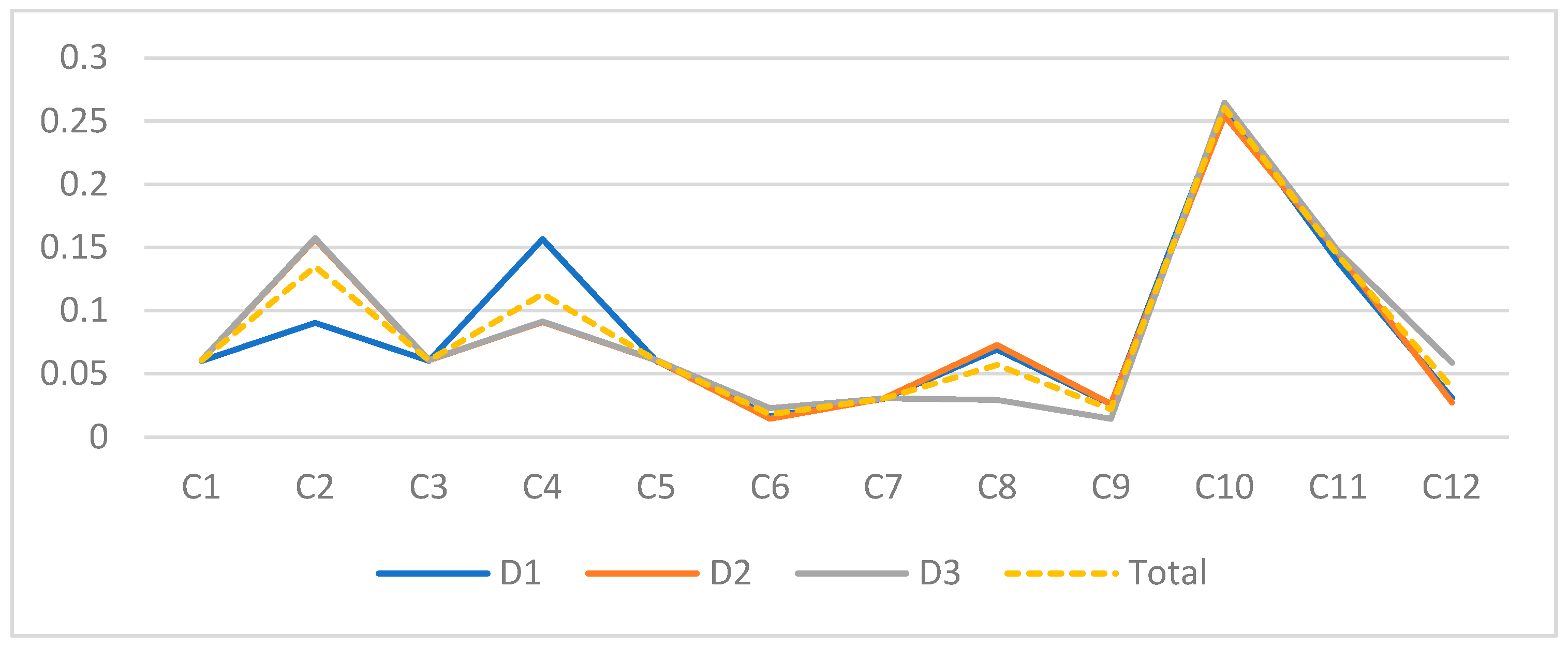
Criteria Symbol	Criteria Weights
	D1	D2	D3	Total
C1	0.0602	0.0606	0.0610	0.0606
C2	0.0903	0.1564	0.1574	0.1347
C3	0.0602	0.0606	0.0610	0.0606
C4	0.1566	0.0909	0.0915	0.1130
C5	0.0602	0.0606	0.0610	0.0606
C6	0.0166	0.0145	0.0229	0.0180
C7	0.0301	0.0303	0.0305	0.0303
C8	0.0692	0.0727	0.0294	0.0571
C9	0.0258	0.0260	0.0146	0.0221
C10	0.2615	0.2545	0.2647	0.2603
C11	0.1385	0.1455	0.1471	0.1437
C12	0.0308	0.0273	0.0588	0.0390

and Figure 1). The pairwise comparison consistency level is acceptable for each DM. For D₁ and D₂, the consistency level is equal to 0.167 and for D₃, the consistency level is equal to 0.125.

One can easily see from Figure 1 that the cost criterion is in first place (the most important) followed by the criterion of security and the criterion of data processing and analytics. The total criteria weights are used in the following.

A list of available IoT platforms on the market that satisfy the requirements is built. To fill this list, an online data search and literature review is employed. Many different IoT platforms are currently available on the market as a result of IoT development, characterized by different characteristics related to usage models and orientation to different fields or availability [72]. There are several IoT platforms that provide infrastructure and services for building and managing IoT applications and solutions. These platforms offer various features, including data analytics, device management, security, and scalability. They cater to a wide range of use cases and requirements, from small-scale projects to large-scale industrial IoT deployments. The classifications of the main IoT platforms were found at Softwaretestinghelp [73] for 13 IoT platforms, Euristiq [74] for 11 IoT platforms, Devteam.space [75] for 10 IoT platforms, Cloudthat [76] for 7 IoT platforms, and Dzone [77] for 11 IoT platforms. There are a set of 21 IoT platforms considered in all the comparative analyses. Some IoT platforms are taken into account in all five comparisons. These are Amazon AWS IoT Core, Cisco IoT Cloud Connect, Google Cloud Platform, IBM Watson IoT, Microsoft Azure IoT Suite, and Oracle IoT. The classifications differ from one analysis to another. For example, Salesforce IoT Cloud is ranked 12 out of 13 by Softwaretestinghelp, 6 out of 11 by Euristiq, and 6 out of 10 by Devteam.space. Amazon AWS IoT Core is ranked 7 out of 13 by Softwaretestinghelp, 2 out of 11 by Euristiq, and 1 by 10 by Devteam.space. Some important IoT platforms are Amazon AWS IoT Core, Cisco IoT Cloud Connect, Google Cloud Platform, IBM Watson IoT, Kaa Enterprise, Microsoft Azure IoT Suite, Oracle IoT, Particle, Salesforce IoT Cloud, ThingsBoard Open-Source IoT Platform, and ThingWorx.

From the IoT platform list, a set of IoT platforms are selected. This set is the alternatives set, composed of 14 IoT platforms: $P=\left\{P_1,P_2,\dots ,P_{14}\right\}$. The IoT platform names are omitted for reasons of confidentiality and market protection.

Each DM evaluates each IoT platform from the set P regarding each of the above-mentioned criteria from the set C in an evaluation matrix. Because many of the considered criteria are qualitative, scores with values from 1 to 10 are used (step 8). The total evaluation matrix $E=\left(e_{ij}\right),i=1,2,\dots ,14;j=1,2,\dots ,12$ is calculated as an average of the three DM evaluation matrices based on Equation (4) (

Table 6. The total evaluation matrix.

IoT Platforms	Criteria
	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
P1	6.667	7.667	5.667	7.667	7.667	7.333	5.333	4.333	3.333	7.333	7.000	5.333
P2	7.667	8.667	7.000	6.667	8.000	7.667	9.000	7.333	4.667	8.667	6.000	6.333
P3	9.333	8.000	8.333	9.000	8.667	7.333	7.667	6.333	7.000	8.667	6.000	7.333
P4	5.667	7.000	6.000	7.667	8.000	9.000	5.333	5.000	6.333	6.000	8.667	7.333
P5	7.333	7.667	6.667	5.667	8.333	7.333	7.000	6.333	5.000	8.000	7.667	5.667
P6	6.333	8.000	6.000	7.333	9.000	9.333	9.000	8.000	8.333	9.667	7.000	4.000
P7	8.333	8.000	8.333	7.000	8.333	8.000	8.333	8.667	7.000	9.667	8.000	8.333
P8	7.667	9.333	6.000	6.667	7.000	6.000	8.333	5.333	6.667	8.000	7.000	4.333
P9	7.333	9.000	7.000	8.000	8.000	5.333	9.333	5.667	7.667	9.000	6.333	4.333
P10	5.000	6.667	6.000	8.667	7.667	5.667	8.000	8.000	6.667	5.667	7.667	6.667
P11	6.333	8.333	9.333	7.000	7.333	8.000	7.333	9.333	9.000	7.333	8.667	7.667
P12	9.333	6.667	9.000	7.333	8.667	8.000	8.667	9.333	8.000	5.667	6.667	7.000
P13	7.667	7.333	9.333	8.000	6.667	5.667	8.667	6.667	7.000	8.333	7.333	5.667
P14	6.667	9.000	8.000	8.333	7.333	7.000	8.333	6.667	5.667	9.000	7.333	6.000

).

The normalized matrices and weighted normalized matrices are calculated for the SAW, VIKOR, TOPSIS, and COPRAS methods based on Equations from step 10. Then, the distances, importance, and utility degree are calculated based on Equations from step 11.

The calculation of the SAW solution is performed based on Equation (24). For VIKOR, the parameter takes the value $\nu =0.5.$ The VIKOR solution is calculated based on Equation (27). For the TOPSIS, the relative distances to the ideal solution are calculated. The TOPSIS solution is calculated based on Equation (32). For the COPRAS method, the solution is calculated based on Equation (33).

The best IoT platform according to the SAW method (respectively, according to the TOPSIS and COPRAS methods) is the IoT platform corresponding to the maximum value of the solution entries. The best IoT platform according to the VIKOR method is the IoT platform corresponding to the minimum value of the solution entries.

The SAW, VIKOR, TOPSIS, and COPRAS solutions are presented in

Table 7. The SAW, VIKOR, TOPSIS, and COPRAS solutions.

IoT Platforms	SAW	COPRAS	VIKOR	TOPSIS
P1	0.1723	0.7525	1	0.2111
P2	0.2158	0.821	0.6673	0.2978
P3	0.3098	0.9373	0.1753	0.617
P4	0.2506	0.8487	0.4961	0.5242
P5	0.1943	0.7939	0.758	0.3148
P6	0.3048	0.9344	0.3597	0.6866
P7	0.2308	0.8834	0.4826	0.5632
P8	0.2867	0.8907	0.3186	0.5647
P9	0.3224	0.9412	0.2219	0.6776
P10	0.2952	0.8918	0.431	0.5783
P11	0.3379	0.9713	0.0952	0.7856
P12	0.3875	1	0.1738	0.7507
P13	0.2826	0.901	0.3271	0.6017
P14	0.243	0.8616	0.473	0.4333
max	0.3875	1	1	0.7856
min	0.1723	0.7525	0.0952	0.2111

.

The solution of the combined method is calculated based on Equations (34)–(43). This solution is the Hybrid Group Multi-Criteria Approach solution (

Table 8. The combined method solution.

IoT Platforms	SAW	COPRAS	VIKOR	TOPSIS	Combined Method
P1	0.000	0.000	0.000	0.000	0.000
P2	0.202	0.277	0.368	0.151	0.998
P3	0.639	0.747	0.911	0.707	3.004
P4	0.364	0.389	0.557	0.545	1.854
P5	0.102	0.167	0.267	0.181	0.717
P6	0.616	0.735	0.708	0.828	2.886
P7	0.272	0.529	0.572	0.613	1.985
P8	0.532	0.558	0.753	0.615	2.459
P9	0.697	0.762	0.860	0.812	3.132
P10	0.571	0.563	0.629	0.639	2.402
P11	0.770	0.884	1.000	1.000	3.654
P12	1.000	1.000	0.913	0.939	3.852
P13	0.513	0.600	0.744	0.680	2.536
P14	0.329	0.441	0.582	0.387	1.739

).

In order to make a comparison and an analysis between the solutions provided by the four methods and the solution provided by our combined method, we ranked the solutions for each method separately.

To obtain the ranking of the IoT platforms, the elements of the SAW, TOPSIS, and COPRAS solutions from Table 7 are ordered in descending order. For the VIKOR method, the elements of the VIKOR solution from Table 7 are ordered in ascending order.

To obtain the ranking of the IoT platforms according to our combined method (from the Hybrid Group Multi-Criteria approach), the elements of the solution presented in the last column of Table 8 are ordered in descending order.

The IoT platform ranking given by our combined method is evaluated by comparison with the IoT platforms ranking given by the SAW, VIKOR, TOPSIS, and COPRAS methods. It is also evaluated using the Spearman correlation.

The IoT platforms ranking of SAW, VIKOR, TOPSIS, COPRAS, and our combined method (from Hybrid Group Multi-Criteria approach) are presented in

Table 9. The IoT platform ranking of SAW, VIKOR, TOPSIS, COPRAS, and combined methods.

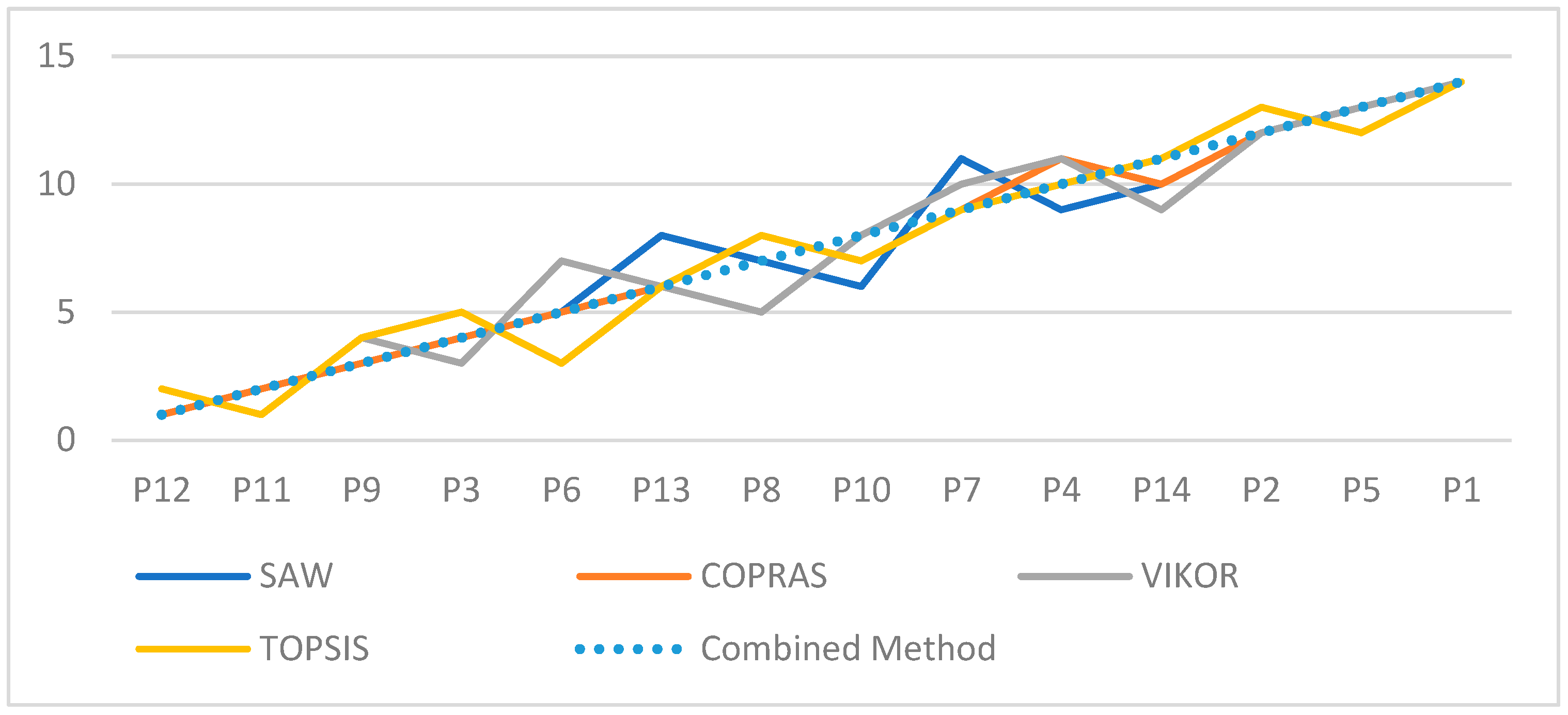
IoT Platforms	Ranks
	SAW	COPRAS	VIKOR	TOPSIS	Combined Method
P12	1	1	2	2	1
P11	2	2	1	1	2
P9	3	3	4	4	3
P3	4	4	3	5	4
P6	5	5	7	3	5
P13	8	6	6	6	6
P8	7	8	5	8	7
P10	6	7	8	7	8
P7	11	9	10	9	9
P4	9	11	11	10	10
P14	10	10	9	11	11
P2	12	12	12	13	12
P5	13	13	13	12	13
P1	14	14	14	14	14

and Figure 2.

Taking into account the considered application, it can be seen that the best IoT platform is P₁₂ according to the SAW, COPRAS, and combined method, and IoT platform P₁₁ according to the VIKOR and TOPSIS methods. The weakest IoT platform is the P₁, according to all methods.

It is observed that the IoT platform rankings obtained with SAW, VIKOR, TOPSIS, and COPRAS are very similar to the IoT platform ranking obtained with our combined method. The ranking differences of our combined method compared to the ranking obtained with these methods are of maximum two positions (example: IoT platforms P₆–P₈, P₁₀, and P₁₄).

The differences between the VIKOR and TOPSIS rankings are greater. Thus, the difference for P₆ is four positions: from 7 (VIKOR) to 3 (TOPSIS), and for P₈, the difference is three positions: from 5 (VIKOR) to 8 (TOPSIS). The difference between the SAW and COPRAS rankings for P₄ is three positions: from 9 (SAW) to 11 (COPRAS) and for P₇, three positions, from 11 (SAW) to 9 (COPRAS).

For this application, the solution of the combined method is the most distant from the solution of the VIKOR method and the closest to the solution of the COPRAS method. The solutions of the methods are the same for IoT platform P₁.

The Spearman correlation of the solutions is presented in

Table 10. The Spearman correlation of solutions.

	SAW	COPRAS	VIKOR	TOPSIS	Combined Method
SAW	1	0.969231	0.942857	0.951648	0.969231
COPRAS	0.969231	1	0.956044	0.973626	0.991209
VIKOR	0.942857	0.956044	1	0.916484	0.960440
TOPSIS	0.951648	0.973626	0.916484	1	0.973626
Hybrid Approach	0.969231	0.991209	0.960440	0.973626	1

.

For this application, the Spearman correlation of the solutions shows that the closest solution of the combined methods (from the Hybrid Group Multi-Criteria approach) is achieved with COPRAS (0.991209), then with TOPSIS (0.973626), SAW (0.969231), and the lastly with VIKOR (0.960440).

6. Conclusions

The purpose of this paper is to prove the usefulness of applying multi-criteria methods for selection problems in IoT, especially when the number of criteria is large. Multi-criteria methods offer an objective and systematic way of making decisions to solve IoT selection problems and can help optimize resource allocation by selecting alternatives that align with an organization’s strategic goals and constraints. They enable the incorporation of decision makers’ preferences and priorities into a decision model, leading to more inclusive and acceptable decisions.

In summary, the paper contains the following:

• An analysis of relevant research in the field of solving selection problems in IoT through multi-criteria methods and a synthesis of the advantages and disadvantages of using multi-criteria methods from a given set of often-used methods in selection problems.
• A comparative study of the SAW, VIKOR, TOPSIS, and COPRAS methods in terms of the advantages, disadvantages, approach, type of normalization, inputs, outputs, measurement scale, aggregation method, obtainment of the order of the alternatives and the best alternative, the level of complexity, and interactivity.
• The proposal of a hybrid group approach that includes the BWM as a weighting method, the multi-criteria methods SAW, VIKOR, TOPSIS, and COPRAS for obtaining several rankings of the alternatives as well as a method for combining them to obtain a unique solution.
• The application of the proposed approach for the selection of an IoT platform from a given set of platforms and a comparison of the solutions obtained with the hybrid approach with the solutions obtained with the SAW, VIKOR, TOPSIS, and COPRAS multi-criteria methods.
• The successful application of the proposed approach involves a careful consideration of some aspects like data quality, the experience of decision makers, the subjectivity of evaluation, the importance of the criteria considered and the computational resources.
• The cost of implementing the proposed approach involves the cost of experts involved in selecting criteria, alternatives, weighting criteria, building the evaluation matrix, in the cost of acquiring data, and in the cost of using software tools. The costs of using the methods can vary depending on the decision problem being considered, and the resources required for data collection, analysis, and decision support.

By providing a structured and rigorous decision-making framework, multi-criteria methods enhance the quality of selection decisions in IoT-type systems. This can lead to better outcomes, cost savings, and improved system performance.