UAV Swarm Centroid Tracking for Edge Computing Applications Using GRU-Assisted Multi-Model Filtering

Abstract

When an unmanned aerial vehicles (UAV) swarm is used for edge computing, and high-speed data transmission is required, accurate tracking of the UAV swarm’s centroid is of great significance for the acquisition and synchronization of signal demodulation. Accurate centroid tracking can also be applied to accurate communication beamforming and angle tracking, bringing about a reception gain. Group target tracking (GTT) offers a suitable framework for tracking the centroids of UAV swarms. GTT typically involves accurate modeling of target maneuvering behavior and effective state filtering. However, conventional coordinate-uncoupled maneuver models and multi-model filtering methods encounter difficulties in accurately tracking highly maneuverable UAVs. To address this, an innovative approach known as 3DCDM-based GRU-MM is introduced for tracking the maneuvering centroid of a UAV swarm. This method employs a multi-model filtering technique assisted by a gated recurrent unit (GRU) network based on a suitable 3D coordinate-coupled dynamic model. The proposed dynamic model represents the centroid’s tangential load, normal load, and roll angle as random processes, from which a nine-dimensional unscented Kalman filter is derived. A GRU is utilized to update the model weights of the multi-model filtering. Additionally, a smoothing-differencing module is presented to extract the maneuvering features from position observations affected by measurement noise. The resulting GRU-MM method achieved a classification accuracy of 99.73%, surpassing that of the traditional IMM algorithm based on the same model. Furthermore, our proposed 3DCDM-based GRU-MM method outperformed the Singer-KF and 3DCDM-based IMM-EKF in terms of the RMSE for position estimation, which provides a basis for further edge computing.

1. Introduction

UAV swarms have emerged as a promising edge computing platform capable of supporting high-speed data transmission by leveraging nodes with strong communication capabilities [1,2,3]. In contrast to conventional satellite systems, which depend on supplementary data like predicted ephemeris information to support phase-locked loop (PLL) operations, highly dynamic UAV swarms face scarcity of easily accessible auxiliary information [4]. This absence of information poses challenges in achieving signal alignment, compensating for Doppler frequency offsets, and other critical operations. To address these challenges, this paper introduces a novel scenario wherein a coordinated UAV swarm is employed for edge computing applications. The proposed approach focuses on ensuring that a high-throughput UAV responsible for ground transmission remains positioned at the centroid of the swarm. Trajectory tracking of the UAV swarm’s centroid using ground-based radar observations is employed to aid with rapid acquisition and robust tracking of the PLL in ground signal demodulation. Moreover, accurate tracking of the UAV swarm’s centroid enables precise beamforming and directionality, resulting in enhanced receiver gain and improved signal reception rates. By emphasizing the tracking of the UAV swarm’s centroid, this research aims to provide solutions specifically tailored to this aspect, contributing to advancements in tracking methodologies within UAV swarm technology.

Some research has been conducted on UAV tracking based on UAV attitude, anti-drone technologies, and remote sensing imagery [5,6,7]. The theory of group target tracking (GTT) provides a flexible framework for effectively monitoring UAV swarms and enabling efficient calculation [8]. By dividing received measurements into groups based on specific criteria, GTT allows for estimating and predicting swarm trajectories and states from a group perspective [9]. The group’s state encompasses both the motion state of the group centroid and the external shape of the group distribution, making accurate tracking of the motion state crucial for the effectiveness of tracking and interception systems. As a result, tracking of maneuvering UAV swarms to achieve efficient edge computing capabilities has gained prominence.

Previous research on tracking maneuvering centroids has primarily focused on motion modeling and filtering algorithms. However, the success of filtering algorithms in achieving the desired tracking accuracy depends on the modeling of the target’s motion, for which prior information is often insufficient [10]. Many models that try to capture the target’s motion, such as the classic Singer [11], current statistical [12], and Jerk models [13], all assume that the target’s acceleration or rate of acceleration change is independent in a decoupled coordinate system. However, most target maneuvers exhibit coupling across different coordinates, particularly from the observer’s coordinate system [10]. To overcome this issue, some studies have adopted dynamic models of target characteristics to represent the control quantity generated by target maneuvers as a random process, such as the two-dimensional model [14], three-dimensional turning model [15,16,17], and flight dynamics model [18,19]. In [19], the authors considered the influence of aircraft attitude angles on target acceleration and utilized a 16-dimensional state extended Kalman filter, significantly improving the prediction accuracy of the target’s state. However, the required attitude angles were unobservable with only position measurements, and the set parameters were limited to specific scenarios, thereby restricting the practical application of this model in tracking aircraft targets.

The various models mentioned above, along with models with different parameters, correspond to distinct maneuvering modes of the target. To address the issue of motion pattern uncertainty in target tracking, a multi-model (MM) algorithm was proposed in [20]. The MM algorithms are classified into three generations: autonomous [21], cooperative [22,23], and variable structure MM methods [24,25,26,27,28,29]. Two challenges arise when employing methods that incorporate multiple filtered states. The first challenge involves using an incomplete set of models to estimate the state, while the second pertains to tracking delays during model transitions [30]. In the IMM algorithm, the transition probability matrix contains information from past models over a period of time. As a result, the IMM algorithm exhibits significant delays in response to model transitions, leading to substantial tracking errors during the initial phase of such transitions [30,31,32,33]. To mitigate model estimation delays, several approaches have been proposed. Among them, the fuzzy-tuned IMM algorithm adjusts the transition probabilities between models [34], while an adaptive neural fuzzy inference system (ANFIS) is used for mobile robot localization [35]. Deep learning techniques have been introduced into the Bayesian filtering framework due to their capabilities of nonlinear mapping and feature extraction using data-driven approaches. Recurrent neural networks (RNNs) excel at extracting features from sequential data, making them widely employed for learning motion models [36,37], noise parameters [38], and Kalman gains [39] in state estimation tasks. When dealing with switching systems, RNNs are combined with IMM methods to learn mode probabilities, which facilitate trajectory estimation, prediction, and human posture estimation. For switching systems, RNNs are combined with IMM methods to learn mode probabilities, which are used to estimate and predict trajectories and estimate human posture [40]. In combination with multi-model tracking, the long short-term memory (LSTM) network is used to replace the transition probability matrix to realize the function of model judgment [41]. Currently, such methods have not been applied to tracking a UAV swarm’s maneuvering centroid.

In summary, tracking a UAV swarm’s maneuvering centroid presents two main challenges in the process of edge computing. One is to achieve a more realistic dynamic modeling of the UAV swarm’s centroid when only position observations are available. Another challenge is accurate centroid tracking in the presence of various maneuverable scenarios and potential model transitions at any time. Thus, we propose multi-model filtering assisted by a GRU network based on a novel 3D coordinate-coupled dynamic model. The key contributions of this paper can be summarized as follows:

• Firstly, we propose an approach for tracking the centroid of a UAV swarm by utilizing a 3D coordinate-coupled dynamic model. In this model, the control quantity is considered a random process, and an unscented Kalman filter is employed.
• Secondly, we introduce a novel GRU-based network that extracts features from position observations. This enables quick and accurate detection of the maneuvering mode. With the detected features, a multi-model filtering method is applied to track the UAV swarm’s centroid.
• Finally, we conduct simulations and experiments to validate the feasibility and superior performance of the proposed algorithm compared with traditional approaches.

The following sections provide further details. Section 2 discusses centroid tracking in GTT and presents the overall framework of our algorithm. Section 3 focuses on the state filtering for the UAV swarm’s centroid based on the dynamic modeling of UAV swarms. Section 4 describes how the GRU network assists with filtering the UAV swarm’s centroid under different maneuvering modes. Section 5 and Section 6 demonstrate the effectiveness of our tracking method through simulated UAV swarm trajectories and flight experiments. Finally, we conclude our work in Section 7.

2. Background Information

The proposed method in this paper aims to improve the accuracy of UAV swarm centroid tracking by utilizing a three-dimensional coordinate-coupled dynamic model and multi-model filtering assisted by a GRU network. The improved tracking results can be used for ground communication by airborne nodes in UAV swarm-based edge computing. Therefore, this section provides the key background information to familiarize readers with the working model of the system and the main principles involved.

To begin with, we introduce the scenario of UAV swarm-based edge computing and centroid tracking in it. Moreover, the working principle of centroid tracking in GTT is introduced. Subsequently, we outline the fundamental principle of modeling unknown control quantities as random processes in target tracking. Finally, we present a comprehensive framework that outlines the proposed tracking method.

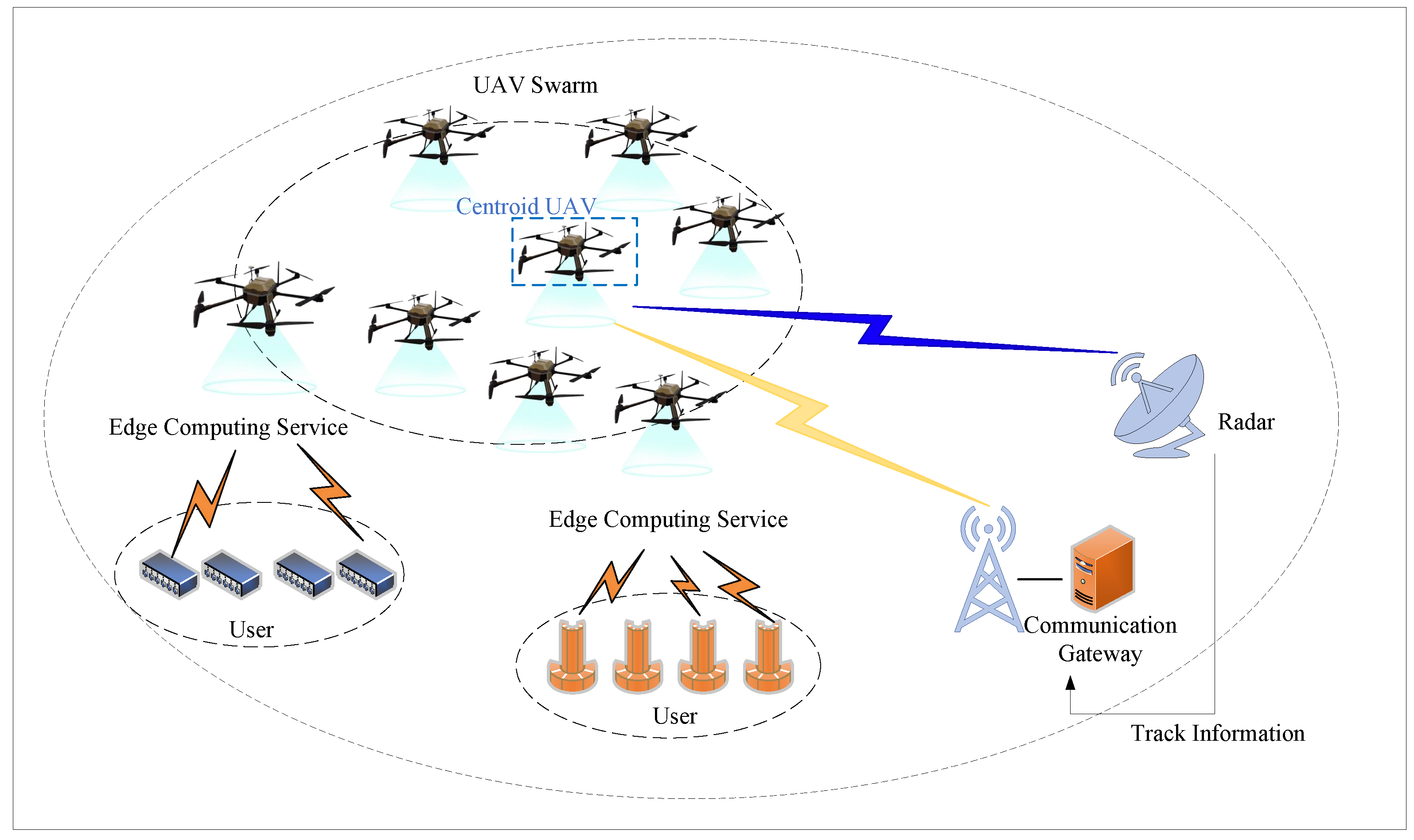
2.1. Centroid Tracking in UAV Swarm-Based Edge Computing

As illustrated in Figure 1, the edge computing architecture based on UAV swarms aims to provide edge computing services for various types of users by integrating a communication node (called a centroid UAV) and multiple UAVs responsible for edge computing. The centroid UAV plays a crucial role in the overall communication and coordination of the management cluster, with the primary responsibility of efficiently distributing and relaying data between edge computing nodes, ensuring high-speed transmission and seamless connectivity of different tasks. At the same time, the centroid UAV is also responsible for high-speed data transmission to the communication gateway. The relative positions between the UAV swarm colonies are pre-programmed so that the main communication node is located at the center of mass of the UAV swarm, which serves as the dynamic anchor point of the whole UAV swarm. Different from satellite communication using ephemeris prediction to assist with the function of PLL operaitons, the trajectory information of a UAV swarm’s centroid is used to assist the acquisition, synchronization, and Doppler frequency offset of ground station signal demodulation. Since the centroid UAV is placed in the centroid position of the UAV swarm in advance, the tracking result of the centroid of the UAV swarm is the track of the centroid UAV. It is not necessary to recalculate the phase center when the trajectory information is used to demodulate the signal. The communication gateway performs two main steps: tracking the centroid of the dUAV swarm by using radar observations and the GTT algorithm. The results of centroid tracking are used to assist with the acquisition, synchronization, beamforming, and angle tracking of the receiving antenna in digital signal demodulation.

A group target, as defined in [42], comprises multiple targets that meet specific criteria. The characteristics of a group encompass its label, centroid motion state, and overall shape, as outlined in [9]. GTT involves five key steps to effectively track UAV swarms: measurement partitioning, group data association, centroid state estimation, group shape estimation, and the detection of group spawning and combination:

1. Measurement partitioning: This step involves dividing the received measurements into groups based on specific criteria. The criteria can be the proximity, similarity in motion characteristics, or any other relevant factors that define a group.

2. Group data association: In this step, the measurements are associated with their corresponding groups. This can be accomplished using various techniques such as nearest neighbor association or probabilistic data association.

3. Centroid state estimation: Once the measurements are associated with their groups, the motion state of the group centroid is estimated. This includes estimating the position, velocity, and other relevant parameters of the centroid.

4. Group shape estimation: In addition to tracking the centroid state, GTT also aims to estimate the external shape of the group distribution. This helps with understanding the spatial arrangement and dynamics of the swarm.

5. Detection of group spawning and combination: UAV swarms are dynamic systems where individual UAVs can join or leave the swarm, and multiple smaller swarms can combine to form a larger swarm. Detecting such events is important for accurate tracking and prediction of swarm behavior.

By following these steps, GTT provides a comprehensive framework for tracking maneuvering UAV swarms and enabling efficient edge computing capabilities. Under predefined criteria, measurement partitioning divides the incoming measurement data into several sets, each representing a distinct group of mobile edge computing (MEC). Group data association links an unlabeled set to the corresponding group track. Shape estimation is utilized to estimate the group’s shape and attitude parameters. The spawning and combination of groups are recorded based on the movement state and shape overlap of the groups, influencing the outcomes (creation or loss of groups) in data association. Group motion state estimation determines the motion state of the group’s centroid using measurements from the same group. The initial step in this process involves obtaining centroid observations from multiple measurements by utilizing established schemes not discussed in this paper. Subsequently, the motion state of the group is estimated through dynamic modeling and nonlinear filtering of the group’s centroid. Centroid tracking, in a strict sense, encompasses both centroid state estimation and group data association. However, this paper solely focuses on the centroid tracking of a single group. The predicted state generated by centroid tracking significantly impacts the accuracy of group association and the spawning and combination of groups, serving as a critical factor in the overall functionality of the tracking system’s edge computing.

2.2. Stochastic Process Modeling of the Control Volume

The unexpected maneuvers of the object are a result of unknown time-varying state controls for the observer. When tracking maneuvering targets, Singer initially suggested modeling the acceleration of maneuvering targets as a zero-mean first-order stationary Markov process, where the acceleration value at a given time depends on the value at neighboring times. By considering the symmetry and attenuation of the correlation function of a stationary random process, the time correlation function $R_a\left(\tau \right)$ with the offset integral $\tau$ for the maneuvering acceleration $a\left(t\right)$ in Singer’s model can be expressed as shown in Equation (1):

$$\begin{array}{c}\hfill R_a\left(\tau \right)=E\left[a\left(t\right)a\left(t+\tau \right)\right]={\sigma }_a^2{e}^{-\alpha \left|\tau \right|}\end{array}$$

(1)

where ${\sigma }_a^2$ denotes the variance of acceleration and $\alpha$ is the maneuvering frequency. In practical tracking applications, because different values of $\alpha$ adapt to different maneuvering scenarios, it is necessary to preset the value according to prior information before filtering. The continuous-time equation of $a\left(t\right)$ can be expressed as shown in Equation (2):

$$\begin{array}{c}\hfill \dot{a}\left(t\right)=-\alpha ·a\left(t\right)+w\left(t\right)\end{array}$$

(2)

where $w\left(t\right)$ represents Gaussian white noise with a variance of $2\alpha ·{\sigma }_a^2$, and the detailed derivation can be found in [11]. The state space for the continuous-time model of one-dimensional target maneuvering is formulated as shown in Equations (3) and (4):

$$\left[\begin{array}{c}\hfill \dot{x}\left(t\right)\hfill \\ \hfill \ddot{x}\left(t\right)\hfill \\ \hfill \stackrel{⃛}{x}\left(t\right)\hfill \end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& -\alpha \end{array}\right]\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill \dot{x}\left(t\right)\hfill \\ \hfill \ddot{x}\left(t\right)\hfill \end{array}\right]+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]w\left(t\right)$$

(3)

$$\left[\begin{array}{c}\hfill \dot{x}\left(t\right)\hfill \\ \hfill \ddot{x}\left(t\right)\hfill \\ \hfill \stackrel{⃛}{x}\left(t\right)\hfill \end{array}\right]=\mathbf{F}\left[\begin{array}{c}\hfill x\left(t\right)\hfill \\ \hfill \dot{x}\left(t\right)\hfill \\ \hfill \ddot{x}\left(t\right)\hfill \end{array}\right]+\mathbf{G}w\left(t\right)$$

(4)

where $x\left(t\right)$, $\dot{x}\left(t\right)$, $\ddot{x}\left(t\right)$, and $\stackrel{⃛}{x}\left(t\right)$ denote the position, velocity, acceleration, and first derivative of acceleration, respectively. Upon discretization with a sampling period of T, the state transition equation for a one-dimensional maneuver is expressed as shown in Equation (5):

$$\begin{array}{cc}\hfill {\mathbf{X}}_{k+1}& \hfill ={\mathbf{F}}_k{\mathbf{X}}_k+{\mathbf{W}}_k=\left[\begin{array}{ccc}1& T& (\alpha T-1+{\mathrm{e}}^{-\alpha T})/{\alpha }^2\\ 0& 1& (1-{\mathrm{e}}^{-\alpha T})/\alpha \\ 0& 0& -{\mathrm{e}}^{-\alpha T}\end{array}\right]{\mathbf{X}}_k+{\mathbf{W}}_k\hfill \end{array}$$

(5)

where ${\mathbf{F}}_k$, ${\mathbf{W}}_k$, and ${\mathbf{X}}_k$ represent the state transition matrix, state noise vector, and state vector at time k and ${\mathbf{X}}_{k+1}$ represents the state vector at time $k+1$. The state noise covariance matrix ${\mathbf{Q}}_k$ in the Kalman filter can be expressed as shown in Equation (6):

$$\begin{array}{c}\hfill {\mathbf{Q}}_k=E\left[{\mathbf{W}}_k{{\mathbf{W}}_k}^{\mathrm{T}}\right]\end{array}$$

(6)

where ${\mathbf{W}}_k$ can be expressed as shown in Equation (7):

$$\begin{array}{c}\hfill {\mathbf{W}}_k={\int }_{kT}^{(k+1)T}{e}^{\mathbf{F}\left[\right(k+1)T-\tau ]}\mathbf{G}w\left(\tau \right)d\tau \end{array}$$

(7)

The covariance matrix for state noise in a more intricate model is fundamentally derived in accordance with Equation (6). Furthermore, the acceleration of maneuvering, which represents unknown controls, can be modeled as a time-dependent second-order model and a “current” statistical model. When dealing with a target that lacks prior information, it is necessary to model the acceleration of each dimension of the target as independent random processes within the coordinate system where the observer’s point of origin is located. This modeling is both essential and feasible in such scenarios. However, in practical scenarios, each control quantity of the UAV swarm’s centroid, generated by maneuvers such as thrust acceleration in the direction of velocity extension, pitch angle, roll angle, and deflection angle control, are independent of one another in the body coordinate system. These controls are better suited to be modeled as independent random processes within the body coordinate system. As a result, this paper derives a new state model and filtering process for tracking the UAV swarm’s centroid based on the dynamic characteristics of the UAV swarm’s centroid.

2.3. Framework of the Proposed Tracking Method

Drawing inspiration from the concepts of the MM algorithm and the utilization of deep learning as demonstrated in [18,41], this paper proposes the utilization of a maneuvering model estimation network to enhance the multi-model centroid tracking of UAV swarms. A noteworthy distinction from [18] lies in the derivation of maneuvering filtering, which exhibits significant differences based on the dynamics model of UAVs. Additionally, due to variations in maneuver types and the essential features that necessitate extraction, certain segments of the network architecture have been redesigned. The tracking framework is divided into four sequential steps:

(Step 1) Initialize filters: The given fused state estimation ${\hat{\mathbf{x}}}_{k-1\left|k-1\right.}$ and the error covariance matrix ${\mathbf{P}}_{k-1\left|k-1\right.}$ at time $k-1$ are updated to ensure their dimensions are appropriate for each filter. Then, the modified fusion state, error covariance matrix, and centroid observations ${\mathbf{z}}_k$ at time k are used as inputs for each filter.

(Step 2) State filtering based on various maneuvering models: The filters employing N maneuvering models produce N state estimations ${\hat{\mathbf{x}}}_{k\left|k\right.}^1,{\hat{\mathbf{x}}}_{k\left|k\right.}^2,\dots ,{\hat{\mathbf{x}}}_{k\left|k\right.}^N$ and an error covariance matrix ${\mathbf{P}}_{k\left|k\right.}^1,{\mathbf{P}}_{k\left|k\right.}^2,\dots ,{\mathbf{P}}_{k\left|k\right.}^N$ at time k.

(Step 3) Model estimation using deep learning: Based on observations of different time epochs ${\mathbf{z}}_k,{\mathbf{z}}_{k-1},\dots ,{\mathbf{z}}_{k-m}$, the maneuvering model estimation network determines the current maneuvering mode of the UAV swarm’s centroid. It outputs weights ${\mu }_1,{\mu }_2,\dots ,{\mu }_N$ corresponding to different maneuver modes.

(Step 4) Fusing the related states and covariance of multiple models: In (Step 2), the outputs of multiple maneuvering filters at time k are combined by a weighted summation with the weights obtained from (Step 3). The fused states ${\hat{\mathbf{x}}}_{k\left|k\right.}$ and the error covariance matrix ${\mathbf{P}}_{k\left|k\right.}$ are also used as inputs at time $k+1$.

3. The Centroid’s UKF with the Proposed 3D Coordinate-Coupled Dynamic Model

At first, drawing inspiration from [43], we represent the tangential load, normal load, and roll angle as factors that affect the three-dimensional position, velocity, pitch angle, and yaw angle of the centroid within a zero-mean first-order stationary Markov decision process. Following this, we design a nine-dimensional unscented Kalman filter, taking into account the aforementioned constraints to effectively track the centroid of the UAV swarm using only position observations, thereby enabling efficient edge computing capabilities.

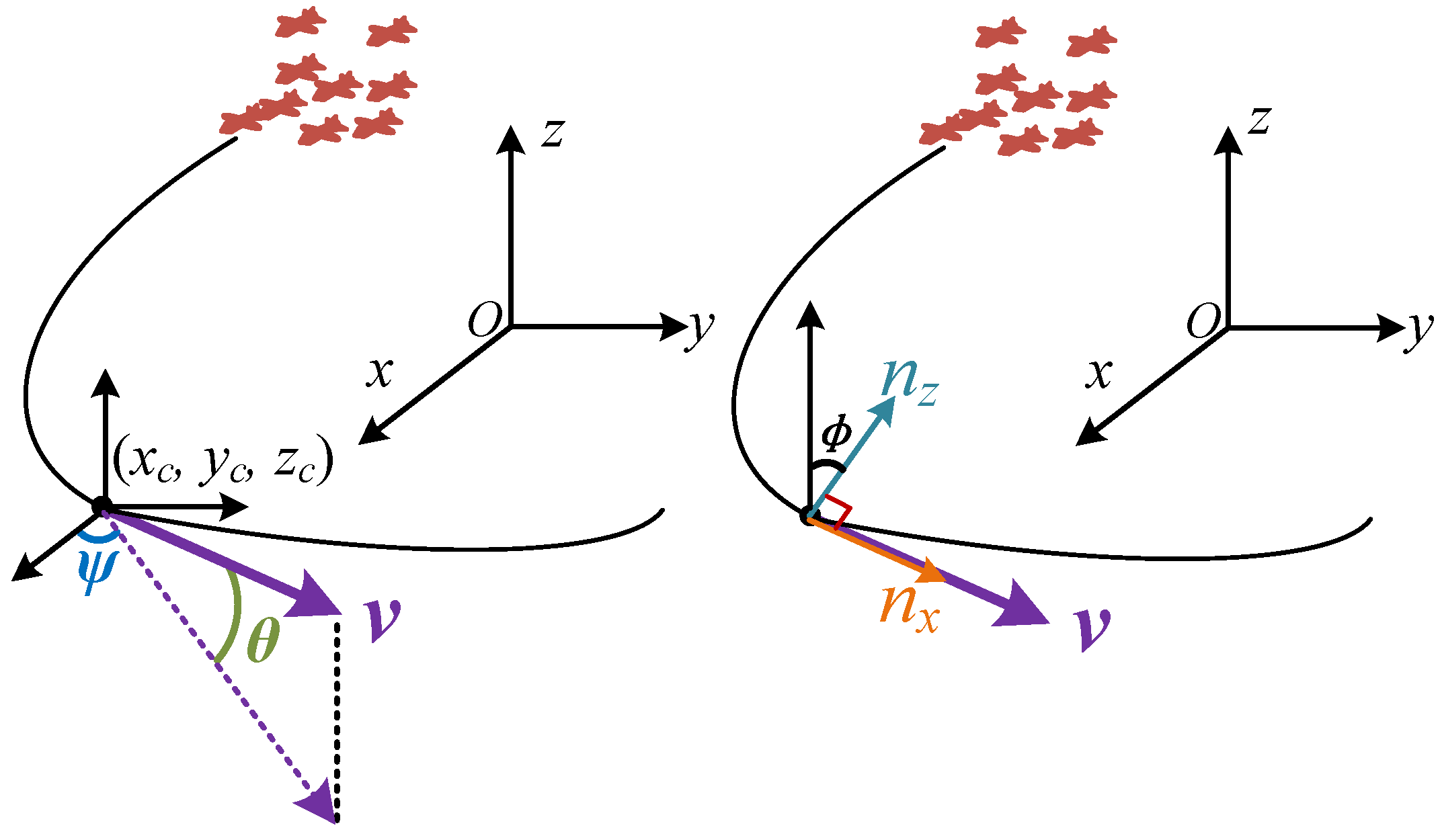
3.1. Modeling Description of the UAV Swarm’s Centroid

As depicted in Figure 2, the reference origin in the Cartesian system is set as the observer, and the position of the UAV swarm can be expressed as $(x_c,y_c,z_c)$. The velocity of the center point relative to the origin of the coordinate system can be expressed as a scalar $v_c$. The pitch angle $\theta$ is defined as the angle between the velocity direction and the XOY plane, while the yaw angle $\psi$ is the angle between the projection of the velocity direction onto the XOY plane and the X axis. It should be noted that “pitch” and “yaw” in this paper describe the trajectory characteristics and should not be confused with the vehicle attitude angles described in [19]:

$$\begin{array}{c}\left\{\begin{array}{l}{\dot{x}}_c=v_{c}cos\theta cos\psi \\ {\dot{y}}_c=v_{c}cos\theta sin\psi \\ {\dot{z}}_c=v_{c}sin\theta \\ {\dot{v}}_c=g(n_x-sin\theta )\\ \dot{\theta }=\frac{g}{v}(n_{z}cos\varphi -cos\theta )\\ \dot{\psi }=\frac{g{n}_{z}sin\varphi }{vcos\theta }\end{array}\right.\end{array}$$

(8)

The state of the centroid is influenced by three control factors: the tangential load $n_x$, normal load $n_z$, and roll angle $\varphi$. The velocity $v_c$ is impacted by the decomposition of thrust into the velocity extension component and the gravitational component. The tangential acceleration of the centroid resulting from the thrust components in the direction of extended motion is denoted as $n_{x}g$, where g represents the gravitational acceleration constant and $n_x$ is the dimensionless tangential load. The pitch and yaw angle indicate the track’s direction and curvature. The control inputs affecting $\theta$ and $\psi$ include the thrust component perpendicular to the velocity direction and the roll angle determining this component’s direction. The normal acceleration of the centroid due to the thrust component perpendicular to the motion direction is defined as $n_{z}g$, with $n_z$ representing the dimensionless normal load. The angle between the normal acceleration and the vertical plane of velocity corresponds to the roll angle $\varphi$. Equation (8) illustrates the relationships governing the states and control variables.

Until it is accurately modeled, all information about the control quantities is unknown to the observer. In addition, changes in the three control quantities are largely independent and uncoupled from each other when maneuvering a swarm of UAVs. Thus, it is appropriate to treat $n_x$, $n_z$, and $\varphi$ as distinct random processes, as outlined previously. In this study, we adopt Singer’s model assumption, positing that $n_x$, $n_z$, and $\varphi$ follow zero-mean first-order stationary Markov decision processes. The continuous-time equations describing these processes can be formulated as shown in Equation (9):

$$\begin{array}{l}\left\{\begin{array}{c}{\dot{n}}_z\left(t\right)=-{\alpha }_{n_z}{n}_z\left(t\right)+w_{n_z}\left(t\right)\hfill \\ {\dot{n}}_x\left(t\right)=-{\alpha }_{n_x}{n}_x\left(t\right)+w_{n_x}\left(t\right)\hfill \\ \dot{\varphi }\left(t\right)=-{\alpha }_{\varphi }\varphi \left(t\right)+w_{\varphi }\left(t\right)\hfill \end{array}\right.\hfill \end{array}$$

(9)

where $w_{n_z}\left(t\right)$, $w_{n_x}\left(t\right)$, and $w_{\varphi }\left(t\right)$ follow the additive white Gaussian noise with variance ${\sigma }_{n_z}^2$, ${\sigma }_{n_x}^2$, and ${\sigma }_{\varphi }^2$, respectively, while ${\alpha }_{n_z}$, ${\alpha }_{n_x}$ and ${\alpha }_{\varphi }$ are the maneuvering frequencies of $n_x$, $n_z$, and $\varphi$, respectively. In addition, $w_{n_z}\left(t\right)$, $w_{n_x}\left(t\right)$, and $w_{\varphi }\left(t\right)$ are zero-mean Gaussian white noise, and their variances are defined as $2{\alpha }_{n_z}{\sigma }_{n_z}^2$, $2{\alpha }_{n_x}{\sigma }_{n_z}^2$, and $2{\alpha }_{n_z}{\sigma }_{\varphi }^2$, respectively. Also, by assuming independence among these control parameters, we can effectively model the dynamics of the UAV swarm during maneuvers.

3.2. Nine-Dimensional UKF of the Centroid State

Integrating the dynamical equations governing the centroid of the swarm with the differential equations concerning the control volume results in a nine-dimensional state vector $\mathbf{x}$, as represented in Equation (10):

$$\begin{array}{c}\hfill \mathbf{x}={\left[x_c,y_c,z_c,v_c,\theta ,\psi ,n_z,n_x,\varphi \right]}^T.\end{array}$$

(10)

This comprehensive state vector encapsulates the essential variables necessary for modeling the UAV swarm’s behavior and interactions during flight maneuvers. By combining these fundamental dynamics, we aim to enhance our understanding of the system’s complex behaviors and optimize the control strategies for improved performance and efficiency.

The continuous-time state space of $\mathbf{x}$ can be expressed as shown in Equation (11):

$$\begin{array}{l}\dot{\mathbf{x}}\left(t\right)=f\left(\mathbf{x}\left(t\right)\right)+\mathbf{Gw}\left(t\right)\hfill \\ =\left[\begin{array}{c}{v}_c\left(t\right)cos\theta \left(t\right)cos\psi \left(t\right)\hfill \\ v_c\left(t\right)cos\theta \left(t\right)sin\psi \left(t\right)\hfill \\ v_c\left(t\right)sin\theta \left(t\right)\hfill \\ g(n_x\left(t\right)-sin\theta \left(t\right))\hfill \\ (g{n}_z\left(t\right)cos\varphi \left(t\right)-gcos\theta \left(t\right))/v_c\left(t\right)\hfill \\ g{n}_z\left(t\right)sin\varphi \left(t\right)/v_c\left(t\right)cos\theta \left(t\right)\hfill \\ -{\alpha }_{n_z}{n}_z\left(t\right)\hfill \\ -{\alpha }_{n_x}{n}_x\left(t\right)\hfill \\ -{\alpha }_{\varphi }\varphi \left(t\right)\hfill \end{array}\right]+\left[\begin{array}{c}0\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \\ w_{n_z}\left(t\right)\hfill \\ w_{n_x}\left(t\right)\hfill \\ w_{\varphi }\left(t\right)\hfill \end{array}\right]\hfill \end{array}$$

(11)

In the realm of tracking nonlinear state equations, common approaches involve the utilization of extended Kalman filters, unscented Kalman filters, or particle filters. In our study, we opted for the unscented Kalman Ffilter (UKF) due to its robustness in handling nonlinear state estimation tasks compared with the extended Kalman filter (EKF). The UKF offers a reliable solution while maintaining a relatively straightforward implementation, making it a preferred choice for our analysis. Additionally, the computational burden associated with the UKF’s iterative process is notably lighter than that of the particle filter, enhancing computational efficiency.

When considering a sampling interval of $T_S$ and accounting for state noise, the discrete-time state equation can be effectively computed as described in Equation (12):

$$\begin{array}{ll}{\mathbf{x}}_k\hfill & ={\mathbf{x}}_{k-1}+\dot{\mathbf{x}}{T}_S\hfill \\ =\hfill & \left[\begin{array}{c}{x}_{c,k-1}+v_{c,k-1}{T}_{S}cos{\theta }_{k-1}cos{\psi }_{k-1}\hfill \\ y_{c,k-1}+v_{c,k-1}{T}_{S}cos{\theta }_{k-1}sin{\psi }_{k-1}\hfill \\ z_{c,k-1}+v_{c,k-1}{T}_{S}sin{\theta }_{k-1}\hfill \\ v_{c,k-1}+g{T}_S(n_{x,k-1}-sin{\theta }_{k-1})\hfill \\ {\theta }_{k-1}+g{T}_S(n_{z,k-1}cos{\varphi }_{k-1}-cos{\theta }_{k-1})/v_{c,k-1}\hfill \\ {\psi }_{k-1}+g{T}_S{n}_{z,k-1}sin{\varphi }_{k-1}/v_{c,k-1}cos{\theta }_{k-1}\hfill \\ n_{z,k-1}-{\alpha }_{n_z}{n}_{z,k-1}{T}_S\hfill \\ n_{x,k-1}-{\alpha }_{n_x}{n}_{x,k-1}{T}_S\hfill \\ {\varphi }_{k-1}-{\alpha }_{\varphi }{\varphi }_{k-1}{T}_S\hfill \end{array}\right]+{\mathbf{w}}_{k-1}\hfill \end{array}$$

(12)

The observation $z_k$, composed of radar measurements (range R, azimuth A, and elevation E), can be expressed as shown in Equation (13), considering measurement errors:

$${\mathbf{z}}_k=\left[\begin{array}{c}{R}_k\hfill \\ A_k\hfill \\ E_k\hfill \end{array}\right]=h\left({\mathbf{x}}_k\right)+{\mathbf{r}}_k=\left[\begin{array}{c}\sqrt{x_{c,k}^2+y_{c,k}^2+z_{c,k}^2}\hfill \\ arctan(y_{c,k}/x_{c,k})\hfill \\ arctan\left(z_{c,k}/\sqrt{x_{c,k}^2+y_{c,k}^2}\right)\hfill \end{array}\right]+\left[\begin{array}{c}{r}_{R,k}\hfill \\ r_{A,k}\hfill \\ r_{E,k}\hfill \end{array}\right]$$

(13)

where the measurement errors vector ${\mathbf{r}}_k$ is additive white noise and its error covariance matrix ${\mathbf{R}}_k$ can be expressed as shown in Equation (14):

$$\begin{array}{c}\hfill {\mathbf{R}}_k=\mathrm{diag}({\sigma }_R^2,{\sigma }_A^2,{\sigma }_E^2)\end{array}$$

(14)

where ${\sigma }_R^2$, ${\sigma }_A^2$, and ${\sigma }_E^2$ are the variances of the observation errors of the range R, azimuth A, and elevation E, respectively. The computation process of the unscented Kalman filter based on the above dynamic model is as follows:

• Initialization
  • Initialize the state estimate ${\hat{\mathbf{x}}}_{1|1}$ and the error covariance matrix ${\mathbf{P}}_{1|1}$. The initialization of ${\hat{\mathbf{x}}}_{1|1}$ can be expressed as shown in Equation (15):

    $$\begin{array}{l}\begin{array}{c}{\hat{x}}_{c,0|0}=R_{0}cos\left(A_0\right)cos\left(E_0\right)\hfill \\ {\hat{y}}_{c,0|0}=R_{0}sin\left(A_0\right)cos\left(E_0\right)\hfill \\ {\hat{z}}_{c,0|0}=R_{0}sin\left(E_0\right)\hfill \\ {\hat{x}}_{c,1|1}=R_{1}cos\left(A_1\right)cos\left(E_1\right)\hfill \\ {\hat{y}}_{c,1|1}=R_{1}sin\left(A_1\right)cos\left(E_1\right)\hfill \\ {\hat{z}}_{c,1|1}=R_{1}sin\left(E_1\right)\hfill \\ {\hat{v}}_{c,1|1}={∥({\hat{x}}_{c,1|1},{\hat{y}}_{c,1|1},{\hat{z}}_{c,1|1})-({\hat{x}}_{c,0|0},{\hat{y}}_{c,0|0},{\hat{z}}_{c,0|0})∥}_2/T_S\hfill \\ {\hat{\theta }}_{c,1|1}=arctan\left(\left({\hat{z}}_{c,1|1}-{\hat{z}}_{c,0|0}\right)/{∥({\hat{x}}_{c,1|1},{\hat{y}}_{c,1|1})-({\hat{x}}_{c,0|0},{\hat{y}}_{c,0|0})∥}_2\right)\hfill \\ {\hat{\psi }}_{c,1|1}=arctan\left(\left({\hat{y}}_{c,1|1}-{\hat{y}}_{c,0|0}\right)/\left({\hat{x}}_{c,1|1}-{\hat{x}}_{c,0|0}\right)\right)\hfill \\ {\hat{n}}_{z,1|1}=0\hfill \\ {\hat{n}}_{x,1|1}=0\hfill \\ {\hat{\varphi }}_{1|1}=0\hfill \end{array}\hfill \end{array}$$

    (15)
    The initialization of the matrix ${\mathbf{P}}_{1|1}$ follows as shown in Equation (16):

    $${\mathbf{P}}_{1|1}=E\left[{\epsilon }_{1|1}{\epsilon }_{1|1}^{\mathrm{T}}\right]=E\left[({\mathbf{x}}_1-{\hat{\mathbf{x}}}_{1|1}){({\mathbf{x}}_1-{\hat{\mathbf{x}}}_{1|1})}^{\mathrm{T}}\right]$$

    (16)

    where ${\epsilon }_{1|1}$ represents the estimated error of ${\hat{\mathbf{x}}}_{1|1}$.
  • Set the initial values for the process noise covariance matrix $\mathbf{Q}$ as shown in Equation (17) and the measurement noise covariance matrix $\mathbf{R}$:

    $$\mathbf{Q}=\mathrm{diag}({\sigma }_{n_z}^2,{\sigma }_{n_x}^2,{\sigma }_{\varphi }^2)$$

    (17)

2.

Augmentation

• Augment the state vector ${\mathbf{x}}_k$ with the process noise vector ${\left[w_{n_z,k},w_{n_x,k},w_{\varphi ,k}\right]}^T$ to form an augmented state vector ${\mathbf{x}}_a$ as shown in Equation (18):

  $${\mathbf{x}}_a={\left[x_{c,k},y_{c,k},z_{c,k},v_{c,k},{\theta }_k,{\psi }_k,n_{z,k},n_{x,k},{\varphi }_k,w_{n_z,k},w_{n_x,k},w_{\varphi ,k}\right]}^{\mathrm{T}}$$

  (18)

• Augment the state covariance matrix ${\mathbf{P}}_{k|k}$ with the process noise covariance matrix $\mathbf{Q}$ to form an augmented covariance matrix ${\mathbf{P}}_a$ as shown in Equation (19):

  $${\mathbf{P}}_a=\left[\begin{array}{cc}{\mathbf{P}}_{k|k}& 0\\ 0& \mathbf{Q}\end{array}\right]$$

  (19)

3.

Sigma Point Generation

• Compute the weight coefficients of the sigma points. The mean weight coefficients follow as shown in Equations (20) and (21):

  $$w_{m,0}=\frac{\lambda }{\lambda +n_a}$$

  (20)

  $$w_{m,i}=w_{c,i}=\frac{1}{2(\lambda +n_a)},i=1,2,\cdots ,2n_a$$

  (21)

  where $n_a$ represents the dimension of the augmented state vector and $\lambda$ is a tunable parameter typically set to $3-n_a$. The covariance weight coefficients can be expressed as shown in Equations (22) and (23):

  $$w_{c,0}=\frac{\lambda }{\lambda +n_a}+(1-{\alpha }^2+\beta )$$

  (22)

  $$w_{c,i}=\frac{1}{2(\lambda +n_a)},i=1,2,\cdots ,2n_a$$

  (23)

  where $\alpha$ and $\beta$ are tunable parameters usually set to $0.5$ and 2, respectively.

• Generate sigma points from the augmented state vector ${\mathbf{x}}_a$ and the corresponding covariance matrix ${\mathbf{P}}_a$ using the unscented transformation as expressed in Equation (24):

  $${\mathbf{X}}_{k|k}^{\left(i\right)}=\left\{\begin{array}{ll}{\mathbf{x}}_a\hfill & i=0\hfill \\ {\mathbf{x}}_a+{\left[\sqrt{(n_a+\lambda ){\mathbf{P}}_a}\right]}_i\hfill & i=1,2,\cdots ,n_a\hfill \\ {\mathbf{x}}_a-{\left[\sqrt{(n_a+\lambda ){\mathbf{P}}_a}\right]}_{i-n_a}\hfill & i=n_a+1,\cdots ,2n_a\hfill \end{array}\right.$$

  (24)

  where ${[·]}_i$ denotes the ith column of a matrix and $\sqrt{·}$ represents the square root of a matrix. By linearly transforming the augmented state vector ${\mathbf{x}}_a$ and combining it with the weight coefficients, we obtain a set of sigma points that represent the state distribution.

4.

State Prediction

• Propagate the sigma points through the nonlinear state transition function $f\left({\mathbf{x}}_k\right)$ to obtain predicted sigma points ${\mathbf{X}}_{k+1|k}^{\left(i\right)}$ as expressed in Equation (25):

  $${\mathbf{X}}_{k+1|k}^{\left(i\right)}=f\left({\mathbf{X}}_{k|k}^{\left(i\right)}\right)$$

  (25)

• Estimate the predicted state ${\hat{\mathbf{x}}}_{k+1|k}$ and the predicted covariance matrix ${\mathbf{P}}_{k+1|k}$ based on the predicted sigma points as expressed in Equations (26) and (27):

  $${\hat{\mathbf{x}}}_{k+1|k}=\sum _{i=0}^{2n_a}{w}_{m,i}{\mathbf{X}}_{k+1|k}^{\left(i\right)}$$

  (26)

  $${\mathbf{P}}_{k+1|k}=\sum _{i=0}^{2n_a}{w}_{c,i}\left({\hat{\mathbf{x}}}_{k+1|k}-{\mathbf{X}}_{k+1|k}^{\left(i\right)}\right){\left({\hat{\mathbf{x}}}_{k+1|k}-{\mathbf{X}}_{k+1|k}^{\left(i\right)}\right)}^{\mathrm{T}}$$

  (27)

5.

Measurement Prediction

• Map the predicted sigma points ${\mathbf{X}}_{k+1|k}^{\left(i\right)}$ through the measurement function $h\left({\mathbf{x}}_k\right)$ to obtain the predicted measurement sigma points ${\mathbf{Z}}_{k+1|k}^{\left(i\right)}$ as expressed in Equation (28):

  $${\mathbf{Z}}_{k+1|k}^{\left(i\right)}=h\left({\mathbf{X}}_{k+1|k}^{\left(i\right)}\right)$$

  (28)

• Estimate the predicted measurement ${\hat{\mathbf{z}}}_{k+1|k}$ and the innovation covariance matrix ${\mathbf{S}}_k$ based on the predicted measurement sigma points as expressed in Equations (29) and (30):

  $${\hat{\mathbf{z}}}_{k+1|k}=\sum _{i=0}^{2n_a}{w}_{m,i}{\mathbf{Z}}_{k+1|k}^{\left(i\right)}$$

  (29)

  $${\mathbf{S}}_{k+1}={\mathbf{R}}_{k+1}+\sum _{i=0}^{2n_a}{w}_{c,i}\left({\hat{\mathbf{z}}}_{k+1|k}-{\mathbf{Z}}_{k+1|k}^{\left(i\right)}\right){\left({\hat{\mathbf{z}}}_{k+1|k}-{\mathbf{Z}}_{k+1|k}^{\left(i\right)}\right)}^{\mathrm{T}}$$

  (30)

6.

Update

• Compute the cross-covariance matrix ${\mathbf{P}}_{\mathbf{xz},k+1}$ between the state and measurement and the Kalman gain ${\mathbf{K}}_{k+1}$ as expressed in Equations (31) and (32):

  $${\mathbf{P}}_{\mathbf{xz},k+1}=\sum _{i=0}^{2n_a}{w}_{c,i}({\mathbf{X}}_{k+1|k}^{\left(i\right)}-{\hat{\mathbf{x}}}_{k+1|k}){({\mathbf{Z}}_{k+1|k}^{\left(i\right)}-{\hat{\mathbf{z}}}_{k+1|k})}^T$$

  (31)

  $${\mathbf{K}}_{k+1}={\mathbf{P}}_{\mathbf{xz},k+1}{\mathbf{S}}_{k+1}^{-1}$$

  (32)

• Update the state estimate ${\hat{\mathbf{x}}}_{k+1}$ and the state covariance matrix ${\mathbf{P}}_{k+1}$ using the actual measurement ${\mathbf{z}}_k$ as expressed in Equations (33) and (34):

  $${\hat{\mathbf{x}}}_{k+1}={\hat{\mathbf{x}}}_{k+1|k}+{\mathbf{K}}_{k+1}({\mathbf{z}}_{k+1}-{\hat{\mathbf{z}}}_{k+1|k})$$

  (33)

  $${\mathbf{P}}_{k+1}={\mathbf{P}}_{k+1|k}-{\mathbf{K}}_{k+1}{\mathbf{S}}_{k+1}{\mathbf{K}}_{k+1}^T$$

  (34)

7.

Iterate

• Repeat steps 3–6 for each new measurement.

4. GRU-Assisted Multi-Model Filtering

In this section, we will focus on the development of a GRU-based network that allows for the extraction of features from position observations. This network plays a crucial role in enabling swift and precise detection of the maneuvering mode. Once the features have been detected, we employ a multi-model filtering approach to effectively track the centroid of the UAV swarm and achieve edge computing.

4.1. Prior Knowledge

The aircraft’s motion is composed of seven basic motion modes, as described in [43]: maintaining the original state of flight, maximum acceleration straight flight, maximum overload left turn, maximum overload right turn, maximum overload climb, maximum overload dive, and maximum deceleration flight. These maneuvers exhibit significant differences in normal load, tangential load, and roll angle. Based on these characteristics, the seven basic maneuvering modes are further divided into four categories.

Mode 1 corresponds to maintaining the original state of flight, where the normal load $n_z$, tangential load $n_x$, and roll angle $\varphi$ remain relatively constant over a period of time.

Mode 2 corresponds to maximum acceleration straight flight and maximum deceleration flight, where $n_x$ changes significantly while $n_z$ and $\varphi$ change insignificantly.

Mode 3 corresponds to maximum overload climb and maximum overload dive, where $n_z$ and $n_x$ change significantly while $\varphi$ changes insignificantly.

Mode 4 corresponds to maximum overload left turn and maximum overload right turn, where $n_z$ and $\varphi$ change significantly while $n_x$ changes insignificantly.

To track the motion of the centroid as it switches between these modes, we employ multi-model filtering. The model transitions are determined based on historical observations of the centroid. The focus of these maneuvering frequency combinations is to differentiate between different types of maneuvers. The optimal values for the maneuvering frequencies may vary from those obtained empirically in this study. Further analysis of the track characteristics of UAV swarms can lead to optimization of the maneuvering frequency values. Although this aspect is not discussed in this work, the methodology of analysis can be found in [11].

4.2. GRU-Based Maneuver Estimation Network

The gated Rrecurrent unit (GRU)-based approach is another variant of recurrent neural networks (RNNs) that is widely used for learning features from sequence data [44]. In this paper, the GRU network is employed to estimate the model probability and replace the calculation of the model transition probability in multi-model filtering. Similar to LSTM, a GRU also utilizes gates to adaptively control the flow of information.

At each time step k, the GRU network maintains a hidden state $h{s}_k$ and a cell state $c{s}_k$. The cell state consists of two gates: the reset gate $r_k$ and the update gate $z{u}_k$. These gates, defined by point-wise sigmoid functions ${\sigma }_g(·)$, determine how much previous information should be forgotten and how much new information should be kept, while ${\mathbf{input}}_k$ represents the input at time step k. The calculation of the hidden state at time k can be summarized by Equation (35):

$$\begin{array}{l}\begin{array}{c}z{u}_k={\sigma }_g({\mathrm{W}}_z·\left[h_{k-1},{\mathbf{input}}_k\right]+{\mathbf{b}}_z)\hfill \\ r_k={\sigma }_g({\mathrm{W}}_r·\left[h_{k-1},{\mathbf{input}}_k\right]+{\mathbf{b}}_r)\hfill \\ {\tilde{h}}_k=tanh({\mathrm{W}}_h·[r_k\odot h{s}_{k-1},{\mathbf{x}}_k]+{\mathbf{b}}_h)\hfill \\ h{s}_k=(1-z{u}_k)\odot h{s}_{k-1}+z{u}_k\odot {\tilde{h}s}_k\hfill \end{array}\hfill \end{array}$$

(35)

In the above equations, ${\mathrm{W}}_{zu}$, ${\mathrm{W}}_r$, and ${\mathrm{W}}_{hs}$ are trainable weight matrices; ${\mathbf{b}}_{zu}$, ${\mathbf{b}}_r$, and ${\mathbf{b}}_{hs}$ are trainable bias vectors; and $tanh\left(·\right)$ denotes the hyperbolic tangent function. The element-wise product operation ⊙ signifies the Hadamard product.

When multiple GRU layers are stacked, the hidden state of the previous layer is used as an input for the next layer, allowing for hierarchical learning of sequential patterns.

The structure of the network is shown in Figure 3. The maneuvering model estimation of a single moment mainly consists of the following two steps:

(Step 1)

Feature extraction: The input to the network consists of multiple observations of the position, including $x_{obs}$, $y_{obs}$, and $z_{obs}$, spanning from the past to the present [45]. At each time step k, the output includes observations of the velocity $v_{obs,k}$, yaw angle ${\psi }_{obs,k}$, and pitch angle ${\theta }_{obs,k}$. While the position observations contain information about $n_x$, $n_z$, and $\varphi$, these characteristics are actually implicit in the second-order differentials between $x_{obs}$, $y_{obs}$, and $z_{obs}$. Moreover, due to measurement noise, using the observations directly as input for the GRU would mask actual changes in the states. To address this, we designed a “smoothing + first-order difference” feature extraction for the network. Specifically, we derive $v_{obs,k}$, ${\psi }_{obs,k}$, and ${\theta }_{obs,k}$ from the first-order differences of the filtered observations, which are then combined into a vector that serves as the input to the GRU layer. To reduce the impact of noise on estimating the motion model without accurately estimating the states of the centroid, we use the classical $\alpha -\beta$ filtering for smoothing the observations, as expressed in Equations (36)–(39) [46].

Prediction:

$$\left[\begin{array}{c}\hfill {\hat{x}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill {\hat{y}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill {\hat{z}}_{\alpha \beta ,k|k-1}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\hat{x}}_{\alpha \beta ,k-1|k-1}\hfill \\ \hfill {\hat{y}}_{\alpha \beta ,k-1|k-1}\hfill \\ \hfill {\hat{z}}_{\alpha \beta ,k-1|k-1}\hfill \end{array}\right]+T_S\left[\begin{array}{c}\hfill {\hat{v}}_{x,k-1|k-1}\hfill \\ \hfill {\hat{v}}_{y,k-1|k-1}\hfill \\ \hfill {\hat{v}}_{z,k-1|k-1}\hfill \end{array}\right]$$

(36)

$$\left[\begin{array}{c}\hfill {\hat{v}}_{x,k|k-1}\hfill \\ \hfill {\hat{v}}_{y,k|k-1}\hfill \\ \hfill {\hat{v}}_{z,k|k-1}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\hat{v}}_{x,k-1|k-1}\hfill \\ \hfill {\hat{v}}_{y,k-1|k-1}\hfill \\ \hfill {\hat{v}}_{z,k-1|k-1}\hfill \end{array}\right]$$

(37)

Update:

$$\left[\begin{array}{c}\hfill {\hat{x}}_{\alpha \beta ,k|k}\hfill \\ \hfill {\hat{y}}_{\alpha \beta ,k|k}\hfill \\ \hfill {\hat{z}}_{\alpha \beta ,k|k}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\hat{x}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill {\hat{y}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill {\hat{z}}_{\alpha \beta ,k|k-1}\hfill \end{array}\right]+\alpha \left[\begin{array}{c}\hfill x_{obs,k}-{\hat{x}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill y_{obs,k}-{\hat{y}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill z_{obs,k}-{\hat{z}}_{\alpha \beta ,k|k-1}\hfill \end{array}\right]$$

(38)

$$\left[\begin{array}{c}\hfill {\hat{v}}_{x,k|k}\hfill \\ \hfill {\hat{v}}_{y,k|k}\hfill \\ \hfill {\hat{v}}_{z,k|k}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\hat{v}}_{x,k|k-1}\hfill \\ \hfill {\hat{v}}_{y,k|k-1}\hfill \\ \hfill {\hat{v}}_{z,k|k-1}\hfill \end{array}\right]+\beta /T_S\left[\begin{array}{c}\hfill x_{obs,k}-{\hat{x}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill y_{obs,k}-{\hat{y}}_{\alpha \beta ,k|k-1}\hfill \\ \hfill z_{obs,k}-{\hat{z}}_{\alpha \beta ,k|k-1}\hfill \end{array}\right]$$

(39)

where ${\left(\widehat{·}\right)}_{\alpha \beta ,k|k-1}$ represents one-step prediction based on $\alpha -\beta$ filtering, ${\left(\widehat{·}\right)}_{\alpha \beta ,k|k}$ represents the smoothed state at time k, ${(·)}_{obs,k}$ represents the observation at time k, and $\left(x,y,z\right)$ and $\left(v_x,v_y,v_z\right)$ represent the position and velocity vector, respectively.

The first-order difference operation used in feature extraction can be derived as shown in Equation (40):

$$\begin{array}{ll}{v}_{obs,k}\hfill & ={∥{\left[{\hat{x}}_{\alpha \beta ,k|k},{\hat{y}}_{\alpha \beta ,k|k},{\hat{z}}_{\alpha \beta ,k|k}\right]}^T-{\left[{\hat{x}}_{\alpha \beta ,k-1|k-1},{\hat{y}}_{\alpha \beta ,k-1|k-1},{\hat{z}}_{\alpha \beta ,k-1|k-1}\right]}^T∥}_2/T_S\hfill \\ {\theta }_{obs,k}\hfill & =arcsin\left(\frac{{\hat{z}}_{\alpha \beta ,k|k}-{\hat{z}}_{\alpha \beta ,k-1|k-1}}{{∥{[{\hat{x}}_{\alpha \beta ,k|k},{\hat{y}}_{\alpha \beta ,k|k},{\hat{z}}_{\alpha \beta ,k|k}]}^T-{[{\hat{x}}_{\alpha \beta ,k-1|k-1},{\hat{y}}_{\alpha \beta ,k-1|k-1},{\hat{z}}_{\alpha \beta ,k-1|k-1}]}^T∥}_2}\right)\hfill \\ {\psi }_{obs,k}\hfill & =arctan\left(({\hat{y}}_{\alpha \beta ,k|k}-{\hat{y}}_{\alpha \beta ,k-1|k-1})/({\hat{x}}_{\alpha \beta ,k|k}-{\hat{x}}_{\alpha \beta ,k-1|k-1})\right)\hfill \end{array}$$

(40)

In theory, the designed feature extraction can potentially learn the necessary features for maneuver detection. However, in practice, the expected increase in classification accuracy was not attained during model training. Further analysis of subsequent results revealed that the limited accuracy, which did not exceed 60%, predominantly stemmed from the narrow intervals between the feature samples and the relatively small absolute changes within individual data points. These factors posed challenges for the computer to precisely calculate the differences due to floating-point precision limitations. To tackle this issue, we experimented with amplifying the differences by multiplying each variable by 10 after calculating the first-order difference. This adjustment aimed to amplify the disparities between data points and facilitate accurate feature learning within a specified level of precision. Following this amplification, the model successfully converged during training, resulting in a classification accuracy of 99.73%.

(Step 2) Regarding model classification, the GRU layer receives a vector that comprises the velocity, yaw angle, and pitch angle. The maneuver model classification is then performed via a fully connected layer, a softmax layer, and a classification layer. The hidden layer contains 200 neurons, and each time step of the GRU layer generates an output.

During model training, the categorical cross-entropy loss function is applied as shown in Equation (41):

$$\begin{array}{c}\hfill L=-\sum _{m=1}^M\sum _{k=1}^{K_m}\sum _{n=1}^N{\mu }_{m,k,n}log\left({\hat{\mu }}_{m,k,n}\right)\end{array}$$

(41)

where M represents the number of trajectories involved in the training process. Each trajectory has its own length and is represented by a sequence of $K_m$ data points. The variable N represents the number of categories, ${\mu }_{m,k,n}$ represents the true probability of a given data point k at a trajectory m belonging to a category n, and ${\hat{\mu }}_{m,k,n}$ indicates the predicted probability.

The model weights were initialized using Glorot initialization, and the ADAM optimizer was employed for optimization. A dropout rate of 0.5 was chosen for the experiment, with network connections being dropped between the final GRU output and the dense classifier. The network underwent 100 training epochs with a learning rate of 0.001 and a gradient threshold of 2.

In this paper, the training data utilized for model training were generated through simulation. The simulation process involved the following steps:

(1)

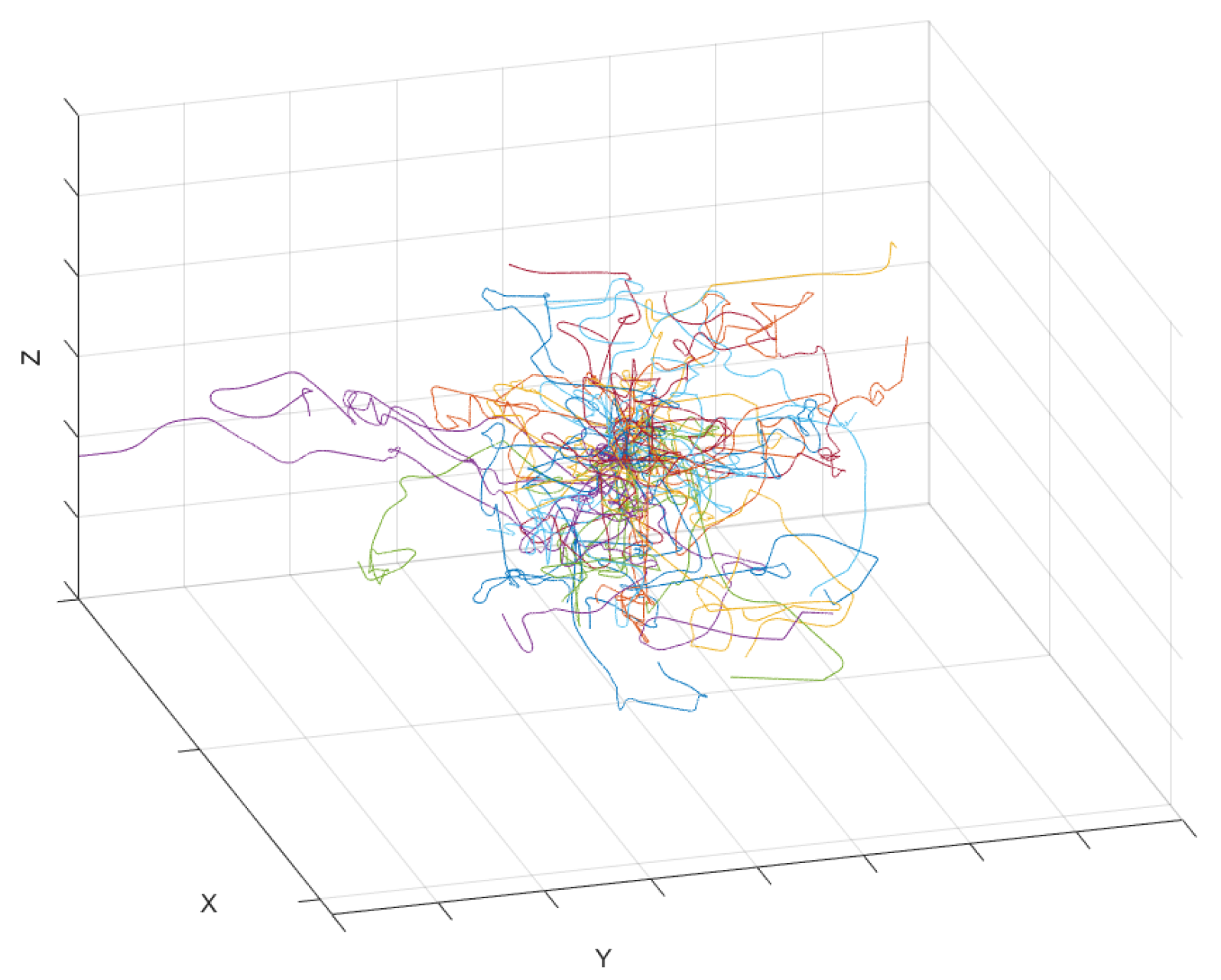
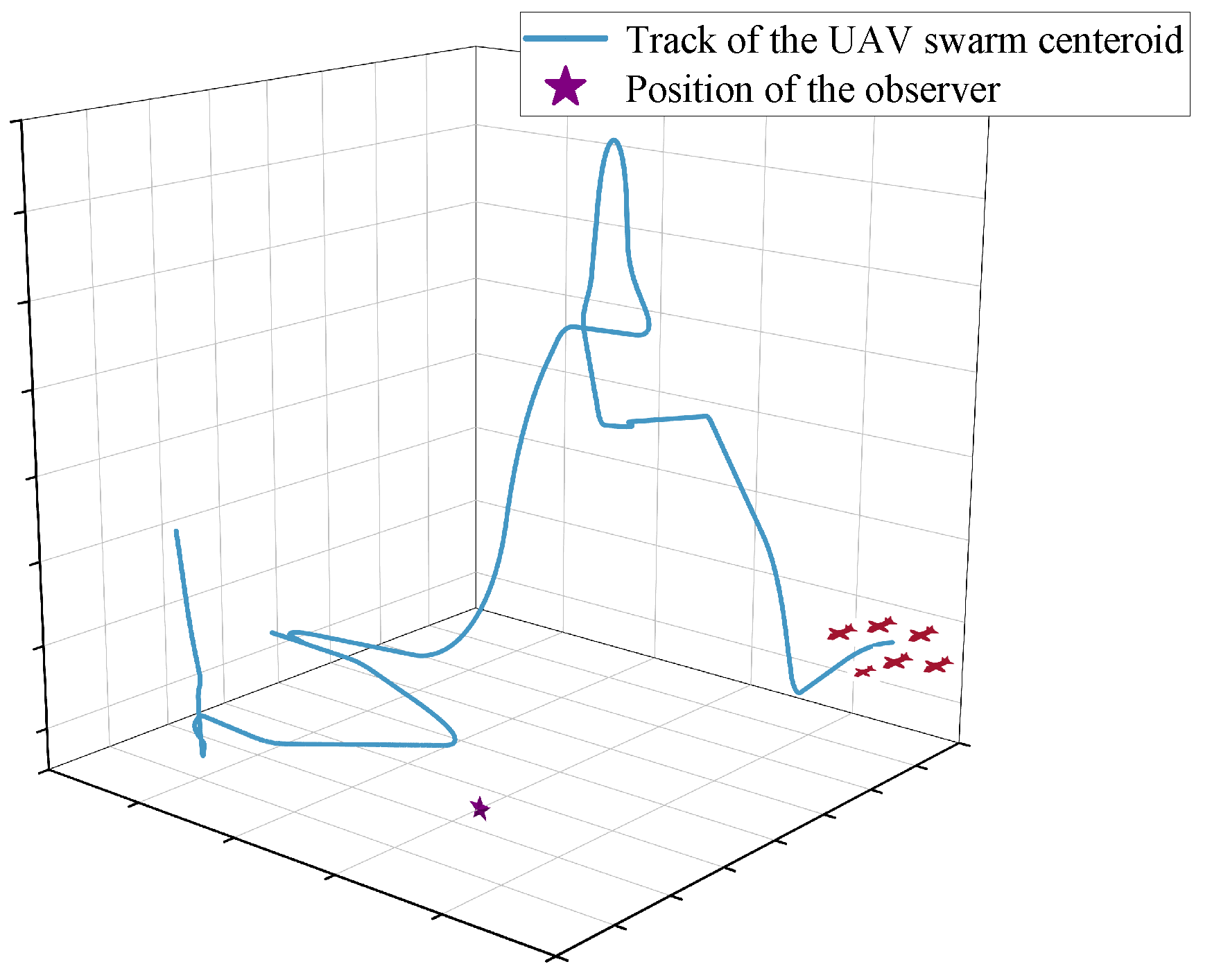
Target generation: A swarm of UAV targets, separated by distances ranging from 5 to 7 m, was generated with their geometric center flying along a predefined trajectory.

(2)

Maneuver and trajectory simulation: The trajectory of the center was divided into several time segments of varying lengths, with each segment randomly corresponding to a maneuver type. The trajectory of the center was simulated based on the selected maneuver type, and the corresponding motion model label was assigned.

(3)

Observation simulation: Observations of the swarm were simulated at a specific resolution, with an observation error having a standard deviation of 8 m along a single coordinate axis and an update frequency of 0.5 s. The centroid observation of the swarm was obtained by combining multiple measurements of the swarm using weighting.

The resulting training data consisted of observed centroid measurements with observation errors and corresponding motion model labels. The trajectory was divided into 50 segments, with a total duration of 75,812 s and an update interval of 0.5 s. The generated tracks are presented in Figure 4.

4.3. Estimation Fusion

At time step k, the UKF estimation and error covariance matrix of the ith model are denoted as ${\hat{\mathbf{x}}}_{k|k}^i$ and ${\mathbf{P}}_{k|k}^i$, respectively. The weight assigned to model i by the maneuver estimation network is denoted as ${\mu }_k^i$. The output state ${\hat{\mathbf{x}}}_{k|k}$ and covariance ${\mathbf{P}}_{k|k}$ of the multi-model filtering can be defined as shown in Equations (42) and (43), respectively:

$$\begin{array}{c}\hfill {\hat{\mathbf{x}}}_{k|k}=\sum _{i=1}^N{\mu }_k^i{\hat{\mathbf{x}}}_{k|k}^i\end{array}$$

(42)

$$\begin{array}{c}\hfill {\mathbf{P}}_{k|k}=\sum _{i=1}^N{\mu }_k^i\left({\mathbf{P}}_{k|k}^i+[{\hat{\mathbf{x}}}_{k|k}^i-{\hat{\mathbf{x}}}_{k|k}]·{[{\hat{\mathbf{x}}}_{k|k}^i-{\hat{\mathbf{x}}}_{k|k}]}^T\right)\end{array}$$

(43)

In [18], the weight ${\mu }_k^i$ is also determined by the considered deep learning network, which restricts its values to either one or zero. In practical scenarios, an alternative approach can be employed where the output of the softmax layer is utilized to assign weights to each model. The reason behind only considering binary values for $\mu$ is not explicitly provided [18]. Furthermore, the paper does not provide a direct comparison between the two methods. To address this gap, we will conduct a thorough analysis and comparison of both approaches in the Section 5. Our objective is to determine which method of assigning weights to models is more suitable for estimation fusion in the context of our study. By evaluating and contrasting these techniques, we aim to provide insights into the advantages and limitations of each approach, enabling us to make informed decisions regarding weight assignment in model fusion for estimation purposes.

5. Simulation

5.1. Simulation Settings

To verify the proposed algorithm, this study carries out simulation experiments that compare the filtering performance of maneuver model estimation and centroid tracking. In the comparative experiments for maneuver model estimation, we adopted the IMM algorithm and set the initial transition probability matrix as shown in Equation (44):

$$\begin{array}{c}\hfill p_{ij}=\left[\begin{array}{cccc}0.25& 0.25& 0.25& 0.25\\ 0.25& 0.25& 0.25& 0.25\\ 0.25& 0.25& 0.25& 0.25\\ 0.25& 0.25& 0.25& 0.25\end{array}\right]\end{array}$$

(44)

The initial mode probabilities were set as shown in Equation (45):

$$\begin{array}{c}\hfill {\mu }^{1:2:3:4}=\left[0.250.250.250.25\right]\end{array}$$

(45)

The validation trajectory’s length was 1213 s, with the observation update frequency set to 0.5 s. The ${\sigma }_R^2$, ${\sigma }_A^2$ and ${\sigma }_E^2$ values were set as 15 m, $0.1^{\circ }$, and $0.1^{\circ }$, respectively. We divided the validated trajectory into 30 segments, with a randomly generated maneuver mode used in each segment. The target’s velocity relative to the coordinate system’s origin fell within the range of (50, 120). The pitch variation for a single time segment was within the range $\left(-\pi /2,\pi /2\right)$, while the yaw variation’s range was $\left(0,2\pi \right)$. We obtained the initial state values for filtering from Equation (23). The track generation process was similar to that in Section 4. Refer to Figure 5 for the tracking scenario. The simulation tool used in this paper is MATLAB 2021A.

5.2. Simulation Results and Analysis

Figure 6 illustrates the training process of the model estimation network. After a predetermined number of 100 iterations, the classification accuracy reached 99.5413%, and the loss function decreased to 0.02419. The network convergence performance was also better, as expected.

Figure 7 illustrates the difference in performance between the traditional IMM and proposed algorithms in estimating motion models. The GRU-assisted algorithm provided higher credibility and promptly reflected model transitions compared with the traditional IMM algorithm.

A 1000 run Monte Carlo simulation of position estimates is shown in Figure 8, which compares the root mean square error (RMSE) values of different algorithms. The IMM-EKF that employed the dynamical model proposed in this paper achieved more accurate state estimation than the Singer model. Overall, GRU-assisted filtering yielded a more accurate state estimation compared with the traditional IMM method. In Figure 9, we show the tracking results of the centroid, comparing the Singer-EKF, IMM-EKF, GRU-assisted filtering (1), and GRU-assisted filtering (2). GRU-assisted filtering (1) and GRU-assisted filtering (2) represent the model weight being zero or one and the model weight being the output of the softmax layer, respectively.

Furthermore, we observed that the reduction in error mainly occurred after model changes, demonstrating the ability of GRU-assisted motion model estimation to promptly reflect mode transitions. There was no significant difference between GRU-assisted filtering (1) and GRU-assisted filtering (2). The smaller RMSE of GRU-assisted filtering (2) may have been due to the retention of some states from other models during model transitions, which increased fault tolerance and mitigates the impact of model weight switching between 0 and 1 at incorrect time steps.

6. Experiments

6.1. Flight Experiments

To further evaluate the effectiveness of the proposed algorithm, flight experiments were conducted using three hexacopter UAVs developed in our laboratory [30]. As shown in Figure 10a, the UAVs were equipped with Langyu SUNNYSKY X5212S brushless motor multirotor motors, Tattu 30,000 mAh batteries, and the DJI A3 flight control system, providing flight endurance of 25 min. Three sets of flight experiments were carried out with different durations, namely 1194 s, 1243 s, and 1223 s. Each UAV was equipped with a BeiDou receiver (SinoGNSS M600mini) to record its real-time position. During each flight experiment, the three UAVs formed a swarm for cooperative flight, as shown in Figure 10b. The centroid trajectories of the swarm during cooperative flight, as depicted in Figure 11, consisted of multiple maneuvering segments. Within the maneuvering capabilities of the UAVs, the specific maneuvers performed were randomly generated by pre-programmed ground routines. Additionally, the YAOFENG RADAR YFR-01C was employed to record radar observations of the UAVs for predicting the motion model and trajectory filtering. The scan interval of the radar was 0.5 s.

The data processing for the experiment was divided into two parts: prediction of the maneuver models and trajectory filtering. In maneuver model prediction, two approaches were employed. The first involved directly using a network trained on a simulated dataset to validate the maneuver model with flight data, while the second approach utilized 70% of the flight data duration for training and the remaining 30% for validation. The training environment was set to mimic the simulation environment. Additionally, trajectory filtering was compared with the Singer-KF and IMM-EKF methods. Figure 12 illustrates the confusion matrix for the proposed deep learning approach in the flight experiment. The false alarm rate for mode estimation by the network trained in the simulation and the retrained network were found to be quite low, validating the algorithm’s capability to detect maneuver models. This also serves as preliminary evidence that the data generation process in the simulation closely approximated reality.

Table 1. The RMSEs of position and velocity estimation for the three flight experiments with GRU-assisted filtering, Singer-KF, and IMM-EKF.

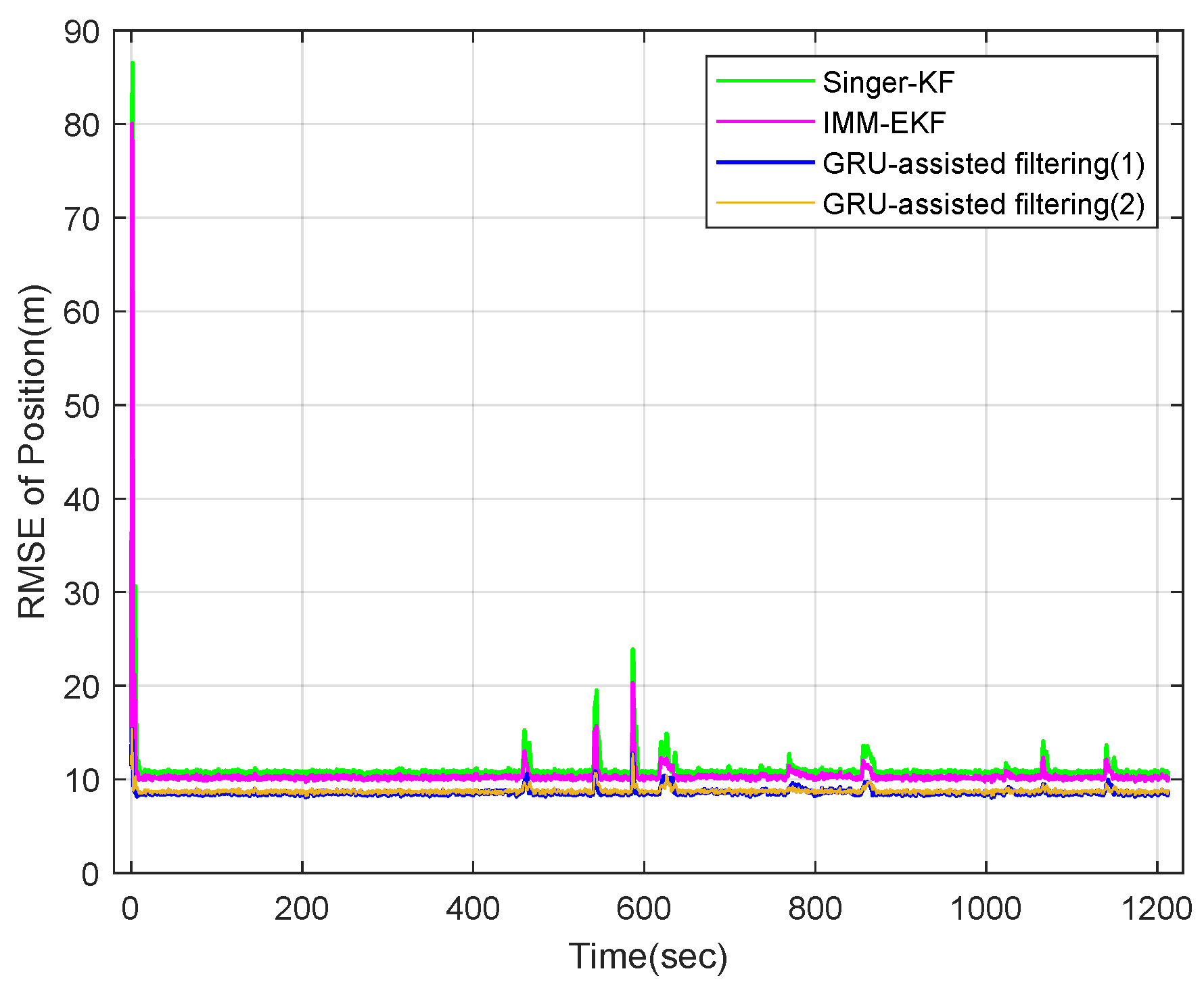
Trajectory	GRU-Assisted Filtering	Singer-KF	IMM-EKF
Flight1 position RMSE (m)	2.5237	3.9419	3.2917
Flight1 velocity RMSE (m/s)	1.6806	2.2451	2.0906
Flight2 position RMSE (m)	2.7068	4.2543	3.3111
Flight2 velocity RMSE (m/s)	1.8814	2.4985	2.1550
Flight3 position RMSE (m)	2.6991	3.8935	3.5317
Flight3 velocity RMSE (m/s)	1.6977	2.3391	2.1863

displays the root mean square error (RMSE) results for position and velocity estimation during the flight experiment. The results demonstrate that the algorithm can more accurately estimate the centroid trajectory of the UAV swarm. Furthermore, the proposed maneuver model and the GRU-assisted multi-model filtering significantly reduced tracking errors.

In practical scenarios, the high dynamic displacement between communicating parties can pose challenges to signal acquisition, synchronization, and stable transmission. Leveraging the spatial relationship between the parties’ displacements to assist with phase acquisition within communication signals can potentially lead to more stable or higher rates of data transmission under the same conditions. Enhanced accuracy in position estimation enables the trajectory information of high-dynamic UAV swarms’ centroids to serve as auxiliary data in communication systems. This auxiliary information, through specific mathematical transformations, can aid in rapid signal demodulation, precise compensation for Doppler frequency shifts, and tracking of communication beam directions within a phase-locked loop framework. Consequently, edge computing based on swarm UAVs can achieve more reliable or high-speed data interaction with the ground in high-dynamic environments.

6.2. Computational Complexity

In this section, the computational complexity of our 3DCDM-based GRU-MM algorithm is discussed in comparison with the Singer-KF and IMM-EKF algorithms by testing the average computation time for a single tracking iteration. To ensure a fair comparison, all algorithms were tested using the same Intel Core i7-8750H 2.2 GHz CPU and 16 GB of RAM. During the trajectory tracking process, our 3DCDM-based GRU-MM algorithm took an average of 17.4 ms per iteration, while the Singer-KF and IMM-EKF algorithms took 3.4 ms and 16.1 ms, respectively. Our 3DCDM-based GRU-MM algorithm achieved higher tracking accuracy without significantly sacrificing computational complexity. When the radar operated in the track-while-scan (TWS) mode with a scan interval of 0.5 s, our proposed method could be applied in real time.

7. Conclusions

Our proposed 3DCDM-based GRU-MM method aims to improve the tracking of maneuvering centroids in UAV swarms, which can significantly enhance the efficiency of mobile edge computing. By adopting a novel 3D coordinate-coupled dynamic model and multi-model filtering assisted by a GRU-based network, our method can better capture complex maneuvers and enhance state estimation accuracy. Furthermore, our proposed GRU-MM method achieved a high classification accuracy of 99.73%. The results demonstrate that our method outperformed traditional models or IMM algorithms in the state estimation of UAV swarms’ maneuvering centroids. The combination of our innovative tracking approach and mobile edge computing opens up new possibilities for advanced applications and services in various fields.

In the context of tracking the centroid of the UAV swarm, future research endeavors will involve exploring more intricate and precise maneuvering models to effectively capture the complex dynamic behaviors exhibited by UAV swarms in high-dynamic environments. This pursuit may involve introducing additional dimensions within dynamic models or considering the impact of uncertainty factors. Moreover, the integration of multiple sources of information will be a focal point, particularly in terms of effectively fusing data from various sensors and communication nodes to enhance the accuracy of UAV swarm state estimation.

Regarding the application of tracking results related to the centroids of UAV swarms, the subsequent step will involve exploring how trajectory information can be transformed to facilitate the enhancement of existing communication systems, specifically in the areas of phase-locked loop (PLL) operations, Doppler frequency estimation, beamforming techniques, and evaluating the implications of these advancements for edge computing.