Barrier-Function-Based Adaptive Fast-Terminal Sliding-Mode Control for a PMSM Speed-Regulation System
Abstract
:1. Introduction
- 1.
- A fast terminal sliding mode surface is proposed, which provides a finite-time convergence speed of system state variables. Therefore, the system has a stronger ability to reject internal and external disturbances.
- 2.
- A barrier-function-based adaptive law is utilized so that control gain is adaptively adjusted in response to the amplitude of disturbance, and the chattering caused by excessive switching gain is reduced. Furthermore, the design of AFTSMC does not require attaining the upper limit of the disturbances.
- 3.
- The experimental results of the proposed method as compared to that of the conventional TSMC are implemented. Both internal and external disturbances are considered to verify the effectiveness of the proposed method.
2. Mathematical Model of PMSM
3. Controller Design
3.1. Traditional TSMC Design
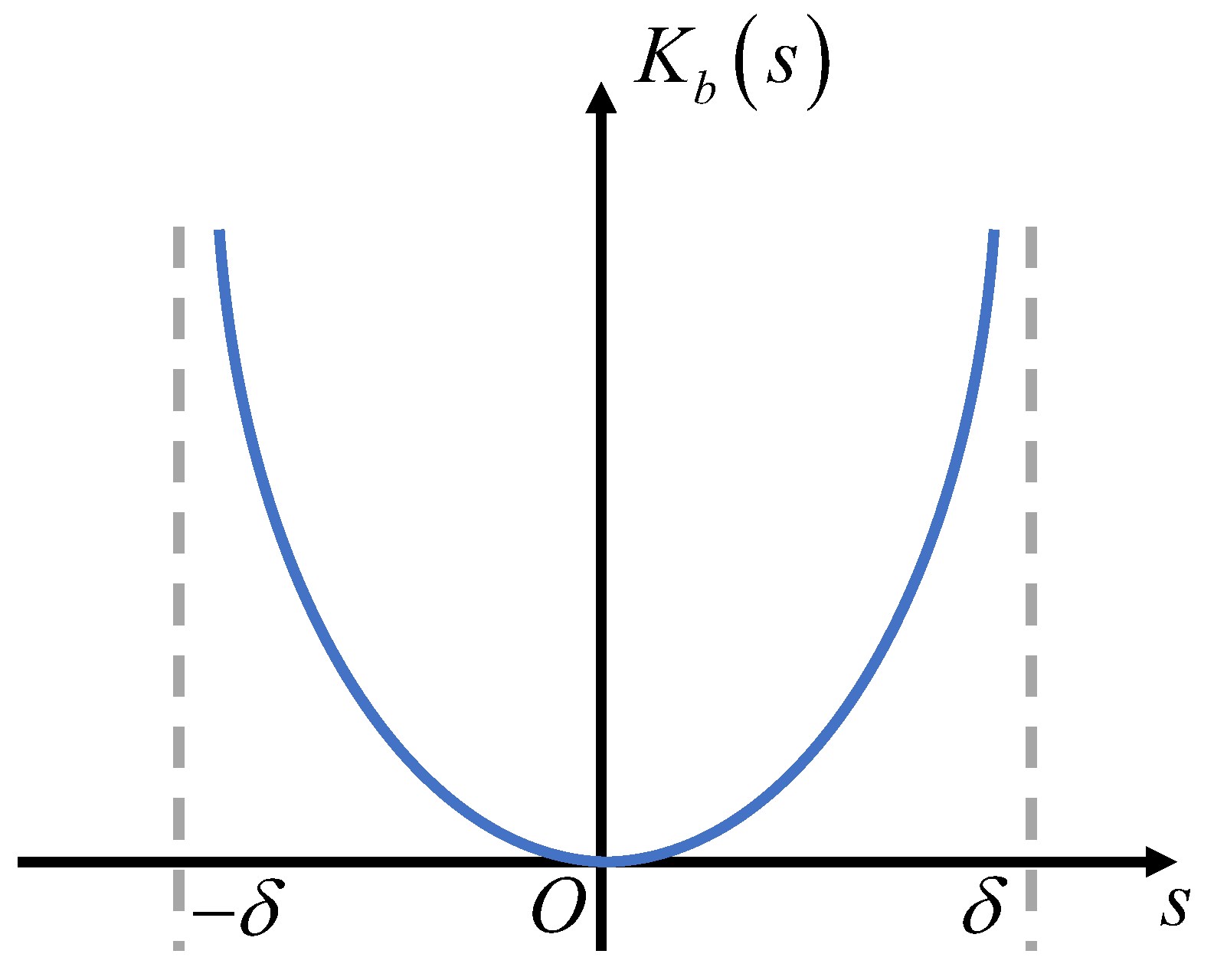
3.2. Barrier-Function-Based AFTSMC Design
- Case I:
- Case 2:
- 1.
- The parameters α and β play a critical role in determining the decay rate of the tracking error on the sliding surface. They also roughly determine the speed-tracking bandwidth, which ultimately contributes to achieving a faster response speed and higher tracking accuracy. It is important to note that a larger bandwidth can amplify high-frequency noise, potentially degrading the overall system performance.
- 2.
- Similarly, the choice of parameter λ influences the convergence time of the system. A larger value of λ results in a smaller convergence time, implying a faster attainment of the desired control objective. However, this could result in an amplification of velocity measurement noises, introducing additional disturbances and potential inaccuracies into the system.
- 3.
- Increasing the value of the parameter leads to an increase in the stiffness of the closed-loop system. However, it should be noted that if is set to a large value, it can inject excess noise into the system.
- 4.
- Increasing the value of the parameter ρ tends to accelerate the convergence speed of the error. However, it can also introduce chattering phenomena into the system. On the other hand, the parameter δ determines the convergence domain. A smaller value of δ leads to higher tracking precision. However, if δ is set too small, it may reduce the convergence speed of the system.
4. Experimental Results
4.1. Speed Response of Motor Starting
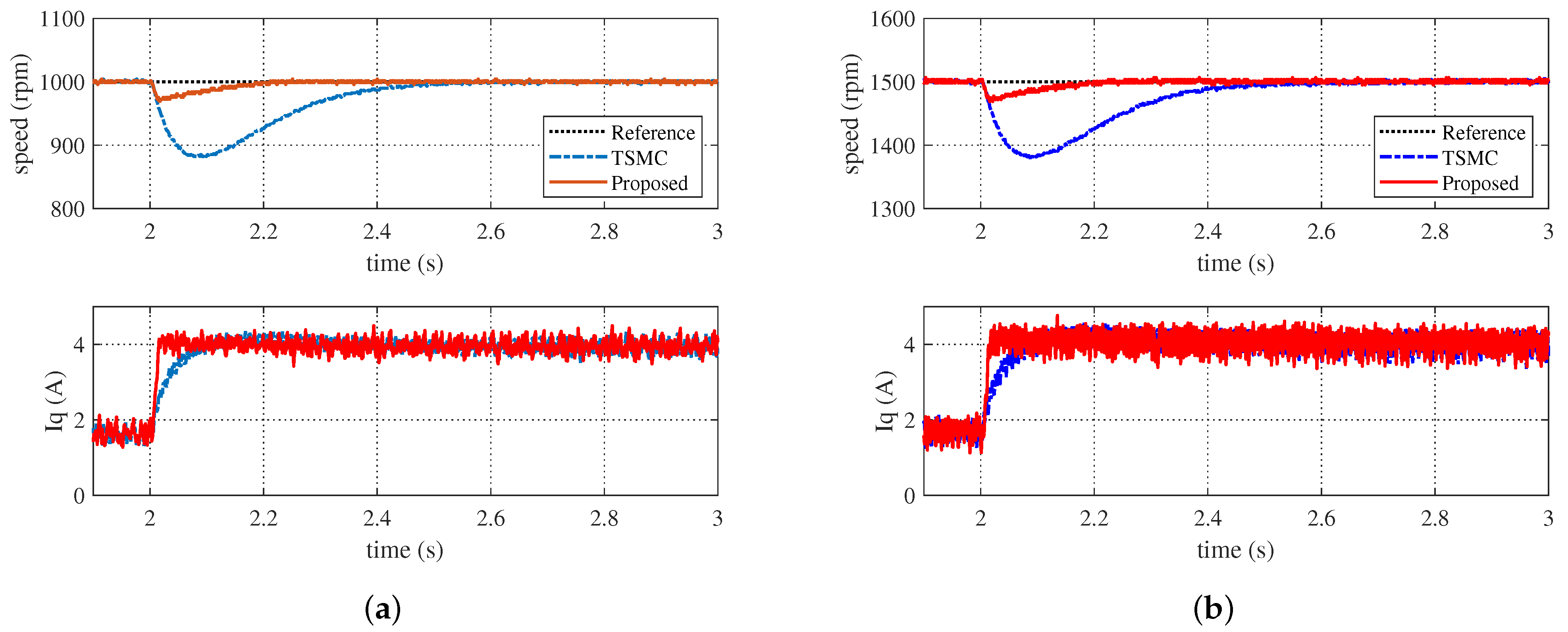
4.2. Speed Response under Sudden Load Torque Changes
4.3. Speed Response under Variable Parameters
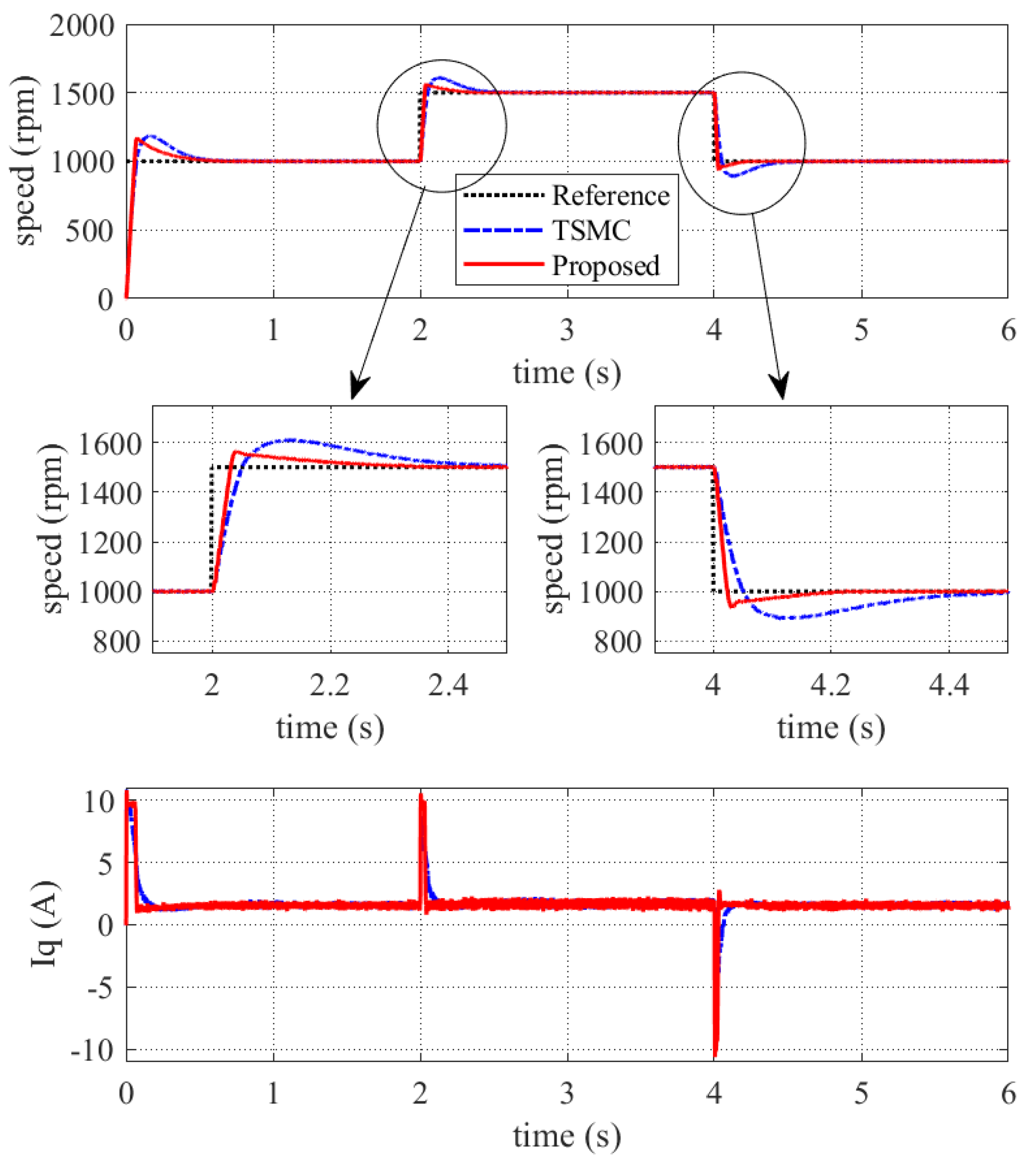
4.4. Variable Speed Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, D.; Zhang, H.; Li, X.; Zhao, H.; Zhang, Y.; Wang, S.; Ahmad, T.; Liu, T.; Shuang, F.; Wu, T. A PMSM Control System for Electric Vehicle Using Improved Exponential Reaching Law and Proportional Resonance Theory. IEEE Trans. Veh. Technol. 2023, 72, 8566–8578. [Google Scholar] [CrossRef]
- Huo, J.; Ji, H.; Yang, P. Research on sensorless control system of permanent magnet synchronous motor for CNC machine tool. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 1592–1595. [Google Scholar]
- Ullah, S.; McDonald, S.P.; Martin, R.; Benarous, M.; Atkinson, G.J. A Permanent Magnet Assist, Segmented Rotor, Switched Reluctance Drive for Fault Tolerant Aerospace Applications. IEEE Trans. Ind. Appl. 2019, 55, 298–305. [Google Scholar] [CrossRef]
- Bensalem, Y.; Abbassi, A.; Abbassi, R.; Jerbi, H.; Alturki, M.; Albaker, A.; Kouzou, A.; Abdelkrim, M.N. Speed tracking control design of a five-phase PMSM-based electric vehicle: A backstepping active fault-tolerant approach. Electr. Eng. 2022, 104, 2155–2171. [Google Scholar] [CrossRef]
- Bensalem, Y.; Abbassi, R.; Jerbi, H. Extended Kalman Filter Based-Sensorless Control of Five-Phase PMSM. In Proceedings of the 2022 5th International Conference on Power Electronics and their Applications (ICPEA), Hail, Saudi Arabia, 29–31 March 2022; pp. 1–7. [Google Scholar]
- Bensalem, Y.; Kouzou, A.; Abbassi, R.; Jerbi, H.; Kennel, R.; Abdelrahem, M. Sliding-Mode-Based Current and Speed Sensors Fault Diagnosis for Five-Phase PMSM. Energies 2022, 15, 71. [Google Scholar] [CrossRef]
- Lin, X.; Wu, C.; Yao, W.; Liu, Z.; Shen, X.; Xu, R.; Sun, G.; Liu, J. Observer-Based Fixed-Time Control for Permanent-Magnet Synchronous Motors With Parameter Uncertainties. IEEE Trans. Power Electron. 2023, 38, 4335–4344. [Google Scholar] [CrossRef]
- Dong, X.; Mao, J.; Yan, Y.; Zhang, C.; Yang, J. Generalized Dynamic Predictive Control for Nonlinear Systems Subject to Mismatched Disturbances With Application to PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 954–964. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, L.; Vazquez, S.; Xu, R.; Dong, Z.; Liu, J.; Leon, J.L.; Wu, L.; Franquelo, L.G. Disturbance and Uncertainty Attenuation for Speed Regulation of PMSM Servo System Using Adaptive Optimal Control Strategy. IEEE Trans. Transp. Electr. 2023, 9, 3410–3420. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Dong, W.; Chen, B.; Lin, C. Neural Network-Based Adaptive Dynamic Surface Control for Permanent Magnet Synchronous Motors. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 640–645. [Google Scholar] [CrossRef] [PubMed]
- Sandre-Hernandez, O.; de Jesus Rangel-Magdaleno, J.; Morales-Caporal, R. Modified model predictive torque control for a PMSM-drive with torque ripple minimisation. IET Power Electron. 2019, 12, 1033–1042. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Discrete-Time Repetitive Control-Based ADRC for Current Loop Disturbances Suppression of PMSM Drives. IEEE Trans. Ind. Informat. 2022, 18, 3138–3149. [Google Scholar] [CrossRef]
- Yu, L.; Huang, J.; Luo, W.; Chang, S.; Sun, H.; Tian, H. Sliding-Mode Control for PMLSM Position Control—A Review. Actuators 2023, 12, 31. [Google Scholar] [CrossRef]
- Levant, A. Chattering Analysis. IEEE Trans. Autom. Control 2010, 55, 1380–1389. [Google Scholar] [CrossRef]
- Zhihong, M.; Yu, X.H. Terminal sliding mode control of MIMO linear systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 1065–1070. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Che, X.; Tian, D.; Jia, P.; Gao, Y.; Ren, Y. Terminal Sliding Mode Control with a Novel Reaching Law and Sliding Mode Disturbance Observer for Inertial Stabilization Imaging Sensor. Sensors 2020, 20, 3107. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A Composite Sliding Mode Control for SPMSM Drives Based on a New Hybrid Reaching Law with Disturbance Compensation. IEEE Trans. Transp. Electr. 2021, 7, 1427–1436. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, Q.; Wang, W.; Zhou, X. Speed Regulation System of a Flux-Modulated Permanent-Magnet in-Wheel Motor Based on Sliding Mode Control and Adaptive Notch Filter. IEEE Trans. Energy Convers. 2018, 33, 2183–2190. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Informat. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved Non-Singular Fast Terminal Sliding Mode Control With Disturbance Observer for PMSM Drives. IEEE Trans. Transp. Electr. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Cupertino, F.; Naso, D.; Mininno, E.; Turchiano, B. Sliding-Mode Control With Double Boundary Layer for Robust Compensation of Payload Mass and Friction in Linear Motors. IEEE Trans. Ind. Appl. 2009, 45, 1688–1696. [Google Scholar] [CrossRef]
- Fei, J.; Wang, H.; Fang, Y. Novel Neural Network Fractional-Order Sliding-Mode Control With Application to Active Power Filter. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3508–3518. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Adaptive Fractional-Order Nonsingular Fast Terminal Sliding Mode Based Robust Tracking Control of Quadrotor UAV With Gaussian Random Disturbances and Uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2265–2277. [Google Scholar] [CrossRef]
- Chalanga, A.; Kamal, S.; Fridman, L.M.; Bandyopadhyay, B.; Moreno, J.A. Implementation of Super-Twisting Control: Super-Twisting and Higher Order Sliding-Mode Observer-Based Approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]
- Balogoun, I.; Marx, S.; Liard, T.; Plestan, F. Super-Twisting Sliding Mode Control for the Stabilization of a Linear Hyperbolic System. IEEE Control. Syst. Lett. 2023, 7, 1–6. [Google Scholar] [CrossRef]
- Huang, Y.; Kuo, T.; Chang, S. Adaptive Sliding-Mode Control for NonlinearSystems With Uncertain Parameters. IEEE Trans. Syst. Man Cybern. Syst. 2008, 38, 534–539. [Google Scholar] [CrossRef] [PubMed]
- Baek, J.; Jin, M.; Han, S. A New Adaptive Sliding-Mode Control Scheme for Application to Robot Manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Obeid, H.; Fridman, L.M.; Laghrouche, S.; Harmouche, M. Barrier function-based adaptive sliding mode control. Automatica 2018, 93, 540–544. [Google Scholar] [CrossRef]
- Chen, L.; Jin, Z.; Shao, K.; Harmouche, M. Sensorless Fixed-Time Sliding Mode Control of PMSM Based on Barrier Function Adaptive Super-Twisting Observer. IEEE Trans. Power Electron. 2023, 39, 3037–3051. [Google Scholar] [CrossRef]
- Dai, B.; Wang, Z. Disturbance Observer-Based Sliding Mode Control Using Barrier Function for Output Speed Fluctuation Constraints of PMSM. IEEE Trans. Energy Convers. 2024, 1–10. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, H.; Liu, J.; Tian, D. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives. ISA Trans. 2019, 88, 113–126. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]




| Description | Value |
|---|---|
| moment of inertia | (kg · m2) |
| frictional coefficient | (N·m·s/rad) |
| rated speed | 3000 (r/min) |
| rated torque | 1.27 (N·m) |
| stator resistance | 0.125 |
| stator inductance | 0.25 (mH) |
| rotor flux | 0.01325 (Wb) |
| pole pairs | 4 |
| Controller | Parameters |
|---|---|
| TSMC | |
| the proposed |
| Controller | OS% | (s) | Speed Decrease with Load Torque (rpm) | Speed Decrease with Parameter Variation (rpm) |
|---|---|---|---|---|
| TSMC under 1000 rpm | 18.16 | 0.497 | 120.4 | 118.0 |
| the proposed under 1000 rpm | 17.00 | 0.293 | 30.4 | 28.0 |
| TSMC under 1500 rpm | 27.53 | 0.536 | 121.0 | 312.0 |
| the proposed under 1500 rpm | 23.87 | 0.384 | 31.0 | 53.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, X.; Ma, Z.; Qi, X.; Li, W.; Niu, H.; Yan, C. Barrier-Function-Based Adaptive Fast-Terminal Sliding-Mode Control for a PMSM Speed-Regulation System. Electronics 2024, 13, 1091. https://doi.org/10.3390/electronics13061091
Che X, Ma Z, Qi X, Li W, Niu H, Yan C. Barrier-Function-Based Adaptive Fast-Terminal Sliding-Mode Control for a PMSM Speed-Regulation System. Electronics. 2024; 13(6):1091. https://doi.org/10.3390/electronics13061091
Chicago/Turabian StyleChe, Xin, Zelong Ma, Xinda Qi, Wenxian Li, Haipeng Niu, and Changxiang Yan. 2024. "Barrier-Function-Based Adaptive Fast-Terminal Sliding-Mode Control for a PMSM Speed-Regulation System" Electronics 13, no. 6: 1091. https://doi.org/10.3390/electronics13061091
APA StyleChe, X., Ma, Z., Qi, X., Li, W., Niu, H., & Yan, C. (2024). Barrier-Function-Based Adaptive Fast-Terminal Sliding-Mode Control for a PMSM Speed-Regulation System. Electronics, 13(6), 1091. https://doi.org/10.3390/electronics13061091







