A Structured Mesh Generation Based on Improved Ray-Tracing Method for Finite Difference Time Domain Simulation
Abstract
:1. Introduction
2. Methods
2.1. Generate Non-Uniform Structured Mesh
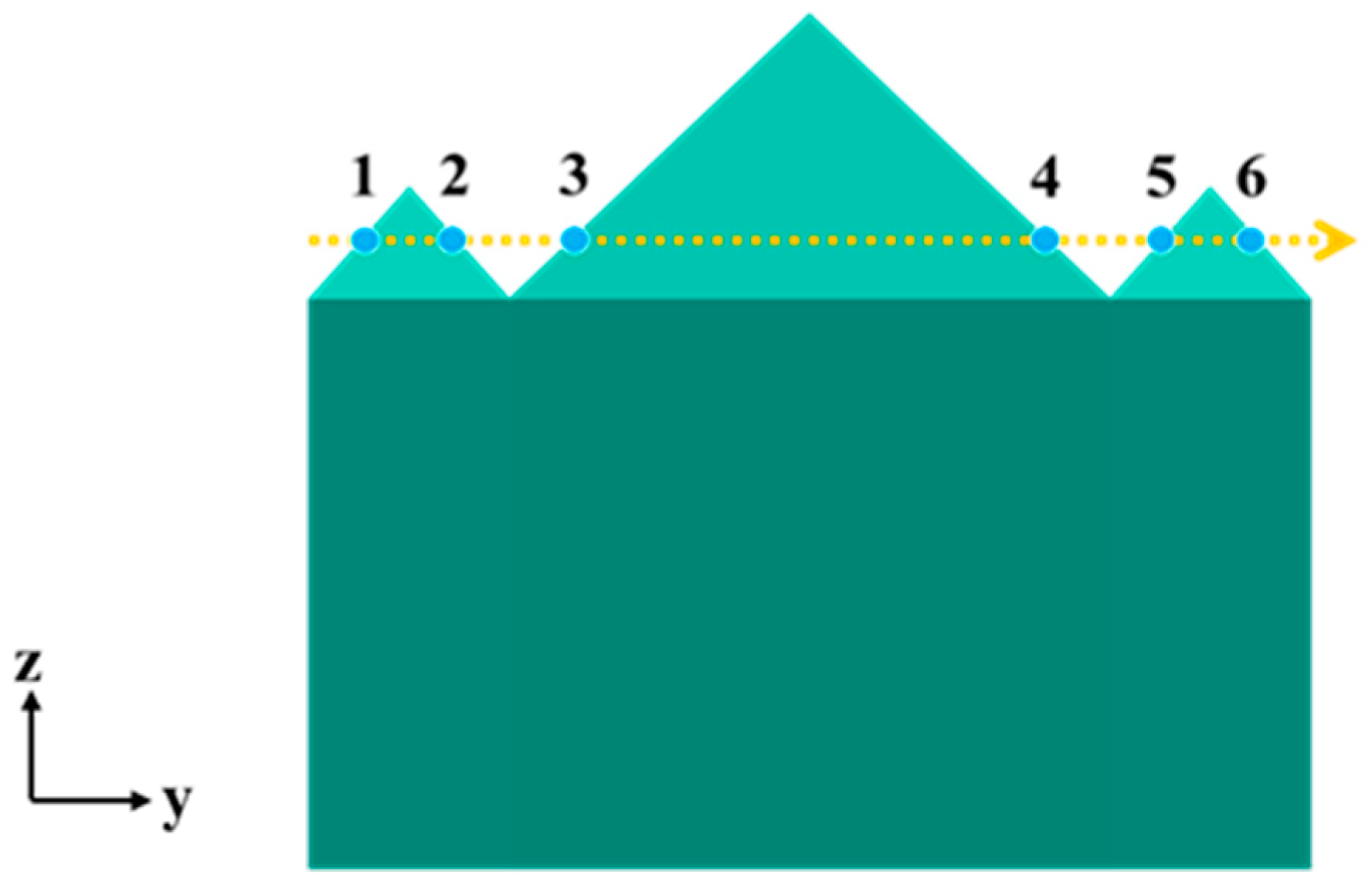
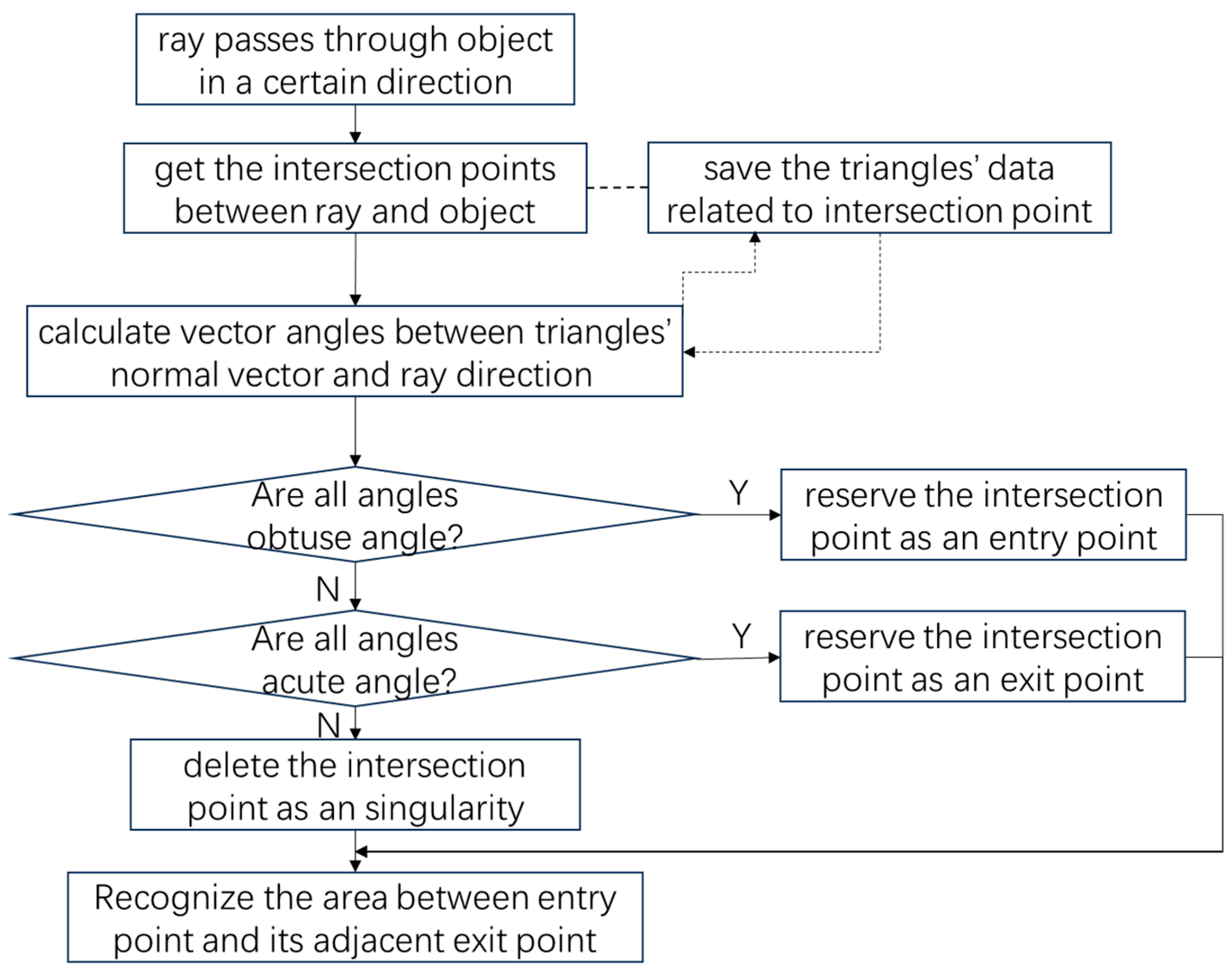
2.2. Recognize Surface Structured Mesh of Object
- 1.
- Project the triangle element ABC onto the XOY plane and mark the projected triangle as A′ B′ C′, as shown in Figure 4.
- 2.
- Based on the vertex coordinates of triangle A′ B′ C′, determine the maximum value and minimum value in the X-direction and the maximum value and minimum value in the Y-direction. Based on these four values, a projected domain (the yellow domain in Figure 5) composed of many rectangular meshes that cover the triangle A′ B′ C′ totally can be obtained. The four vertex coordinates of the projected domain are recorded as (), (), (), (), respectively.
- 3.
- For all the rectangle meshes in the projected domain, the vector cross multiplication method is used to determine whether the mesh center point P is located inside A′ B′ C′. It first connects lines PA′, PB′, and PC′ and obtains three vectors , , and . It then calculates × , × and × . If the three cross product results are all positive or negative simultaneously, point P is located inside the projection triangle A′ B′ C′, as shown in Figure 6a. Otherwise, point P is located outside of the projection triangle A′ B′ C′, as shown in Figure 6b.
- 4.
- For the point P that is located inside the projected triangle A′ B′ C′, it substitutes its projection coordinates (, ) to the plane equation of triangle ABC as follows:where , , are the vector components of the normal vector of triangle ABC in the X, Y and Z direction, respectively. (, , ) is the coordinate of an arbitrary point in triangle ABC. Then, , the z-coordinate of the projection point P′ in triangle ABC, as shown in Figure 7, can be solved. After that, the coordinate (, , ) of point P′ is determined; subsequently, the structured mesh including point P′ is recognized as the surface structured mesh of the object, as shown in Figure 8.
2.3. Recognize Internal Structured Mesh of Object
3. Results of Numerical Experiments
3.1. SU30 Aircraft
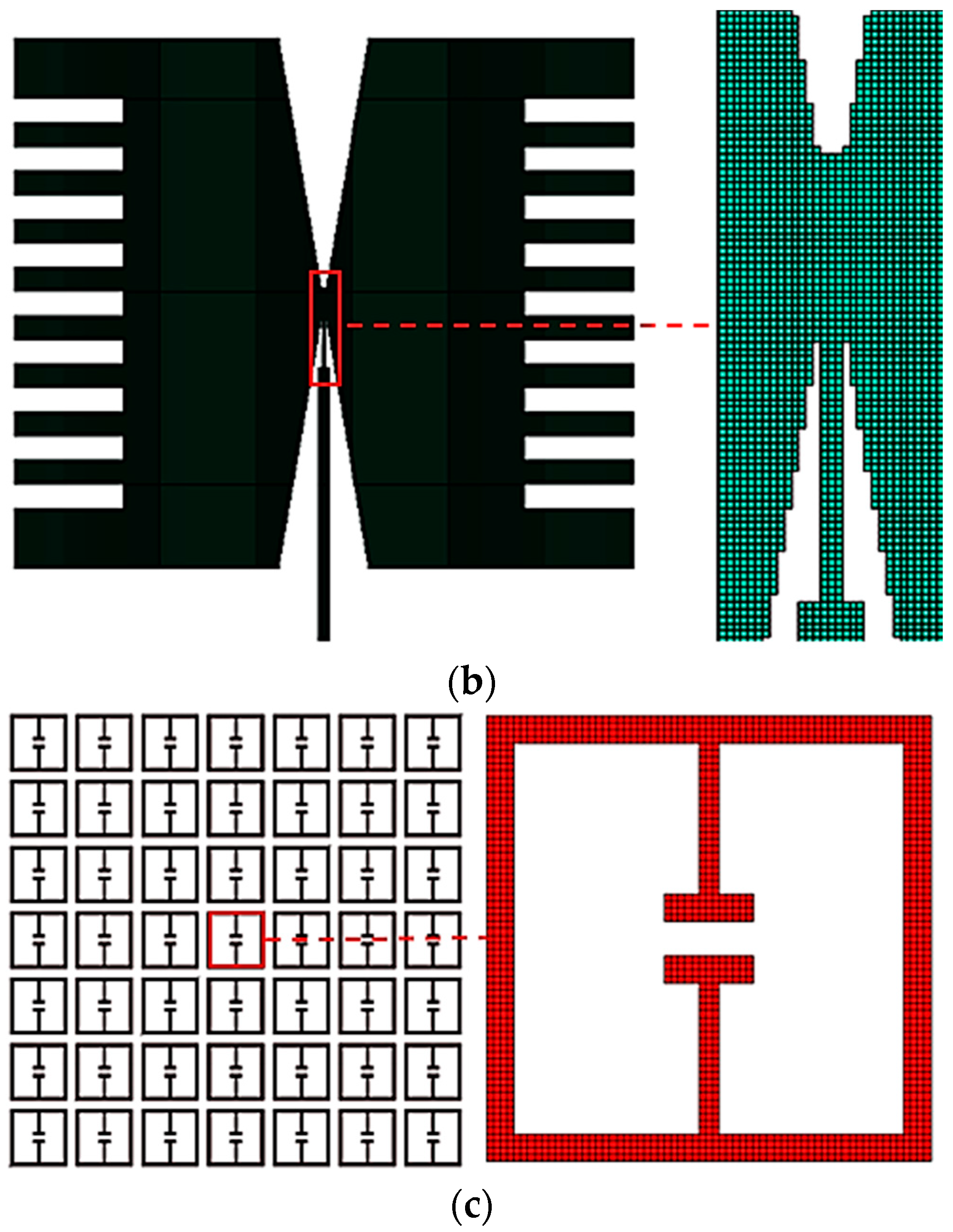
3.2. Bow-Tie Antenna
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Sun, W.; Balanis, C.A.; Purchine, M.P.; Barber, G. Three-dimensional automatic FDTD mesh generation on a PC. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Ann Arbor, MI, USA, 28 June–2 July 1993; pp. 30–33. [Google Scholar]
- Gheonjian, A.; Jobava, R. Non-uniform conforming mesh generator for FDTD scheme in 3D cylindrical coordinate system. In Proceedings of the 5th International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED), Tbilisi, Georgia, 3–6 October 2000; pp. 41–44. [Google Scholar]
- Waldschmidt, G.; Taflove, A. Three-dimensional CAD-based mesh Generator for the Dey-Mittra conformal FDTD algorithm. IEEE Trans. Antennas Propag. 2004, 52, 1658–1664. [Google Scholar] [CrossRef]
- Okoniewski, M.; Okoniewska, E.; Stuchly, M.A. 3D sub-gridding algorithm for FDTD. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Newport Beach, CA, USA, 18–23 June 1995; pp. 232–235. [Google Scholar]
- Junkin, G.; Parron, J. A Robust 3D Mesh Generator for the Dey-Mittra Conformal FDTD Algorithm. In Proceedings of the Second European Conference on Antennas and Propagation, EuCAP 2007, Edinburgh, UK, 11–16 November 2007; pp. 1–6. [Google Scholar]
- Schuhmann, R.; Weiland, T. An improved implementation of nonorthogonal FDTD using triangular fillings. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Atlanta, GA, USA, 21–26 June 1998; pp. 600–603. [Google Scholar]
- Berens, M.K.; Flintoft, I.D.; Dawson, J.F. Structured Mesh Generation: Open-source automatic nonuniform mesh generation for FDTD simulation. IEEE Antennas Propagat. Mag. 2016, 58, 45–55. [Google Scholar] [CrossRef]
- Hong, L.; Kaufman, A.E. Fast projection-based ray-casting algorithm for rendering curvilinear volumes. IEEE Trans. Vis. Comput. Graph. 1999, 5, 322–332. [Google Scholar] [CrossRef]
- Holland, R. Pitfalls of staircase meshing. In IEEE Transactions on Electromagnetic Compatibility; IEEE: New York, NY, USA, 1993; Volume 35, pp. 434–439. [Google Scholar]
- Chung, P.Y.; Wu, C.; Navarro, E.A.; Litva, J. A circular mesh scheme for the non-orthogonal finite difference time domain method. In Proceedings of the IEEE Antennas and Propagation Society International Symposium. 1995 Digest, Newport Beach, CA, USA, 18–23 June 1995; Volume 1, pp. 240–243. [Google Scholar]
- Li, Y.; Chen, J. Design of Miniaturized High Gain Bow-Tie Antenna. IEEE Trans. Antennas Propag. 2022, 70, 738–743. [Google Scholar] [CrossRef]























| Method | Simulation Time |
|---|---|
| conventional ray-tracing method | 30.01 s |
| improved ray-tracing method | 32.98 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Guo, J.; Mou, C.; Xu, Z.; Wang, J. A Structured Mesh Generation Based on Improved Ray-Tracing Method for Finite Difference Time Domain Simulation. Electronics 2024, 13, 1189. https://doi.org/10.3390/electronics13071189
Chen J, Guo J, Mou C, Xu Z, Wang J. A Structured Mesh Generation Based on Improved Ray-Tracing Method for Finite Difference Time Domain Simulation. Electronics. 2024; 13(7):1189. https://doi.org/10.3390/electronics13071189
Chicago/Turabian StyleChen, Juan, Jiale Guo, Chunhui Mou, Zikun Xu, and Jianguo Wang. 2024. "A Structured Mesh Generation Based on Improved Ray-Tracing Method for Finite Difference Time Domain Simulation" Electronics 13, no. 7: 1189. https://doi.org/10.3390/electronics13071189
APA StyleChen, J., Guo, J., Mou, C., Xu, Z., & Wang, J. (2024). A Structured Mesh Generation Based on Improved Ray-Tracing Method for Finite Difference Time Domain Simulation. Electronics, 13(7), 1189. https://doi.org/10.3390/electronics13071189






