Comparative Evaluation of Three-Phase Three-Level Flying Capacitor and Stacked Polyphase Bridge GaN Inverter Systems for Integrated Motor Drives
Abstract
:1. Introduction
2. Operating Principles
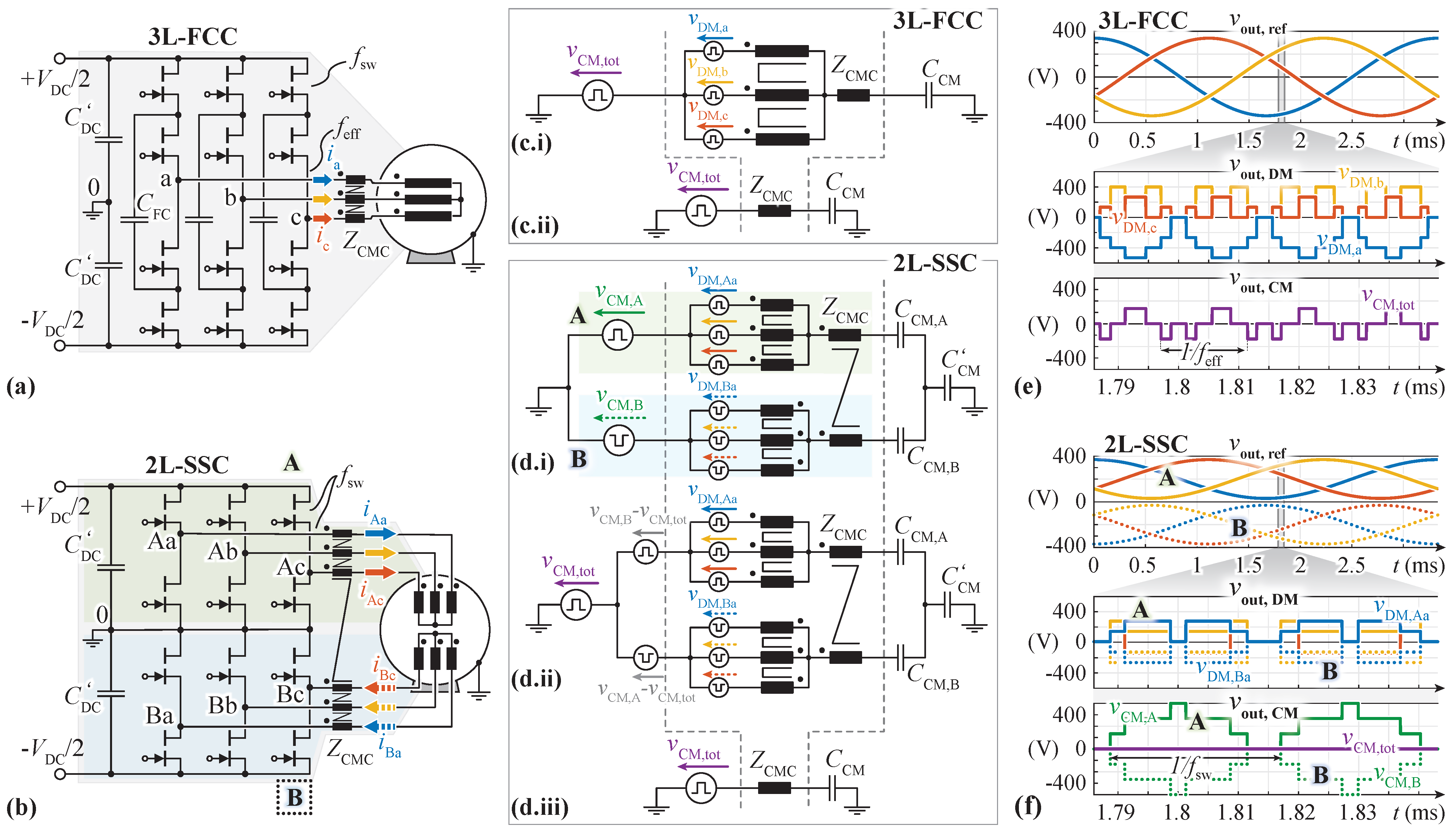
2.1. 3L-FCC
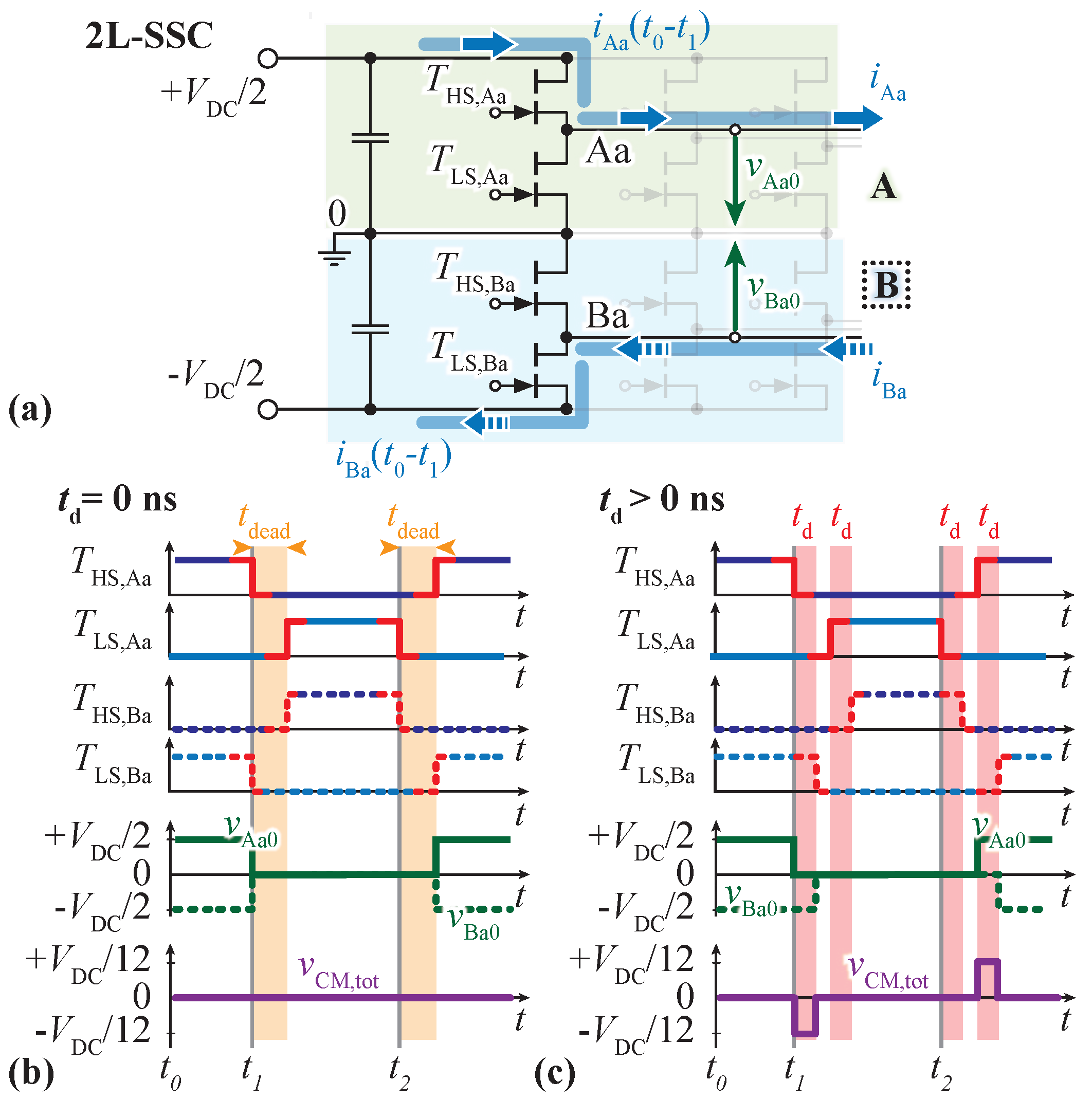
2.2. 2L-SSC
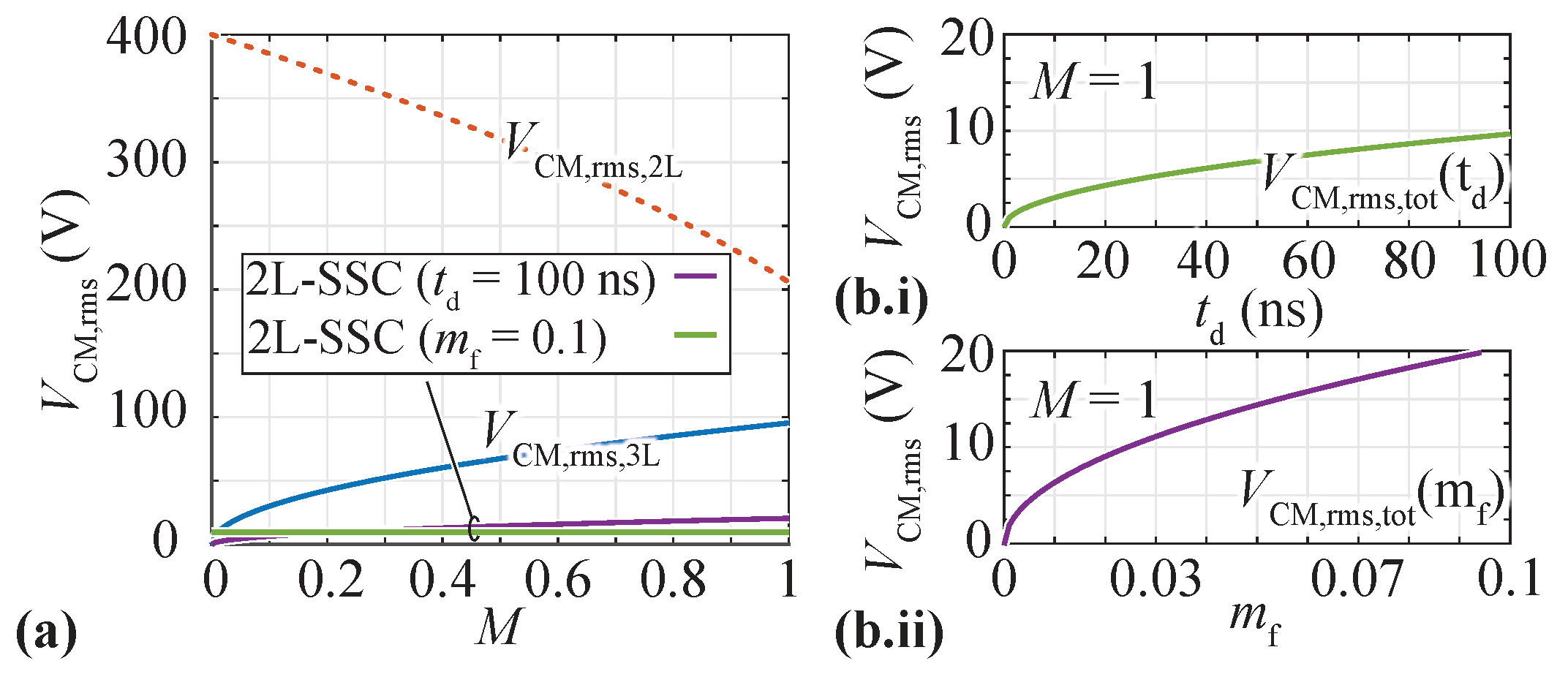
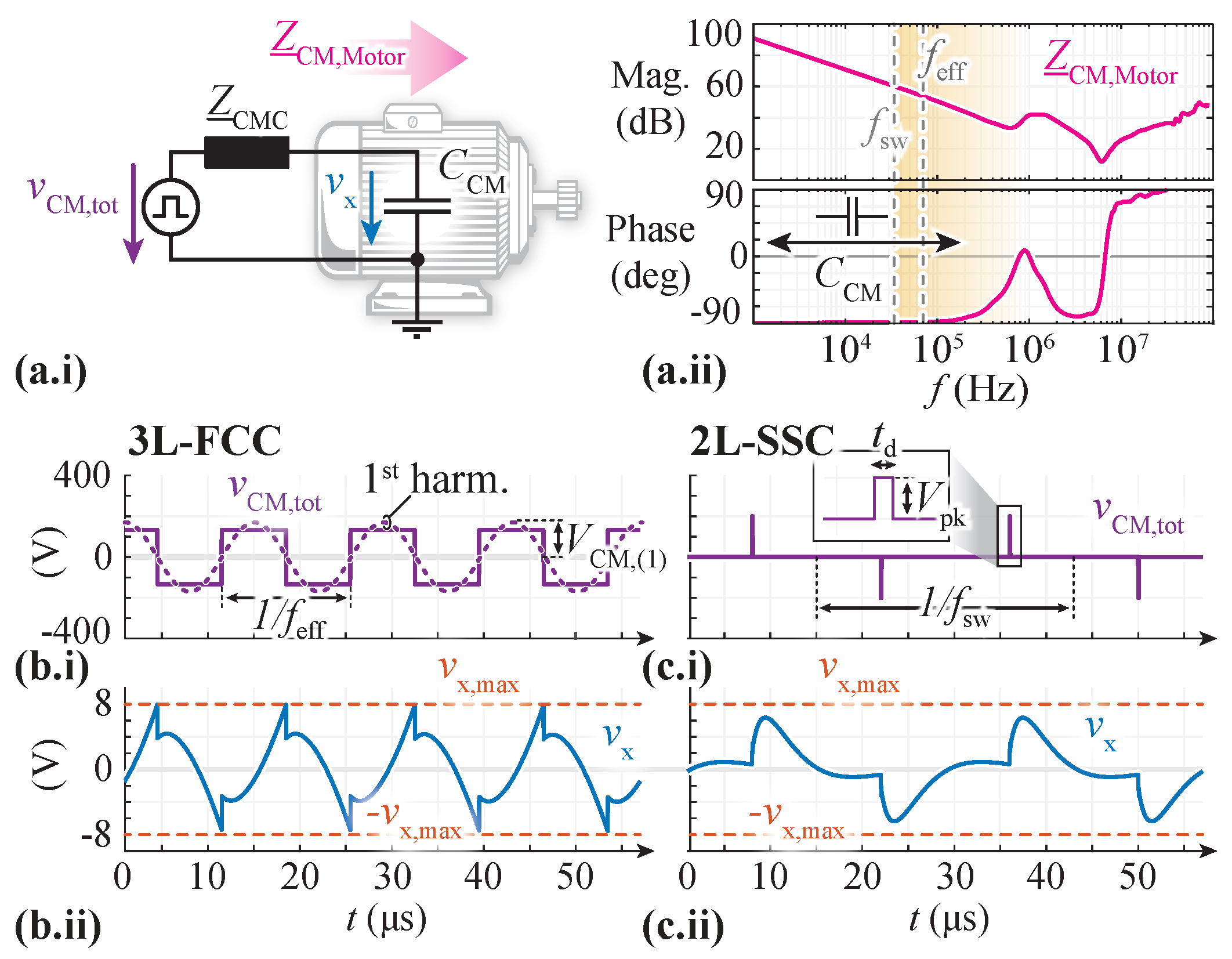
2.3. Quantitative Comparison of Resulting CM Voltages
3. Design Considering Short-Term Overload Capability
3.1. Semiconductors
3.2. Flying Capacitors
3.3. High Frequency (HF) DC-Link Capacitors
- 3L-FCC: Only the switching states of the two complementary semiconductors next to the DC-link capacitor (cf. and in Figure 4a) define the HF component of the DC-link current regardless of the switching state of the other semiconductors (cf. and Figure 4a). Consequently, the HF DC-link voltage ripple (contrary to the FC voltage ripple) is directly related to the device switching frequency (and not the effective switching frequency at the switch nodes). Hence, as seen from the DC-link, the inverter behaves like a standard three-phase 2L inverter. For the design, in a first-step approximation, only a single phase leg is considered. It can then be assumed that the full HF current is covered by the HF DC-link capacitors, which leads to a required capacitance value offor a duty cycle of with a desired peak-to-peak voltage ripple of [38]. Similar to the FCs, an overload operation with determines the required capacitance.Two series connected rows of, in total, 176 X6S ceramic capacitors, each rated for 450 (C5750X6S2W225K250KA, , [37]), can be used for the implementation (i.e., every row with a value of to account for the series connection). This large number of discrete capacitors for the DC-link realization can be impractical for industrial applications. Alternatives with fewer discrete devices (e.g., pre-assembled CeraLink capacitor units [39] or even film capacitors) would increase the converter volume, but simplify manufacturing and possibly contribute to increased reliability (i.e., fewer discrete devices and soldering connections that can potentially break). Note that to comply with the thermal limitation of the capacitors, the total rms current of , based on a 2L motor drive derived in [40], must be taken into account. According to Figure 1a, the DC-midpoint (marked with “0”) can be used as a ground reference, but remains completely unloaded.
- 2L-SSC: The 2L-SSC consists of two stacked three-phase 2L-inverters, each with their own HF DC-link capacitor at half the DC-link voltage. Due to the inverted switching patterns and phase currents, the currents drawn from their respective HF DC-link capacitors are identical for both inverters A and B. Thus, the HF voltage ripple limitation can be applied to inverter A and inverter B independently. Using the same single-phase approximation introduced above for the 3L-FCC, the required capacitance per stacked inverter can be approximated with (7) and (since the respective voltage ripples will be summed up directly due to the identical DC-link currents of inverter A and inverter B). All in all, the series connection of the two results in an identical total DC-link capacitance value as for the 3L-FCC. Hence, it can be built in the same way and for identical rms current loading.
| 3L-FCC | 2L-SSC | |
|---|---|---|
| Inverter Output | ||
| Semiconductors | ||
| (*) | ||
| DC-link Cap. | ||
| [38] | ||
| [40] | ||
| Flying Cap. | ||
| - | ||
| [29] | - | |
| [29] | - | |
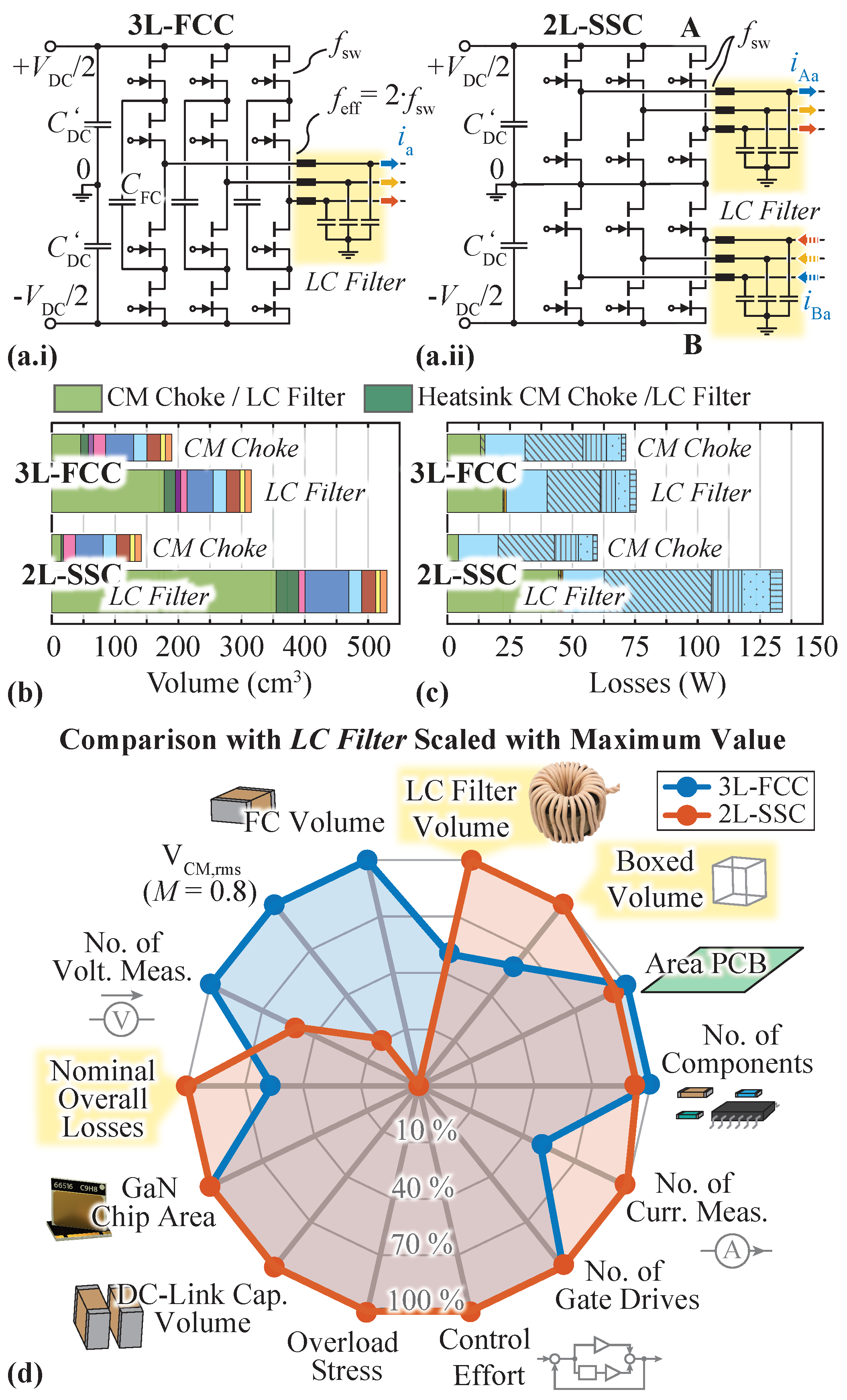
3.4. Exemplary CM Choke Designs
3.4.1. Derivation of the CM Model
3.4.2. Worst-Case CM Voltage Design Criteria
- 3L-FCC: In conventional PSPWM, the worst-case occurs for sinusoidal modulation (i.e., with a modulation limit of , without a third harmonic CM voltage injection) when one of the phases passes through the peak output voltage with, e.g., phase leg duty cycles of , . The resulting simulated CM voltage is shown in Figure 5(b.i), together with its dominating first harmonic component at with a maximum amplitude of . In order to comply with the given design specifications, the excitation of the first harmonic has to be attenuated to a maximum peak amplitude of over (red dashed line in Figure 5(b.ii)). All higher-order harmonics are not explicitly addressed with this approach, as they are, first, of lower amplitude in the first place, and, second, attenuated ideally substantially stronger than the first harmonic (characteristic of a low-pass filter formed by the motor CM capacitance and the CM choke impedance ). Consequently, a CM choke design with an impedance satisfyingis required for the 3L-FCC. For the design process can be modeled with (8) as .As a side remark: Note that the dead time (usually in the range of several 10 s of ns) has a negligible influence on the worst-case CM voltage of the 3L-FCC for the given switching frequency and the resulting effective frequency at the switch-node (= ).
- 2L-SSC: As discussed in Section 2.2, a significant reduction in the total CM voltage can be achieved thanks to CM cancellation. Thereby, if the two stacked inverters do not switch simultaneously (cf. Figure 2c), only small CM voltage spikes remain, which is, e.g., the case for a delay between the switching transitions of inverter A and B as a result of propagation delay mismatches and/or active DC-link balancing actions with correction factor . As every single one of these voltage spikes charges the motor CM capacitance , the CM choke has to be designed to limit the increase in voltage during those CM spikes. Thereby, the largest voltage-time area (i.e., the longest spike duration with the highest spike amplitude) defines the worst-case, and thus, the required choke impedance .In the case at hand, a delay of the corresponding switching actions in the 2L-SSC between inverter A and inverter B of is assumed. This is a very conservative upper limit, given that typical propagation delay (mismatches) are in the order of a few 10 ns if high-quality ICs and PCB layouts are used (e.g., in the case of the hardware components in Table 3, the gate driver (1EDN7511B [43]) and the signal isolator (ADuM120N [44]) are both specified with a propagation delay variation of approximately 10 in their respective datasheets). However, choosing a very conservative value of of also accounts for CM voltage spikes caused by potential active DC-link balancing (i.e., in Section 2.2).Then, in general, six voltage spikes of duration and of amplitude result per switching period. The largest instantaneous voltage-time area (i.e., the worst-case scenario) occurs for (i.e., all bridge legs operate with a duty cycle ). In this operating point, the six voltage spikes are temporally aligned/superimposed such that only two CM voltage spikes per switching period with amplitudes remain, as depicted in Figure 5(c.i). Note that coincides mostly with the motor standstill operation (i.e, no back-EMF hence low/no inverter output voltage amplitude), where the bearings show a resistive instead of capacitive behavior [27]. However, it is a valid worst-case scenario, which accounts for all possible operating points.In contrast to the 3L-FCC above, the first harmonic component does not sufficiently characterize the CM voltage spikes. Therefore, the following approach is suggested: only the inductive part of the choke, i.e., , is considered, which is still a significant part of the impedance at , reducing the CM model of Figure 5(a.i) to a simple (resonant) circuit. During the voltage spike of duration , essentially the full spike voltage is applied over the choke (given that is small by design), giving rise to a current increase and, hence, an accumulation of stored energy in the CM choke. After the CM voltage spike, this energy is transferred to , leading to a peak voltage amplitude of . The subsequently expected characteristic oscillation of an resonant circuit is strongly damped in reality thanks to the (so far) neglected , i.e., the peak voltage is expected to be slightly lower and the oscillation is finished before the next voltage spike occurs. Consequently, with this approach, the design criterion of (i.e., ) is deduced via the energy balance as
3.4.3. CM Choke Realization
- Possible core saturation caused by the leakage flux (corresponding to a leakage inductance of several , depending on the inductor design) can be considered already in the design phase [42];
- The core and winding temperatures should be maintained below 155 [45] (coinciding with NEMA motor insulation temperature rating Class F [46]). With the majority of the losses originating from the winding, i.e., copper losses, the choke can, e.g., be pressed to the motor housing/inverter baseplate using a Thermal Interface Material (TIM) to achieve sufficient conductive heat transfer. Therefore, a straightforward thermal model consists of a parallel connection of a thermal capacitance (copper winding) and a thermal resistance (cooling path through the copper windings to the side of choke contacting the TIM and then the path through the TIM itself onto the motor housing/inverter baseplate). Starting from the nominal operating point (defined by the thermal resistance only) the choke should not overheat within the 3 overload operation, despite the strongly increased winding losses during this period.
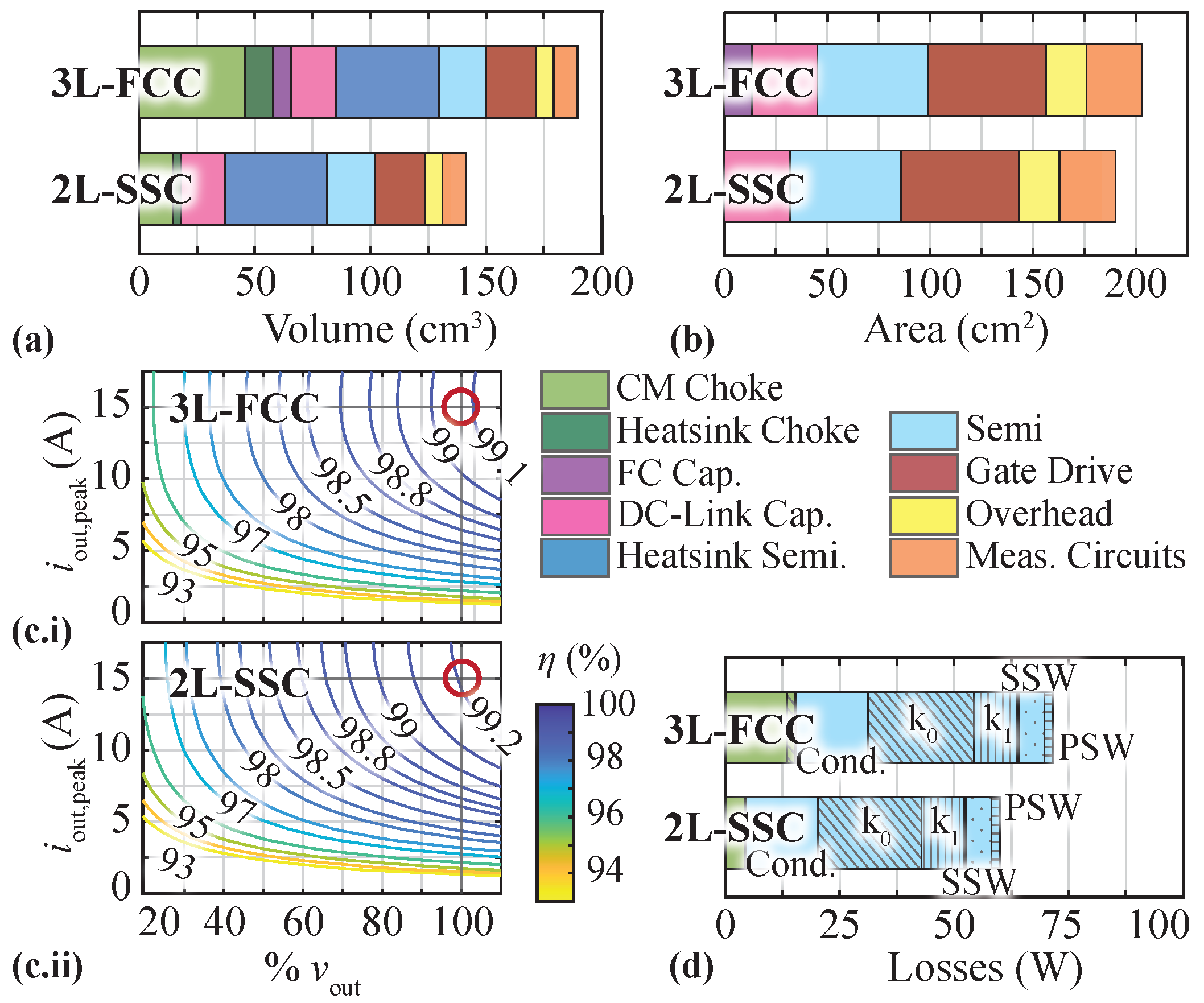
3.5. Resulting IMD Designs
| 3L-FCC | 2L-SSC |
|---|---|
| Power Transistors | |
| GaN Systems GS66516T (
650
,
25
), 2 × parallel per position; 27.2 mm2 device chip area [48] | |
| Gate Driver and Gate Drive Insulator | |
| Infineon 1EDN7511B [43] Analog Devices ADuM121N [44] | |
| CM Choke | |
| VITROPERM 500F [45] L2030-W514, 2× stacked; 3× 19 turns of solid copper wire (); , | VITROPERM 500F [45] L2025-W380, 1× stacked; 6x 6 turns of solid copper wire (); , |
| DC-Link Capacitors | |
| Min.
20
, 176 × C5750X6S2W225K250KA (X6S,
,
450
), i.e., two rows of 88 caps in series | |
| Flying Capacitors | |
| 11 , 24 × C5750X6S2W225K250KA (X6S, , 450 ) per phase | |
| Required PCB Areas according to [5] | |
| Paralleled semiconductors per half-bridge: 9.0 cm2 | |
| Gate drive circuit per half-bridge: 9.5 cm2 | |
| Overhead per half-bridge: 3.3 cm2 | |
| Single voltage/current measurement circuit: 4.5 cm2 | |
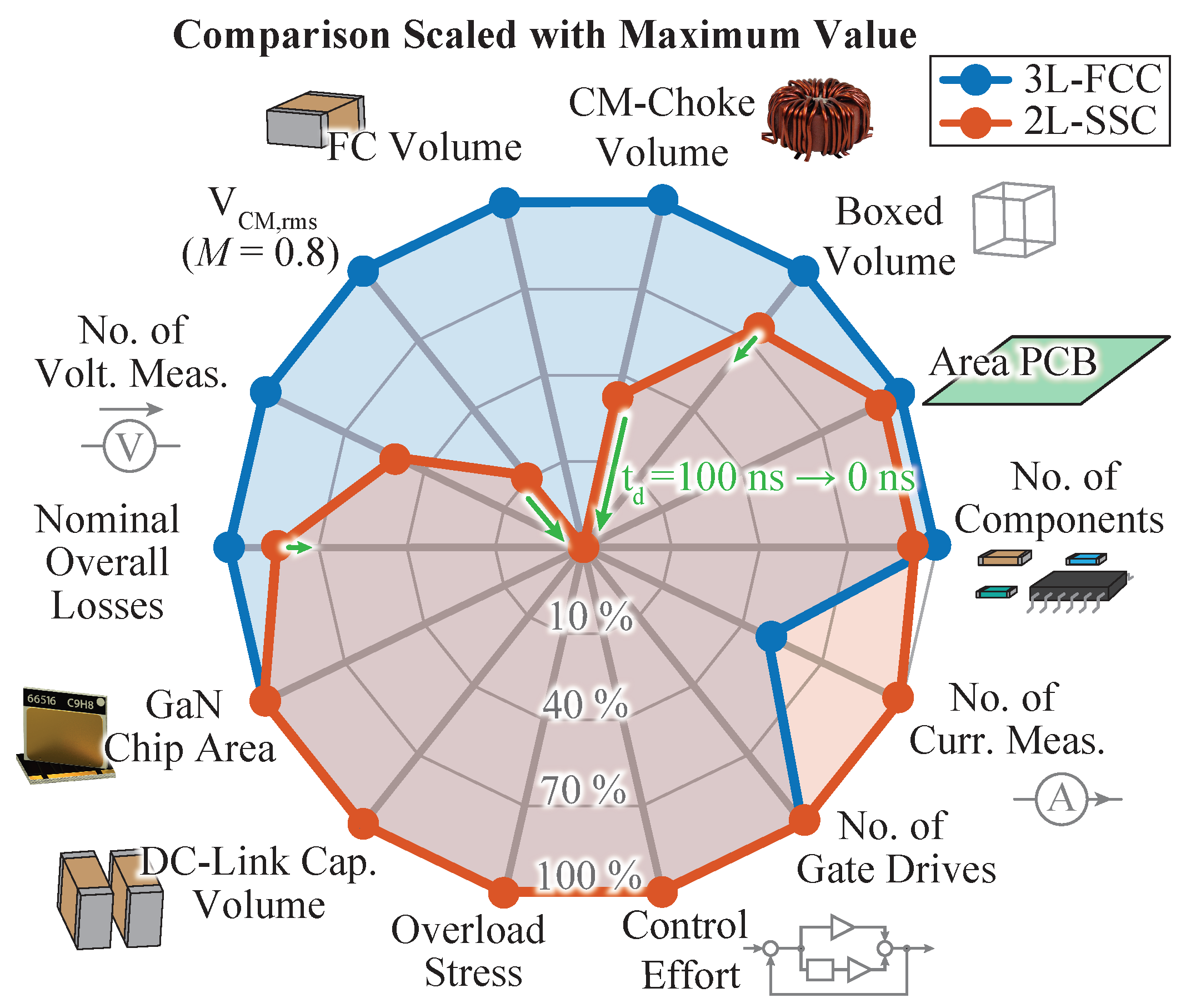
4. Comparative Evaluation
4.1. Mechanical Realization Effort
4.2. Losses and Overload Capability
4.3. Measurement Effort
4.4. Control Effort
4.5. Alternate Scenario: Low Motor Phase Inductance
4.6. Alternate Scenario: Full Sine-Wave Output Filter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3L-FCC | Three-Level Flying Capacitor Converter |
| 2L-SSC | Two Series-Stacked Two-Level three-phase Converters |
| AC | Alternating Current |
| CM | Common Mode |
| DC | Direct Current |
| DM | Differential Mode |
| FC | Flying Capacitor |
| FCC | Flying Capacitor Converter |
| EDM | Electric Discharge Machining |
| EMI | Electromagnetic Interference |
| ESR | Equivalent Series Resistance |
| FOC | Field-Oriented Control |
| GaN | Gallium Nitride |
| HEMT | High Electron Mobility Transistor |
| HF | High Frequency |
| IMD | Integrated Motor Drive |
| PMSM | Permanent Magnet Synchronous Motor |
| PWM | Pulse Width Modulation |
| PSPWM | Phase-Shifted PWM |
| RMS | Root Mean Square |
| SPBI | Stacked Polyphase Bridge Inverter |
| SVPWM | Space Vector PWM |
| TIM | Thermal Interface Material |
| VSD | Variable Speed Drive |
List of Symbols
| Symbol | Description | Unit |
| Inductance per Turn Squared | H | |
| Motor CM Capacitance | F | |
| Part of the Motor CM Capacitance | F | |
| , | Motor CM Capacitance of Winding-Set A and B | F |
| DC-Link Capacitance | F | |
| Split DC-Link Capacitance | F | |
| Flying Capacitor Capacitance | F | |
| Parasitic Winding Capacitance | F | |
| Motor CM Capacitance between a Winding-Set and Earth in the employed 18-Phase PMSM | F | |
| Motor Rotor-Frame Capacitance | F | |
| Motor Winding-Winding Capacitance (between Winding-Sets in the employed 18-Phase PMSM) | F | |
| , | Motor Winding-Frame Capacitance of Winding-Set A and B | F |
| , | Motor Winding-Rotor Capacitance of Winding-Set A and B | F |
| Motor Winding-Winding Capacitance (between Winding-Set A and B) | F | |
| d | Duty Cycle | |
| , , | Phase Duty Cycles | |
| Max. Peak-Peak DC-Link Voltage Ripple | V | |
| Peak-Peak FC Voltage Ripple | V | |
| Max. Peak-Peak FC Voltage Ripple | V | |
| Peak-Peak Voltage Ripple | V | |
| f | Frequency | Hz |
| Effective Frequency | Hz | |
| Inverter Output Frequency | Hz | |
| Max. Inverter Output Frequency | Hz | |
| Device Switching Frequency | Hz | |
| , | Current of Phase a of Inverter A and B | A |
| Inductor Current | A | |
| Phase Output Current | A | |
| Phase Output Current Amplitude during Overload | A | |
| Peak Output Current | A | |
| Max. RMS Current | A | |
| Inductive Part of CM Choke | H | |
| M | Modulation Index | |
| Balancing Correction Factor | ||
| Complex Relative Permeability | ||
| Number of Winding Turns | ||
| Protective Earth | ||
| Semiconductor Switching Losses | W | |
| Resistive Part of CM Choke Model (i.e., represents the Core Losses) | ||
| Semiconductor On-State Resistance | ||
| Semiconductor Thermal Resistance | K/W | |
| CM Choke Winding Resistance | ||
| , | Gate Signals | |
| Effective Period | s | |
| Time Delay between Switching Signals of Inverter A and B | s | |
| Dead Time between Turn-Off and Complementary Transistor Turn-On of a Bridge Leg | s | |
| , | High-Side Semiconductor Gate Signal of Phase a of Inverter A and B | |
| Max. Semiconductor Junction Temperature | °C | |
| , | Switch Node Voltages of Inverter A and B referenced to “0” (DC-Midpoint) | V |
| Voltage over Motor Bearing/over | V | |
| Bias Voltage | V | |
| Amplitude of First Order Harmonic of the CM Voltage | V | |
| , | CM Voltages of Inverter A and B | V |
| Total CM RMS Inverter Output Voltage | V | |
| Total CM Inverter Output Voltage | V | |
| , , | DM Phase Voltages | V |
| Nominal Semiconductor Blocking Voltage | V | |
| Phase Output Voltage Amplitude | V | |
| Reference Output Voltage | V | |
| CM Voltage Spike Amplitude of 2L-SSC | V | |
| Switched Output Voltage | V | |
| Peak CM Voltage at the Motor | V | |
| Max. Peak CM Voltage at the Motor | V | |
| Complex CM Choke Impedance | ||
| Calculated CM Choke Impedance | ||
| Measured CM Impedance of 18-Phase PMSM configured as Dual-Winding-Set Motor with One Winding-Set Unconnected (=OPEN) | ||
| Measured CM Impedance of 18-Phase PMSM configured as Dual-Winding-Set Motor with One Winding-Set Connected to PE | ||
| Measured CM Impedance of 18-Phase PMSM configured as Single-Winding-Set Motor |
Appendix A. Asymmetries in the Motor
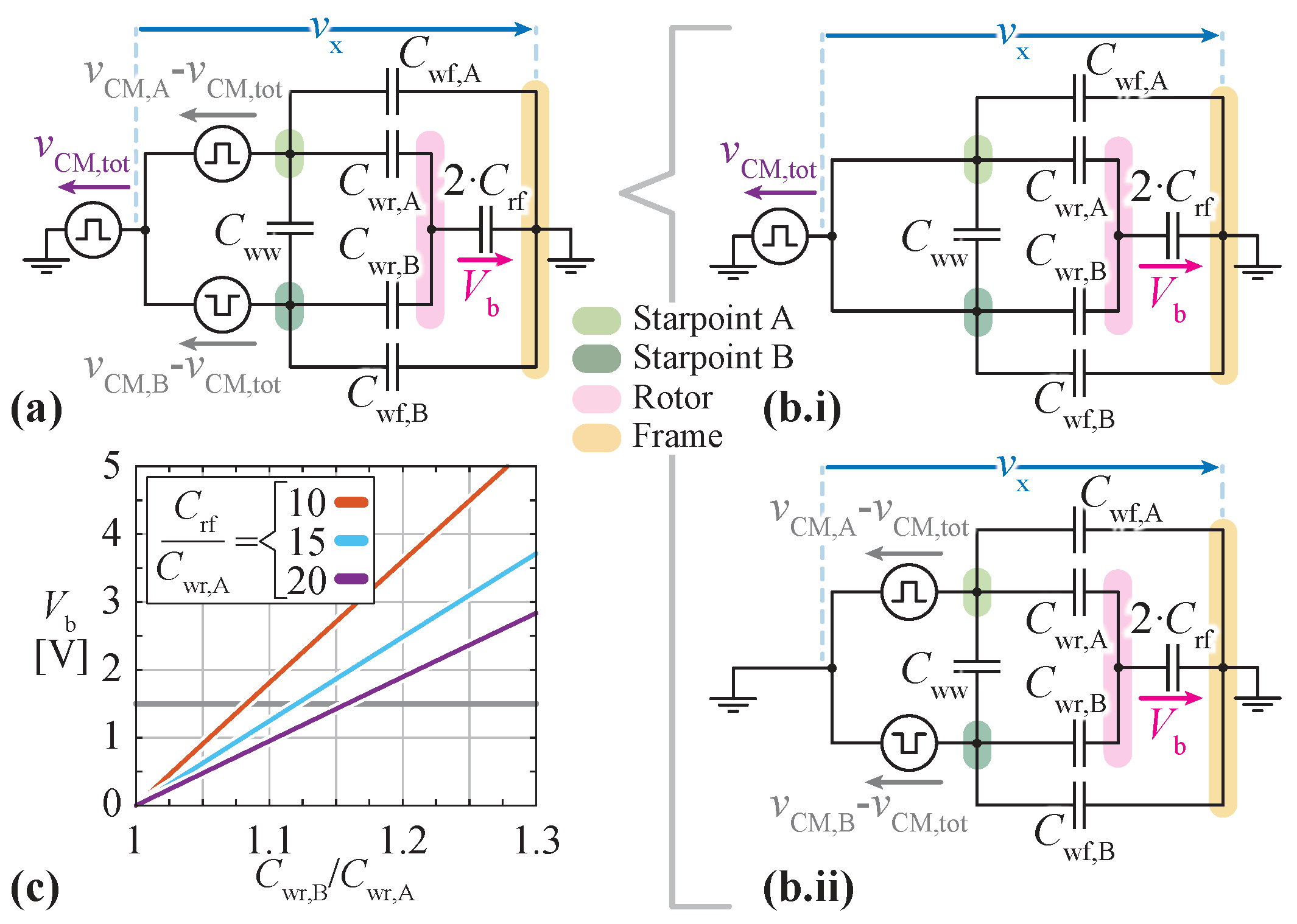
Appendix B. Additional Motor Impedance Measurements

References
- Jahns, T.M.; Dai, H. The Past, Present, and Future of Power Electronics Integration Technology in Motor Drives. CPSS Trans. Power Electron. Appl. 2017, 2, 197–216. [Google Scholar] [CrossRef]
- Sauer, A. The DC-Factory: Energy Efficient. Robust. Forward-Looking, 1st ed.; Carl Hanser Verlag: Munich, Germany, 2021. [Google Scholar]
- Teichmann, R.; Bernet, S. A Comparison of Three-Level Converters Versus Two-Level Converters for Low-Voltage Drives, Traction, and Utility Applications. IEEE Trans. Ind. Appl. 2005, 41, 855–865. [Google Scholar] [CrossRef]
- Cittanti, D.; Guacci, M.; Mirić, S.; Bojoi, R.; Kolar, J.W. Comparative Evaluation of 800V DC-Link Three-Phase Two/Three-Level SiC Inverter Concepts for Next-Generation Variable Speed Drives. In Proceedings of the 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 1699–1704. [Google Scholar] [CrossRef]
- Rohner, G.; Gfrörer, T.; Niklaus, P.S.; Bortis, D.; Schweizer, M.; Kolar, J.W. Comparative Evaluation of Three-Phase Three-Level GaN and Seven-Level Si Flying Capacitor Inverters for Integrated Motor Drives Considering Overload Operation. IEEE Access 2024, 12, 7356–7371. [Google Scholar] [CrossRef]
- Holtz, J. Selbstgeführter Wechselrichter. German Patent DE2339034C2, 1 August 1973. [Google Scholar]
- Baker, R.H. Bridge Converter Circuit. U.S. Patent US4270163A, 26 May 1981. [Google Scholar]
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, 17, 518–523. [Google Scholar] [CrossRef]
- Brown, M. SIEMENS Standard Drives Application Handbook. 1997. Available online: https://cache.industry.siemens.com/dl/files/430/1160430/att_36835/v1/applications_e.pdf (accessed on 5 June 2022).
- Ye, Z.; Lei, Y.; Liao, Z.; Pilawa-Podgurski, R.C.N. Investigation of Capacitor Voltage Balancing in Practical Implementations of Flying Capacitor Multilevel Converters. IEEE Trans. Power Electron. 2022, 37, 2921–2935. [Google Scholar] [CrossRef]
- Iyer, R.K.; Petric, I.Z.; Bayliss, R.S.; Brooks, N.C.; Pilawa-Podgurski, R.C.N. A High-Bandwidth Parallel Active Balancing Controller for Current-Controlled Flying Capacitor Multilevel Converters. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 775–781. [Google Scholar] [CrossRef]
- Papamanolis, P.; Neumayr, D.; Kolar, J.W. Behavior of the Flying Capacitor Converter under Critical Operating Conditions. In Proceedings of the 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 628–635. [Google Scholar] [CrossRef]
- Norrga, S.; Jin, L.; Wallmark, O.; Mayer, A.; Ilves, K. A Novel Inverter Topology for Compact EV and HEV Drive Systems. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON), Vienna, Austria, 10–13 November 2013; pp. 6590–6595. [Google Scholar] [CrossRef]
- Deplazes, R. Neue Transformatorlose Schaltungstopologie für Traktionsantriebe auf der Basis von 3-Stern-Asynchronmaschinen. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 1999. (In German) [Google Scholar] [CrossRef]
- Han, Y. Design, Modeling, and Control of Multilevel Converter Motor Drive with Modular Design and Split Winding Machine. In Proceedings of the 15th IEEE Workshop on Control and Modeling for Power Electronics (COMPEL), Santander, Spain, 22–25 June 2014. [Google Scholar] [CrossRef]
- Nikouie, M.; Zhang, H.; Wallmark, O.; Nee, H.P. A Highly Integrated Electric Drive System for Tomorrow’s EVs and HEVs. In Proceedings of the IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017. [Google Scholar] [CrossRef]
- Pan, Z.; Shrestha, G.; Schweizer, M.; Leppanen, V.M. Cell Voltage Balancing of a Series-Connected Multiphase BLDC Motor Drive. In Proceedings of the International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 969–974. [Google Scholar] [CrossRef]
- Sierra-Gonzalez, A.; Pescetto, P.; Alvarez-Gonzalez, F.; Heriz, B.; Trancho, E.; Lacher, H.; Ibarra, E.; Pellegrino, G. Full-Speed Range Control of a Symmetrical Six-Phase Automotive IPMSM Drive With a Cascaded DC-Link Configuration. IEEE Trans. Ind. Appl. 2023, 59, 3413–3424. [Google Scholar] [CrossRef]
- Bringezu, T.; Biela, J. Comparison of Optimized Motor-Inverter Systems Using a Stacked Polyphase Bridge Converter Combined with a 3-, 6-, 9-, or 12-Phase PMSM. In Proceedings of the European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Han, Y. Integrated Modular Motor Drive Design with GaN Power FETs. IEEE Trans. Ind. Appl. 2015, 51, 3198–3207. [Google Scholar] [CrossRef]
- Von Jauanne, A.; Zhang, H. A Dual-Bridge Inverter Approach to Eliminating Common-Mode Voltages and Bearing and Leakage Currents. IEEE Trans. Power Electron. 1999, 14, 43–48. [Google Scholar] [CrossRef]
- Han, D.; Lee, W.; Li, S.; Sarlioglu, B. New Method for Common Mode Voltage Cancellation in Motor Drives: Concept, Realization, and Asymmetry Influence. IEEE Trans. Power Electron. 2018, 33, 1188–1201. [Google Scholar] [CrossRef]
- Lee, K.; Benson, M.; Dong, X.; Moon, J.; Lee, W. Common-Mode EMI Noise Analysis of Neutral-Point-Less (NPL) Multilevel X-type Inverter. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024. [Google Scholar]
- Skibinski, G.; Kerkman, R.; Schlegel, D. EMI Emissions of Modern PWM AC Drives. IEEE Ind. Appl. Mag. 1999, 5, 47–80. [Google Scholar] [CrossRef]
- Evo, M.T.; Alzamora, A.M.; Zaparoli, I.O.; Paula, H.D. Inverter-Induced Bearing Currents: A Thorough Study of the Cause-and-Effect Chains. IEEE Ind. Appl. Mag. 2023, 29, 57–66. [Google Scholar] [CrossRef]
- Brown, N.R.; Jahns, T.M.; Lorenz, R.D. Power Converter Design for an Integrated Modular Motor Drive. In Proceedings of the IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 1322–1328. [Google Scholar] [CrossRef]
- Muetze, A. Bearing Currents in Inverter-Fed AC-Motors. Ph.D. Thesis, Technical University of Darmstadt, Darmstadt, Germany, 2003. [Google Scholar]
- Dahl, D.; Sosnowski, D.; Schlegel, D.; Kerkman, R.; Pennings, M. Gear Up Your Bearings. IEEE Ind. Appl. Mag. 2008, 14, 45–53. [Google Scholar] [CrossRef]
- Barth, C.B.; Assem, P.; Foulkes, T.; Chung, W.H.; Modeer, T.; Lei, Y.; Pilawa-Podgurski, R.C.N. Design and Control of a GaN-Based, 13-Level, Flying Capacitor Multilevel Inverter. IEEE Trans. Emerg. Sel. Top. Power Electron. 2020, 8, 2179–2191. [Google Scholar] [CrossRef]
- Khazraei, M.; Sepahvand, H.; Corzine, K.A.; Ferdowsi, M. Active Capacitor Voltage Balancing in Single-Phase Flying-Capacitor Multilevel Power Converters. IEEE Trans. Ind. Electron. 2012, 59, 769–778. [Google Scholar] [CrossRef]
- Stillwell, A.; Candan, E.; Pilawa-Podgurski, R.C.N. Active Voltage Balancing in Flying Capacitor Multi-Level Converters With Valley Current Detection and Constant Effective Duty Cycle Control. IEEE Trans. Power Electron. 2019, 34, 11429–11441. [Google Scholar] [CrossRef]
- Mocevic, S.; Aeloiza, E.; Tremelling, D.; Kadachigov, P.; Harnefors, L. DC-Link Stability of Stacked Polyphase Bridges Supplying Multiphase Induction Machine Having Common-Duty-Ratio Control. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE USA), Nashville, TN, USA, 29 October–2 November 2023. [Google Scholar] [CrossRef]
- Nikouie, M.; Wallmark, O.; Jin, L.; Harnefors, L.; Nee, H.P. DC-Link Stability Analysis and Controller Design for the Stacked Polyphase Bridges Converter. IEEE Trans. Power Electron. 2017, 32, 1666–1674. [Google Scholar] [CrossRef]
- Bringezu, T.; Biela, J. Control of a 9-Phase PMSM with Stacked Polyphase Bridge Converter Including DC Source Impedance. In Proceedings of the 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023. [Google Scholar] [CrossRef]
- Zhang, D.; Leibl, M.; Mühlethaler, J.; Huber, J.; Kolar, J.W. Modeling and Comparison of CM and DM EMI Pre-Filter Noise Emissions of Three-Phase Voltage and Current DC-Link Converters. IEEE Trans. Power Electron. (TPEL) 2024. under review. [Google Scholar]
- GaN Systems. GS66516T Datasheet. 2021. Available online: https://gansystems.com (accessed on 13 April 2023).
- TDK. C5750X6S2W225K250KA Datasheet. 2022. Available online: https://product.tdk.com (accessed on 25 September 2023).
- Infineon. Input Capacitor (DCLINK) Calculation for Single Phase Motor Bridge—Application Note Z8F80483545. 2023. Available online: https://www.infineon.com/dgdl/Infineon-Input_capacitor_calculation_for_single_motor_bridge-AN-ApplicationNotes-v01_00-EN.pdf?fileId=8ac78c8c8929aa4d0189d5bbe46d21f8 (accessed on 22 June 2023).
- TDK Electronics. CeraLink Capacitors. 2024. Available online: https://www.tdk-electronics.tdk.com/en/1054426/products/product-catalog/ceramic-capacitors/ceralink-capacitors (accessed on 22 June 2023).
- Kolar, J.W.; Round, S. Analytical Calculation of the RMS Current Stress on the DC-Link Capacitor of Voltage-PWM Converter Systems. IEE Proc.-Electr. Power Appl. 2006, 153, 535. [Google Scholar] [CrossRef]
- Kolar, J.W.; Azurza Anderson, J.; Miric, S.; Haider, M.; Guacci, M.; Antivachis, M.; Zulauf, G.; Menzi, D.; Niklaus, P.S.; Minibock, J.; et al. Application of WBG Power Devices in Future 3-Φ Variable Speed Drive Inverter Systems—“How to Handle a Double-Edged Sword”. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 12–18 December 2020. [Google Scholar] [CrossRef]
- Heldwein, M.L.; Dalessandro, L.; Kolar, J.W. The Three-Phase Common-Mode Inductor: Modeling and Design Issues. IEEE Trans. Ind. Electron. 2011, 58, 3264–3274. [Google Scholar] [CrossRef]
- Infineon. 1EDN7511B. 2022. Available online: https://www.infineon.com/cms/de/product/power/gate-driver-ics/1edn7511b/ (accessed on 3 February 2024).
- Infineon. ADuM121N. 2016. Available online: https://www.analog.com/en/products/adum121n.html (accessed on 3 February 2024).
- VACUUMSCHMELZE. EMC Products Based on Nanocrystalline VITROPERM. 2021. Available online: https://staging.vacpim.com/03_Documents/Brochures/EMC%20Products%20based%20on%20Nanocrystalline%20VITROPERM.pdf (accessed on 12 November 2023).
- NEMA, N.E.M.A. Motors and Generators MG 1. 2019. Available online: https://www.nema.org/ (accessed on 5 April 2022).
- Plexim GmbH. Electrical Engineering Software; Plexim GmbH: Zurich, Switzerland, 2023. [Google Scholar]
- Rohner, G.; Gfrörer, T.; Niklaus, P.S.; Huber, J.; Bortis, D.; Schweizer, M.; Kolar, J.W. Hardware-Based Comparative Analysis of Multilevel Inverter Topologies for Integrated Motor Drives Considering Overload Operation. IEEE Open J. Power Electron. 2023, 4, 934–944. [Google Scholar] [CrossRef]
- Karttunen, J.; Kallio, S.; Peltoniemi, P.; Silventoinen, P.; Pyrhönen, O. Decoupled Vector Control Scheme for Dual Three-Phase Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2014, 61, 2185–2196. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Choi, W.; Sarlioglu, B. High-Speed Electric Machines: Challenges and Design Considerations. IEEE Trans. Transport. Electrific. 2016, 2, 2–13. [Google Scholar] [CrossRef]
- Haider, M.; Niklaus, P.S.; Madlener, M.; Rohner, G.; Kolar, J.W. Comparative Evaluation of Gate Driver and LC-Filter Based dv/dt-Limitation for SiC-Based Motor-Integrated Variable Speed Drive Inverters. IEEE Open J. Power Electron. 2023, 4, 450–462. [Google Scholar] [CrossRef]


| Parameter | Value | |
|---|---|---|
| DC-Link Voltage | 800 V | |
| Nominal Output Power | 7.5 kW | |
| Nominal Peak Phase Current Amp. | ||
| Overload Peak Phase Current Amp. | ||
| Overload Duration | ||
| Device Switching Frequency | 35 kHz | |
| Max. Inverter Output Frequency | ||
| Motor Case (Ambient) Temperature | 90% | |
| Min. Nominal Inverter Efficiency | 99% | |
| Max. Peak CM Volt. at the Motor | 1% of | |
| Max. Peak-Peak DC-link Volt. Ripple | 1% of | |
| Max. Peak-Peak FC Volt. Ripple | 10% of |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rohner, G.; Huber, J.; Mirić, S.; Kolar, J.W. Comparative Evaluation of Three-Phase Three-Level Flying Capacitor and Stacked Polyphase Bridge GaN Inverter Systems for Integrated Motor Drives. Electronics 2024, 13, 1259. https://doi.org/10.3390/electronics13071259
Rohner G, Huber J, Mirić S, Kolar JW. Comparative Evaluation of Three-Phase Three-Level Flying Capacitor and Stacked Polyphase Bridge GaN Inverter Systems for Integrated Motor Drives. Electronics. 2024; 13(7):1259. https://doi.org/10.3390/electronics13071259
Chicago/Turabian StyleRohner, Gwendolin, Jonas Huber, Spasoje Mirić, and Johann W. Kolar. 2024. "Comparative Evaluation of Three-Phase Three-Level Flying Capacitor and Stacked Polyphase Bridge GaN Inverter Systems for Integrated Motor Drives" Electronics 13, no. 7: 1259. https://doi.org/10.3390/electronics13071259
APA StyleRohner, G., Huber, J., Mirić, S., & Kolar, J. W. (2024). Comparative Evaluation of Three-Phase Three-Level Flying Capacitor and Stacked Polyphase Bridge GaN Inverter Systems for Integrated Motor Drives. Electronics, 13(7), 1259. https://doi.org/10.3390/electronics13071259







